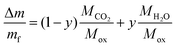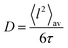Mobility of hydrous species in amorphous calcium/magnesium carbonates

Abstract

Amorphous calcium carbonate (ACC) is commonly found in many biological materials. As ACC readily crystallizes into calcite, stabilizers, such as anions, cations or macromolecules, often occur to avoid or delay unwanted crystallization. In biogenic ACC, magnesium is commonly present as one of the stabilizing agents. It is generally thought that the presence of mobile water in ACC is responsible for its limited stability and that the strong interaction of Mg²⁺ with water stabilizes the amorphous structure by retarding dehydration of ACC. To test this hypothesis, we studied the mobility of hydrous species in the model materials ACC, amorphous magnesium carbonate (AMC) and amorphous calcium/magnesium carbonate (ACMC), using quasi elastic neutron scattering (QENS) which is highly sensitive to the dynamics of H atoms. We discovered that hydrous species in the considered amorphous materials consist of water and hydroxide ions, as magnesium ions are incorporated in a ratio of 1 to about 0.6 with OH⁻. Surprisingly, we found that there is no evidence of translational diffusion of water and hydroxides when calcium is present in the samples, showing that hydrous species are highly static. However, we did observe diffusion of water in AMC with similar dynamics to that found for water in clays. Our results suggest that Mg²⁺–water interactions alone are not the only reason for the high stability of AMC and ACMC. The stabilizing effect of Mg ions, in addition to Mg–water binding, is likely to be caused by binding to hydroxide in amorphous calcium carbonates. In fact, the incorporation of hydroxides into the amorphous phase results in a mineral composition that is incompatible with any of the known Ca/Mg-carbonate crystal phases, requiring large scale phase separation to reach the composition of even the basic magnesium carbonate minerals artinite and hydromagnesite.

---

Introduction

Magnesium substituted calcium carbonate is a widespread biogenic mineral.^1–5 Calcite, the thermodynamically stable polymorph of calcium carbonate, is often not directly formed from solution, but rather through a series of polymorphs starting with an amorphous precursor known as amorphous calcium carbonate (ACC).^6–9 The stability of ACC is a key factor in its role as a biomineral precursor and in biogenic ACC stabilizers are often present, most commonly Mg ions.¹ The stabilizing effect of Mg²⁺ is frequently attributed to the high dehydration energy of magnesium ions, relative to calcium ions,^10,11 which retards the dehydration of the ACC⁸ and hence prevents crystallization. The stability of synthetic ACC has been studied extensively both with^8,12,13 and without^{6,7,9,14–17} the incorporation of Mg²⁺. In magnesium-free ACC the stability has been suggested to depend on the mobility of water molecules^17–19 and NMR studies^14,20 have suggested that several types of water exist in ACC: translationally rigid, restricted mobile and liquid-like H₂O.¹⁷ However, recent studies have indicated that the water in ACC is mainly structural (i.e. binding to ions)²¹ and may kinetically stabilize the amorphous network via hydrogen bonding to the carbonates.²² Incorporating magnesium into the ACC phases increases the lifetime of the amorphous phase in solution from a few minutes⁷ to several hours.¹² However, it is unclear if and how magnesium affects the dynamics of the water molecules inside the amorphous phase. In this work, we investigate the dynamics of water in different Mg-containing samples ranging from Mg free ACC to calcium free amorphous magnesium carbonate (AMC) using quasi elastic neutron scattering (QENS). The QENS instrument IRIS²³ was chosen given its wide dynamic range from a few ps to tens of ps, the range used to study translation diffusion in bulk and confined water in many mesoporous materials.^24–27 This range also covers the time scales for confined rotational motion of hydrous species in both clays and zeolites.^26,28 Compositional analysis of the samples revealed that, unlike calcium ions, magnesium ions coprecipitate with hydroxide ions generated by the sodium carbonate salt upon dissolution. This results in a composition of Ca_1−xMg_x(CO₃)_1−0.32(4)x(OH)_0.64(8)x·nH₂O. Five samples were chosen for analysis with x = 0, 0.22(2), 0.52(2), 0.73(2) and 1, and with n = 1.1–1.2. Our analysis reveals that the hydrous species in all calcium containing samples do not show any translational diffusion within the resolution of the instrument and that the high stability of AMC compared to ACC is likely due, in addition to the higher dehydration energy of the magnesium ions, to the strong interaction between magnesium and hydroxide ions. Also, if hydroxy groups are incorporated in the solid, an additional dehydroxylation step is required before crystallization and this can slow down the kinetics of the transformation. Moreover, we found that part of the water in AMC does show jump diffusion with a jump distance of 2.66(8) Å and a residence time of 15.4(1) ps, giving a diffusion constant of 7.6(3) × 10⁻¹⁰ m² s⁻¹.

Results

Sample characterization

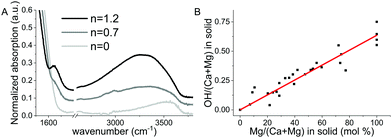
To assess the composition of the prepared materials, the samples were measured with inductively coupled plasma-optical emission spectroscopy (ICP-OES), thermogravimetric analysis (TGA) (Fig. S1, ESI†) and Fourier transform infrared spectroscopy (FTIR) (Fig. 1A). FTIR analysis was performed on the AMC sample with three hydration levels n = 1.2, 0.5 and 0 (respectively the as prepared material and two samples obtained by heating at temperatures of 100 °C and 180 °C for 2 hours). The FTIR analysis showed that the O–H stretching and H–O–H bending modes of water decrease in intensity with dehydration, as expected, and that only the band at 3600 cm⁻¹ remains after full dehydration (Fig. 1A). Given that after complete dehydration there is no presence of a H₂O bending band and that the position of the O–H stretching band is characteristic of basic O–H groups it was concluded that hydroxide ions are present in the magnesium-containing amorphous sample. On the other hand, it was previously shown that hydroxides are only incorporated in ACC in trace amounts unless NaOH is added during the synthesis,¹⁶ which was not the case of the samples studied here. Combining these results, it was determined that the synthesized samples consist of Ca, Mg (determined from ICP-OES), CO₃²⁻, OH⁻ and H₂O (identified from FTIR and quantified from TGA). To quantify the amount of hydrous species within the samples, TGA data were analyzed as follows. Taking charge neutrality into account we can assume a composition of:

Ca_1−xMg_x(CO₃)_1−y(OH)_2y·nH₂O

Fig. 1 (A) FTIR spectrum of AMC with n = 0, 0.7 and 1.2, showing the O–H stretches centered at 3400 cm⁻¹ and the H₂O bending at 1650 cm⁻¹. After full dehydration, the component of the O–H stretching at around 3600 cm⁻¹ remains, while the water bending band disappears, indicating the presence of basic hydroxide groups. (B) OH⁻ content as a function of Mg²⁺ incorporated into ACC/AMC as derived from TGA and ICP measurements.

The TGA measurement showed two mass losses, one at ∼100 °C (loss of water) and the second between 250 °C and 800 °C where the following decomposition takes place:²⁹

Ca_1−xMg_x(CO₃)_1−y(OH)_2y → Ca_1−xMg_xO + (1 − y)CO₂ + yH₂O

Naming m_f and Δm the final mass of the remaining oxide and the mass loss from 250–800 °C, respectively, i.e. loss of water and carbon dioxide during decomposition, y can be determined from the TGA data using the following relation:

Here M_CO2 and M_H2O are the molar masses of CO₂ and H₂O, respectively, and M_ox is the molar mass of the calcium/magnesium oxide (i.e. Ca_1−xMg_xO). Several samples with 0 ≤ x ≤ 1 were measured and 2y = OH/(Ca + Mg) was plotted as a function of x in Fig. 1B. As can be seen, 2y correlates linearly with x with a slope, obtained by fitting, of 0.64(8). The final composition of the samples could be described by the general formula Ca_1−xMg_x(CO₃)_1−0.32(4)x(OH)_0.64(8)x·nH₂O with 0 ≤ x ≤ 1 (Fig. 1). The analysis of the weight losses at temperatures below 250 °C further showed a hydration level n = H₂O/(Ca + Mg) of 1.1–1.2 for all samples.

Fixed elastic window scan (FEWS)

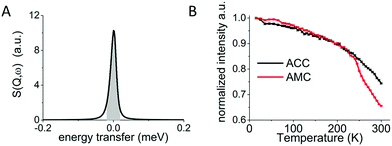
Fig. 2 shows the integrated intensity of the elastic line (energy transfer = 0) as a function of temperature. Since any diffusion occurring faster than the resolution limit of the instrument results in a decrease in the intensity of the elastic line, by following the temperature dependent variation of this peak (Fig. 1A) one can identify phase transitions in the samples, such as the melting of any bulk or confined water.²⁷ For ACC a steady decrease in the intensity is observed from 5 K to 300 K with no apparent phase transition. For AMC the same steady decrease is observed from 5 K to ∼240 K after which a drop in intensity is observed indicating a change in dynamics.

Fig. 2 (A) QENS measurement at a single temperature showing the elastic line at energy transfer = 0 with the area of the elastic line marked in grey given by the resolution of the IRIS instrument of 17.5 μeV. (B) Fixed elastic window scan of ACC and AMC calculated from the integrated intensity of the elastic line in (A), normalized to the integrated intensity of the elastic peak at 5 K.

Quasi elastic neutron scattering (QENS)

To compare the broadening of the elastic line between the samples, the measured spectra were averaged over Q to give a single spectrum for each sample (Fig. 3).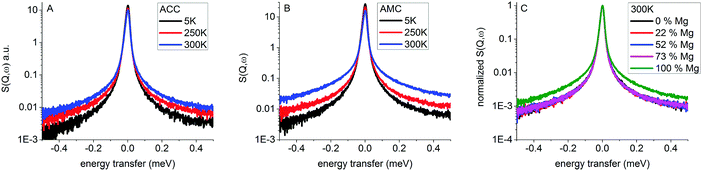

Fig. 3 Q integrated QENS spectra of ACC (A) and AMC (B) at 5, 250 and 300 K and QENS spectra at 300 K for all samples (C).

ACC and AMC samples both show increasing line broadening with increasing temperature. However, most of the elastic line is still present, showing that most of the hydrogen is not mobile on a time scale below 75 ps, which is the resolution limit of the instrument. For ACC (Fig. 3A) and AMC (Fig. 3B) the line broadening increases with temperature as expected since hydrogen mobility generally increases with temperature. For AMC the increase from 250 K to 300 K is significantly higher than for ACC as already suggested by the FEWS results (Fig. 2). For samples with varying magnesium content, the spectra of all samples were normalized to the height of the elastic line to compare the line broadening. From the normalized spectra (Fig. 3C), it is clear that the ACC and ACMC samples have similar line broadening while the AMC sample exhibits a significantly broader elastic line, which indicates that hydrogen is more mobile.

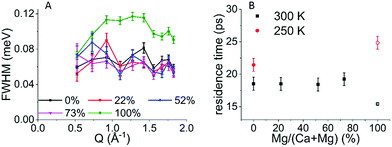
To determine the type of hydrogen motion, the Q dependent QENS spectra acquired on the 50 detectors of an IRIS spectrometer were binned into 10 groups, in order to gain sufficient signal to noise ratio, and were processed as follows. For each Q and for all samples, the line profile was fitted by a convolution of the elastic line measured at 5 K and a single Lorentzian peak function (Fig. S2 and S3 in the ESI†). A fit using two Lorentzian peaks was also performed but without any improvement, indicating that only a single type of motion is observed. The FWHM of each Lorentzian is reported in Fig. 4A for all samples. In the case of translational diffusion an increase in the FWHM of the elastic line with Q is expected,^24,30 while for confined rotational motion the FWHM of the elastic line should be independent of Q.²⁸ Despite the noise in the data (Fig. 4A) it is clear that there is no increase in line broadening for ACC and the three ACMC samples with Q indicating that the motion observed is confined. By fitting the FWHM with a straight line the residence time (t) for the confined rotational motion of the calcium containing samples was calculated for each sample as t = 2ℏ/HWHM, where HWHM is the half width at half maximum and ℏ is the reduced Planck's constant. The resulting residence time vs. magnesium concentration is shown in Fig. 4B. A small increase of the FWHM with Q, typical of translational diffusion, is observed only for the AMC sample, for Q values from 0.5 to 1 Å⁻¹. Because of the much higher QENS signal in the AMC sample, reasonable signal to noise levels could be achieved with 25 detector groups giving more points in the low Q region. With this binning, the Hall–Ross³⁰ jump diffusion model fits the data better than the straight line used for confined rotational motion (see Fig. S4 for details, ESI†). Therefore, diffusion of water within the solid cannot be excluded for AMC. From the Hall–Ross model we estimate a Gaussian distribution of jump distances with a mean jump distance of 2.66(8) Å and a residence time of 15.4(1) ps. The presence of water diffusing in AMC at 300 K can also explain the drop observed after 250 K in the FEWS measurement (Fig. 2B).

Fig. 4 (A) FWHM of the Lorentzian used to fit the QENS spectra (measured at 300 K) as a function of Q for all samples. (B) The residence time of the confined rotational motion of H calculated from the FWHM shown in A and the jump diffusion residence time determined for the AMC sample (open square).

Discussion

A first finding that emerges from our results regards the composition of Mg-containing amorphous carbonates. Previous studies have addressed the synthesis of AMC,^29,31–33 but the incorporation of hydroxide ions within ACMC/AMC has not been reported so far, to the best of our knowledge. A second interesting observation is that, in calcium containing samples, we do not find translational diffusion of hydrous species comparable to that of liquid or loosely bound water, indicating that the water molecules in these samples are mainly structural. This is in agreement with recent neutron and X-ray pdf analyses of ACC that showed that water molecules preferentially form H-bonds with anions rather than with other water molecules.²¹ When compared to a scenario where water causes instabilities due to the presence of pores of mobile water,¹⁹ our results support the notion that, instead, structural water helps to stabilize the amorphous network²² regardless of its Mg content.

ACC/ACMC/AMC composition

The composition of AMC has been previously reported as MgCO₃·nH₂O.^29,31–33 However, performing FTIR on dehydrated samples indicated the presence of hydroxide ions in the magnesium containing samples and this was also confirmed by the mass loss seen from TGA analysis, which showed a mass loss too low to be consistent with a pure carbonate sample. The high levels of OH⁻ incorporation with magnesium in ACMC/AMC is consistent with the lower solubility of Mg(OH)₂³⁴ than MgCO₃.³⁵ The incorporation of OH⁻ in ACC is well studied^16,36,37 and only trace amounts are incorporated unless the synthesis is carried out at high pH, by adding NaOH.¹⁶ This is not surprising as CaCO₃³⁸ is less soluble than Ca(OH)₂.³⁹ To the best of our knowledge only a handful of AMC studies have been published,^29,31–33 and there the OH⁻ content of the material has not been reported. For this reason, it is difficult to say if the incorporation of hydroxide is a general feature or if it is only a feature of our synthesis. However, if this is a general feature of AMC it is likely to have an important role in the higher kinetic stability of AMC and ACMC, as hydroxides are known to stabilize magnesium-free ACC, where OH⁻ containing ACC exhibits longer crystallization times in solution and higher crystallization temperatures during heating.¹⁶

Hydrogen mobility

The confined rotational motion of the water molecules and possibly of the hydroxide ions is most likely a reorientation of the O–H bond (of water or hydroxide ions) between H-bonding sites (i.e. with the hydrogen pointing towards oxygen of a neighboring water, carbonate or hydroxide) in the local environment. This confined rotational motion implies that hydrous species are bound for ∼18 ps to one of the available oxygens in its near vicinity before switching to an adjacent site. A residence time of ∼18 ps, as found for confined rotational motion in ACC/ACMC, is comparable to typical times reported for reorientational motion of water in other hydrated minerals (e.g. clays²⁶ and zeolites²⁸) and one order of magnitude slower than what is found in liquid water at room temperature.²⁴ At low Mg²⁺ contents, hydrogens from water are likely to be preferentially hydrogen bonded to carbonate molecules similar to what we have recently shown for ACC.²¹ The translational motion observed in AMC, but not in ACC or ACMC, is comparable in jump distance and residence time with what was been reported for 2-dimensional water in vermiculite and montmorillonite,^25,26 suggesting that water molecules diffuse, in AMC, in a confined space. However, it must be noticed that there is still a large elastic signal at high Q (Fig. S3, ESI†) and only a part of the water in AMC exhibits this relatively faster dynamics. The lack of jump diffusion in the ACC/ACMC samples suggests that calcium may prevent fast dynamics of the water molecules more effectively than magnesium. This is somewhat counterintuitive given the higher dehydration energy of the magnesium ion.^10,11 The presence of a small fraction of water molecules characterized by this faster dynamic may be related to the higher coordination number of the calcium ion allowing for more water molecules to bind per cation. In the case of AMC, as the Mg ion can accommodate less water, a small fraction of molecules is relatively free to diffuse within the solid. However, without a detailed structural description of AMC and ACMC it is difficult to quantitatively describe the properties of these water molecules.

The existence of liquid-like water in amorphous carbonates has been suggested by several NMR studies.^14,17 The presence of this kind of water within the materials studied here seems to be however unlikely. Residence times and jump distances for confined H₂O molecules in clays and mesoporous compounds have been reported between 2 and 43 ps and between 1.1 and 3.9 Å, respectively.^25,26 Bulk liquid water has much faster diffusion with a residence time of 1.25 ps and a jump distance of 1.29 Å.²⁴ Translational diffusion of water exhibits residence times larger than 75 ps (the resolution limit of the IRIS instrument) and 15 ps, respectively, for ACC/ACMC and AMC. This indicates that the large majority of water in these materials is structural. Although structural, water can still slowly diffuse through the material as has been predicted by MD simulations.⁴⁰ Assuming a similar jump distance to that in AMC and using the equation

where l is the jump distance and τ the residence time,²⁴ one can calculate an upper limit for the diffusion coefficient (D) of about 1.57 × 10⁻¹⁰ m² s⁻¹. MD simulations, however, have suggested diffusion coefficients as much as 5 orders of magnitude lower.⁴⁰ Given the relatively slow diffusion of water in these systems it is unlikely that the mobility of the internal water plays a large role in initiating ACC crystallization compared to the much higher mobility of water at the surface of ACC that may be present. This is consistent with the long life time of ACC under vacuum (>6 months)⁴¹ or in confinement¹⁴ compared to the lifetime in solution (minutes).^7,9

On the mechanism of stabilization

To form the anhydrous minerals calcite or magnesite, water has to be removed from the material by diffusion. In this sense, as a structural component in the amorphous phase, water can be thought to stabilize against crystallization,²² but if nucleation occurs the water would be released forming bulk water that will promote crystallization^41,42 as it also provides mobility for the ions. The addition of magnesium may slow down the dehydration dynamics, and hence retard the transformation of ACC, as the free energy of solvation for Mg is 60% higher than for Ca.⁴³ Furthermore, the consequential incorporation of hydroxide ions may have an additional important effect. Hydroxide incorporation in ACC is known to increase the crystallization temperature and its lifetime in solution.¹⁶ In AMC the effect of hydroxides has been less explored but the composition of the AMC is not compatible with any of the mixed hydroxide/carbonate phases, given that the OH/CO₃ ratio in AMC is ∼1, while it is 2 in artinite⁴⁴ and 0.5 in hydromagnesite.⁴⁵ AMC, therefore, when exposed to increasing temperatures, maintains its amorphous structure up to 400 °C when the carbonate and hydroxides contemporaneously decompose.²⁹ This crystallization temperature is much higher than the highest temperature reported for non-OH containing ACC.^15,36 Also in solution the AMC phase is kinetically more stable than the ACC phase.^12,46 However, it is unclear if the solubility of AMC is higher or lower than ACC, as the values are not reported in the literature. Based on the fact that MgCO₃ is more soluble than calcite³⁵ but Mg(OH)₂ is less soluble than calcite, Ca(OH)₂ and MgCO₃,³⁴ both Mg²⁺ and OH⁻ can only be in solution in very low concentration. This reflects the large binding affinity of the species and for this reason, probably, OH⁻ ions are incorporated in the amorphous precipitates. This strong magnesium-hydroxide binding in the amorphous phases may provide an additional barrier to dissolution/recrystallization in the magnesium containing samples compared to ACC.^12,46 Yet, the lifetime of the amorphous phase in solution should not be purely associated with the structure and composition of the amorphous phase, as it also depends on other factors such as the rate of nucleation of the crystalline phases.

Conclusions

By analyzing the composition of ACC/ACMC/AMC it is found that Mg substitution in ACC does not occur by simply replacing one calcium ion with a magnesium one but by incorporating hydroxide ions together with magnesium, giving rise to substituted phases with a composition of Ca_1−xMg_x(CO₃)_1−0.32x(OH)_x0.64·nH₂O with 0 ≤ x ≤ 1 and n = 1.1–1.2. Therefore, it is important to consider the presence of hydroxide ions in amorphous carbonates, especially when they contain small divalent cations that tend to have very low solubility of their hydroxide minerals, as OH ions can significantly affect the stability of the amorphous phase. As for the motion of hydrous species in ACC/ACMC we found that this is spatially confined in the time range below 75 ps. We also determined that H-bonds’ residence time between reorientation events is around 18 ps for ACC and ACMC (with 0 ≤ x ≤ 0.73). In AMC, a fraction of water molecules exhibits translational diffusion with a residence time of 15.4 ps. Since no translational diffusion was detected in ACC/ACMC, based on the instrument resolution and assuming a similar jump distance to AMC, we could determine an upper limit for the water diffusion coefficient in ACC/ACMC of D_max = 1.57 × 10⁻¹⁰ m² s⁻¹, thereby ruling out the presence of liquid or liquid-like water in ACC/ACMC.

Materials and methods

Materials synthesis

ACC/AMC was synthesized by rapid mixing of 20 mL 1 M (Ca/Mg)Cl₂ (CaCl₂·2H₂O ≥ 99%, MgCl₂·6H₂O 99–102%, Sigma Aldrich) solution with 480 mL Na₂CO₃ (Na₂CO₃·10H₂O 99.999%, Sigma Aldrich) to get an initial concentration of 40 mM of both the carbonate and Ca/Mg ions. The solution was filtered, after which the solid was washed with cold ethanol (99.8%, Sigma Aldrich) and dried in a vacuum desiccator for a minimum of 24 h.

ICP-OES

Ca and Mg contents were determined by ICP using a Perkin Elmer optima 8000 ICP-OES spectrometer (Perkin Elmer, Waltham, MA, US).

TGA-DSC

Thermogravimetric analysis was performed on a TGA/DSC (SENSYS evo TGA-DSC, SETARAM instrumentation, Caluire, France). The samples were placed in a corundum crucible and heated from 25–800 °C at 2° min⁻¹.

QENS

Quasi elastic neutron scattering was performed on the IRIS instrument²³ at ISIS-TS1 using a pyrolytic graphite 002 analyser (STFC Rutherford Appleton Laboratory, Didcot, UK). The samples were measured from −0.4 to 0.4 meV in ω and from 0.42 to 1.85 Å⁻¹ in Q. ∼2 grams of sample was place in an annular aluminium can with 2 mm sample thickness. ACC and AMC were measured at 5 K, 250 K and 300 K for 6 hours while ACMC with Mg/(Ca + Mg) = 0.22, 0.52 and 0.73 was measured at 300 K for 6 hours. Fixed elastic window scan was performed on ACC and AMC from 5 K to 300 K with 5 K resolution and 20 min exposure per step. Data reduction and analysis were performed in Mantid.⁴⁷

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank ISIS for allocation of beam time at the IRIS instrument and Dr Sanghamitra Mukhopadhyay and Dr Victoria Garcia Sakai for support with the QENS measurements. We are grateful to Ms Jeannette Steffen of the Max Planck Institute of Colloids and Interfaces for support with the ICP measurements and to Yael Politi for critically reading the manuscript and suggesting substantial improvements. Open Access funding provided by the Max Planck Society.

References

1. L. Addadi, S. Raz and S. Weiner, Taking Advantage of Disorder: Amorphous Calcium Carbonate and Its Roles in Biomineralization, Adv. Mater., 2003, 15(12), 959–970.
2. J. H. E. Cartwright, A. G. Checa, J. D. Gale, D. Gebauer and C. I. Sainz-Díaz, Calcium Carbonate Polyamorphism and Its Role in Biomineralization: How Many Amorphous Calcium Carbonates Are There?, Angew. Chem., Int. Ed., 2012, 51(48), 11960–11970.
3. S. Mann, Biomineralization: Principles and Concepts in Bioinorganic Materials Chemistry, Oxford University Press, 2001, vol. 5.
4. S. Weiner, Y. Levi-Kalisman, S. Raz and L. Addadi, Biologically Formed Amorphous Calcium Carbonate, Connect. Tissue Res., 2003, 44(1), 214–218.
5. S. Weiner, I. Sagi and L. Addadi, Choosing the Crystallization Path Less Traveled, Science, 2005, 309(5737), 1027–1028.
6. P. Bots, L. G. Benning, J.-D. Rodriguez-Blanco, T. Roncal-Herrero and S. Shaw, Mechanistic Insights into the Crystallization of Amorphous Calcium Carbonate (ACC), Cryst. Growth Des., 2012, 12(7), 3806–3814.
7. J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, The Kinetics and Mechanisms of Amorphous Calcium Carbonate (ACC) Crystallization to Calcite, via Vaterite, Nanoscale, 2011, 3(1), 265–271.
8. J. D. Rodriguez-Blanco, S. Shaw, P. Bots, T. Roncal-Herrero and L. G. Benning, The Role of pH and Mg on the Stability and Crystallization of Amorphous Calcium Carbonate, J. Alloys Compd., 2012, 536(Suppl. 1), S477–S479.
9. A. C. S. Jensen, M. Hinge and H. Birkedal, Calcite Nucleation on the Surface of PNIPAM-PAAc Micelles Studied by Time Resolved In Situ PXRD, CrystEngComm, 2015, 17(36), 6940–6946.
10. F. Lippmann, Sedimentary Carbonate Minerals, Springer Science & Business Media, 2012, vol. 6.
11. Y. Politi, D. R. Batchelor, P. Zaslansky, B. F. Chmelka, J. C. Weaver, I. Sagi, S. Weiner and L. Addadi, Role of Magnesium Ion in the Stabilization of Biogenic Amorphous Calcium Carbonate: A Structure−Function Investigation, Chem. Mater., 2010, 22(1), 161–166.
12. J. D. Rodriguez-Blanco, S. Shaw, P. Bots, T. Roncal-Herrero and L. G. Benning, The Role of Mg in the Crystallization of Monohydrocalcite, Geochim. Cosmochim. Acta, 2014, 127, 204–220.
13. J. Ihli, Y.-Y. Kim, E. H. Noel and F. C. Meldrum, The Effect of Additives on Amorphous Calcium Carbonate (ACC): Janus Behavior in Solution and the Solid State, Adv. Funct. Mater., 2013, 23(12), 1575–1585.
14. J. Ihli, W. C. Wong, E. H. Noel, Y.-Y. Kim, A. N. Kulak, H. K. Christenson, M. J. Duer and F. C. Meldrum, Dehydration and Crystallization of Amorphous Calcium Carbonate in Solution and in Air, Nat. Commun., 2014, 5, 3169.
15. Z. Zou, L. Bertinetti, Y. Politi, A. C. S. Jensen, S. Weiner, L. Addadi, P. Fratzl and W. J. E. M. Habraken, Opposite Particle Size Effect on Amorphous Calcium Carbonate Crystallization in Water and during Heating in Air, Chem. Mater., 2015, 27(12), 4237–4246.
16. D. J. Tobler, J. D. Rodriguez Blanco, H. O. Sørensen, S. L. S. Stipp and K. Dideriksen, Effect of pH on Amorphous Calcium Carbonate Structure and Transformation, Cryst. Growth Des., 2016, 16(8), 4500–4508.
17. M. P. Schmidt, A. J. Ilott, B. L. Phillips and R. J. Reeder, Structural Changes upon Dehydration of Amorphous Calcium Carbonate, Cryst. Growth Des., 2014, 14(3), 938–951.
18. Y. G. Bushuev, A. R. Finney and P. M. Rodger, Stability and Structure of Hydrated Amorphous Calcium Carbonate, Cryst. Growth Des., 2015, 15, 5269–5279.
19. A. L. Goodwin, F. M. Michel, B. L. Phillips, D. A. Keen, M. T. Dove and R. J. Reeder, Nanoporous Structure and Medium-Range Order in Synthetic Amorphous Calcium Carbonate, Chem. Mater., 2010, 22(10), 3197–3205.
20. S. Kababya, A. Gal, K. Kahil, S. Weiner, L. Addadi and A. Schmidt, Phosphate–Water Interplay Tunes Amorphous Calcium Carbonate Metastability: Spontaneous Phase Separation and Crystallization vs. Stabilization Viewed by Solid State NMR, J. Am. Chem. Soc., 2015, 137(2), 990–998.
21. A. C. S. Jensen, S. Imberti, S. F. Parker, E. Schneck, Y. Politi, P. Fratzl, L. Bertinetti and W. J. E. M. Habraken, Hydrogen Bonding in Amorphous Calcium Carbonate and Molecular Reorientation Induced by Dehydration, J. Phys. Chem. C, 2018, 122(6), 3591–3598.
22. S. Sen, D. C. Kaseman, B. Colas, D. E. Jacob and S. M. Clark, Hydrogen Bonding Induced Distortion of CO₃ Units and Kinetic Stabilization of Amorphous Calcium Carbonate: Results from 2D ¹³C NMR Spectroscopy, Phys. Chem. Chem. Phys., 2016, 18, 20330–20337.
23. S. I. Campbell, M. T. F. Telling and C. J. Carlile, The Optimisation of Analyser Geometry in Near-Backscattering Spectrometers – IRIS on the ISIS-Pulsed Source, Physica B, 2000, 276–278, 206–207.
24. J. Teixeira, M. C. Bellissent-Funel, S. H. Chen and A. J. Dianoux, Experimental Determination of the Nature of Diffusive Motions of Water Molecules at low Temperatures, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1913–1917.
25. N. T. Skipper, P. A. Lock, J. O. Titiloye, J. Swenson, Z. A. Mirza, W. S. Howells and F. Fernandez-Alonso, The Structure and Dynamics of 2-Dimensional Fluids in Swelling Clays, Chem. Geol., 2006, 230(3–4), 182–196.
26. J. Swenson, R. Bergman and W. S. Howells, Quasielastic Neutron Scattering of Two-Dimensional Water in a Cermiculite Clay, J. Chem. Phys., 2000, 113(7), 2873–2879.
27. E. Mamontov, D. R. Cole, S. Dai, M. D. Pawel, C. D. Liang, T. Jenkins, G. Gasparovic and E. Kintzel, Dynamics of Water in LiCl and CaCl2 Aqueous Solutions Confined in Silica Matrices: A Backscattering Neutron Spectroscopy Study, Chem. Phys., 2008, 352(1–3), 117–124.
28. P. D. Shepherd, W. W. Kagunya, S. I. Campbell, A. P. Chapple, J. W. Dreyer, R. J. Humphreys, M. Kemali, M. Mercer and D. K. Ross, Water Dynamics in Na Zeolite P by QENS, Physica B, 1997, 234–236, 914–916.
29. A. V. Radha, A. Fernandez-Martinez, Y. Hu, Y.-S. Jun, G. A. Waychunas and A. Navrotsky, Energetic and Structural Studies of Amorphous Ca_1−xMg_xCO₃·nH₂O (0 < x < 1), Geochim. Cosmochim. Acta, 2012, 90, 83–95.
30. P. L. Hall and D. K. Ross, Incoherent neutron scattering functions for random jump diffusion in bounded and infinite media, Mol. Phys., 1981, 42(3), 673–682.
31. C.-J. Lin, S.-Y. Yang, S.-J. Huang and J. C. C. Chan, Structural Characterization of Mg-Stabilized Amorphous Calcium Carbonate by Mg-25 Solid-State NMR Spectroscopy, J. Phys. Chem. C, 2015, 119(13), 7225–7233.
32. Z. Lei, S. Sun and P. Wu, Ultrafast, Scale-Up Synthesis of Pure and Stable Amorphous Carbonate Mineral Nanoparticles, ACS Sustainable Chem. Eng., 2017, 5(6), 4499–4504.
33. C. E. White, N. J. Henson, L. L. Daemen, M. Hartl and K. Page, Uncovering the True Atomic Structure of Disordered Materials: The Structure of a Hydrated Amorphous Magnesium Carbonate (MgCO₃·3D₂O), Chem. Mater., 2014, 26(8), 2693–2702.
34. O. S. Pokrovsky and J. Schott, Experimental Study of Brucite Dissolution and Precipitation in Aqueous Solutions: Surface Speciation and Chemical Affinity Control, Geochim. Cosmochim. Acta, 2004, 68(1), 31–45.
35. P. Bénézeth, G. D. Saldi, J.-L. Dandurand and J. Schott, Experimental Determination of the Solubility Product of Magnesite at 50 to 200 °C, Chem. Geol., 2011, 286(1–2), 21–31.
36. N. Koga, Y. Nakagoe and H. Tanaka, Crystallization of Amorphous Calcium Carbonate, Thermochim. Acta, 1998, 318(1–2), 239–244.
37. H.-W. Wang, L. L. Daemen, M. C. Cheshire, M. K. Kidder, A. G. Stack, L. F. Allard, J. Neuefeind, D. Olds, J. Liu and K. Page, Synthesis and Structure of Synthetically Pure and Deuterated Amorphous (basic) Calcium Carbonates, Chem. Commun., 2017, 53(20), 2942–2945.
38. A. De Visscher and J. Vanderdeelen, Estimation of the Solubility Constant of Calcite, Aragonite, and Vaterite at 25 °C Based on Primary Data Using the Pitzer Ion Interaction Approach, Monatsh. Chem., 2003, 134(5), 769–775.
39. I. Lambert and H. L. Clever, Alkaline Earth Hydroxides in Water and Aqueous Solutions, Elsevier, 2013, vol. 52.
40. R. Innocenti Malini, Y. G. Bushuev, S. A. Hall, C. L. Freeman, P. M. Rodger and J. H. Harding, Using Simulation to Understand the Structure and Properties of Hydrated Amorphous Calcium Carbonate, CrystEngComm, 2016, 18(1), 92–101.
41. F. Konrad, F. Gallien, D. E. Gerard and M. Dietzel, Transformation of Amorphous Calcium Carbonate in Air, Cryst. Growth Des., 2016, 16(11), 6310–6317.
42. M. Albéric, L. Bertinetti, Z. Zou, P. Fratzl, W. Habraken and Y. Politi, The Crystallization of Amorphous Calcium Carbonate is Kinetically Governed by Ion Impurities and Water, Adv. Sci., 2018, 5(5), 1701000.
43. M. Pavlov, P. E. Siegbahn and M. Sandström, Hydration of Beryllium, Magnesium, Calcium, and Zinc Ions Using Density Functional Theory, J. Phys. Chem. A, 1998, 102(1), 219–228.
44. M. Akao and S. Iwai, The Hydrogen Bonding of Artinite, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33(12), 3951–3953.
45. M. Akao and S. Iwai, The Hydrogen Bonding of Hydromagnesite, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33(4), 1273–1275.
46. G. Montes-Hernandez and F. Renard, Time-Resolved in Situ Raman Spectroscopy of the Nucleation and Growth of Siderite, Magnesite, and Calcite and Their Precursors, Cryst. Growth Des., 2016, 16(12), 7218–7230.
47. O. Arnold, J.-C. Bilheux, J. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal and M. Gigg, Mantid—Data Analysis and Visualization Package for Neutron Scattering and μSR Experiments, Nucl. Instrum. Methods Phys. Res., 2014, 764, 156–166.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp01782d

---