Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure of supramolecular astaxanthin aggregates revealed by molecular dynamics and electronic circular dichroism spectroscopy†
Grzegorz
Zajac
 a,
Ewa
Machalska
a,
Agnieszka
Kaczor
ab,
Jiří
Kessler
c,
Petr
Bouř
a,
Ewa
Machalska
a,
Agnieszka
Kaczor
ab,
Jiří
Kessler
c,
Petr
Bouř
 *c and
Malgorzata
Baranska
*ab
*c and
Malgorzata
Baranska
*ab
aFaculty of Chemistry, Jagiellonian University, Gronostajowa 2, Krakow 30-387, Poland. E-mail: baranska@chemia.uj.edu.pl
bJagiellonian Centre for Experimental Therapeutics (JCET), Jagiellonian University, Bobrzynskiego 14, Krakow 30-348, Poland
cInstitute of Organic Chemistry and Biochemistry, Academy of Sciences, Flemingovo náměstí 2, Prague, 16610, Czech Republic. E-mail: bour@uochb.cas.cz
First published on 13th June 2018
Abstract
Biomolecular aggregation is omnipresent in nature and important for metabolic processes or in medical treatment; however, the phenomenon is rather difficult to predict or understand on the basis of computational models. Recently, we found that electronic circular dichroism (ECD) spectroscopy and closely related resonance Raman optical activity (RROA) are extremely sensitive to the aggregation mechanism and structure of the astaxanthin dye. In the present study, molecular dynamics (MD) and quantum chemical (QC) computations (ZIndo/S, TDDFT) are used to link the aggregate structure with ECD spectral shapes. Realistic absorption and ECD intensities were obtained and the simulations reproduced many trends observed experimentally, such as the prevalent sign pattern and dependence of the aggregate structure on the solvent type. The computationally cheaper ZIndo/S method provided results very similar to those obtained by TDDFT. In the future, the accuracy of the combined MD/QC methodology of spectra interpretation should be improved to provide more detailed information on astaxanthin aggregates and similar macromolecular systems.
Introduction
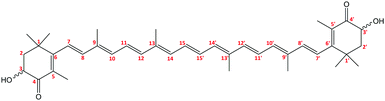
We concentrate on the astaxanthin dye (3,3′-dihydroxy-β,β-carotene-4,4′-dione, AXT, Fig. 1), because it is a convenient system to study, important in biology and potentially useful in human medicine. This red xanthophyll can be obtained by carotene oxidation as well as de novo synthesis by several organisms.1–8 Humans and animals cannot produce it and because AXT exhibits similar metabolic and physiological functions to β-carotene, zeaxanthin and lutein5 it must be supplied by food.2,4,9AXT chemistry is important for biological functions. The hydroxyl and keto-groups on terminal β-ionone rings contribute to AXT's antioxidative capacity and prevent UV light photooxidation of lipids.2,10–12 The relatively long polyene chain is responsible for strong absorption of green and blue light, and it also largely determines the aggregation properties via π–π stacking interactions. AXT is often attached to proteins (carotenoproteins) and lipoproteins (carotenolipoproteins), or esterified with fatty acids (monoester or diester forms), which makes it more resistant to oxidization, heat and light degradation.2,4,5,13–18
The conjugated bonds can adopt both the trans and cis conformations,19,20 although the trans-form prevails.14,21 Each molecule has two chiral centres at the C3 and C3′ atoms giving rise to two enantiomers (3R,3′R) and (3S,3′S) and one meso form (3R,3′S).17 Six conformers are generated due to mutual orientation of the ionone rings (gauche and trans conformations).19,22 These variations of structure influence the bioavailability of AXT.16,20,21,23
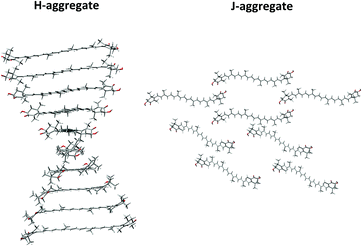
We and others also noticed the ability of chiral xanthophyll molecules to form a wide range of supramolecular assemblies.24–35 Typically, aggregation occurs when water is added to an AXT solution in an organic solvent.36,37 Aggregation almost always results in significant spectroscopic changes, often sensitive to aggregate type. AXT forms two types: H-aggregates, characterized by a blue-shifted strong electronic absorption band around 400 nm, and J-aggregates exhibiting a red-shift. The H-aggregates are characterised by tight “card-pack” stacking where the polyene chains are more or less parallel to each other, while J-aggregates with “head-to-tail” or “herring bone” orientation of the conjugated chains are looser.26,33,34,38,39 Formation of a particular assembly depends on the balance of intermolecular forces between molecular constituents, such as hydrogen bonds, electrostatic forces, and van der Waals interactions.30,34,36 In spite of gross phenomenological models of the H and J aggregates, however, detailed mutual arrangements of the monomers in them is not known.
Chiroptical spectroscopy, such as electronic circular dichroism (ECD) and Raman optical activity (ROA) were found to be very convenient to study aggregation.19,27,29,32,35,40,41 In addition, we reported a new phenomenon, aggregation-induced resonance Raman optical activity (AIRROA), which seems to be general for chiral xanthophylls, such as astaxanthin, zeaxanthin, lutein and its derivatives.24–27 The importance of AIRROA lies in the enormous enhancement of the “ordinary” ROA spectra, as these would be immeasurably weak for monomeric (non-aggregated) molecules.
However, while (non-resonance) ROA intensities can be computed relatively easily, a straightforward simulation methodology for AIRROA does not exist. Simulations are needed in structure–function studies of biomolecules, to provide a link between the spectral shapes and system geometry. As a first step, in the present study, we concentrate on the dependence of the CD spectra on the aggregation, because CD intensities were shown to be directly related to the resonance ROA effects.42 In particular, according to a one electronic resonant state model, the ROA sign is determined by the CD intensity at the excitation wavelength.
Although we currently cannot model larger-scale ordering of the aggregates, molecular dynamics simulations on limited models (the AXT dimer and decamer) are used to understand formation of different supramolecular structures in different solvent mixtures, and the results are compared to experimental data. The molecular dynamics methodology has been suggested for AXT also in the past,43 but according to our current knowledge, the dependence of the aggregation geometry and its spectral features on the solvent type has not been theoretically studied yet. Absorption and CD intensities are simulated using both time dependent density functional theory (TD-DFT) and a faster Zerner's intermediate neglect of differential overlap method (ZIndo/S).44–46 The ZIndo/S approach was particularly developed for large-size molecular systems including aggregates.47–52
The results indicate that the combination of experimental and theoretical approaches provides a solid basis for interpretation of the experimental data, including information about the structure and chirality of the aggregates, and the aggregation mechanism.
Experimental
The aggregate preparation and experimental spectra were reported previously.25,26 Briefly, the aggregates were prepared by mixing 0.3 mL 1.0 × 10−4 M AXT acetone stock solution with 2.7 mL distilled water (H-aggregate), or with 0.6 mL acetone and 2.1 mL distilled water (J-aggregate), thereby obtaining solutions with 1.0 × 10−5 M concentration. A monomer AXT reference solution was prepared by mixing 0.3 mL stock solution with 2.7 mL acetone.Electronic absorption (EA) and electronic circular dichroism spectra were measured in a quartz cell (optical path length 1 cm), in the 330–900 nm spectral range, using Jasco J-815 and UV-vis PerkinElmer Lambda-35 spectrometers, respectively.
Calculations
Arbitrary models
Arbitrary models of H and J-aggregates of (3S,3′S)-AXT were created from 10 and 8 molecules in the most stable conformation (-GG).16,19,41 The monomer was optimized at the CAM-B3LYP/Def2SVP theoretical level, using the Gaussian 09 E.01 package.53 The initial geometries were constructed according to the structures previously proposed for similar H and J-aggregates of carotenoids; their spectra modelled on the basis of exciton theory and supramolecular exciton chirality reproduced the experimental data reasonably well.32,54–56 The monomers in the H-aggregate have been arranged into a helical, parallel orientation, with 5 Å distance and 20° angle between the polyene chains of neighbouring molecules (Fig. 2). For the J-aggregation the monomers were arranged into two twisted layers (40°) and separated by 25 Å (Fig. S1, ESI†).Molecular dynamics
Two solutions of acetone and water mixed in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and 3
9 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 ratios were selected based on experimental knowledge,25,26,57 as these mixtures favour formation of the H and J-aggregates of AXT, respectively. Two models of both the H and J aggregates were investigated (dimers and decamers), differing by the numbers of included AXT molecules. To compare obtained electronic spectra of aggregates with non-aggregated AXT, we performed a monomer simulation as well, where a single AXT molecule was placed in acetone.
7 ratios were selected based on experimental knowledge,25,26,57 as these mixtures favour formation of the H and J-aggregates of AXT, respectively. Two models of both the H and J aggregates were investigated (dimers and decamers), differing by the numbers of included AXT molecules. To compare obtained electronic spectra of aggregates with non-aggregated AXT, we performed a monomer simulation as well, where a single AXT molecule was placed in acetone.
MD simulations were performed using the Amber 14,58 Packmol59,60 and VMD61 programs. The general amber force field (GAFF) has been used. To model the monomer, one AXT molecule was placed into the centre of a cubic box (40 × 40 × 40 Å3) and the remaining space was filled with 511 acetone molecules. In the dimer models, two AXT molecules parallel to each other separated by 20 Å were put in the same box and the remaining space was filled with a mixture of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1869 and 150
1869 and 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1454 acetone
1454 acetone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water molecules, corresponding to the 1
water molecules, corresponding to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 or 3
9 or 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 volume ratio, respectively, needed for H and J-aggregation. Finally, the decamer models consisted of ten AXT molecules randomly distributed in a larger box (80 × 80 × 80 Å3), and additional 407
7 volume ratio, respectively, needed for H and J-aggregation. Finally, the decamer models consisted of ten AXT molecules randomly distributed in a larger box (80 × 80 × 80 Å3), and additional 407![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 and 1221
128 and 1221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 acetone
767 acetone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water molecules (for the 1
water molecules (for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 or 3
9 or 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 volume ratios).
7 volume ratios).
All the simulations have been performed using nVT ensembles (T = 300 K), Langevin dynamics with the collision frequency 2 ps−1, a non-covalent interaction cutoff at 8 Å, the particle mesh Ewald (PME) method, and a 1 fs integration time step. To account for the electron conjugation presumably not well represented in GAFF, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C torsion angles in the polyene chain (except for C5–C6–C7–C8 and C5′–C6′–C7′–C8′) were restrained to 180°, using a harmonic force constant of 1.8 × 10−2 kcal mol−1 rad2. After 0.5 ns equilibration, production runs of 20 ns (the monomer), 205 ns (dimers) and 110 ns (decamers) were performed. Geometry frames were saved every 10 ps. From hundred monomer frames, evenly distributed in time within the 20 ns simulation, the solvent molecules were deleted and CD and EA spectra were simulated. The dimers and decamers were allowed to aggregate for 5 ns and 30 ns, respectively. Thousand dimer frames evenly distributed over the remaining 200 ns and 400 decamer frames evenly distributed over the remaining 80 ns were used to simulate the spectra, as for the monomer. The simulation conditions are summarized in Table 1.
C torsion angles in the polyene chain (except for C5–C6–C7–C8 and C5′–C6′–C7′–C8′) were restrained to 180°, using a harmonic force constant of 1.8 × 10−2 kcal mol−1 rad2. After 0.5 ns equilibration, production runs of 20 ns (the monomer), 205 ns (dimers) and 110 ns (decamers) were performed. Geometry frames were saved every 10 ps. From hundred monomer frames, evenly distributed in time within the 20 ns simulation, the solvent molecules were deleted and CD and EA spectra were simulated. The dimers and decamers were allowed to aggregate for 5 ns and 30 ns, respectively. Thousand dimer frames evenly distributed over the remaining 200 ns and 400 decamer frames evenly distributed over the remaining 80 ns were used to simulate the spectra, as for the monomer. The simulation conditions are summarized in Table 1.
| Model | No. of AXT | No. of water molecules | No. of acetone molecules | Water volume [%] | Box size [Å] | Simulation time [ns] | No. of clusters |
|---|---|---|---|---|---|---|---|
| Monomer | 1 | 0 | 511 | 0 | 40 × 40 × 40 | 20 | 100 |
Dimer 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9 |
2 | 1869 | 50 | 90 | 40 × 40 × 40 | 205 | 1000 |
Dimer 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 7 |
2 | 1454 | 150 | 70 | 40 × 40 × 40 | 205 | 1000 |
Decamer 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9 |
10 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 128 |
407 | 90 | 80 × 80 × 80 | 110 | 400 |
Decamer 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 7 |
10 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
1221 | 70 | 80 × 80 × 80 | 110 | 400 |
Electronic absorption and electronic circular dichroism
Transition energies, oscillator and rotation strengths for the first 100 (arbitrary models), 40, 80 and 100 (monomer, dimer and decamer) singlet electronic transitions were calculated using the ZIndo/S method. For the monomers and dimers analogous calculations were performed using TD-DFT, with the CAM-B3LYP functional and the Def2SVP basis set. The EA and ECD curves were obtained by convolution with Gaussian functions of 0.2 eV half width at full maximum, using the CD Spec Tech program62,63 and averaged over the MD snapshots.Results and discussion
Main features in experimental EA and ECD of AXT aggregates
The electronic absorption is dominated by the strong transition between the S0(11Ag−) → S2(11Bu+) states coming from the polyene chain chromophore.64 The S0 → S2 excitation does not exhibit any resolvable vibrational structure, which is sometimes observed for carotenoids with conjugated carbonyl groups. The H- and J-aggregates are characterized by the blue and red shift of the main electronic absorption band and the appearance of corresponding strong Cotton effects in CD. In the case of the J-aggregate in acetone–water mixed solutions, a red shift (from 478 to 515 and 551 nm) of the S0 → S2 excitation is observed. Note that two major types of AXT H-aggregates have been discussed in the literature,25,26 one with a blue shift of the S0 → S2 excitation from 492 to 386 nm in DMSO–water mixed solutions (H1-aggregate), and one with a minor blue shift from 478 to 469 nm in acetone–water mixed solutions (H2-aggregate). The monomers do not possess prominent rotatory strength at this transition. Supposedly, prepared samples with prevalent H- and J-aggregates are always mixtures of more aggregate subtypes and monomers.EA and ECD of arbitrary models
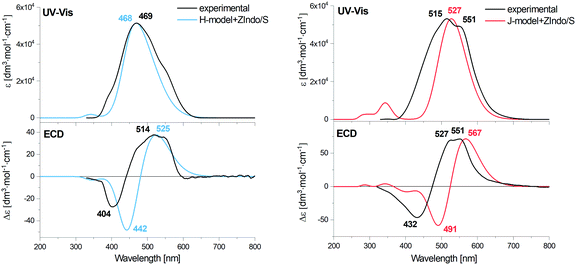
The theoretical spectra of the arbitrary aggregate models are compared to experimental data in Fig. 3. One can see that the positions of the main absorption bands both for the H- and J-aggregates are very close to the experimental ones. For J the main experimental band exhibits a substructure that is not reproduced. The calculated characteristic blue and red shifts of this transition for the H- and J-aggregates with respect to the monomer can be seen in Fig. S3 in the ESI,† and agree with the observations.ECD of both models exhibits Cotton effects (positive/negative at longer/shorter wavelengths) in the S0 → S2 excitation region, similar to the experimental spectra, however theoretical ECD couplets (zero-line crossings) are shifted to longer wavelengths, more than the absorption band, which we attribute to an effect of inhomogeneous line broadening and splitting caused by longer-range coupling, impossible to simulate at this stage.
MD simulations
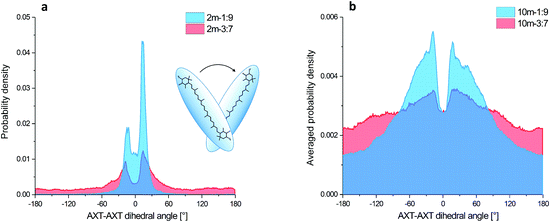
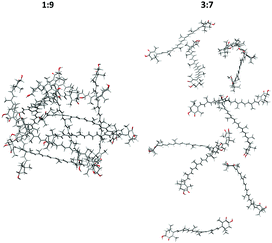
The aggregation process and basic structural information (parallel or head to tail organization) of the four MD models are apparent from the AXT–AXT distances and the C6AXT1–C6′AXT1–C6′AXT2–C6AXT2 torsional angles. Their histograms and dependencies on the simulation time are plotted in Fig. 4 and ESI† (Fig. S4–S7).In the case of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-dimer system (Fig. S4(a), blue curve, ESI†), the aggregation starts almost immediately (<3 ns) when the initial distance of 20 Å shortens to about 5 Å, more precisely it fluctuates between 3 and 10 Å during the remaining 202 ns. This corresponds to a tightly organized structure of the H-aggregate. The parallel orientation of aggregated AXT is confirmed by the AXT–AXT dihedral angle histogram (Fig. 4(a), blue). The highest probability is observed between −30° and 30°, with two maxima at 13° and −13°.
9-dimer system (Fig. S4(a), blue curve, ESI†), the aggregation starts almost immediately (<3 ns) when the initial distance of 20 Å shortens to about 5 Å, more precisely it fluctuates between 3 and 10 Å during the remaining 202 ns. This corresponds to a tightly organized structure of the H-aggregate. The parallel orientation of aggregated AXT is confirmed by the AXT–AXT dihedral angle histogram (Fig. 4(a), blue). The highest probability is observed between −30° and 30°, with two maxima at 13° and −13°.
In the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimer model the molecules move more freely as can be seen in Fig. S4(a) in the ESI† (red curve). The AXT–AXT distance varies between 3 and 25 Å during the entire 205 ns simulation. The looser structure of the 3
7-dimer model the molecules move more freely as can be seen in Fig. S4(a) in the ESI† (red curve). The AXT–AXT distance varies between 3 and 25 Å during the entire 205 ns simulation. The looser structure of the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimer is also confirmed by the dihedral angle histogram (Fig. 4(a), red). Contrary to the 1
7-dimer is also confirmed by the dihedral angle histogram (Fig. 4(a), red). Contrary to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-dimer, all angles can be adopted, albeit with a low probability density. Probability maxima (−18° and 14°), however, are nearly at the same angles as for the 1
9-dimer, all angles can be adopted, albeit with a low probability density. Probability maxima (−18° and 14°), however, are nearly at the same angles as for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-dimer. In terms of partial integral probabilities, 8.3% of AXT pairs in the 1
9-dimer. In terms of partial integral probabilities, 8.3% of AXT pairs in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-dimer and 59.5% of pairs in the 3
9-dimer and 59.5% of pairs in the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimer adopt the dihedral angle between −180° and −30° or 30° and 180° characteristic of weaker binding.
7-dimer adopt the dihedral angle between −180° and −30° or 30° and 180° characteristic of weaker binding.
For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-decamer the starting averaged distance between all AXT molecules of approximately 33 Å shrank to about 15 Å after 20 ns; it oscillates between 12 and 18 Å, thus indicating a tightly packed structure and similar behaviour to the 1
9-decamer the starting averaged distance between all AXT molecules of approximately 33 Å shrank to about 15 Å after 20 ns; it oscillates between 12 and 18 Å, thus indicating a tightly packed structure and similar behaviour to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-dimer model. However, the aggregation time is considerably longer (Fig. S6(a), blue curve, ESI†). The angular distribution is broader, but the two maxima (−18° and 17°) corresponding to the two preferred stacking angles are the same (Fig. 4(b), blue).
9-dimer model. However, the aggregation time is considerably longer (Fig. S6(a), blue curve, ESI†). The angular distribution is broader, but the two maxima (−18° and 17°) corresponding to the two preferred stacking angles are the same (Fig. 4(b), blue).
For the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-decamer model the averaged distance decreases from 37 Å to 26 Å in 8 ns, and then varies between 23 and 32 Å (Fig. S6(a), red curve, ESI†). The probability density of the dihedral angles is similar to that for the 3
7-decamer model the averaged distance decreases from 37 Å to 26 Å in 8 ns, and then varies between 23 and 32 Å (Fig. S6(a), red curve, ESI†). The probability density of the dihedral angles is similar to that for the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimer, just broader (Fig. 4(b), red).
7-dimer, just broader (Fig. 4(b), red).
The simulation thus agrees well with the observations, indicating that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 solvent mixture supports tight and nearly parallel organization of AXT molecules, with two most-preferred values of the dihedral angle. On the other hand, the 3
9 solvent mixture supports tight and nearly parallel organization of AXT molecules, with two most-preferred values of the dihedral angle. On the other hand, the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 mixture leads to a more weakly associated supramolecular structure, allowing considerable freedom to AXT–AXT orientations and distances.
7 mixture leads to a more weakly associated supramolecular structure, allowing considerable freedom to AXT–AXT orientations and distances.
EA and ECD of MD clusters
A few examples of typical MD clusters of AXT dimers and decamers (without solvent molecules) are shown in Fig. 5 and 6. In almost all extracted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
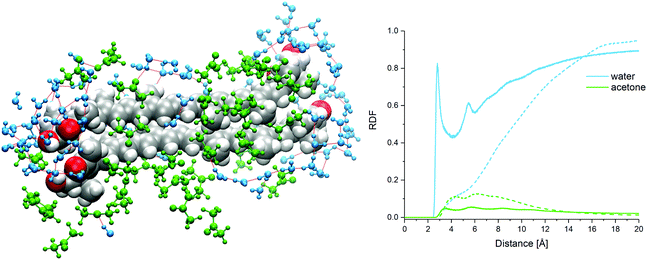
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-dimer clusters, the AXT molecules are oriented in parallel to each other and tightly packed. About three aggregate types can be recognized (Fig. 5(a–c)), characterized by different values of the dihedral angles, distances, and ring orientations. In the a and c clusters, the terminal rings are connected by the hydrogen bonding between the hydroxyl and carbonyl group and bridging water molecules (Fig. 7).
9-dimer clusters, the AXT molecules are oriented in parallel to each other and tightly packed. About three aggregate types can be recognized (Fig. 5(a–c)), characterized by different values of the dihedral angles, distances, and ring orientations. In the a and c clusters, the terminal rings are connected by the hydrogen bonding between the hydroxyl and carbonyl group and bridging water molecules (Fig. 7).
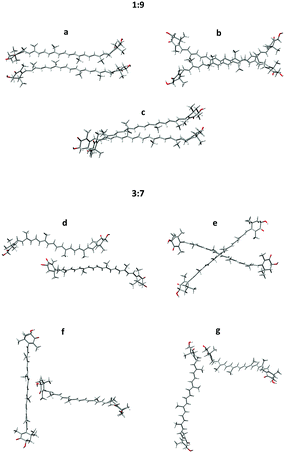 | ||
Fig. 5 Typical structures taken from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 (a–c) and 3 9 (a–c) and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (d–g) dimer MD simulation models; (a–c) parallel dimers, (d) the serial dimer, (e) the X-dimer, (f) the T-dimer, (g) the L-dimer. 7 (d–g) dimer MD simulation models; (a–c) parallel dimers, (d) the serial dimer, (e) the X-dimer, (f) the T-dimer, (g) the L-dimer. | ||
The 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimers, contrary to 1
7-dimers, contrary to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, are less associated, and prefer different orientations. Four major types of the 3
9, are less associated, and prefer different orientations. Four major types of the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimers are exemplified as the serial dimer (Fig. 5d), X-dimer (Fig. 5e), T-dimer (Fig. 5f) and L-dimer (Fig. 5g). Parallel dimers similar to these found for the 1
7-dimers are exemplified as the serial dimer (Fig. 5d), X-dimer (Fig. 5e), T-dimer (Fig. 5f) and L-dimer (Fig. 5g). Parallel dimers similar to these found for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 system are also encountered, but they are less frequent. UV-vis and ECD spectra of selected structures are presented together with experimental spectra in Fig. S8 and S9, ESI.† Some of the structures reproduce well the experimental shapes (1
9 system are also encountered, but they are less frequent. UV-vis and ECD spectra of selected structures are presented together with experimental spectra in Fig. S8 and S9, ESI.† Some of the structures reproduce well the experimental shapes (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-c and 3
9-c and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-d,e,f), but others rather give opposite signs (1
7-d,e,f), but others rather give opposite signs (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-b and 3
9-b and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-g) or the wrong intensity (1
7-g) or the wrong intensity (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-a). It is worth noting that the presented “typical” structures cannot substitute for the variety of all dimers in the MD clusters. Spectral averaging over typical structures would be problematic due to the large degree of freedom in the real solution.65
9-a). It is worth noting that the presented “typical” structures cannot substitute for the variety of all dimers in the MD clusters. Spectral averaging over typical structures would be problematic due to the large degree of freedom in the real solution.65
The decamers show similar behaviour to the dimers. The computed geometries are consistent with structural models proposed previously.43 (Note that a helical longer-range arrangement was also proposed for carotenoid aggregates,34 this however, is not possible to simulate reliably with our computational means).
The simulation thus provides useful insight into the underlying processes of aggregation. It confirms that the low concentration of acetone (in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 model) is favourable for hydrophobic attraction of AXT molecules, although all weak interactions (electrostatic, π–π stacking, van der Waals forces, and hydrogen bonding) participate. At higher acetone concentrations the hydrophobic attraction is weaker. A similar situation was described for AXT aggregation in mixed water–ethanol solutions.43
9 model) is favourable for hydrophobic attraction of AXT molecules, although all weak interactions (electrostatic, π–π stacking, van der Waals forces, and hydrogen bonding) participate. At higher acetone concentrations the hydrophobic attraction is weaker. A similar situation was described for AXT aggregation in mixed water–ethanol solutions.43
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7” system, nevertheless they stabilize at about the 700 cluster average. Note that the equilibration required rather long MD simulation times, to allow an average of a sufficient number of independent (uncorrelated) geometry frames, i.e., separated by long time intervals.
7” system, nevertheless they stabilize at about the 700 cluster average. Note that the equilibration required rather long MD simulation times, to allow an average of a sufficient number of independent (uncorrelated) geometry frames, i.e., separated by long time intervals.
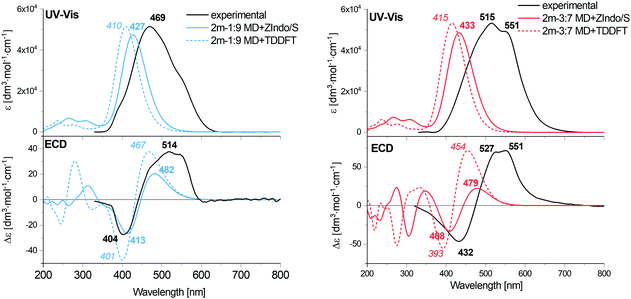 | ||
Fig. 8 Calculated EA and ECD spectra of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and 3 9 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 AXT dimers, averaged over 1000 MD clusters, combined with the experimental data for H and J-aggregates of AXT. 7 AXT dimers, averaged over 1000 MD clusters, combined with the experimental data for H and J-aggregates of AXT. | ||
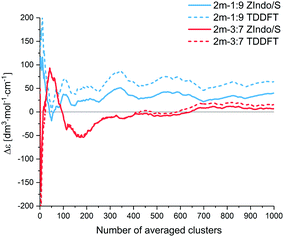 | ||
Fig. 9 ECD intensities (Δε) of simulated AXT dimers at 482 nm (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ZIndo/S), 467 nm (1 9 ZIndo/S), 467 nm (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 TD-DFT), 479 nm (3 9 TD-DFT), 479 nm (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 ZIndo/S) and 454 nm (3 7 ZIndo/S) and 454 nm (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 TD-DFT) as a function of the number of averaged clusters. 7 TD-DFT) as a function of the number of averaged clusters. | ||
For both dimers, the maximum of the main UV-vis band is predicted at shorter wavelengths compared to the experimental spectra. For the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimer model this shift is considerably more prominent. Both dimer models and both theoretical methods lead to the same positive/negative (at high/low wavenumber) ECD couplet, which is also observed in the experimental spectra of AXT aggregates. This couplet results from splitting of the AXT excited energy levels during the interactions. The sign of the couplet corresponds to the “positive” chirality in the dimers, i.e. to the slight prevalence of the positive torsional angles as indicated by the histograms, both for the 1
7-dimer model this shift is considerably more prominent. Both dimer models and both theoretical methods lead to the same positive/negative (at high/low wavenumber) ECD couplet, which is also observed in the experimental spectra of AXT aggregates. This couplet results from splitting of the AXT excited energy levels during the interactions. The sign of the couplet corresponds to the “positive” chirality in the dimers, i.e. to the slight prevalence of the positive torsional angles as indicated by the histograms, both for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and 3
9 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimers (Fig. 4(a)).
7-dimers (Fig. 4(a)).
An alternate representation of the results may be a comparison of the monomer, J and H aggregate EA and ECD spectra, as done for the experiment and computation in the ESI:† Fig. S2 (experiment), S15 and S16 (ZIndo/TDDFT theories). The detailed line structure of the simulated spectra can also be seen in the ESI† (Fig. S18–S21). Some experimental trends are not well-reproduced, such as the blue and red shifts of the absorption maxima of the H and J aggregates, if compared to the monomer. The theoretical maxima remain almost constant. The aggregation also broadens the experimental signal, leading to a distinct signal at 551 nm for the J aggregate attributed to its two different forms,57,66 which is not seen in theory (see Fig. S2, ESI†). Supposedly the dimer model is too crude to reproduce all aspects of the structure of the loose J-aggregation; the H-aggregate experiment is reproduced much better, which is consistent with the “card-packing” concept where the short-range interactions reasonably-well reproduced by the model dominate.
The TDDFT and ZIndo/S methods gave quite similar results in the region of the main absorption band, while the calculation times were significantly (∼50 times) shorter for the former one. TDDFT gives only slightly higher transition energies and ECD intensities.
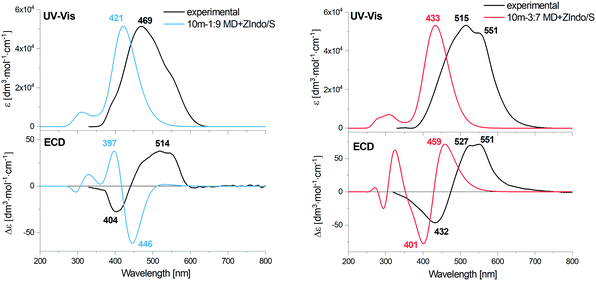 | ||
Fig. 10 Calculated EA and ECD spectra of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and 3 9 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 AXT decamers, averaged over 400 MD clusters, combined with the experimental data of H- and J-aggregates of AXT. 7 AXT decamers, averaged over 400 MD clusters, combined with the experimental data of H- and J-aggregates of AXT. | ||
The simulated ECD curves are more complex than for the dimer; roughly speaking the “−/+” couplet becomes a “+ − +” w-shape. For the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-model the theoretical shape is more or less consistent with the experiment, as for the dimers, while for the 1
7-model the theoretical shape is more or less consistent with the experiment, as for the dimers, while for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 system the longest-wavelength predicted positive intensity is unrealistically low. The models thus have clear limits in reproducing the complex aggregation equilibria. Note, for example, that in some H-aggregates the helicity could be switched within a few hours,25 which is clearly beyond the scope of the present MD simulations.
9 system the longest-wavelength predicted positive intensity is unrealistically low. The models thus have clear limits in reproducing the complex aggregation equilibria. Note, for example, that in some H-aggregates the helicity could be switched within a few hours,25 which is clearly beyond the scope of the present MD simulations.
Conclusions
We devised several models to simulate the aggregation process and spectral properties of astaxanthin aggregates, to understand the dependence of the aggregate structure on the environment, and to link their optical activity expressed as ECD spectral intensities to the geometry. For simulation of the absorption and ECD spectra the two ZIndo/S and TD-DFT approaches appeared both suitable and provided about the same results, which opened the way to simulate larger aggregates with the computationally cheaper ZIndo/S method. The molecular dynamics simulations (Amber/GAFF) reproduced the different aggregation behaviour observed for the low-and high-acetone concentrations very well. The lower-one (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 models) provided tight “H-type” aggregates, whereas for the higher content (3
9 models) provided tight “H-type” aggregates, whereas for the higher content (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) AXT molecules were ordered less, which is believed to be the principal characteristic of the “J-aggregates”. MD also provided detailed structural information (e.g. torsional angles and distances between AXT molecules) as well as the solvent distribution in the first AXT solvation sphere that so far cannot be directly obtained from experiment. Both the aggregate types are predicted to comprise two dominant conformations, with positive and negative values of torsional angles. However the distribution in the 3
7) AXT molecules were ordered less, which is believed to be the principal characteristic of the “J-aggregates”. MD also provided detailed structural information (e.g. torsional angles and distances between AXT molecules) as well as the solvent distribution in the first AXT solvation sphere that so far cannot be directly obtained from experiment. Both the aggregate types are predicted to comprise two dominant conformations, with positive and negative values of torsional angles. However the distribution in the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7-dimer is broader and spans all the angles. Hydrophobic forces are responsible for the attraction of AXT molecules in the 1
7-dimer is broader and spans all the angles. Hydrophobic forces are responsible for the attraction of AXT molecules in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9-dimer, however, the H-bond network (Fig. 7) around the polar terminal groups also may stabilize the interaction of monomers.
9-dimer, however, the H-bond network (Fig. 7) around the polar terminal groups also may stabilize the interaction of monomers.
The dimer models also reproduced the prevalent chirality well as reflected in ECD band shapes and signs, nevertheless the decamer model and a more detailed comparison with experiment indicated that the structure–spectra relationship is more complex than it is possible to model with the available computational means. In spite of the limited precision we consider the present study as an important step to rationalize the rich ECD and ROA spectroscopic data in terms of the structure; in the future an improved MD/QM methodology is likely to become an indispensable tool to reveal the structure and reactivity of astaxanthin and similar biomolecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Science Centre (grant no. DEC-2015/19/N/ST4/00185, DEC-2017/24/T/ST4/00454) and GACR (16-05935S). This research was supported in part by PL-Grid Infrastructure.References
- M. Baranska, M. Roman, J. Cz. Dobrowolski, H. Schulz and R. Baranski, Curr. Anal. Chem., 2013, 9, 108–127 CrossRef.
- M. Olaizola and M. E. Huntley, Recent Adv. Mar. Biotechnol. Vol. 9 Biomater. Bioprocessing, 2003, vol. 9, pp. 143–164 Search PubMed.
- F. X. Cunningham and E. Gantt, Plant Cell, 2011, 23, 3055–3069 CrossRef PubMed.
- G. R. Lorenz and R. T. Cysewski, Trends Biotechnol., 2000, 18, 160–167 CrossRef PubMed.
- M. Guerin, M. E. Huntley and M. Olaizola, Trends Biotechnol., 2003, 21, 210–216 CrossRef PubMed.
- E. A. Johnson, Int. Microbiol., 2003, 6, 169–174 CrossRef PubMed.
- J. D. Fontana, M. B. Chocial, M. Baron, M. F. Guimaraes, M. Maraschin, C. Ulhoa, J. A. Florêncio and T. M. Bonfim, Appl. Biochem. Biotechnol., 1997, 63–65, 305–314 CrossRef PubMed.
- T. Ide, M. Hoya, T. Tanaka and S. Harayama, Biochem. Eng. J., 2012, 65, 37–43 CrossRef.
- C. Vílchez, E. Forján, M. Cuaresma, F. Bédmar, I. Garbayo and J. M. Vega, Mar. Drugs, 2011, 9, 319–333 CrossRef PubMed.
- H. Li, P. Zhang, X. Song and W. Wang, Chin. J. Chem., 2011, 29, 1535–1540 CrossRef.
- C. Yuan, Z. Jin and X. Xu, Carbohydr. Polym., 2012, 89, 492–496 CrossRef PubMed.
- N. E. Polyakov, A. Magyar and L. D. Kispert, J. Phys. Chem. B, 2013, 117, 10173–10182 CrossRef PubMed.
- P. Bhosale and P. S. Bernstein, Arch. Biochem. Biophys., 2007, 458, 121–127 CrossRef PubMed.
- I. Higuera-Ciapara, L. Félix-Valenzuela and F. M. Goycoolea, Crit. Rev. Food Sci. Nutr., 2006, 46, 185–196 CrossRef PubMed.
- N. Anarjan, I. A. Nehdi and C. P. Tan, Chem. Cent. J., 2013, 7, 1–11 CrossRef PubMed.
- A. Kaczor and M. Baranska, Anal. Chem., 2011, 83, 7763–7770 CrossRef PubMed.
- V. M. Moretti, T. Mentasti, F. Bellagamba, U. Luzzana, F. Caprino, G. M. Turchini, I. Giani and F. Valfrè, Food Addit. Contam., 2006, 23, 1056–1063 CrossRef PubMed.
- B. Durbeej and L. A. Eriksson, Chem. Phys. Lett., 2003, 375, 30–38 CrossRef.
- G. Zajac, A. Kaczor, S. Buda, J. Młynarski, J. Frelek, J. C. Dobrowolski and M. Baranska, J. Phys. Chem. B, 2015, 119, 12193–12201 CrossRef PubMed.
- B. Subramanian, N. Tchoukanova, Y. Djaoued, C. Pelletier, M. Ferron and J. Robichaud, J. Raman Spectrosc., 2014, 45, 299–304 CrossRef.
- G. N. Coral-Hinostroza, T. Ytrestøyl, B. Ruyter and B. Bjerkeng, Comp. Biochem. Physiol., Part C: Toxicol. Pharmacol., 2004, 139, 99–110 CrossRef PubMed.
- A. Kaczor, K. Turnau and M. Baranska, Analyst, 2011, 136, 1109–1112 RSC.
- B. A. Clevidence and J. G. Bieri, Methods Enzymol., 1993, 214, 33–46 Search PubMed.
- M. Dudek, G. Zajac, A. Kaczor and M. Baranska, J. Raman Spectrosc., 2017, 48, 673–679 CrossRef.
- M. Dudek, G. Zajac, A. Kaczor and M. Baranska, J. Phys. Chem. B, 2016, 120, 7807–7814 CrossRef PubMed.
- G. Zajac, A. Kaczor, A. Pallares Zazo, J. Mlynarski, M. Dudek and M. Baranska, J. Phys. Chem. B, 2016, 120, 4028–4033 CrossRef PubMed.
- G. Zajac, J. Lasota, M. Dudek, A. Kaczor and M. Baranska, Spectrochim. Acta, Part A, 2017, 173, 356–360 CrossRef PubMed.
- F. Zsila, J. Deli and M. Simonyi, Planta, 2001, 213, 937–942 CrossRef PubMed.
- F. Zsila, Z. Bikádi, J. Deli and M. Simonyi, Chirality, 2001, 13, 446–453 CrossRef PubMed.
- M. Simonyi, Z. Bikádi, F. Zsila and J. Deli, Chirality, 2003, 15, 680–698 CrossRef PubMed.
- F. Zsila, J. Deli, Z. Bikádi and M. Simonyi, Chirality, 2001, 13, 739–744 CrossRef PubMed.
- F. Zsila, Z. Bikádi, Z. Keresztes, J. Deli and M. Simonyi, J. Phys. Chem. B, 2001, 105, 9413–9421 CrossRef.
- H. H. Billsten, V. Sundström and T. Polívka, J. Phys. Chem. A, 2005, 109, 1521–1529 CrossRef PubMed.
- S. Köhn, H. Kolbe, M. Korger, C. Köpsel, B. Mayer, H. Auweter, E. Lüddecke, H. Bettermann and H.-D. Martin, in Carotenoids: Volume 4: Natural Functions, ed. G. Britton, S. Liaaen-Jensen and H. Pfander, Birkhäuser Basel, Basel, 2008, pp. 53–98 Search PubMed.
- C. Köpsel, H. Möltgen, H. Schuch, H. Auweter, K. Kleinermanns, H.-D. Martin and H. Bettermann, J. Mol. Struct., 2005, 750, 109–115 CrossRef.
- J. Hempel, C. N. Schädle, S. Leptihn, R. Carle and R. M. Schweiggert, J. Photochem. Photobiol., A, 2016, 317, 161–174 CrossRef.
- A. V. Ruban, P. Horton and A. J. Young, J. Photochem. Photobiol., B, 1993, 21, 229–234 CrossRef.
- J. Olsina, M. Durchan, B. Minofar, T. Polivka and T. Mancal, 2012, Arxiv: 1208.4958.
- I. E. Apanasenko, O. Y. Selyutina, N. E. Polyakov, L. P. Suntsova, E. S. Meteleva, A. V. Dushkin, P. Vachali and P. S. Bernstein, Arch. Biochem. Biophys., 2015, 572, 58–65 CrossRef PubMed.
- F. Zsila, Z. Bikádi, J. Deli and M. Simonyi, Tetrahedron Lett., 2001, 42, 2561–2563 CrossRef.
- G. Zajac, A. Kaczor, K. Chruszcz-Lipska, J. C. Dobrowolski and M. Baranska, J. Raman Spectrosc., 2014, 45, 859–862 CrossRef.
- L. A. Nafie, Chem. Phys., 1996, 205, 309–322 CrossRef.
- K. J. Karki, S. Samanta and D. Roccatano, J. Phys. Chem. B, 2016, 120, 9322–9328 CrossRef PubMed.
- M. C. Zerner, G. H. Loew, R. F. Kirchner and U. T. Mueller-Westerhofflc, J. Am. Chem. Soc., 1980, 102, 589–599 CrossRef.
- J. E. Ridley and M. C. Zerner, Theor. Chim. Acta, 1976, 42, 223–236 CrossRef.
- J. Ridley and M. Zerner, Theor. Chim. Acta, 1973, 32, 111–134 CrossRef.
- M. G. Cory, M. C. Zerner, X. Hu and K. Schulten, J. Phys. Chem. B, 1998, 102, 7640–7650 CrossRef.
- J. Alonzo, W. M. Kochemba, D. L. Pickel, M. Ramanathan, Z. Sun, D. Li, J. Chen, B. G. Sumpter, W. T. Heller and S. M. Kilbey II, Nanoscale, 2013, 5, 9357–9364 RSC.
- G. Bringmann, K. Maksimenka, T. Bruhn, M. Reichert, T. Harada and R. Kuroda, Tetrahedron, 2009, 65, 5720–5728 CrossRef.
- R. A. Alvarez-Puebla, C. Valenzuela-Calahorro and J. J. Garrido, Sci. Total Environ., 2006, 358, 243–254 CrossRef PubMed.
- S. Blumstengel, F. Meinardi, P. Spearman, A. Borghesi, R. Tubino and G. Chirico, J. Chem. Phys., 2002, 117, 4517–4525 CrossRef.
- S. Chandrasekaran, M. Aghtar, S. Valleau, A. Aspuru-Guzik and U. Kleinekathöfer, J. Phys. Chem. B, 2015, 119, 9995–10004 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc, Wallingford CT, 2016 Search PubMed.
- F. C. Spano, J. Am. Chem. Soc., 2009, 131, 4267–4278 CrossRef PubMed.
- M. Simonyi, Z. Bikádi, F. Zsila and J. Deli, Chirality, 2003, 15, 680–698 CrossRef PubMed.
- M. Kasha, H. R. Rawls and M. Ashraf El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 Search PubMed.
- C. Köpsel, H. Möltgen, H. Schuch, H. Auweter, K. Kleinermanns, H. D. Martin and H. Bettermann, J. Mol. Struct., 2005, 750, 109–115 CrossRef.
- D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, I. T. E. Cheatham, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, AMBER 14, University of California, San Francisco, 2014 Search PubMed.
- J. M. Martínez and L. Martínez, J. Comput. Chem., 2003, 24, 819–825 CrossRef PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef PubMed.
- C. L. Covington and P. L. Polavarapu, CDspecTech: Computer programs for calculating similarity measures of comparison between experimental and calculated dissymmetry factors and circular intesity diferentials, version22.0, 2017, https://sites.google.com/site/cdspectech1/ Search PubMed.
- C. L. Covington and P. L. Polavarapu, Chirality, 2017, 29, 178–192 CrossRef PubMed.
- H. A. Frank and R. L. Christensen, in The Carotenoids, Vol. 4: Natural Functions, ed. H. Britton, G. Liaaen-Jensen and S. Pfander, Birkhäuser, Basel, 4th edn, 2008, pp. 167–188 Search PubMed.
- G. Pescitelli, L. Di Bari and N. Berova, Chem. Soc. Rev., 2011, 40, 4603 RSC.
- L. Lu, T. Hu and Z. Xu, Spectrochim. Acta, Part A, 2017, 185, 85–92 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp01742e |
| This journal is © the Owner Societies 2018 |