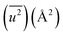Size effects on rhodium nanoparticles related to hydrogen-storage capability

Abstract

To unveil the origin of the hydrogen-storage properties of rhodium nanoparticles (Rh NPs), we investigated the electronic and crystal structures of the Rh NPs using various synchrotron based X-ray techniques. Electronic structure studies revealed that the hydrogen-storage capability of Rh NPs could be attributed to their more unoccupied d-DOSs than that of the bulk near the Fermi level. Crystal structure studies indicated that lattice distortion and mean-square displacement increase while coordination number decreases with decreasing particle size and the hydrogen-absorption capability of Rh NPs improves to a greater extent with increased structural disorder in the local structure than with that in the mean structure. The smallest Rh NPs, having the largest structural disorder/increased vacancy spaces and the smallest coordination number, exhibited excellent hydrogen-storage capacity. Finally, from the bond-orientational order analysis, we confirmed that the localized disordering is distributed more over the surface part than the core part and hydrogen can be trapped on the surface part of Rh NPs which increases with a decrease in NP diameter.

---

1 Introduction

The study of materials enabling the efficient storage and safe transport of fuel gases, particularly hydrogen gas, has mainly focused on areas such as metal–organic frameworks,^1–3 carbon materials,^4,5 and hydrogen-storage alloys.^6–8 Hydrogen-storage alloys are metallic materials that have a unique ability to store hydrogen compactly and safely as a consequence of the stability of their hydrides.^9,10 Recently, nanoparticles of such metals have attracted much attention as advanced materials of new hydrogen-storage alloys.^11–13 Rhodium (Rh) is an effective catalyst for various chemical reactions in the 4d transition metal series.^14–16 The synthesis of metal nanoparticles (NPs) to improve their catalytic activities and obtain unexpected properties is a very hot topic owing to the quantum size effects and high surface-area-to-volume ratios exhibited by the NPs.^17–19 For instance, while bulk Rh metal does not absorb hydrogen, Rh NPs do.¹⁴ Kusada et al. observed that the hydrogen-storage capacity of Rh NPs increases with decreasing particle size.²⁰ They also reported that the enthalpy of hydrogen storage in the Rh NPs changes from endothermic to exothermic with decreasing particle sizes, with critical sizes between 7.1 and 10.5 nm. These phenomena might be caused by a change in the electronic state of Rh with decreasing particle size.^10,14 However, the origin of the hydrogen-storage properties and performance of Rh NPs can hardly be described as one parameter and has not yet been revealed. Therefore, understanding the electronic and crystal structures of such NPs is very important for understanding their catalyst properties. In particular, the absorption of hydrogen by metal NPs is expected to occur in their core part as well as on their surface part.

X-ray photoelectron spectroscopy (XPS) is a useful technique for probing the electronic properties of solids.^21,22 However, as described before,²³ it is very difficult to detect a bulk electronic structure of NPs with a wrapping layer by using conventional XPS. Synchrotron-based hard X-ray photoelectron spectroscopy (HAXPES), which has high brilliance and exhibits large probing depths, is widely used to investigate the bulk electronic structure of materials^24,25 and this kind of NPs.²³ High-energy X-ray diffraction (HEXRD)^26,27 and extended X-ray absorption fine structure (EXAFS)^28–31 analysis using synchrotron X-rays are also useful tools for observing structural information in long- and short-range orders. Furthermore, a reverse Monte Carlo (RMC) modeling method allows us to generate 3-dimensional structure models from HEXRD data.³²

In this study, we investigated the electronic and crystal structures of Rh NPs of various particle sizes (2.4, 4.0, 7.1, and 10.5 nm), using synchrotron-based X-ray techniques including the HAXPES, X-ray absorption fine structure (XAFS), and HEXRD coupled with the RMC modeling method. To help unveil the origin of their hydrogen-absorption ability, we analysed the particle size dependence of the d-band center, lattice distortion, coordination number, long- and short-range order, mean-square displacement, and volume fraction of cavities of the Rh NPs.

2 Experimental

2.1 Sample preparation

We investigated Rh NPs of four different sizes (2.4–10.5 nm), as shown in Table 1. The Rh NPs were fabricated by the chemical reduction method using RhCl₃·3H₂O as the metal precursor and poly(N-vinyl-2-pyrrolidone) (PVP) as the stabilizing agent. Ethylene glycol (EG) was used as both the solvent and the reducing agent. The detailed procedure is described in ref. 20. The particle size of the prepared samples was determined from transmission electron microscopy (TEM) images. The details of the determination of NP size from the size histograms and temperature dependences for the hydrogen pressure–composition (PC) isotherms are also described in supporting notes 1 and 2 (ESI†).

Table 1 Reaction conditions for the synthesis of fcc Rh NPs and their hydrogen-storage capacity (H/Rh)²⁰

Size (TEM)/nm	Metal precursor/mmol	Solvent/mL	PVP/mmol	H/Rh
2.4 ± 0.5	RhCl3·3H2O/1.0	EG/220	10.0	0.225
4.0 ± 0.7	RhCl3·3H2O/2.0	EG/220	10.0	0.185
7.1 ± 1.2	RhCl3·3H2O/2.0	EG/110	5.0	0.130
10.5 ± 1.5	RhCl3·3H2O/5.0	EG/200	5.0	0.067

---

2.2 Hard X-ray photoelectron spectroscopy (HAXPES)

HAXPES measurements were performed by employing a linearly polarized X-ray beam in the horizontal plane with a photon energy of 5.95 keV at the undulator beamline BL15XU of the National Institute for Materials Science (NIMS) at SPring-8 in Japan. The total energy resolution was estimated to be 240 meV with a pass energy of 200 eV using a standard Au sample. All HAXPES spectra were recorded at room temperature. To eliminate the charge-up phenomenon, all the NPs were mixed with carbon powder. The corresponding inelastic mean free path (IMFP: λ), which was calculated using the TPP-2M equation,³³ was approximately 5.6 nm for metallic Rh. The corresponding effective information depth was approximately 17–18 nm (3λ), greater than the diameter of the largest NPs. Hence, we were able to obtain information regarding the electronic structure of the Rh NPs.

2.3 High-energy X-ray diffraction (HEXRD)

High-energy XRD experiments were performed at a beamline BL04B2 of SPring-8 in Japan using X-rays of 61.37 keV in photon energy (λ = 0.202 Å). The measurements were taken in the symmetric transmission geometry. The HEXRD data were corrected for background, polarization, and absorption and were then normalized to the structure factor and Fourier transformed using the SPring-8 BL04B2 analysis software.

2.4 X-ray absorption fine structure (XAFS)

XAFS measurements of the Rh K-edge (23.22 keV) were performed using a Si(311) double-crystal monochromator at beamline BL01B1 of SPring-8, Japan. All XAFS spectra were obtained in transmission mode at room temperature. The powder samples were used to fill the hole of a copper plate of 0.5 mm in thickness using Kapton tape on both sides. The inner diameter of the hole was 3.0 mm. The intensities of the incident and transmitted X-ray beams were collected using ionization chambers located in front and behind the respective samples. To extract the XAFS oscillation, |χ(k)| (where k is the photoelectron wavenumber), from the obtained absorption spectra, the extrapolated pre-edge background absorption was subtracted first. The resulting curve was then normalized by dividing the jump in the absorption at the edge. Data processing and analysis of the XAFS spectra were performed using the Athena and Artemis programs of the IFEFFIT software package.³⁴

2.5 Reverse Monte Carlo (RMC) method

RMC simulations were performed using RMC_POT software³⁵ to construct the 3-dimensional atomic configuration and to calculate the volume fraction of cavities for Rh NPs of three different sizes (2.4, 4.0, and 7.1 nm). RMC_POT provides RMC simulation on the assumption of the NPs in sphere shapes under non-periodic boundary conditions. Here, the diameter of spherical samples was determined from TEM images in Table 1. The RMC run was carried out for each system whose configuration closely resembles that of a spherical NP. The simulations were guided by the experimental structure factor S(Q) and were stopped when the RMC computed and experimental data agreed very well over the entire range of wave vectors (Q = 20 Å⁻¹). An average coordination constraint of first neighbors was enforced the coordination number, as obtained from the results of XAFS experiments.

3 Results and discussion

3.1 Electronic structure: HAXPES

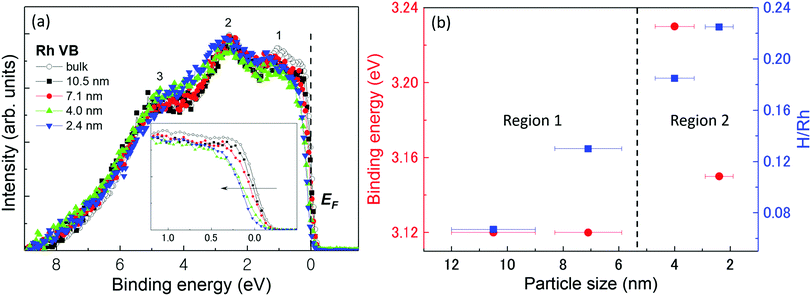
Fig. 1(a) shows the VB HAXPES spectra of bulk Rh and Rh NPs with different particle sizes. To ensure proper comparison between the spectra, the following steps were implemented: (1) all VB spectra were recorded in the same energy region (0–9 eV), (2) the background caused by carbon powder was properly subtracted, (3) the Shirley background was subtracted³⁶ and (4) the VB area intensity was normalized. For ease of discussion, peaks 1, 2, and 3 have been tagged in the VB HAXPES spectra. According to our previous density functional theory (DFT) calculations,²³ peak 1 arose from the Rh 4d density of states (DOS). Peak 2 was mainly composed of the Rh 4d partial DOS. Peak 3 was mainly composed of Rh 4d and 5s partial DOSs. The Rh 5p DOS just uniformly distributed in both peaks 2 and 3. The most apparent difference in the spectra is that the intensity of peak 1 was higher for bulk Rh than for the Rh NPs. The calculated s-DOS was most intense at the bottom of the d-band far away from the Fermi edge (E_F), as shown in Supplementary Fig. 5 of ref. 23, similarly to the Ag case. This suggested that the difference between the 4d DOSs near the Fermi edge caused by the coordination number³⁷ of bulk Rh and Rh NPs may be the reason why the bulk Rh cannot store hydrogen. This result indicates that the metal d state is an important parameter for estimating the chemical molecular adsorption barrier of noble metal surfaces. The inset of Fig. 1(a) shows an enlargement of the photoemission spectra in the vicinity of the Fermi edge. The VB DOS shifts obviously toward a higher binding energy with decreasing particle size. In particular, for the 4.0 nm and 2.4 nm diameter Rh NPs, the Fermi edge onsets in the VB HAXPES spectra were not the usual metallic Fermi edge, with steep slopes away from the Fermi edge. This phenomenon probably originated from the final state effect caused by the photoholes left behind in the NPs during the photoemission process³⁸ and the effective number of the neighbors of a given atom decreases as the particle size decreases, consequently, the interaction of the d-electrons localized on neighboring atoms is expected to decrease.³⁹

Fig. 1 VB HAXPES spectra and hydrogen-storage capacity: (a) VB HAXPES spectra of bulk Rh and Rh NPs of different particle sizes. The black empty circles, black squares, red circles, green up triangles, and blue down triangles in (a) represent bulk Rh, and 10.5 nm, 7.1 nm, 4 nm, and 2.4 nm Rh NPs, respectively. The inset of (a) is the enlarged VB spectra near the Fermi edge. (b) Centre of gravity of the VB spectra (red circles) and hydrogen-storage capacity (blue squares) of the NPs as a function of particle size.

Generally, the electronic structure change due to hydrogen absorption would be like that due to alloying reaction as a metallic bond, not covalent character within the host–guest framework. In fact, for not only Rh but also other 3d, 4d, and 5d metals, the electronic structures especially the d-band structures are very important for adsorption hydrogen.^40,41 It has been shown that the activity of metal catalysts strongly depends on the coordination number of the metal atoms. Hammer and Nørskov⁴² proposed the so-called d-band model to explain trends in the catalytic activities of metal surfaces, films, and clusters.

The strength of the interaction and the occupancy of the resulting states, which are directly related to the potential barrier for adsorption, can be reflected by the position of the d-band center. According to their study,⁴² the d-band width becomes smaller and the d-band center tends to move away from E_F with decreasing coordination number. Therefore, the center of gravity of each VB HAXPES spectrum, which is called the d-band-center position, was plotted as shown by the red circles in Fig. 1(b). The relative hydrogen-storage capacity of the Rh NPs is also plotted in the figure with the blue squares. It is obvious that the hydrogen-storage capacity of the NPs linearly increased as their diameter was decreased.²⁰ However, the d-band center positions for the 10.5 nm and 7.1 nm diameter Rh NPs were almost the same. As the particle size was decreased from 7.1 nm to 4.0 nm, the center position is shifted away from E_F. It then shifted towards E_F from 4.0 nm to 2.4 nm. The whole behaviour of the d-band center position deviated from that predicted by the d-band-center theory.

The 4.0 nm diameter Rh NPs, the d-band center of which was the most shifted away from E_F, did not have the highest hydrogen-storage capacity. This suggested that the hydrogen-storage capacity may be determined by structural parameters, not the position of the d-band center. Here, the structural parameters included lattice parameters, atomic bond length, surface area, lattice distortion, coordination number, mean-square displacement, and cavity. Notably, the d-band widths of the 4.0 nm and 2.4 nm diameter Rh NPs were slightly smaller than that of the 10.5 nm and 7.1 nm diameter Rh NPs, suggesting d-band rehybridization in these smaller NPs. Furthermore, the limitation condition may exist for d-band theory when explaining the hydrogen-storage capacity of NPs.

3.2 Structural characterization: HEXRD, XAFS and RMC structure modeling

To fully understand the origin of the hydrogen-absorption ability of Rh NPs, we carried out a structural characterization using HEXRD and XAFS. Fig. 2(a) shows the XRD patterns of all the prepared Rh NPs. The full-width-at-half-maximum (FWHM) of the diffraction peaks became sharper with an increase in mean particle size, which was obtained from TEM observations.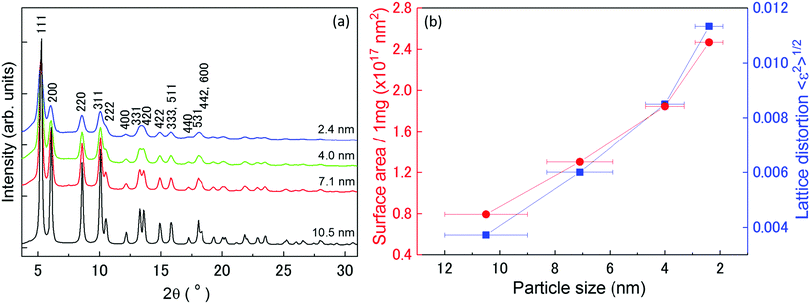

Fig. 2 XRD patterns, surface area and lattice distortion: (a) XRD patterns of Rh NPs at room temperature. The incident X-ray energy was 61.37 keV with a wavelength of 0.202 Å. Fifteen Bragg peaks (from 111 to 600) were used to determine the average crystalline domain size of the Rh NPs, as shown in Fig. S4 (ESI†). (b) Dependence of surface area of crystalline domains (red circles) and lattice distortion (blue squares), as obtained from the Rietveld analysis, on particle size.

All the XRD patterns were analysed using the Rietveld refinement method⁴³ with the pseudo-Voigt function. The results of the Rietveld refinement analysis are shown in Fig. S3 (ESI†). The plot shows the refined XRD patterns, residuals, Bragg peak positions, and R_wp and R_B agreement factors. In the refinement, the Rh fractional position and occupancy were considered to be fixed. Other parameters such as lattice constants, B factor, scale factor, and peak-shape function parameters were taken as free parameters. The B factor is defined as the mean-square displacement and is related to atomic thermal vibration. The space group associated with fcc Rh NPs is Fm3̄m. The evaluated average domain size, lattice parameter, the nearest neighbour distance (R_NN), unit-cell volume, the number of unit cells, B factor, Debye–Waller factor 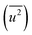, lattice distortion, and the domain surface area of the NPs are listed in Table 2.

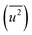Table 2 Average crystalline domain size, lattice parameter, the nearest neighbour distance (R_NN), unit volume, the number of unit cells, B factor, Debye–Waller factor , lattice distortion, and the domain surface area of Rh NPs obtained by Rietveld refinement of the HEXRD data

Sample	Rh 2.4 nm	Rh 4.0 nm	Rh 7.1 nm	Rh 10.5 nm
Crystalline domain size (nm)	1.97	2.63	3.73	6.12
a (Å)	3.8133 ± 0.0007	3.8094 ± 0.0004	3.8121 ± 0.0002	3.8091 ± 0.0002
R NN (Å)	2.6964 ± 0.0005	2.6937 ± 0.0003	2.6955 ± 0.0001	2.6935 ± 0.0001
Unit volume (Å^3)	55.4480	55.2815	55.3961	55.2685
Number of unit cells	72.5	172.5	491.3	2167.3
B factor (Å^2)	0.30 ± 0.03	0.27 ± 0.02	0.29 ± 0.01	0.28 ± 0.01
	0.0038 ± 0.0004	0.0034 ± 0.0003	0.0037 ± 0.0001	0.0035 ± 0.0001
Lattice distortion	0.0113	0.0085	0.0060	0.0037
Domain surface area (×10^17 nm^2)	2.47	1.84	1.30	0.79

---

To reveal the origin of the hydrogen-storage properties of the Rh NPs, we plotted the particle size dependence of the surface area of the crystalline domains, lattice distortion, and mean-square displacement. Fig. 2(b) shows the relationship between the surface area of the crystalline domains (red circles)/lattice distortion ratio (blue square), obtained from Rietveld analysis and particle size, as obtained from TEM results. The surface area was calculated using the following equation: A_surface = N × 4π(D/2)², assuming that the NPs are spherical in shape. Here, A_surface denotes the surface area of the crystalline domains, N is the number of domains per 1 mg of Rh NPs, and D is the average crystalline domain size. N is defined by the following equation: N = (number of Rh atoms per 1.0 mg)/(number of Rh atoms per domain). The details for the calculation of N are described in supporting note 5 (ESI†). The surface area of the crystalline domains increased with a decrease in NP diameter. This result indicates that the hydrogen-storage capacity is closely related to the surface area of the crystalline domains, and can be interpreted as the main reason why the 10.5 nm and 7.1 nm diameter Rh NPs had different hydrogen-storage capacities even though their VB spectra (Fig. 1(b)) were almost the same.

In the calculation of lattice distortion, based on the assumption that the absorption of hydrogen on Rh NPs occurs on all crystalline planes, not only the close-packed (111) lattice planes, the lattice distortion was determined using all 15 lattice planes (from (111) to (600)). The crystal lattice distortion 〈ε²〉^1/2 of the Rh NPs at various domain sizes was calculated using the following equation:^44,45

Here, K (= 0.9 if nanoparticles are assumed to be spherical) is the shape factor. Lattice distortion in Fig. 2(b) increased with a decrease in NP diameter. The hydrogen-storage capacity of the Rh NPs can be attributed to this phenomenon, together with the result of the surface area in Fig. 2(b). In other words, larger surface area and lattice distortion result in large hydrogen-storage capacity for the Rh NPs.

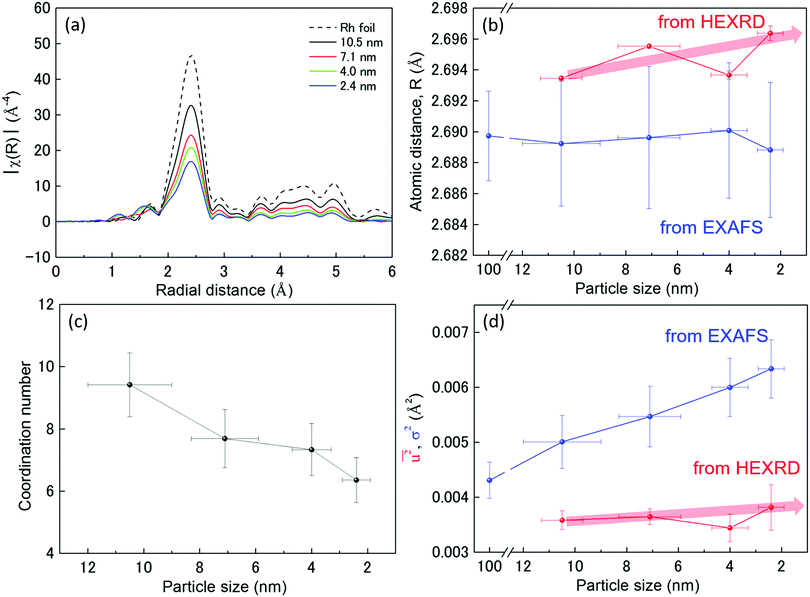
Fig. 3(a) show the Fourier transformed (FT) magnitude |χ(R)| of k³χ(k) for the experimental K-edge XAFS spectra of Rh foil and Rh NPs (Fig. S5, ESI†). All the |χ(R)| peaks in the spectrum of the Rh foil were present in the spectra of all the Rh NPs (Fig. 3(a)). This result indicates that an fcc Rh local structure existed in at least part of the 2.4 to 10.5 nm diameter Rh NPs. The behaviour of the experimental Rh K-edge XAFS spectra was reflected in the fit of the FT magnitudes |χ(R)| of k³χ(k) of these spectra, assuming that the local structure in both Rh foil and Rh NPs can be represented by a single-term contribution. The mean interatomic Rh–Rh distance (R_Rh–Rh), coordination number (CN), and Debye–Waller parameter (σ²) evaluated from the fitting are listed in Table 3. Rh foil was also used as a reference to obtain the value of R_Rh–Rh, reduction factor (S_o²), and σ². This value of S_o² was used in the following study of the atomic structure of the Rh NPs (Table 3), in which the CN for the Rh NPs were obtained by dividing the corresponding variable S_o² × CN by S_o² = 0.994. From XAFS results in Fig. 3(b), the mean interatomic Rh–Rh distance (R_Rh–Rh) of Rh NPs was confirmed to be equal to that of Rh foil. However, the nearest neighbour distance (R_NN) and the lattice parameter from HEXRD tend to increase with decreasing particle size, except for the 4.0 nm diameter Rh NPs. This size effect on the lattice parameters was not in agreement with results from previous studies on metallic NPs.^46–52 Furthermore, the abnormal change in R_NN for the 4.0 nm diameter Rh NPs can be interpreted as one of the reasons why the 2.4 nm diameter Rh NPs had a higher hydrogen-storage capacity than the 4.0 nm diameter Rh NPs, even though the d-band center of the Rh 2.4 nm diameter NPs was closer to E_F than that of the 4.0 nm diameter Rh NPs in Fig. 1(b).

Fig. 3 Local structure information from XAFS analysis: (a) FT magnitudes |χ(R)| of k³χ(k) of Rh foil (dashed black lines) and Rh NPs of different sizes: D = 10.5 nm (solid black line), D = 7.1 nm (solid red line), D = 4.0 nm (solid green line) and D = 2.4 nm (solid blue line). (b) Dependence of atomic distance, R, on particle size. (c) Dependence of coordination number (CN) for mean structure (red circles) and local structure (blue circles) on particle size. (d) Dependence of mean-square displacement for mean structure (red circles) and local structure (blue circles) on particle size.

Table 3 Mean interatomic Rh–Rh distance (R_Rh–Rh), coordination number (CN), and Debye–Waller parameter (σ²) of Rh NPs obtained using a single shell fit of the XAFS data. Rh foil was used as a reference to establish the values of R_Rh–Rh, reduction factor (S_o²), and σ²

Sample	Rh 2.4 nm	Rh 4.0 nm	Rh 7.1 nm	Rh 10.5 nm	Rh foil
R Rh–Rh (Å)	2.6888 ± 0.0044	2.690 ± 0.0044	2.6896 ± 0.0046	2.6892 ± 0.0040	2.6897 ± 0.0029
S o ^2					0.994 ± 0.077
CN	6.355 ± 0.719	7.333 ± 0.840	7.688 ± 0.936	9.419 ± 1.022
σ ^2 (Å^2)	0.0063 ± 0.0005	0.0060 ± 0.0005	0.0055 ± 0.0006	0.0050 ± 0.0005	0.0043 ± 0.0003

---

Fig. 3(c) shows the relationship between the coordination number (CN) and particle size. The apparent decrease in CN, compared with the 12 of the Rh bulk metal, may be associated with the increase in the number of unoccupied sites in each unit cell and localized disordering. This also indicates that the smaller particle tends to have more vacancy spaces or the larger one tends to be denser. These results, along with the results of surface area and lattice distortion in Fig. 2(b), are advantageous for the hydrogen-absorption capacity in terms of crystal structures of the Rh NPs.

Fig. 3(d) shows the dependence of the mean-square displacement of the mean structure (red circles, 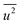) and local structure (blue circles, σ²) on particle size. The value of 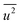(Debye–Waller factor) is estimated from B, defined as⁵³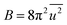, in Table 2 and regarded as indicative of the relative thermal vibrational motion of different parts of the structure relative to the mean structure (in the bulk). Atoms with a small 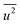belong to parts of the structure that are well ordered. In contrast, atoms with a large 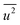generally belong to parts of the structure that are very flexible or more sensitive to the ambient environment. In contrast, strictly speaking, σ² is not a Debye–Waller factor. The Debye–Waller factor is a term commonly used in diffraction to describe the attenuation of the scattered intensity caused by the displacement of atoms away from a lattice point. For XAFS, the analogous Debye–Waller factor would describe the attenuation of χ(k) caused by the thermal and static disorder in the bond length or local structure. The value of 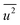, obtained from HEXRD, slightly increased with decreasing particle size, except for the 4.0 nm diameter Rh NPs. The value of σ², obtained from XAFS, also increased with a decrease in particle size. These results mean that the mean-square displacement/disorder greatly affects the hydrogen-storage capacity of Rh NPs. It has been noted that the value of σ² is considerably larger than that of 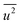for the same particle size. This result suggests that the hydrogen-absorption capability of Rh NPs improves more as the mean-square displacement in the local structure increases than that in the mean crystal structure.

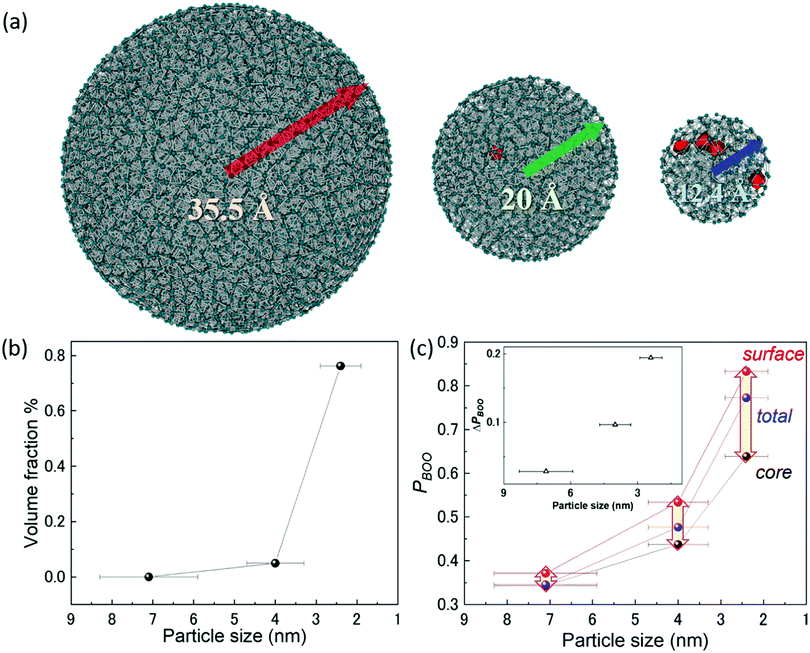
To fully reveal the size effect of the hydrogen-storage capacity of Rh NPs, the cavities and bond-orientational order (BOO) parameter^54,55 within Rh NPs were calculated with RMC structure modeling based on high-energy X-ray diffraction data. It is well known that hydrogen is more likely to be trapped on grain boundary or dislocations in metals.⁵⁶ It is also expected that hydrogen can be absorbed on cavities in their entire volume. Notably, RMC structure modeling is suitable to investigate the local structure of isolated and finite-sized spherical NPs and to determine the 3-dimensional atomic positions.³² The RMC experimental and simulated structure factor data sets for Rh NPs (2.4, 4.0, and 7.1 nm) are shown in Fig. S6 (ESI†). The RMC configuration models of Rh NPs reproduced the experimental total structure factor S(Q) with a good agreement. Fig. 4(a) shows the atomic configuration and cavity distribution obtained from RMC structure modeling. Here, the cavities were presented in red. The position and volume size of cavities were determined from a Dirichlet–Voronoi construction using the atomic positions and the cavity centers.⁵⁷ From this cavity analysis, we confirm that there was no cavity within the 7.1 nm diameter Rh NPs. In contrast, the volume fractions of the cavities for the 2.4 nm and 4.0 nm Rh NPs were 0.76 and 0.05%, respectively. Namely, the volume fraction of the cavities increased with a decrease in NP diameter (Fig. 4(b)). This result indicates that the total cavity volume contributes to the hydrogen-storage capacity, and the cavities can be induced by the increase of unoccupied sites and localized disordering. Fig. 4(c) shows the relationship between the parameter P_BOO and particle size for a core part and a surface part of Rh NPs. This P_BOO value means the deviation of the local structure from the ideal crystal structure.⁵⁵ If P_BOO is zero, the local structure is regarded as ideal. The details of the calculation of BOO and P_BOO are described in supporting note 7 (ESI†). Here, the whole volume of Rh NPs was divided into a core part and a surface part on the basis of the distance of 0.33 nm from the surface. The parameter P_BOO increased with a decrease in NP diameter. This result indicates that the localized disordering of Rh NPs increased with a decrease in NP diameter and was in agreement with the result shown in Fig. 3(c). It has been noted that P^surface_BOO is bigger than P^core_BOO in a same size and the difference between P^surface_BOO and P^core_BOO increased with a decrease in NP diameter (see the inset of Fig. 4(c)). This result indicates that localized disordering is distributed over the surface part than the core part a lot; the effect on localized disordering at the surface part increased with a decrease in NP diameter. It is expected that the probability that hydrogen can be trapped on the surface part of Rh NPs increases with a decrease in NP diameter. The structural information obtained in the present work will contribute to the design and improvement of the functionality of nanosized metals.

Fig. 4 Cavity and local structure information from 3-dimensional RMC models: (a) 3-dimensional atomic configuration and cavity distribution. The cavities were presented in red. (b) Dependence of volume fraction of cavities on the particle size. (c) Dependence of the deviation of the bond-orientational order from an ideal fcc structure on the particle size. If P_BOO is zero, the local structure is regarded as ideal. The inset of (c) shows the difference of P_BOO between a core part and a surface part.

4 Conclusions

We have investigated the size dependence of the hydrogen-storage properties of Rh nanoparticles (NPs) using various synchrotron-based X-ray techniques including HAXPES, HEXRD, XAFS and also analyzed the cavities inside Rh NPs using the RMC method. The principal findings from these measurements are as follows. (1) In the VB HAXPES spectra, the intensity of peak 1 (the occupied d-DOS) was higher for bulk Rh than for Rh NPs. This indicates that the unoccupied d-DOS of Rh NPs may be more than that of bulk Rh. (2) The electronic structures of the 2.4 nm and 4.0 nm diameter Rh NPs were very different from those of the other sizes. The narrowing of the d-band width with decreasing particle size suggested that the d-band rehybridization occurred in these smaller NPs. (3) With decreasing particle size, the domain surface area, lattice distortion, vacancy spaces, and mean-square displacement increased and the coordination number decreased. These results can explain the hydrogen-storage capacity of the Rh NPs. (4) The hydrogen-storage capability of the Rh NPs increased to a greater extent with the mean-square displacement in the local structure than that in the mean crystal structure. (5) The volume fraction of the cavities inside the Rh NPs increased with decreasing particle size. The cavities can be induced by the increase of unoccupied sites in each unit cell and localized disordering. From the result of P_BOO, the effect on localized disordering at the surface part increased with a decrease in NP diameter. As a result, it is expected that the probability that hydrogen absorbed on the surface part of the Rh NPs increases with a decrease in NP diameter. It is hoped that these findings will be helpful in understanding the correlation between hydrogen-storage properties and electronic and crystal structure parameters in these new functional NPs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partly supported by ACCEL (JPMJAC1501) of the Japan Science and Technology Agency (JST). The HAXPES spectra were obtained at the NIMS synchrotron X-ray station of SPring-8 under Proposal No. 2013A4908. The HEXRD and XAFS measurements were carried out at SPring-8 with the approval of the Japan Synchrotron Radiation Institute under Proposal No. 2016A1292 and 2016B1033. This work was also partly supported by the Ministry of Education, Culture, Sports, Science and Technology of Japan (OS: 15K04616).

References

1. P. K. Capon, A. Burgun, C. J. Coghlan, R. S. Crees, C. J. Doonan and C. J. Sumby, CrystEngComm, 2016, 18, 7003–7010.
2. J. Goldsmith, A. G. Wong-Foy, M. J. Cafarella and D. J. Siegel, Chem. Mater., 2013, 25, 3373–3382.
3. Y. Liu, J. F. Eubank, A. J. Cairns, J. Eckert, V. C. Kravtsov, R. Luebke and M. Eddaoudi, Angew. Chem., Int. Ed., 2007, 46, 3278–3283.
4. Y. Xia, Z. Yang and Y. Zhu, J. Mater. Chem. A, 2013, 1, 9365–9381.
5. R. Ströbel, J. Garche, P. Moseley, L. Jörissen and G. Wolf, J. Power Sources, 2006, 159, 781–801.
6. M. M. Li, C. C. Yang, C. C. Wang, Z. Wen, Y. F. Zhu, M. Zhao, J. C. Li, W. T. Zheng, J. S. Lian and Q. Jiang, Sci. Rep., 2016, 6, 27601.
7. M. D. Ward, Science, 2003, 300, 1104–1105.
8. L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358.
9. F. A. Lewis, The Palladium Hydrogen System, Academic Press, London, 1967.
10. Hydrogen in Metals, ed. G. Alefeld and J. Völkl, Springer, Berlin, 1978.
11. S. K. Konda and A. Chen, Mater. Today, 2016, 19, 100–108.
12. H. Kobayashi, M. Yamauchi, H. Kitagawa, Y. Kubota, K. Kato and M. Takata, J. Am. Chem. Soc., 2008, 130, 1818–1819.
13. H. Kobayashi, M. Yamauchi, H. Kitagawa, Y. Kubota, K. Kato and M. Takata, J. Am. Chem. Soc., 2008, 130, 1828–1829.
14. H. Kobayashi, H. Morita, M. Yamauchi, R. Ikeda, H. Kitagawa, Y. Kubota, K. Kato and M. Takata, J. Am. Chem. Soc., 2011, 133, 11034–11037.
15. D. W. Goodman and C. H. F. Peden, J. Phys. Chem., 1986, 90, 4839–4843.
16. E. Bergene, O. Tronstad and A. Holmen, J. Catal., 1996, 160, 141–147.
17. A. Zaluska, L. Zaluski and J. Ström-Olsen, J. Alloys Compd., 1999, 288, 217–225.
18. R. Kubo, J. Phys. Soc. Jpn., 1962, 17, 975–986.
19. A. Henglein, Chem. Rev., 1989, 89, 1861–1873.
20. K. Kusada, H. Kobayashi, R. Ikeda, H. Morita and H. Kitagawa, Chem. Lett., 2013, 42, 55–56.
21. M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2–11.
22. H. S. Kim, M. Kang, M. W. Song, J. W. Park and B. R. Min, React. Kinet. Catal. Lett., 2004, 81, 251–257.
23. A. Yang, O. Sakata, K. Kusada, T. Yayama, H. Yoshikawa, T. Ishimoto, M. Koyama, H. Kobayashi and H. Kitagawa, Appl. Phys. Lett., 2014, 105, 153109.
24. K. Kobayashi, M. Yabashi, Y. Takata, T. Tokushima, S. Shin, K. Tamasaku, D. Miwa, T. Ishikawa, H. Nohira, T. Hattori, Y. Sugita, O. Nakatsuka, A. Sakai and S. Zaima, Appl. Phys. Lett., 2003, 83, 1005–1007.
25. K. Kobayashi, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601, 32–47.
26. N. Bedford, C. Dablemont, G. Viau, P. Chupas and V. Petkov, J. Phys. Chem. C, 2007, 111, 18214–18219.
27. C. Song, O. Sakata, L. S. R. Kumara, S. Kohara, A. Yang, K. Kusada, H. Kobayashi and H. Kitagawa, Sci. Rep., 2016, 6, 31400.
28. Y. F. Nishimura, T. Hamaguchi, S. Yamaguchi, H. Takagi, K. Dohmae, T. Nonaka and Y. Nagai, J. Phys.: Conf. Ser., 2016, 712, 012067.
29. V. V. Srabionyan, A. L. Bugaev, V. V. Pryadchenko, L. A. Avakyan, J. A. van Bokhoven and L. A. Bugaev, J. Phys. Chem. Solids, 2014, 75, 470–476.
30. Y. Oumellal, K. Provost, C. M. Ghimbeu, A. M. de Yuso and C. Zlotea, Nanotechnology, 2016, 27, 465401.
31. C.-M. Lin, T.-L. Hung, Y.-H. Huang, K.-T. Wu, M.-T. Tang, C.-H. Lee, C. T. Chen and Y. Y. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125426.
32. L. S. R. Kumara, O. Sakata, S. Kohara, A. Yang, C. Song, K. Kusada, H. Kobayashi and H. Kitagawa, Phys. Chem. Chem. Phys., 2016, 18, 30622–30629.
33. S. Tanuma, C. J. Powell and D. R. Penn, Surf. Interface Anal., 1988, 11, 577–589.
34. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
35. O. Gereben and V. Petkov, J. Phys.: Condens. Matter, 2013, 25, 454211.
36. D. A. Shirley, Phys. Rev. B: Solid State, 1972, 5, 4709–4714.
37. B. Hvolbak, T. V. Janssens, B. S. Clausen, H. Falsig, C. H. Christensen and J. K. Nørskov, Nano Today, 2007, 2, 14–18.
38. A. Tanaka, Y. Takeda, T. Nagasawa, H. Sasaki, Y. Kuriyama, S. Suzuki and S. Sato, Surf. Sci., 2003, 532–535, 281–286.
39. I. Konomi, S. Hyodo and T. Motohiro, J. Catal., 2000, 192, 11–17.
40. R. Griessen and A. Driessen, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 4372–4381.
41. B. Hammer and J. K. Nørskov, Nature, 1995, 376, 238.
42. B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129.
43. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
44. X. Zhong, B. Yang, X. Zhang, J. Jia and G. Yi, Particuology, 2012, 10, 365–370.
45. A. Gaber, M. A. Abdel-Rahim, A. Y. Abdel-Latief and M. N. Abdel-Salam, Int. J. Electrochem. Sci., 2014, 9, 81–95.
46. W. H. Qi, M. P. Wang and Y. C. Su, J. Mater. Sci. Lett., 2002, 21, 877–878.
47. W. H. Qi and M. P. Wang, J. Nanopart. Res., 2005, 7, 51–57.
48. E. Z. da Silva and A. Antonelli, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17057–17060.
49. R. Lamber, S. Wetjen and N. I. Jaeger, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10968–10971.
50. P. A. Montano, G. K. Shenoy, E. E. Alp, W. Schulze and J. Urban, Phys. Rev. Lett., 1986, 56, 2076–2079.
51. P. A. Montano, W. Schulze, B. Tesche, G. K. Shenoy and T. I. Morrison, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 672–677.
52. G. Apai, J. F. Hamilton, J. Stohr and A. Thompson, Phys. Rev. Lett., 1979, 43, 165–169.
53. R. W. James, The Optical Principles of the Diffraction of X-rays, Ox Bow Press, Woodbridge, Conn., 1962.
54. P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784–805.
55. O. Seo, O. Sakata, J. M. Kim, S. Hiroi, C. Song, L. S. R. Kumara, K. Ohara, S. Dekura, K. Kusada, H. Kobayashi and H. Kitagawa, Appl. Phys. Lett., 2017, 111, 253101.
56. W. Xiao and W. Geng, J. Nucl. Mater., 2012, 430, 132–136.
57. I. Heimbach, F. Rhiem, F. Beule, D. Knodt, J. Heinen and R. O. Jones, J. Comput. Chem., 2017, 38, 389–394.

---

Footnote

† Electronic supplementary information (ESI) available: Rietveld analysis, crystalline domain size, X-ray absorption fine structure (XAFS) spectra, particle size distributions of Rh NPs, reverse Monte Carlo (RMC) simulation, bond-orientational order (BOO) parameter, and hydrogen pressure–composition (PC) isotherms (Fig. S1–S6 and Table S1). See DOI: 10.1039/c8cp01678j

---