The excess electron at polyethylene interfaces

Abstract

This work investigates the energy and spatial properties of excess electrons in polyethylene in bulk phases and, for the first time, at amorphous vacuum interfaces using a pseudopotential single-electron method (Lanczos diagonalisation) and density functional theory (DFT). DFT calculations are made employing two approaches: with pseudopotentials/plane waves and the local-density approximation; and with all-electron Gaussian basis functions at the B3LYP level of theory, supplemented with a lattice of ghost atoms. All three methods predict similar spatial localisation of the excess electron, but a reliable comparison of its energy can only be made between the Lanczos and DFT using Gaussian bases. While Lanczos predicts that an excess electron would preferentially localise in nanovoids with diameters smaller than 1 nm, DFT suggests that it would localise on surfaces in nanovoids larger than 1 nm. Overall we conclude that in DFT studies of polyethylene/vacuum interfaces at the current level of theory, orbital-based methods provide a useful representation of excess electron properties.

---

I. Introduction

Electron trapping processes are central to energy transfer in nature¹ and to a wide range of technologies including photocatalysis,² photovoltaics,^3,4 organic thin film transistors, light-emitting diodes,⁵ radiation damage and repair,^6,7 and in DNA based molecular electronics,^8,9 and electrical insulation.¹⁰ In particular, electron trapping processes have been linked to dielectric breakdown in polymeric insulator shielding,¹¹ which is significant for high-voltage cables used for power transmission. Around 9% of the generated electricity is lost through transmission and distribution,¹² amounting to an estimated financial loss of 3 trillion U.S. dollars a year worldwide. In the light of these financial and technological challenges, the present work investigates the nature of interface trap states in polymeric materials¹³ and their representation in single and multi-electron models. Our focus is on polyethylene, chemically the simplest organic insulator which is used in a wide range of applications from home electric devices to high-voltage cables.¹⁴ Although dry low-density polyethylene has a very low electrical conductivity (10⁻¹⁶ S cm⁻¹),¹⁵ this material still traps electrons (and holes) that are injected through contact with the conductor, forming a space charge of excess electrons. The traps are gap states caused by physical¹⁶ and chemical disorder,¹⁷ including interfaces and impurities. On the one hand, the electrostatic forces arising from trapped electrons, are thought to lower the energy barriers to local conformational change producing microvoids,¹⁸ which eventually initiate the failure of polyethylene insulating materials through aging and dielectric breakdown.^11,19 On the other hand, the creation of new interfaces through the mixing of nanoparticles with polymers to produce nanocomposites has been reported to improve dielectric properties.²⁰ Therefore, we need a much better understanding of the behaviour of excess electrons at polyethylene interfaces to address key technological phenomena such as the aging and breakdown of insulators and nanodielectrics.

As a first step, this work studies the energy and localisation of excess electrons in polyethylene in bulk, and at interfaces with vacuum. These excess-electron properties have been calculated using Lanczos diagonalisation and single-electron semi-empirical pseudopotentials, which we refer to hereinafter as the ‘Lanczos method’. The Lanczos method has been used to study pure systems such as alkanes,^21,22 rare gases,^21,23 and water.²⁴ In previous work we have used this pseudopotential approach to predict the density of states for excess electrons in bulk polyethylene, including the mobility edge between delocalised states and those states representing electrons localised (trapped) at nanovoids in bulk polyethylene with radii of up to 0.4 nm.²⁵ The Lanczos polyethylene pseudopotential was fitted to experimental data for the energy of excess electrons in alkanes (from a difference in work functions of electrons in a metal in vacuum and the same metal in the alkane fluid,²⁶ so with respect to a zero of potential in vacuum away from the metal surface) and ab initio data.²² For materials with complex chemistries the Lanczos method is more difficult to apply since we would need a semi-empirical pseudopotential for each component. This limitation could be overcome by using, for example, all-electron density functional theory (DFT) methods. However, it is yet unclear how to determine excess-electron properties in DFT; an important question given importance of electron localisation physics,^27–29 chemistry,^30,31 and biology,³² and the focus of the present work.

In this work, we use DFT and Lanczos calculations to investigate the behaviour of excess electrons at vacuum interfaces of polyethylene. This behaviour is evaluated as function of polyethylene morphology (lamellar and amorphous) and the vacuum gap d. We then compare the results obtained from two DFT methods and to Lanczos’. The first uses the CRYSTAL14 code³³ at the B3LYP³⁴ level of theory and LCAO Gaussian basis sets (in what follows the LCAO basis is assumed to comprise Gaussian functions). The second uses Quantum Espresso³⁵ with Becke88 and Perdew86 for the exchange–correlation (LDA + BP) and a plane wave basis. This comparison of Lanczos and DFT approaches provides insight into the question of how best to represent the excess electron in DFT.

In previous work using DFT, two Kohn–Sham orbitals have been routinely chosen to represent the excess-electron states. The more common choice is the lowest-unoccupied molecular orbital (LUMO) of the neutral N-electron system,^36,37 which assumes that this orbital's energy is that of an electron added to a neutral N electron system. However, in principle at least, the LUMO in DFT is unsuitable to describe any polarisation effects exerted by an added electron. The second choice is the highest-occupied molecular orbital (HOMO) of the charged N + 1 system.³⁸ This HOMO contributes to the ground state total energy and is correlated with the other N electrons (see Discussion in ref. 31). The HOMO of the N + 1 electron system can be rigorously identified in exact DFT with the electron affinity (A) of the N-electron system (cf. Fig. 1 in ref. 31 and Discussion therein). We however employ a hybrid functional so that it remains to be seen to what extent the HOMO(N + 1) provides a good approximation to the true excess electron energy.

Our manuscript is organised as follows. In Section II, we briefly describe the methods employed to build the bulk and interfacial systems and the parameterisation of the DFT and Lanczos calculations (the full methodology is given in the ESI†). In Section III, we present the degree of localisation of excess electrons in lamellar systems and compare with previous studies. We next show the degree of localisation and energies for the bulk and interfacial systems of amorphous polyethylene. Finally, Section V concludes with our main findings and implications for future work.

II. Methodology

We study two models of bulk polyethylene: a bulk crystal (C) composed of 4 chains with 24 carbons bonded across the periodic boundaries, and an amorphous polyethylene (A) phase built with four rings of 20 (or 40) carbons each with no terminal methyl groups. These amorphous configurations are prepared with Materials Studio using the COMPASS2³⁹ force field with no periodic boundaries in the x direction to avoid splitting the chains when the vacuum is imposed. The cubic simulation cell has a length of 1.29 nm and a density⁴⁰ of 0.86 g cm⁻³. Our lamellar (L) polyethylene systems are composed of four chains with initially 20 carbon atoms in each one. Chains are folded in the x direction parallel to the surface normal vector of the yz plane by adding four methylene groups including across the periodic boundaries (see Fig. 1). The lateral dimensions of the systems are set to 0.986 and 0.74 nm in the y and z directions,⁴¹ respectively, with a length of 2.68 nm in the x direction. Surfaces are created by separating both folded faces with vacuum of thickness 0.1, 0.5, 1.0, 1.5, 2.0, and 3.0 nm. The geometry of all systems is optimised with the ab initio package CP2k⁴² in its QUICKSTEP⁴³ implementation.⁴⁴

Fig. 1 Molecular models of the polyethylene phases. Panels (a and b) show the four lamellar chains contained inside a black parallelepiped which represents the simulation cell with a vacuum gap of 1.0 nm in the x-direction. The chains are replicated above and below to illustrate the bonds across the periodic boundaries in the y direction. To build the lamellar chains we first place four chains of 20 carbons (–CH₂) inside the central cell. Then, we bond two neighbouring chains with four –CH₂– groups in the y-direction at each of the two chain endings. At the y axis periodic boundaries we also add two 4 –CH₂– groups to create a semi-infinite lamella. An equivalent bulk crystalline polyethylene system comprises four chains of 24 carbons as shown in panels (c and d) bonded across the periodic boundaries in the z direction.

The optimised configurations are then used as input for calculations with the codes Quantum Espresso and CRYSTAL14 which both use periodic boundary conditions. The Quantum Espresso plane-wave code uses local-density approximation (LDA) supplemented by Becke88 and Perdew86 for the exchange–correlation (LDA + BP). Plane-wave calculations are restricted to neutral systems due to the difficulty with convergence for charged interfaces.⁴⁵ CRYSTAL14 was used to perform all-electron calculations at the B3LYP theory level. This exchange–correlation functional has given excellent estimates of band gaps⁴⁶ and optical gaps⁴⁷ of extended systems. We use a standard 6-31G**^48,49 basis set to represent the local atomic orbitals as primitive Gaussian functions. The calculations are made for systems with N and N + 1 electrons (with background positive charge) using the same simulation cell parameters and nuclear configuration. The optimised configurations from CP2k are also used as an input to run the Lanczos method.²² Full details of our computational methodology are given in the ESI.† Representative configurations of these phases are shown in Fig. 1.

III. Results and discussion

We first calculate the electronic (fundamental) band gap for bulk polyethylene phases before reporting the effect of vacuum gaps in Fig. 2. For bulk crystalline polyethylene using CRYSTAL14 (B3LYP and Gaussian basis) we obtain a band gap of 8.79 eV. This value is in excellent agreement with the experimental result of 8.8 eV.^37,50 Other authors have also found good agreement with Gaussian basis sets. For example, in their study of all trans polyethylene with Gaussian sets and two local-density functionals, Miao et al.⁵¹ obtained band gaps of 7.7 eV with Gaspar–Kohn–Sham (GKS) and 8.0 with Perdew–Zunger (PZ). In contrast, the band gap in our crystalline polyethylene system decreases to 6.22 eV using LDA + BP and plane waves (PW) in the Quantum Espresso package. This value is in agreement with that of 6.46 eV reported by Serra and colleagues^36,52 who employed LDA (BP and BLYP) and plane waves. More recently, Chen et al.⁵³ obtained a gap of 6.9 eV using plane waves and the PBE functional in the VASP code. In addition to these crystalline values, in the present work we provide gaps for the lamellar and amorphous phases. Forming a lamellar phase lowers the CRYSTAL14 band gap slightly to 8.2 eV while an amorphous phase lowers it to 8.09 eV (and 7.56 eV with ghost atoms, see below). In conclusion, we find that the band gap in non-crystalline polyethylene; lamellar and amorphous, is reduced by 6.7% and 8.0% with respect to the pure crystalline structure.

Fig. 2 Electronic band gaps, calculated as the difference between the LUMO's and HOMO's of the N electron systems of lamellar (a) and amorphous (b) polyethylene without (red solid circles) and with (black triangles) ghost atoms. Ghost atoms separated by 0.185 nm as a function of the vacuum gap.

Creating free space above the polyethylene surface is similar to generating voids and defects in studies of semiconductors. Previous studies have found it necessary to use so-called ghost atoms in an augmented basis set to ensure that the electrons can penetrate this space to lower the total energy.^54–56 In our study we have added a lattice of ghost hydrogen atoms⁵⁷ throughout the simulation cell. These atoms represent points in space where the electronic orbitals are defined by Gaussian functions but have no electronic or nuclear charges. The construction of ghost-atom lattices is detailed in the ESI.†Fig. 2 shows that ghost atoms have a dramatic effect on the band gaps, lowering them by over an eV, and changing their variation with the slab separation. The band gap now falls with increasing slab separation rather than increasing. Clearly not using a basis augmented with ghost atoms restricts the excess electron in an unphysical way even for bulk amorphous polyethylene (see Fig. 3). The excellent agreement with the experimental band gap for the basis without ghost atoms must then be seen as fortuitous. We note in passing that an augmented basis is also required for fluid methane. In previous work⁵⁸ we showed that neither the LUMO(N) nor the HOMO(N + 1) DFT (CRYSTAL14) energy levels could represent the experimental methane excess electron energy as a function of density, except for the highest liquid density. However, using an augmented basis DFT gives good agreement with the experiment over a wide range of densities.⁵⁹ Introducing a lattice of ghost atoms requires a new parameter to be set: the distance d_g between ghost atoms. This approach is in contrast to using ghost atoms in vacancy calculations, where a real atom at a position r is replaced by a ghost atom. One method of choosing d_g would be to find the minimum in the total energy as a function of this distance. We find that the total energy decreases marginally (<0.001%) with d_g but that for d_g < 0.141 nm the code fails to converge, so total energy is not a useful function in this respect. However, the LUMO(N) and HOMO(N + 1) energies for the polyethylene/vacuum systems are relatively insensitive to d_g for d_g ≤ 0.185 nm (see Fig. 3). We therefore have some freedom in choosing this parameter and we choose d_g = 0.185 nm.

Fig. 3 Energies of the HOMO (a) of the charged N + 1 system and the LUMO (b) of the neutral N system of amorphous polyethylene in bulk (red dots) and with gaps of 2.0 nm (black triangles) and 4.0 nm (blue squares) as a function of the separation between ghost atoms.

In Fig. 4 we plot the excess electron density for a representative bulk amorphous polyethylene configuration using each method: Lanczos ground-state, PW LUMO(N), LCAO HOMO(N + 1), LCAO LUMO(N), LCAOG HOMO(N + 1), and LCAOG LUMO(N), where G signifies the augmented basis with ghosts. These images show that the LCAO method without ghost atoms misplaces the excess electron. All other DFT methods localise the electron in agreement with Lanczos. An analysis of the overlap of the excess electron wave function Ψ with the ground state Lanczos wave function Ψ_l, measured as the dot product 〈Ψ|Ψ_l〉 for five configurations (see Fig. S1, ESI†) indicates that the LCAO LUMO(N) and the PW LUMO(N) show the best agreement with averages of 〈Ψ|Ψ_l〉 = 0.65 and 0.67, respectively.

Fig. 4 Red isosurfaces where the excess electron sits in bulk amorphous polyethylene when using each method: Lanczos (a), plane waves (d), and LCAO (b and e), and LCAO with ghosts (c and f). The meshed isosurfaces show an excess electron density of 3.0 × 10⁻⁴ electrons per Bohr³. Yellow spheres in panels (c and f) represent the hydrogen ghost atoms (separated by 0.185 nm) in the polyethylene chains, which are painted in green for carbons and blue for hydrogens.

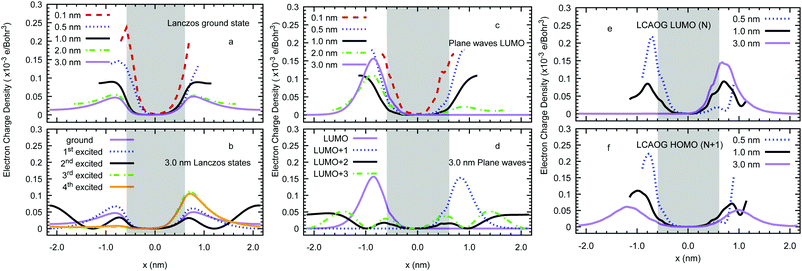
Fig. 5(a) illustrates the average profiles of the charge density of the excess electron for the vacuum gaps formed by lamellar surfaces from the single electron Lanczos calculation. The extra electron prefers to localise away from the slab (bulk-like) regions for all separations, showing a transition in its cross-sectional profile from small to larger separations. For separations larger than 2.0 nm the excess electron prefers to be located near the surface on the vacuum side with the wave function decaying exponentially towards the centre of the gap (normal to the surface). In the plane of the interface the charge density is delocalised. For slits smaller than 2.0 nm the charge density on opposing surfaces overlaps to give a parabolic profile across the gap. Note that the average profiles at d = 3.0 nm are asymmetric with respect to the origin of coordinates since the optimised geometry is not perfectly symmetric. In addition, Fig. 5(b) shows that the first three excited states localise near the interface for d = 3.0 nm, whereas the fourth excited state lies at the middle of the vacuum slab.

Fig. 5 Cross-sectional averages of the excess-electron charge density for lamellar polyethylene slabs (grey) with vacuum gaps of 0.1, 0.5, 1.0, 2.0, and 3.0 nm. Panel (a) shows the ground-state level of excess electron from the Lanczos method and panel (b) the four consecutive excited states at 3.0 nm. Panel (c) illustrates the LUMO calculated with DFT using plane waves and LDA + BP of the N system (c) and panel (d) the four first LUMOs at 3.0 nm.

Fig. 5(c) illustrates the average profiles of the plane wave LUMO(N) charge density for the neutral lamellar surfaces separated by d = 0.1, 0.5, 1.0, 2.0, and 3.0 nm. These profiles are very similar to those from Lanczos shown in Fig. 5(a) and (b), except the electron density peaks further away from the surface (around 0.5 nm at d = 3 nm). A significant difference is detected at d = 3.0 nm, where LUMO+2 and LUMO+3 are observed to form states extended throughout the vacuum, as shown by Fig. 5(d). Our LUMO+3 disagrees with that predicted by Righi et al.³⁶ since theirs resembles the conduction band of bulk lamellar polyethylene with the electron density residing in the bulk phase.

Fig. 6(a) shows that for amorphous polyethylene the excess electron (from Lanczos) forms a surface state in a similar fashion to the lamellar phase at d = 3.0 nm. We have 65.3% of the excess electron in a region between 0.2 nm inside each surface and 0.7 nm into the vacuum, the peak in the electron density is at 0.2 nm above the polyethylene surface. In contrast to the lamellar phase, it is now the second excited state that is extended into the vacuum as shown in Fig. 6(b). Fig. 6(c) presents the cross-sectional averages of the LUMO of neutral systems calculated with plane waves. Despite the change in the surface morphology from lamellar to amorphous and the increase of the cross sectional area of the simulation cell from 0.729 (= 0.986 × 0.740) nm² in the former to 1.674 (= 1.294 × 1.294) nm² in the latter, the charge densities look similar with a small fraction inside the slab as d increases. The only qualitative difference is the complete loss of symmetry of the LUMO at 3.0 nm. However, looking at the LUMO+1, this state is only 0.03 eV more positive in energy (i.e. of the order of k_BT, where k_B is the Boltzmann's constant) and it is likely they both represent the same state, restoring the symmetry. Fig. 6(e and f) compares the cross-sectional averages, from CRYSTAL14 with ghost atoms, of the electron density of LCAOG LUMO(N) and HOMO(N + 1) for the amorphous surfaces at the B3LYP level of theory. The density of the LUMO(N) peaks around 0.2 nm above the interface for a gap of 3 nm in agreement with Lanczos and plane wave DFT while for the HOMO(N + 1) the peak is further out at 0.5 nm or more above the interface. The decay of the excess electron density into the vacuum is exponential for Lanczos and DFT^60,61 (see Fig. S2, ESI†) yielding localisation lengths l_loc for the 4 nm vacuum gap of 0.24 nm for Lanczos, 0.31 nm for the PW LUMO(N), 0.31 nm for LCAOG LUMO(N), and 0.14 nm for the LCAOG HOMO(N + 1). We note that while the excess electron is delocalised in the directions parallel to the interface in our semi-infinite flat periodic surface model, in a real material the electron may well localise in y and z as well due to irregularities or the finite size of the surface.

Fig. 6 Cross-sectional averages of the excess-electron charge density in amorphous polyethylene slabs of the ground and excited states of the Lanczos method (a and b), the LUMO(N) of DFT using plane waves and LDA + BP (c and d) for vacuum gaps between 0.1 and 3.0 nm, and the LUMO(N) (e) and HOMO(N + 1) (f) using DFT with LCAOG basis functions and B3LYP with gaps of 0.5, 1.0, and 3.0 nm with ghost atoms separated by 0.185 nm.

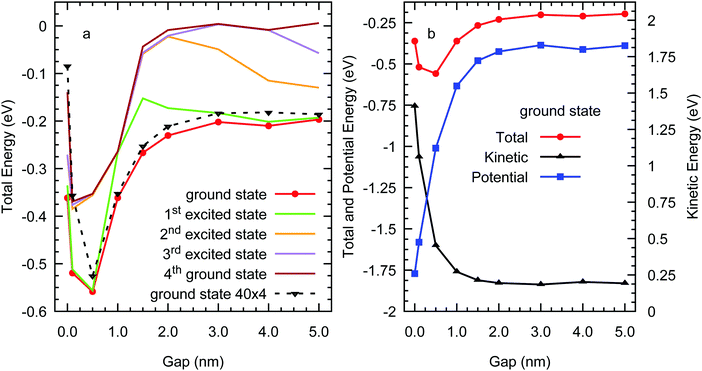
We now focus on the variation of the kinetic, potential, and total energies of the excess electron in amorphous polyethylene with the vacuum gap d calculated using the Lanczos method, as illustrated in Fig. 7. In the bulk material the excess electron energy is −0.37 eV, agreeing with the much larger systems of bulk polyethylene studied in our previous work,²⁵ dropping as we add vacuum to a minimum of −0.53 eV at d = 0.5 nm and then increasing to plateau at around −0.2 eV for d > 2.0 nm. This implies that an excess electron would prefer to localise in the bulk phase or a small planar void, rather than in a vacuum gap wider than 1.0 nm. For the larger system of four chains with 40 carbons each, Fig. 7(a) shows that the excess electron energy is more negative for surface states than in the bulk with a value of −0.09 eV at d = 0 nm. The excess electron energies of the two systems are in good agreement except for the bulk where there are clearly system size effects which is to be expected as we have shown previously that the electron trapping is in naturally occurring nanovoids whose distribution will depend on system size and nanostructure. The minimum in the excess electron energy for planar vacuum gaps between 0.1 and 1.0 nm is also consistent with our previous study of the excess electron energy of spherical nanovoids in bulk polyethylene, although the energy of the planar gaps falls off more rapidly with d. The behaviour of the kinetic and potential energies, which plateau rapidly as the gap increases as expected as the excess-electron charge density is localised at the polyethylene surfaces on the vacuum side. The excess electron is not present away from the surface and hence, the kinetic energy is not a decaying function of ∼d², which would be the case if the wave function was extended throughout the vacuum, whilst the potential energy becomes much more positive with increasing d as the localised electron interacts only with the closest surface. To summarise, the Lanczos method implies that an excess electron in polyethylene containing nanovoids either formed naturally in the amorphous phase or due to cracks or other imperfections that are nanoscale in at least one dimension, would localise preferentially in spaces with gaps less than 1.0 nm either as a surface state (localised normal to the plane) on a planar surface or inside a nanovoid localised in three dimensions.

Fig. 7 Lanczos ground-state energies of the excess electron and the four excited states for amorphous polyethylene (a) four chains with 20 carbons except as noted, and (b) ground-state kinetic and potential energy components.

Fig. 8 shows the energy of the LUMO(N), LCAOG excess electron compared to the Lanczos ground state in amorphous polyethylene. In order to make a meaningful comparison with Lanczos and with DFT data for different vacuum gaps, the LUMO(N) energies must be corrected to a common energy scale. We make this correction with respect to the zero of the electrostatic potential at the centre of the vacuum gaps, as it has been done previously in metal–organic frameworks (MOF).⁶² The average Hartree potential at the centre of the vacuum is observed to approach a negligible value, both for LUMO(N) and HOMO(N + 1) LCAOG, as shown in Fig. S3 (ESI†). In the case of the HOMO(N + 1) the decay takes place further from the polyethylene slab, which is expected given that the Hartree potential in this case includes the contribution due to the excess electron. This implies that the electrostatic potential drop at the polyethylene surfaces is negligible, in full agreement with our DFT calculations reported in ref. 22 and with simple electrostatic considerations: there should be no dipole correction at all as long as the molecules are not drastically truncated at the surfaces, since the atoms that make up polyethylene have no permanent dipoles. In contrast to the Lanczos data, using the LUMO(N) energy as an approximation to the excess-electron energy E_ee, implies that an excess electron would prefer to localise in vacuum gaps d ≥ 1 nm, rather than in smaller gaps. The LUMO(N) energy is small and positive for d < 0.2 nm where Lanczos is small and negative. Nonetheless, there is excellent agreement between the two approaches for d ≥ 2 nm with E_ee = −0.2 eV within the accuracy of both calculations. The HOMO(N + 1) energies, agree very well with Lanczos for small gaps, but are around 0.5 eV more negative for large gaps. If we take the HOMO(N + 1) as representative of the excess electron then there is a slight preference for localisation in gaps in the range 1 to 2 nm. For the plane-wave data. The Hartree potential shows huge variation across the vacuum gaps and we cannot correct it to a zero of potential. Previous work using this approach has reported energy differences between energy levels, not absolute values.³⁶ Nevertheless the data are shown as a dotted line in Fig. 8, falling as approximately 1/d.

Fig. 8 DFT predictions of the excess electron energy: LUMO(N), HOMO (N + 1) vs. vacuum gap thickness in amorphous polyethylene using B3LYP with ghost atoms separated by 0.185 nm, corrected to the vacuum level compared to Lanczos ground-state energies. The LUMO(N) with plane waves is also shown uncorrected to vacuum level.

IV. Conclusion

We have compared various DFT methods of estimating the properties of an excess electron with data from the single electron pseudopotential approach using Lanczos diagonalisation. All methods localise the excess electron similarly (with an extended basis for CRYSTAL14) with more of less equivalent localisation sites and localisation lengths. Only the LUMO(N) and HOMO(N + 1) obtained from CRYSTAL14 can be corrected to a reference zero potential energy at infinity. The plane wave method used here employs core pseudopotentials which make it impossible to calculate the average Hartree potential reliably however higher order methods employed with plane waves such as GW (see for example⁶³) may give more reliable predictions.

Although the Lanczos method predicts a minimum in the excess electron energy for vacuum gaps between 0.1 and 1.0 nm at around −0.6 eV, DFT suggests that the excess electron would prefer to localise on surfaces with vacuum gaps larger than 1 nm. Both LUMO(N) and Lanczos agree that the energy of an excess electron in planar vacuum gaps larger than 2 nm is around −0.2 eV. The HOMO(N + 1) energies differ from those of the LUMO(N) and the ground state of Lanczos by a shift of nearly 0.5 eV for larger gaps. On the other hand, LUMO(N) energy differs from Lanczos and HOMO(N) for bulk polyethylene by a similar amount. While the differences between the two approaches are significant at this level of theory, the current work has not considered polaronic effects that could distort the local nuclear configuration and change the energy of excess electrons in the vacuum gaps. We note though that for the bulk polyethylene system the effect on localisation energies has been found to be small⁶⁴ of less than 0.1 eV. In Fig. 8, it can be seen that the Lanczos energies lie within the predictions of both methods.

Overall, the similarity between the LUMO(N) with the HOMO(N + 1) orbitals using a Gaussian basis with ghosts atoms and their agreement with Lanczos are encouraging and we conclude that in DFT studies of polyethylene/vacuum interfaces at the current level of theory, these orbital-based methods provide a useful representation of excess electron properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support of EPSRC through grant EP/N002288/1, Advanced Polymer Material for Energy Security, POLYMAT and HPC support through ARCHER project e446. D. C. acknowledges financial support from the Ministerio de Economía y Competitividad of Spain, Grant No. FIS2016-80244-P.

References

1. P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168.
2. M. A. Henderson, J. M. White, H. Uetsuka and H. Onishi, J. Am. Chem. Soc., 2003, 125, 14974–14975.
3. C. J. Lombardo, M. S. Glaz, Z. E. Ooi, D. A. Vanden Bout and A. Dodabalapur, Phys. Chem. Chem. Phys., 2012, 14, 13199–13203.
4. C. Groves, J. C. Blakesley and N. C. Greenham, Nano Lett., 2010, 10, 1063–1069.
5. L. G. Kaake, P. F. Barbara and X. Y. Zhu, J. Phys. Chem. Lett., 2010, 1, 628–635.
6. B. L. Mahaney and K. Meek, J. Biochem., 2009, 417, 639–650.
7. Z. G. Yu and X. Song, Phys. Rev. Lett., 2001, 86, 6018–6021.
8. Y. Okahata, T. Kobayashi, K. Tanaka and M. Shimomura, J. Am. Chem. Soc., 1998, 120, 6165–6166.
9. R. Rinaldi, E. Branca, R. Cingolani, R. Di Felice, A. Calzolari, E. Molinari, S. Masiero, G. Spada, G. Gottarelli and A. Garbesi, Ann. N. Y. Acad. Sci., 2002, 960, 184–192.
10. I. L. Hosier, A. S. Vaughan and S. G. Swingler, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 2309–2322.
11. L. A. Dissado and J. C. Fothergill, Electrical Degradation and Breakdown in Polymers, P. Peregrinus, London, 1992.
12. According to the International Electrotechnical Commission: http://www.iec.ch/ (accessed February 2018).
13. H. T. Nicolai, M. Kuik, G. A. H. Wetzelaer, B. de Boer, C. Campbell, C. Risko, J. L. Brédas and P. W. M. Blom, Nat. Mater., 2012, 11, 882–887.
14. The first polyethylene insulated cable was a mile of submarine cable between the Isle of Wight and the mainland of England installed by Dean's company in 1938, see J. A. Allen, Studies in Innovation in the Steel and Chemical Industries, Manchester University Press, Manchester, 1967.
15. S. Virtanen, A. S. Vaughan, L. Yang, F. Saiz and N. Quirke, Dielectric Breakdown Strength and Electrical Conductivity of Low Density Polyethylene Octyl-nanosilica Composite, Proceedings of the 2016 Conference on Electrical Insulation and Dielectric Phenomenon, IEEE, 2016, pp. 58–61.
16. M. Meunier and N. Quirke, J. Chem. Phys., 2000, 113, 369–376.
17. M. Meunier, A. Aslanides and N. Quirke, J. Chem. Phys., 2001, 115, 2876–2881.
18. G. Dlubek, T. Lupke, H. M. Fretwell, M. A. Alam, A. Wutzler and H. J. Radusch, Acta Polym., 1998, 49, 236–243; G. Dlubek, K. Saarinen and H. M. Fretwell, J. Polym. Sci., Part B: Polym. Phys., 1998, 36, 1513–1528.
19. A. Toureille, Rev. Gen. Electr., 1991, 8, 15–20.
20. D. Ma, T. A. Hugener, R. W. Siegel, A. Christerson, E. Mårtensson, C. Önneby and L. S. Schadler, Nanotechnology, 2005, 16, 724–731.
21. B. Space, D. F. Coker, Z. H. Lui, B. J. Berne and G. Martyna, J. Chem. Phys., 1992, 97, 2002–2021.
22. D. Cubero, N. Quirke and D. F. Coker, J. Chem. Phys., 2003, 119, 2669–2679.
23. Z. Liu and B. J. Berne, J. Chem. Phys., 1993, 99, 9054–9069.
24. I. A. Shkrob, W. J. Glover, R. E. Larsen and B. J. Schwartz, J. Phys. Chem. A, 2007, 111, 5232–5243.
25. Y. Wang, D. MacKernan, D. Cubero, D. Coker and N. Quirke, J. Chem. Phys., 2014, 140, 154902.
26. R. Reininger, U. Asaf, I. T. Steinberger and S. Basak, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 4426–4432.
27. F. M. Izrailev and N. M. Makarov, Phys. Rev. Lett., 2009, 102, 203901.
28. S. Selcuk and A. Selloni, Nat. Mater., 2016, 15, 1107–1112.
29. F. Baletto, C. Cavazzoni and S. Scandolo, Phys. Rev. Lett., 2005, 95, 176801.
30. C. E. Ekuma, V. Dobrosavljević and D. Gunlycke, Phys. Rev. Lett., 2009, 118, 106404.
31. E. J. Baerends, O. V. Gritsenko and R. van Meer, Phys. Chem. Chem. Phys., 2013, 15, 16408–16425 . Note the state labelled LUMO(M−), the LUMO of the neutral system M modified by the addition of an excess electron corresponds to the HOMO(N + 1) in this work.
32. A. A. Krokhin, V. M. K. Bagci, F. M. Izrailev, O. V. Usatenko and V. A. Yampol'skii, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085420.
33. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D’Arco, Y. Noel, M. Causa, M. Rerat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317.
34. T. P. M. Goumans and R. A. Catlow, Phys. Chem. Chem. Phys., 2007, 9, 2146–2152.
35. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. Fabris, G. Fratesi, S. de Gironcoli, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
36. C. M. Righi, S. Serra, E. Tosatti, S. Scandolo and G. Santoro, Phys. Rev. Lett., 2001, 87, 076802.
37. M. Unge, T. Christen and C. Törnkvist, Electronic structure of polyethylene – -crystalline and amorphous phases of pure polyethylene and their interfaces, Annual Report Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), IEEE, 2012, pp. 525–530.
38. S. Serra, S. Iarlori, E. Tosatti, S. Scandolo, M. C. Righi and G. E. Santoro, Chem. Phys. Lett., 2002, 360, 487–493.
39. H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364.
40. To match the value used in ref. 26 for amorphous low-density polyethylene. The experimental material is a mixture of different morphologies with different local densities.
41. Taken from the values of orthorhombic unit cells of long-alkane chains found with X-ray diffraction. See C. W. Bunn, Trans. Faraday Soc., 1939, 35, 482–491.
42. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Comput. Mol. Biosci., 2014, 4, 15–25.
43. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
44. See ESI† for details.
45. See for example discussion on plane wave forum http://www.mail-archive.com/pw_forum@pwscf.org/ (accessed January 2018).
46. J. Muscat, A. Wander and N. M. Harrison, Chem. Phys. Lett., 2001, 342, 397–401.
47. L. Bernasconi, S. Tomic, M. Ferrero, M. Rerat, R. Orlando, R. Dovesi and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195325.
48. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218.
49. G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090.
50. K. J. Less and E. G. Wilson, J. Phys. C: Solid State Phys., 1973, 6, 3110–3120.
51. M. S. Miao, P. E. Van Camp, V. E. Van Doren, J. J. Ladik and J. W. Mintmire, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 10430–10435.
52. S. Serra, S. Iarlori, E. Tosatti, S. Scandolo and G. Santoro, Chem. Phys. Lett., 2000, 331, 339–345 . See also D. Ceresoli, M. C. Righi, E. Tosatti, S. Scandolo, G. Santoro and S. Serra, J. Phys.: Condens. Matter, 2005, 17, 4621.
53. L. Chen, T. D. Huan and R. Ramprasad, Sci. Rep., 2017, 7, 6128.
54. M. De La Pierre, P. Karamanis, J. Baima, R. Orlando, C. Pouchan and R. Dovesi, J. Phys. Chem. C, 2013, 117, 2222–2229.
55. R. A. Evarestov, A. V. Bandura, M. V. Losev, E. A. Kotomin, Yu F. Zhukovskii and D. Bocharov, J. Comput. Chem., 2008, 29, 2079–2087.
56. A. D. Yau, E. F. C. Byrd and B. M. Rice, J. Phys. Chem. A, 2009, 113, 6166–6171.
57. For further discussions on the application of ghost atoms, the reader is referred to T. Clark, A handbook of computational chemistry, Wiley, New York, 1995, pp. 289–301; F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1886; S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031.
58. F. Saiz, N. Quirke, L. Bernasconi and D. Cubero, Chem. Phys. Lett., 2016, 664, 143–148.
59. F. Saiz and N. Quirke, Unpublished.
60. P. W. Anderson, Phys. Rev., 1958, 109, 1492–1505.
61. J. J. Ludlam, S. N. Taraskin, S. R. Elliott and D. A. Drabold, J. Phys.: Condens. Matter, 2005, 17, L321–L327.
62. K. T. Butler, C. H. Hendon and A. Walsh, J. Am. Chem. Soc., 2014, 136, 2703–2706.
63. L. Chen, T. D. Huan, Y. Cardona Quintero and R. Ramprasad, J. Mater. Sci., 2016, 51, 506–512.
64. D. Cubero and N. Quirke, J. Chem. Phys., 2004, 120, 7772–7778.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp01330f

---