Modeling gas-diffusion electrodes for CO2 reduction†
Received
28th February 2018
, Accepted 4th June 2018
First published on 4th June 2018
Abstract
CO2 reduction conducted in electrochemical cells with planar electrodes immersed in an aqueous electrolyte is severely limited by mass transport across the hydrodynamic boundary layer. This limitation can be minimized by use of vapor-fed, gas-diffusion electrodes (GDEs), enabling current densities that are almost two orders of magnitude greater at the same applied cathode overpotential than what is achievable with planar electrodes in an aqueous electrolyte. The addition of porous cathode layers, however, introduces a number of parameters that need to be tuned in order to optimize the performance of the GDE cell. In this work, we develop a multiphysics model for gas diffusion electrodes for CO2 reduction and used it to investigate the interplay between species transport and electrochemical reaction kinetics. The model demonstrates how the local environment near the catalyst layer, which is a function of the operating conditions, affects cell performance. We also examine the effects of catalyst layer hydrophobicity, loading, porosity, and electrolyte flowrate to help guide experimental design of vapor-fed CO2 reduction cells.
Introduction
A great deal of interest has arisen in the design and development of solar-fuel generators for carrying out electrochemical CO2 reduction (CO2R), as this process offers a potential route for the storage of solar energy into chemical bonds. Depending on the choice of catalyst, CO2 can be reduced to products such as CO, CH4, C2H4, etc. Most of what is known about CO2R is based on experiments conducted with planar electrodes immersed in an aqueous electrolyte saturated with CO2.1–4 However, the current density of such systems is limited significantly by poor mass transport to the cathode due to the low diffusivity and solubility of CO2 in water and the thickness of the mass-transfer boundary layers near the electrode that are typically 60 to 160 μm.5–7 As a consequence, the mass-transfer limited current density based on the geometric area of the cathode is on the order of 10 mA cm−2. Another factor limiting CO2 availability in aqueous systems is the acid/base reaction of CO2 with hydroxide ions (OH−), which results in an even lower limiting current density than that approximated by Fick's law.8 A recent analysis has shown that for CO2R systems to be economically feasible, it is necessary to improve the current density by at least one order of magnitude.9 One of the promising approaches for achieving this target is to use vapor-fed cells with gas-diffusion electrodes (GDEs). In such systems, current densities up to 360 mA cm−2 for CO2R have been demonstrated.10–15
The porous electrodes in GDE systems have a number of design parameters that can be tuned to optimize the performance of the system. As shown in Fig. 1, the GDE is comprised of a porous catalyst layer (CL) and a diffusion medium (DM). The DM is typically a hydrophobic carbon layer that consists of a macroporous gas-diffusion layer (GDL) and a microporous layer (MPL). The DM serves several purposes. First, it provides a porous medium through which CO2 can diffuse to the CL; second, it mechanically supports the CL; and third, it provides electronic conductivity for electrons to flow from the current collector and external circuit to the CL. Most commercial DMs are PTFE treated to be hydrophobic; ideally, the DM remains dry throughout its use (no electrolyte leakage or condensation). Catalyst particles mixed with a (ionic) binder are deposited onto the MPL to form the CL. The binder holds the catalyst particles together and may provide ionic conductivity within the CL.
 |
| | Fig. 1 Schematic of a gas diffusion electrode. | |
The exact microstructure of the CL is not well known. Cook et al. first proposed a schematic illustrating a “triple-phase interface” region where the CO2R reaction occurs, and many have argued that the high current densities achievable with GDEs is attributable to a high concentration of CO2 at the gas/solid interface, thereby overcoming the low solubility of CO2 in water.16 However, the hypothesis that a triple-phase interface is essential for the high performance of a GDE is probably not correct for two reasons: (1) At NTP (20 °C and 1 atm), the gas-phase concentration of CO2 is 42 mM. This level is only 30% higher than that of dissolved CO2 (33 mM) and cannot account for the order of magnitude increase in CO2R current density observed experimentally. (2) Recent experimental and theoretical work have demonstrated the importance of water and hydrated cations on the elementary processes involved in CO2R.17,18 Therefore, we propose that it is necessary for the catalyst to be covered with electrolyte in order to be active. This means that although CO2 is supplied to the GDE from the gas phase, the reactant at the catalyst site is still dissolved CO2.
The performance of a GDE greatly depends on the local environment within the CL and the balance between transport phenomena and reaction kinetics. Based on the capillary pressure, CL pore-size distribution and their wettability, the pores can be either flooded (Fig. 2a) or dry (Fig. 2c). The partially wetted CL case depicted in Fig. 2b occurs when there is a mixture of flooded and dry pores. Flooded pores completely eliminate gas channels within the CL, resulting in high mass-transport resistances for gaseous reactants. Dry pores will be inactive due to the lack of aqueous electrolyte and an ionic pathway. The film of electrolyte in the wetted pores needs to be thin to minimize CO2 transport resistance to the catalyst, but thick enough to maintain good ionic conductivity within the CL. The fraction of flooded pores is defined as the saturation, S, and is a function of the capillary-pressure, which is the difference between the liquid- and gas-phase pressures.19 At low capillary pressures, only small hydrophilic pores will be flooded. As the capillary pressure increases, other pores become flooded in the following order: large hydrophilic pores, large hydrophobic pores, and eventually small hydrophobic pores. Therefore, to control CL wetting, one needs to adjust the pore-size distribution or the wettability of the CL pores.
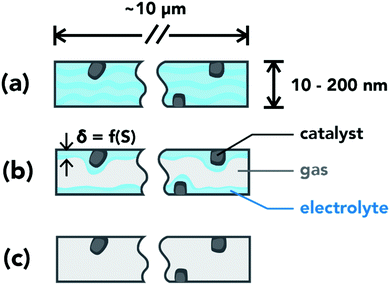 |
| | Fig. 2 Schematic of pore conditions in the catalyst layer. (a) Flooded pore: pore volume filled with electrolyte. (b) Wetted pore: a thin layer of electrolyte covers the pore walls. (c) Dry pore: catalyst inactive due to lack of an ionic pathway. | |
Because the structure of GDEs is complex and CO2R in such systems involves the simultaneous occurrence of many physical processes, it is very hard, if not impossible, to assess the impact of a particular change in the composition and structure of the CL without a detailed model that accounts for the complex chemistry and physics interrelationships. Attempts to optimize GDE performance experimentally have been devoted, for the most part, to Sn electrodes used to produce formic acid. Wu et al. have found that increasing the CL thickness beyond 9 μm had no effect on the overall activity; however, the reason for this behaviour was not given.20 Both Wu et al. and Wang et al. have shown that changing the CL composition can affect the total current density and faradaic efficiency (FE) of a Sn GDE.20,21 Other parameters such as catalyst morphology, fabrication methods, etc. have also been studied experimentally and a detailed survey of different GDE systems has been reported by Endrodi et al.22 While there have been numerous experimental designs of GDEs, there have been only a limited number of efforts on the modeling of vapor-fed CO2R systems. In terms of modeling, Delacourt et al. presented a model for a vapor-fed cell with an aqueous buffer layer between the cathode and the membrane.23 They assumed that dissolved CO2 is in equilibrium with bicarbonate and carbonate ions and these are the main reactants, assumptions that have later been shown not to be valid in regions near the catalyst.8 They also considered the CL as an interface rather than a domain of finite thickness. More recently, Wu et al. developed a comprehensive model for a microfluidic flow cell with GDEs.24 While they considered a finite thickness for the CL, they neglected bicarbonate acid/base reactions occurring within this region and focused on the overall cell performance rather than the influence of the composition and structure of the CL and how these factors govern the overall cell performance.
The objective of this work is to develop a comprehensive model for a GDE with particular attention devoted to capturing the details of physical and chemical processes occurring in the CL. To this end, we consider the GDE design most commonly used for CO2R that has been implemented in a cell with continuous electrolyte supply (Fig. 1).12–15 We chose Ag as the catalyst because it produces only two gaseous products, H2 and CO, with > 90% FE to CO.1,15 Our model focuses on the CL region and investigates how the local environments in the CL, such as the distributions of CO2, OH−, and water change with varying operating conditions and CL properties. We describe quantitatively the advantages of GDEs over planar electrodes, and compare the three CL cases: a flooded CL (flooded case), a uniformly wetted CL (ideally wetted case), and a CL described by the saturation curve (saturation curve case). Finally, we explore the effects of varying GDE design parameters (hydrophilicity, loading, and porosity) and operating conditions (electrode potential and electrolyte flowrate).
Theory
Physical model
The one-dimensional, macro-homogeneous model assumes isothermal, steady-state conditions. The model does not account for the anisotropy of GDEs, for which a higher-dimensional model is needed. The higher-dimensional aspects of transport in GDLs are not expected to impact the results significantly since the in-plane diffusion is faster than the through-plane diffusion and the transport through the GDL is only vapor phase and not limiting.25,26 The CL is assumed to consist of spherical nanoparticles of Ag with radius rnp that are loosely packed and bound by a binder and have intrinsic porosity εoCL (the solid volume fraction is (1 − εoCL)). The liquid and gas volume fractions are εoCLS and εoCL(1 − S), respectively. For the flooded case, only solid and liquid phases exist in the CL domain.
For the ideally wetted and saturation curve cases, the amount of liquid in the CL is determined by the CL saturation (S is assumed constant for the ideally wetted case). The saturation vs. capillary–pressure relationship (saturation curve) measured for a fuel-cell CL is used due to the expected similarities with that of the CL in a GDE.27 Although empirical in this work, the saturation curve can be related theoretically to structural properties such as the pore-size distribution.28 However, it is important to note that the saturation curve will change depending on the composition of the CL, and the method used to produce the CL. When describing CL wettability, the saturation curve was shifted up (down) by 0.1 unit saturation for a more hydrophilic (hydrophobic) CL. This assumes that the CL pore-size distribution remains unchanged, but the fraction of hydrophilic pores is increased (decreased) by 0.1 unit. An equivalent thin-film thickness, δTF,eq, is derived from geometric arguments based on the CL saturation by evenly distributing the electrolyte throughout the CL,
| |  | (1) |
where
rp,CL is the mean CL pore radius.
For the ideally wetted CL case, a uniform 10 nm thick electrolyte thin film is assumed. This thickness corresponds to the CL saturation at zero capillary pressure (S = 0.64), and is representative of the electrolyte thin-film thickness observed in fuel-cell CLs.29 While a distribution of the thin-film thickness δTF may be more accurate, it has been shown in fuel-cell models that the difference between using δTF,eq and δTF is insignificant, especially within the kinetically controlled regime.30 The DM is assumed to be completely dry (S = 0), with solid volume fraction, 1 − εoDM, and gas volume fraction, εoDM. Fig. 3 shows the two modeling domains, CL and DM, of the model. The DM consists of only solid and gas phases, as it is assumed to be completely dry. If flooded, the CL consists of only solid and liquid phases (hatched portion is liquid in this case); otherwise, all solid, liquid and gas phases exist in the CL for the wetted case (hatched portion is gas phase in this case).
 |
| | Fig. 3 Graphical illustration (not to scale) of the modeling domains and different phases within the CL and DM. Hatched portion in the CL domain will be either liquid phase (L) for the flooded case, or gas phase (G) for the ideally wetted and saturation curve cases. Solid phase (S) consists of Ag nanoparticles in the CL and carbon substrate in the DM. The volume fractions for the three phases in the CL is labelled to the left of the graph. | |
The gas phase contains CO2, H2, and CO. An almost 100% CO2 feed condition is assumed for all simulations (trace quantities of the other species are included for numerical stability and do not impact the results). The bulk electrolyte is 0.5 M KHCO3 and is assumed to flow parallel to the CL surface. The electrolyte contains six species: dissolved CO2, K+, H+, OH−, HCO3−, and CO32−. Dissolved CO and H2 are neglected in the model since they have limited solubility.31 Dilute-solution theory is used for liquid-phase species, and the water concentration is assumed to be constant. This assumption may break down at high current densities, for which local concentrations within the CL become substantial, as will be shown below. We note that concentrated-solution theory requires additional diffusion coefficients that are not readily available, and the general trends obtained using dilute-solution theory are not expected to change significantly with the corrected parameters. Bubbling induced convection of liquid electrolyte inside the pores of the CL is neglected considering the small capacity and thickness of the distributed electrolyte thin films, and large amounts of reaction area and nucleation sites. Although a simplification, this assumption should not significantly impact the mass-transport effects within the porous electrode.
Two charge transfer reactions occur in the CL, CO2R, which is assumed to be only CO evolution reaction (COER),15
| | | CO2(aq) + H2O + 2e− → CO + 2OH− | (2) |
and H
2 evolution reaction (HER) in acidic and basic environments,
| | | 2H2O + 2e− → H2 + 2OH− | (4) |
A first-order dependence on CO2 concentration for COER is assumed, considering that the first electron transfer to CO2 molecule (CO2 + e− → CO2˙−) is the rate-limiting step (RLS).32,33 HER undergoes different mechanisms in acidic and basic environments. For acidic HER, a first-order dependence on proton concentration is assumed. This assumption is valid when either the Heyrovsky step or the Volmer step is the RLS, which is more likely than the Tafel step as it is a chemical step (as opposed to an electron transfer step).34 Tafel kinetics are assumed to simulate conditions away from equilibrium. Gaseous CO2 dissolves in the electrolyte at a rate estimated using Fick's law. Acid/base carbonate and water-dissociation reactions occur in the electrolyte and are treated as kinetic expressions (i.e., equilibrium is not assumed).
| |  | (5) |
Governing equations
The mass balance for each species within the CL and the DM can be written as| | | ∇·ni = RCT,i + RB,i + RPT,i | (6) |
where ni is the mass flux, RCT,i, RB,i and RPT,i are the volumetric charge-transfer reactions, homogeneous bulk reactions, and phase-transfer source terms, respectively. RCT,i and RPT,i apply to both gas- and liquid-phase species, while RB,i only applies to liquid-phase species.
Gas-phase transport
The gaseous species flux consists of a diffusive term and a convective term,where ji is the diffusive mass flux of species i, ρi is the mass density of species i, and ug is the mass-averaged fluid velocity. The diffusive flux is calculated using a mixture averaged diffusion model,35| |  | (8) |
where ωi is the mass fraction of species i, ρg is the gaseous mixture density, Mn is the average molar mass of the mixture 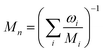 , and Deffi is the effective diffusion coefficient for species i. The diffusion coefficient is composed of a mass-averaged Stefan–Maxwell diffusivity, Dmi, and Knudsen diffusivity, DKi, occurring in parallel,
, and Deffi is the effective diffusion coefficient for species i. The diffusion coefficient is composed of a mass-averaged Stefan–Maxwell diffusivity, Dmi, and Knudsen diffusivity, DKi, occurring in parallel,| | 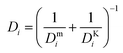 | (9) |
where| |  | (10) |
and| | 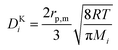 | (11) |
Here, rp,m is the average pore radius of the porous medium m, and yi and Mi are the molar fraction and weight of species i, respectively. Additionally, for flow through a porous medium (the CL and the DM), the effective diffusivity is corrected for the porosity, εm, and tortuosity, τm, of the medium using the Bruggeman relationship,
| |  | (12) |
The liquid volume fraction, i.e. the saturation of the porous medium, is used to calculate the gas volume fraction,
where
εom is the void fraction of the porous medium when
S = 0. Note here that
εDM =
εoDM based on the assumption that the DM is completely dry (
i.e.,
S = 0).
To describe the mass-averaged velocity field, ug, in the porous medium, Darcy's law is used,
| | 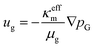 | (14) |
where
κeffm is the effective permeability of the porous medium m,
μg is the fluid viscosity, and
pG is the total gas pressure. The effective permeability is calculated as
where
κsat,m is the saturated permeability and
κr,m is the relative permeability.
κsat,m is determined by the structure of the medium according to the Carman–Kozeny equation,
36| |  | (16) |
The value of κosat,m is given in Table 1. The relative permeability assumes a cubic dependence on the saturation, so that37
Table 1 Model parameters
| Parameter |
Value |
Unit |
Ref. |
| Operating conditions |
|
T
|
293.15 |
K |
|
|
P
|
1 |
atm |
|
|
q
l
|
0.5 |
ml min−1 |
8
|
|
|
| Electrode geometry |
|
|
|
|
L
elec
|
0.02 |
m |
11
|
|
A
elec
|
7.5 × 10−6 |
m2 |
11
|
|
|
| Gas phase species |
|
D
H2–CO
|
0.743 |
cm2 s−1 |
39
|
|
D
H2–N2
|
0.779 |
cm2 s−1 |
39
|
|
D
H2–CO2
|
0.646 |
cm2 s−1 |
39
|
|
D
CO–N2
|
0.202 |
cm2 s−1 |
39
|
|
D
CO–CO2
|
0.152 |
cm2 s−1 |
39
|
|
D
N2–CO2
|
0.165 |
cm2 s−1 |
39
|
|
|
| Liquid phase species |
|
D
K+
|
1.957 × 10−5 |
cm2 s−1 |
34
|
|
D
H+
|
9.311 × 10−5 |
cm2 s−1 |
34
|
|
D
OH−
|
5.293 × 10−5 |
cm2 s−1 |
34
|
|
D
HCO3−
|
1.185 × 10−5 |
cm2 s−1 |
34
|
|
D
CO3−
|
0.923 × 10−5 |
cm2 s−1 |
34
|
|
D
CO2
|
1.910 × 10−5 |
cm2 s−1 |
39
|
|
|
| DM |
|
L
DM
|
325 |
μm |
40
|
|
ε
DM
|
0.8 |
|
40
|
|
σ
DM
|
220 |
S m−1 |
40
|
|
κ
osat,DM
|
1.34 × 10−12 |
m2 |
40
|
|
|
| CL |
|
m
loading
|
2 |
mg cm−2 |
|
|
ε
CL
|
0.5 |
|
|
|
σ
CL
|
100 |
S m−1 |
41
|
|
κ
osat,DM
|
16 × 10−16 |
m2 |
42
|
|
r
np
|
5 × 10−8 |
m |
43
|
|
|
| Charge transfer reactions |
|
U
oHER
|
0 |
V |
34
|
|
i
Ao,HER
|
9.79 × 10−4 |
mA cm−2 |
1
|
|
α
Ac,HER
|
0.27 |
|
1
|
|
i
Bo,HER
|
1.16 × 10−6 |
mA cm−2 |
1
|
|
α
Bc,HER
|
0.36 |
|
1
|
|
U
oCOER
|
−0.11 |
V |
34
|
|
i
o,COER
|
4.71 × 10−4 |
mA cm−2 |
1
|
|
α
c,COER
|
0.44 |
|
1
|
|
|
| Homogeneous reactions |
|
k
1
|
3.71 × 10−2 |
s−1 |
38
|
|
k
2
|
59.44 |
s−1 |
38
|
|
k
3
|
2.23 × 103 |
L mol−1 s−1 |
38
|
|
k
4
|
6.0 × 109 |
L mol−1 s−1 |
38
|
The Nth gaseous species fraction is determined from
| |  | (18) |
Liquid-phase transport
The flux of aqueous species can be broken into diffusion and migration terms (Nernst–Planck)| | | nj = −Deffjρl∇ωj + zjujFρlωj∇ϕl | (19) |
where zj is the charge and uj is the mobility of aqueous species j, respectively, ρl is the liquid density, and ϕl is the liquid-phase potential. The liquid-phase effective diffusivity also assumes a Bruggeman relation, eqn (12). The mobility can be determined from Nernst–Einstein relationship| |  | (20) |
To determine the concentration profiles for all ionic species and the potential, an additional equation is required, which is provided by electroneutrality
| |  | (21) |
Electron transport
Charge conservation and Ohm's law govern the electronic potential ϕs and current is,| |  | (22) |
andwhere is is the current density in the solid phase, il is the current density in the liquid phase, ik is the local partial current density for reaction k, av is the active surface area defined in the follow section, and σeffs,m is the effective electrical conductivity of the solid material in medium m, corrected by the Bruggeman correlation (eqn (12)).
Charge-transfer reactions
Charge-transfer reactions occur in the CL at the solid/liquid interface. The CL thickness, LCL, and specific surface area, aov, are determined by| |  | (24) |
and| |  | (25) |
respectively, where mloading is the mass loading of the catalyst nanoparticles. The active surface area for the saturation curve case is corrected by CL saturation, av = aovS, since only those catalyst particles in contact with liquid electrolyte are active.
The charge-transfer reactions contribute to the source term for gas-phase species H2 and CO, as well as liquid-phase species H+ and OH−,
| | 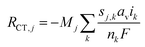 | (26) |
where
F is Faraday's constant,
nk is the number of electrons transferred,
sj,k is the stoichiometric coefficient (negative for reactants and positive for products) for species
j in reaction
k. Since cathodic electrode potentials away from equilibrium are simulated, the CO and H
2 current densities are calculated using Tafel kinetics,
| |  | (27) |
and
| |  | (28) |
The exchange-current densities, io,k, and transfer coefficients, αc,k, are obtained by fitting eqn (27) and (28) to experimental data for planar electrodes immersed an aqueous electrolyte after correcting for mass-transport effects (see Fig. S2, ESI†).1 Reference concentrations for both CO2 and H+ are taken to be 1 M. The surface overpotential is given by
| |  | (29) |
where
Uok is the standard reduction potential for reaction
k.
Homogeneous bulk reactions and CO2 dissolution
Source terms resulting from homogenous bulk reactions for the aqueous species j are calculated using apparent rate constants measured by Schulz et al.38| | 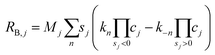 | (30) |
Forward reaction-rate constants for equation n, kn, are listed in Table 1 and reverse reaction rate constants are calculated from
| |  | (31) |
where
Kn is the equilibrium constant listed in
eqn (5).
Gas-phase CO2 dissolves into the electrolyte at the gas/liquid interface. For a wetted CL, the gas-to-liquid mass-transfer coefficient, kGL,CO2, is dependent on the thickness of the electrolyte film covering the pore walls in the CL, δTF, and the species diffusivity,
| |  | (32) |
The rate of CO2 dissolution, RPT,CO2, then contributes to the source term for CO2 by
| | | RPT,CO2 = avkGL,CO2MCO2(HCO2pGyCO2 − cCO2(aq)) | (33) |
where
HCO2 is Henry's constant for CO
2,
cCO2(aq) is the dissolved CO
2 concentration.
RPT,CO2 is negative for gas-phase CO
2 (representing consumption) and positive for liquid-phase CO
2 (representing production).
Boundary conditions
At the electrolyte/CL boundary, the Sherwood–Reynold–Schmidt correlation is used to determine the mass-transfer coefficient,| | 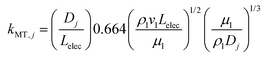 | (34) |
where Lelec is the electrode length, ρl and μl are the density and viscosity of the electrolyte, respectively, and vl is the electrolyte flow velocity, which is calculated from the electrolyte flow rate divided by the cross-sectional area of flow channel, vl = ql/Aelec. The aqueous species flux is set to zero at the CL/DM boundary, and| | | nj = ρlkMT,j(ωbj − ωj) | (35) |
at the electrolyte/CL boundary, where ωbj is the mass fraction in the bulk electrolyte. The gas feed composition is set to 99.8 mol% CO2, 0.1 mol% H2 and 0.1 mol% CO at the DM/gas channel boundary. Gaseous species flux is set to RPT,CO2/av for CO2, and zero for H2 and CO at the CL/DM boundary (flooded case) or electrolyte/CL boundary (ideally wetted and saturation curve cases).
The electrolyte potential is set to zero as a reference. il = 0 at the CL/DM boundary, and is = 0 at the electrolyte/CL boundary must be satisfied. The electronic potential is varied from −0.6 V to −2.2 V vs. SHE at the DM/gas channel boundary.
Numerical method
The above equations are solved using COMSOL Multiphysics 5.3 using MUMPS general solver. The maximum mesh sizes were set to 0.01 μm and 3.25 μm for the CL and DM domain, respectively; a total of 481 mesh elements were used. The solution was independent of increasing mesh elements. Model parameters are listed in Table 1.
Results and discussion
Model validation
Fig. 4 compares the results of simulations and experimental measurements by Hatsukade et al. for planar electrodes and by Verma et al. for GDEs. A detailed description of the experimental setups can be found in ref. 1 and 15. The model captures the order of magnitude increase in partial CO current density in the GDE compared to the planar electrode. Discrepancies between the simulations and experiments may be due to: (1) lack of information on CL properties used in the experiments; (2) inadequacy of the rate parameters extracted from the data on metal, planar foils for the nanoparticles used in GDEs;44 (3) failure of the one-dimensional model to capture properly the true current-density distribution. These discrepancies will be investigated in future work.
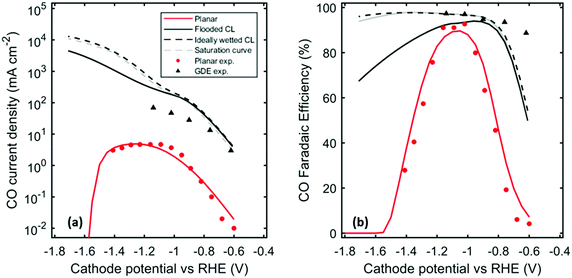 |
| | Fig. 4 (a) CO partial current density and (b) CO Faradaic efficiency (other product is hydrogen, plotted in S3) as a function of Cathode potential vs. RHE for the planar case, flooded case, ideally wetted case, saturation curve case, compared to experimental data measured by Hatsukade et al. and Verma et al.1,11 | |
Fig. 4a shows that for cathode potentials below −1.1 V vs. RHE, the CO partial current density for the GDE is more than an order of magnitude higher than that for the case of planar electrodes, independent of whether the CL in the GDE is flooded or wetted. This difference can be attributed to two main factors. The first is because the GDE contains a higher concentration of catalytically active sites per unit geometric cathode area than does the planar catalyst. This is a consequence of the porous structure of the GDE. The specific interfacial area, aov, for GDEs used in fuel cells have been measured to be in the range of 106 to 108 m−1, depending on the structure, material, deposition method, etc. of the CL.43,45,46 We have assumed a value of aov = 3 × 107 m−1 for the CL, calculated using eqn (25). This corresponds to a roughness factor of 114, which explains the two orders of magnitude higher current density at low overpotentials. For cathode potentials more negative than −1.1 V vs. RHE, the difference between the CO partial current densities for the GDE and planar electrode systems grows dramatically. This is because the mass-transfer resistance for the GDE is much lower than that for the planar-electrode system. At potentials more negative than −1.1 V vs. RHE, the planar electrode becomes CO2 mass-transfer limited, whereas the CO current densities for the GDE continue to increase exponentially with overpotential as expected if the electrode is kinetically controlled (see eqn (27)). CO2 mass transfer to the catalyst of the GDE is much more effective than for the planar electrode because the distance over which mass transfer through the electrolyte occurs is much smaller. For the CL of the GDE, the diffusion layer is in the range of 0.01 to 10 μm, depending on the saturation of the CL, which is much smaller than the boundary-layer thickness for a planar electrode (60 to 160 μm).7
One interesting phenomena to note is how the CO current density and CO FE decrease after reaching a maximum. This is due to the reaction of CO2 with OH− (see eqn (2) and (4)). As the potential is made more cathodic, the HER current density continues to increase exponentially (eqn (4)), producing more OH− that will react with the already limited CO2 near the electrode. The consumption of CO2 results in the drop in CO current density as well as the FE, while the H2 FE continues to increase. This effect is most noticeable for the planar-electrode system.
Results of flooding in the CL
While the current density is high for a flooded CL, the selectivity towards CO starts to decrease around −1 V vs. RHE (Fig. 4a). Even though fully flooded within the CL, the GDL is assumed to remain dry and consequently the catalyst at the CL/GDL interface can still promote CO2R. As the electrode is driven to more cathodic potentials and the rate of CO2R rises, the concentration of CO2 in the CL near the electrolyte decreases (Fig. 5a). The local CO current density shifts towards the CL/DM boundary, where gas-phase CO2 is supplied (Fig. 5c). The local CO current density at the electrolyte/CL boundary does not drop as rapidly as it does at the center of the CL because bicarbonate anions from the bulk can decompose to produce CO2. This phenomenon is also in agreement with recent publications showing HCO3− as a carbon source for CO2R to CO.3,4 Because of the equilibrium relationships for the reactions listed in eqn (5), a 0.5 M KHCO3 solution not equilibrated with gaseous CO2 will decompose and produce approximately 5 mM aqueous CO2 to maintain equilibrium. This is why CO2R continues to occur near the electrolyte/CL boundary at high overpotentials. The uneven distribution of CO current density for a flooded CL results in poor utilization of the catalyst. At high cathodic potentials, the overpotential for both CO2R and HER are high. Catalyst sites that are CO2 limited continue to perform HER, causing the drop in CO FE.
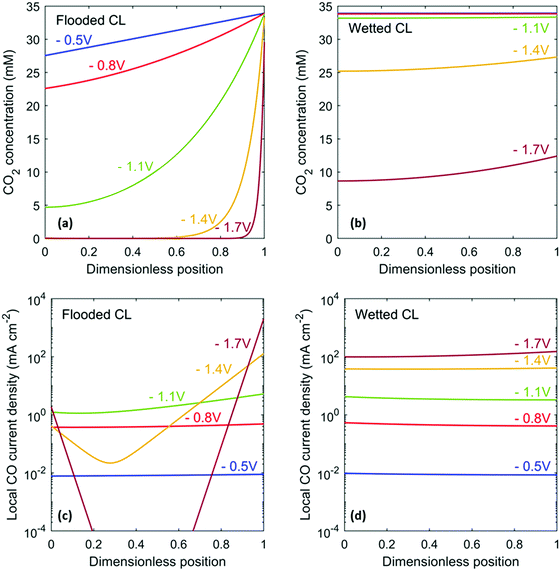 |
| | Fig. 5 CO2 concentration profile (a and c) and local CO current density (b and d) within the catalyst layer for the flooded case (a and b) and the ideally wetted case (c and d). The dimensionless position is scaled using the CL thickness, where 0 is the electrolyte/CL boundary, and 1 is the CL/GDL boundary. | |
A partially wetted CL performs better than a flooded CL in terms of both the CO partial current density and the CO FE, especially at high current densities (high overpotentials). Wetted pores allow gas-phase CO2 to penetrate throughout the CL, resulting in a more even distribution of dissolved CO2 and local CO current density even at high overpotentials (Fig. 5b and d). The high current densities in GDEs cause high alkalinity in the electrolyte within the CL as one OH− is produced for each electron consumed. This effect is more severe for the wetted CL because it operates at a higher current density than does the flooded CL (Fig. 6). High pH leads to a high K+ cation concentration, which is required to maintain electroneutrality in the electrolyte in the CL. The high concentrations in the CL also implies a sharp concentration gradient at the electrolyte/CL boundary. For CO current densities above 1.5 A cm−2, K2CO3 may start precipitating from the solution.31 However, the increased concentration of the counter-ion may also beneficially amplify cation effects, where cations near the electrode stabilize CO2R intermediates for non Ag CO2R catalysts.18
 |
| | Fig. 6 (a) pH profile and (b) potassium cation concentration profile within the catalyst layer for the flooded case (solid lines) and wetted case (dashed lines). | |
Describing saturation/hydrophilicity in the CL
The ideally wetted CL case assumes a constant uniform thin film of electrolyte throughout the CL. However, the CL local environment will change as the electrode consumes CO2 and produces CO and H2. Incorporating the saturation curve to describe liquid distribution in the CL results in a slightly lower CO current density and FE than the wetted CL case since only 64% of the total catalyst surface area is active. As the current density increases, the total pressure in the gas phase drops near the electrolyte/CL boundary and more of the CL pores become flooded (Fig. 7a). The effective permeability of the CL decreases according to eqn (15), causing a lower CO2 concentration near the electrolyte/CL boundary and a decrease in local CO current density (Fig. 7b). H2 current density is unaffected since its rate does not depend on concentrations of dissolved gaseous species (Fig. S3, ESI†).
 |
| | Fig. 7 (a) Saturation and (b) local CO current density as a function of position within the catalyst layer at different potentials for the saturation curve case. | |
Fig. 8 shows the effect of changing the hydrophilicity/hydrophobicity of the CL. At low overpotentials, a more hydrophilic CL (higher saturation for a given capillary pressure) enhances performance because it improves pore wetting, giving a higher specific active interfacial area. However, a hydrophilic CL also becomes flooded more easily, leading to worse performance at more cathodic potentials. Thus, there is an optimum that is dependent on operating conditions and desired efficiency and rate (current density).
 |
| | Fig. 8 Change in CO current density as a function of cathode potential vs. RHE for a more hydrophilic CL (blue) and a more hydrophobic CL (orange). | |
Effects of catalyst layer loading and porosity
The effect of reducing the catalyst loading (i.e., the mass of catalyst per CL geometric area) and, hence, decreasing the CL thickness was examined. For a kinetically controlled system, reducing catalyst loading by 50%, halves the current density, as can be seen in Fig. 9 at low overpotentials. However, the change in CO partial current density for the case of 0.5× catalyst loading becomes less significant as the overpotential increases because of the lower mass-transfer resistances in a thinner CL. The trend reverses around −1 V vs. RHE, showing the balance between current density and pH: high current density increases CL pH, which can suppress CO current density by the reaction of CO2 and OH−. The poor catalyst utilization in flooded GDEs eventually becomes detrimental at high current densities (i.e. electrode potentials lower than −1.2 V vs. RHE), and a lower catalyst loading under such conditions can actually enhance the CO current density.
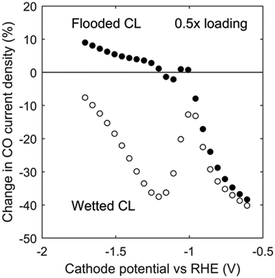 |
| | Fig. 9 Change in CO current density as a function of cathode potential vs. RHE at 0.5× loading (0.5× CL length) for the flooded case (filled circles) and the ideally wetted case (hollow circles). | |
Another property that can be changed is the CL porosity. Increasing porosity enhances gas transport by increasing the gas permeability (eqn (16)) and effective diffusivity (eqn (12)), but requires an increase in the CL thickness to maintain a constant catalyst loading (eqn (24)). Fig. 10 shows that it is more effective to increase porosity for a wetted CL than a flooded CL. This makes sense since the mass-transport limitation is more severe in a flooded CL, and increasing its thickness will aggravate the uneven local CO current-density distribution shown in Fig. 5b. For a wetted CL, doubling the CL porosity can improve the current density by about 100 mA cm−2 at −1.1 V vs. RHE.
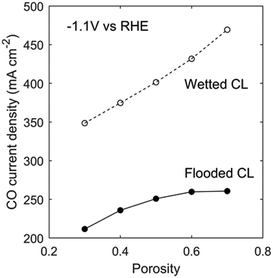 |
| | Fig. 10 CO current density as a function of CL porosity for the flooded case (filled circles) and the ideally wetted case (hollow circles). | |
Effects of electrolyte flowrate
Increasing the electrolyte flowrate improves the mass transport of ionic species and helps to maintain the CL local environment near that of the bulk electrolyte. This is important for GDEs considering the high pH and cation concentration caused by the high current density (Fig. 6). However, the model demonstrates that increasing electrolyte flowrate may not be the most effective method to improve electrode performance. As shown in Fig. 11, to achieve a 100 mA cm−2 increase in CO current density at −1.1 V vs. RHE, it is necessary to increase the electrolyte flowrate by an order of magnitude.
 |
| | Fig. 11 CO current density as a function of electrolyte flow rate for the flooded case (filled circles) and the ideally wetted case (hollow circles). | |
Conclusions
We have developed a framework for modeling GDEs for CO2 reduction. The model captures basic species transport mechanisms (Nernst–Planck for ionic species in liquid electrolyte and Stefan–Maxwell for gas-phase species), concentration-dependent charge-transfer kinetics (Tafel equations) and the acid/base kinetics of CO2 reaction with OH− to form HCO3− and CO32− in the electrolyte. The model was used to explore design space for physical properties and analyze inherent transport and kinetic tradeoffs. It was demonstrated and quantified how a GDE improves CO2R performance by providing a higher active surface area and lower mass-transfer resistances. Electrode properties such as wettability, catalyst loading, and porosity impact the inherent local CO2 concentration due to the balance between transport through the CL and the reaction of CO2 with produced hydroxide ions. This balance is sensitive to the operating conditions of the GDE and therefore the optimal property values depend on the desired current density. Our results show that tuning CL wettability can significantly affect the resulting CO current density and CO FE. At high current densities (>100 mA cm−2), it is important to prevent flooding of the CL, as this may lead to an uneven distribution of CO2 within the CL and poor utilization of the catalyst. In such a case (operating a flooded CL at high current densities), decreasing the catalyst layer loading may actually improve the CO partial current density and catalyst utilization. The amount of liquid in the CL varies depending on position and operating current density, which in turn affects the local CO partial-current-density distribution within the CL. Manipulation of the porosity and electrolyte flowrate can also improve the CO partial current density by as much as twice the amount. The insights gained from the model described in this study can be used to guide the design of GDEs for CO2R.
List of symbols
| Roman | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
a
v
| Specific surface area, m−1 |
|
A
elec
| Cross sectional area of the flow channel, m2 |
|
c
i
| Concentration of species i, mol m−3 |
|
D
i
| Diffusivity of species i, m2 s−1 |
|
F
| Faraday's constant, C mol−1 |
|
H
i
| Henry's constant of species i, mol atm−1 |
|
i
α
| Current density in phase α, mA cm−2 |
|
i
o,k
| Exchange current density of reaction k, mA cm−2 |
|
j
i
| Diffusive mass flux of species i, g m−2 s−1 |
|
k
gl
| Mass-transfer coefficient at the gas/liquid interface, m s−1 |
|
k
n
| Rate constant for homogeneous reaction n, s−1 or L mol−1 s−1 |
|
L
| Length, m |
|
m
loading
| Catalyst loading, g m−2 |
|
M
i
| Molar mass of species i, g mol−1 |
|
M
n
| Average molar mass of gaseous mixture, g mol−1 |
|
n
i
| Mass flux of species i, g m−2 s−1 |
|
n
k
| Number of electrons transferred in reaction k |
|
p
α
| Total pressure in phase α, atm |
|
q
l
| Electrolyte flow rate, ml min−1 |
|
r
np
| Catalyst nanoparticle radius, m |
|
r
p,m
| Pore radius in medium m |
|
R
| Gas constant, J mol−1 K−1 |
|
R
β,i
| Volumetric rate of reaction of species i from bulk reaction β, g m−3 s−1 |
|
s
j,k
| Stoichiometric coefficient of species j in reaction k |
|
S
| Saturation |
|
T
| Temperature, K |
|
u
β
| Mass-averaged fluid velocity of fluid β, m s−1 |
|
u
i
| Mobility of species i, s mol kg−1 |
|
U
k
| Reference potential of reaction k, V |
|
v
l
| Electrolyte flow velocity, m s−1 |
|
y
i
| Mole fraction of species i |
|
z
i
| Charge of species i |
| Greek | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
α
k
| Transfer coefficient of reaction k |
|
δ
TF
| Electrolyte thin film thickness |
|
ε
m
| Porosity of medium m |
|
η
s,k
| Surface overpotential of reaction k, V |
|
κ
m
| Permeability of medium m, m2 |
|
μ
β
| Viscosity of fluid β, Pa s |
|
ρ
i
| Mass density of species i, g cm−3 |
|
ρ
α
| Density of species phase α, g cm−3 |
|
σ
m
| Conductivity in medium m, S m−1 |
|
τ
m
| Tortuosity of medium m |
|
ϕ
α
| potential of phase α, V |
|
ω
i
| Mass fraction of species i |
| Subscript | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| B | Bulk |
| CL | Catalyst layer |
| CT | Charge transfer |
| DM | Diffusion medium |
| eq | Equivalent |
| g | Gaseous mixture |
|
i
| Species |
|
j
| Species |
|
k
| Reaction |
| l | Liquid |
| np | Nanoparticle |
| p | Pore |
| PT | Phase transfer |
| s | Solid |
| TF | Electrolyte thin film |
| Superscript | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| o | Intrinsic value or standard state |
| ref | Reference |
| eff | Effective |
| K | Knudsen |
| m | Mass-averaged |
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This material is based upon work performed by the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy under Award Number DE-SC0004993.
References
- T. Hatsukade, K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Phys. Chem. Chem. Phys., 2014, 16, 13814–13819 RSC.
- K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5, 7050–7059 Search PubMed.
- S. Zhu, B. Jiang, W. B. Cai and M. Shao, J. Am. Chem. Soc., 2017, 139, 15664–15667 CrossRef PubMed.
- D. Hursan and C. Janaky, ACS Energy Lett., 2018, 3, 722–723 CrossRef PubMed.
- N. Gupta, M. Gattrell and B. MacDougall, J. Appl. Electrochem., 2006, 36, 161–172 CrossRef.
- M. R. Singh, E. L. Clark and A. T. Bell, Phys. Chem. Chem. Phys., 2015, 17, 18924–18936 RSC.
- E. L. Clark, J. Resasco, A. Landers, J. Lin, L.-T. Chung, A. Walton, C. Hahn, T. F. Jaramillo and A. T. Bell, ACS Catal., 2018 DOI:10.1021/acscatal.8b01340.
- H. Hashiba, L. C. Weng, Y. K. Chen, H. K. Sato, S. Yotsuhashi, C. X. Xiang and A. Z. Weber, J. Phys. Chem. C, 2018, 122, 3719–3726 Search PubMed.
- S. Verma, B. Kim, H. R. Jhong, S. Ma and P. J. Kenis, ChemSusChem, 2016, 9, 1972–1979 CrossRef PubMed.
- K. Ogura, R. Oohara and Y. Kudo, J. Electrochem. Soc., 2005, 152, D213–D219 CrossRef.
- D. T. Whipple, E. C. Finke and P. J. A. Kenis, Electrochem. Solid State Lett., 2010, 13, D109–D111 CrossRef.
- B. Kim, F. Hillman, M. Ariyoshi, S. Fujikawa and P. J. A. Kenis, J. Power Sources, 2016, 312, 192–198 CrossRef.
- B. Kim, S. Ma, H.-R. Molly Jhong and P. J. A. Kenis, Electrochim. Acta, 2015, 166, 271–276 CrossRef.
- S. Ma, R. Luo, S. Moniri, Y. C. Lan and P. J. A. Kenis, J. Electrochem. Soc., 2014, 161, F1124–F1131 CrossRef.
- S. Verma, X. Lu, S. Ma, R. I. Masel and P. J. Kenis, Phys. Chem. Chem. Phys., 2016, 18, 7075–7084 RSC.
- R. L. Cook, R. C. Macduff and A. F. Sammells, J. Electrochem. Soc., 1990, 137, 607–608 CrossRef.
- M. R. Singh, Y. Kwon, Y. Lum, J. W. Ager, 3rd and A. T. Bell, J. Am. Chem. Soc., 2016, 138, 13006–13012 CrossRef PubMed.
- J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, J. Am. Chem. Soc., 2017, 139, 11277–11287 CrossRef PubMed.
-
F. A. L. Dullien, Porous media: fluid transport and pore structure, Academic Press, San Diego, 1992 Search PubMed.
- J. J. Wu, P. P. Sharma, B. H. Harris and X. D. Zhou, J. Power Sources, 2014, 258, 189–194 CrossRef.
- Q. N. Wang, H. Dong, H. Yu and H. B. Yu, J. Power Sources, 2015, 279, 1–5 CrossRef.
- B. Endrodi, G. Bencsik, F. Darvas, R. Jones, K. Rajeshwar and C. Janaky, Prog. Energy Combust. Sci., 2017, 62, 133–154 CrossRef.
- C. Delacourt and J. Newman, J. Electrochem. Soc., 2010, 157, B1911–B1926 CrossRef.
- K. Wu, E. Birgersson, B. Kim, P. J. A. Kenis and I. A. Karimi, J. Electrochem. Soc., 2014, 162, F23–F32 CrossRef.
- I. Nitta, T. Hottinen, O. Himanen and M. Mikkola, J. Power Sources, 2007, 171, 26–36 CrossRef.
- M. S. Ismail, D. B. Ingham, K. J. Hughes, L. Ma and M. Pourkashanian, Int. J. Hydrogen Energy, 2015, 40, 10994–11010 CrossRef.
- I. V. Zenyuk, P. K. Das and A. Z. Weber, J. Electrochem. Soc., 2016, 163, F691–F703 CrossRef.
- A. Z. Weber, J. Power Sources, 2010, 195, 5292–5304 CrossRef.
- F. C. Cetinbas, R. K. Ahluwalia, N. Kariuki, V. De Andrade, D. Fongalland, L. Smith, J. Sharman, P. Ferreira, S. Rasouli and D. J. Myers, J. Power Sources, 2017, 344, 62–73 CrossRef.
- A. Chowdhury, C. J. Radke and A. Z. Weber, ECS Trans., 2017, 80, 321–333 CrossRef.
-
CRC handbook of chemistry and physics, CRC Press, Cleveland, Ohio, 1977 Search PubMed.
-
Y. Hori, in Modern Aspects of Electrochemistry, ed. C. G. Vayenas, R. E. White and M. E. Gamboa-Aldeco, Springer New York, New York, NY, 2008, pp. 89–189 Search PubMed.
- L. D. Chen, M. Urushihara, K. R. Chan and J. K. Norskov, ACS Catal., 2016, 6, 7133–7139 CrossRef.
-
J. S. Newman and K. E. Thomas-Alyea, Electrochemical systems, J. Wiley, Hoboken, N.J., 3rd edn, 2004 Search PubMed.
-
R. Taylor and R. Krishna, Multicomponent mass transfer, Wiley, New York, 1993 Search PubMed.
- P. C. Carman, Chem. Eng. Res. Des., 1997, 75, S32–S48 CrossRef.
- A. Z. Weber and J. Newman, Chem. Rev., 2004, 104, 4679–4726 CrossRef PubMed.
- K. G. Schulz, U. Riebesell, B. Rost, S. Thoms and R. E. Zeebe, Mar. Chem., 2006, 100, 53–65 CrossRef.
-
E. L. Cussler, Diffusion, mass transfer in fluid systems, Cambridge University Press, Cambridge Cambridgeshire, New York, 1984 Search PubMed.
- A. El-Kharouf, T. J. Mason, D. J. L. Brett and B. G. Pollet, J. Power Sources, 2012, 218, 393–404 CrossRef.
- C. Y. Du, P. F. Shi, X. Q. Cheng and G. P. Yin, Electrochem. Commun., 2004, 6, 435–440 CrossRef.
- I. V. Zenyuk, E. Medici, J. Allen and A. Z. Weber, Int. J. Hydrogen Energy, 2015, 40, 16831–16845 CrossRef.
- T. Soboleva, X. Zhao, K. Malek, Z. Xie, T. Navessin and S. Holdcroft, ACS Appl. Mater. Interfaces, 2010, 2, 375–384 Search PubMed.
- A. Salehi-Khojin, H.-R. M. Jhong, B. A. Rosen, W. Zhu, S. Ma, P. J. A. Kenis and R. I. Masel, J. Phys. Chem. C, 2013, 117, 1627–1632 Search PubMed.
- S. Thiele, R. Zengerle and C. Ziegler, Nano Res., 2011, 4, 849–860 CrossRef.
- H. Schulenburg, B. Schwanitz, N. Linse, G. N. G. Scherer, A. Wokaun, J. Krbanjevic, R. Grothausmann and I. Manke, J. Phys. Chem. C, 2011, 115, 14236–14243 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp01319e |
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab and
Adam Z.
Weber
*ab and
Adam Z.
Weber
 *a
*a



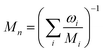 , and Deffi is the effective diffusion coefficient for species i. The diffusion coefficient is composed of a mass-averaged Stefan–Maxwell diffusivity, Dmi, and Knudsen diffusivity, DKi, occurring in parallel,
, and Deffi is the effective diffusion coefficient for species i. The diffusion coefficient is composed of a mass-averaged Stefan–Maxwell diffusivity, Dmi, and Knudsen diffusivity, DKi, occurring in parallel,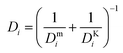

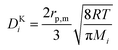

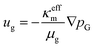







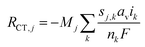



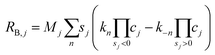


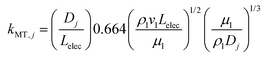







![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)




