Interaction between amino-functionalized inorganic nanoshells and acid-autocatalytic reactions

Abstract

Amino-functionalized inorganic silica nanoshells with a diameter of 511 ± 57 nm are efficiently used as hydrogen ion binders with a base dissociation constant of (1.2 ± 0.1) × 10⁻⁴. The hydrogen removal has been shown to produce reaction–diffusion fronts of constant propagation velocity in the autocatalytic chlorite–tetrathionate reaction when it is run in thin planar slices of nanoshell-containing agarose gel to exclude all convection related effects. By controlling the exact amount of amino-functionalized hollow nanospheres in the gel matrix it is possible to finely tune the propagation velocity of the chemical front in the 0.1–10 cm h⁻¹ range. Remarkably, this can be achieved with very low amino-functionalized hollow inorganic nanosphere loadings between 0.1–0.01 (m V⁻¹)%. The front width has also been determined experimentally, which increases by a factor of two with one magnitude decrease in the front velocity.

---

1 Introduction

Spatiotemporal structures of self-organized reactions can interact with a self-assembly on a much smaller lengthscale.¹ Nanoparticles have been shown to be regulated with a pH-oscillator^2–4 or an autocatalytic reaction resulting in acidic fronts utilizing buoyancy.⁵ Under different conditions, the aggregation and disaggregation of these nanoparticles can be influenced. If the functional groups, attached to the surface of the nanoparticles, are capable of dissociation in a basic medium, the electrostatic force overcompensates the van der Waals force^2,3,5,6 which leads to the disappearance of the coherence of these nanoparticles. The relationships between the nanoparticles and nonlinear reactions have allowed further perspectives: the mechanical properties of pH-responsive hydrogels, used for drug delivery or therapy,⁷ can also be affected by these chemical systems.^4,8

Although the existence of spatial patterns in nature is one of the most common phenomena, their detailed investigation started only in the middle of the 20th century. One of the first steps was Alan Turing's reaction–diffusion model⁹ in which stationary structures can evolve. From this time, a large number of reactions yielding spatiotemporal patterns have been thoroughly studied. The well known Belousov–Zhabothinsky reaction¹⁰ was the first exhibiting both oscillatory and excitable behavior in the form of target patterns or spirals. Various Landolt-type reactions, like the thiourea–iodate–sulfite reaction,¹¹ and the bromate–sulfite–ferrocyanide,¹² the ferrocyanide–iodate–sulfite,¹³ and the halogen-free hydrogen–peroxide–sulfite systems,¹⁴ have been able to produce intriguing labyrinthine and Turing structures. The iodate–arsenous acid^15,16 and the chlorite–tetrathionate reaction¹⁷ served as models to study the buoyancy effects on simple chemical fronts.¹⁸ The properties of these reactions have also been studied in different structured media to elicit their particular mechanism.^19,20

One of the model reactions giving rise to pH-fronts reproducibly is the chlorite–tetrathionate (CT) reaction. The reaction is an autocatalytic process in which hydrogen ions play the role of an autocatalyst. The thermodynamically most favorable but experimentally not observable stoichiometric equation proposed by Nagypál and Epstein²¹ is

7ClO₂⁻ + 2S₄O₆²⁻ + 6H₂O → 7Cl⁻ + 8SO₄²⁻ + 12H⁺ (1)

with a rate equation of r = k[S₄O₆²⁻][ClO₂⁻][H⁺]² describing supercatalysis. The equation, however, can still be used for the initial period of the reaction in the presence of slight chlorite-ion excess.^22,23 For experimental conditions with the initial concentration ratio set to [ClO₂⁻]₀/[S₄O₆²⁻]₀ ≈ 4, it was found that the observed stoichiometry is

8.5ClO₂⁻ + 2S₄O₆²⁻ + 6H₂O → 7.5Cl⁻ + ClO₃⁻ + 8SO₄²⁻ + 12H⁺ (2)

which provides the same amount of the autocatalyst with respect to the limiting reactant tetrathionate i.e., 6[S₄O₆²⁻]₀.^{24, 25}

Using a highly viscous or gelled, elastic reaction medium like gelatin, polyacrylamide or agarose, where convection is negligible, pure reaction–diffusion fronts develop, so the effect of diffusion as a sole transport process can be investigated.^26–30 Typically an initially planar front retains its shape during propagation unless the mobility of the autocatalyst is significantly lower than that of the reactants. If the autocatalyst is reversibly immobilized, the initial planar symmetry can be lost and a cellular structure may appear.^26–30

In this work, our aim is to study how a self-assembly with a nanometer length scale can influence a macroscopic self-organizing system of a millimeter size. Namely, the influence of hollow inorganic nanospheres (HINS)^31–33 on the pH reaction–diffusion front arising from the CT model reaction is investigated experimentally. Furthermore the impact is quantified by determining the characteristics of the reaction–diffusion fronts such as front velocity or width.

2 Experimental

The amino-functionalized hollow nanospheres were synthesized as described previously³³ and summarized in the ESI.† To conduct the reactions, we used analytical-grade reagents except for sodium chlorite, which had 80% purity. The experiments were carried out in an agarose gel matrix³⁴ to avoid convection and hence, diffusion was the only transport process to consider. Accordingly, the final mixture contained, besides the two reagents – sodium chlorite and potassium tetrathionate – bromophenol blue as an indicator and amino-functionalized hollow silica nanospheres to bind hydrogen ions as summarized in Table 1. The initial pH was set to pH = 11.96 ± 0.02 with the addition of sodium hydroxide to inhibit the self-initiation of the reaction.

Table 1 Reagent concentrations in the gel

Component	Concentration
Potassium tetrathionate	3.13 mM
Sodium chlorite	12.5 mM
Sodium dodecyl sulfate	5.25 mM
Bromophenol blue	0.18 mM
Agarose	11.25 mg cm^−3

---

The analysis of the nanoparticle size distribution was based on the pictures taken by scanning electron microscope similar to those shown in Fig. 1. The monodisperse HINS have an average diameter of 511 ± 57 nm based on measurements of 400 spheres (for the details see the ESI†). Thus, we do not have to consider any size fluctuation effects on the pattern formation. To ensure reproducibility, we have stabilized the nanospheres by creating a suspension containing sodium hydroxide, sodium dodecyl sulfate, and the nanoparticles with concentrations of 1.48–2.96 mg cm⁻³. Fig. 1(c and d) illustrates that even a three-minute long sonication does not damage the structure of the hollow nanospheres. As a first step of the gel preparation, ultrasound sonication (ν = 37 kHz; Elma S60H Elmasonic) was used for 13 s to ensure homogeneous distribution of the suspension. Then to an appropriate volume (1–7 cm³) of suspension we added 90 mg of solid agarose. The beaker was covered by a glass plate and heated for 13 min under continuous stirring (Thermolyne Cimarec 2 hotplate, stirring at 300 rpm and 100 °C). The beaker was then cooled down for 2 minutes using another magnetic stirrer (Velp Scientifica microstirrer, 550 rpm) at room temperature. During this period, the condensed water drops were poured back into the solution to keep the solution volume constant. An appropriate volume of potassium tetrathionate and bromophenol blue stock solutions were pipetted into the mixture. Sodium chlorite was added into the solution 2 minutes later. The mixture was then poured into a 1.25 mm-deep, Plexi mold and covered with another Plexi plate. The mixture was polymerized for 50 minutes at room temperature (T = 25 ± 1 °C). The liquid was removed from the gel with a paper towel and 1.5 cm × 7 cm pieces were cut. We placed 3–4 gel strips into a 2 mm-deep vessel, parallel and 5 mm apart. Small pieces, 1.5 cm × 5 cm, were then cut off from each gel and a drop of 0.04 M sulfuric acid was added to the top. When the entire piece turned yellow, we wiped off the liquid acid from the surface of the gel and attached the two parts to induce front propagation. Finally, to prevent evaporation we closed the mold with tape around the edges.

Fig. 1 SEM images of the hollow inorganic nanospheres at various sonication times: 0 min (a), 1 min (b), 3 min (c), and 6 min (d).

The front propagation was monitored with a video camera (Unibrain 1394 Innovators) using an LED light source which irradiated the reaction vessel from below. The velocity of the front propagation was determined from the photos taken at 1–10 min intervals by determining the front position as a function of time.

The average dissociation constant of the amino-HINS was determined with potentiometric titrations at constant ionic strength (I = 0.5 mol dm⁻³) using a pH-meter (Thermo Orion 420). First a 50 ml sodium nitrate solution (c = 0.5 mol dm⁻³) was titrated with 0.01 mol dm⁻³ HCl which was followed by the titration of the solution with the same composition and 15.6 mg amino–HINS. The same procedure was followed but the solutions were titrated with 0.01 mol dm⁻³ NaOH. From the titrations of the acid the number of amino groups can be determined considering the –NH₂ + H⁺ ⇌ −NH₃⁺ equilibrium, while the titrations with NaOH yield the number of appropriate ammonium ions.

The amount of hydrogen ions was calculated for all cases. To obtain the number of aminogroups for a given volume of acid we subtracted the number of hydrogen ions in the sodium nitrate solution from that in the presence of the nanospheres. After the equivalence point the difference (Δn_H⁺) became constant, giving the number of amino groups of the HINS. The same procedure was performed using the titrations with a base but the difference in the number of hydroxide ions (Δn_OH⁻) gives the number of ammonium ions of the HINS. We also measured the initial pH of the solution from which the hydroxide ion concentration ([OH⁻]) was calculated. Finally,

was used to estimate the average dissociation constant.

3 Results and discussion

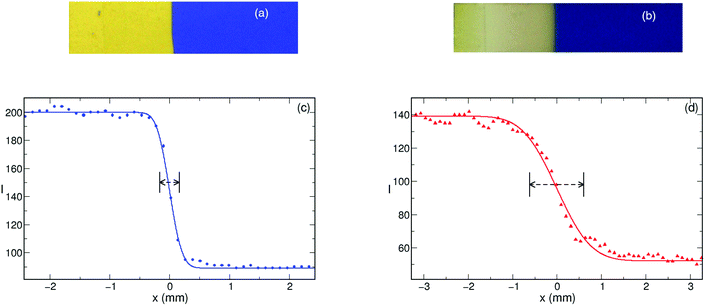
To characterize the hydrogen ion binding capacity of the amino–HINS, we have determined the dissociation constant (K_b) from parallel titrations which is estimated to be K_b = (1.2 ± 0.1) × 10⁻⁴. This suggests that the nanoparticles are a stronger base than ammonia in water, and hence hydrogen ions can be easily removed from the system, which makes the amino-functionalized HINS an effective hydrogen ion removal agent.

Upon initiation, a planar, narrow reaction zone develops separating the blue colored reactant from the yellow colored products when HINS are added to the system. The autocatalytic reaction zone in the form of a reaction–diffusion front propagates through the gel with its shape sustained as shown in Fig. 2 when 15 mg or less nanoshells are introduced. Thus, the effect of the addition of the nanospheres is visually not observable; the gel appears homogeneous and the initial symmetry is kept throughout the experiments. A slight change in the yellow color corresponding to the product state in Fig. 2(b) is due to the slow oxidation of the indicator by the produced chlorine dioxide.

Fig. 2 Front images in the absence of nanoparticles at t = 7 min (a) and with 15 mg nanoparticle content at t = 230 min (b) with their front profiles (c and d) in gels of V = 8 cm³. The fitted cumulative normal distribution function is shown by solid lines and the appropriate front width is indicated with arrows. The length of the gel strips is 6.5 cm (a) and 5.8 cm (b).

For the system with 15 mg nanoshells to reach the same position as for a nanoparticle-free one, significantly greater time is needed which proves that the amino groups bind the autocatalyst and the reaction rate slows down because of the decrease in the concentration of the autocatalyst. A further increase to 20 mg, however, results in so much hydrogen binding that front propagation cannot be sustained.

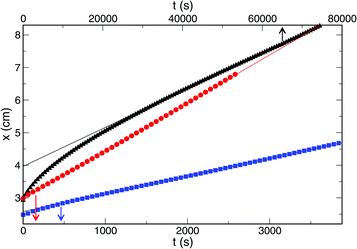
The front evolution was monitored and, after a transition period, we have found that the front position changes with time linearly (see Fig. 3), hence, the front velocity is constant. The actual value, however, is strongly affected by the amount of amino-functionalized nanospheres present in the system.

Fig. 3 Front position as a function of time for gels (V = 8 cm³) with 5 mg, 10 mg, and ▲ 15 mg nanoshells. The solid lines represent the fitted straight lines to determine the front velocity. The arrows point towards the corresponding timescale.

The addition of only 15 mg of nanospheres in 8 ml gel results in a decrease by an order of magnitude of the front velocity as shown in Fig. 4.

Fig. 4 Front velocity as a function of the nanosphere amount in gels of V = 8 cm³ in volume.

In previous works^26,27 carboxylate groups were immobilized into a polyacrylamide gel via preparing a polyacrylamide–sodium methacrylate copolymer. The addition of 18 mM carboxylate ions as sodium methacrylate (corresponding to 60% binding of the autocatalyst) not only resulted in a similar decrease in the front velocity but also affected the pattern formation as the cellular acidity front developed from the initial planar one. The binding capability of the HINS is significantly stronger since the addition of 12 mg HINS—corresponding to 43% binding of the hydrogen ion—results in the same lowering of the front velocity. Thus, the amino-functionalized HINS have a stronger effect on front propagation speed than the introduction of immobilized carboxylate groups into a polyacrylamide–sodium methacrylate copolymer.

To check for diffusion-driven lateral instability in the gel, we have conducted experiments in which we cut the gel into wider pieces (∼6 cm × 4 cm). The initial planar symmetry was kept for all the bindings where front propagation is sustained suggesting that the effective diffusion coefficient³⁵ was not lowered as previously^26,27 because HINS are not immobilized in the gel, and the movement of the nanoparticles is freely possible.

The effect of the binding on the other property of the front, namely its width has also been investigated. A cumulative normal distribution function is fitted to the sigmoid shape of the stable front profile, and the standard deviation associated with it is taken as the reaction front width. Fig. 5 shows that even in the absence of the nanospheres, the front width is 200 μm which does not increase significantly until ≈40% of hydrogen is bound by the HINS. The significant number of nanospheres makes the removal of hydrogen more efficient resulting in lower reaction rate and substantial widening of the reaction front. The larger front width also indicates the increasing contribution of diffusion to the evolving structure.

Fig. 5 Front width as a function of the nanosphere amount in gels of V = 8 cm³ in volume.

4 Conclusion

In summary, we have shown that amino-functionalized hollow silica nanospheres can be effectively utilized to control propagation of pH fronts. Compared to the immobilized carboxylate groups, the amount of HINS needed to observe the slowing down by the same magnitude is significantly lower. Furthermore the one magnitude decrease in the front velocity results in at least a factor of two increase in the front width as was determined experimentally.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Preliminary experiments of Evelin Rauscher are gratefully acknowledged. This work was supported by the National Research, Development and Innovation Office (K112531) and GINOP-2.3.2-15-2016-00013 projects.

References

1. G. M. Whitesides and B. A. Grzybowski, Self-assembly at all scales, Science, 2002, 295, 2418–2421.
2. I. Lagzi, B. Kowalczky, D. Wang and B. A. Grzybowski, Nanoparticle oscillation and fronts, Angew. Chem., Int. Ed., 2010, 49, 8616–8619.
3. J. H. Jang, M. Orbán, S. Wang and D. S. Huh, Adsorption-desorption oscillation of nanoparticles on a honeycomb-patterned pH-responsive hydrogel surface in a closed reaction system, Phys. Chem. Chem. Phys., 2014, 16, 25296–25305.
4. I. Varga, I. Szalai, R. Mészáros and T. Gilányi, Pulsating pH-responsive nanogels, J. Phys. Chem. B, 2006, 110, 20297–20301.
5. B. Bohner, G. Schuszter, H. Nakanishi, D. Zámbó, A. Deák, D. Horváth, Á. Tóth and I. Lagzi, Self-assembly of charged nanoparticles by an autocatalytic reaction front, Langmuir, 2015, 31, 12019–12024.
6. D. Zámbó, K. Suzuno, Sz. Pothorszky, D. Bárdfalvy, G. Holló, H. Nakanishi, D. Wang, D. Ueyama, A. Deák and I. Lagzi, Self-assembly of like charged nanoparticles into Voronoi diagrams, Phys. Chem. Chem. Phys., 2016, 18, 25735–25740.
7. J. P. Best, M. P. Neubauer, S. Javed, H. H. Dam, A. Fery and F. Caruso, Mechanics of pH-responsive hydrogel capsules, Langmuir, 2013, 29, 9814–9823.
8. V. Labrot, P. De Kepper, J. Boissonade, I. Szalai and F. Gauffre, Wave pattern driven by chemomechanical instabilities in responsive gels, J. Phys. Chem. B, 2005, 109, 21476–21480.
9. A. M. Turing, The chemical basis of morphogenesis, Philos. Trans. R. Soc., B, 1952, 237, 37–72.
10. I. R. Epstein and J. A. Pojman, An introduction to nonlinear chemical dynamics: Oscillations, waves patterns, and chaos, Oxford University Press, New York, 1998.
11. J. Horváth, I. Szalai and P. D. Kepper, An experimental design method leading to chemical Turing patterns, Science, 2009, 324, 772–775.
12. I. Molnár and I. Szalai, Kinetic and diffusion-driven instabilites in the bromate-sulfite-ferrocyanide system, J. Phys. Chem. A, 2017, 121, 1900–1908.
13. I. Szalai and P. D. Kepper, Patterns of the ferrocyanide-iodate-sulfite reaction revisited: The role of immobilized carboxylic functions, J. Phys. Chem. A, 2008, 112, 783–786.
14. I. Szalai, J. Horváth, N. Takács and P. D. Kepper, Substained self-organizing pH patterns in hydrogen peroxide driven aqueous redox systems, Phys. Chem. Chem. Phys., 2011, 13, 20228–20234.
15. A. Hanna, A. Saul and K. Showalter, Detailed studies of propagating fronts in the iodate oxidation of arsenous acid, J. Am. Chem. Soc., 1982, 104, 3838–3844.
16. J. A. Pojman, I. R. Epstein, T. J. McManus and K. Showalter, Convective effects on chemical waves. Simple convection in the iodate-arsenous acid system, J. Phys. Chem., 1991, 95, 1299–1306.
17. L. Szirovicza, I. Nagypál and E. Boga, An algorithm for the design of propagating acidity fronts, J. Am. Chem. Soc., 1989, 111, 2842–2845.
18. D. Horváth, T. Bánsági and Á. Tóth, Orientation-dependent density fingering in an acidity front, J. Chem. Phys., 2002, 117, 4399–4402.
19. I. R. Epstein, Coupled chemical oscillators and emergent system properties, Chem. Commun., 2014, 50, 10758–10767.
20. I. R. Epstein, V. K. Vanag, A. C. Balázs, O. Kuksenok, P. Dayal and A. Bhattacharya, Chemical oscillators in structured media, Acc. Chem. Res., 2012, 45, 2160–2168.
21. I. Nagypál and I. R. Epstein, Fluctuations and stirring rate effects in the chlorite-thiosulfate reaction, J. Phys. Chem., 1986, 90, 6285–6292.
22. Á. Tóth, D. Horváth and A. Siska, Velocity of front propagation in reaction-diffusion fronts of the chlorite-tetrathionate reaction, J. Chem. Soc., Faraday Trans., 1997, 93, 73–76.
23. A. K. Horváth, I. Nagypál, G. Peintler and I. R. Epstein, Autocatalysis and self-inhibition: Coupled kinetic phenomena in the chlorite-tetrathionate reaction, J. Am. Chem. Soc., 2004, 126, 6246–6247.
24. A. K. Horváth, I. Nagypál and I. R. Epstein, Three autocatalysts and self-inhibition in a single reaction: A detailed mechanism of the chlorite-tetrathionate reaction, Inorg. Chem., 2006, 45, 9877–9883.
25. A. K. Horváth, A three-variable model for the explanation of the “supercatalytic” effect of hydrogen ion in the chlorite-tetrathionate reaction, J. Phys. Chem. A, 2005, 109, 5124–5128.
26. Á. Tóth, I. Lagzi and D. Horváth, Pattern formation in reaction-diffusion systems: Cellular acidity fronts, J. Phys. Chem., 1996, 100, 14837–14839.
27. D. Horváth and Á. Tóth, Diffusion-driven front instabilities in the chlorite-tetrathionate reaction, J. Chem. Phys., 1998, 108, 1447–1451.
28. M. Fuentes, M. N. Kuperman, J. Boissonade, E. Dulos, F. Gauffre and P. D. Kepper, Dynamical effects induced by long range activation in nonequilibrium reaction-diffusion system, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 056205.
29. F. Gauffre, V. Labrot, J. Boissonade, P. De Kepper and E. Dulos, Reaction-diffusion patterns of the chlorite-tetrathionate system in a conical geometry, J. Phys. Chem. A, 2003, 107, 4452–4456.
30. I. Szalai, F. Gauffre, V. Labrot, J. Boissonade and P. D. Kepper, Spatial bistability in a pH autocatalytic system: From long to short range activation, J. Phys. Chem. A, 2005, 109, 7843–7849.
31. E. Soto-Cantu, R. Cueto, J. Koch and P. S. Russo, Synthesis and rapid characterization of amine-functionalized silica, Langmuir, 2012, 28, 5562–5569.
32. X. Du and J. He, Amino-functionalized silica nanoparticles with center-radially hierarchical mesopores as ideal catalyst carriers, Nanoscale, 2012, 4, 852–859.
33. D. G. Dobó, D. Berkesi and Á. Kukovecz, Morphology conserving aminopropyl functionalization of hollow silica nanospheres in toluene, J. Mol. Struct., 2017, 1140, 83–88.
34. J.-Y. Xiongm, J. Narayanan, X.-Y. Liu, T. K. Chong, S. B. Chen and T.-S. Chung, Topology evolution and gelation mechanism of agarose gel, J. Phys. Chem. B, 2005, 109, 5638–5643.
35. G. Schuszter, T. Gehér-Herczeg, Á. Szücs, Á. Tóth and D. Horváth, Determination of the diffusion coefficient of the hydrogen ion in hydrogels, Phys. Chem. Chem. Phys., 2017, 19, 12136–12143.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp01053f

---