Open Access Article
Open Access ArticleRed-shifting and blue-shifting OH groups on metal oxide surfaces – towards a unified picture
Getachew G.
Kebede
 a,
Pavlin D.
Mitev
a,
Pavlin D.
Mitev
 a,
Wim J.
Briels
bc and
Kersti
Hermansson
a,
Wim J.
Briels
bc and
Kersti
Hermansson
 *a
*a
aDepartment of Chemistry-Ångström, Uppsala University, Box 538, Uppsala, SE-75121, Sweden. E-mail: kersti@kemi.uu.se
bComputational Biophysics, University of Twente, Box 217, Enschede 7500 AE, The Netherlands
cForschungszentrum Jülich, ICS 3, Jülich D-52425, Germany
First published on 17th March 2018
Abstract
We analyse the OH vibrational signatures of 56 structurally unique water molecules and 34 structurally unique hydroxide ions in thin water films on MgO(001) and CaO(001), using DFT-generated anharmonic potential energy surfaces. We find that the OH stretching frequencies of intact water molecules on the surface are always downshifted with respect to the gas-phase species while the OH− groups are either upshifted or downshifted. Despite these differences, the main characteristics of the frequency shifts for all three types of surface OH groups (OHw, OsH and OHf) can be accounted for by one unified expression involving the in situ electric field from the surrounding environment, and the gas-phase molecular properties of the vibrating species (H2O or OH−). The origin behind the different red- and blueshift behaviour can be traced back to the fact that the molecular dipole moment of a gas-phase water molecule increases when an OH bond is stretched, but the opposite is true for the hydroxide ion. We propose that familiarity with the relations presented here will help surface scientists in the interpretation of vibrational OH spectra for thin water films on ionic crystal surfaces.
1. Introduction
The stabilities, structures, and reactivities of metal oxide surfaces and nanoparticles under ambient conditions are strongly affected by their hydration–hydroxylation. Here especially the water molecules residing closest to the metal oxide are targets of intense scientific interest as they are the molecules most drastically modified by the surface and often even subject to dissociation. Spectroscopic signals from dissociated and intact water molecules on many metal oxide surfaces have been presented in the literature over the years (see, for example, ref. 1–9) and here vibrational and electron spectroscopies have emerged as being especially informative. Thus, recently, some of the seemingly most simple and prototypic water/oxide systems, such as H2O/MgO(100),2,3 H2O/CaO(100),5,6 H2O/ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)8 and H2O/rutile-TiO2(110),9 have been targets of vibrational spectroscopic studies of various flavors such as IRRAS (Infrared reflection–absorption spectroscopy), SFG (sum-frequency generation), and FTIR (Fourier transform Infra-red) spectroscopy with an ATR (attenuated internal total reflection) device.
0)8 and H2O/rutile-TiO2(110),9 have been targets of vibrational spectroscopic studies of various flavors such as IRRAS (Infrared reflection–absorption spectroscopy), SFG (sum-frequency generation), and FTIR (Fourier transform Infra-red) spectroscopy with an ATR (attenuated internal total reflection) device.
Theoretical investigations are critically important in the field of vibrational spectroscopy, and most of the experimental studies today contain supporting vibrational calculations. The special value of calculations is that they can provide both detailed local structure information and detailed, well resolved, spectral information: together these two advantages help to decipher complex experimental spectra for complex systems. Moreover, such calculations often have the power to take us further and provide an explanation, or a rationale, behind the experimentally observed spectral features. The objective of this paper is to present a unifying, systematizing framework that relates the vibrational dynamics of surface OH groups to their chemical environment for both OH− and H2O simultaneously.
We will show that in the analysis of experimental or calculated OH spectra it is not helpful to treat all groups as water-like. We find that all the dissociated OH groups present for different water coverages on MgO(001) and CaO(001) are indeed hydroxide ions, and this has consequences for how they respond to perturbations from their environments. Thus we find that the intact water molecules on the surface are always downshifted with respect to the unperturbed (gas-phase) molecule while the OH− groups are either upshifted or downshifted with respect to the gas-phase ion. We will also show that in spite of these differences it is possible to treat the surface water molecules and surface hydroxide ions on an equal footing, using a simple and intuitive electrostatic analysis involving the electric field from the surroundings as the descriptor. The electric field has been found to be quite a useful local useful local descriptor in the context of the OH vibrational downshift of perturbed water molecules in various situations, such as in uniform electric fields in the gas phase,10,11 water clusters,12,13 liquid water,14,15 and in crystalline hydrates.16 However, as far as we are aware, our treatment in this paper represents a new way of looking at OH vibrations on ionic surfaces.
Our hope is that our new model will simplify future interpretations of water OH vibrational spectra for surface systems where electrostatic interactions play an important role, which is the case on metal oxide surfaces.
2. Systems and methods
2.1 Systems
Water clusters (monomers, dimers, and trimers) on MgO(001) and CaO(001) as well as overlayers of 1.0 and 1.25 monolayer (ML) coverages are studied in this paper. Two of these structures are shown in Fig. 1. A full monolayer is defined as 1 adsorbed water molecule per surface cation (or formula unit). The starting geometries for the geometry optimizations were taken from the previously reported 1.0 ML and 1.25 ML overlayer structures on MgO(001) and CaO(001) by Włodarczyk et al.2 and Zhao et al.,5 respectively. For the overlayers and the trimer on MgO(001), some of the water molecules dissociate and form two types of hydroxides, namely OsH or OHf. The s in Os stands for “surface” and the f in Hf stands for “free”. Due to the stronger basicity of CaO, water molecules near its surface are more likely to dissociate than in the case of MgO, and to give rise to many non-equivalent OH groups.Altogether we examine 56 structurally unique intact H2O molecules and 34 structurally unique OH− ions, covering a range of different situations from weak to strong “intermolecular” interactions. The H2O/MgO(001) and H2O/CaO(001) systems were modelled as 3-D periodic boxes, consisting of slabs of four substrate layers, plus the water adsorbate layer and a 15 Å thick vacuum region. The calculated lattice constants of 4.25 Å for bulk MgO(001) and 4.83 Å for bulk CaO(001) were used to build the clean slabs. In all interface calculations, water molecules were adsorbed only on one side of the slab.
2.2 Electronic structure calculations
We recently found17 that the optPBE-vdW functional18 predicted the adsorption energy of water on MgO(001) in agreement with the experimental isosteric heat of adsorption, and we have chosen this functional for our study here. All calculations were performed with the VASP program.19–22 The electron-core interactions were described using the PAW formalism.23,24 For H, O, Mg and Ca, the 1s1, 2s22p4, 2p63s2 and 3p64s2 electrons, respectively, were treated as valence electrons. All calculations were performed with a plane-wave kinetic energy cutoff of 400 eV and a 4 × 4 × 1 Monkhost–Pack k-point mesh. Only the Γ point was used for the gas-phase water molecule and hydroxide ion. We used Gaussian smearing with a width of 0.1 eV in all cases.Full geometry optimizations were performed for all atoms in all systems, except that the atoms residing in the two “bottom” layers of the ionic slabs were kept fixed. The conjugate-gradient algorithm was used for the structure optimizations and cell parameters and atomic coordinates were considered to be converged when the forces acting on the atoms were less than 0.0021 eV Å−1. A convergence criterion of 10−7 eV for the total energy was used in the electronic self-consistent calculations.
2.3 Calculation of anharmonic OH frequencies
We have calculated all OH stretching vibrational frequencies using a 1-dimensional (1D) uncoupled OH vibrational model. In this model, each OH potential energy curve is constructed so as to allow the vibrating OH bond (in a H2O molecule or OH− group) to contract and stretch along the OH bond, keeping the center of mass of the OH group fixed while the remaining parts of the system were kept fixed at their optimized positions. We used a reduced mass of 0.94808 amu for the vibrating OH oscillator and 19 energy points were generated along the potential energy curve with a step size of 0.06 Å. More precisely, we used 12 energy points above and 7 below the equilibrium OH distance, re.The 1D vibrational Schrödinger equation was then solved for the vibrational energy levels using the discrete variable basis-set representation (DVR) approach of Light et al.25,26 The anharmonic stretching frequencies were calculated by taking the energy difference between the ground and first excited vibrational eigenstates.
This computational approach has previously been used by us to calculate OH frequencies of water molecules and hydroxide ions in crystals16,27,28 and on surfaces29 as well as in liquid water30 and ionic aqueous solutions.31
2.4 Calculation of electric field from the environment
The external electric field exerted on the surface OH groups from its surroundings is a central concept in this study. For an OH oscillator that belongs to an intact water molecule all neighbours outside that water molecule constitute the external world. Other appropriate names for this field might have been the in situ field, on-site field, or perhaps intrinsic field to pinpoint that we are not dealing with any externally applied electric field, but we have chosen the term external field to emphasize that it is generated by all the short- and long-range neighbours outside the targeted hydroxide ion or water molecule.Wannier orbitals and their centres32 were calculated from the final electronic wave function using the WANNIER90 program.33 The electric field generated by the surroundings at a probe site was calculated from the positions and charges of the Wannier centres and the nuclei (with any accompanying core electrons as described by the PAW pseudopotentials) using the GULP34 program. The on-site electric field calculated with this program contains both the self-field of the probed water molecule (or hydroxide ion) itself and the external electric field from the surroundings. Since we want to describe the effect of the gas-to-surface OH frequency shifts in terms of the surroundings only, the self-field generated by the internal charge sites of the probed water molecule or hydroxide ion were removed “manually” from the total on-site field value.
For each investigated OH group, in each of our structurally optimized surface systems, the equilibrium position of the H nucleus was selected as the probe site where the electric field strength was evaluated, and it is the field component along the OH bond that was monitored, as we have found that the electric field components perpendicular to the vibrating OH bond have only a negligible effect on the OH frequency. We denote it E‖, sometimes E‖@H. The field direction is defined according to the standard physics definition (i.e. from plus to minus).
2.5 Calculation of molecular dipole moments and dipole moment derivatives
The dipole moments of the isolated (μ0) water molecule and hydroxide ion were calculated from the positions and charges of their nuclei and four occupied Wannier centers, and similarly for the species on the surface (μbound). The induced dipole moment was calculated from μbound − μ0. The dipole moments were calculated with respect to the center-of-mass of the oscillating OH bond. For water, the dipole moment value does not depend on the reference position. For the charged hydroxide ion it does, but the expressions that we will make use of involve the first derivatives of dipole moments with respect to rOH, and therefore the choice of reference point will again be unimportant. The dipole moment derivative was evaluated at the bound state equilibrium distance re,bound, using a 5-point numerical differential formula.3. Results
3.1 The electric field as the origin of the gas-to-surface frequency shifts
The calculated uncoupled, anharmonic OH frequencies, ν(OH), for the intact water molecules, adsorbed on either MgO(001) or CaO(001) are plotted in Fig. 2a. They span a large range, from about 3600 cm−1 down to about 2100 cm−1. Actually, this is also true for most of the individual adsorbate systems in the figure, except for the smallest water clusters. Note that the spread is not due to couplings, as these are uncoupled vibrations; instead, the spread directly mirrors the spread in the strengths of the external perturbations exerted from the surroundings on the individual water molecules. Going now to the dissociated water molecules in Fig. 2c, we find somewhat more structure in the data points: one highly populated group of frequencies between about 3600 and 3470 cm−1, immediately below which there is a more sparsely distributed group with values all the way down to about 2000 cm−1. We can identify the uppermost group of frequencies with the structural motif that is commonly referred to as the OHf type in the literature. The frequencies lying between about 3410 and 3300 cm−1 originate from OsH groups that are weakly bound to OHf. Finally, the more low-lying set of frequencies also originate from OsH groups, but those which are strongly bound to the OHf.In order to bring some logics and systematics into the presentation of all these data we display the same data in Fig. 2b and d, but now plotted against the probed electric field strength E‖. The result is impressive: all points nicely follow arc-like curves. The two curves are similar but not identical. The largest frequency in Fig. 2b lies close to E‖ = 0.0 a.u, but in Fig. 2d it occurs at E‖ ≈ 0.05 a.u., below which no frequencies can be found since none of the hydroxide groups in our sample experiences small external fields. The latter may partly be a consequence of the relatively small tilts of the OH− groups from the surface normal compared to the water molecules which often lie flat on the surface (cf.Fig. 1b). It may also be so that environments giving smaller fields than 0.05 a.u. do not lead to water dissociation. In each of the two figures we have marked the frequencies at E‖ = 0.0, i.e. the gas-phase frequencies. We note that for the intact water molecules all the frequencies are downshifted (red-shifted) with respect to this point while for the dissociated water molecules there exist oscillators which are upshifted (blue-shifted) with respect to the gas-phase value.
The two frequency vs. field curves just discussed are shown together in Fig. 3, together with the corresponding curves (dashed) obtained from MP2 calculations presented in ref. 10 for a water molecule and a hydroxide ion exposed to uniform electric fields of varying strengths directed along the OH stretch coordinate. The frequency-field curves in ref. 10 were found to be parabola-like for both water and hydroxide, but with their respective maxima at different positions. For H2O, the maximum was found10,11 to lie to the left of the zero-field line (cf.Fig. 3) resulting in redshifts for all positive (i.e. natural, realistic) fields. This is indeed consistent with experimental data: we are not aware of any experimental situation or system where an OH oscillator belonging to a bound water molecule is not red-shifted compared to the gas-phase water frequency. For the OH− ion in a uniform electric field, on the other hand, the maximum was found to lie on the positive field side.10 This implies that at small and intermediate fields, a frequency upshift with respect to the gas-phase frequency will occur, while with increasing fields finally very large downshifts appear. Indeed it is known from experiments, e.g. by Lutz and his co-workers,35–37 that hydroxide ions in crystalline hydroxides display both downshifts and upshifts compared to the gas-phase OH− frequency.
 | ||
| Fig. 3 The same correlations as in Fig. 2(b) and (d) but here the water and hydroxide OH groups are plotted together to highlight that they follow two different ‘ν(OH) vs. E‖’ correlations. The dashed curves are taken from ref. 10 where the author performed MP2 calculations for a water molecule and a hydroxide ion in uniform electric fields of varying strengths. Here and in the following, the circles for the data points have the same meaning as in Fig. 2. | ||
In this paper, we observe that the surface OH groups found on the hydrated–hydroxylated MgO and CaO surfaces qualitatively follow the behaviour of the two ideal uniform-field systems. Thus, the intact surface water molecules essentially follow the uniform-field curve for H2O, while the OHf (blue half-filled rings) and OsH (red half-filled rings) data points display a similar behaviour to the uniform-field curve for the OH− ion. Bader-type atomic charges38 were calculated, and the net charges of the dissociated water OH groups in the various MgO and CaO surface systems studied here were found to lie in the range from −0.7 to −0.9 e, i.e. they can be classified as hydroxide ions. It is interesting to note that all the OHf groups in our sample accumulates close to the turning point of the frequency vs. field curve, while the OsH groups lie further to the right on the curve. The former are all blueshifted with respect to the gas-phase OH− ion, while all of the OsH vibrations (except one) are redshifted, most of them even strongly so. We believe that these findings are likely to hold for hydroxylated metal oxide surfaces in general, at least in the absence of a second water layer.
3.2 Perturbation from the surface and the co-adsorbates
In this section, we will provide a rationale behind the different water and hydroxide OH frequency redshift and blueshift behaviour displayed in Fig. 3. One of our intact surface water molecules is used as the example in Fig. 4a, namely the water monomer on the MgO(001) surface, and more specifically the OH leg which binds to the surface (cf.Fig. 1a). The black curve in the figure (Vgas, or equivalently, V0) is the calculated potential energy for the isolated gas-phase molecule, with rOH being the uncoupled OH stretching coordinate. The red curve marked Vbound is the corresponding calculated potential energy for our selected water molecule on the surface, shifted so as to coincide with the unperturbed curve at rOH = 0.80 Å.The total perturbation exerted by the environment will be denoted the external potential Vext(rOH), defined by Vbound(rOH) = V0(rOH) + Vext(rOH). Vext is shown in the upper half of Fig. 4a, again shifted so as to coincide with the other two curves at rOH = 0.80 Å.
The Vext curve is seen to have a negative slope at the gas-phase equilibrium distance re,gas and in fact everywhere in the figure, and we claim that the sign of the slope determines the sign of the gas-to-surface frequency shift; this claim will be substantiated in the coming sections.
We now turn to a dissociated water molecule. The bottom part of Fig. 4c presents three parabola-like potential energy curves, one for a surface-bound OsH hydroxide ion (red curve), one for a gas-phase hydroxide ion (black curve) and one for a surface-bound OHf hydroxide ion (blue curve). The upper part of the figure shows the corresponding Vext potential energy curves. As in the previous case, all curves were drawn to coincide for rOH equal to 0.8 Å. The chosen OsH ion is one of the strongly red-shifted OH− groups in Fig. 3, and is seen to be accompanied by a Vext curve with a negative slope everywhere, while the OHf ion is accompanied by a Vext curve with a positive slope in Fig. 4c and it is one of the blueshifted OH groups. This means that our findings are in agreement with our claim above, i.e. that the sign of the slope is consistent with the direction of the frequency shift.
Ten more examples from our bound intact surface water molecules on MgO(100) and CaO(100) are shown in Fig. 4b and seven more of the bound hydroxides in Fig. 4d; a variety of strongly and weakly bound environments are represented in both cases. The water molecules are seen to all have Vext curves with negative slopes everywhere, while the hydroxide ions display either negative (always OsH ions) or positive slopes (always OHf ions), and this is indeed consistent with our results in Fig. 2 and 3 where the OsH groups were all found to be downshifted in frequency compared to the gas-phase ion, and the OHf groups were upshifted. The colour of each curve indicates the direction of our calculated gas-to-surface frequency shift.
In conclusion, Fig. 3 and 4 together paint a consistent picture. All blueshifted OH groups are exposed to an external perturbation with a positive slope, and all redshifted OH groups are exposed to an external perturbation with a negative slope. The effect of an external potential with a negative slope is to move the equilibrium distance to larger values (weaken the bond), and to make the potential energy curve flatter and the harmonic force constant smaller. The opposite in all respects is true for the blueshifted OH oscillators. The curvature of Vext never opposes the shift direction predicted by the slope.
For future reference, we now introduce some notations/definitions:
| V0(rOH) = k02·(rOH − re,gas)2 + k03·(rOH − re,gas)3 +… | (1a) |
| Vbound(rOH) = kbound2·(rOH − re,bound)2 + kbound3·(rOH − re,bound)3 +… | (1b) |
| Vext(rOH) = kext1·(rOH − re,gas) + kext2·(rOH − re,gas)2 +… | (1c) |
The centers of the expansions for the free and bound potentials are their respective equilibrium distances, thereby removing a linear term. For the external potential the center has been chosen to be re,gas. With these definitions we find that the shift of the harmonic force constant up to the quadratic term becomes10
 | (2) |
In a perturbative treatment both the harmonic frequency shift (Δω = ωbound − ω0) and the anharmonic frequency shift (Δν = νbound − ν0) are related to Δk2 through the following relations
 | (3a) |
 | (3b) |
A derivation of the last two equations is presented in the Appendix.
Eqn (2) allows us to make a more quantitative comparison of the impacts of the kext1 and kext2 terms on the harmonic force constant Δk2 and thereby also on the OH frequency shifts by way of eqn (3a) and (3b). Thus for each OH oscillator in our study, a quadratic fit to the VASP-calculated external potential Vext was performed and Fig. 5 displays Δk2 as a function of the field at each OH oscillator. It is seen that for both intact and dissociated water molecules, eqn (2) is dominated by the kext1 term. For fields up to about 0.1 a.u., which is the field range where the qualitative redshift/blueshift difference between water and OH− manifests itself, it is sufficient to approximate the external potential as being linear in the stretch coordinate. For both water and hydroxide, k02 is positive and k03 is negative, and so the sign of the prefactor of kext1 is positive and the sign of kext1 will determine the sign of Δk2.
In the next subsection we present a simple electrostatic model to understand the rationale behind the field variations of the frequencies of the surface OH oscillators. In that model we will use eqn (2), setting kext2 = 0.
3.3 Interpretation – a dipolar model gives the direction
The number written to the right of each Vext curve in Fig. 4b and d is the field value that we have discussed extensively already, i.e. the field parallel to the vibrating OH bond, produced by surrounding charges, and evaluated at the bound H equilibrium position, re,bound. This is now our descriptor of the external environment of each surface OH group.In ref. 10 and 11, as mentioned, isolated water and OH− species in uniform electric fields were studied, and it was shown that, in both cases, Vext is well approximated by a dipolar electrostatic model. Here we propose to use the same model with the uniform field being replaced by E‖@H. Using the expressions given in ref. 10 and 11 and applying eqn (1c), we get
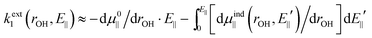 | (4) |
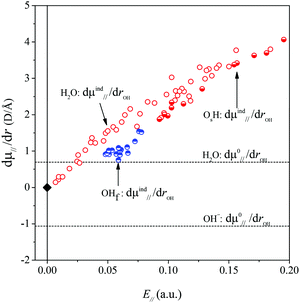
As we are primarily interested in a qualitative analysis, we assume that dμind‖ (rOH, E‖)/drOH is approximately proportional to the field over an appreciably large range of field values. Eqn (4) then becomes
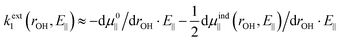 | (5a) |
 | (5b) |
The derivatives are displayed in Fig. 6. The symbol α represents the ‖,‖ component of the dipole polarizability tensor of the OH oscillator, and the prime denotes a differentiation with respect to the stretch coordinate, taken at the gas-phase equilibrium point re,gas. The α′ values were obtained from linear fits to our calculated dμind‖/drOHvs. electric field data, for small to modest field strengths.
Using eqn (2), (3) and (5) we then calculated the harmonic and anharmonic frequency shifts within our dipolar model and plotted the anharmonic shift in Fig. 7, together with the results from our VASP calculations. Given the many of approximations, the results are surprisingly good. We therefore accept the model as a reasonable approximation to reality and analyze the difference in behavior between the water and the hydroxide oscillators.
 | ||
| Fig. 7 Comparison of the DFT results and the dipolar model results for the surface-induced frequency shift Δν = νbound − νgas plotted against E‖. | ||
Inspection of eqn (5a) shows that the sign of dμ0‖/dr and the relative magnitudes of dμ0‖/dr and dμind‖(E‖)/drOH will determine the magnitude and sign of kext1, which in turn will determine the sign and magnitude of Δν and the position of the maximum in the frequency vs. field correlation curves in Fig. 3. We find that all quantities in the second term of eqn (5a) are positive for all the surface OH oscillators while dμ0‖/drOH has different signs for water and hydroxide: +0.62 D Å−1 for water and −1.14 D Å−1 for hydroxide with our chosen DFT functional. It is the sign of dμ0‖/dr which is the ultimate origin behind the different frequency vs. field behavior of the water molecule and the OH− groups in Fig. 3. The negative sign for OH− will give rise to a parabola with a maximum for a positive field value.
This can easily be formalized as follows. From eqn (5b) we find that the frequency shifts as a function of the field lie on concave (since α0′ is positive in all cases) parabola. The maxima of these parabolas occur where  . Since
. Since  is positive for the water oscillator the maximum for the water parabola falls at a negative field value; a negative field value never occurs in the in situ situations studied here, and seldom, if ever, in any equilibrium scenarios in nature either, as they would be energetically unfavourable. As a result the maximum occurs at zero field and all frequencies are downshifted. By a similar reasoning, since
is positive for the water oscillator the maximum for the water parabola falls at a negative field value; a negative field value never occurs in the in situ situations studied here, and seldom, if ever, in any equilibrium scenarios in nature either, as they would be energetically unfavourable. As a result the maximum occurs at zero field and all frequencies are downshifted. By a similar reasoning, since  is negative for the hydroxide oscillator, its maximum frequency shift occurs at a positive field value. The value of kext1 at this point is equal to
is negative for the hydroxide oscillator, its maximum frequency shift occurs at a positive field value. The value of kext1 at this point is equal to 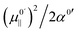 , which is positive. For field values between zero and
, which is positive. For field values between zero and  , the hydroxide oscillator will therefore be upshifted. In our present study no fields occur below
, the hydroxide oscillator will therefore be upshifted. In our present study no fields occur below  , and so all oscillators in fields between
, and so all oscillators in fields between  and
and 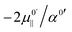 are upshifted.
are upshifted.
The underlying reason for the different signs of dμ0‖/drOH for gas-phase water and hydroxide is related to the fact that when the gas-phase hydroxide ion is stretched, a very complex electron redistribution occurs, which leads to a net decrease in the dipole moment, and simultaneously makes it favourable for the hydroxide to contract when placed in an electric field. The water molecule, on the other hand, behaves like most molecules: the dipole moment increases if the OH bonds are stretched, and the system gains energy by elongating when exposed to an electric field.39
Further analysis performed by us suggests that, seemingly, the almost perfect agreement between the VASP and model results for water at high fields is at least partly due to error compensation. The neglect of the kext2 term in the dipolar model is compensated by a too large slope of the kext1 term in the same model, which in turn is likely due to the neglect of the non-electrostatic interactions (orbital overlap). For the hydroxide on the other hand, we find that the kext1 term from the dipolar model is quite similar to that from VASP, and that it is mainly the lack of the kext2 term that causes the discrepancy with the VASP results.
4. Summary and concluding remarks
This paper is an effort to rationalize the sign and size of the OH frequency shifts observed experimentally for water on metal oxide surfaces, namely OsH, OHf, and OHw groups, the latter from intact water molecules. In total the paper analyses 90 unique surface OH groups – intact water molecules as well as hydroxide groups. The first part of the title of this paper is “Red-shifting and blue-shifting OH groups on metal oxide surfaces”, which reflects the phenomenon that OHw groups appear to always be redshifted by their surroundings at the surface, while the hydroxide ions can be either red- or blueshifted depending on the strength of the OH group's interaction with its environment.The second part of the title is “towards a unified picture” and we have demonstrated, using a simple electrostatic dipolar model, that not only can the surface-induced frequency shift for OsH and OHf be described by one and the same model but also OHw. The model is expressed by eqn (5). All three OH groups are part of the same general scheme where the main ingredients are the external electric field (E‖@H) from the surroundings as well as the permanent and induced dipole moment derivatives along the OH stretching coordinate. We concluded that it is the sign of dμ0/drOH which is the ultimate origin behind the different frequency shifting behaviour of the water molecules and the OH− groups.
Our dipolar model succeeds in describing the qualitative behaviour of gas-to-surface OH frequency shifts on metal oxide surfaces with both molecularly and dissociatively adsorbed water molecules. It may be valuable to extend this work to a broader range of metal oxides, with different ionicity and acid–base properties, in future work. It will also be interesting to explore to what extent this model holds for more water-rich interfaces. Work along this line is underway.
Conflicts of interest
There are no conflicts to declare.Appendix: perturbation model
Since we want to discuss both the harmonic and the anharmonic frequency shifts, we assume that all potential curves can be described by the Morse function| V(rOH) = De·[1 − exp(−a(rOH − re))]2 | (A1) |
 | (A2) |
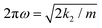 , as can also be seen by putting k3 equal to zero (m is the reduced mass of the oscillator).
, as can also be seen by putting k3 equal to zero (m is the reduced mass of the oscillator).
The total potential energy curve is then represented by the sum of an unperturbed gas-phase part augmented with a small perturbation. Since the perturbation can be represented by a quadratic polynomial, we may set kbound3 = k03 and kbound2 = k02 + Δk2 with Δk2 being small. Notice that k02 is half the second derivative of the gas-phase potential energy curve, at the re,gas value, etc. To first order in the small parameter we then get that the anharmonic frequency shift Δν = νbound − ν0 is given by
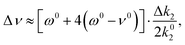 | (A3) |
An expression for Δk2 can be obtained by applying a second-order perturbation to the Vgas potential energy curve,10 defined in eqn (1a) in the main text.
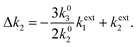 | (A4) |
The expression for the harmonic shift, Δω is obtained by putting the second term between brackets equal to zero, or, equivalently, by setting ν0 equal to ω0. Since k02 is positive for both OHw and OH− and k03 is negative, we conclude that both contributions to Δk2 have the same sign. As long as kext1 and kext2 have the same sign, one may say that either of them determines the sign of Δk2. With the first contribution to Δk2 being the largest, we conclude that the sign of kext1 determines the sign of Δk2. Moreover, since the factor between square brackets in the expression for Δν is always positive, we conclude that indeed the sign of kext1 determines the sign of the gas-to-surface frequency shift.
Acknowledgements
This work is supported by the Swedish Research Council (Vetenskapsrådet). Funding from the National Strategic e-Science program eSSENCE is greatly acknowledged. The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX and NSC.References
- J. Heidberg, B. Redlich and D. Wetter, Adsorption of Water Vapor on the MgO(100) Single Crystal Surface, Berichte Bunsenges. Für Phys. Chem., 1995, 99, 1333–1337 CrossRef CAS.
- R. Włodarczyk, M. Sierka, K. Kwapień, J. Sauer, E. Carrasco, A. Aumer, J. F. Gomes, M. Sterrer and H.-J. Freund, Structures of the Ordered Water Monolayer on MgO(001), J. Phys. Chem. C, 2011, 115, 6764–6774 Search PubMed.
- E. Carrasco, A. Aumer, J. F. Gomes, Y. Fujimori and M. Sterrer, Vibrational spectroscopic observation of ice dewetting on MgO(001), Chem. Commun., 2013, 49, 4355–4357 RSC.
- M. J. D. Low, N. Takezawa and A. J. Goodsel, Infrared study of hydroxyls on active CaO, J. Colloid Interface Sci., 1971, 37, 422–429 CrossRef CAS.
- X. Zhao, X. Shao, Y. Fujimori, S. Bhattacharya, L. M. Ghiringhelli, H.-J. Freund, M. Sterrer, N. Nilius and S. V. Levchenko, Formation of Water Chains on CaO(001): What Drives the 1D Growth?, J. Phys. Chem. Lett., 2015, 6, 1204–1208 CrossRef CAS PubMed.
- Y. Fujimori, X. Zhao, X. Shao, S. V. Levchenko, N. Nilius, M. Sterrer and H.-J. Freund, Interaction of Water with the CaO(001) Surface, J. Phys. Chem. C, 2016, 120, 5565–5576 CAS.
- H. Noei, H. Qiu, Y. Wang, E. Löffler, C. Wöll and M. Muhler, The identification of hydroxyl groups on ZnO nanoparticles by infrared spectroscopy, Phys. Chem. Chem. Phys., 2008, 10, 7092–7097 RSC.
- F. Viñes, A. Iglesias-Juez, F. Illas and M. Fernández-García, Hydroxyl Identification on ZnO by Infrared Spectroscopies: Theory and Experiments, J. Phys. Chem. C, 2014, 118, 1492–1505 Search PubMed.
- G. A. Kimmel, M. Baer, N. G. Petrik, J. VandeVondele, R. Rousseau and C. J. Mundy, Polarization- and Azimuth-Resolved Infrared Spectroscopy of Water on TiO2(110): Anisotropy and the Hydrogen-Bonding Network, J. Phys. Chem. Lett., 2012, 3, 778–784 CrossRef CAS PubMed.
- K. Hermansson, Redshifts and blueshifts of OH vibrations, Int. J. Quantum Chem., 1993, 45, 747–758 CrossRef CAS.
- K. Hermansson, Electric-field effects on the OH vibrational frequency and infrared absorption intensity for water, J. Chem. Phys., 1993, 99, 861–868 CrossRef CAS.
- S. Sen, M. Boda, S. V. Lata and G. N. Patwari, Internal electric fields in small water clusters [(H2O)n; n = 2–6], Phys. Chem. Chem. Phys., 2016, 18, 16730–16737 RSC.
- K. Hermansson, J. Lindgren and M. M. Probst, Non-additivity of OH frequency shifts in ion-water systems, Chem. Phys. Lett., 1995, 233, 371–375 CrossRef CAS.
- S. A. Corcelli, C. P. Lawrence and J. L. Skinner, Combined electronic structure/molecular dynamics approach for ultrafast infrared spectroscopy of dilute HOD in liquid H2O and D2O, J. Chem. Phys., 2004, 120, 8107–8117 CrossRef CAS PubMed.
- B. M. Auer and J. L. Skinner, IR and Raman spectra of liquid water: Theory and interpretation, J. Chem. Phys., 2008, 128, 224511 CrossRef CAS PubMed.
- A. Sen, P. D. Mitev, A. Eriksson and K. Hermansson, H-bond and electric field correlations for water in highly hydrated crystals, Int. J. Quantum Chem., 2016, 116, 67–80 CrossRef CAS.
- G. G. Kebede, D. Spångberg, P. D. Mitev, P. Broqvist and K. Hermansson, Comparing van der Waals DFT methods for water on NaCl(001) and MgO(001), J. Chem. Phys., 2017, 146, 064703 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. C. Light, I. P. Hamilton and J. V. Lill, Generalized discrete variable approximation in quantum mechanics, J. Chem. Phys., 1985, 82, 1400–1409 CrossRef CAS.
- Z. Bacic and J. C. Light, Theoretical Methods for Rovibrational States of Floppy Molecules, Annu. Rev. Phys. Chem., 1989, 40, 469–498 CrossRef CAS.
- P. D. Mitev, A. Eriksson, J.-F. Boily and K. Hermansson, Vibrational models for a crystal with 36 water molecules in the unit cell: IR spectra from experiment and calculation, Phys. Chem. Chem. Phys., 2015, 17, 10520–10531 RSC.
- K. Hermansson, G. Gajewski and P. D. Mitev, Origin of the OH Vibrational Blue Shift in the LiOH Crystal, J. Phys. Chem. A, 2008, 112, 13487–13494 CrossRef CAS PubMed.
- G. G. Kebede, P. D. Mitev, P. Broqvist, J. Kullgren and K. Hermansson, Hydrogen-Bond Relations for Surface OH Species, J. Phys. Chem. C, 2018, 122, 4849–4858 CAS.
- K. Hermansson, S. Knuts and J. Lindgren, The OH vibrational spectrum of liquid water from combined ab initio and Monte Carlo calculations, J. Chem. Phys., 1991, 95, 7486–7496 CrossRef CAS.
- K. Hermansson, P. A. Bopp, D. Spångberg, L. Pejov, I. Bakó and P. D. Mitev, The vibrating hydroxide ion in water, Chem. Phys. Lett., 2011, 514, 1–15 CrossRef CAS.
- N. Marzari and D. Vanderbilt, Maximally localized generalized Wannier functions for composite energy bands, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 12847–12865 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Wannier90: a tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- J. D. Gale, GULP: a computer program for the symmetry-adapted simulation of solids, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- H. D. Lutz, H. Möller and M. Schmidt, Lattice vibration spectra. Part LXXXII. Brucite-type hydroxides M(OH)2 (M = Ca, Mn, Co, Fe, Cd)—IR and Raman spectra, neutron diffraction of Fe(OH)2, J. Mol. Struct., 1994, 328, 121–132 CrossRef CAS.
- H. D. Lutz, Coordination Chemistry, Springer, Berlin, Heidelberg, 1995, pp. 85–103 Search PubMed.
- B. Weckler and H. D. Lutz, Near-infrared spectra of M(OH)Cl (M = Ca, Cd, Sr), Zn(OH)F, γ-Cd(OH)2, Sr(OH)2, and brucite-type hydroxides M(OH)2 (M = Mg, Ca, Mn, Fe, Co, Ni, Cd), Spectrochim. Acta, Part A, 1996, 52, 1507–1513 CrossRef.
- R. F. W. Bader and C. F. Matta, Atomic Charges Are Measurable Quantum Expectation Values:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Rebuttal of Criticisms of QTAIM Charges, J. Phys. Chem. A, 2004, 108, 8385–8394 CrossRef CAS.
A Rebuttal of Criticisms of QTAIM Charges, J. Phys. Chem. A, 2004, 108, 8385–8394 CrossRef CAS. - K. Hermansson, OH bonds in electric fields: electron densities and vibrational frequency shifts, Chem. Phys. Lett., 1995, 233, 376–382 CrossRef CAS.
| This journal is © the Owner Societies 2018 |