Is a cross-β-sheet structure of low molecular weight peptides necessary for the formation of fibrils and peptide hydrogels?†
Niranjan V.
Ilawe
a,
Reinhard
Schweitzer-Stenner
*b,
David
DiGuiseppi
b and
Bryan M.
Wong
 *a
*a
aDepartment of Chemical & Environmental Engineering, and Materials Science & Engineering Program, University of California-Riverside, Riverside, CA 92521, USA. E-mail: bryan.wong@ucr.edu; Web: http://www.bmwong-group.com Tel: +1-951-827-2163
bDepartment of Chemistry, Drexel University, Philadelphia, PA 19104, USA. E-mail: rschweitzer-stenner@drexel.edu; Web: http://www.schweitzer-stenner.com Tel: +1-215-895-2268
First published on 17th April 2018
Abstract
Short peptides have emerged as versatile building blocks for supramolecular structures and hydrogels. In particular, the presence of aromatic amino acid residues and/or aromatic end groups is generally considered to be a prerequisite for initiating aggregation of short peptides into nanotubes or cross β-sheet type fibrils. However, the cationic GAG tripeptide surprisingly violates these rules. Specifically, in water/ethanol mixtures, GAG peptides aggregate into very long crystalline fibrils at temperatures below 35 °C where they eventually form a spanning network structure and, thus, a hydrogel. Two gel phases are formed in this network, and they differ substantially in chirality and thickness of the underlying fibrils, their rheological parameters, and the kinetics of oligomerization, fibrilization, and gel formation. The spectroscopic data strongly suggests that the observed fibrils do not exhibit canonical cross β-sheet structures and are indicative of a yet unknown secondary conformation. To complement our unusual experimental observations in this perspective article, we performed large-scale DFT calculations to probe the geometry and spectroscopic properties of these GAG oligomers. Most importantly, our experimental and computational results yield rather unconventional structures that are not reminiscent of classical cross-β-sheet structures, and we give two extremely likely candidates for oligomer structures that are consistent with experimental amide I′ profiles in IR and vibrational circular dichroism (VCD) spectra of the two gel phases.
1 Introduction
The folding of a polypeptide into a conformation with a well-defined secondary and tertiary structure generally requires that it contain 100 residues or more. This is close to the chain length that is necessary to produce a well-defined hydrophobic core. Additionally, with regard to the secondary structure of folded proteins, right-handed α-helices, β-sheets, and a variety of other turn structures are of similar importance. Their respective contribution depends on the specifics of the amino acid sequence. However, over the last 15–20 years, β-sheets in particular, have gained prominence in the field of protein and peptide science, since they have emerged as the dominant secondary structures in protein and peptide aggregates such as amyloid fibrils.1–6 However, several differences between β-sheets in proteins and amyloid fibrils are noteworthy. In proteins, the need for compactness frequently gives rise to highly twisted structures of β-sheets and bent structures of strands. β-sheet barrels in protein-like porin7 or the horseshoe structure of ribonuclease inhibitors are good examples of these, which are composed of an outer shell of α-helices and an inner shell of highly curved β-sheets.8 On the contrary, amyloid fibrils are formed by extended cross β-sheets that can extend over hundreds of nanometers. Compared with the situation in proteins, sheet twisting (if existing at all) is helical and regular (ca. 0–20° per strand).9–11 This facilitates stacking and, thus, the development of protofibrils and fibrils.12 While the classical folding process generally requires fairly long polypeptide chains, β-sheet dominated ordered aggregates can be formed even with very short peptides comprised of only two or three residues.13–15 This is indicative of a unique stability bestowed by this secondary structure onto such peptide aggregates.1Over the last ten years, such short low-molecular weight peptides with two or three peptide groups have emerged as a versatile tool for a bottom-up approach towards the formation of a variety of supramolecular nanostructures such as tubes, spheres, and tapes.4,6,16–18 Research in this field was initiated by the discovery of the Gazit group which found that even diphenylalanine peptides can self-aggregate into nanotubes in hexafluoro-2-propanol.19 Furthermore, modifications of this peptide by the addition of aromatic (fluorenylmethoxycarbonyl, Fmoc) and aliphatic (tert-butyloxycarbonyl, t-Boc) end groups have substantially increased the propensity for self-assembly.17,18,20–22 For example, the replacement of phenylalanine groups by less hydrophobic groups in these systems does not impede the formation of nanostructures.6,21–23 Similarly, adding an Fmoc group to the N-terminal of even partially aromatic di- and tripeptides facilitates the formation of hydrogels if the peptide is dissolved in dimethylsuloxide followed by a dilution in water.21 Gelation of such Fmoc-terminated peptides can be achieved in water by first dissolving the peptide at alkaline pH followed by a switch to acidic pH in order to protonate the C-terminal carboxyl group.24,25 These hydrogels exhibit quite substantial strength as documented by their large modulus (G′) values, which generally lie in the 103 Pa regime, and by their rather large loss factor (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ 0.2).20 The self-aggregation of all these peptides is thought to be driven by π–π stacking between aromatic groups, which facilitates the formation of β-sheets and higher order structures such as β-sheet-containing ribbons, tapes, and fibrils.21,26,27 The pivotal role of these π–π interactions for the stacking of β-sheets has recently been highlighted by computational work done by the Ulijn group,14 who predicted that dipeptides with strong aromatic side chains (i.e. F and W) show the highest propensity for aggregation and self-assembly into higher order structures. However, somewhat at variance with the predictions of the above study, recent studies revealed that FmocAA can self-assemble into hydrogels with rather large G′ values (ca. 5 kPa) and intermediate loss factors (0.035).25
δ ≈ 0.2).20 The self-aggregation of all these peptides is thought to be driven by π–π stacking between aromatic groups, which facilitates the formation of β-sheets and higher order structures such as β-sheet-containing ribbons, tapes, and fibrils.21,26,27 The pivotal role of these π–π interactions for the stacking of β-sheets has recently been highlighted by computational work done by the Ulijn group,14 who predicted that dipeptides with strong aromatic side chains (i.e. F and W) show the highest propensity for aggregation and self-assembly into higher order structures. However, somewhat at variance with the predictions of the above study, recent studies revealed that FmocAA can self-assemble into hydrogels with rather large G′ values (ca. 5 kPa) and intermediate loss factors (0.035).25
All the above-cited studies on short peptides are indicative of a mutual dependence of β-sheet propensity and hydrophobic interactions as the driving force that causes the formation of supramolecular structures by low molecular weight peptides. Therefore, it came as a surprise when Milorey et al. reported the formation of a rather peculiar hydrogel after dissolving ca. 200 mM cationic GAG in 55 mol% ethanol/45 mol% water.28 A bright field microscopy image revealed a sample spanning network of crystalline-like fibrils with several hundred micrometers in length. Subsequently, DiGuiseppi et al. found that neutral zwitterionic GHG forms a similar hydrogel at even tenfold lower concentrations in water.29 Even though the imidazole ring of histidine carries some hydrophobicity, its propensity for self-assembly is generally not considered as large as the previously mentioned aromatic groups.15 Rheological experiments revealed rather large G′ values (20 kPa at 23 °C and nearly 100 kPa at 10 °C) and a moderate loss factor (0.035 at 23 °C and ca. 0.04 at 10 °C) for GAG in ethanol/water.30
Thus far it has been generally assumed that supramolecular structures formed by even very short di- and tripeptides underlie canonical cross β-sheet conformations of protofilaments. However, this notion has recently been challenged for the aggregation process which precedes the gelation of FmocAA in acidic aqueous solution. Mostly based on the result of MD simulations, Mu et al. proposed that even in the aggregated state, the alanine residues predominantly sample polyproline II (pPII) conformations.24 In principle, this claim seems credible since a plethora of experimental results obtained over the last ten years clearly suggest that alanine residues have a very high propensity for pPII in water with mole fractions between 0.7 and 0.85.31–34 However, it is unclear how this conformation can be maintained in sheet-like structures. A rather detailed analysis of the amide I′ band spectrum of FmocAA gels led Fleming et al. to the opposite conclusion, and they interpret the observed position of amide I′ bands as a clear indicator of a cross-β-sheet structure.35 In a more recent paper, Eckes et al. reaffirmed the non-β-sheet option based on somewhat indirect evidence from diffraction patterns and the gelation of a modified peptide FmocALac (lactic acid).25 The authors utilize a comparison of their gelators' IR spectra to argue that they cannot be used as an indicator of a β-sheet structure.
Somewhat stronger evidence for the possibility that short peptides can self-aggregate into rather long non-β-sheet structures recently emerged from the IR-spectra of GAG gels formed in water/ethanol, which shows amide I′ regions that are clearly distinct from the classical β-sheet spectrum (vide infra). This observation is more meaningful than a similar one made with FmocAA, because the intrinsic spectral differences between the amide I′ modes of the carbamate (N-terminal) and the peptide group (N-terminal) of the latter complicates the spectral analysis. The canonical redshift of amide I can be expected even for β-sheet structures formed by very short peptides with, e.g., only two peptide groups, owing to comparatively strong interstrand excitonic coupling between adjacent strands.36 In the case of GAG in the utilized water–ethanol mixtures, the mixing of wavefunctions is further facilitated by the close proximity of the wavenumbers of the N- and C-terminal amide I′ modes.37 The absence of a canonical β-sheet structure in the GAG gel phases are further corroborated by their far UV circular dichroism (UVCD) spectra,30 which exhibit a positive, rather than a negative, maximum in the region between 210 and 220 nm. In the case of a cross-β-sheet structure, one would expect a negative maximum. CD spectroscopy is not a suitable tool for the structural analysis of Fmoc-peptides owing to strong interactions between electronic transitions in the Fmoc moiety and the two peptide groups.
This perspective article includes new computational methods to augment and determine possible conformations of GAG oligomers that are consistent with the observed IR and vibrational circular dichroism (VCD) spectra of the two gel phases that we observed for GAG in the above water/ethanol mixtures. We employed additional experimental data (fluorescence and light microscopy) to further demonstrate the difference between the two gel phases. Large-scale DFT calculations were used to obtain two very plausible candidates for the oligomer structures that underlie the crystalline fibrils of GAG gels. To the best of our knowledge this is the first time that a geometry optimization is performed on the peptide oligomers of this size. Specifically, our work identifies two possible structures for which the predicted spectroscopic properties are in excellent agreement with corresponding experimental data. The peculiar properties of the obtained oligomers suggest that they might be representative of oligomers formed by tripeptides in aqueous solutions. Generally, our results demonstrate that DFT calculations can be a formidable tool to explore the peptide conformations in oligomers formed in the initial phase of peptide fibrillization.
2 Materials & methods
2.1 Material
A solvent mixture of 55 mol% ethanol (200 proof, Pharmco-Aaper)/45 mol% deionized water was first prepared. Deuterated solvents, D2O and ethan(ol)-d (EtOD), were purchased for vibrational spectroscopy studies to avoid the interference of the water bending mode with the amide I region as well as vibrational mixing between amide I and water bending modes.38 EtOD is the deuterated ethyl alcohol with the alcoholic hydrogen replaced by a deuterium. D2O and EtOD were purchased from Sigma-Aldrich in 99.9% purity. Solutions of cationic glycylalanylglycine (GAG) (>98% purity, Bachem) were then dissolved in the solvent mixture. The pH of each solution was adjusted to about 2 by adding HCl (ACS grade, Ricca Chemical Company).2.2 Fluorescence spectroscopy
Fluorescence measurements were performed at 10 and 23 °C using a 1 cm path length ICL quartz cell on a Perkin Elmer LS55 Luminescence Spectrometer. Emission spectra were recorded between 450 and 600 nm with a 440 nm excitation wavelength and a scanning speed of 100 nm min−1. Excitation and emission slit widths of 5 and 10 nm, respectively, were used. The temperature was controlled using a PerkinElmer PTP1 Peltier Temperature Programmer and a PCB 1500 Water Peltier System. Samples were allowed to sit at the required temperature for at least two minutes before scanning was performed.2.3 Bright field microscopy
Images were taken using an Olympus Model BX51 Microscope equipped with a PixeLINK PL-A662 camera. A 10× objective lens was used to provide a total magnification of 100×.2.4 Computational methods
All quantum chemical calculations in this study utilized density functional theory (DFT) calculations in conjunction with the dispersion-corrected, range-separated ωB97XD functional as implemented in the Gaussian 09 package. This functional has been previously used by us39–42 and others43–46 to successfully model a variety of different properties in peptide-based systems that involve both dispersion and hydrogen-bonding interactions. All the geometries were optimized with a large cc-pVDZ basis set in the presence of an aqueous polarizable continuum model (PCM). Geometry optimizations and harmonic frequencies at the same level of theory were calculated to verify that these stationary points were local minima. With the vibrational frequencies properly calculated, both the IR and VCD spectral intensities were calculated for all of the considered oligomers. The IR and VCD spectral intensities were calculated using the PyVib247 program which uses the Gaussian checkpoint file as input.3 Results and discussion
3.1 Spectroscopy and microscopy
In an earlier paper, we reported spectroscopic and rheological data that indicated the existence of two different gel phases produced by the self-assembly of GAG in ethanol/water mixtures at temperatures above and below 15 °C, which we now term phase I and II, respectively.28Fig. 1 compares the amide I′ region of the IR and VCD spectra phases formed in 55 mol% ethanol/45 mol% D2O at 10 °C and 23 °C. Differences between the two gel phases are clearly revealed by these data. For example, while two amide I′ bands appear in both IR spectra at 1646 and 1670 cm−1, the band at the lower wavenumber is narrower and more intense in the spectrum of the phase II (10 °C) gel. Moreover, for both phases the IR spectrum does not resemble those of classical β-sheet structures, which are generally dominated by a very strong band between 1610 and 1630 cm−1 even in the spectrum of short peptide fibrils.21,35 Similarly, the very weak band generally observed around 1690 cm−1 in the presence of antiparallel β-sheets is missing in these spectra. The corresponding VCD signals are both large (nearly two orders of magnitude more intense than the common signals of peptide monomers33), but exhibit opposite signs (negative couplet for phase I and a positive one for phase II). Such enhanced VCD signals of amide I′ are generally diagnostic of long helically twisted fibrils.11,48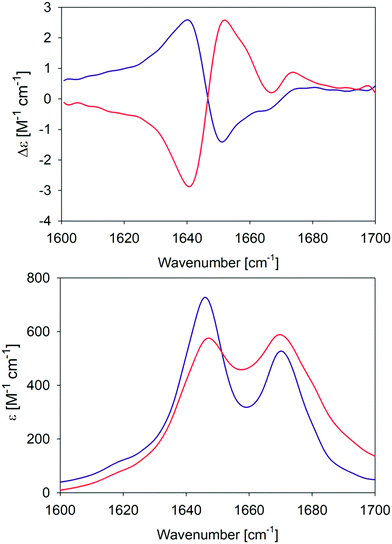 | ||
| Fig. 1 Amide I′ region of the VCD (upper panel) and IR (lower panel) spectra of the GAG gel phase at 10 °C (blue) and 23 °C (red). The two VCD spectra and the IR spectrum of the 10 °C gel phase were already reported by Farrell et al.30 | ||
In order to further characterize the two gel phases, we measured the kinetics of the corresponding fibril formation by recording the time-dependence of thioflavin-T fluorescence (Fig. 2). This fluorophore is a well-established indicator of fibrillization, which normally results from the formation of a supramolecular structure generally formed by the self-assembly of cross β-sheet structures.49 The fluorescence kinetics in Fig. 2 shows a rather peculiar and interesting behavior. At 10 °C, the underlying process is rather fast. The fluorescence exhibits a maximum at ca. 10 minutes and subsequently levels off at a value of 200. Such intermediate maxima are often observed in the fluorescence kinetics of amyloid formation.50–52 These data suggests that fibrillization occurs on a much shorter time scale than gelation (not completed even after 60 minutes) but that it is more or less in sync with the formation of the chiral aggregates probed by the VCD signal of amide I′ (cf.Fig. 8 in Farrell et al.30). It is faster than the corresponding pre-gelation process probed by UVCD that was found to be completed after 25 minutes.
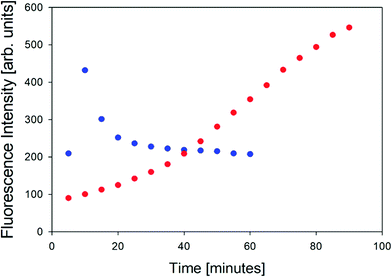 | ||
| Fig. 2 Thioflavin fluorescence intensity measured at approximately 496 nm of the GAG gel at 10 °C (blue) and 23 °C (red). | ||
The situation is totally different at 23 °C. Here, aggregation (probed by IR and VCD), pre-gelation (probed by UVCD), and gelation itself (probed by G′, G′′) proceed on a very similar time scale (completed within ca. 15 minutes), while the fluorescence has reached its maximum only after about 75 minutes. Strangely, this seems to suggest that gelation does not require the formation of fibrils. Alternatively, the data could indicate that protofibrils formed at an earlier state can be crosslinked to achieve gelation, while the local viscosity that the fluorophore probes is still not low enough to induce fluorescence.
The microscopy images reveal differences between the fibrillar structures of the two phases (Fig. 3). In phase I, the fibrils look like thin needles with diameters in the range of 10 μm or less. They can apparently aggregate into thicker bundles and form a rather densely packed sample that spans a structural network in some locations. On the other hand, the image of isolated fibrils in phase II shown in Fig. 3 suggests that they are overall thicker with some thinner fibrils stuck at their periphery. In the more densely packed region of the sample spanning network, the branched character of the fibrils that lead to the formation of fractal structures is clearly observed.
 | ||
| Fig. 3 Bright field microscope image of 200.0 mM GAG in a 0.55 mol% ethanol/45 mol% water formed at 0 °C (left) and 23 °C (right). | ||
All these observations clearly reveal the existence of two different gel phases due to the formation of differently structured peptide fibrils. From the IR spectra, one infers that the corresponding secondary structures are indeed not classical β-sheets. In what follows, we describe the results of large-scale DFT calculations that yield structures of GAG aggregates consistent with our spectroscopic data for amide I′.
3.2 DFT-calculations
We began our DFT calculations with the optimization of a cationic GAG monomer in implicit solvent (water). As expected, this yielded an extended β-strand conformation (Fig. S1, ESI†). Generally, the formation of peptide fibrils involves a nucleation phase in which oligomers of different sizes form an amorphous aggregate, which at some point, converts into a more ordered β-sheet structure in a cooperative ‘folding’ process.53,54 However, the kinetic data reported by Farrell et al. suggest that the formation of more regular structures starts rather early for both gel phases.30 Therefore, we decided to investigate how oligomers of GAG could be formed via hydrogen bonding between the peptide's functional groups (NH, CO, NH3+, and COOH). As recently inferred from spectroscopic data, such an aggregation into ordered structures could be facilitated by the accumulation of peptides at water/ethanol interfaces.37 Accordingly, we started the first calculation by moving two optimized monomers into close proximity (i.e. hydrogen bonding distance) with a parallel orientation to allow for the formation of a dimer. We chose parallel oriented peptides since earlier evidence suggested that in the case of β-sheet aggregation, the helical twisting of a parallel β-sheet structure is more likely to produce an enhancement of amide I′ VCD than the twisting of an antiparallel structure.11 Since the use of an explicit solvent is prohibitively costly at the selected level of theory for any optimization of GAG oligomers, all oligomer calculations were performed in implicit solvent, first in water and subsequently in implicit ethanol, for selected oligomers. Furthermore, all amide and ammonium protons in the oligomers were replaced by deuterons to allow for a direct comparison with our experiment. The dimer structure was then optimized as described in the Materials & methods section. For the trimer structure, we proceeded using the result of the dimer optimization and added an optimized monomer to the structure which was further optimized. Similarly, higher order oligomers were created and optimized in succession by adopting the same concept. This strategy is in line with the expectation on how the primary nucleation step of peptide/protein self-assembly proceeds.50,53 We recently argued, based on spectroscopic data, that this initial formation of oligomers is likely to be caused by the accumulation of peptides at water–ethanol interfaces that catalyze the nucleation process.37 This still somewhat hypothetical model is based on observations of rather different changes of N- and C-terminal amide I band positions and chemical shifts in 1H NMR spectra in response to the addition of ethanol to water.37 The existence of interfaces between non-ideally mixed water and ethanol as well as between water and methanol had earlier been inferred from Raman experiments and MD simulations, respectively.55,56 This process was continued until we obtained an optimized octamer. The final optimized geometries of all the oligomers are shown in Table S4 (ESI†). Fig. S2 and S3 (ESI†) show how the amide I′ region develops in the IR and VCD spectrum of the optimized oligomers. The respective spectra calculated for the heptamer and octamer are shown in Fig. 4. Note that all spectra were normalized on the number of peptides incorporated in the optimized oligomer, so that they are directly comparable. Specifically, for the monomer in implicit water, the calculation yielded two AI′ bands with the band at lower wavenumbers being nearly twice as intense as that at higher wavenumbers. This is in line with expectations for the β-strand structure that emerged from the optimization process. Similarly, the VCD is heavily negatively biased, which is again diagnostic of cationic tripeptides adopting β-strands.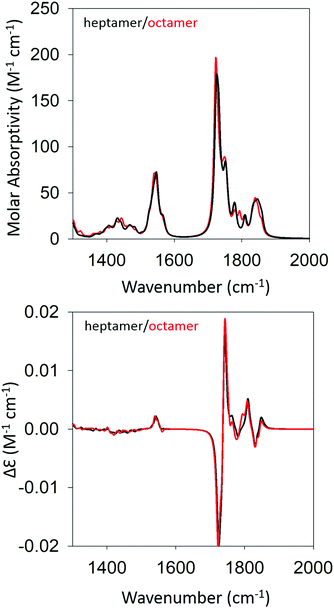 | ||
| Fig. 4 Calculated IR (top) and VCD spectra (bottom) of a geometry optimized GAG heptamer (black) and octamer (red) with parallel strand orientation. | ||
The IR spectra of the larger oligomers reveal a growing asymmetry of the two amide I′ bands with the lower wavenumber band increasing its intensity at the expense of the band at higher wavenumbers. Moreover, both bands also exhibit a blueshift. The corresponding VCD signal increases significantly and becomes rather structured for the trimer and tetramer, which reflects the underlying distribution of excitonic states. Once the number of GAG exceeds four, the VCD signal develops into a very intense negative couplet, as observed for the gel phase I at 23 °C. In short, the calculated changes in the amide I′ region are in close correspondence to experimental observations (Fig. 1 and ref. 30). However, the calculated VCD enhancement is less pronounced than the experimental one since the observed enhancement certainly reflects additional contributions from long twisted fibrils/filaments, which could not be handled by DFT calculations due to system size constrains. Nevertheless, our results suggest that the observed enhanced negative couplet could have indeed emerged as the result of a protofilament and filament formation that just involves the continuation of the growth process that started with oligomerization.
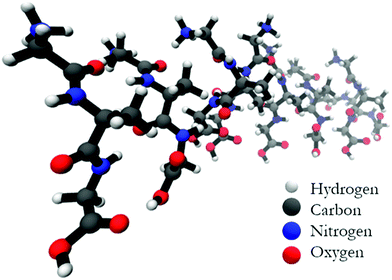
Fig. 5 shows the optimized structure of the octamer. The structures of the trimer and the pentamer are shown in Fig. S4 (ESI†). Even by inspection one recognizes rather different conformations of individual peptides. Table 1 lists the dihedral angles of all peptides in the octamer while the corresponding angles of the other oligomers are listed in Table S1 (ESI†). A closer inspection of these values reveals an interesting pattern. In particular, for the octamer, the secondary structure sequence of the peptides reads as βp, βp, βT, γinv, βext, pPII, βext, and pPII (βp: parallel β-sheet like conformation, βext: extended β-strand like conformation, βT: conformation located between the traditional β-strand/β-sheet region and pPII,33γinv: inverse γ-turn). An inspection of the structures obtained for the other oligomers also reveals a mixture of pPII, β, and γinv. Obviously, the occurrence of γinv and, to a lesser extent, of pPII conformations, adds substantially to the overall left-handed chirality of the structure, thus explaining the observed VCD enhancement. Consequently, the observed structure can be described as a not fully regular repeat of rather classical secondary structures, which produces some limited disorder on the tertiary level.
| Peptide no. | Ψ 1 | ϕ 2 | Ψ 2 | ϕ 3 | Conformation |
|---|---|---|---|---|---|
| 1 | −169 | −125 | 135 | −69 | β p |
| 2 | −163 | −127 | 146 | −60 | β p |
| 3 | −148 | −122 | 168 | −64 | β ext/βT |
| 4 | −150 | −85 | 83 | −106 | γ inv |
| 5 | −168 | −153 | 156 | −115 | β ext |
| 6 | −166 | −92 | 156 | −160 | pPII |
| 7 | −161 | −177 | 158 | −84 | β ext |
| 8 | −157 | −62 | 163 | −63 | pPII |
At this stage, one may wonder whether a calculation in implicit water is really representative for the oligomerization and aggregation process of GAG in a water–ethanol mixture. Our choice of the solvent would be problematic if the presence of ethanol was essential for the stability of oligomers and fibrils. However, as shown by Farrell et al., one can take ethanol out of the gel without effecting its stability.30 Moreover, the recent results of NMR-studies on the sol phase of our ternary mixture suggest that the ethanol functions more as a facilitator of the gelation process. Since our computational protocol actually starts with a situation (i.e. peptides in close proximity), which in our experiments is promoted by the accumulation of GAG at water–ethanol interfaces, the choice of the solvent might not matter much for the secondary and tertiary structure of GAG oligomers and filaments. Nevertheless, to test this hypothesis further we optimized a GAG octamer in implicit ethanol. The resulting optimized secondary structure sequence reads as pPII(βT), βp, βext, γinv, βext, βT, βext, and pPII. The respective dihedral angles are listed in Table S2 (ESI†). The structure of the first peptide contains a geometry that is intermediate between pPII and βT. While the sequence is somewhat different from what we observed for implicit water, the secondary structure ingredients are the same. It is therefore not surprising that the calculated IR- and VCD-profiles in the amide I′ region are very similar (data not shown).
Based on the agreement between calculated and experimental spectra, one would be tempted to conclude that the obtained semi-ordered oligomer represents secondary and tertiary structure of the filaments that eventually form the experimentally obtained fibrils of gel phase I. However, we felt that it was necessary to check whether an antiparallel arrangement of peptides would actually yield a similar agreement with our experimental data or whether it could even produce spectra more in line with those of the low temperature gel phase II. To check for these possibilities, we performed the same series of calculations for antiparallel oriented peptides. We optimized the structure of GAG oligomers for such a scenario using the same protocol adopted for the oligomers with parallel oriented peptides. All optimizations were again performed with implicit water as solvent. Fig. S5 and S6 (ESI†) show the development of the IR and VCD profiles in the amide I′ region for all the oligomers. The final optimized geometries of all the oligomers in anti-parallel are shown in Table S5 (ESI†). The calculated spectra of the heptamer and octamer are shown in Fig. 6. For the IR band profiles, the development is similar to what we observed for parallel peptides, i.e. a redshift combined with a substantial increase of the lower wavenumber amide I′ band. This increase is even more pronounced than that observed for parallel peptides. Interestingly, such an increase of intensity in the lower wavenumber is exactly what we observed when we lowered the temperature of the gel to 10 °C (phase II). The corresponding VCD signals of the dimer, trimer, and tetramer still resemble a negative couplet with a fine structure exhibited by the positive component. However, starting at the pentamer level, the signal switches to a positive couplet with some additional fine structure on the blue side. The enhancement is slightly less pronounced than it is for the parallel oriented peptides. Overall, the calculated VCD reproduces our observation for gel phase II at least on a qualitative level. It is reasonable to assume that the agreement with experiment would improve with increasing oligomer numbers because a higher oscillator rotational strength would accumulate in only a few excitonic states. This issue is discussed in more detail below.
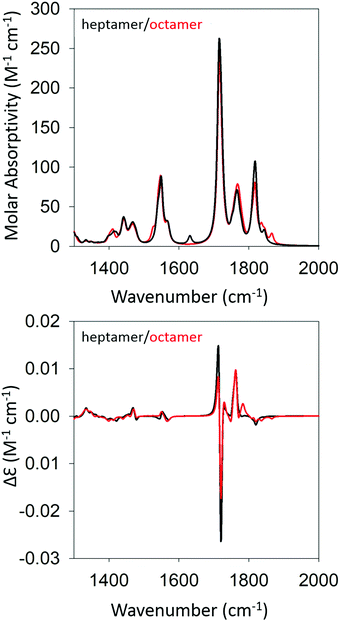 | ||
| Fig. 6 Calculated IR (top) and VCD spectra (bottom) of a geometry optimized GAG heptamer (black) and octamer (red) with antiparallel strand orientation. | ||
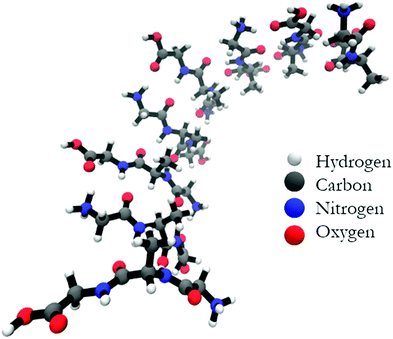
Fig. 7 shows the structure of the optimized anti-parallel octamer. The trimer and pentamer structures are shown in Fig. S7 (ESI†). Overall, the octamer resembles one half of a ring. Based on the growth of the oligomer structure, as documented by the structures in Fig. S8 (ESI†), one can assume that a full ring would have formed if we had been able to optimize a 16-mer. This is a very peculiar structure, which could serve as a template for the formation of a nanopore. An analysis of backbone structures of the optimized oligomers (Table 2 and Table S2, ESI†) shows that all peptides are either in a βa-strand (a: antiparallel) or an extended β-strand-like conformation. This implies that the optical activity of the oligomers results solely from the overall twisted tertiary structure and is not due to the conformations of the individual tripeptides. The obtained structure is somewhat reminiscent of the horseshoe structure of the inner shell of the ribonuclease inhibitor.8 The large twisting should be the reason for the absence of characteristic β-strand fingerprints in the calculated IR and VCD spectra, i.e. a significant amide I′ downshift and a very small VCD signal.
| Peptide no. | Ψ 1 | ϕ 2 | Ψ 2 | ϕ 3 | Conformation |
|---|---|---|---|---|---|
| 1 | −158 | −120 | 157 | 121 | β |
| 2 | −163 | −157 | 165 | 168 | β |
| 3 | −155 | −151 | 142 | −164 | β |
| 4 | −162 | −141 | 142 | −169 | β |
| 5 | −159 | −143 | 139 | −165 | β |
| 6 | 174 | −141 | 146 | −160 | β |
| 7 | −155 | −141 | 146 | 148 | β |
| 8 | −165 | −143 | 141 | −177 | β |
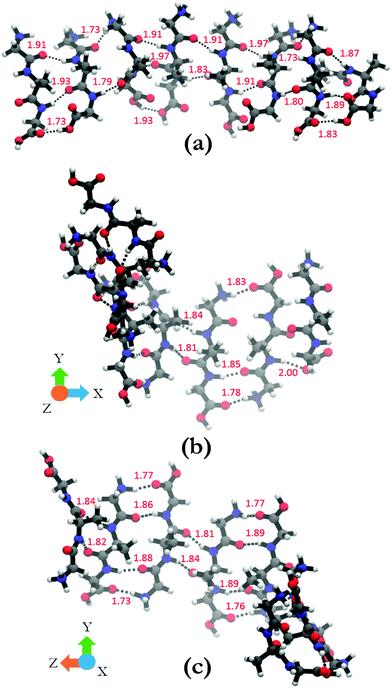
In order to shed some light on the underlying cause for the two very different oligomer structures obtained for the parallel and antiparallel oriented GAGs, we analyze the hydrogen bonds between C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups as acceptors and NH, NH3+, and OH groups as donors. The hydrogen bonding pattern of the octamers with parallel and antiparallel oriented GAGs are shown in Fig. 8. For the octamer with parallel peptides, we observed an interpeptide hydrogen bond pattern of 3–2–3–2–3–2–3 (from right to left). Most of the hydrogen bond pairs are formed between the carbonyl and amide groups of the peptide, with the exception of the interface between strand 2 and 3 (from the right) where the N-terminal carbonyl group of strand 3 is bound to the NH3+ group of strand 2. The third hydrogen bonding between the terminal strands occurs between carboxyl groups. The results of this analysis confirm the hypothesis of Farrell et al.,30 which suggests that the multitude of functional groups of GAG can promote some type of non-conventional fibril structure.
O groups as acceptors and NH, NH3+, and OH groups as donors. The hydrogen bonding pattern of the octamers with parallel and antiparallel oriented GAGs are shown in Fig. 8. For the octamer with parallel peptides, we observed an interpeptide hydrogen bond pattern of 3–2–3–2–3–2–3 (from right to left). Most of the hydrogen bond pairs are formed between the carbonyl and amide groups of the peptide, with the exception of the interface between strand 2 and 3 (from the right) where the N-terminal carbonyl group of strand 3 is bound to the NH3+ group of strand 2. The third hydrogen bonding between the terminal strands occurs between carboxyl groups. The results of this analysis confirm the hypothesis of Farrell et al.,30 which suggests that the multitude of functional groups of GAG can promote some type of non-conventional fibril structure.
The situation is much less convoluted for the conformation of the antiparallel oriented GAG octamer. The interpeptide hydrogen bond pattern reads as 1–3–2–4–2–4–2 (Fig. 8(b) and (c)). In addition to the traditional CO–HN interstrand hydrogen bonds, additional hydrogen bonding occurs between adjacent NH3+ and COOH groups which adds stability to the obtained octamer conformation. The antiparallel octamer would therefore be energetically favored and entropically disfavored over the corresponding parallel arrangement, which might explain why the former is observed at lower temperatures.30
3.3 Delocalization of excited vibrational states
In canonical β-sheet structures, amide I/I′ vibrations of adjacent peptide groups in different strands are vibrationally coupled, predominantly due to transition dipole coupling.36,57,58 If one treats the system quantum mechanically, one obtains a delocalization of the excited states' wavefunctions. In an ideal rippled antiparallel β-sheet, only two of multiple delocalized vibrations are IR-active.57 While the intense one is heavily redshifted to lower wavenumbers and corresponds to an Au-representation of the C2h point group of a local unit cell, the other one is blue shifted and assignable to a Bu-representation. It is also generally very weak. In the Au case, all CO groups of a chain formed by hydrogen-bond-connected peptide groups in different strands vibrate in phase, so that their transition dipole moments add up. Deviations from the ideal structure lead to the activation of additional modes.59 This causes a broadening of the most intense band and produces some detectable intensities over a very broad range of wavenumbers between 1610 and 1690 cm−1. In the case of an ideal parallel β-sheet, there are in principle more IR active modes (2 or 3, depending on the point group of the unit cell), but only one (with the lowest wavenumber) dominates.60Apparently, the structures that emerged from our geometry optimizations cannot be characterized as ideal sheets. However, the question arises as to what extent do these structures still facilitate the delocalization of amide I modes? To answer this question, we plot the CO displacements of the carbonyl groups of the two octamers for particular amide I′ modes that carry a significant transition dipole moment and/or rotational strength. The plots are shown in Fig. S8 and S9 (ESI†). For the two modes that contribute most to the strong negative signal of the VCD and the intense low wavenumber IR band, the vibrations are heavily delocalized over the N-terminal peptide groups. For the modes at the C-terminal, delocalization is only significant for one of the two modes (1723 cm−1). For the two modes contributing significantly to the positive VCD signal and to the weaker higher wavenumber amide I′ band, delocalization is obtained over both chains for the 1739 cm−1 vibrations, while the 1743 cm−1 mode appears somewhat more localized, which exhibits rather dominant contributions from the N-terminal vibration of the 3rd and C-terminal amide I′ vibration of the 5th GAG. Overall, the spectrum of modes with modest IR intensity and rotational strengths is rather broad (Fig. S6, ESI†), which in view of the fairly heterogeneous set of secondary peptide structures, is not surprising.
However, the situation is somewhat different for the structure formed by antiparallel GAGs. First of all, there are only two excitonic transitions that contribute significantly to the positive couplet of the VCD. These are also the only two contributors to the intense low wavenumber IR band. This focusing of oscillator strength in just a few excitonic transitions leads to a narrowing of the band and an increase of the peak intensity, as also seen experimentally for the low temperature gel phase (Fig. S9, ESI†). The displacement distributions indicate a very high degree of delocalization along both the N- and the C-terminal chains of peptide carbonyls. Additionally, for both cases the displacement distributions seem to approach the shape of standing waves, a behavior expected from more ideal structures with a higher degree of local symmetry. Altogether, this analysis shows that amide I′ vibrations are delocalized in both structures, though to a different extent.
3.4 Implications for fibrilization
What do the obtained structures of peptide oligomers mean for understanding the formation of very long and thick fibrils? First of all, we recall that the kinetic studies of Farrell et al., as well as the fluorescence kinetics in Fig. 2, show that the aggregation phase probed by changes of amide I′ in IR and VCD spectra precedes gelation of GAG in ethanol/water. Generally, the formation of amorphous oligomers is considered to be the first step of peptide self-assembly, which can then develop further into protofilaments, filaments, and fibrils (we ignore here the option that oligomer formation occurs off-pathway).1,53 However, in our case the kinetics probed by changes of the amide I′ IR and VCD intensities suggest that GAG forms more ordered, non-conventional sheets during the initial phase of the self-aggregation process, which subsequently develop into filaments, fibrils, and finally into a sample spanning network.Consequently, the oligomers optimized in this study should thus be considered as a snapshot of early aggregation events, which involve a constant growth process from fairly ordered oligomers into long sheets. For parallel oriented GAG, these sheets contain mixtures of peptides exhibiting pPII, β-strand, and γinv conformations rather than the canonical β-sheet structure. On the other hand, the β-strand content of oligomers formed by antiparallel oriented peptides look rather normal, but the curved and heavily twisted structure is far from expected.
How can these two types of oligomers grow into larger structures? Octamers of parallel oriented peptides can easily grow in the direction of its main axis via the hydrogen bonding mechanism visualized in Fig. 8. In principle, such a sheet can grow laterally via hydrogen bonding between N- and C-terminal groups. The protonated carboxylic acid groups can function as donors and acceptors for hydrogen bonds, and the N-terminal can donate a hydrogen bond to a C-terminal group of another oligomer even if it is involved in intrastrand hydrogen bonding. The alanine side chains of a sheet point into the same direction allowing for hydrophobic stacking between different oligomers/sheets/filaments to form a bilayer structure. Such filaments grow further in all three dimensions to form the crystalline fibrils shown in Fig. 3; in parallel, a sample-spanning network could be built up at a very early stage.
The situation would be different for the antiparallel oriented GAG octamer. Based on the structure, it is very reasonable to assume that an increase of the oligomer by further addition of peptides would create a ring structure. The diameter of this ring would be approximately 18 Å. Different rings could react via their terminal groups to form very stable nanopores or very thin nanotubes. These tubes would have a very smooth surface, which would allow just for the formation of rod like assemblies shown in Fig. 3.
The differences between the geometry-optimized structures may explain the rather different fluorescence kinetics observed at 10 °C and 23 °C. For phase II, the size of the proposed nanotubes would be large enough to accommodate thioflavin, which could diffuse into their interior practically in sync with the formation of protofibrils. In the protofibrils, their rotational motion would be very restricted, and fluorescence would thus be induced. Since all alanine side chains point inward, the interior is very hydrophobic. The much less regular structure proposed for phase I would certainly produce a lot of hydrophobic cavities but it would take time for the fluorophore to diffuse into these cavities. Some of the cavities might even be too large to restrict the rotational motion of the fluorophore. As a consequence, fibrillization would actually occur faster than the measured fluorescence kinetics.
How do the results of our study compare with the structure analysis of FmocAA peptides which yielded somewhat unspecified sheet structures with a majority of alanine residues adopting pPII-like conformations?24,25 As a matter of fact, our results for the phase I of GAG gels are not qualitatively different. Depending on the choice of the implicit solvent, between 2 and 3 of the residue structures of the obtained octamers were found to adopt pPII. If the obtained secondary structures are an indicator of the situation in long fibrils, we could expect up to 38% pPII, 50% β-strand, and 12% inverse γ-turns. Overall, one could characterize this structure as a disordered β-sheet. The DFT calculations allowed us to identify the modes of hydrogen bonding that allows for the formation of such disordered structures. The situation is of course different for the antiparallel oligomers, where the overall β-strand content is practically 100%. However, the curvature of the structure, while occurring in proteins, is unconventional for peptide fibrils.
One might argue that the growth into crystalline fibrils could eliminate the specifics of the obtained octamers (i.e. the occurrence of pPII and γinv-turns, or the bent structure of the antiparallel oligomer) to produce canonical helically twisted fibrils. This could lead to the observed enhancement of the amide I′ VCD; however, it would also lead to a larger downshift of the major excitonic amide I′ transition.11 The very fact that the spectral changes of the IR spectrum that emerged from our calculation reproduce our experimental observations strongly suggests that structures of the sheets in the observed fibrils are not so different from what we observed for GAG oligomers.
4 Conclusions
In conclusion, experimental observations are clearly indicative of the existence of two gel phases of ternary GAG–water–ethanol mixtures. The DFT studies on GAG oligomers presented in this perspective produced spectral features in the amide I′ region of IR and VCD spectra that are in very good agreement with experimental observations. In particular, we observe that the optimized conformations of these oligomers reveal rather unconventional structures, which are not reminiscent of the classical cross β-sheet structures of peptide and protein fibrils. Additionally, for parallel-oriented peptides we observed a structure that resembles an irregular repeat of pPII, β-strand, and inverse γ turn structures. On the contrary, antiparallel-oriented peptides adopt canonical β-strand structures, but the highly curved sheet structure bears little similarities with reported cross β-strand structures of peptide fibrils. Finally, we note that self-aggregation of GAG is made possible entirely by hydrogen bonding, while interactions between aliphatic side chains are certainly of secondary importance.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Mr. Daniel Hagarman for assisting us with the microscopy work on GAG gels. This project is supported in part by a grant from the National Science Foundation to R. S. S. (DMR-1707770). N. V. I. and B. M. W. acknowledge the National Science Foundation for the use of supercomputing resources through the Extreme Science and Engineering Discovery Environment (XSEDE), Project No. TG-CHE150040.References
- C. M. Dobson, Trends Biochem. Sci., 1999, 24, 329–332 CrossRef CAS PubMed.
- J. L. Jimenez, E. J. Nettleton, M. Bouchard, C. V. Robinson, C. M. Dobson and H. R. Saibil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 9196–9201 CrossRef CAS PubMed.
- K. Rajagopal and J. P. Schneider, Curr. Opin. Struct. Biol., 2004, 14, 480–486 CrossRef CAS PubMed.
- L. M. De Leon Rodriguez, Y. Hemar, J. Cornish and M. A. Brimble, Chem. Soc. Rev., 2016, 45, 4797–4824 RSC.
- A. Vitalis and R. V. Pappu, J. Comput. Chem., 2008, 30, 673–699 CrossRef PubMed.
- A. R. Hirst, I. A. Coates, T. R. Boucheteau, J. F. Miravet, B. Escuder, V. Castelletto, I. W. Hamley and D. K. Smith, J. Am. Chem. Soc., 2008, 130, 9113–9121 CrossRef CAS PubMed.
- W. C. Wimley, Curr. Opin. Struct. Biol., 2003, 13, 404–411 CrossRef CAS PubMed.
- G. I. Yakovlev, V. A. Mitkevich and A. A. Makarov, Mol. Biol., 2006, 40, 867–874 CrossRef CAS.
- R. Johnson, Nat. Chem., 2013, 5, 251 CrossRef.
- J. Wang, S. Gülich, C. Bradford, M. Ramirez-Alvarado and L. Regan, Structure, 2005, 13, 1279–1288 CrossRef CAS PubMed.
- T. J. Measey and R. Schweitzer-Stenner, J. Am. Chem. Soc., 2011, 133, 1066–1076 CrossRef CAS PubMed.
- L. C. Serpell, Biochim. Biophys. Acta, Mol. Basis Dis., 2000, 1502, 16–30 CrossRef CAS.
- G. Colombo, P. Soto and E. Gazit, Trends Biotechnol., 2007, 25, 211–218 CrossRef CAS PubMed.
- R. V. Ulijn, N. Bibi, V. Jayawarna, P. D. Thornton, S. J. Todd, R. J. Mart, A. M. Smith and J. E. Gough, Mater. Today, 2007, 10, 40–48 CrossRef CAS.
- P. W. Frederix, G. G. Scott, Y. M. Abul-Haija, D. Kalafatovic, C. G. Pappas, N. Javid, N. T. Hunt, R. V. Ulijn and T. Tuttle, Nat. Chem., 2015, 7, 30–37 CrossRef CAS PubMed.
- A. R. Hirst, B. Escuder, J. F. Miravet and D. K. Smith, Angew. Chem., Int. Ed., 2008, 47, 8002–8018 CrossRef CAS PubMed.
- L. Adler-Abramovich and E. Gazit, Chem. Soc. Rev., 2014, 43, 6881–6893 RSC.
- E. R. Draper and D. J. Adams, Chem., 2017, 3, 390–410 CAS.
- M. Reches and E. Gazit, Science, 2003, 300, 625 CrossRef CAS PubMed.
- J. Raeburn, C. Mendoza-Cuenca, B. N. Cattoz, M. A. Little, A. E. Terry, A. Zamith Cardoso, P. C. Griffiths and D. J. Adams, Soft Matter, 2015, 11, 927–935 RSC.
- R. Orbach, I. Mironi-Harpaz, L. Adler-Abramovich, E. Mossou, E. P. Mitchell, V. T. Forsyth, E. Gazit and D. Seliktar, Langmuir, 2012, 28, 2015–2022 CrossRef CAS PubMed.
- N. Javid, S. Roy, M. Zelzer, Z. Yang, J. Sefcik and R. V. Ulijn, Biomacromolecules, 2013, 14, 4368–4376 CrossRef CAS PubMed.
- C. Tang, A. Smith, R. Collins, R. Ulijn and A. Saiani, Langmuir, 2009, 25, 9447–9453 CrossRef CAS PubMed.
- X. Mu, K. M. Eckes, M. M. Nguyen, L. J. Suggs and P. Ren, Biomacromolecules, 2012, 13, 3562–3571 CrossRef CAS PubMed.
- K. M. Eckes, X. Mu, M. A. Ruehle, P. Ren and L. J. Suggs, Langmuir, 2014, 30, 5287–5296 CrossRef CAS PubMed.
- M. Mezei, P. J. Fleming, R. Srinivasan and G. D. Rose, Proteins: Struct., Funct., Genet., 2004, 55, 502–507 CrossRef CAS PubMed.
- M. Ghosh, M. Halperin-Sternfeld, I. Grigoriants, J. Lee, K. T. Nam and L. Adler-Abramovich, Biomacromolecules, 2017, 18, 3541–3550 CrossRef CAS PubMed.
- B. Milorey, S. Farrell, S. E. Toal and R. Schweitzer-Stenner, Chem. Commun., 2015, 51, 16498–16501 RSC.
- D. DiGuiseppi and R. Schweitzer-Stenner, J. Raman Spectrosc., 2016, 47, 1063–1072 CrossRef CAS.
- S. Farrell, D. DiGuiseppi, N. Alvarez and R. Schweitzer-Stenner, Soft Matter, 2016, 12, 6096–6110 RSC.
- K. Chen, Z. Liu and N. R. Kallenbach, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15352–15357 CrossRef CAS PubMed.
- Z. Shi, K. Chen, Z. Liu and N. R. Kallenbach, Chem. Rev., 2006, 106, 1877–1897 CrossRef CAS PubMed.
- A. Hagarman, T. J. Measey, D. Mathieu, H. Schwalbe and R. Schweitzer-Stenner, J. Am. Chem. Soc., 2010, 132, 540–551 CrossRef CAS PubMed.
- S. Toal, D. Meral, D. Verbaro, B. Urbanc and R. Schweitzer-Stenner, J. Phys. Chem. B, 2013, 117, 3689–3706 CrossRef CAS PubMed.
- S. Fleming, P. W. J. M. Frederix, I. Ramos Sasselli, N. T. Hunt, R. V. Ulijn and T. Tuttle, Langmuir, 2013, 29, 9510–9515 CrossRef CAS PubMed.
- C. Lee and M. Cho, J. Phys. Chem. B, 2004, 108, 20397–20407 CrossRef CAS.
- D. DiGuiseppi, B. Milorey, G. Lewis, N. Kubatova, S. Farrell, H. Schwalbe and R. Schweitzer-Stenner, J. Phys. Chem. B, 2017, 121, 5744–5758 CrossRef CAS PubMed.
- X. G. Chen, R. Schweitzer-Stenner, S. A. Asher, N. G. Mirkin and S. Krimm, J. Phys. Chem., 1995, 99, 3074–3083 CrossRef CAS.
- M. A. Saeed, A. Pramanik, B. M. Wong, S. A. Haque, D. R. Powell, D. K. Chand and M. A. Hossain, Chem. Commun., 2012, 48, 8631 RSC.
- M. A. Saeed, B. M. Wong, F. R. Fronczek, R. Venkatraman and M. A. Hossain, Cryst. Growth Des., 2010, 10, 1486–1488 CAS.
- M. A. Hossain, M. A. Saeed, A. Pramanik, B. M. Wong, S. A. Haque and D. R. Powell, J. Am. Chem. Soc., 2012, 134, 11892–11895 CrossRef CAS PubMed.
- N. V. Ilawe, A. E. Raeber, R. Schweitzer-Stenner, S. E. Toal and B. M. Wong, Phys. Chem. Chem. Phys., 2015, 17, 24917–24924 RSC.
- E. E. Dahlke, R. M. Olson, H. R. Leverentz and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 3976–3984 CrossRef CAS PubMed.
- S. Chakraborty, K. Yamada, S. I. Ishiuchi and M. Fujii, Chem. Phys. Lett., 2012, 531, 41–45 CrossRef CAS.
- S. Murase, N. Haspel, L. Del Valle, E. Perpète, C. Michaux, R. Nussinov, J. Puiggalí and C. Alemán, RSC Adv., 2014, 4, 23231–23241 RSC.
- S. I. Ishiuchi, K. Yamada, S. Chakraborty, K. Yagi and M. Fujii, Chem. Phys., 2013, 419, 142–152 CrossRef.
- M. Fedorovsky, PyVib2, a program for analyzing vibrational motion and vibrational spectra, 2007, http://pyvib2.sourceforge.net Search PubMed.
- S. Ma, X. Cao, M. Mak, A. Sadik, C. Walkner, T. B. Freedman, I. K. Lednev, R. K. Dukor and L. A. Nafie, J. Am. Chem. Soc., 2007, 129, 12364–12365 CrossRef CAS PubMed.
- C. Xue, T. Lin, D. Chang and Z. Guo, R. Soc. Open Sci., 2017, 4, 160696 CrossRef PubMed.
- P. Arosio, P. F. Knowles and S. Linse, Phys. Chem. Chem. Phys., 2015, 17, 7606–7618 RSC.
- P. Arosio, M. Beeg, L. Nicoud and M. Morbidelli, Chem. Eng. Sci., 2012, 78, 21–32 CrossRef CAS.
- J. S. Schreck and J. M. Yuan, J. Phys. Chem. B, 2013, 117, 6574–6583 CrossRef CAS PubMed.
- T. P. J. Knowles, C. A. Waudby, G. L. Devlin, S. I. A. Cohen, A. Aguzzi, M. Vendruscolo, E. M. Terentjev, M. E. Welland and C. M. Dobson, Science, 2009, 326, 1533–1537 CrossRef CAS PubMed.
- S. Auer, C. M. Dobson, M. Vendruscolo and A. Maritan, Phys. Rev. Lett., 2008, 101, 258101 CrossRef PubMed.
- K. Egashira and N. Nishi, J. Phys. Chem. B, 1998, 102, 4054–4057 CrossRef CAS.
- S. Dixit, J. Crain, W. C. Poon, J. L. Finney and A. K. Soper, Nature, 2002, 416, 829–832 CrossRef CAS PubMed.
- S. Krimm and J. Bandekar, Adv. Protein Chem., 1986, 38, 181–364 CrossRef CAS PubMed.
- R. Schweitzer-Stenner, J. Phys. Chem. B, 2012, 116, 4141–4153 CrossRef CAS PubMed.
- J. Kubelka and T. A. Keiderling, J. Am. Chem. Soc., 2001, 123, 12048–12058 CrossRef CAS PubMed.
- J. Bandekar and S. Krimm, Biopolymers, 1988, 27, 909–921 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp00691a |
| This journal is © the Owner Societies 2018 |