 Open Access Article
Open Access ArticleConnectivity-driven bi-thermoelectricity in heteroatom-substituted molecular junctions†
Sara
Sangtarash
 *,
Hatef
Sadeghi
*,
Hatef
Sadeghi
 * and
Colin J.
Lambert
* and
Colin J.
Lambert
 *
*
Quantum Technology Centre, Department of Physics, Lancaster University, LA14YB Lancaster, UK. E-mail: s.sangtarash@lancaster.ac.uk; h.sadeghi@lancaster.ac.uk; c.lambert@lancaster.ac.uk
First published on 12th March 2018
Abstract
To improve the thermoelectric performance of molecular junctions formed by polyaromatic hydrocarbon (PAH) cores, we present a new strategy for enhancing their Seebeck coefficient by utilizing connectivities with destructive quantum interference combined with heteroatom substitution. Starting from the parent PAH, with a vanishing mid-gap Seebeck coefficient, we demonstrate that the corresponding daughter molecule obtained after heteroatom substitution possesses a non-zero, mid-gap Seebeck coefficient. For the first time, we demonstrate a “bi-thermoelectric” property, where for a given heteroatom and parent PAH, the sign of the mid-gap Seebeck coefficient depends on connectivity and therefore the daughter can exhibit both positive and negative Seebeck coefficients. This bi-thermoelectric property is important for the design of tandem thermoelectric devices, where materials with both positive and negative Seebeck coefficients are utilized to boost the thermovoltage. Simple parameter-free rules for predicting the Seebeck coefficient of such molecules are presented, which form a powerful tool for designing efficient molecular thermoelectric devices.
Introduction
The ability to convert waste heat into electricity via the Seebeck effect is an attractive technology, because it is silent, environmentally friendly and when operated in reverse enables Peltier cooling.1 Recently, the ability to measure the Seebeck coefficient of single molecules has revealed that quantum interference (QI) plays a fundamental role in determining their room temperature thermoelectric properties.2 In a molecular-scale junction,3,4 transport properties are determined by the probability T(E) that electrons with energy E can pass from one electrode to another. In particular, the Seebeck coefficient S is proportional to the slope of the natural logarithm of T(E), evaluated at the Fermi energy EF of the electrodes, provided T(E) changes linearly with E in the scale of kBT.5 Most thermoelectric devices utilize inorganic materials, which are difficult to process and have limited global supply. Therefore in recent years, organic thermoelectric materials have been investigated as a possible alternative,6,7 resulting in a body of experimental measurements showing that single organic molecules bridging two metallic electrodes can exhibit negative and positive Seebeck coefficients ranging from ∼−30 μV K−1 for fullerene families8–12 to +38 μV K−1 in oligophenyldithiol derivatives.13–18Although theory predicts that a large Seebeck coefficient of ∼−500 μV K−1 is possible in Au/C60/Au junctions,8 the measured values are far from this theoretical value, because the Fermi energy does not lie close to a transport resonance, where a high slope of T(E) and a high Seebeck coefficient is expected. The reported experimental values8–10 could be further enhanced by electrostatic gating to ∼−50 μV K−1.9 However electrostatic gating is not desirable, because a thermoelectric device is designed to generate a voltage, whereas gating consumes electrical power. Furthermore, because the coupling to electrostatic gates is usually weak, the voltages needed to move resonances towards the Fermi energy can be rather large. Since high slopes of T(E) associated with resonances appear to be inaccessible without gating, high slopes due to the anti-resonances might be more useful. In organic molecules such as polycyclic aromatic hydrocarbons (PAHs), anti-resonances occur when two de Broglie waves with similar amplitudes, but opposite phases meet each other after travelling from one electrode to another through different paths.19 Since the lengths of such paths depends on the connection points at which electrons are injected into and collected from the PAH core, such QI effects are connectivity dependent.
Results and discussion
The aim of this paper is to show how connectivity and anti-resonances in PAHs20–22 can be exploited to achieve high Seebeck coefficients. As an alternative to electrostatic gating, we discuss how thermoelectric properties can be tuned by heteroatom substitution.22,23 For the first time, we demonstrate a “bi-thermoelectric” property, where for a given heteroatom, the sign of the mid-gap Seebeck coefficient depends on connectivity and therefore both positive and negative Seebeck coefficients can be exhibited by a given molecular core. We derive simple parameter free rules to predict the Seebeck coefficient of PAHs molecules, which provide a powerful tool for designing future efficient thermoelectric devices.In this paper, we discuss two groups of molecules: bipartite PAH molecules, in which even numbered atoms are connected to odd numbered atoms only, and heteroatom-substituted bipartite PAHs. We start by considering PAH molecules such as benzene, naphthalene, anthracene, pyrene and anthanthrene, which can be represented by bipartite lattices (see Fig. S1 in the ESI†). In these lattices, each site represents a p-orbital connected to a nearest neighbour by a π–π coupling. Fig. 1a shows an example of the bipartite lattice representing benzene. Fig. 1a shows core transmission coefficients τlm(E) between different pairs of injection and collection sites l,m obtained using the definition τ(E) ∝ |(E − H)−1|2 where H is tight binding (Hückel) Hamiltonian of core. The quantities τlm(E) capture the contribution to transmission from the core of the PAH, without reference to the electrodes. For the same connectivities l,m, Fig. 1c shows the full transmission coefficient Tlm(E) obtained from a corresponding DFT material-specific mean field Hamiltonian. The details of these transport calculations are given in the methods section. For each choice of (l,m), the associated electrical conductance Glm is given by Glm = G0Tlm(EF) where G0 is the conductance quantum and EF is the Fermi energy. Fig. 1a and c show that the transmission coefficient T2,5(E) between sites 2,5 is much higher than the transmission T2,6(E) between sites 2,6 for energies E in the vicinity of middle of HOMO–LUMO gap, for both the simple tight binding model (Fig. 1a in the vicinity of E/γ = 0) and the more complex multi-orbital DFT Hamiltonian (Fig. 1c in the vicinity of E = 0.8 eV) in agreement with experiments.24,25 This connectivity dependence illustrates a general property of PAHs,20,21 namely provided the Fermi energy is close to the vicinity of middle of HOMO–LUMO gap (mid-HL), when a PAH core is weakly coupled to the electrodes, the conductances between odd to odd (i.e. 1,3) or even to even (i.e. 2,6) sites are low due to a destructive QI, whereas the conductances between any odd and even (i.e. 2,5) sites are high due to a constructive QI.
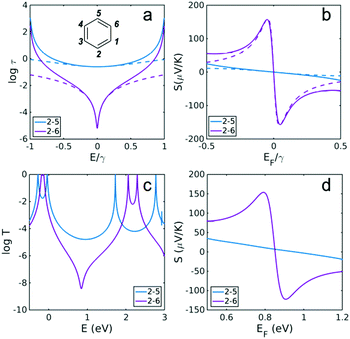 | ||
| Fig. 1 Transmission coefficients and Seebeck coefficients for different connectivities of benzene. When considering the connectivity dependence of transport properties, what seems a natural labelling system to a physicist often conflicts with chemical convention and therefore here we have used both conventions. In what follows, a pair of indices, n,m refers to the ‘physics conventions’ whereas a pair of indices in curly brackets {n,m} refer to the chemical convention. For example the chemical convention {1,4}-connectivity for para, {1,3}-for meta and {1,2}-for ortho correspond to the physics labelling of 2,5 for para, 2,4 for meta and 2,3 for ortho. (a) Using the physics numbering in the inset, the blue curve shows the core transmission coefficient for 2,5 {1,4} para connectivity and the purple curve shows the core transmission coefficient for 2,6 {1,3} meta connectivity, obtained from the definition τ(E) ∝ G(E)2 (see Methods for more details). (b) Seebeck coefficient obtained from the τ(E) in (a) at T = 300 K. (c) The full transmission coefficient T(E) for connectivities obtained using DFT (d) corresponding DFT Seebeck coefficient at room temperature. Dashed lines in (a and b) are obtained using the mid-gap theory of thermoelectricity presented in the ESI,†eqn (3) and (4) and coincide with the solid lines near the middle of the HOMO–LUMO gap. | ||
For a given transmission coefficient, the Seebeck coefficient S can be calculated for different Fermi energies EF at a given temperature (see Methods). Fig. 1b shows the room-temperature (T = 300 K) Seebeck coefficient for different connectivities to benzene obtained from the core transmissions of Fig. 1a. The transmission spectrum is symmetric about E = 0 and therefore S vanishes when EF coincides with the middle of the HOMO–LUMO gap, (i.e. when EF = 0). However, different connectivities behave differently in the vicinity of EF = 0. S is much lower for constructive-QI connectivities such as 2,5 since in the vicinity of mid-HL gap, the transmission function is small (see Fig. 1a) compared with the 2,6 connectivity. This is a general feature of bipartite PAH molecules, for which the Seebeck coefficient at Fermi energies above and below the mid-gap is greater for destructive-QI cases compared with constructive cases. Fig. 1d shows that this behaviour is also found in DFT calculations of S. Fig. 1d shows the Seebeck coefficient of benzene connected to two gold electrodes through acetylene linkers (see ESI† for the molecular structure of the junction) using two different connectivities. Clearly S passes through zero near the gap center (EF ∼ 0.8 eV shown shaded in Fig. 1d), but when EF is either side of the mid-gap, S is higher for the 2,6 connectivity (destructive) compared with the 2,5 connectivity (constructive). Although destructive connectivity can produce large positive and negative Seebeck coefficients, in a real experiment, environmental effects, including fluctuations in the electrodes, would randomly shift the destructive interference minimum to either side of EF and produce non-zero values of S, but with random signs, whose ensemble average would be low. Therefore in what follows, we propose a general strategy to bias the sign and increase the magnitude of S in such PAH molecules, by introducing a heteroatom at an appropriate position to shift the energy at which destructive QI occurs.
By choosing different heteroatoms and connectivities, we demonstrate that one can systematically control this energy and shift destructive QI to above or below the Fermi energy, thereby creating HOMO or LUMO-dominated devices with negative or positive Seebeck coefficients. We find (see mid-gap theory below) that after heteroatom substitution at site lo, the mid-gap Seebeck coefficient S is a product of two parameters; i.e. S = εlo![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ij. The first parameter (εlo) depends on whether or not the heteroatom donates or accepts electrons, but not on connectivity i or j and the second term
ij. The first parameter (εlo) depends on whether or not the heteroatom donates or accepts electrons, but not on connectivity i or j and the second term ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ij depends on connectivity and the location of the substitution site lo. Since the sign of
ij depends on connectivity and the location of the substitution site lo. Since the sign of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ij depends on the choice of connectivity, the mid-gap Seebeck coefficient for a given heteroatom can be positive or negative, depending on connectivity. We called this property “bi-thermoelectricity”. Note that if an electrostatic field is applied to a molecular junction, which shifts anti-resonances relative to the Fermi energy, then the slope of the transmission function at the Fermi energy and the Seebeck coefficient could indeed change sign. However as mentioned in the introduction, electrostatic gating is not desirable, because a thermoelectric device is designed to generate a voltage, whereas gating consumes electrical power. Therefore we reserve the term ‘bi-thermoelectricity’ to describe materials, which can exhibit Seebeck coefficients of both signs, without electrostatic gating.
ij depends on the choice of connectivity, the mid-gap Seebeck coefficient for a given heteroatom can be positive or negative, depending on connectivity. We called this property “bi-thermoelectricity”. Note that if an electrostatic field is applied to a molecular junction, which shifts anti-resonances relative to the Fermi energy, then the slope of the transmission function at the Fermi energy and the Seebeck coefficient could indeed change sign. However as mentioned in the introduction, electrostatic gating is not desirable, because a thermoelectric device is designed to generate a voltage, whereas gating consumes electrical power. Therefore we reserve the term ‘bi-thermoelectricity’ to describe materials, which can exhibit Seebeck coefficients of both signs, without electrostatic gating.
To demonstrate that introducing a heteroatom changes the sign and magnitude of the Seebeck coefficient, we now consider a benzene ring with nitrogen N substituents at site number 1 (inset of Fig. 2a). Fig. 2a shows the transmission coefficient obtained using a simple tight-binding model, in which the heteroatom is taken into account by inserting non-zero site energy εlo ≠ 0 at the site occupied by the heterotaom, while all other site energies are zero. It is apparent that both odd-to-odd (i.e. 3,5) and even-to-even (i.e. 2,4) connectivities show destructive QI and the anti-resonance associated with odd-to-odd (i.e. 3,5) connectivity has not moved from the mid-HL gap. The constructive connectivities (i.e. 2,5) are not affected by heteroatom substitution at site 1, whereas the destructive QI feature of even–even connectivities (i.e. 2,6 and 2,4) has moved to higher or lower energies. This is in agreement with our analysis in ref. 22, which predicts that when the heteroatom is substituted into an odd-numbered site (i.e. site 1 in Fig. 1a) the transmission coefficient of odd–odd and even–odd connectivities are unchanged, whereas those of even–even connectivities are shifted.
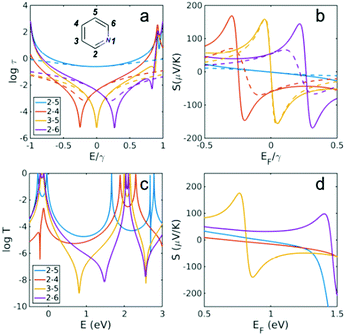 | ||
| Fig. 2 Transmission coefficient and Seebeck coefficient for different connectivities of pyridine. (a) Transmission coefficient for connectivities 2,5, 2,4, 3,5 and 2,6 (inset of a) when heteroatom substituted at site 1 (εlo = −0.25) using a simple description of τ(E) ∝ G(E)2 (see Methods for more details). (b) The Seebeck coefficient corresponding to τ(E) at T = 300 K. (c) Full transmission coefficient T(E) for connectivities in (a), obtained using DFT and (d) the corresponding Seebeck at room temperature. Dashed lines in (a) and (b) are obtained using the simple description of transmission and Seebeck coefficient from eqn (3) and (4) below. | ||
Fig. 2b shows that the corresponding Seebeck coefficient profile moves with the anti-resonance. In an experiment where the Fermi energy of the parent PAH is coincident with the minimum of a destructive interference feature, and therefore a low ensemble-averaged Seebeck coefficient is predicted, departure of the anti-resonance from the mid-HL gap creates a robust, well-defined high Seebeck coefficient. In addition, shifting the anti-resonance away from the mid-HL gap using heteroatom substitution leads to a higher conductance as we recently predicted22 and confirmed by experiment.23 This simultaneous increase of the Seebeck coefficient and conductance is expected to lead to a device with higher efficiency. Fig. 2c and d show the DFT-predicted transmission coefficient and Seebeck coefficient in the presence of a nitrogen heteroatom connected to gold electrodes (see ESI† for the structures). It is apparent that except for the 2,4 connectivity, all the main features predicted using the simple TB model of p-orbital transport are also obtained from DFT, which takes into account material specific properties, sigma orbitals and charge transfer due to the heteroatom substitution.
In the case of 2,4 connectivity, the anti-resonance at E/γ = −0.25 in Fig. 2a is much closer to the HOMO in the DFT results (i.e. near E = −0.2 eV) and therefore the simple parameter free rules for the core transmission do not reproduce the DFT results. In other words, the Fano line shape of the red curve in Fig. 2b does not appear within the HOMO–LUMO gap in the red curve of Fig. 2d. This difference arises, because magic number theory is aimed at teasing out the role of connectivity alone using the simplest possible Hamiltonian and deliberately ignores other complexities, which may occur in real molecules. In particular the electronic structure of the linker groups connecting the central core to the electrodes is assumed to be unaffected by connectivity. Fig. S4 of the ESI† shows that this is indeed the case for all molecules except, 2,4, where the symmetry of the HOMO is strongly broken. As discussed in ref. 26, this means that the HOMO orbital product is much smaller than the LUMO orbital product and therefore the anti-resonance moves away from the mid-gap, towards the HOMO.
Consider a molecule which possesses only a HOMO molecular orbital ψH(rl) of energy EH and a LUMO molecular orbital ψL(rl) of energy EL, whose Green's function is given by
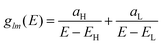 | (1) |
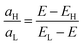 | (2) |
The molecular orbitals of all molecules are shown in Fig. S4 of the ESI,† where the intercepts between the vertical guide lines and the points of connection between the acetylene linkers and the central 6-fold ring show the points at which molecular orbitals ψH(rl), ψL(rl), ψH(rm) and ψL(rm) are to be evaluated. (Red = positive and blue = negative.) As expected, for the para-connected molecules, the orbital products aL and aH have opposite signs, so no interference dip occurs within the HOMO–LUMO gap. On the other hand, for the meta-connected molecules, the orbital products have the same sign. One exception to this is the meta-2,4 molecule, where ψH(rm) is almost zero. In this case, aH ≪ aL and therefore the interference dip is expected to be close to the HOMO. This expectation is confirmed by Fig. 2c, where the red curve shows that the interference dip has indeed moved close to the HOMO.
From the point of view of ‘magic number’ theory, the differences between the red curves of Fig. 2a and c means that the simple approximation of modelling the heteroatom using only a simple site energy εlo should be modified. As shown in Fig. S5 of the ESI,† when this additional complexity is introduced, the interference dip is indeed shifted towards the HOMO.
The TB model calculations of Fig. 2a and b reveal the surprising property of connectivity-driven bi-thermoelectricity in molecular junctions. As shown in Fig. 2a, for a given heteroatom substitution (i.e. nitrogen N), the anti-resonance due to the 2,4 connectivity moves to a lower energy, whereas the anti-resonance due to the 2,6 connectivity moves to a higher energy (Fig. 2b). Therefore as shown in Fig. 2b, in the vicinity of mid-HL gap (around EF = 0), the 2,4 connectivity produces a negative Seebeck coefficient, whereas the 2,6 connectivity possesses a positive Seebeck coefficient. This behaviour is also predicted for more complicated molecules such as naphthalene, anthracene, pyrene and anthanthrene (Fig. 3–6).
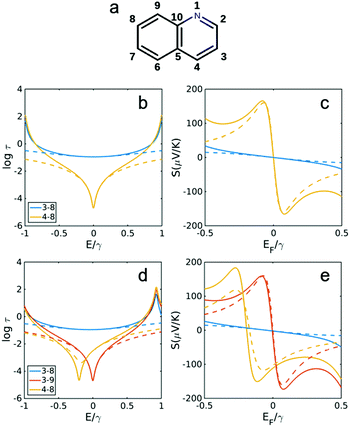 | ||
| Fig. 3 Transmission and Seebeck coefficients for different connectivities of naphthalene with and without heteroatom substitution in site 1 (a). Transmission coefficient using the definition τ(E) ∝ G(E)2 (see Methods for more details) for connectivities 3,8, 4,8 and 3,9 in (b) naphthalene (without N in a) and (d) quinolone shown in (a). (c and e) Seebeck coefficient corresponding to τ(E) in b, d at T = 300 K. Dashed lines are obtained using simple description of transmission and Seebeck coefficient from eqn (3) and (4) below. | ||
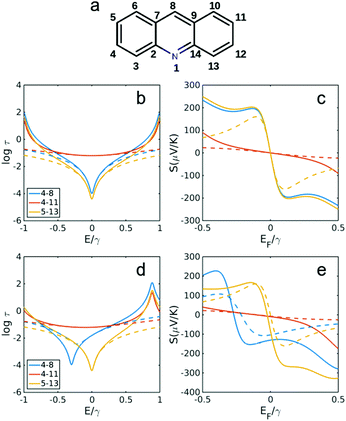 | ||
| Fig. 4 Transmission and Seebeck coefficients for different connectivities of anthracene with and without heteroatom substitution in site 1 (a). Transmission coefficient using simple description of τ(E) ∝ G(E)2 for connectivities 4,8, 4,11 and 5,13 in (b) anthracene (without N in a) and (d) with N substitution in site 1 as shown in (a). (c and e) Seebeck coefficient correspond to τ(E) in b, d at T = 300 K. Dashed lines are obtained using simple description of transmission and Seebeck coefficient from eqn (3) and (4) below. | ||
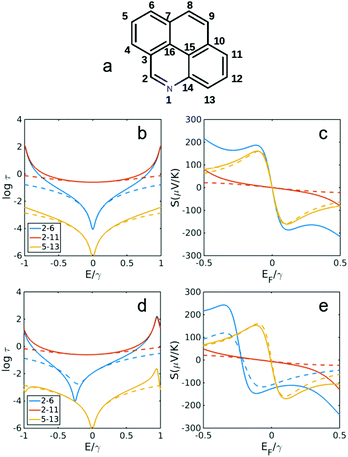 | ||
| Fig. 5 Transmission and Seebeck coefficients for different connectivities of pyrene with and without heteroatom substitution in site 1 (a). Transmission coefficient using simple description of τ(E) ∝ G(E)2 (see Methods for more details) for connectivities 2,6, 2,11 and 5,13 in (b) pyrene (without N in a) and (d) with N substitution shown in (a). (c and e) Seebeck coefficient corresponding to τ(E) in b, d at T = 300 K. Dashed lines are obtained using simple description of transmission and Seebeck coefficient from eqn (3) and (4) below. | ||
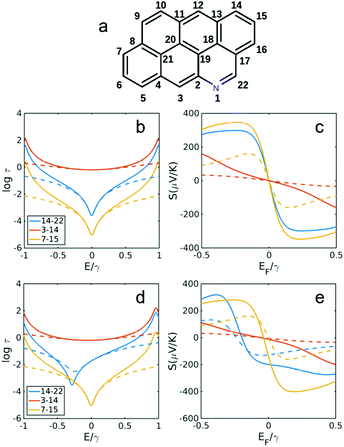 | ||
| Fig. 6 Transmission and Seebeck coefficients for different connectivities of anthanthrene with and without heteroatom substitution in site 1 (a). Transmission coefficient using simple description of τ(E) ∝ G(E)2 for connectivities 14,22, 3,14 and 7,15 in (b) anthanthrene (without N in a) and (d) with N substitution in site 1 as shown in (a). (c and e) Seebeck coefficient correspond to τ(E) in b, d at T = 300 K. Dashed lines are obtained using simple description of transmission and Seebeck coefficient from eqn (3) and (4) below. | ||
As mentioned above, if an anti-resonance happens to be located at the Fermi energy, then the sign of the Seebeck coefficient will be sensitive to slight shifts in the position of the anti-resonance and the ensemble-averaged Seebeck coefficient will be low. However, introducing a heteroatom will move the anti-resonance away from the mid-gap, so the slope of the transmission coefficient and hence the sign of the Seebeck coefficient becomes better-defined and insensitive to small variations. Consequently, the Seebeck coefficient of the daughter can be more robust than that of the parent.
Fig. 3 and 4 show the results for naphthalene and anthracene with and without heteroatom substitution (Fig. 3a and 4a), obtained using the TB model (corresponding DFT calculations was shown in Fig. S2 in the ESI†). All constructive connectivities (odd to even connectivities shown in Fig. 3b, d and 4b, d) possess a smaller Seebeck coefficient (shown in Fig. 3c, e and 4c, e) compared with destructive connectivities (i.e. odd to odd or even to even connectivities). It should be noted that heteroatom substitution has no effect on constructive connectivities and would change the energy in which destructive QI happens only for even to even (odd to odd) connectivities when heteroatom substituted on odd (even) site. For example, in naphthalene, when a heteroatom is substituted at the odd site 1 (Fig. 3a), the destructive QI energy is changed for 4,8 connectivity (Fig. 3c and e), whereas the destructive QI energy for connectivity 3,9 is unchanged. In addition, the odd–even constructive connectivities are not affected in all cases (i.e. 3,8 in naphthalene shown in Fig. 3b and d and 4,11 in anthracene shown in Fig. 4b and d). Consequently, thermopower is also only affected for even to even (odd to odd) destructive connectivities when a heteroatom is substituted on an odd (even) site, as shown in Fig. 3c and e for naphthalene and Fig. 4c and e for anthracene.
Fig. 5 and 6 show the transmission and Seebeck coefficient for two larger molecules, pyrene and anthanthrene with and without heteroatoms (Fig. 5a and 6a). Fig. 5b, d and 6b, d show the transmission coefficient for pyrene, pyrene with heteroatom substitution, anthanthrene and anthanthrene with heteroatom substitution, respectively. The corresponding Seebeck coefficients are shown in Fig. 5c, e and 6c, e. These results demonstrate that all qualitative conclusions made for smaller molecular cores (i.e. benzene, pyridine, naphthalene, quinolone, anthracene with and without heteroatoms) are preserved for larger molecules. Furthermore, the maximum Seebeck coefficient increases with the size of the molecule. For example, for the connectivities that are affected by heteroatom substitution, the maximum Seebeck coefficient is ∼169 μV K−1 in pyridine (2,4 connectivity in Fig. 2b), ∼184 μV K−1 in quinolone (4,8 connectivity in Fig. 3e), ∼227 μV K−1 in heteroatom substituted anthracene (4,8 connectivity in Fig. 4e), ∼242 μV K−1 in heteroatom substituted pyrene (2,6 connectivity in Fig. 5e) and ∼319 μV K−1 in heteroatom substituted anthanthrene (14,22 connectivity in Fig. 6e). This demonstrates that the maximum Seebeck coefficient increases with the size of molecular core. Furthermore, this tuning of the position of the QI energy and the Seebeck coefficient by heteroatom substitution is confirmed by a more material-specific calculations shown in Fig. S2 of the ESI.†
Mid-gap theory of thermoelectricity
To rationalize the results of Fig. 1–6, we now present an analytic theory of thermoelectricity for Fermi energies near the mid-gap of PAH molecules. Recently we predicted that for molecules, whose central core is weakly connected to external electrodes, provided the Fermi energy lies within the HOMO–LUMO gap, the ratio of conductances σi,j and σl,m associated with connectivities i and j or l and m is given by the ‘magic ratio rule’ (MRR)20,21σi,j/σl,m = τi,j(EF)/τl,m(EF) = [Mi,j(EF)/Ml,m(EF)]2, where τi,j(EF) and τl,m(EF) are core transmission coefficients and contain no information about the electrodes except via the parameter EF. If H is a Hamiltonian matrix describing the isolated core, then the core transmissions are given by τi,j(E) = |Gi,j(E)|2, where G is the corresponding Green's function matrix G = (E − H)−1. Mi,j(E) is proportional to Gi,j(E), with a constant of proportionality which does not depend on i, j, but may depend on E. The constant of proportionality cancels in the above ratios and is chosen to yield the simplest possible values for the “magic numbers” Mi,j(EF). A simple parameter-free description of electrical conductance through polyaromatic hydrocarbon (PAH) cores is then obtained by assuming EF = E0, where E0 is the middle of the HOMO–LUMO gap and identifying the Hamiltonian H of the core with a simple connectivity matrix C, whose entries are either Cij = −1 if sites i, j are nearest neighbours or Cij = 0 otherwise. This yields σi,j ∝ [Mi,j(E0)]2, where Mi,j(E0) ∝ (E0 − C)−1. It was shown experimentally that this simple rule can predict the statistically-most-probable experimental conductance ratios measured in for example a break-junction set up.20,21 The remarkable agreement between conductance ratios obtained from the quantities Mi,j(E0) and experimental measurements carried out by different groups,20 led us to refer to them as ‘magic numbers.’ We now generalize the above theory to describe the Seebeck coefficient of molecules whose central core is weakly connected to external electrodes.The above expressions are valid, because provided the Fermi energy lies within the HOMO–LUMO gap, when electrons of energy E passing from one electrode to another enter the core at orbital i and leave the core from orbital j, the transmission coefficient T(E) is proportional to τi,j(E). The low-bias, electrical conductance is given by the Landauer formula σi,j = G0T(EF), where T(E) is transmission coefficient and G0 = 2e2/h is the quantum of conductance. This form of the Landauer formula is valid, provided the transmission coefficient does not vary significantly on the scale of kBT, where T is the temperature and kB = 8.6 × 10−5 eV K−1 is Boltzmann's constant. Similarly the Seebeck coefficient is given by
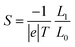 | (3) |
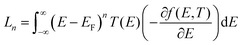 is the n-th moment of
is the n-th moment of 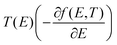 and f(E) = (1 + exp((E − EF)/kBT))−1 is the Fermi–Dirac distribution function. Hence for a connectivity i, j, the core Seebeck coefficient can be written
and f(E) = (1 + exp((E − EF)/kBT))−1 is the Fermi–Dirac distribution function. Hence for a connectivity i, j, the core Seebeck coefficient can be written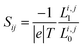 | (4) |
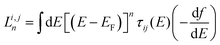 . Provided the transmission coefficient does not vary significantly on the scale of kBT, it is useful to approximate τij(E) by
. Provided the transmission coefficient does not vary significantly on the scale of kBT, it is useful to approximate τij(E) by| τij(E) = τ(0)ij + (E − EF)τ(1)ij + (E − EF)2τ(2)ij | (5) |
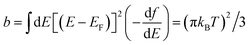 . Dashed lines in the left panel of Fig. 1–6 show the transmission coefficient obtained using this approximation. It is apparent that this is a good approximation in the vicinity of middle of the HOMO–LUMO gap. From τij(E) and eqn (4), we obtain
. Dashed lines in the left panel of Fig. 1–6 show the transmission coefficient obtained using this approximation. It is apparent that this is a good approximation in the vicinity of middle of the HOMO–LUMO gap. From τij(E) and eqn (4), we obtain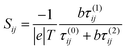 | (6) |
For bipartite PAH cores with equal numbers of odd ‘o’ sites and even ‘e’ sites at the mid-HL gap and for EF = 0, Sij = 0. On the other hand, if EF ≠ 0, the behaviour of Sij(EF) in the vicinity of EF = 0 is quite different for odd–even compared with even–even and odd–odd connectivities. It could be shown (see ESI†) that
(a) When i is odd and j is even or vice versa, assuming that b and EF are small compared with τ(0)ij(0)/τ(2)ij(0) yields
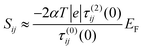 | (7) |
(b) On the other hand, when i, j are both odd or both even, τ(0)ij(0) = 0. Hence
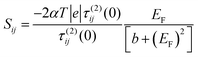 | (8) |
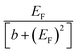 and therefore exhibits a Fano lineshape.2 If the aromatic core contains a heteroatom, whose site energy εlo differ from that of carbon, it can be shown (see ESI†) that
and therefore exhibits a Fano lineshape.2 If the aromatic core contains a heteroatom, whose site energy εlo differ from that of carbon, it can be shown (see ESI†) thatSij = εlo![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ij ij | (9) |
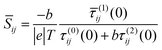 | (10) |
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ij which depends on connectivity, but not on the nature of the heteroatom. Since the sign of the mid-gap Seebeck coefficient depends on connectivity, heteroatom substituted PAHs are bi-thermoelectric. Furthermore, the mid-gap Seebeck coefficient between even and even or odd and even sites is no longer zero, because τ(1)ij(0) no longer vanishes. On the other hand the mid-gap Seebeck coefficient between odd and odd sites remains at zero. These features are clearly present in the right-hand columns of Fig. 2–6.
ij which depends on connectivity, but not on the nature of the heteroatom. Since the sign of the mid-gap Seebeck coefficient depends on connectivity, heteroatom substituted PAHs are bi-thermoelectric. Furthermore, the mid-gap Seebeck coefficient between even and even or odd and even sites is no longer zero, because τ(1)ij(0) no longer vanishes. On the other hand the mid-gap Seebeck coefficient between odd and odd sites remains at zero. These features are clearly present in the right-hand columns of Fig. 2–6.
One effect of heteroatom substitution, in which a carbon is replaced by another atom such as nitrogen or sulphur, is the introduction of a local electrostatic potential. If the heteroatom is nitrogen, then it will be electron withdrawing and the local potential is negative. Therefore nitrogen substitution decreases the molecular orbital energies. This movement to more negative values is evident in Table S4 (ESI†), where all energies of the nitrogen-substituted ‘daughter’ molecules are more negative than those of the unsubstituted ‘parent.’ At a tight-binding level, this is modelled by choosing the site energy εlo to be lower than the site energy of the carbons in the parent. On the other hand substitution by an electron donating heteroatom such as sulphur would introduce a negative electrostatic potential, which increases molecular energy levels. This is modelled by choosing the parameter εlo to be greater than the site energy of the carbons in the parent. This effect is independent of connectivity. In contrast, our mid-gap theory and the results of Fig. 2a and c show that the movement of the anti-resonance relative to the mid-gap is determined both by εlo, and by connectivity.
Conclusion
We have presented a new strategy for improving the Seebeck coefficient of PAH molecules. First we used a simple tight binding model to illustrate the main principles and then showed that the predicted trends are present in calculations based on density functional theory.For the parent PAH, before heteroatom substitution, we predict that the Seebeck coefficient Sij, corresponding to connectivities i, j has the following properties:
(a) When i is odd and j is even or vice versa, Sij is proportional to EF, where EF is the Fermi energy, relative to the middle of the HOMO–LUMO gap. Hence Sij vanishes at the gap centre.
(b) When i, j are both odd or both even, Sij is proportional to 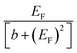 and therefore exhibits a Fano lineshape. Again Sij again vanishes at the gap centre EF = 0.
and therefore exhibits a Fano lineshape. Again Sij again vanishes at the gap centre EF = 0.
Starting from the parent PAH, whose mid-gap Seebeck coefficient is predicted to vanish, we demonstrated that the corresponding daughter molecule obtained after heteroatom substitution possesses a non-zero mid-gap Seebeck coefficient. These trends are confirmed by calculations based on density functional theory.
The above predictions would be of interest experimentally, when the Seebeck coefficient of a parent molecule is measured to have large sample-to-sample fluctuations in sign and a small average, since such behaviour signals the presence of a destructive interference feature close to the parental Fermi energy. In this case, we predict that heteroatom substitution will lead to a decrease in the sample-to-sample fluctuations and a larger ensemble-averaged value of S, whose sign depends both on connectivity and on the electron donating or withdrawing character of the heteroatom.
This means that the same molecule can exhibit both positive and negative Seebeck coefficients, without external electrostatic gating. This bi-thermoelectric property is important for the design of tandem thermoelectric devices, where materials with both positive and negative Seebeck coefficents are needed to boost the thermo-voltage. The use of bi-thermoelectric molecules ensures that the two materials are completely compatible.
Computational methods
The optimized geometry and ground state Hamiltonian and overlap matrix elements of each structure was self-consistently obtained using the SIESTA27 implementation of density functional theory (DFT). SIESTA employs norm-conserving pseudo-potentials to account for the core electrons and linear combinations of atomic orbitals to construct the valence states. The generalized gradient approximation (GGA) of the exchange and correlation functional is used with the Perdew–Burke–Ernzerhof parameterization (PBE) a double-ζ polarized (DZP) basis set, a real-space grid defined with an equivalent energy cut-off of 250 Ry. The geometry optimization for each structure is performed to the forces smaller than 40 meV Å−1. The mean-field Hamiltonian obtained from the converged DFT calculation or a simple tight-binding Hamiltonian was combined with our Gollum28 quantum transport code to calculate the phase-coherent, elastic scattering properties of the each system consist of left (source) and right (drain) leads and the scattering region. The transmission coefficient T(E) for electrons of energy E (passing from the source to the drain) is calculated via the relation T(E) = Trace(ΓR(E)GR(E)ΓL(E)GR†(E)). In this expression,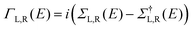 describe the level broadening due to the coupling between left (L) and right (R) electrodes and the central scattering region,
describe the level broadening due to the coupling between left (L) and right (R) electrodes and the central scattering region, 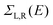 are the retarded self-energies associated with this coupling and
are the retarded self-energies associated with this coupling and 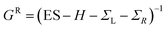 is the retarded Green's function, where H is the Hamiltonian and S is overlap matrix. Using obtained transmission coefficient (T(E)), the conductance G and Seebeck coefficient S could be calculated as G = G0L0 and S = −L1/eTL0 where
is the retarded Green's function, where H is the Hamiltonian and S is overlap matrix. Using obtained transmission coefficient (T(E)), the conductance G and Seebeck coefficient S could be calculated as G = G0L0 and S = −L1/eTL0 where 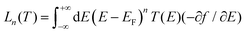 where G0 = 2e2/h is the conductance quantum, f(E) = (1 + exp((E − EF)/kBT))−1 is the Fermi–Dirac distribution function, T is the temperature and kB = 8.6 × 10−5 eV K−1 is Boltzmann's constant.
where G0 = 2e2/h is the conductance quantum, f(E) = (1 + exp((E − EF)/kBT))−1 is the Fermi–Dirac distribution function, T is the temperature and kB = 8.6 × 10−5 eV K−1 is Boltzmann's constant.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. S. thanks European Commission (EC) for a Marie Curie Early Stage Researcher position within EC FP7 ITN Molecular-Scale Electronics “MOLESCO” project no. 606728. H. S. acknowledges the Leverhulme Trust for Leverhulme Early Career Fellowship no. ECF-2017-186. This work was also supported by UK EPSRC grant no. EP/M014452/1 and EP/N017188/1.Notes and references
- F. J. Disalvo and F. J. Disalvo, Science, 2012, 703, 1997–2000 Search PubMed.
- C. J. Lambert, H. Sadeghi and Q. H. Al-galiby, C. R. Phys., 2016, 17, 1084–1095 CrossRef CAS.
- H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2017, 17, 4611–4618 CrossRef CAS PubMed.
- S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410 CrossRef CAS PubMed.
- H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2015, 15, 7467–7472 CrossRef CAS PubMed.
- L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Chem. Soc. Rev., 2016, 45, 4285–4306 RSC.
- L. Cui, R. Miao, C. Jiang, E. Meyhofer and P. Reddy, J. Chem. Phys., 2017, 146, 92201 CrossRef.
- C. Evangeli, K. Gillemot, E. Leary, M. T. González, G. Rubio-Bollinger, C. J. Lambert and N. Agraït, Nano Lett., 2013, 13, 2141–2145 CrossRef CAS PubMed.
- Y. Kim, W. Jeong, K. Kim, W. Lee and P. Reddy, Nat. Nanotechnol., 2014, 9, 881–885 CrossRef CAS PubMed.
- S. K. Yee, J. A. Malen, A. Majumdar and R. A. Segalman, Nano Lett., 2011, 11, 4089–4094 CrossRef CAS PubMed.
- S. K. Lee, M. Buerkle, R. Yamada, Y. Asai and H. Tada, Nanoscale, 2015, 7, 20497–20502 RSC.
- L. Rincón-García, A. K. Ismael, C. Evangeli, I. Grace, G. Rubio-Bollinger, K. Porfyrakis, N. Agraït and C. J. Lambert, Nat. Mater., 2015, 15, 289–293 CrossRef PubMed.
- P. Reddy, S. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568–1571 CrossRef CAS PubMed.
- J. A. Malen, P. Doak, K. Baheti, T. Don Tilley, R. A. Segalman and A. Majumdar, Nano Lett., 2009, 9, 1164–1169 CrossRef CAS PubMed.
- A. Tan, J. Balachandran, S. Sadat, V. Gavini, B. D. Dunietz, S. Y. Jang and P. Reddy, J. Am. Chem. Soc., 2011, 133, 8838–8841 CrossRef CAS PubMed.
- J. R. Widawsky, W. Chen, H. Vázquez, T. Kim, R. Breslow, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2013, 13, 2889–2894 CrossRef CAS PubMed.
- D. Kim, P. S. Yoo and T. Kim, J. Korean Phys. Soc., 2015, 66, 602–606 CrossRef CAS.
- W. Chang, B. Russ, V. Ho, J. J. Urban and R. A. Segalman, Phys. Chem. Chem. Phys., 2015, 17, 6207–6211 RSC.
- H. Sadeghi, J. a Mol, C. S. Lau, G. A. D. Briggs, J. Warner and C. J. Lambert, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2658–2663 CrossRef CAS PubMed.
- S. Sangtarash, C. Huang, H. Sadeghi, G. Sorohhov, J. Hauser, T. Wandlowski, W. Hong, S. Decurtins, S. X. Liu and C. J. Lambert, J. Am. Chem. Soc., 2015, 137, 11425–11431 CrossRef CAS PubMed.
- Y. Geng, S. Sangtarash, C. Huang, H. Sadeghi, Y. Fu, W. Hong, T. Wandlowski, S. Decurtins, C. J. Lambert and S. X. Liu, J. Am. Chem. Soc., 2015, 137, 4469–4476 CrossRef CAS PubMed.
- S. Sangtarash, H. Sadeghi and C. J. Lambert, Nanoscale, 2016, 8, 13199–13205 RSC.
- X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z.-Y. Y. Xiao, W. Hong, C. J. Lambert and S.-X. X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176 CrossRef CAS PubMed.
- D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur, T. Wandlowski, M. R. Bryce and C. J. Lambert, Nat. Commun., 2015, 6, 6389 CrossRef CAS PubMed.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. Van Der Zant, Angew. Chem., Int. Ed., 2013, 52, 3152–3155 CrossRef CAS PubMed.
- C. J. Lambert and S. X. Liu, Chem. – Eur. J., 2017 DOI:10.1002/chem.201704488.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garcìa, J. Junquera, P. Ordejòn and D. Sànchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 93029 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp00381e |
| This journal is © the Owner Societies 2018 |
