TEMPO-oxidised cellulose nanofibrils; probing the mechanisms of gelation via small angle X-ray scattering

Abstract

The structure of dispersions of TEMPO-oxidised cellulose nanofibrils (OCNF), at various concentrations, in water and in NaCl aqueous solutions, was probed using small angle X-ray scattering (SAXS). OCNF are modelled as rod-like particles with an elliptical cross-section of 10 nm and a length greater than 100 nm. As OCNF concentration increases above 1.5 wt%, repulsive interactions between fibrils are evidenced, modelled by the interaction parameter ν_RPA > 0. This corresponds to gel-like behaviour, where G′ > G′′ and the storage modulus, G′, shows weak frequency dependence. Hydrogels can also be formed at OCNF concentration of 1 wt% in 0.1 M NaCl(aq). SAXS patterns shows an increase of the intensity at low angle that is modelled by attractive interactions (ν_RPA < 0) between OCNF, arising from the screening of the surface charge of the fibrils. Results are supported by ζ potential and cryo-TEM measurements.

---

Introduction

Cellulose is the most abundant natural polymer.¹ It can be produced in various forms (such as nanofibrils,^2–5 nanocrystals,^6–8 microbeads⁹), from a variety of sources (wood pulp,¹ bacteria,¹⁰ tunicates¹¹), is biocompatible^1,12 and environmentally friendly. Strong hydrogen bonds between cellulose fibrils maintain the fibrils in a hierarchical organisation, and prevent fibril dispersion in aqueous suspensions.¹³ To counteract this strong fibril aggregation and enhance the stability of dispersions in water, diverse methods of surface modification,^13–15 such as the TEMPO-oxidation method,^13,14 have been developed.

The 2,2,6,6-tetramethylpiperidine-1-oxyl radical (TEMPO)-mediated oxidation of cellulose fibrils introduces negatively-charged carboxyl groups on the surface of the cellulose fibrils,^13,14 resulting in easy-to-disperse negatively-charged oxidised cellulose nano-fibrils (OCNF) with high surface charge (<−30 mV in ζ potential) and large aspect ratio (5–10 nm cross-section, and 100 nm to several μm in length).¹⁴

OCNF have been used to form hydrogels modulated by concentration,¹⁶ pH¹⁷ or in presence of additives, such as salt,^2,17,18 surfactant^2,19 or alcohols.²⁰ This makes them promising materials for several applications such as their use in cosmetics, as rheology modifiers (e.g. thickener, gelling agent, stabilizer),² scaffolds for tissue engineering²¹ or as drug-delivery carriers.^22,23 Among these possible additives, addition of monovalent salts has been showed to trigger gelation at concentrations of 0.1 M.² The stability of OCNF in suspensions is often described by the balance between non-covalent interactions (such as van der Waals and hydrogen bonding, electrostatic and hydrophobic interactions) following the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory.^17,18,24 Fukuzumi et al. employed the DLVO theory to calculate the interaction potential between fibrils and demonstrated that the addition of counter-ions to the suspensions screened the electrostatic repulsion force between OCNF, hence disturbing the stability of the OCNF suspensions.¹⁸ Understanding the aggregation mechanism of cellulose nanofibrils is of crucial importance to control the properties of the hydrogels, such as the mesh size, and hence tune the material properties for the desired applications.^25,26

A powerful tool to probe structural changes in aqueous solutions is small angle X-ray scattering (SAXS). Indeed, this, non-invasive, in situ technique not only provides information on the shape of the particles, such as OCNF, in dispersions, but also allows studies of the interactions between particles in such suspensions. Recently, Mao et al. have studied in detail the shape and sizes of OCNF in aqueous dispersions in the dilute regime, where particle–particle interactions can be neglected.²⁷ The aim of this paper is to model OCNF suspensions at higher concentrations, characterising the effect of fibril concentration and salt addition using SAXS, and compare these with the rheological observations, to shed some light on the gelation mechanisms involved in these systems.

Material and methods

Sample preparation

OCNF, prepared as described previously using TEMPO/NaOCl/NaBr oxidation^13,14 of wood pulp followed by high-pressure homogenisation, were provided by Croda®, as a ca. 8 wt% solids paste in water. The degree of oxidation, corresponding to the carboxylate group content of the nanofibrils as a function of number of anhydroglucose units, was determined to be 25% by conductometric titration.^21,26,28

OCNF were purified in order to remove salts and preservatives. Approximatively 20 g of OCNF was dispersed in 100 mL of deionized water (DI, 18.2 MΩ cm) and stirred at room temperature for 30 min. Then the dispersion was acidified to pH 3 using 1 M aqueous HCl solution and dialysed against DI (cellulose dialysis tubing MWCO 12 400) for 3 days and the DI replaced daily. The dialysed OCNF was processed via mechanical shear (ULTRA TURRAX, IKA T25 digital, 30 minutes at 6500 rpm) and the pH adjusted to 7 using 0.1 M NaOH. After a second dialysis step, the dispersion was diluted to ca. 2 wt% and dispersed using a sonication probe (Ultrasonic Processor, FB-505, Fisher), via a series of 1 s on 1 s off pulse mode for a net time of 5 min at 60% amplitude (i.e. a power of 300 W) on ca. 45 mL of the dispersion placed in an ice bath.

The OCNF solution was freeze-dried and 2.5 wt% and 3 wt% dispersions were prepared by mixing OCNF powder and DI water and stirring the solution overnight. Lower concentrations of OCNF dispersions were prepared by diluting OCNF stock solution to final OCNF concentrations of 0.4; 0.6; 0.8; 1; 1.5; 2; 2.5 or 3 wt%. Dispersions with salt were prepared by diluting OCNF stock solution with aqueous NaCl solution to final OCNF concentration of 2 wt% and NaCl concentration of 0; 0.1; 0.2; 0.3; 0.4 or 0.5 M.

Methods

SAXS measurements were performed at Diamond Light Source (Didcot, Oxfordshire), on the I22 beamline with a beam energy of E = 12.4 keV and wavelength λ = 1 Å. The data were collected using a Pilatus P3-2M (Silicon hybrid pixel detector, DECTRIS). Multiple frames of 100 ms were recorded for a total of 7 s. Radiation damage, inducing a change in the SAXS pattern, was observed after a few seconds of exposure, thus only the frames corresponding to the first second of measurement were kept and averaged. The probed q-range was 0.003–0.3 Å⁻¹ where q is the scattering vector. Samples were loaded in 1.5 mm diameter glass capillary tubes and sealed. For the absolute intensity calibration, scattering patterns of the empty capillary and the capillary filled with DI water were also recorded. The value of the constant intensity contribution of water is equal to 0.016 cm⁻¹ on absolute scale.²⁹ Capillaries containing the water and salt solutions were also recorded for solvent subtraction.

Complementary measurements were made at SOLEIL synchrotron (Saclay, France), also using a beam wavelength of λ = 1 Å, and with a probed q-range of 0.006–0.3 Å⁻¹. 10 frames of 100 ms were recorded using a PCCD170170 (AVIEX).

The measured scattered intensity I(q) (cm⁻¹) is defined for isotropic suspensions as:³⁰

I(q) = nΔρ²P(q)S(q) + bkg (1)

n is the number of objects per unit volume. Δρ = ρ_c − ρ₀ is the difference between the scattering length density of the dispersed particles (ρ_c) and the scattering length density of the solvent (ρ₀) (in cm⁻²). P(q) is the form factor which describes the shape and size of the particles (in cm⁻⁶). S(q) is the structure factor and describes interference of the X-ray beam with multiple objects, thus usually associated with particle–particle interactions. Finally, bkg is the background.

In agreement with previous studies^27,28 and TEM measurements, cellulose fibrils were modelled as rigid cylinders with a length L, an elliptical cross section (with a major radius R_max and an ellipticity 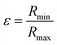ratio between the minor and the major radii, R_min and R_max respectively) and a uniform scattering length density (ρ_c).

P(q) = P(q, R_max, ε, L, σ) = 〈F_CS²(q, R_max, ε)〉_σP_rod(q, L) (2)

withthe form factor associated to the ellipsoidal cross-section, andthe form factor of an infinitely thin rod, with . If needed, the polydispersity in size on the cross-section, 〈·〉_σ is taken into account via the Schulz–Zimm distribution, i.e.:with

In some cases, for comparison, a variation of the model was used. In that case, the cylinders are considered as not completely rigid, but presenting a flexibility in their length. The model of semi-flexible cylinders has been previously described by Pedersen and Schurtenberger,³¹ with the form factor being expressed as:

P(q) = P(q, R_max, ε, L, σ) = 〈F_CS²(q, R_max, ε)〉_σP_flex(q, L_C, b_Kuhn) (6)

P_flex, the contribution associated with the flexible length of the cylinders, depends on two parameters, the contour length L_C, and the Kuhn length b_Kuhn. The contour length corresponds to the overall length of the fibrils (equivalent to L in the rigid cylinders model). The Kuhn length is two times the persistence length, and is an indication of the flexibility of the fibrils. A complete description of P_flex can be found in ref. 31, and is not repeated here.

Finally, in the semi-dilute regime, the interactions between the cylinders, either rigid or flexible, have been described using the Random Phase Approximation (RPA):^32,33

The parameter ν_RPA is associated with the second virial coefficient describing the pair interaction between cylinders:³³In most cases, the interactions U(r) studied in the RPA model are of the “excluded volume” type, with cylinders defined as impenetrable. Using mean-field theory, all pair interactions are averaged between cylinders, and in that case ν_RPA is named the excluded volume parameter.³² This model has been developed and extensively studied for semi flexible cylinders,^33–35 but was later shown to be valid for interacting rigid cylinders.^30,32 Notably, the theory depicts accurately the interactions at work in the isotropic-to-nematic phase transition in rigid cylinder suspensions.³²

Monte–Carlo simulations³⁶ have shown that cylinder–cylinder interactions are better depicted using the polymer reference interaction site model (PRISM),³⁷ similar to the RPA model:

with

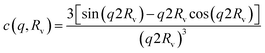
In that case, on top of the excluded volume parameter, ν_RPA, previously described, the term c(q, R_v) is associated with a local excluded volume along the fibril. This local volume corresponds on each point along the length of the fibril to a sphere of radius R_v which is not accessible to any other fibril. The PRISM model is often used at high concentration of objects, where interactions between cylinders are high and induce a broad peak to appear around 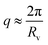. Let us note that this extra parameter has influence only at much higher interactions than the one studied in this paper. R_v was then fixed to R_max the maximum radius of OCNF fibrils, and for the range of “weak interactions” studied here, the structure factor is:

S(q) = S_PRISM(q, ν_RPA, R_max) ≅ S_RPA(q, ν_RPA) (10)

For simplicity we will hence describe interactions as following the Random Phase Approximation model.

In addition to SAXS, rheological measurements were performed using a stress-controlled rheometer (Discovery HR-3, TA Instruments®) equipped with a sandblasted plate–plate geometry (40 mm or 12 mm in diameter depending on the measurements). The samples were used without any further processing and the edge of the geometry was covered with a thin layer of mineral oil to prevent evaporation of water. Three types of experiments were conducted. Amplitude strain sweep measurements of the storage and loss moduli G′ and G′′ were conducted at ω = 10 rad s⁻¹. A strain amplitude of 0.1%, within the linear viscoelastic regime, was chosen for frequency sweep measurements. Finally, steady flow measurements were performed to study the viscosity response of the sample to shearing, with a shear rate ranging from 10⁻² to 10² s⁻¹.

Transmission electron microscopy (TEM) measurements were carried out using a JEM-2100 Plus (JEOL, USA), at an operating voltage of 200 kV. TEM grid was prepared by drop-deposition of OCNF at 0.025 wt%, negatively stained using uranyl acetate (2 M). Excess solution was removed and the sample left to dry prior to experiment. To study the effect of salt on the dispersions, cryo-TEM measurements were carried out on a JEM-2200FS (JEOL, Japan), operated at 200 kV. The samples were vitrified in a controlled environment vitrification system with relative humidity close to 100% at room temperature. A small volume (about 5 μL) of OCNF solution at 0.1 wt%, without salt or with 0.1 M NaCl respectively, was deposited on lacey carbon-coated cupper grids and excess fluid was gently removed by blotting. The grids were then directly plunged into liquid ethane. Grids were stored in liquid nitrogen until being transferred to the electron microscope.

Results

Gels formed by OCNF suspensions at various concentrations

Before studying the formation of cellulose gels, OCNF were observed in TEM (see Fig. 1a, b, and Fig. S1 in ESI†). Their shape consists of long fibrils with a length of hundreds of nm and a cross-section around 5 nm. From averaging 175 measurements, both the diameter and the length of the fibrils were estimated to be D = 7 ± 2 nm and L = 160 ± 60 nm respectively (statistics are given in Fig. 1c and d). A histogram of the diameter shows a broad distribution of sizes between 4–12 nm, reflecting the elliptical nature of the fibril cross-section.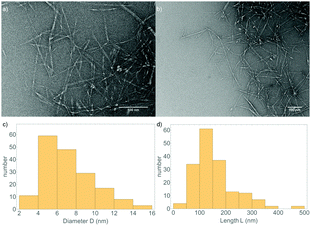

Fig. 1 (a and b) TEM micrographs of OCNF at 0.025 wt%, stained with uranyl acetate. (c and d) Size distribution of the diameter and length of the fibrils over 175 measurements.

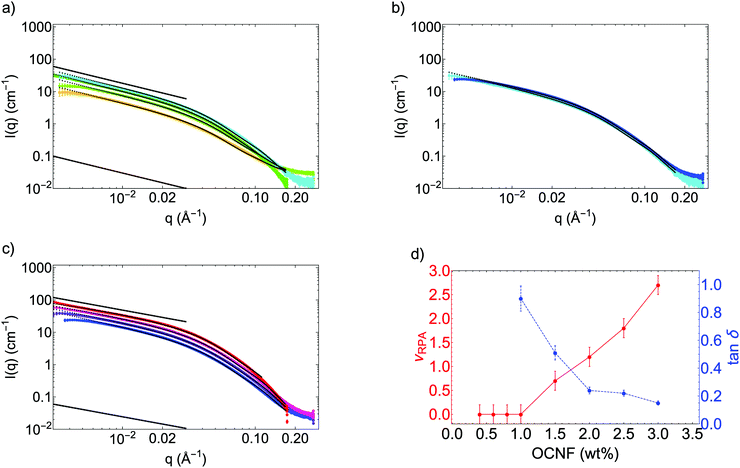
SAXS data of OCNF suspensions at various concentrations were measured on the I22 beamline (see Fig. 2 and Fig. S2 in ESI†). In agreement with the TEM measurements, OCNF were modelled by a form factor of rigid cylinders, with the length L fixed at 160 nm (as L cannot be measured in SAXS at this q-range) and an elliptical cross-section (R_max and ε = R_min/R_max are given in Table 1).

Fig. 2 (a–c) SAXS patterns I(q) vs. q in absolute scaling of OCNF at various wt%: (a) 0.4 wt% (yellow), 0.6 wt% (pale green), 0.8 wt% (green) and 1 wt% (cyan) giving the signal of non-interacting fibrils; (b) 1 wt% (cyan) and 1.5 wt% (blue) which shows the emergence of a repulsive interaction between OCNF fibrils and (c) 1.5 wt% (blue), 2 wt% (violet), 2.5 wt% (pink) and 3 wt% (red) fitted using the model of interacting fibrils. All the fits are given by the black dots. The dashed line highlights the slope at low angles. (d) Comparison between the interaction parameter ν_RPA (solid red line) and tan δ = G′′/G′ (dashed blue line) measured in rheology at ω = 1 rad s⁻¹.

Table 1 Table of the parameters found by fitting of the SAXS data for OCNF dispersions at various wt% via the RPA (PRISM) model for rigid cylinders. Length of the fibrils has been fixed at L = 160 nm using results from TEM measurements

OCNF wt%	0.4	0.6	0.8	1	1.5	2	2.5	3
n (×10^12 cm^−3)	7 ± 1	12 ± 1	16 ± 2	20 ± 2	24 ± 3	33 ± 4	47 ± 7	67 ± 10
R max (nm)	5.1 ± 0.1	5.1 ± 0.1	5.1 ± 0.1	5.1 ± 0.1	5.1 ± 0.1	5.1 ± 0.1	5.1 ± 0.1	5.1 ± 0.1
ε	0.27 ± 0.02	0.27 ± 0.02	0.27 ± 0.02	0.27 ± 0.02	0.27 ± 0.02	0.27 ± 0.02	0.27 ± 0.02	0.27 ± 0.02
R min (nm)	1.4 ± 0.1	1.4 ± 0.1	1.4 ± 0.1	1.4 ± 0.1	1.4 ± 0.1	1.4 ± 0.1	1.4 ± 0.1	1.4 ± 0.1
ν RPA	0	0	0	0	0.7 ± 0.2	1.2 ± 0.2	1.8 ± 0.2	2.7 ± 0.2

---

We note that Mao et al. described the fibrillar cross-section using the Gaussian-approximate parallelepiped model (GAP), essentially describing the cross-section as a parallelepiped with semicircles ends.²⁷ Instead, here we used a slightly simpler model, with fewer fitting parameters, describing an ellipsoidal cross-section. This gives a satisfactory fit to the SAXS data (see residuals in Fig. S2, ESI†) and the cross-section dimensions found are consistent with those previously observed by Mao et al.

For concentrations ≤1 wt%, the SAXS data can be well-fitted by this form factor only, without any interactions between the fibrils (Fig. 2a). Notably, the scattering at small angles follows, on a log–log plot, a q⁻¹ slope, characteristic of rigid elongated objects such as rods or cylinders. The dimensions of the fibrils (R_max and ε) are found not to be dependent on the concentration and consistent with the TEM measurements. The number of objects per unit volume increases with concentration as expected (see the increase in intensity in Fig. 2a and the parameters found for the fits in Table 1). These SAXS patterns of rigid rods, observed in this dilute regime, are consistent with previous results found for cellulose nanocrystals^38,39 or cellulose nanofibrils at similar concentrations.^27,40,41 These are also consistent with the high value measured for the Young's modulus of OCNF (around 100 GPa) using AFM.⁴²

Between 1 and 1.5 wt% (Fig. 2b), there is no observable increase of the intensity at low angles; as a change in the slope is observed in the small angle region (0.005 ≤ q ≤ 0.03 Å⁻¹). In that q-range, the slope evolves from a q⁻¹ behaviour at 1 wt% to a less pronounced exponent at 1.5 wt%. This decrease in the slope can only be attributed to a change in the structure factor S(q), due to repulsive interactions appearing between fibrils at 1.5 wt%. This can be more easily observed by plotting the effective structure factor S(q) only (see Fig. S2, ESI†). For concentrations ≥1.5 wt%, S(q) diverges from 1 at low q, signalling interactions.

The SAXS pattern at 1.5 wt% is well-modelled by adding to the fit the structure factor described in the Materials and methods section. Data fitting gives an excluded volume parameter ν_RPA = 0.7 (Fig. 2d and Table 1). The positive sign of ν_RPA indicates that the fibril–fibril interaction is repulsive and the value of ν_RPA is related to the strength of the interaction and the concentration of the interacting fibrils.⁴³ν_RPA corresponds to the excluded volume parameter between the repulsive fibrils.³³

For higher concentrations, the SAXS data can only be fitted including interactions between fibrils (Fig. 2c, and S(q) in Fig. S2, ESI†), with further reduction of the slope at small angles: the observed slope at small-angles follows a q^{−0.6 to 0.7} power law at 3 wt% instead of q⁻¹ for non-interacting fibrils, as seen below 1 wt%. Contrary to fractal systems (where slopes of q^−Dm, with 2 ≤ Dm ≤ 4, can be observed), this slope does not describe a fractal organisation, but the emergence of repulsive interactions, effectively lowering the intensity measured in this q-range. This is clearly observed by plotting S(q) versus q (Fig. S2, ESI†), where S(q) is found to be below 1 in this q-range.

Further increase in intensity (i.e. in the number of objects per unit volume) is also observed, and, more importantly, the ν_RPA parameter increases linearly in this concentration range (see Table 1 and Fig. 2d), as this parameter depends on the concentration of interacting OCNF. A monotonic increase in the concentration would result in a monotonic increase in the parameter ν_RPA. Moreover, for high enough values of ν_RPA, denoting significant fibril–fibril interactions, the influence of a local excluded volume, described by the radius R_v in the PRISM model (see Material and methods), can no longer be neglected. Indeed, theoretical SAXS patterns of the same fibril form factor at different values of ν_RPA (Fig. S3 in ESI†) demonstrate the emergence of a correlation peak in the small angle region for high interactions. The position of this correlation peak, which signals the isotropic to nematic phase transition, is associated with the value of R_v. For OCNF, this correlation peak is not observed for concentrations ≤3 wt%. It has nonetheless been recently observed by Bertsch et al. for suspensions of cellulose nanocrystals at 5 wt%.⁴⁴ Interestingly, a similar correlation peak was also observed by Uhlig et al., for dispersions of different types of cellulose nanocrystals at very low concentration (below 1 wt%).⁴⁵ Nonetheless, it was noted by the authors that, in their case, their nanocrystals were forming liquid-crystalline aggregates in solution, instead of the homogeneous dispersions obtained using TEMPO-oxidised cellulose nanofibrils.¹³

Reproducibility of these results was confirmed by complementary measurements made at SOLEIL synchrotron (Fig. S4, ESI†). A different batch of OCNF, prepared in the same conditions, showed rigorously similar SAXS patterns and fits parameters.

These results from SAXS have to be considered in regards to the rheology measurements (Fig. 2d and Fig. S5, ESI†). OCNF suspensions are shear-thinning for concentrations ≥0.6 wt% (Fig. S5a, ESI†). Nevertheless, measurable G′, corresponding to G′ > G′′ (characteristic of a gel) were observed both in frequency and amplitude sweeps only at concentrations above 1 wt%; and G′ ≫ G′′ only for samples above 2 wt% (Fig. S5b and c, ESI†).

A gel-like behaviour is evidenced by two criteria: and a value of G′ only weakly dependant of the frequency of oscillation.⁴⁶ Both are evidenced here for OCNF suspensions ≥1.5 wt%, which corresponds to the minimal concentration where interactions between fibrils are needed to fit the SAXS data (see Fig. 2d giving both ν_RPA and tan δ upon OCNF concentration and Fig. S5b (ESI†) giving G′ and G′′ measurements upon frequency sweeps).

It is known that suspensions of anisotropic particles will exhibit a gel-like behaviour as concentration is increased. This is due to particle orientation in the suspension as the isotropic-to-nematic phase transition is approached.^47,48 The ν_RPA parameter expresses increasing interactions between fibrils due to crowding effects, but it has been shown that the nematic interaction associated with fibril–fibril orientation plays a significant role in the overall structure factor only at concentrations close to c*, the concentration of the isotropic-to-nematic transition.³² Hence, our results indicate that a small crowding of OCNF is enough to form a physical gel, even without the fibrils having a nematic orientation within the sample at rest.

Gels of OCNF in presence of salt

OCNF are negatively charged particles, and addition of small amounts of monovalent salts, such as NaCl, is enough to allow the formation of self-standing gels.^2,17,18 Addition of salt not only has dramatic effects on the rheological properties of the sample, with a strong gel-like behaviour observed in presence of salt^2,18 (see Fig. S6, ESI†), but also on the structural properties measured in SAXS.⁴¹ Indeed, comparing SAXS patterns of OCNF at 1 wt% without NaCl or with 0.1 M NaCl (Fig. 3) demonstrates a complete superimposition of the data at large angles (associated with the fibril cross-section) between the two samples; whereas at small angles an increase of the signal is noted, with a slope changing from q⁻¹ for the sample without salt to q^−1.6 in the presence of salt. The same type of changes was also observed for cellulose nanocrystals in presence of salt.³⁹

Fig. 3 SAXS patterns I(q) vs. q in absolute scaling of OCNF at 1 wt% without salt (cyan) and with 0.1 M of NaCl (orange). The black dots are the fits made using the model of rigid cylinders, without interactions (when no NaCl is added) and with attractive interactions (with 0.1 M of NaCl). The grey dashed line is the fit made using the semi-flexible cylinders model for the sample with 0.1 M NaCl.

Two models were investigated to explain this change in the small-angle region. The first model, of semi-flexible fibrils, assumes that OCNF present some flexibility along their length, defined by two parameters: the contour length L_C, which represents the overall length of the fibrils (and corresponds to the length L of the rigid fibril model), and a Kuhn length b_Kuhn, which is twice the persistence length, corresponding to the length over which the fibril can be considered as rigid.^31,34 Parameters associated with the cross-section of the fibrils (R_max and ε) are unchanged. This model, used for example to describe worm-like micelles,³⁴ relies on a change of the form factor of the fibrils – reflecting a change of their shape – and implies that the fibrils experience a physical change of their rigidity, possibly due to the appearance of points of contact between fibrils, associated with the addition of counter-ions on the surface.

The second model does not rely on any change in the form factor of the fibrils, but assumes that the change in slope is due to interactions, attractive this time, between the fibrils, mirroring the effect of repulsive interactions on SAXS pattern of cylindrical scatterers. van der Schoot and Odijk have calculated the structure factor for rodlike particles interacting by van der Waals forces.⁴⁹ They showed that when writing the pair correlation function between two rods, and the associated structure factor, two cases arise depending on the angle γ between the two rods. If γ is extremely small (the rods are almost parallel to each other), the description of the structure factor requires the calculation of the third virial coefficient between the rods. For any other angle γ (rods not parallel), the structure factor is similar to the one developed in the random phase approximation, by replacing ν_RPA with ν_RPA = ν_vdW + ν_rep, with ν_vdW the second virial coefficient associated to attraction forces, and ν_rep the second virial coefficient due to repulsion forces. Let us note that when no salt is added, OCNF are strongly repulsive (ν_vdW ≪ ν_rep) and ν_RPA ≅ ν_rep, result given by the random phase approximation theory. When the surface charge of the fibrils is screened, then ν_vdW ≫ ν_rep and ν_RPA ≅ ν_vdW < 0. In a gel network where fibrils are disorganised, it is much more probable that fibrils are not parallel to each other. Therefore, we have decided to generalize the random phase approximation structure factor with ν_RPA < 0. Indeed, since the ν_RPA parameter is associated with the overall second virial coefficient of the cylinders, attractive interactions would result in a negative value for this parameter.^50,51 For a more detailed depiction of the structure factor with attractive interactions, the use of the third virial coefficient is recommended.⁴⁹ Nonetheless this simplified structure factor is enough to capture the main feature of the data.

Both models provide reasonable fits to the data (fits illustrated in Fig. 3, parameters in Table 2), with data at small angles slightly better fitted for the semi-flexible fibril model. Indeed, in the interacting rigid fibril model, the use of a negative second virial coefficient, without taking into account higher orders in the pair correlation function between rods, gives a mathematical singularity at the smallest angles, as already discussed by van der Schoot and Odijk.⁴⁹ In the presence of salt, the parameters associated with the fibril cross-section are unchanged and are found to be similar for both models. The semi-flexible model gives a Kuhn length b_Kuhn = 24 ± 2 nm, more than five times lower than the overall length of the fibrils, suggesting highly flexible particles. On the other hand, the second model gives exactly the same parameters for the shape of the fibrils with and without salt added, and a negative ν_RPA value (−3.2) when NaCl is present, corresponding, as previously described, to attractive interactions between the fibrils.

Table 2 Table of the parameters found by fitting of the SAXS data for 1 wt% OCNF without NaCl, with NaCl via the RPA (PRISM) model for rigid cylinders and with NaCl via the semi-flexible cylinders model

NaCl (M)	0	0.1	0.1
Model	Rigid cylinders	Rigid cylinders + interactions	Semi-flexible cylinders
R max (nm)	5.1 ± 0.1	5.1 ± 0.1	5.1 ± 0.1
ε	0.27 ± 0.02	0.27 ± 0.02	0.27 ± 0.02
L (or LC, nm) (fixed)	160	160	160
ν RPA	0	−3.2 ± 0.2	—
b Kuhn (nm)	—	—	24 ± 2

---

To better comprehend the physical meaning of those two models and help discriminate between them, cryo-TEM measurements have been carried out on both samples at 0.1 wt% of OCNF (Fig. 4 and Fig. S7, ESI†) to study the flexible or rigid nature of the fibrils,⁵² and ζ potential measurements were conducted to measure surface charge. Examination of cryo-TEM micrographs does not provide evidence for a change in flexibility of the fibrils, which appear straight both with and without salt, as expected from elastic modulus measurements on a single fibril.⁴² However, the two samples seem to exhibit very different OCNF organisation, with some local nematic order observed in the sample without salt (Fig. S7, ESI†), while sample containing salt presents a more random orientation of the fibrils, appearing to be forming a 3D network, consistent with the formation of a gel.

Fig. 4 Cryo-TEM micrographs of (a) OCNF at 0.1 wt% without salt and (b) OCNF at 0.1 wt% with NaCl 0.1 M.

This apparent “network” observed in presence of salt allows a mesh size to be defined as the average distance between two “nodes” (i.e. apparent contact points between fibrils) of the network. A rough measurement over 15 nodes between fibrils gives a value of 30 ± 10 nm (see Fig. S8, ESI†). This is of a similar order of magnitude to the Kuhn length derived from the flexible cylinder modelling of the SAXS data. The mesh size measured here can be indicative only, as cryo-TEM micrographs are a 2D projection of a 3D organisation, which would bias any precise measurement. Nonetheless, this suggests that the q value where the SAXS signal deviates from the q⁻¹ slope of rigid cylinders, modelled by the Kuhn length in the semi-flexible cylinders model, corresponds to the mesh size of the network. Hence, the value of the Kuhn length obtained from the fits can be directly associated to the mesh size of the gel network.

On the other hand, the nature of the change of interactions between OCNF is well captured by the attractive interaction model. But, as it is defined here, it does not allow an accurate description of the resulting fractal network organization of OCNF. Of course, one must be extremely cautious in interpreting cryo-TEM images, as the sample preparation procedure may significantly alter the fibril dispersion. Nonetheless, those results are a valid indication that the fibrils do not experience a change of their shape, but rather a reorganisation of OCNF in the sample.

Furthermore, a change in interactions between fibrils is expected from ζ potential measurements. OCNF exhibit a measured ζ potential value of ζ = −61 ± 3 mV in water against −22 ± 1 mV in 0.1 M NaCl. As −30 mV is often considered as the limit below which negative colloidal particles are stable in dispersions, and above which they aggregate, a decrease of the charge on the fibrils implies a decrease of the repulsive interactions between them. Yet, the potential of interaction between fibrils is often expressed as the sum of two contributions, electrostatic repulsion and van der Waals attraction.^17,18,24 The limit of −30 mV hence is equivalent to the limit between electrostatic repulsion dominating (ζ < −30 mV) and van der Waals attraction dominating (0 ≥ ζ > −30 mV). As previously evidenced by Fukuzumi et al.,¹⁸ increasing the salt concentration decreases the strength of the electrostatic repulsion, and the overall potential becomes attractive, reflected in attractive interactions required to model the SAXS data.

Further evidence of the effect of salt on the OCNF interaction is found in the SAXS study of OCNF suspensions at 2 wt% with various concentrations of salt, conducted at SOLEIL synchrotron (Fig. 5). This sample without salt is fitted including repulsive interactions (ν_RPA = 1.7 ± 0.2). Increasing the concentration of salt results in a gradually decreasing ν_RPA parameter, that becomes negative above 0.1 M NaCl, indicating that the particles enter an attractive regime at high concentration of salt (see Fig. 5b). Those results are a direct evidence of a change in the balance of interactions between electrostatic repulsion and van der Waals attraction between OCNF.

Fig. 5 (a) SAXS patterns I(q) in arbitrary units vs. q of OCNF at 2 wt% with various NaCl concentrations: without salt (yellow), 0.1 M (green), 0.2 M (cyan), 0.3 M (blue), 0.4 M (pink) and 0.5 M (red). Curves have been shifted for clarity. The fits are given in black dots. (b) Interaction parameter ν_RPA found by the fits upon salt concentration. The grey area is associated to repulsive interactions while the white area corresponds to attractive interactions between the fibrils.

To summarize, analysis of the SAXS measurements show that the addition of salt changes the interactions between OCNF. Gelation is triggered by attractive interactions between the fibrils arising from the screening of the electrostatic repulsion of OCNF.

Fitting the SAXS data with the RPA (or PRISM) structure factor of rigid cylinders and a negative value of ν_RPA is sufficient to capture the main features of the structural changes in the system. It is also possible to provide a good fit to the data using a purely phenomenological model of semi-flexible cylinders, which allows, via the Kuhn length b_Kuhn, an estimation of the mesh size of the gel network.

Conclusions

Careful analysis of SAXS data allows elucidation of the mechanisms of gelation and deconvolution of interactions of OCNF aqueous dispersions. Notably, the effects of fibril concentration and salt addition have been characterised and used to determine a suitable model for fitting SAXS data from such systems. In agreement with TEM measurements and fitting of SAXS patterns of dilute samples, OCNF can be described as long rigid cylinders with an elliptical cross-section. With increasing concentration of OCNF, excluded volume interactions start to become important, modelled by the random phase approximation and the interaction parameter ν_RPA > 0. The measurement of these repulsive interactions in the SAXS pattern corresponds to a tan δ = G′′/G′ < 1 and low-frequency dependence of G′ in rheology, indicating physical gel-like behaviour. This links the formation of a gel to a crowding effect of the particles in dispersion in this semi-dilute regime, without further ordering. When salt is added, a noticeable difference is observed in the SAXS pattern, with an increase of the signal at small angles, ascribed to attractive interactions between the fibrils. As a first approximation, the data have been fitted using the same random phase approximation model for the structure factor, with a value of ν_RPA < 0, corresponding to a negative second virial coefficient of the fibrils – in agreement with the occurrence of attractive interactions between OCNF. This is supported by cryo-TEM images, that reveal no change in fibril shape, but point to a possible reorganisation; ζ potential measurements that show a diminution of the surface charge of OCNF and SAXS measurements of OCNF at different salt concentrations, which pinpoint the slow change from a regime where the fibrils experience repulsive interactions to the attractive regime due to the screening of the electrostatic repulsions between OCNF. By studying both the excluded volume effect from OCNF concentration variation and the attractive interactions due to charge screening in the presence of salt, a better understanding of the mechanisms of gelation of these OCNF suspensions is gained. This will provide the basis for understanding and describing the effect of other additives, such as alcohols or surfactants.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank EPSRC for funding this project (grant EP/N033310/1). Mr Vincenzo Calabrese thanks the University of Bath for PhD studentship funding. Dr Nick Terril and Dr Andy Smith on I22 are thanked for assistance with SAXS experiments at Diamond Light Source Ltd (experiments no. SM3691 and SM16364-1). Dr Thomas Bizien and Dr Javier Pérez on Swing at SOLEIL are also thanked (proposal 20170502). Mrs Ursula Potter (Microscopy and Analysis Suite, University of Bath) and Dr Anna Carnerup (Lund University) are thanked for their assistance in TEM and cryo-TEM measurements. The Technology Strategy Board (TSB), UK is acknowledged for funding under the “Sustainable Materials” collaborative R&D call (project number: TS/H000240/1). All data supporting this paper are openly available from the University of Bath data archive at https://doi.org/10.15125/BATH-00471.

Notes and references

1. D. Klemm, B. Heublein, H.-P. Fink and A. Bohn, Angew. Chem., Int. Ed., 2005, 44, 3358–3393.
2. R. J. Crawford, K. J. Edler, S. Lindhoud, J. L. Scott and G. Unali, Green Chem., 2012, 14, 300–303.
3. O. Nechyporchuk, M. N. Belgacem and J. Bras, Ind. Crops Prod., 2016, 93, 2–25.
4. R. K. Johnson, A. Zink-Sharp, S. H. Renneckar and W. G. Glasser, Cellulose, 2009, 16, 227–238.
5. I. Siró and D. Plackett, Cellulose, 2010, 17, 459–494.
6. J. George and S. N. Sabapathi, Nanotechnol., Sci. Appl., 2015, 8, 45–54.
7. S. J. Eichhorn, Soft Matter, 2011, 7, 303–315.
8. Y. Habibi, L. A. Lucia and O. J. Rojas, Chem. Rev., 2010, 110, 3479–3500.
9. J. Coombs O'Brien, L. Torrente-Murciano, D. Mattia and J. L. Scott, ACS Sustainable Chem. Eng., 2017, 5, 5931–5939.
10. S. Hestrin and M. Schramm, Biochem. J., 1954, 58, 345–352.
11. Y. Zhao, Y. Zhang, M. E. Lindström and J. Li, Carbohydr. Polym., 2015, 117, 286–296.
12. F. G. Torres, S. Commeaux and O. P. Troncoso, J. Funct. Biomater., 2012, 3, 864–878.
13. T. Saito, Y. Nishiyama, J.-L. Putaux, M. Vignon and A. Isogai, Biomacromolecules, 2006, 7, 1687–1691.
14. A. Isogai, T. Saito and H. Fukuzumi, Nanoscale, 2011, 3, 71–85.
15. M. Hasani, E. D. Cranston, G. Westman and D. G. Gray, Soft Matter, 2008, 4, 2238–2244.
16. Q. Wu, Y. Meng, S. Wang, Y. Li, S. Fu, L. Ma and D. Harper, J. Appl. Polym. Sci., 2014, 131, 40525.
17. A. B. Fall, S. B. Lindström, O. Sundman, L. Ödberg and L. Wågberg, Langmuir, 2011, 27, 11332–11338.
18. H. Fukuzumi, R. Tanaka, T. Saito and A. Isogai, Cellulose, 2014, 21, 1553–1559.
19. N. Quennouz, S. M. Hashmi, H. S. Choi, J. W. Kim and C. O. Osuji, Soft Matter, 2016, 12, 157–164.
20. M. A. da Silva, V. Calabrese, J. Schmitt, D. Çelebi, J. L. Scott and K. J. Edler, in preparation.
21. J. C. Courtenay, M. A. Johns, F. Galembeck, C. Deneke, E. M. Lanzoni, C. A. Costa, J. L. Scott and R. I. Sharma, Cellulose, 2017, 24, 253–267.
22. M. M. Abeer, M. C. I. M. Amin and C. Martin, J. Pharm. Pharmacol., 2014, 66, 1047–1061.
23. D. Çelebi, R. H. Guy, K. J. Edler and J. L. Scott, Int. J. Pharm., 2016, 514, 238–243.
24. S. M. Notley, Phys. Chem. Chem. Phys., 2008, 10, 1819–1825.
25. L. Jowkarderis and T. G. M. van de Ven, Soft Matter, 2015, 11, 9201–9210.
26. M. A. Johns, A. Bernardes, E. Ribeiro De Azevêdo, F. E. G. Guimarães, J. P. Lowe, E. M. Gale, I. Polikarpov, J. L. Scott and R. I. Sharma, J. Mater. Chem. B, 2017, 5, 3879–3887.
27. Y. Mao, K. Liu, C. Zhan, L. Geng, B. Chu and B. S. Hsiao, J. Phys. Chem. B, 2017, 121, 1340–1351.
28. Y. Habibi, H. Chanzy and M. R. Vignon, Cellulose, 2006, 13, 679–687.
29. O. Glatter and O. Kratky, Small Angle X-Ray Scattering, Academic Press, 1982.
30. S. Manet, J. Schmitt, M. Impéror-Clerc, V. Zholobenko, D. Durand, C. L. P. Oliveira, J. S. Pedersen, C. Gervais, N. Baccile, F. Babonneau, I. Grillo, F. Meneau and C. Rochas, J. Phys. Chem. B, 2011, 115, 11330–11344.
31. J. S. Pedersen and P. Schurtenberger, Macromolecules, 1996, 29, 7602–7612.
32. T. Shimada, M. Doi and K. Okano, J. Chem. Phys., 1988, 88, 2815–2821.
33. S. F. Edwards, Proc. Phys. Soc., 1966, 88, 265–280.
34. C. A. Dreiss, Soft Matter, 2007, 3, 956–970.
35. M. Daoud, J. P. Cotton, B. Farnoux, G. Jannink, G. Sarma, H. Benoit, R. Duplessix, C. Picot and P. G. de Gennes, Macromolecules, 1975, 8, 804–818.
36. L. Cannavacciuolo, J. S. Pedersen and P. Schurtenberger, Langmuir, 2002, 18, 2922–2932.
37. K. S. Schweizer and J. G. Curro, Adv. Polym. Sci., 1994, 116, 319–377.
38. P. Terech, L. Chazeau and J. Y. Cavaille, Macromolecules, 1999, 32, 1872–1875.
39. F. Cherhal, F. Cousin and I. Capron, Langmuir, 2015, 31, 5596–5602.
40. Y. Su, C. Burger, B. S. Hsiao and B. Chu, J. Appl. Crystallogr., 2014, 47, 788–798.
41. L. Geng, X. Peng, C. Zhan, A. Naderi, P. R. Sharma, Y. Mao and B. S. Hsiao, Cellulose, 2017, 24, 5417–5429.
42. S. Iwamoto, W. Kai, A. Isogai and T. Iwata, Biomacromolecules, 2009, 10, 2571–2576.
43. J. S. Pedersen, in Neutrons, X-Rays and Light, ed. T. Zemb and P. Lindner, Elsevier Science, 2002, ch. 16.
44. P. Bertsch, S. Isabettini and P. Fischer, Biomacromolecules, 2017, 18, 4060–4066.
45. M. Uhlig, A. Fall, S. Wellert, M. Lehmann, S. Prévost, L. Wågberg, R. von Klitzing and G. Nyström, Langmuir, 2016, 32, 442–450.
46. G. Kavanagh and S. B. Ross-Murphy, Prog. Polym. Sci., 1998, 23, 533–562.
47. A. Mourchid, A. Delville and P. Levitz, Faraday Discuss., 1995, 101, 275–285.
48. M. E. Cates, S. M. Fielding, D. Marenduzzo, E. Orlandini and J. M. Yeomans, Phys. Rev. Lett., 2008, 101, 068102.
49. P. van der Schoot and T. Odijk, J. Chem. Phys., 1992, 97, 515–524.
50. A. Quigley and D. R. Williams, Eur. J. Pharm. Biopharm., 2015, 96, 282–290.
51. D. Rosenbaum, P. C. Zamora and C. F. Zukoski, Phys. Rev. Lett., 1996, 76, 150–153.
52. R. Kumar, G. C. Kalur, L. Ziserman, D. Danino and S. R. Raghavan, Langmuir, 2007, 23, 12849–12856.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp00355f

‡ Current address: Nanobiophysics, MESA+ Institute for Nanotechnology, Faculty of Science and Technology, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands.

---