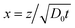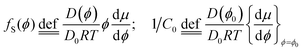Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaporation, diffusion and self-assembly at drying interfaces†
K.
Roger
 *a,
E.
Sparr
*a,
E.
Sparr
 *b and
H.
Wennerström
*b and
H.
Wennerström
 b
b
aLaboratoire de Génie Chimique/Université de Toulouse, CNRS, INPT, UPS, Toulouse, France. E-mail: kevin.roger@ensiacet.fr
bDiv Physical Chemistry, Dept Chemistry, Lund University, Sweden. E-mail: emma.sparr@fkem1.lu.se
First published on 21st March 2018
Abstract
Water evaporation from complex aqueous solutions leads to the build-up of structure and composition gradients at their interface with air. We recently introduced an experimental setup for quantitatively studying such gradients and discussed how structure formation can lead to a self-regulation mechanism for controlling water evaporation through self-assembly. Here, we provide a detailed theoretical analysis using an advection/diffusion transport equation that takes into account thermodynamically non-ideal conditions and we directly relate the theoretical description to quantitative experimental data. We derive that the concentration profile develops according to a general square root of time scaling law, which fully agrees with experimental observations. The evaporation rate notably decreases with time as t−1/2, which shows that diffusion in the liquid phase is the rate limiting step for this system, in contrast to pure water evaporation. For the particular binary system that was investigated experimentally, which is composed of water and a sugar-based surfactant (α-dodecylmaltoside), the interfacial layer consists in a sequence of liquid crystalline phases of different mesostructures. We extract values for mutual diffusion coefficients of lamellar, hexagonal and micellar cubic phases, which are consistent with previously reported values and simple models. We thus provide a method to estimate the transport properties of oriented mesophases. The macroscopic humidity-independence of the evaporation rate up to 85% relative humidities is shown to result from both an extremely low mutual diffusion coefficient and the large range of water activities corresponding to relative humidities below 85%, at which the lamellar phase exists. Such a humidity self-regulation mechanism is expected for a large variety of complex system.
Introduction
Water evaporation is a phenomenon we all witness from an early age, although its apparent simplicity quickly dissipates as we are taught science basics. Indeed, liquid water is stable between 0 °C and 100 °C and yet it can convert to its gaseous form at ambient temperatures. This apparent paradox is explained by the necessity to consider the full system, including both liquid water and the gas phase surrounding it. Only when this gas phase is saturated with water vapor, at 100% relative humidity, will evaporation stop. Predicting the evaporation rate of pure water remains a challenging task since a collection of different limiting steps can be encountered, such as diffusion or convection in the gas phase and thermal transfer to the interface. Aqueous systems often contain solutes that exhibit negligible evaporation rates. Water evaporation then results in an increased concentration of the solute close to the air–liquid interface, which often makes diffusion in the liquid phase the rate limiting transport process. Interestingly, an increased number of components in the system can thus lead to a simplified description of the evaporation phenomenon. The concentration gradient can significantly impact the properties of the system. For example, Kabalnov and Wennerström2 showed that dispersed colloidal particles diffuse away from the air–liquid interface in the gradient created by water evaporation in a mixed solvent. An application of this effect is found in the prevention of the drying out at the tip of ink-pens, when not in use. More dramatic effects can occur when the gradient gives rise to the appearance of new phases close to the air–liquid interface.1,3–6 These structures have a strong influence on diffusion and other transport properties.6,7 The control of drying processes thus crucially depends on the understanding of the physico-chemical processes giving rise to structure and composition gradients at the air–liquid interface of multi-component solutions. Such an understanding also impacts the description of filtration and centrifugation processes as well as that of transport across out-of-equilibrium biological membranes as, for example, found in the skin and the liquid tear film on our eyes.8–11A challenge in the description of the transport processes during evaporation is that the systems are highly non-ideal and they can show a rich phase behavior. A detailed experimental characterization of the interfacial region is a prerequisite for obtaining a relevant understanding of the phenomena. In a recent publication,1 we presented experimental investigations showing the formation of interfacial multilayer structures on drying aqueous solutions, using a capillary setup that allows for detailed mapping of gradients in composition and structure. In the present paper, we focus on providing a theoretical description of evaporation from non-ideal solutions, using additional experimental results and theoretical analysis. Section 1 contains a report of experimental results that are particularly relevant for the theoretical analysis. Section 2 describes a general scaling law that analytically follows from Fick's second law for diffusion in non-ideal systems. Section 3 consists in a quantitative evaluation of mutual diffusion coefficients for aligned mesophases. Section 4 contains a discussion of a humidity self-regulation mechanism exhibited in amphiphile/water solution and its extension to complex systems.
Results and discussion
1. Experimental findings
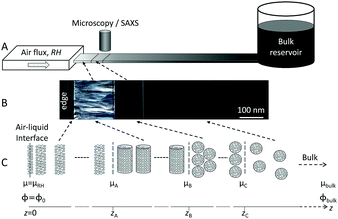 | ||
| Fig. 1 (A) Schematic representation of the drying setup consisting of a rectangular capillary connected to a large reservoir containing the aqueous solution and placed in front of an air flux of controlled relative humidity, as previously described.1 (B) Top view of the capillary under drying placed in between crossed polarizers under an optical microscope. (C) Associated microstructures and chemical potential gradients. | ||
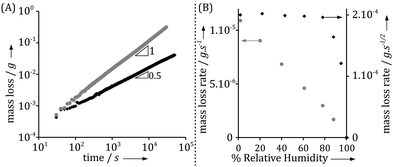
Time resolved SAXS and IR microscopy measurements show that while both the positions of the phase boundaries and composition at a given position vary with time, the observations could always be rescaled to the same profiles within each phase between the phase boundaries.1 Optical microscopy enables an easy monitoring of the growth of the mesophases with time, and thus provides rescaling factors. Fig. 3A displays the thickness increase over time of the different phases observed in the interfacial layer formed in the surfactant/water system. Remarkably, the thickness of all phases increases linearly with the square root of time, for all relative humidities. This is consistent with the measured macroscopic mass loss due to evaporation (Fig. 2A). The thickness of the outer phase in contact with air varies with the relative humidity at the boundary, while the thicknesses of all inner phases are seemingly independent of boundary conditions. At relative humidities above 85%, the outer lamellar phase disappears and the hexagonal phase becomes the outer phase. The relative humidity of this phase transition coincides with the analogous phase transition in equilibrium conditions, as confirmed by sorption calorimetry measurements.1Fig. 3B shows that the ratio between the thicknesses of two inner (hexagonal and micellar cubic) phases is independent of variations in RH at RH < 85%, while the ratio between the thickness of the outer phase, which is in contact with air, and the thickness of an inner phase varies with the RH boundary condition. Interestingly, the profile in Fig. 3B is very similar to the one extracted from the macroscopic measurements for evaporation rates from the same system (Fig. 2B). Fig. 3C shows that, at a given relative humidity, the ratio between two phases is almost constant over time. It is also noticed that the outer lamellar phase is much thinner compared to the inner phases with higher water contents, which decreases the precision of its thickness determination compared to the inner phases. Similar observations have also been made for other binary and ternary water–surfactant and water–lipid systems.1
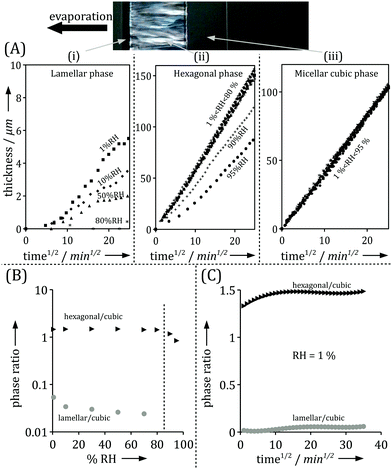 | ||
| Fig. 3 (A) Thickness variations with time of the lamellar phase (i), hexagonal phase (ii) and micellar cubic phase (iii), which scale with the square root of time (adapted from ref. 1). (B) Ratio of thicknesses between the hexagonal and cubic phases (black) is constant over most of the humidity range, while the ratio of thicknesses between the lamellar and hexagonal phases (grey) varies with RH until the lamellar phase disappears at 85% RH. (C) Ratio of thicknesses between the hexagonal and cubic phases (black), and the lamellar and cubic phases (grey) over time at a given RH. The ratios are constant after a transition regime. Experiments were performed using the milli-fluidic drying cell in Fig. 1A where the bulk solution contained 15 wt% α-dodecylmaltoside surfactant/water solution. | ||
To further investigate the role of the boundary condition we monitored the response to an abrupt relative humidity change in the gas phase. Fig. 4 shows how the different phase boundaries move in response to an instantaneous change in RH from 1% to 95%. There is momentarily a condensation of water at the interface and a change in the direction of diffusional flow. The lamellar phase disappears and the hexagonal phase responds and becomes thinner as its inner boundary moves towards the air/liquid interface. Within an hour, the system has fully adjusted to the new boundary condition and the diffusional flow reverts to its original direction throughout the system. Note that the thickness of the inner micellar cubic remains virtually unaffected by the change in the boundary condition. The relatively fast response indicates that the majority of molecular degrees of freedom are in, or close to, equilibrium and respond quickly to the changes caused by the dynamic processes.
The experimental observations summarized in Fig. 2–4, as well as those reported in ref. 1 clearly demonstrate a remarkable consistency between experimental observations of microscopic and macroscopic properties of the drying interfaces in the amphiphile–water systems. There are clear trends in the experimental data that calls for explanations. The observed t1/2 time dependence in Fig. 2B, 3A and 4 is notably indicative of a diffusion controlled rate-limiting process. In the following section, we explore theoretically what predictions follow from Fick's first and second laws for both ideal and non-ideal systems.
2. Scaling law for ideal and non-ideal systems
Our aim is now to provide a theoretical description of water evaporation from non-ideal solutions, limited by diffusion in the liquid and under unidirectional advection, which corresponds to our experimental conditions.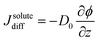 | (1) |
Combined with the equation of continuity, one arrives at Fick's second law
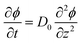 | (2) |
Here we use the volume fraction ϕ to denote concentrations and D0 is the diffusion coefficient of the pure solvent. As an example, consider the example in which a solution of the volatile solute at the concentration ϕsolutediff in a non-volatile solvent is exposed to a flowing gas. The volatile solute will evaporate at the surface, triggering a diffusion of solute molecules towards this surface. At the air–liquid interface (z = 0), the concentration of the solute is zero and it grows towards the bulk value ϕsolutediff away from the surface (z > 0). The partial differential eqn (2) can be transformed into an ordinary differential equation by introducing the variable transformation to a dimensionless parameter x;
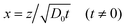 | (3) |
 | (4) |
The evaporation rate, which is defined as the mass of the evaporated solute per unit time, dm(t)/dt, can be written using either a local or an integral approach:
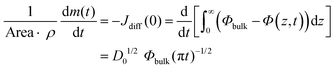 | (5) |
Interestingly, this simple model yields a diffusion-limited signature that is very similar to what is observed in all our experiments, even though such a model lacks several crucial elements. Firstly, in the system that we study experimentally the solvent, water, evaporates rather than the solute. An advective term must thus be included in the model to take into account the liquid flow from the reservoir, which compensates the evaporated volume of water. Secondly, amphiphiles/water solutions are strongly deviating from ideality. Thirdly, the diffusion coefficient is not a constant and it depends on the concentration in each position. Fourthly, the gradient in chemical potential allows for the formation of other phases in addition to the bulk homogeneous solution. Despite these considerable additional difficulties, some major qualitative features of eqn (4) remain relevant for the complex case, as will be discussed in the following section.
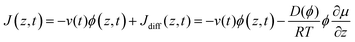 | (6) |
In the second equality, we have introduced a generalization of Fick's first law, which accounts for non-ideality in the thermodynamics by specifying the driving force as the gradient in chemical potential, μ, rather than the gradient in concentration, Φ. The chemical potential of water (μw) is directly related to the water activity (aw) and the relative humidity (RH) as
Δμw = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(RH/100) = RT ln(RH/100) = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(aw) ln(aw) | (7) |
In eqn (6), we also allow for a concentration dependence of the diffusion coefficient. The equation of continuity results in
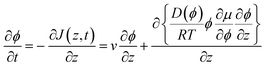 | (8) |
Boundary conditions are set by ϕ(z = ∞) = ϕbulk and ϕ(0) = ϕ0, where the second boundary condition is determined by the condition that the solvent water is in equilibrium with the gas phase with controlled RH. In addition, the net solute flow is zero at the air–liquid interface, J(0,t) = 0, so that the transport due to the advective flow is cancelled by the diffusive flow at this position. It follows from eqn (6) that
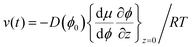 | (9) |
It is a formidable task to solve eqn (8) for a typical non-ideal system. However, it is possible to obtain a substantial simplification of the problem by making the variable transformation of eqn (3). Similar to the simple example of eqn (4), the partial differential eqn (8) can be transformed into an ordinary differential equation by introducing the variable transformation to a dimensionless parameter x, expressed in eqn (3):
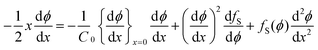 | (10) |
with the boundary conditions at x = 0 and x = ∞ preserved. The condition in eqn (9) has been used to eliminate v(t) in eqn (8), a full derivation is presented in ESI.† Even though it is difficult to obtain an explicit solution of eqn (10), there exists a specific solution ϕ(x) satisfying the time independent boundary conditions at both ends of the capillary. This solution describes the functional form of the concentration profile. The profile at a given time, t1, is then obtained by the using the coordinate transformation of eqn (3) so that
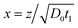 . This leads to the significant prediction that the shape of the concentration profile is preserved during the process, while the length scale increases proportionally to the square root of time. Even without explicitly solving the diffusion equations, we can conclude that all properties that are proportional to the length-scale increase linearly with the square root of time. The fundamental reason for a scaling behavior is that there is no external length-scale in the problem.
. This leads to the significant prediction that the shape of the concentration profile is preserved during the process, while the length scale increases proportionally to the square root of time. Even without explicitly solving the diffusion equations, we can conclude that all properties that are proportional to the length-scale increase linearly with the square root of time. The fundamental reason for a scaling behavior is that there is no external length-scale in the problem.
In deriving eqn (10) we have assumed that ϕ(z) is a continuous function that is differentiable for all values of z. This condition is not fulfilled for the case where there is a phase change in the interfacial layer, which indeed may occur in the concentration gradient in, for example, amphiphile–water systems. If we assume local equilibrium in the gradient, the position of the phase change is determined by the local thermodynamic conditions. When such a change occurs at some position, z1, the chemical potential, μ(z), is still a continuous function, while there are discontinuities in the function describing the concentration profile, Φ(z), as well as the function describing the variation in the diffusion coefficient at various positions in the interfacial film, D(z). For the formal solution of eqn (10) it is then necessary to treat the different single-phase regions separately and then join them by boundary conditions determined by thermodynamic conditions at the phase boundaries (Fig. 1C). There is again no introduction of an external length-scale. Thus, there is a unique solution in the variable x (eqn (3)), and one preserves the property of a unique concentration profile with a real space length-scale that increases as the square root of time.
We have arrived at some specific predictions about the concentration profile without explicitly solving the diffusion equation. These predictions are based on three assumptions. The first is the validity of the generalized form of Fick's second law. The second assumption is that the state of the system is determined by the local thermodynamic variables so that phase boundaries occur at the same local chemical potentials in the gradient as in the equilibrium bulk systems. The third and more specific assumption is that the rate limiting transport process for the evaporation is the diffusion in the condensed phase.
Under the assumption of local thermodynamic equilibrium, phase transitions occur at given volume fractions {Φi}, which are determined by bulk thermodynamics. A given phase thus exists within a composition range {Φa, Φb} (Fig. 1C). For a given relative humidity at the air–liquid interface, eqn (10) yields a given concentration profile ΦRH(x). The stability region of a given phase characterized by {Φa, Φb} corresponds to a constant value of (xa − xb). The distance between these phase boundaries is then:
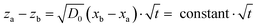 | (11) |
The experimental data in Fig. 3 clearly demonstrate such t1/2 dependence with high accuracy. The slope of the curve is proportional to 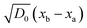 , which depends on the relative humidity only for the phase in contact with air. It follows from eqn (11) that the ratio between the thicknesses of two such phases should be constant in time, which is also shown in the experimental data displayed in Fig. 3B.
, which depends on the relative humidity only for the phase in contact with air. It follows from eqn (11) that the ratio between the thicknesses of two such phases should be constant in time, which is also shown in the experimental data displayed in Fig. 3B.
The magnitude of the advective flow, v, is given by eqn (9), which can be rewritten using the variable transformation of eqn (3):
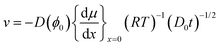 | (12) |
This shows that v decreases with the inverse square root of time. The mass evaporation rate is then given by:
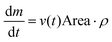 | (13) |
Overall, theoretical and experimental scaling behavior are in excellent agreement, without making any specific assumptions on the characteristics of the systems in terms of how diffusion coefficient and chemical potential vary in the gradient. This agreement supports the main assumption of the model, which is that diffusion in the condensed phase is the rate-limiting process for water evaporation in the present systems.
3. Quantitative evaluation of mutual diffusion coefficients in mesophases
The scaling law derived in the previous section provides a generic description of evaporation, but it remains to interpret the specific quantitative parameters such as pre-factors and proportionality constants. Mathematically, the characteristics of the system are contained in the function fS(Φ) and the constant C0 in eqn (10). In principle, these two quantities can be calculated if the concentration profile in the layer and the activity–concentration isotherm are known. It would then be possible to obtain values of the diffusion coefficient at all concentrations, D(Φ). In practice, this procedure will be limited mainly by the spatial resolution of the concentration measurement, in particular, for the thin outer phase that is in contact with air.1 Another limitation in precision is the activity–concentration isotherm determination at high relative humidity (RH) based on sorption techniques. In this section, we use a simpler approach based on an approximation supported by experimental observations and theoretical scaling in order to extract the order of magnitudes of mutual diffusion coefficients of the different phases.Using infra-red microscopy, we have monitored the concentration gradient in the capillary. Within experimental error, the concentration gradient is observed to linearly vary with z within a given phase.1 Furthermore, the IR data show that the concentrations at the boundaries between two phases in the non-equilibrium gradient correspond to their equilibrium counterparts. A drastic change in the boundary conditions at the air–liquid interface result in a rapid response of the system as illustrated in Fig. 4. This shows that the self-assembly reorganization time is much shorter than the time needed for the build-up of the gradient, which is consistent with the local equilibrium hypothesis. The rapid reorganization time and the fact that the concentration gradients are approximately linear suggest that a quantitative evaluation of the parameters characterizing the system can be obtained within a quasi steady-state approximation.
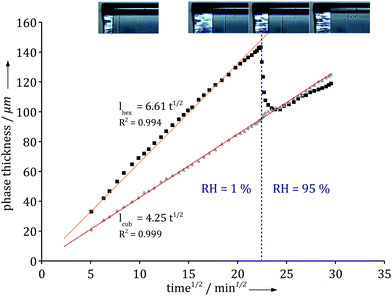 | ||
| Fig. 4 Thickness variation with time of the hexagonal phase (black squares) and the micellar cubic phase (grey triangles) upon a change in the air relative humidity. The hexagonal phase responds and reaches a slower increase as expected from Fig. 3, while the micellar cubic phase is completely insensitive to the change. Experiments were performed using the milli-fluidic drying cell in Fig. 1A where the bulk solution contained 15 wt% α-dodecylmaltoside surfactant/water solution. | ||
The essence of the quasi steady-state approximation is to assume that at a given moment in time the flow in the system is the same as for a system at steady state with the same thickness and the same concentration at the boundaries. The scaling law ensures that the final result does not depend on the choice of the specific time. Using this approximation one can estimate mutual diffusion coefficients in this system, neglecting the effect of non-equilibrium dynamics.
At steady state, 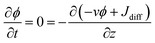 . Therefore, the net flux −vϕ + Jdiff is constant over the whole capillary. Since the net flux is zero at the evaporation boundary, it is thus zero everywhere. It follows from eqn (6) that:
. Therefore, the net flux −vϕ + Jdiff is constant over the whole capillary. Since the net flux is zero at the evaporation boundary, it is thus zero everywhere. It follows from eqn (6) that:
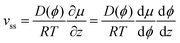 | (14) |
We assume a constant average diffusion coefficient within a phase, since the main concentration dependence of D is caused by a change in the mesostructure. Integrating eqn (14) between the corresponding phase boundaries Φ2 and Φ1 yields:
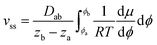 | (15) |
Eqn (15) allows a quantitative evaluation of the mutual diffusion coefficient under the quasi-steady-state approximation:
| Dab = vss(zb − za)/(μb − μa) | (16′) |
This equation can be alternatively expressed with time-independent quantities using the scaling law:
| Dab = v0(xb − xa)/(μb − μa) | (16′′) |
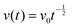 .
.
We can extract v0 values from gravimetric measurements of water evaporation under the conditions of quasi steady-state, thicknesses through optical microscopy images, and the activity–composition isotherm through sorption calorimetry measurements.1 We can thus evaluate the mutual diffusion coefficients for the different phases using eqn (16). For the present system, the average constant diffusion coefficient for the lamellar phase is estimated to (1.2 ± 0.2) × 10−12 m2 s−1, for the hexagonal phase the estimated diffusion coefficient is (3.4 ± 1.0) × 10−11 m2 s−1 and for the micellar cubic phase we obtain D = (8.0 ± 2.0) × 10−10 m2 s−1. Strikingly, the mutual diffusion coefficient varies roughly by an order of magnitude between the different phases, and is always at least one order of magnitudes lower than the self-diffusion coefficient of water in a pure aqueous solution. In addition, taking explicitly the non-ideality of the system through the activity–composition relationship was found to be crucial in the quantitative evaluation.
We now turn towards a comparison of these mutual diffusion coefficients values with simple models and other published values. The lamellar phase is a one-dimensional liquid crystalline structure, which can be described as an alternating stack of hydrophobic layers, the hydrocarbon chains, and hydrophilic layers, the hydrophilic heads and water. If we consider a repetition unit consisting of one hydrophobic layer and one hydrophilic layer, we can estimate the effective diffusion coefficient of water through this repetition unit16 (see ESI†). This effective coefficient will strongly depend on the orientation of the stack with respect to the flux. In the capillary, stacks are orthogonal to the water flux, as evidenced by the anisotropic SAXS patterns. This is the alignment that most efficiently hinders water evaporation at the surface as water molecules must cross the hydrophobic layers in which they have a low solubility. The rate-limiting step is thus water diffusion through hydrophobic layer for self-diffusion and most likely also for the mutual diffusion. For such an oriented lamellar structure, the perpendicular diffusion coefficient can be estimated simply based on the structure dimensions, local diffusion coefficients in water and in hydrocarbon and the oil/water partition coefficient16 to (2.1 ± 0.6) × 10−12 m2 s−1 (for more details, see ESI†). This value is in close agreement with the value obtained from our experiments, which is consistent with the modelling of the structure/transport relationship for the lamellar phase. If the lamellar phase was instead oriented with lamellae parallel to the flux, a larger diffusion coefficient would be expected, although the activity–composition relationship would be unchanged. This highlights the predominant role of mesostructure orientation in this transport problem. There exists a large collection of permeability measurements for phospholipid bilayers in the literature. For liquid crystalline bilayers composed of dioleoyl phosphatidylcholine (C18:1 chains), permeability values ranging between P = 3–13 × 10−4 m s−1 have been reported,20–23 which corresponds to specific resistances to diffusive transport of ρ = P·dbilayer/2 = 0.72–3.1 × 10−12 m2 s−1, where dbilayer is the bilayer thickness taken as 4.8 nm. This range of values is compatible with the mutual diffusion coefficient we evaluated for the DDM (12C:0). Our method is thus an alternate mean to evaluate water transport across bilayers in of oriented lamellar phases rather than monitoring release from unilamellar vesicles.
In the hexagonal and micellar cubic phase, there exists continuous pathways for water to diffuse through hydrophilic regions, which gives rise to faster self-diffusion compared to the lamellar phase. In the water gradient, the channels between the rods in the hexagonal phase become narrower. At the phase boundary towards the lamellar phase, the hexagonal phase contains around 12 wt% water, while at the other phase boundary towards the micellar cubic phase, the hexagonal phase contains around 47 wt% water.1,13 This difference in water content explains the difference in diffusion coefficients for the micellar cubic and hexagonal phases. The hydrophilic layers are constituted of water and maltoside chains. Nilsson and Söderman17 showed that the water self-diffusion in such systems is similar to water self-diffusion in the corresponding aqueous sugar solutions. In our system, the diffusion coefficient values obtained for the hexagonal and the micellar cubic phases indeed fall within the expected range for the corresponding sucrose/water solutions.18,19
A direct consequence of the low diffusion coefficient of the outer oriented lamellar phase at the air–liquid interface is the low value of the evaporation rate, given by eqn (15). The system spontaneously forms an efficient barrier against evaporation, which is sufficient to induce a change in the transport limiting step compared to pure water.
4. Evaporation rate and humidity self-regulation
Fig. 2 demonstrates that there are qualitative differences in the behavior of the evaporation rate between pure water and the surfactant system. For the latter system, the rate decreases in time as t−1/2, which signifies the rate-limiting step is the diffusion in the liquid phase. The rate is thus determined by the magnitude of the diffusion coefficient in the condensed phase. During evaporation, there appears a sequence of phases in the interfacial region and it follows from the results of the previous section that the thicknesses of the respective phases adjust to give (nearly) the same diffusional flow in the different phases. The observation that the lamellar phase is much thinner than the hexagonal and cubic ones shows that it has a much lower mutual diffusion coefficient.We now turn to a practical consequence of the step in the diffusion coefficient profile occurring at the phase boundary. As shown in Fig. 2B, the evaporation rate is virtually constant up to 85% RH in the air. This qualitative behavior is very similar to what is found for stratum corneum, the outer layer of our skin,10,24–26 and the non-linear transport behavior strongly contrasts with the evaporation rate from a pure water solution (Fig. 2B). In this section, we want to unveil the microscopic origin of such a behavior and discuss its generality. The mass evaporation rate writes as:
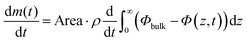 | (17) |
This integral formulation can be rewritten to explicit the various phases of the system, lamellar (0,a), hexagonal (a,b), micellar cubic (b,c) and micellar (c,∞):
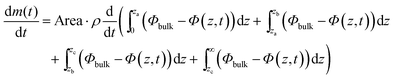 | (18) |
The experimental data suggests that the concentration gradient within a phase is approximately linear, which is consistent with quasi-steady-state and leads to:
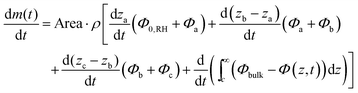 | (19) |
In practice, this behavior should be common in complex aqueous solutions, containing amphiphiles, polymers and colloids. Indeed, in the vicinity of the air–liquid interface, water is scarce. Therefore, the water activity rapidly changes with concentration, which ensures an extended range of existence for the driest phase formed by the system. Furthermore, structures formed in the water poor region tend to optimize the hydration of the solute, which will lead to low mutual diffusion coefficients. Nonetheless, the quality of this evaporation self-regulation will depend on the exact values of the diffusion coefficient and the activity range at which the least permeable structure exists. In the experimental system presented, an extremely low diffusion coefficient is achieved in the driest phase where the lamellae are oriented perpendicularly to the evaporation flow. If the lamellae were oriented parallel to the evaporation flow, which would correspond to the same activity profile, the self-regulation behavior would be weaker as the lamellar phase would exhibit a similar growth rate as the hexagonal phase.
Conclusions
In this article, we presented an experimental and theoretical investigation of water evaporation from aqueous solutions of amphiphilic molecules. Using milli-fluidic drying cells, we monitored the build-up of interfacial structure composed of several liquid crystalline phases at the air–liquid interface. This interphase corresponds to a gradient in both composition and mesostructure, which spontaneously forms in response to the non-equilibrium conditions imposed by evaporation. Several mesophases of distinct structures and thus transport properties are formed within this interphase. All time-dependent quantities exhibit a square root of time scaling. Analyzing the advection/diffusion transport equation for non-ideal solutions we demonstrate that this scaling law is a general consequence of diffusion limited transport in the liquid phase. The scaling law is valid independently of the characteristics of the system, such as diffusion coefficient and activity profiles as long as the evaporation is diffusion controlled.We extracted values of mutual diffusion coefficients for the different mesophases encountered along the gradients. The driest phase possesses a lamellar structure with lamellae oriented perpendicularly to the water flow and exists over a large range of relative humidities below 85% RH. The mutual diffusion coefficient was measured as (1.2 ± 0.2) × 10−12 m2 s−1, which agrees with a simple structure model and literature data for lamellar bilayers.16 Our method thus enables the measurement of mutual diffusion coefficients in aligned structures.
We discussed a striking macroscopic behavior observed in such systems, but also in biological systems such as stratum corneum, which is the independence of the evaporated mass with relative humidity. This macroscopic behavior rests on a structure with low water mutual diffusion coefficient at the air–liquid interface, which exists over a large range of water activity. In practice, this behavior is expected to be general to complex aqueous solutions, containing amphiphiles, polymers and colloids.
To conclude, our results suggest that in order to describe drying, filtration and centrifugation of complex aqueous systems, a non-ideal and non-equilibrium thermodynamic description based on activity and diffusion coefficient profiles is required.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Knut and Alice Wallenberg Foundation, KAW (E. S. and H. W.) and the Swedish Research Council is gratefully acknowledged for financial support both through regular grants (E. S.) and the Linnaeus Center of Excellence ”Organizing molecular matter” (E. S., K. R. and H. W.). Agence Nationale de la Recherche is acknowledged for financial support through grant ANR-17-CE-09-0004-01 COATING (K. R.).Notes and references
- K. Roger, M. Liebi, J. Heimdal, Q. D. Pham and E. Sparr, Controlling water evaporation through self-assembly, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10275–10280 CrossRef CAS PubMed.
- A. Kabalnov and H. Wennerström, Diffusion in evaporating solutions, Soft Matter, 2009, 5, 4712–4718 RSC.
- B. M. D. O’Driscoll, E. Milsom, C. Fernandez-Martin, L. White, S. J. Roser and K. J. Edler, Thin films of polyethylenimine and alkyltrimethylammonium bromides at the air/water interface, Macromolecules, 2005, 38, 8785–8794 CrossRef.
- T. Mokhtari, K. Edler, T. Nylander and E. Sparr, Interfacial films in mixed CTAB-PEI systems can be regulated by the properties of the vapor phase, Langmuir, 2014, 30, 9991 CrossRef CAS PubMed.
- G. Cevc, W. Fenzl and L. Sigl, Surface-Induced X-Ray Reflection Visualization Of Membrane Orientation And Fusion Into Multibilayers, Science, 1990, 249, 1161–1163 CAS.
- C. Åberg, E. Sparr, K. J. Edler and H. Wennerström, Nonequilibrium phase transformations at the air-liquid interface, Langmuir, 2009, 25, 12177–12784 CrossRef PubMed.
- C. Åberg, E. Sparr and H. Wennerström, Lipid phase behaviour under steady state conditions, Faraday Discuss., 2012, 161, 151–166 RSC.
- J. Cwiklik, Tear film lipid layer: A molecular level view, Biochim. Biophys. Acta, 2016, 1858, 2421 CrossRef PubMed.
- D. L. Leiske, C. E. Miller, L. Rosenfeld, C. Cerretani, A. Ayzner, B. Lin, M. Meron, M. Senchyna, H. A. Ketelson, D. Meadows, S. Srinivasan, L. Jones, C. J. Radke, M. F. Toney and G. G. Fuller, Molecular structure of interfacial human meibum films, Langmuir, 2012, 28, 11858 CrossRef CAS PubMed.
- I. H. Blank, J. Moloney, A. G. Emslie, I. Simon and C. Apt, The diffusion of water across the stratum corneum as a function of its water content, J. Invest. Dermatol., 1984, 82, 188–194 CrossRef CAS PubMed.
- S. Björklund, J. Engblom, K. Thuresson and E. Sparr, A water gradient can be used to regulate drug transport across skin, J. Controlled Release, 2010, 143, 191–200 CrossRef PubMed.
- J. Leng, B. Lonetti, P. Tabeling, M. Joanicot and A. Ajdari, Microevaporators for Kinetic Exploration of Phase Diagrams, Phys. Rev. Lett., 2006, 96, 084503 CrossRef PubMed.
- X. Auvray, C. Petipas, R. Anthore, I. Rico and A. Lattes, X-ray Diffraction Study of Mesophases of Cetyltrimethylammonium Bromide in Water, Formamide and Glycerol, J. Phys. Chem., 1989, 93, 7458–7464 CrossRef CAS.
- E. L. Cussler, Diffusion and Mass Transfer in Fluid Systems, University Press, Cambridge, 2nd edn, 1997 Search PubMed.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, John Wiley & Sons, New York, 2002 Search PubMed.
- D. F. Evans and H. Wennerström, The Colloidal Domain. Where Physics, Chemistry, Biology and Technology meet, VCH Publishers, Inc., New York, 1999, ch. 6 Search PubMed.
- F. Nilsson, O. Söderman and I. Johansson, Physical−Chemical Properties of the n-Octyl β-d-Glucoside/Water System. A Phase Diagram, Self-Diffusion NMR, and SAXS Study, Langmuir, 1996, 12, 902–908 CrossRef CAS.
- H. C. Price, J. Mattsson and B. J. Murray, Sucrose diffusion in aqueous solution, Phys. Chem. Chem. Phys., 2016, 18, 19207–19216 RSC.
- I. A. Farhat, E. Loisel, P. Saez, W. Derbyshire and J. M. V. Blanshard, The effect of sugars on the diffusion of water in starch gels: a pulsed field gradient NMR study, Int. J. Food Sci. Technol., 1997, 32, 377–387 CAS.
- Y. Graziani and A. Livne, Water permeability of bilayer lipid membranes. Sterol-lipid interaction, J. Membr. Biol., 1972, 7, 275 CrossRef CAS PubMed.
- A. Finkelstein, Water movement through lipid bilayers, pores and plasma membranes: Theory and reality, John Wiley and Sons Ltd, New York, 1987, vol. 4 Search PubMed.
- K. Olbrich, W. Rawicz, D. Needham and E. Evans, Water Permeability and Mechanical Strength of Polyunsaturated Lipid Bilayers, Biophys. J., 2000, 79, 321–327 CrossRef CAS PubMed.
- J. C. Mathai, S. Tristram-Nagle, J. F. Nagle and M. L. Zeidel, Structural determinants of water permeability through the lipid membrane, J. Gen. Physiol., 2008, 131, 69–76 CrossRef CAS PubMed.
- B. Cravello and A. Ferri, Relationships between skin properties and environmental parameters, Skin Res. Tech., 2008, 14, 180–186 CrossRef PubMed.
- S. Björklund, A. Nowacka, J. A. Bouwstra, E. Sparr and D. Topgaard, Characterization of the dynamics of the molecular components of intact stratum corneum using natural abundance 13C solid-state NMR, PLoS One, 2013, 8, e61889 Search PubMed.
- A. Alonso, N. Meirelles, V. Yushmanov and M. Tabak, Water increases the fluidity of intercellular membranes of stratum corneum: correlation with water permeability, elastic, and electric resistance properties, J. Invest. Dermatol., 1996, 106, 1058–1063 CrossRef CAS PubMed.
- E. Sparr and H. Wennerström, Responding phospholipid membranes - Interplay between hydration and permeability, Biophys. J., 2001, 81, 1014–1028 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp00305j |
| This journal is © the Owner Societies 2018 |