Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
All-atom molecular dynamics simulations of spin labelled double and single-strand DNA for EPR studies†
C.
Prior
,
L.
Danilāne
and
V. S.
Oganesyan
 *
*
School of Chemistry, University of East Anglia, Norwich, NR4 7TJ, UK. E-mail: v.oganesyan@uea.ac.uk
First published on 16th April 2018
Abstract
We report the first application of fully atomistic molecular dynamics (MD) simulations to the prediction of electron paramagnetic resonance (EPR) spectra of spin labelled DNA. Models for two structurally different DNA spin probes with either the rigid or flexible position of the nitroxide group in the base pair, employed in experimental studies previously, have been developed. By the application of the combined MD-EPR simulation methodology we aimed at the following. Firstly, to provide a test bed against a sensitive spectroscopic technique for the recently developed improved version of the parmbsc1 force field for MD modelling of DNA. The predicted EPR spectra show good agreement with the experimental ones available from the literature, thus confirming the accuracy of the currently employed DNA force fields. Secondly, to provide a quantitative interpretation of the motional contributions into the dynamics of spin probes in both duplex and single-strand DNA fragments and to analyse their perturbing effects on the local DNA structure. Finally, a combination of MD and EPR allowed us to test the validity of the application of the Model-Free (M-F) approach coupled with the partial averaging of magnetic tensors to the simulation of EPR spectra of DNA systems by comparing the resultant EPR spectra with those simulated directly from MD trajectories. The advantage of the M-F based EPR simulation approach over the direct propagation techniques is that it requires motional and order parameters that can be calculated from shorter MD trajectories. The reported MD-EPR methodology is transferable to the prediction and interpretation of EPR spectra of higher order DNA structures with novel types of spin labels.
Introduction
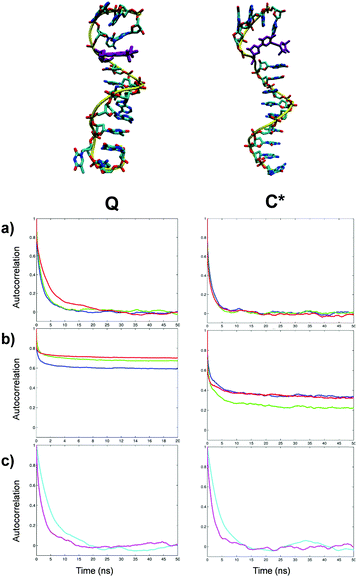
The internal dynamics and conformational variability of DNA are known to be crucial to its biological functions including interaction with proteins and expression of the genetic code.1,2 Because of the semi-flexible nature of DNA its dynamic regime consists of multiple contributions from breathing, bending and twisting modes, as well as groove fluctuations of the helix. Analysis of such motions is challenging and has been the subject of extensive studies. Various experimental techniques including nuclear magnetic resonance (NMR),3 fluorescence,4 dynamic light scattering5 and Fourier transform infrared difference spectroscopy6 amongst others have been utilised to probe different motional components. Electron Paramagnetic Resonance (EPR) with introduced spin labels is a particularly suitable spectroscopic technique to study the dynamics and conformational changes in complex bio-molecular systems such as DNA. EPR, being a ‘fast’ magnetic technique, is able to directly resolve molecular dynamics and structural changes on the sub-nanosecond time scale.7–11 Furthermore, due to recent advances in spin labelling methodologies (e.g. the use of click chemistry) an increasingly wide range of spin labels are being developed for DNA studies by EPR, allowing greater sequence selectivity.12–17 However, the need to introduce a synthetic spin label with its own internal dynamics, combined with the potential to influence the local DNA structure might significantly complicate the analysis of EPR data. Additionally, global tumbling motions of relatively short DNA fragments employed in many model experimental studies are significant on the EPR timescale, thus requiring sophisticated spectral modelling to interpret the results.7,9 In the case of nitroxide labels attached via flexible tethers this typically requires the fitting of EPR spectra with multiple adjustable parameters using the slowly relaxing local structure (SRLS) model of Freed and co-workers7 with global tumbling rates based on hydrodynamic theory.18,19Spin labels such as the quinolonyl derived Q (Fig. 1)10 or alkyne tethered labels such as the cytosine derived C* (Fig. 1)20 (or the analogous thymine derived T*21) were the first ones developed by Robinson and co-workers for DNA studies using EPR.8–11,20,22 These labels were assumed to report accurately on the motions of the host DNA, with the spectra typically interpreted through the application of either diffusion of a rigid cylinder10 or weakly bending rods9 models. In particular the Q spin label is assumed to exhibit negligible internal motion, as well as being highly thermally stable. However it has no natural analogue and requires a synthetic 2-aminopurinyl complementary base pair, P (Fig. 1), with the effect on the local dynamics and structure unclear from EPR alone.10
C* represents an alkyne-linked spin label covalently attached to conventional base pairs and thus is assumed to be less structurally perturbing.10,11 Although such labels have been demonstrated to be highly sensitive to the dynamics of DNA duplexes, they exhibit internal rotation about the alkyne linkage that potentially compromises the structural and dynamic information obtained from the analysis of EPR spectra.11
Over the past decade novel approaches have been developed allowing for the prediction of motional Continuous wave (CW) EPR spectra from molecular dynamics (MD) simulations by either indirect23–25 or direct propagation25–29 calculation methods. MD-EPR prediction techniques can greatly simplify the interpretation and analysis of EPR experimental spectra, and hence provide unambiguous conclusions about molecular order and motions. They have been successfully applied to spin labelled proteins24,27–31 and soft matter systems such as liquid crystals, both thermotropic and lyotropic.32–35 Fully atomistic MD simulations have already provided significant insights into the sequence-dependent flexibility of DNA.36–40 In particular it is becoming increasingly apparent that DNA sequences can adopt a wide variety of conformations, depending on the chemical environment, and that generally the structure of DNA should be considered in terms of conformational ensembles.40,41 In the past modelling studies on DNA have been hindered by the lack of generating sufficiently long MD trajectories required for representing adequately the helix properties on different timescales.41 Recent advances in computing power and refined force fields, such as the recently parameterised parmbsc1,42 allow the accurate description of conformational behaviour with trajectories of up to 10 μs currently achievable at least for relatively short DNA chains.40
The purpose of this paper was to achieve the following. Firstly, given that the EPR spectra are highly sensitive to the motions and order of the spin probes, simulation of EPR line shapes from the results of MD provides an ultimate test bed for the force fields currently employed to model DNA and also RNA structures. Additionally we have analysed the perturbing effects from the presence of spin probes on the DNA local structure. Secondly, the use of fully atomistic MD combined with MD-EPR simulation methodology allowed us to provide detailed quantitative analysis of different motional contributions, both internal and global associated with the spin probe's and DNA motions, respectively, into the dynamics of the Q and C* labels in both duplex and single-stranded DNA fragments. Finally, the application of fully atomistic MD simulations for modelling single strand and duplex labelled DNA complexes allowed us to test the validity of previously employed simplified models for the simulation and interpretation of EPR spectra that are based on the application of so-called Model-Free (M-F) approach. The M-F approach assumes that the global and local motions are independent. In addition, in many simulation strategies employed previously the local dynamics of the label was assumed to be in the so-called fast motional regime on the EPR timescale that justifies the partial averaging of the magnetic tensors A and g.22,43 The advantage of performing MD is that the statistically averaged parameters employed in such models can be readily calculated from MD trajectories and used in the simulation of the EPR spectra. In our case both global (DNA) and local (nitroxide spin probe) motional contributions have an impact on CW X-band EPR spectra thus making the reported DNA systems an ideal test bed for simplified models.
Computational methods
Molecular dynamics modelling
Initial 14-mer DNA configurations were constructed using the analysis module of the w3DNA web server developed by Olson and co-workers.44 Conventional base pairs were modelled using the parmbsc1 force field.42 Parameters for both spin labels have been generated in analogy with other spin probes developed by us previously, initially in the General AMBER force field (GAFF)45 and subsequently adapted to the parmbsc1 format. Quantum chemical calculations of Q and C* were performed with the Gaussian 09 software package.46 Force field parameters for the new atom types of the nitroxide moieties (the unsaturated carbon atoms of the nitroxide ring, the saturated carbon atoms of the nitroxide ring, the nitrogen and the oxygen) were taken from a combination of geometry optimization calculations in the gas phase and previous calculations. Equilibrium bond lengths and angles were taken directly from minimized energy structures. Force constants were interpolated using the reference values in the AMBER99 force field47 and the quantum mechanical calculations of Barone and co-workers.48,49 In the case of the C* label two dummy atoms in the triple bond (see Fig. S1 of ESI†) were introduced in order to define the torsional rotation between the cytosine and nitroxide rings. The parameters for the dihedral angle were determined by fitting to the QM potential energy scan. Partial charges for spin labels were calculated using a multi-conformational Restrained Electrostatic Potential (RESP) fit47 at the HF/6-31G* level of theory. The calculated force field parameters and partial charges for the Q and C* probes are included in the ESI† (Fig. S1–S3 and Tables S1–S5). The SPC/E water model50 was used with the Smith–Dang ion parameters for sodium counter ions51 with the systems compositions given in Table 1. All MD calculations were performed using the AMBER 1452 software package.| Sequence | Number of water molecules | Length of trajectorya (ns) |
|---|---|---|
| a Equilibration time is given in brackets. | ||
| [5′-d(GCC-TAC-ATG-QGA-CG)-5′-d(CGT-CPC-ATG-TAG-GC)] | 6780 | 700 (700) |
| [5′-d(GCC-TAC-ATG-C*GA-CG)-5′-d(CG-TCG-CAT-GTA-GGC)] | 7000 | 700 (700) |
| [5′-d(GCT-TAA-GCT-QCG-CG)] | 6370 | 700 (700) |
| [5′-d(GCC-TAC-ATG-C*GA-CG)] | 6450 | 600 (600) |
An NPT ensemble was maintained at a pressure of 1 atm using the Berendsen algorithm53 with a coupling constant of 5 ps. The SHAKE algorithm54 was used to maintain the hydrogen bond lengths. The centre of mass motion was removed every 20 ps to limit the build-up of translational kinetic energy, allowing for a time step of 2 fs to be used. Long range electrostatic interactions were accounted for using the Particle Mesh Ewald55 method with a cut-off of 10 Å. Systems were equilibrated for 700 ns prior to production runs of 700 ns. DNA conformational analysis was performed using the software from the w3DNA web server.44
Rotational autocorrelation functions
The autocorrelation function of each vector,![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) , associated with either the magnetic axes of the nitroxide head group of each spin label or the principal axes of DNA, can be calculated from an MD trajectory using the following expression:34
, associated with either the magnetic axes of the nitroxide head group of each spin label or the principal axes of DNA, can be calculated from an MD trajectory using the following expression:34 | (1) |
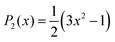 | (2) |
The local motional component of the probes and the global tumbling of the DNA were separated as follows. The global DNA motion was approximated by the dynamics of the principal axes of the tensor of inertia of each DNA fragment. Because of the effectively nearly cylindrical shape of DNA the X/Y principal components of the rotational tensor become poorly resolved for different moments of time. Thus they were estimated using the vector between the C1′ (glycosidic link) atoms of two complementary base pairs. The local motions of the probes (motions in the DNA fixed frame) were extracted using a mass-weighted RMS structural fit with the Ptraj module of AmberTools.56 In the M-F framework the motional and order parameters were obtained from the fitting of autocorrelation functions for the local and global motions using eqn (3) and (4), respectively, derived using the M-F formalism of Lipari and Szabo.34,57
 | (3) |
 | (4) |
According to these authors, for Markovian type motions the correlation function for internal dynamics can be generally expressed as a series of exponentials.57 Indeed, for many molecular systems the autocorrelation function for local dynamics can be well approximated by three different motional contributions and one time independent term S2 which is the square of the generalised local order parameter (eqn (3)). In eqn (3) index i corresponds to x, y, or z magnetic axes and wi are the weighting factors associated with the motional contributions. The effective local correlation time is calculated as ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) i = w1τi1 + w2τ2i + w3τ3i. Eqn (4) corresponds to the model of the free axial rotational diffusion of an DNA fragment where the components of the rotational diffusion tensor D⊥ and D‖ are related to correlation times according to τi = 1/(6Di).34,57
i = w1τi1 + w2τ2i + w3τ3i. Eqn (4) corresponds to the model of the free axial rotational diffusion of an DNA fragment where the components of the rotational diffusion tensor D⊥ and D‖ are related to correlation times according to τi = 1/(6Di).34,57
Direct prediction of EPR spectra from MD trajectories
A previously reported trajectory-based method that employs the numerical solution of the Stochastic Liouville Equation (SLE) in the Langevin form for the spin density matrix has been used for the simulation of the EPR line shapes.25,28 A program developed and described previously by one of us26 has been employed. The relatively long MD trajectories generated in this work allowed the simulation of CW EPR spectra directly by propagation of the spin density matrix along the entire sampling time without further approximations. In the program, single MD trajectories are used to calculate the variation in time of the averaged transverse magnetisation and, eventually, the EPR line shapes.26 At each time increment the propagation of the density matrix was carried out in Hilbert space using both eigenvalues and eigenvectors of the Spin–Hamiltonian as reported previously.29 Statistical averaging was achieved by the “sliding time window technique”, allowing the use of single MD trajectories for predicting EPR line shapes.25,28At the X-band the spectrum is dominated by the anisotropic hyperfine coupling A tensor and, under the condition of intermediate field approximation, the three hyperfine coupling lines are the functions of the calculated dynamical trajectory Ω(t)
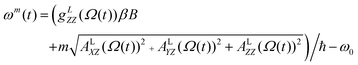 | (5) |
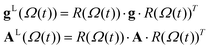 | (6) |
In (5)ω0, β, ℏ and B are the resonance frequency, Bohr magneton, Planck's constant and magnetic field respectively and m = ±1, 0. Note that there is no hyperfine contribution to the central line (m = 0). The orientational history of the magnetic axes in the fixed frame of the simulation box is calculated and processed. The EPR spectral line shapes of nitroxide spin labels are determined entirely by the variation with time of two angles that define the orientation of the applied magnetic field to the principal axis of the nitroxide group. The z axis of the nitroxide ring (coincident with the direction of the pz-orbital of N) is calculated from the cross-product of the unit vectors of two N–C bonds of the nitroxide ring (see Fig. 1).28,33 The x axis is calculated as a projection vector of the N–O bond on the nitroxide plane (defined by the C–N–C atoms) and the y axis is taken as a cross-product of the z and x vectors.
Prediction of EPR spectra using a combination of MD simulations and the Model-Free approach
Most recently we have reported the simulation of EPR line shapes using the M-F approach with the motional parameters extracted from the MD trajectories of lyotropic liquid crystals doped with a paramagnetic spin probe in a range of different aggregation states, namely, micro-aggregates, micelles, rods and lamellar states.34 EPR line shapes were simulated by solving the SLE in the Fokker–Planck (F–P) form.58,59 Thus a combined MD-EPR methodology allowed us to test directly the validity of the application of the M-F approach coupled with the partial averaging of magnetic tensors due to fast local motions34,60,61 to systems with complex multi-component molecular dynamics by comparing the resulting EPR spectra to those simulated directly from MD trajectories and also to the experimental ones.The advantage of using all-atom MD simulations is that both the motional and order parameters employed in the M-F approach can be readily calculated from the MD outputs. In most of lyotropic aggregate states reported in ref. 34 the internal dynamics of the probe was sufficiently fast for partial averaging of the magnetic tensors. In addition, because of the bulk structures the orientations of the principal components of the partially averaged magnetic tensors of the spin probe were well defined in each of the aggregate states. In the spin labelled DNA fragments the orientation of the partially averaged principal tensor components is not a priori obvious making them ideal systems to test the application of the M-F approach combined with the partial averaging of A and g by fast local motions in a general case. Both the values and the orientations of partially averaged principal components of the magnetic tensors were calculated from MD using the following procedure. Firstly, both tensors were averaged according to the following equations:
| 〈A〉ij = Axx〈lxi·lxj〉 + Ayy〈lyi·lyj〉 + Azz〈lzi·lzj〉 | (7) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) whose columns are the eigenvalues (projection cosines) that define the orientations of the averaged principal tensor components in the DNA fixed frame.
whose columns are the eigenvalues (projection cosines) that define the orientations of the averaged principal tensor components in the DNA fixed frame.Ā = ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ·〈A〉· ·〈A〉·![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) T T | (8) |
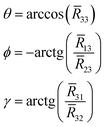 | (9) |
Transformation from the DNA fixed frame into the frame defined by the directions of the principal components of the partially averaged magnetic tensor is shown in Fig. S4 of ESI.† Our results showed that Ā and ḡ were nearly collinear and as such only the rotational angles for Ā were used in the simulations of EPR. They are reported in Table 4 for all systems. Together with the partially averaged values of Ā and ḡ and the global rotational diffusional coefficients (correlation times), obtained from the fitting of the autocorrelation function using eqn (4), they were used for the simulation of the EPR spectra using M-F approach.
Calculation of magnetic parameters
Magnetic parameters, namely the principal values of both A and g tensors, were calculated using the B3LYP functional with the N07D62,63 basis set as implemented in the Gaussian 09 software package.46 Structures were first optimised in the gas phase followed by optimisation in water using the polarizable continuum solvent scheme. Hyperfine coupling tensor A is calculated by combining contributions from the Fermi contact and anisotropic spin dipole coupling.64,65 Importantly, the calculation of magnetic parameters from first principles makes the entire MD-EPR simulation approach fully predictive.Results and discussion
The principal values of the g and A tensors calculated by DFT methods indicate that the magnetic parameters of both C* and Q probes are close to each other (Table 2). Excellent agreement is found between the predicted g and A values and those obtained from EPR measurements on the immobilised Q spin label (gxx = 2.0076, gyy = 2.0061, gzz = 2.0028; Axx = 6.68 G, Ayy = 5.41 G, Azz = 33.90 G) available from the literature,10 confirming the accuracy of the B3LYP/N07D model for calculation of these parameters for second row elements and nitroxide radicals.62,63,66 The calculated values were, therefore, used without scaling for the direct prediction of EPR spectra.| Spin label | g xx | g yy | g zz | A xx | A yy | A zz |
|---|---|---|---|---|---|---|
| Q | 2.0087 | 2.0061 | 2.0021 | 6.18 | 6.29 | 33.60 |
| C* | 2.0078 | 2.0069 | 2.0021 | 6.16 | 6.27 | 33.77 |
Effect of attached spin label on duplex DNA structure
Within the duplex DNA both spin labels Q and C* were found to remain base-stacked for the entire MD trajectories. The calculated RMSD of the DNA backbone with terminal base pairs removed (C* 1.72 Å, Q 2.16 Å) gives values in agreement with those typically reported for B-DNA (1.6–2.2 Å).40 The small fluctuations observed for this parameter in labelled DNA fragments confirm the structural stability of both duplexes over the course of the production trajectory (see Fig. S5 of ESI†).For the C* label, which is a modified cytosine base, comparison with the corresponding unlabelled sequence has been performed by calculating several geometric parameters of the helical base pair step using the analysis tools of the 3DNA program.44 The results are presented in Table S6 of ESI.† Good agreement between the twist, roll, slide and rise is observed between the average structures for the labelled and unlabelled sequences denoted by the red and blue lines, respectively, in Fig. S6 of ESI.† The shift and tilt of the average structures display slightly lower agreement, however in each case the geometry of selected random frames shows this to be within the expected deviation of the DNA structure caused by motions. Sugar pucker angles (phase), which are closely related to the backbone conformation, are within one degree difference between the unlabelled and labelled sequences (Table S6 of ESI†). Additionally, the average amplitude values are within the range of 25°–45°, as observed for standard B-DNA structures.67 Both the calculated structural parameters and the RMSD results unambiguously confirm that the C* label has a negligible perturbing effect on the geometry and flexibility of the host sequence, in agreement with conclusions based on experimental studies.11 Since the Q probe and its complementary base pair P both have no natural equivalents to draw a comparison with, calculation of their geometric parameters have not been attempted.
Contributions to the dynamics of spin labels in duplex DNA fragments
The re-orientational autocorrelation functions of the magnetic axes of Q label are presented in Fig. 2a. The autocorrelation functions of the magnetic axes of Q obtained by excluding the global DNA tumbling are presented in Fig. 2b. The motional and order parameters obtained from the fitting of autocorrelation functions are given in Table 3 (for all DNA models reported in this paper the fitted curves are presented in the ESI†). Due to the rigidity of Q, in duplex DNA the local re-orientational motions of all three magnetic axes demonstrate a high degree of order (see Table 3). Among the three the y axis exhibits the greatest local order with the local motions arising mainly from tilting about this axis. A less pronounced twisting motion about the x axis causes rotation of y and z. The z axis exhibits the lowest order. The results of the fitting of the autocorrelation functions of both the local motions of the probe and the global DNA tumbling (Fig. 2c) are presented in Table 3. The effective correlation times for local motions are calculated from the three motional contributions obtained from the fitting of the relevant autocorrelation functions using eqn (3). The results of the fitting are given in Table S7 of ESI.† Fitting of the autocorrelation function for the principal axes of the labelled DNA duplex with an axial model (eqn (4)) yields the correlation times for the global diffusion, namely, τ⊥ = 6.21 ns and τ‖ = 2.99 ns. Since the local motion of Q is highly restrained (Si > 0.9 for all three magnetic vectors), the autocorrelation functions of the magnetic axes (Fig. 2a) closely resemble those of the principal DNA axes (Fig. 2c), confirming that the dynamics of Q in duplex DNA adequately represents the global motion of the entire DNA fragment.10 Notably, τ⊥ ≈ 2τ‖, as would be expected for a 14-mer fragment where the long cylinder axis is roughly twice the length of the short axis.11 Both components of the global motion are approximately 1.5 times faster than those reported by Okonogi et al. (τ⊥ = 9.89 ns, τ‖ = 4.43 ns)8 using the hydrodynamic theory of Tirado and de la Torre for a duplex DNA of this size.18,19 The principal difference is that the hydrodynamic theory treats DNA as a rigid rod,18 whereas in our all-atom MD simulations DNA flexibility is naturally present and has an impact on the global motional rates. The value of τ⊥ is close to that reported by Miller et al. using an isotropic rotational diffusion model for the fitting of the EPR spectrum (τIso = 7.6 ns).10| Label | Temp. (K) | τ ⊥ (ns) | τ ‖ (ns) |
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) x
(ns)
x
(ns) |
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) y
(ns)
y
(ns) |
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) z
(ns)
z
(ns) |
S x | S y | S z |
|---|---|---|---|---|---|---|---|---|---|
a
τ
⊥ and τ‖ represent the correlation times of the axial components of global diffusion. ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) x, x, ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) y, y, ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) z, Sx, Sy and Sz represent the effective correlation times and order parameters of the local motions of the probes. 95% confidence bounds for all parameters are provided in ESI. z, Sx, Sy and Sz represent the effective correlation times and order parameters of the local motions of the probes. 95% confidence bounds for all parameters are provided in ESI.
|
|||||||||
| Duplex | |||||||||
| Q | 293 | 6.21 | 2.99 | 0.22 | 0.27 | 0.19 | 0.91 | 0.96 | 0.90 |
| C* | 293 | 7.02 | 2.88 | 0.25 | 0.21 | 0.13 | 0.78 | 0.66 | 0.64 |
| 273 | 13.10 | 5.23 | 0.30 | 0.23 | 0.12 | 0.80 | 0.68 | 0.65 | |
| Single-strand | |||||||||
| Q | 293 | 4.76 | 1.23 | 0.72 | 1.06 | 0.88 | 0.77 | 0.82 | 0.84 |
| C* | 293 | 3.75 | 0.96 | 1.43 | 1.23 | 1.12 | 0.60 | 0.51 | 0.60 |
| 273 | 9.65 | 1.91 | 1.66 | 1.41 | 1.08 | 0.60 | 0.51 | 0.60 | |
The EPR spectrum predicted directly by propagation of the MD trajectory (Fig. 3 red line) is found to be in good agreement with the experimental one (black line) reported by Miller et al.10 Such a validation against a highly sensitive spectroscopic technique confirms the reasonable accuracy of the MD model employed in this work. In addition, we have performed a simulation of the EPR spectrum using the M-F approach with the motional parameters extracted from MD (Tables 3 and 4), assuming an axially symmetric rotational diffusion model of the rigid rod of the DNA fragment and partial averaging of magnetic parameters of the probe. The resulting spectrum, simulated using Easyspin software,68 is presented as the blue line in Fig. 3 and found to be in good agreement with the line shape predicted directly and completely from the MD trajectory. Firstly, this suggests that the internal motions of the Q probe are highly restrained and thus have a negligible contribution to the overall motion and that Q indeed serves as an adequate reporter of the DNA motions. Secondly, this also confirms the validity of the application of the M-F approach to duplex DNA with the Q label. The apparent absence of the split in the low field region of the lineshape by both prediction methods is attributed to a slight overestimation of the global rotation diffusion of the DNA duplex by the SPC/E water model resulting in a somewhat reduced value of global τ⊥. This is in agreement with the results from the fitting of the EPR spectrum reported previously.10
 | ||
| Fig. 3 Comparison between experimental (black) and predicted directly and completely from MD (red) EPR spectra of Q-labelled duplex DNA at 293 K. Experimental EPR spectrum is reproduced from ref. 10 with permission from the American Chemical Society. The blue line represents the spectrum calculated using the M-F approach with the motional parameters extracted from MD. Homogeneous broadening parameter corresponding to 1.70 Gauss was used in all simulations. | ||
| Label | T (K) | g xx | g yy | g zz | A xx | A yy | A zz | ϕ | θ | γ |
|---|---|---|---|---|---|---|---|---|---|---|
| a Since the principal axes of partially averaged Ā and ḡ tensors are nearly collinear only the rotational angles corresponding to Ā are shown. Angles are given in degrees. | ||||||||||
| Duplex | ||||||||||
| Q | 293 | 2.0085 | 2.0060 | 2.0024 | 6.73 | 7.60 | 31.74 | −58.21 | 17.14 | −29.97 |
| C* | 273 | 2.0071 | 2.0066 | 2.0034 | 7.42 | 11.70 | 27.08 | 73.33 | 13.48 | −40.52 |
| 293 | 2.0069 | 2.0065 | 2.0034 | 7.68 | 11.51 | 27.01 | −62.09 | 14.37 | 84.37 | |
| Single-strand | ||||||||||
| Q | 293 | 2.0080 | 2.0062 | 2.0028 | 7.36 | 8.32 | 30.39 | −87.35 | 18.17 | −16.03 |
| C* | 273 | 2.0070 | 2.0059 | 2.0039 | 8.72 | 12.97 | 24.51 | −45.16 | 16.54 | −84.79 |
| 293 | 2.0067 | 2.0061 | 2.0040 | 10.75 | 11.88 | 23.58 | 72.30 | 41.62 | −23.40 | |
The autocorrelation functions calculated from MD for the total and local motions of the C* spin probe and the dynamics of the principal rotation axes of the labelled DNA duplex are presented in subpanels (a), (b) and (c), respectively, of Fig. 4. Similar to the Q label, C* demonstrates the complex multi-component dynamics with the very fast decay on the 1–100 ps time scale attributed to the local motion of the probe. The situation is however principally different from Q in several aspects. Firstly, autocorrelation functions with the global motion excluded (Fig. 4b) confirm that the rotation and bending of the alkyne tether leads to C* experiencing a considerably lower local order than Q for all three magnetic vectors. Secondly, rotation along the tether is associated with the most prominent re-orientational motion leading to the highest order parameter calculated for the x magnetic axis. However, measurement of the dihedral angle between the plane of the cytosine base and the nitroxide ring of the C* label (Fig. S7 of ESI†) indicates that, as has been inferred in the study of the related T* label, rotation about the alkyne linkage is not free.
This confirmed the previous assumption that due to a short tether the nitroxide group is effectively trapped in the major groove11 (Fig. 4). Rotation along the single bond of the tether leads to the averaging of the Azz and Ayy magnetic principal values of the nitroxide moiety resulting in a narrower predicted EPR line shape at 293 K (Fig. 5 top red curve) compared to the one corresponding to the Q label at the same temperature, confirming the higher level of rotational flexibility of the C* label in duplex DNA.
 | ||
| Fig. 5 (a) Comparison between EPR spectra of C*-labelled duplex DNA at 293 K simulated directly and completely from MD (red) and indirectly using the M-F approach with the motional parameters extracted from MD (blue) (b) comparison among EPR spectra of the C*-labelled duplex DNA at 273 K simulated directly and completely from MD (red), using the M-F approach with the parameters extracted from MD (blue) and the experimental one (solid black). The experimental EPR spectrum is reproduced from ref. 20 with permission from Taylor and Francis. | ||
The EPR spectrum simulated using the M-F approach with the motional parameters extracted from MD (Tables 3 and 4) is presented as the top blue line in Fig. 5. It has reasonably good agreement with the one simulated directly and completely from the relevant MD trajectory confirming the validity of the M-F approach for this system. Indeed, according to the calculated effective correlation times shown in Table 3 the partially restrained local dynamics of C* remains in the fast motional regime (<1 ns) at 293 K. Previously it has been shown that the EPR spectra of the closely related thymine derived spin label T* could be fitted with a simplified model which assumes that the fast axial local motion (τL < 1 ns22) partially averages the magnetic parameters.43 Robinson and co-workers using both T* and the double alkyne-bridged analogue T** demonstrated that the location of the nitroxide group in the major groove hinders local motions for alkyne-bridged labels in duplex DNA.11
In order to compare the predicted EPR spectrum with the experimental one available from the literature we have performed an additional MD simulation at 273 K.20 The results are compared as bottom lines in Fig. 5. A reasonable agreement between the predicted directly from MD (red line) and experimental (solid black line) EPR line shapes is observed. As in the case with the Q label (Table S7 of ESI†), fitting of the autocorrelation function of the local dynamics of the magnetic axes for the C* label required a minimum of three motional components on the 10 ps, 100 ps and 1–5 ns timescales (Table S9 of ESI†). The value of the Sx local order parameter for C* (0.80 at 273 K) was found to be very close to that reported by Fischhaber (0.77 at 273 K)20 and decreases slightly with increasing temperature (Table 3). Simulation using the M-F approach with partially averaged local magnetic tensors is presented as a blue line and is in good agreement with both the spectra predicted using the direct propagation method and the experimental one. Some discrepancy (narrowing down of some spectral features) is attributed to the presence of the slow motional mode in the local dynamics of C* (third component in the fitting of autocorrelation functions, see Table S9, ESI†) which is outside the fast motional regime, the condition that is required for the use of the partial averaging of the magnetic tensors. As a result, the slow motional contribution becomes underestimated in the simulated spectrum. Apparently, such effects are less pronounced when the local order parameter is high as evident from the agreement between the simulated EPR spectra by two methods of the DNA duplex with the Q label. Also, as expected, there was little difference between the motional parameters extracted for the global dynamics of both DNA duplexes labelled with Q and C* (see Fig. 2c, 4c and Table 3).
Contributions to the dynamics of spin labels in single-strand DNA fragments
The autocorrelation functions calculated from MD for the total and local motions of both probes and the dynamics of the principal rotation axes of the single-strand DNA structures are presented in subpanels (a), (b) and (c), respectively, of Fig. 6. The subpanels on the left and on the right correspond to the strands labelled with Q and C* probes, respectively. In the single-strand sequences folding of the outer base pairs and temporary disruption of stacking of individual bases both enable a greater degree of local motional flexibility for both Q and C* labels than in duplex DNA. This is confirmed by the autocorrelation functions calculated from MD for local motions of the probes (Fig. 6b) where the local order of the magnetic axes of both Q and C* is lower than that in the corresponding duplex forms. As in the case of the duplex DNA the autocorrelation function of the local motion is well represented by three motional modes (Table 3). For both C* and Q-labelled single-strand fragments the global diffusion remains highly axial with τ⊥ > 3.8τ‖ but with both correlation times smaller compared to the duplex form, as expected, (Table 3).Interestingly, the effective correlation times for the local motions of the probes were somewhat slower than those observed in the duplex forms. At the same time the order parameters for both spin labels attached to the single-stand DNA fragments are noticeably reduced compared to the cases of labelled duplexes. Both differences can be explained by the emergence of additional modes of motion in both labels with larger amplitudes but slower correlation times when not fully stacked.
As with the duplex DNA, the autocorrelation functions of the magnetic axes of Q in the single strand DNA in the laboratory frame (Fig. 6a left) are very close to the ones corresponding to the principal axes of the single-strand DNA (Fig. 6c left). This indicates that Q label in the single-strand structure bears a significant motional contribution from the latter thus serving as an adequate reporter of the DNA motions. In contrast, in the case of C*-labelled singe-strand DNA the nitroxide group of the spin probe is no longer trapped within the major groove with the rotation around the alkyne tether becoming relatively unrestricted. This is confirmed by the calculated time evolution of the dihedral angle between the plane of the cytosine base and the nitroxide ring of C* showing an increased frequency of flips between the 0° and 180° angles in the case of a single strand (Fig. S7 of ESI†). The greater mobility of C* label results in a more noticeable difference observed between the correlation functions of the magnetic axes of C* (Fig. 6a right) and the principal axes of the single-strand DNA fragment (Fig. 6c right). EPR spectra predicted directly and completely from relevant MD trajectories of single strand DNA are shown as red lines in (a), (b) and (c) of Fig. 7 for the Q labelled fragment at 293 K, the C* labelled fragment at 293 K and the C* labelled fragment at 273 K, respectively. In order to compare the predicted EPR spectrum with the experimental one available from the literature20 we have performed an additional MD simulation at 273 K. The result is presented in Fig. 7c demonstrating very good agreement with experiment thus confirming the accuracy of the force field employed in this study.
 | ||
| Fig. 7 (a and b) Comparison between EPR spectra at 293 K simulated directly and completely from MD (red) and indirectly using the M-F approach with the parameters extracted from MD (blue) of single strand DNA fragments labelled with Q and C*, respectively; (c) comparison among EPR spectra of C*-labelled single strand DNA at 273 K simulated directly and completely from MD (red), using the M-F approach with the parameters extracted from MD (blue) and the experimental one (solid black). The experimental EPR spectrum is reproduced from ref. 20 with permission from Taylor and Francis. | ||
As one would expect, the line shapes for both spin labels are much narrower compared to their counterparts in the duplex form. Two factors contribute to the narrowing of the line shapes in both cases, namely, the decreased correlation times of the global DNA tumbling by a factor of ∼1.5 and the reduction of the order parameters of the attached probes.
Simulations of EPR spectra using the M-F approach assuming axially symmetric rotational diffusion of the DNA fragments combined with partial averaging of magnetic axes of the probes are shown by a blue line for each of the cases (a), (b) and (c). For single-strand DNA labelled with Q the simulated spectrum is in perfect agreement with the one predicted directly from MD (Fig. 7a) thus confirming the validity of the F-M approach in this case. The same conclusion can be drawn for the case of single-stranded DNA labelled with C* at 273 K (Fig. 7c). The situation is noticeably different in the case of the single-strand C* labelled DNA fragment at 293 K where the simulation by the M-F approach appears to result in much narrower EPR features compared to the ones by the direct method (Fig. 7b). This can be explained as follows. Although the local dynamics of the probes in all three cases (a), (b) and (c) does not strictly satisfy the fast motional regime due to the presence of a slow motional mode (τ3 ∼ 4 ns) (see Table S13 of ESI†) in the case (a) because of the high motional restriction of Q (S = 0.84) the impact of such a slow mode on the spectrum becomes negligible. In the case (c) the global tumbling of the DNA fragment is much slower (τ ∼ 9 ns) compared to the label's local motion thus minimising the impact of its slowest local mode on the EPR line shape. The situation is different for the case (b) where the correlation time of the local slow mode (τ3 ∼ 4 ns), as well as the total local effective correlation time (τ ∼ 1 ns), become comparable to the correlation time of global motion (τ ∼ 3.75 ns) making the impacts from local and global motional both equally significant for the EPR line shape. As a result, the partial averaging of A and g magnetic tensors, used in the EPR simulation procedure, clearly underestimates the effect of local motions of the C* label on the EPR spectrum.
Finally, it is instructive to inspect the sensitivity of the predicted from MD EPR spectra to the choice of force fields employed in DNA modelling. For that reason we have performed an additional simulation of the DNA duplex with the Q spin label at 293 K with the parm99 force field.69 Parm99, combined with the TIP3P water model, has been used previously to study DNA conformations as well as DNA interactions with proteins.70,71 The motion and order parameters extracted from the MD simulation are presented in Tables S15 and S16 (ESI†). Fig. S20 of ESI† shows that the predicted from MD EPR spectrum is significantly narrower compared to both the experimental spectrum and the one simulated using the force field parameters employed in this work. Narrowing of the hyperfine coupling lines in the EPR spectrum is attributed mainly to the use of the TIP3P water model which noticeably underestimates the viscosity of water molecules72 and consequently overestimates the rotational diffusion of DNA. In contrast, the SPC/E water model is known for a reasonably adequate representation of water diffusion.72 This was recently confirmed in the MD-EPR combined study of different micellar aggregates in water,34 demonstrating the high feasibility of using our MD-EPR simulation methodology as a test bed for MD force field models. We have therefore also performed an MD simulation using parm99 combined with the SPC/E water model on single-strand DNA labelled with C* at 273 K. Single strand DNA structures have wider amplitudes of local motions that are expected to be more sensitive to DNA force field parameters describing base-base and base-probe interactions. Motional and order parameters extracted from MD run are presented in Tables S17 and S18 (ESI†). Fig. S21 of the ESI,† compares the predictions from the MD EPR spectrum to both the experimental one and the one simulated using the parmbsc1 force field. The results confirm that parmbsc1 provides a better agreement with the EPR experiment compared to parm99.
Conclusions
This study reports the first simulation of the CW EPR spectra of spin labelled DNA fragments in both duplex and single-strand forms from fully atomistic MD simulations. Force field models were developed for two structurally different spin probes, namely, Q and C*, that were the first ones introduced to the studies of DNA structures by EPR spectroscopy. Firstly, EPR spectra predicted directly and completely from the resulting MD trajectories using the direct propagation method demonstrate good agreement with the experimental spectra thus confirming the accuracy of the recently improved version of the parmbsc1 force field for DNA MD modelling. Secondly, structural analysis concludes that the effect of the modified cytosine spin label C* on the helical geometry of the duplex DNA is minimal with the nitroxide group partially restrained within the major groove of duplex DNA. As expected, the data obtained at the fully atomistic level confirm the higher mobility of C* compared to the quinolonyl derived probe Q with the latter shown to be an accurate reporter on the global DNA tumbling. Thirdly, our combined MD–EPR methodology allowed us to test the validity of the application of the M-F approach combined with the partial averaging of the local motions of the probe in the simulation and interpretation of EPR spectra. The 14-mer spin labelled DNA fragments with both local and global motional contributions having a prominent effect on the EPR line shapes serve as an ideal test bed for the M-F approach. Our results conclude that the M-F approach coupled with partial averaging of magnetic tensors provides an adequate simulation of the EPR spectra when the local motions fall within the fast motional regime and/or are highly restrained. The methods, however, become inadequate when the correlation times of the local and global motional contributions become comparable. It is important to note that parameters employed in the simulation of EPR line shapes by the M-F approach can be readily generated from MD trajectories. The calculation of the relevant autocorrelation functions usually requires much shorter trajectory lengths (<100 ns for DNA fragments in this work) compared to the ones required in the direct propagation method. Thus, in many cases the M-F based EPR simulation methodology using relatively short MD trajectories would be advantageous for the prediction and analysis of EPR spectra compared to direct propagation techniques. This would be crucial in cases of large higher order DNA structures where long scale MD simulations would be challenging or impractical at the all-atom level. Recent advances in click chemistry have led to the design of flexible, base-independent methods for the spin labelling of nucleic acids,12,73–75 making the EPR studies of DNA increasingly attractive. Several nitroxide based probes representing an improvement over Q and C* in terms of DNA labelling have been recently reported including base independent labelling for both DNA and RNA.73–75 The MD-EPR simulation methodology reported in this work is transferable to the novel DNA labels thus broadening the potential of EPR applications to study the assembly and conformational changes of higher order DNA structures such as the four way Holliday junction.76 For instance, as have been recently discovered, the assembly of such structures can be induced by small molecules with potential for medical and nanotechnology applications.77,78 Such MD-EPR applications are currently in progress.Conflicts of interest
There are no conflicts to declare.Acknowledgements
VSO gratefully acknowledges financial support of this work from EPSRC (grants EP/H020411/1 and EP/L001322/1). The authors wish to thank the Research and Computing Service at the University of East Anglia for access to the High Performance Computing Cluster.Notes and references
- S. C. Schultz, G. C. Shields and T. A. Steitz, Science, 1991, 253, 1001 CrossRef CAS PubMed.
- Z. A. E. Waller, B. J. Pinchbeck, B. S. Buguth, T. G. Meadows, D. J. Richardson and A. J. Gates, Chem. Commun., 2016, 52, 13511–13514 RSC.
- M. X. Fernandes, A. Ortega, M. C. López Martínez and J. García de la Torre, Nucleic Acids Res., 2002, 30, 1782–1788 CrossRef CAS PubMed.
- S. Georghiou, T. D. Bradrick, A. Philippetis and J. M. Beechem, Biophys. J., 1996, 70, 1909–1922 CrossRef CAS PubMed.
- W. Eimer, J. R. Williamson, S. G. Boxer and R. Pecora, Biochemistry, 1990, 29, 799–811 CrossRef CAS PubMed.
- S. Rüdisser, A. Hallbrucker and E. Mayer, J. Am. Chem. Soc., 1997, 119, 12251–12256 CrossRef.
- Z. Liang, J. H. Freed, R. S. Keyes and A. M. Bobst, J. Phys. Chem. B, 2000, 104, 5372–5381 CrossRef CAS.
- T. M. Okonogi, A. W. Reese, S. C. Alley, P. B. Hopkins and B. H. Robinson, Biophys. J., 1999, 77, 3256–3276 CrossRef CAS PubMed.
- T. M. Okonogi, S. C. Alley, A. W. Reese, P. B. Hopkins and B. H. Robinson, Biophys. J., 2002, 83, 3446–3459 CrossRef CAS PubMed.
- T. R. Miller, S. C. Alley, A. W. Reese, M. S. Solomon, W. V. McCallister, C. Mailer, B. H. Robinson and P. B. Hopkins, J. Am. Chem. Soc., 1995, 117, 9377–9378 CrossRef CAS.
- E. J. Hustedt, J. J. Kirchner, A. Spaltenstein, P. B. Hopkins and B. H. Robinson, Biochemistry, 1995, 34, 4369–4375 CrossRef CAS PubMed.
- S. A. Shelke and S. T. Sigurdsson, Eur. J. Org. Chem., 2012, 2291–2301 CrossRef CAS.
- S. A. Shelke, G. B. Sandholt and S. T. Sigurdsson, Org. Biomol. Chem., 2014, 12, 7366–7374 CAS.
- M. M. Haugland, A. H. El-Sagheer, R. J. Porter, J. Peña, T. Brown, E. A. Anderson and J. E. Lovett, J. Am. Chem. Soc., 2016, 138, 9069–9072 CrossRef CAS PubMed.
- M. M. Haugland, J. E. Lovett and E. A. Anderson, Chem. Soc. Rev., 2018, 47, 668–680 RSC.
- U. Jakobsen, S. A. Shelke, S. Vogel and S. T. Sigurdsson, J. Am. Chem. Soc., 2010, 132, 10424–10428 CrossRef CAS PubMed.
- O. Schiemann, P. Cekan, D. Margraf, T. F. Prisner and S. T. Sigurdsson, Angew. Chem., Int. Ed., 2009, 48, 3292–3295 CrossRef CAS PubMed.
- M. M. Tirado and J. G. de la Torre, J. Chem. Phys., 1980, 73, 1986–1993 CrossRef CAS.
- J. Garcia de la Torre, M. C. Lopez Martinez and J. J. Garcia Molina, Macromolecules, 1987, 20, 661–666 CrossRef CAS.
- P. L. Fischhaber, A. W. Reese, T. Nguyen, J. J. Kirchner, E. J. Hustedt, B. H. Robinson and P. B. Hopkins, Nucleosides Nucleotides, 1997, 16, 365–377 CAS.
- A. Spaltenstein, B. H. Robinson and P. B. Hopkins, Biochemistry, 1989, 28, 9484–9495 CrossRef CAS PubMed.
- E. J. Hustedt, A. Spaltenstein, J. J. Kirchner, P. B. Hopkins and B. H. Robinson, Biochemistry, 1993, 32, 1774–1787 CrossRef CAS PubMed.
- H.-J. Steinhoff and W. L. Hubbell, Biophys. J., 1996, 71, 2201–2212 CrossRef CAS PubMed.
- C. Beier and H.-J. Steinhoff, Biophys. J., 2006, 91, 2647–2664 CrossRef CAS PubMed.
- V. S. Oganesyan, SPR: Electron Paramagnetic Resonance, The Royal Society of Chemistry, 2015, vol. 24, pp. 32–61 Search PubMed.
- V. S. Oganesyan, J. Magn. Reson., 2007, 188, 196–205 CrossRef CAS PubMed.
- D. Sezer, J. H. Freed and B. Roux, J. Am. Chem. Soc., 2009, 131, 2597–2605 CrossRef CAS PubMed.
- V. S. Oganesyan, Phys. Chem. Chem. Phys., 2011, 13, 4724–4737 RSC.
- S. C. DeSensi, D. P. Rangel, A. H. Beth, T. P. Lybrand and E. J. Hustedt, Biophys. J., 2008, 94, 3798–3809 CrossRef CAS PubMed.
- V. S. Oganesyan, F. Chami, G. F. White and A. J. Thomson, J. Magn. Reson., 2017, 274, 24–35 CrossRef CAS PubMed.
- E. Kuprusevicius, G. White and V. S. Oganesyan, Faraday Discuss., 2011, 148, 283–298 RSC.
- F. Chami, M. R. Wilson and V. S. Oganesyan, Soft Matter, 2012, 8, 6823–6833 RSC.
- E. Kuprusevicius, R. Edge, H. Gopee, A. N. Cammidge, E. J. L. McInnes, M. R. Wilson and V. S. Oganesyan, Chem. – Eur. J., 2010, 16, 11558–11562 CrossRef CAS PubMed.
- C. Prior and V. S. Oganesyan, Chem. – Eur. J., 2017, 23, 13192–13204 CrossRef CAS PubMed.
- V. S. Oganesyan, E. Kuprusevicius, H. Gopee, A. N. Cammidge and M. R. Wilson, Phys. Rev. Lett., 2009, 102, 013005 CrossRef CAS PubMed.
- W. K. Olson and V. B. Zhurkin, Curr. Opin. Struct. Biol., 2000, 10, 286–297 CrossRef CAS PubMed.
- F. Lankaš, J. Šponer, P. Hobza and J. Langowski, J. Mol. Biol., 2000, 299, 695–709 CrossRef PubMed.
- M. Pasi, J. H. Maddocks, D. Beveridge, T. C. Bishop, D. A. Case, T. Cheatham, P. D. Dans, B. Jayaram, F. Lankas, C. Laughton, J. Mitchell, R. Osman, M. Orozco, A. Pérez, D. Petkevičiūtė, N. Spackova, J. Sponer, K. Zakrzewska and R. Lavery, Nucleic Acids Res., 2014, 42, 12272–12283 CrossRef CAS PubMed.
- K. M. Kosikov, A. A. Gorin, V. B. Zhurkin and W. K. Olson, J. Mol. Biol., 1999, 289, 1301–1326 CrossRef CAS PubMed.
- P. D. Dans, L. Danilāne, I. Ivani, T. Dršata, F. Lankaš, A. Hospital, J. Walther, R. I. Pujagut, F. Battistini, J. L. Gelpí, R. Lavery and M. Orozco, Nucleic Acids Res., 2016, 44, 4052–4066 CrossRef CAS PubMed.
- R. Galindo-Murillo, D. R. Roe and T. E. CheathamIii, Nat. Commun., 2014, 5, 5152 CrossRef CAS PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Perez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goni, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpi, C. Gonzalez, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2016, 13, 55–58 CrossRef CAS PubMed.
- S. P. Van, G. B. Birrell and O. H. Griffith, J. Magn. Reson., 1974, 15, 444–459 CAS.
- G. Zheng, X.-J. Lu and W. K. Olson, Nucleic Acids Res., 2009, 37, 240–246 CrossRef PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, USA, 2009.
- P. Cieplak, W. D. Cornell, C. Bayly and P. A. Kollman, J. Comput. Chem., 1995, 16, 1357–1377 CrossRef CAS.
- V. Barone, A. Bencini, M. Cossi, A. D. Matteo, M. Mattesini and F. Totti, J. Am. Chem. Soc., 1998, 120, 7069–7078 CrossRef CAS.
- E. Stendardo, A. Pedone, P. Cimino, M. Cristina Menziani, O. Crescenzi and V. Barone, Phys. Chem. Chem. Phys., 2010, 12, 11697–11709 RSC.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757–3766 CrossRef CAS.
- D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, I. T. E. Cheatham, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, University of California, San Francisco, 2014 Search PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comp. Physiol., 1977, 23, 327–341 CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- G. Lipari and A. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- C. F. Polnaszek, G. V. Bruno and J. H. Freed, J. Chem. Phys., 1973, 58, 3185–3199 CrossRef CAS.
- J. H. Freed, G. V. Bruno and C. F. Polnaszek, J. Phys. Chem., 1971, 75, 3385–3399 CrossRef CAS.
- B. J. Gaffney and H. M. McConnell, J. Magn. Reson., 1969, 1974(16), 1–28 Search PubMed.
- W. L. Hubbell and H. M. McConnell, J. Am. Chem. Soc., 1971, 93, 314–326 CrossRef CAS PubMed.
- V. Barone, P. Cimino and E. Stendardo, J. Chem. Theory Comput., 2008, 4, 751–764 CrossRef CAS PubMed.
- V. Barone and P. Cimino, J. Chem. Theory Comput., 2009, 5, 192–199 CrossRef CAS PubMed.
- N. Rega, M. Cossi and V. Barone, J. Chem. Phys., 1996, 105, 11060–11067 CrossRef CAS.
- V. Barone, Chem. Phys. Lett., 1996, 262, 201–206 CrossRef CAS.
- L. Hermosilla, P. Calle and J. M. Garcia de la Vega, RSC Adv., 2015, 5, 62551–62562 RSC.
- R. E. Dickerson, Nucleic Acids Res., 1989, 17, 1797–1803 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- T. E. Cheatham, P. Cieplak and P. A. Kollman, J. Biomol. Struct. Dyn., 1999, 16, 845–862 CAS.
- C. Rauch, M. Trieb, F. R. Wibowo, B. Wellenzohn, E. Mayer and K. R. Liedl, J. Biomol. Struct. Dyn., 2005, 22, 695–706 CAS.
- Y. X. Yu and S. Fujimoto, Sci. China: Chem., 2013, 56, 524–532 CrossRef CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. B, 2001, 105, 24a CrossRef.
- S. A. Shelke, G. B. Sandholt and S. T. Sigurdsson, Org. Biomol. Chem., 2014, 12, 7366–7374 CAS.
- U. Jakobsen, S. A. Shelke, S. Vogel and S. T. Sigurdsson, J. Am. Chem. Soc., 2010, 132, 10424–10428 CrossRef CAS PubMed.
- M. M. Haugland, A. H. El-Sagheer, R. J. Porter, J. Pena, T. Brown, E. A. Anderson and J. E. Lovett, J. Am. Chem. Soc., 2016, 138, 9069–9072 CrossRef CAS PubMed.
- M. A. Karymov, M. Chinnaraj, A. Bogdanov, A. R. Srinivasan, G. H. Zheng, W. K. Olson and Y. L. Lyubchenko, Biophys. J., 2008, 95, 4372–4383 CrossRef CAS PubMed.
- L. A. Howell, Z. A. E. Waller, R. Bowater, M. O'Connell and M. Searcey, Chem. Commun., 2011, 47, 8262–8264 RSC.
- L. A. Howell, R. A. Bowater, M. A. O'Connell, A. P. Reszka, S. Neidle and M. Searcey, ChemMedChem, 2012, 7, 792–804 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp08625c |
| This journal is © the Owner Societies 2018 |