The kinetics and mechanism of oxidation of reduced phosphovanadomolybdates by molecular oxygen: theory and experiment in concert

Abstract

The reactivity of the H₅PV₂Mo₁₀O₄₀ polyoxometalate and its analogues as an electron transfer and electron transfer–oxygen transfer oxidant has been extensively studied in the past and has been shown to be useful in many transformations. One of the hallmarks of this oxidant is the possibility of its re-oxidation with molecular oxygen, thus enabling aerobic catalytic cycles. Although the re-oxidation reaction was known, the kinetics and mechanism of this reaction have not been studied in any detail. Experimentally, we show that both the one- and two-electron reduced polyoxometalate are reactive with O₂, the two-electron one more so. The reactions are first-order in the polyoxometalate and O₂. Solvents also have a considerable effect, protic solvents being preferred over aprotic ones. H₅PV₂Mo₁₀O₄₀ was reduced either by an electron transfer reaction (H₂) or an electron transfer–oxygen transfer reaction (Ph₃P). Similar rate constants and activation parameters were observed for both. DFT calculations carried out on the re-oxidation reactions strongly suggest an inner-sphere process. The process involves first the formation of a coordinatively unsaturated site (CUS) and subsequently the binding of O₂ to form superoxo and then peroxo η²-O₂ adducts. Most interestingly, although vanadium is the reactive redox centre as well as a necessary component for the oxidative activity of H₅PV₂Mo₁₀O₄₀, and a CUS can be formed at both Mo and V sites, O₂ coordination occurs mostly at the Mo CUSs, preferably those where the vanadium centers are distal to each other.

---

Introduction

Molecular oxygen is a very attractive oxidant for the oxidative transformation of industrially relevant substrates. However, its direct interaction with organic compounds, particularly in the oxidation of hydrocarbons, is characterized by low selectivity because of radical chain reactions associated with the prevalence of oxo and peroxo radical intermediates. One alternative approach for use of dioxygen is its use as a terminal oxidant in oxidase type reactions, such as those catalysed by Pd compounds,¹ or those catalysed by phosphovanadomolybdates, notably the H₅PV₂Mo₁₀O₄₀ of the α-Keggin structure.^2–9 In the latter reactions, substrates are typically activated by electron transfer (ET) to yield either a dehydrogenated product or an oxygenated product by further oxygen transfer (OT). Over the years, reactions involving C–H, C–C and C–M bond activation as well as oxidation of sulphides have been studied.^7–9 Importantly, the reduced catalyst, whose structure has been studied by EPR experiments^10,11 and DFT calculations,¹² can be re-oxidized by molecular oxygen. This spatiotemporal separation between the substrate oxidation and the catalyst regeneration is responsible for high selectivity of such reactions. It should be stressed, as indicated in Scheme 1, that the reaction of one equivalent of H₅PV₂Mo₁₀O₄₀ with one equivalent of substrate or reducing agent typically leads first to an observable intermediate consisting of an oxidized substrate and reduced H₅PV₂Mo₁₀O₄₀.^7–12 In principle, in the presence of O₂ two scenarios can be considered for a catalytic reaction that includes re-oxidation of the reduced H₅PV₂Mo₁₀O₄₀: (i) product formation as shown in Scheme 1 followed by catalyst re-oxidation; and (ii) direct aerobic oxidation of the intermediate as recently demonstrated in the oxidation of benzene.¹³

Scheme 1 Oxidation of generic substrates (S) by H₅PV₂Mo₁₀O₄₀.

Thus, although much is known about the mechanisms of substrate oxidation, much less is known about the reactions of reduced polyoxometalates with oxygen. It has thus been shown that a Fe(II)-substituted polyoxotungstate binds O₂,¹⁴ but more generally the re-oxidation of reduced polyoxotungstates with O₂ in water has been shown to proceed by an outer-sphere electron transfer (ET).^15–17 The mechanism is less clear in the case of phosphovanadomolybdates. Moreover, although the redox potentials for different α-Keggin polyoxometalates show the following general trend, polyoxotungstates < polyoxomolybdates < polyoxovanadomolybdates,¹⁸ the rates of their aerobic re-oxidation are not correlated with the redox potential: polyoxotungstates (seconds) ≫ polyoxovanadomolybdates (minutes) ≫ polyoxomolybdates (days). It was suggested that aerobic re-oxidation of H₆PV^VV^IVMo₁₀O₄₀ after reaction with α-terpinene occurs through inner-sphere electron transfer to oxygen,¹⁹ but other publications suggest different scenarios.^20–22 Herein, we examine the mechanism of oxidation of reduced H₅PV₂Mo₁₀O₄₀ by O₂ under conditions similar to practical catalytic oxidation applications. In order to understand the mechanism at the atomic and electronic level, the experimental studies were combined with density functional theory (DFT) calculations. It is known that important factors for O₂ activation include, but are not limited to, redox potential, solvent, spin state, ligand architecture, and additional co-reductants.^23,24 In this work we have considered the oxidation of H₆PV₂Mo₁₀O₄₀ and H₇PV₂Mo₁₀O₄₀ by molecular oxygen.

Results and discussion

Kinetics of aerobic oxidation

As can be seen from Scheme 1 the reaction of H₅PV₂Mo₁₀O₄₀ (the oxidized compound, 1_ox) with substrates either by an ET dehydrogenation or an ET–OT oxygenation is intrinsically a two-electron process. However, self-exchange ET between polyoxometalates is fast,^2,15,17 that is, the two-electron reduced H₇PV₂Mo₁₀O₄₀ (1_red2e) can readily react with 1_ox to yield the one-electron reduced H₆PV₂Mo₁₀O₄₀ (1_red1e). According to our calculations, this interaction is exergonic by 3.73 kcal mol⁻¹ in acetonitrile and is favoured kinetically by the strong acidic nature of the surface protons. Therefore, the substrate/1_ox ratio can be manipulated to form either 1_red1e or 1_red2e. Molecular hydrogen, H₂, is the simplest reducing agent, since there is no product formed besides 1_red1e or 1_red2e. Thus, 1_red1e and 1_red2e can be formed by the reaction of 0.5 equivalents and 1.0 equivalent of H₂ with 1_ox, respectively, as in eqn (1):

H₂ + 1_ox → 1_red2e and 1_red2e + 1_ox → 1_red1e (1)

In the reaction of either the one- or two-electron reduced species (1_red) with O₂ in CH₃CN, 1 equivalent of O₂ was consumed per 2 equivalents and 4 equivalents, respectively, of 1_red2e and 1_red1e, as determined by volumetric measurements, Table S1 (ESI‡). Therefore, we conclude that 1_red2e and 1_red1e react with O₂ according to eqn (2) and (3), respectively:

2H₇PV₂Mo₁₀O₄₀ + O₂ → 2H₅PV₂Mo₁₀O₄₀ + 2H₂O (2)

4H₆PV₂Mo₁₀O₄₀ + O₂ → 4H₅PV₂Mo₁₀O₄₀ + 2H₂O (3)

The kinetics of reoxidation of 1_red in acetonitrile was studied spectrophotometrically, by following the disappearance of the reduced polyoxometalate blue colour at 750 nm. Typical kinetic curves are shown in Fig. S1 (ESI‡). The reaction order with respect to the concentration [1_red] was determined by measuring the initial rate, −d[1_red]/dt, as a function of the initial concentration of [1_red], [1_red]₀, at a constant initial concentration of [O₂]. The linear increase in the initial rate with the increase in 1_red over a wide range of [1_red]₀ reveals the reaction to be first-order with respect to [1_red] reduced by either 1 or 2 electrons, Fig. S2 (ESI‡). Similarly, the linear dependence of the initial rate on [O₂]₀, Fig. S3 (ESI‡), indicates that the reaction is first order with respect to O₂. Therefore, the direct reaction of 1_red with O₂ obeys the rate law as shown in eqn (4):

d[1_red]/dt = k[1_red]₀[O₂]₀ (4)

From this equation, one can calculate a rate constant for 1_red1e, k₂₉₈ = 0.09 ± 0.02 M⁻¹ s⁻¹. This rate constant is two orders of magnitude lower than that for oxidation of one electron reduced polyoxotungstates in water.¹⁵ The rate constant for the reoxidation of 1_red2e is k₂₉₈ = 0.9 ± 0.1 M⁻¹ s⁻¹, which is an order of magnitude higher than that measured for 1_red1e. In addition, once the blue colour associated with 1_red disappeared, iodometric titration revealed that no H₂O₂ was present in the reaction mixture, although this does not rule out the possibility of H₂O₂ as a fast-reacting oxidizing intermediate. Indeed, a control experiment on the oxidation of 1_red1e by H₂O₂ yielded a rate constant, k₂₉₈ = 3.2 ± 0.8 M⁻¹ s⁻¹, which is significantly higher than the one with O₂ as oxidant.

It is worth noting that the initial rates, V₀, for the aerobic oxidation of 1_red are solvent dependent – although as seen in Table 1, V₀(1_red2e) is always greater than V₀(1_red1e). Generally, the reactions are faster in protic solvents compared to aprotic ones, although addition of trifluoroacetic acid positively affects the rates in aprotic solvents, while the effect is small for protic solvents. The rate constants are not correlated with the redox potential of 1 in the various solvents.

Table 1 Initial rates for oxidation of 1_red reduced by H₂ in different solvents

Solvent	V 0(1red2e) M s^−1 × 10^7	V 0(1red1e) M s^−1 × 10^7	E (V)
Conditions: 0.25 mM 1red, 1 bar air, 25 °C. The redox potentials were obtained by cyclic voltammetry (see the Experimental section) and standardized versus Fc/Fc^+. Since the solubility of O2 depends somewhat on the solvent, the dependence of the rate of reoxidation of 1red is presented in terms of initial rates V0 rather than rate constants. nd – not determined.
Water	8.4 ± 0.9	3.70 ± 0.4	0.50
0.1 M H2SO4	21.8 ± 2.5	4.48 ± 0.4	0.52
AcOH	15.7 ± 1.5	4.21 ± 0.4	0.38
MeOH	15.1 ± 1.6	2.92 ± 0.3	nd
Acetonitrile	3.6 ± 0.5	0.36 ± 0.06	0.49
Sulfolane	0.6 ± 0.1	0.12 ± 0.02	0.50
DMSO	2.8 ± 0.3	0.12 ± 0.02	0.40
Diglyme	3.1 ± 0.4	0.24 ± 0.03	0.45

---

In addition to the reduction of 1_ox by H₂, the reduced polyoxometalate was also formed by a typical but simple ET–OT reaction, that is, the oxidation of triphenylphosphine to the corresponding oxide, Scheme 2. At 25 °C, the ion pair formed as a result of electron transfer can be observed by EPR, Fig. S4 (ESI‡). A ³¹P NMR measurement at this point shows no formation of triphenylphosphine oxide, which however can easily be formed by heating the mixture to 70 °C.

Scheme 2 The ET–OT oxygenation of triphenylphosphine.

The rate constants as well as the transition state energies found for the oxidation of 1_red formed by reduction with either H₂ or Ph₃P are presented in Table 2. As one can see, there is some small variation in the values obtained, but they are very similar and likely within experimental uncertainty. Notable is the large negative value of ΔS^#, pointing towards an organized rate-limiting state.

Table 2 Rate constants and activation parameters for the aerobic oxidation of 1_red formed by different reducing agents (RA)

RA	1red	k 298, M^−1 s^−1	ΔH^#298, kcal mol^−1	ΔS^#298, cal mol^−1 K^−1	ΔG^#298, kcal mol^−1
Conditions: 0.50 mM 1red in CH3CN, 1 bar air. Data from Fig. S5 and S6 (ESI).
H2	1red1e	0.09 ± 0.02	8.4	−32.6	18.3
H2	1red2e	0.9 ± 0.1	5.4	−39.8	17.3
Ph3P	1red1e	0.05 ± 0.01	8.3	−36.6	19.2
Ph3P	1red2e	0.7 ± 0.1	6.5	−36.5	17.4

---

Computational results

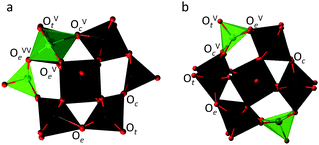
The overall reactions of oxygen reduction by H₇PV₂Mo₁₀O₄₀ and H₆PV₂Mo₁₀O₄₀ according to eqn (2) and (3) are energetically highly favourable: ΔG₂₉₈ = −57.2 and −50.3 kcal mol⁻¹ in acetonitrile, respectively. However, the first step of the interaction, that is the abstraction of the first H-atom or coupled proton–electron transfer (CPET), is endergonic by 13.5 kcal mol⁻¹ for 1_red2e and 16.9 kcal mol⁻¹ for 1_red1e. This is in agreement with the strongly negative one-electron reduction potential of oxygen (which is −0.33 V vs. NHE in water at pH 7, 25 °C).²⁵ The interaction between an acidic surface hydrogen of 1_red1e and apolar O₂ leads to a highly unstable intramolecular complex before hydrogen transfer that is 22.4 kcal mol⁻¹ above the energy of the reactants. The subsequent activation barrier for H transfer is 29.8 kcal mol⁻¹, prohibitively high for a room temperature reaction. See Fig. S7 (ESI‡) for optimized structures for outer sphere complexes. We were unable to locate a similar precursor complex and transition state for 1_red2e using our computational approximation. In both cases the probability of the outer-sphere H-transfer is expected to be extremely low since CPET or H-atom transfers are viewed as vibrational processes that require at least weak hydrogen bonding between the reaction centres.^26–28

Due to the absence of spin restrictions, electron transfer (ET) is often considered the most probable initial stage of oxygen activation.^29,30 Our calculations showed that in spite of the high oxidation potential of oxygen and the presence of lone pair electrons, ET and PT from the reduced polyoxometalates are unacceptably high in energy, especially in the gas phase, Table S2 (ESI‡). These results, together with the experimental observations that (a) a catalytic amount of Cu⁺ does not influence the rate of the oxidation reaction and (b) H₂O₂ was not observed as an intermediate in the reaction mixture, prompted us to consider an inner-sphere mechanism for aerobic oxidation of 1_red. By way of example, we consider the (1,2) and (1,11) isomers of the [PV₂Mo₁₀O₄₀]^q− anion (Fig. 1), which have two vanadium atoms at the proximal and distal positions, respectively, to each other. These isomers were chosen because they represent two different structure types with different reactivity that have been previously observed.^10–12 According to our calculations, the (1,2) isomers of 1_ox and 1_red1e are 1.5 and 2.2 kcal mol⁻¹ more stable, respectively, than the (1,11) isomer. In contrast, the (1,11) isomer of 1_red2e is 0.6 kcal mol⁻¹ more stable than the corresponding (1,2) isomer.

Fig. 1 Surface oxygen atoms in the 1,2 (a) and 1,11 (b) isomers of the [PV₂Mo₁₀O₄₀]^q− anion.

All 12 metal atoms in the Keggin structure are hexa-coordinated with oxo ligands and thus are not likely to coordinate O₂. However, we have previously shown that the tendency of vanadium atoms in high oxidation states towards a reduced coordination number facilitates the formation of defect structures with coordinatively unsaturated sites (CUSs). Depending on which bonds are broken, V or Mo CUSs could be formed.¹² Further calculations reported here show that reduction of the polyoxometalate tends to slightly decrease the energetic cost for such defect formation, while protonation slightly increases it, Table 3. The experimentally observed accelerating effect of protic solvents presents an additional indirect proof for CUS formation as an important stage of interaction.

Table 3 Stability of V and Mo CUSs (ΔG₂₉₈ in acetonitrile, kcal mol⁻¹) compared to the corresponding intact structures

	(1,2)V CUS	(1,2)Mo CUS	(1,11)Mo CUS
The energies of 2e-reduced structures in the triplet state are shown in parentheses. The optimized structures of the V and Mo CUS are shown in Fig. S8 (ESI).
H5PV2Mo10O40	20.54	16.50	16.25
[H5PV2Mo10O40]^−	19.58	17.85	14.10
H6PV2Mo10O40	22.28	16.93	14.35
[H6PV2Mo10O40]^−	17.64 (19.69)	13.75 (17.94)	15.08 (16.71)
H7PV2Mo10O40	18.64 (19.96)	15.32 (18.86)	15.54 (21.03)

---

The bonding analysis, Fig. S9 (ESI‡), shows that one of the V–O–V bonds represents the weakest bridging bond in the 1_ox (1,2) isomer. Breaking of this bond together with one of the adjacent weak Mo–O or V–O bonds leads to molybdenum- or vanadium-centred CUSs, respectively. The electron spin density in intact 1_red is distributed between t_1u orbitals that are nonbonding with respect to V–O and t_2g orbitals that are strongly antibonding with respect to Mo–O, Fig. S10 (ESI‡). Therefore, the reduction of phosphovanadomolybdates most strongly destabilizes Mo–O bonds, making the formation of molybdenum centred CUSs more preferential. Thus, for the (1,2) isomer of 1_red, the formation of a Mo CUS is preferred by 2–5 kcal mol⁻¹ relative to its V counterpart. Moreover, Mo CUSs are usually slightly less endergonic for the (1,11) isomer, especially for 1_red1e. In contrast to the intact 1_red2e structures that have triplet ground states, closed-shell electronic configurations are 1.3–5.5 kcal mol⁻¹ more stable for the defect structures. Finally, it is also notable that the presence of water as a coordinated ligand stabilizes defect structures, especially for the 1_ox and 1_red1e with V CUSs, Table S3 and Fig. S11 (ESI‡).

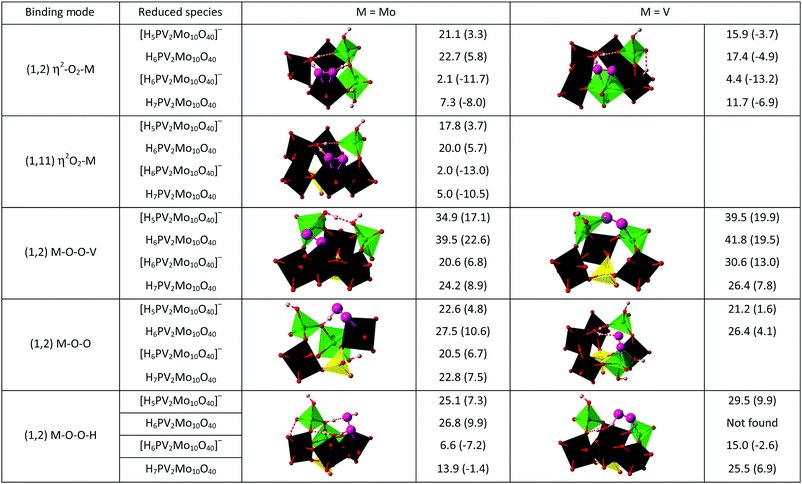
Now given that the calculations have shown that the CUSs of 1 are viable species, they can be also considered as excellent candidates for the ligation of O₂ and its activation by an inner sphere reaction. Side-on η²-O₂, end-on η¹-O₂ and η²-O₂H as well as bridged M–O–O–M coordination modes of O₂ at molybdenum and vanadium sites are shown in Chart 1, together with their calculated stabilities. Selected bond lengths, vibrational frequencies and atomic charges of these complexes are assembled in Table S4 (ESI‡). The most notable observation is that the side-on η²-O₂ coordination to either Mo or V in defect structures was found to be the most energetically favourable for the one-electron reduced polyoxometalate. This also holds true for the two-electron reduced polyoxometalate, although here also certain M–O–O–H species were stable, albeit still less than the side-on η²-O₂ species. In all considered (1,2) isomers, oxygen binding and activation is preferred at a molybdenum CUS where longer O–O bonds, lower O–O vibrational frequencies, and greater transfer of electron density were found (Table S4, ESI‡) compared to the vanadium CUS. The only exception is the end-on coordination mode, for which V superoxo complexes are slightly more stable than the corresponding Mo complexes. The (1,11) isomer possesses only Mo sites that show oxygen binding affinity qualitatively similar to that of the (1,2) isomer.

Chart 1 Typical O₂ modes of ligation to reduced species of 1 and their calculated stabilities. The free energy, ΔG₂₉₈, kcal mol⁻¹, of the species is given relative to the intact polyoxometalate and to the relevant defect structures (in parentheses). All the complexes are in the lowest possible spin state, that is singlet or doublet. These are the lowest-energy states that were found at the level of theory employed.

These findings can be explained by π-repulsion caused by metal interactions with σ- and π-donating oxygen ligands, and this effect is stronger for V than for Mo because of the difference in atomic sizes.¹² For superoxo complexes, the electron transfer from 1_red to O₂ is comparable for side-on and end-on coordination modes, resulting in quite similar stabilities of these complexes. In contrast, effective 2e-backdonation from metal to O₂ in side-on peroxo complexes results in their dramatically higher stability. Indeed, for a V³⁺ complex with bulky amine ligands that does not suffer from π-repulsion, the side-end peroxo complex was found to be much stronger than in our case (ΔH = −75.0 ± 2.0 kcal mol⁻¹) with a much smaller energy difference between the two isomers (4.2 kcal mol⁻¹), favouring η² binding.³¹

Having the defect structures with CUSs and their oxygen complexes in side-on and end-on binding modes as possible intermediates, the mechanism of inner-sphere oxidation 1_red can be studied in more detail. The first reaction considered was the stoichiometric oxidation of four H₆PV₂Mo₁₀O₄₀, 1_red1e, species by O₂ on three different coordinatively unsaturated sites – Mo CUS in (1,11) and Mo and V CUS in (1,2) isomers, Fig. 2.

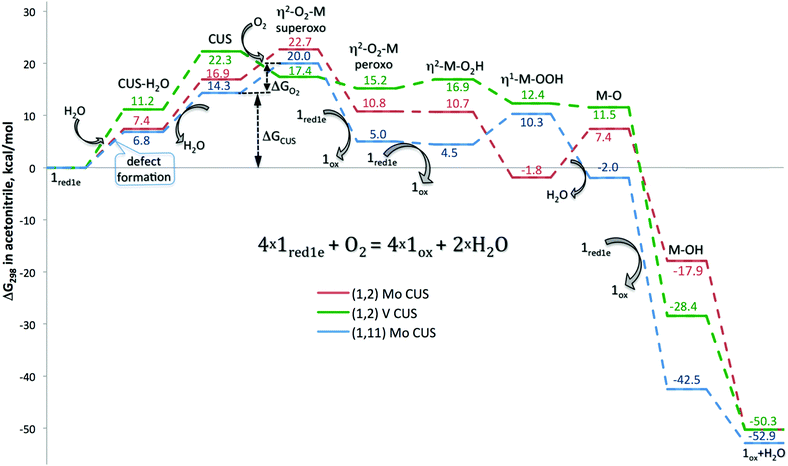Fig. 2 Reaction profiles for the oxidation of H₆PV₂Mo₁₀O₄₀, 1_red1e. All points are local minima on the corresponding potential energy surfaces.

Inspection of the reaction profiles in Fig. 2 shows that defect formation and oxygen coordination are the highest energy states in acetonitrile at room temperature. For activation at vanadium, the enthalpy-controlled reaction of V CUS formation would appear to be the rate determining state of the reaction. In contrast, for the Mo CUS, entropy-controlled oxygen coordination represents the limiting state. Energetically, reactions on both Mo and V CUSs have lower barriers than that for the outer-sphere CPET (vide supra).

Transformation of superoxo to peroxo complexes by hydrogen transfer from another 1_red1e species significantly stabilizes oxygen coordination on the Mo CUS. Protonation of coordinated oxygen and subsequent water dissociation are endergonic at this stage by 5–10 kcal mol⁻¹. Hydrogen transfer from the third 1_red1e species causes transformation from the side-on to the end-on M–OOH coordination mode, in which intramolecular proton transfer and consequent water dissociation take place. These intermediate reactions proceed with small changes in energy, and most of the complexes remain endergonic with respect to the reactants. Transfer of the fourth H-atom completes 4e O₂ reduction and proceeds with strong energy gain. These energetic trends qualitatively resemble the outer-sphere oxygen reduction (Table S2, ESI‡). The last strongly exergonic stage is water dissociation and recovery of 1_ox.

Although all points in Fig. 2 correspond to local minima on the corresponding potential energy surface, we believe that the activation barriers are well approximated by the calculated energies of the intermediate structures. The first reaction, formation of defect structures with CUSs, is the only individual step for which a substantial activation barrier could be anticipated. For the most unstable V CUS in the 1_ox isomer, we found a late transition state that was only 3.12 kcal mol⁻¹ higher in energy than the final defect structure. In spite of numerous efforts, we were unable to locate a saddle point on the way to other defect structures, presumably because of close geometric and energetic proximity of the local minima corresponding to the final state. Moreover, the presence of water further stabilizes the transition state. The second reaction is the formation of the η²-O₂–M adducts in the absence of spin restriction for the interaction of 1_red1e with oxygen in its ground state. Finally, self-exchange hydrogen transfer from other 1_red1e species at the next stages of the interaction is fast and is favoured kinetically by the strong acidic nature of the surface protons, vide supra. Reorganization of the η²-O₂ coordination mode to η¹-OOH and the following water dissociation smoothly proceed on the energetic scale and are facilitated by hydrogen bonding (see the corresponding structures in Chart 2). Thus, we believe that the reaction profiles in Fig. 2 represent not only the thermodynamics, but also the kinetics of the 1_red1e oxidation reaction.

Chart 2 The most stable O₂ adducts to the (1,2) isomer of 1_red2e with different spin states and their Gibbs free energy, O–O bond stretching vibrational frequency and Atomic Polar Tensor (APT) charges on oxygen atoms (Q_O). The ΔG₂₉₈ values are relative to the plenary, non-defect structure.

Reoxidation of 1_red2e shows specific features, related mainly to the spin state of the systems. As mentioned above, the defect structures of the 2e-reduced polyoxometalates have singlet electronic configurations in the ground state, but the triplet states are only a few kcal mol⁻¹ higher in energy, and thus, the oxygen complexes may have different multiplicities, Scheme 3. Interaction between the defect structures in the singlet state with an oxygen molecule results in the formation of a superoxo η²-O₂ adduct in the triplet state. Oxygen interaction with the defect structures in the triplet state might lead to superoxo complexes in the open shell singlet (OSS) electronic configuration. In both cases, consequent intramolecular ET yields closed-shell η²-O₂ peroxo complexes.

Scheme 3 Schematic representation of oxygen interactions with metals of various electronic states.

Depending on the spin state, oxygen coordination to 1_red2e features various kinds of interaction, from weak bonding (quintet) to superoxo (triplet) and peroxo (singlet), Chart 2 and Fig. S12 (ESI‡).³² For some superoxo complexes, we succeeded in locating spin symmetry-broken solutions. Calculations show that the OSS states are lower in energy and correspond to somewhat stronger O₂ activation than the triplet state.

The calculated reaction profiles for the oxidation reaction of 1_red2e are shown in Fig. 3. In contrast to 1_red1e, water coordination does not promote defect formation in these complexes, or only barely does so. Very similar to the case for the re-oxidation of 1_red1e, the two-competitive rate-limiting states in these systems are defect formation and barrier-less (spin allowed, Scheme 3) O₂ coordination with formation of the triplet superoxo η²-O₂ adduct. The next stage of the interaction, intramolecular ET resulting in a much more stable singlet peroxo η²-O₂ complex, could potentially have a finite barrier. However, for such transition metal systems, spin crossing probabilities were shown to be close enough to unity, so that they will not materially affect reaction rates.³³ The subsequent stages of the reaction are very similar to those for the re-oxidation of 1_red1e and involve intermolecular H-transfers from another 1_red2e species, resulting in dissociation of two water molecules and recovery of the intact Keggin structure. As in the case of 1e-reduced polyoxometalates, inspection of the reaction profiles in Fig. 3 shows that for Mo CUSs, oxygen coordination represents the highest energy state of the pathway. In contrast, for activation at vanadium, V CUS defect formation would appear to be the rate determining factor of the reaction while the following O₂ coordination proceeds with some energy gain in this case.

Fig. 3 Reaction profiles for the oxidation of H₇PV₂Mo₁₀O₄₀, 1_red2e.

Although, using the broken spin-symmetry approximation, we found the OSS η²-O₂ superoxo complexes to be more stable than their triplet isomers (vide infra), these reaction profiles are energetically less favourable because of the high energy of the previous stage of interaction, i.e. formation of the defect structure in the triplet state.

In order to bridge between the experimental and computational kinetic data, the energetic span model of Kozuch and co-workers can be applied.^34–36 This model is based on Eyring's transition state theory together with the concept of rate-determining states rather than rate-determining steps. In such a way, one can retrieve the computed activation energies for oxidation of different forms of 1_red on three coordinatively unsaturated sites, Table 4.

Table 4 Calculated apparent activation energies for the aerobic oxidation of different forms of 1_red

1red		ΔH^#298, kcal mol^−1	ΔS^#298, cal mol^−1 K^−1	ΔG^#298, kcal mol^−1
1red1e	Mo (1,2)	14.6	−27.2	22.7
	Mo(1,11)	10.2	−33.1	20.0
	V (1,2)	24.5	7.4	22.3
1red2e	Mo (1,2)	13.8	−27.6	22.0
	Mo(1,11)	11.5	−28.2	19.9
	V (1,2)	19.3	2.2	18.6

---

The following conclusions could be drawn from the comparison of experimental and computational data presented in this work.

(i) The experimental results showed that the oxidations with O₂ of both the one- and two-electron reduced polyoxometalates are first-order in 1_red and O₂ with entropy-driven kinetics. The intermediate species shown in Chart 2 found by computation supported an inner sphere mechanism of these oxidation reactions with oxygen coordination as a rate determining state. Together, inspection of the reaction profiles for oxidation of 1_red and kinetic parameters collected in Table 4 show that the stationary points defining the overall apparent activation barrier for Mo CUSs are always the energies of the superoxo complexes. In accordance with the experimental results, these reactions are entropy-driven. The rate-limiting state for oxygen activation on V is clearly enthalpy-driven CUS formation. This reaction pathway is higher in energy than that on the Mo CUS for 1_red1e and thus is not expected to be experimentally observed for 1e-reduced polyoxometalates. For 1_red2e, both reaction pathways are energetically comparable; however, Mo CUSs are more common than V CUSs in H₅PV₂Mo₁₀O₄₀ (only two out of five isomers have V atoms in adjoining positions, and even in these cases there are 7 V–O–Mo bonds per each V–O–V bond). Thus, we expect that depending on the relative number of isomers and on the reaction temperature, the kinetics of the Mo CUS or V CUS driven reaction profiles could be observed in the experiments.

(ii) It is notable that theoretically O₂ activation by 1_red1e is slightly preferred for the (1,11) isomer compared to the (1,2) isomer. In fact, in an EPR experiment where one can differentiate between 1_red1e species with vicinal and distal vanadium atoms,^10,11 we found that the species associated with distal isomers, e.g. the (1,11) isomer, were oxidized faster than the species associated with vicinal vanadium atoms.

(iii) Since the reduction of O₂ to H₂O is a four-electron process, additional intermolecular electron transfer and proton transfer steps are needed to split the O–O bond and form water after initial interaction of O₂ with the reduced polyoxometalate. The fact that the reaction is first-order in the polyoxometalate and O₂, together with the calculated energies of the intermediate hydrogen transfer reactions, clearly indicates that these latter reactions are fast relative to the O₂ activation step.

(iv) For 1_red2e, the experimental and computed kinetic parameters (ΔG^#, ΔH^# and ΔS^#) are similar and also very similar to those found for 1_red1e. The slight difference in the experimentally found ΔG^# explains the faster rate constant found for 1_red2e, but this is not so obvious from the calculated data.

Experimental

Preparation of the reduced polyoxometalate

The oxidized plenary Keggin compound, H₅PV₂Mo₁₀O₄₀, 1_ox, was prepared using the published method.³⁷ One- or two-electron reduced forms were prepared in organic solvents by reduction with H₂ using a 10% Pt/C catalyst or with organic substrates. The degree of reduction was spectrophotometrically verified at 750 nm by titration with m-chloroperbenzoic acid and verified also by oxidation using a standardized solution of Br₂ as oxidant. The reduced polyoxometalate was stored under argon. Precise values for the extinction coefficient ε of the one- or two-electron reduced polyoxometalates were determined by titration with m-chloroperbenzoic acid. Using this method, for 1_red1e an extinction coefficient of ε₇₅₀ = 1.1 + 0.2 × 10³ M⁻¹ cm⁻¹ was found and for 1_red2e, ε₇₅₀ = 2.2 + 0.3 × 10³ M⁻¹ cm⁻¹.

Kinetics measurements

Reactions of reduced 1_red with O₂ were carried out in various organic solvents. Known amounts of 1_red were treated with a solution saturated with pure O₂, air or O₂/Ar mixtures in spectrophotometric cuvettes. Measurements were carried out on an Agilent 8453 diode array spectrometer equipped with a temperature controller nominally accurate to 0.1 °C. Changes in absorption with time at various concentrations and temperatures were observed at 750 nm. The initial rates were derived from these absorption versus time data when plots were linear (about 10% conversion). The solubility of O₂ in air-equilibrated CH₃CN is 1.6 mM or 8.1 mM in O₂ saturated CH₃CN at 25 °C.^38,39

Cyclic voltammetry

Measurements were carried out at 25 °C under an argon atmosphere using an EC-Lab VCP-201 electrochemical workstation (BioLogic Science Instruments). A standard three-electrode electrochemical cell was employed with a glassy carbon disk (surface area 0.071 cm²) as the working electrode, a platinum wire as the counter electrode, and Ag wire as the reference electrode. The scan rate used was 100 mV s⁻¹. Potentials measured versus Ag/Ag⁺ were converted to the Fc/Fc⁺ (Fc = ferrocene) scale by analysis of cyclic voltammetry of ferrocene in acetonitrile under same conditions (0.1 M Bu₄NClO₄ 50 mM trifluoroacetic acid) in acetonitrile.

Computational methods

All computations were done using a locally modified version of the Gaussian 09 package.⁴⁰ Geometry optimizations and harmonic frequency evaluations were performed using the nonempirical GGA density functional^41,42 PBE⁴³ in conjunction with the PC1 basis set. The latter is a combination of Jensen's polarization consistent pc-1 basis set^44–46 for the main group elements and V and the Stuttgart–Dresden–Dolg (SDD) basis set-RECP (relativistic energy-consistent pseudopotential) combination⁴⁷ for molybdenum; to the latter, a single f-type polarization function was added, the exponent being the geometric average of the two f-exponents given by Martin and Sundermann.⁴⁸ This combination is of double-ζ plus polarization quality. In order to speed up the calculations, we applied the density fitting (DF) approximation^49–51 for calculating the two-electron (Coulomb) integrals. This approximation is known to speed up pure-DFT calculations on large systems by 1–2 orders of magnitude. The auxiliary basis sets required for this were generated by the automatic algorithm as implemented in Gaussian 09. Thus, geometries of all the complexes were optimized at the PBE-DF/PC1 level of theory without symmetry constraints. Subsequently, single-point calculations at the optimized geometries were performed using the empirical hybrid meta-GGA functional M06⁵² combined with the same basis set (M06/PC1), as well as using the PBE functional but combined with a larger AUG-PC1 basis set. The AUG-PC1 basis set represents a combination of the aug-pc-1 basis set on the main group elements and vanadium^{44–46,53,54} and the SDD basis set with added f basis functions on molybdenum. The final level of theory applied in the present work is thus the additivity approximation E_e[M06/AUG-PC1] ≈ E[PBE-DF/AUG-PC1] − E[PBE-DF/PC1] + E[M06/PC1].

Bulk solvent effects of the acetonitrile medium have been calculated at the M06/PC1 level via the self-consistent reaction field (SCRF) method,⁵⁵ using the continuum solvation model COSMO as implemented in Gaussian 09.^56,57 Dispersion interactions within the computed structures are partially accounted for in the M06 functional. Adding the D3 empirical dispersion correction term,^58,59 further improved the energies by considering long interactions. No D3(BJ) parameters for M06 are available from the Grimme group;⁶⁰ as we optimized parameters for many additional functionals in the framework of a large benchmark project for noncovalent interactions,⁶¹ we found the D3(BJ) optimization for M06 to be divergent.

Oxygen is a triplet in its ground state while oxidized products usually have a closed-shell electronic configuration. Therefore, reactions of molecular oxygen often involve a step of intersystem crossing. Thus, we considered doublet and quartet states for 1e-reduced complexes and closed- and open-shell singlet, triplet and quintet states for 2e-reduced complexes. Spin contamination was negligible for all wave functions except for open-shell singlets, for which the broken-symmetry wave functions were contaminated by triplet state with 〈S²〉 close to 1. In this case the energy was corrected using the sum method of Cramer and Ziegler⁶² according to the equation

where E_S+T is the energy of the broken symmetry unrestricted DFT wave function for the optimized geometry; E_T is the energy of the triplet state with the same geometry; and 〈S²〉 is the value obtained in the calculations.

The calculations were performed for two isomers, (1,2) with adjacent vanadium atoms and (1,11) with the most distant vanadium atoms. If not stated otherwise, the energetic results present Gibbs free energy in acetonitrile at 298 K and relate to the (1,2) isomer. Presented enthalpy values involve the same corrections as ΔG, i.e. correction for AUG-PC1, Grimme's dispersion correction D3 for M06 functional and solvation correction.

Conclusions

This combined experiment and computational study provides, for the first time, important insights into the oxidation by O₂ of one- and two-electron reduced H₅PV₂Mo₁₀O₄₀ species, which is one of the key steps in many aerobic catalytic cycles.^7–9 The experimental kinetic studies show that the reactions are first-order in both the polyoxometalate and O₂, where the rate constants are somewhat higher for the two-electron reduced species. Solvents have a considerable effect, protic solvents being preferred over aprotic solvents—presumably the protons are aiding in the formation of coordinatively unsaturated sites (CUSs). Reduction of H₅PV₂Mo₁₀O₄₀ by an ET (H₂) or ET–OT (Ph₃P) reaction showed similar reoxidation kinetics (rate constants and activation parameters). The entropy of activation is strongly negative, indicating a significant reorganization energy in the transition state because two species interact to form one species. DFT calculations and experiments carried out on the re-oxidation reactions suggest an inner-sphere process for O₂ activation in contrast with what was observed with the isostructural tungstates.^15–17 The reaction pathways proceed by the formation of a CUS, and then the binding of O₂, to form a superoxo η²-O₂ adduct. After formation of this superoxo η²-O₂ adduct, additional inter- and intra-molecular ET and CPET steps lead to O–O bond cleavage and formation of H₂O. Most interestingly, although vanadium is the reactive redox centre for oxidation of substrates (reducing agents) and a necessary component for the oxidative activity of H₅PV₂Mo₁₀O₄₀—and a CUS can be formed at both Mo and V sites—O₂ coordination occurs at the Mo CUSs, preferably those where the vanadium centres are distal to each other. This may be at least a partial explanation of the unique activity of H₅PV₂Mo₁₀O₄₀, as opposed to monomeric or oligomeric vanadates, such as decavanadate where V(IV) species are inert to oxidation with O₂.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Israel Science Foundation Grants 763/14 and 1358/15, the Israel Ministry of Science and Technology, and the Lise Meitner Centre for Computational Quantum Chemistry. The authors would like to thank Mr Nitai Sylvetsky for assistance with editing the manuscript.

Notes and references

1. S. S. Stahl, Angew. Chem., Int. Ed., 2004, 43, 3400–3420.
2. I. V. Kozhevnikov, Catalysis by Polyoxometalates, Wiley, Chichester, England, 2002.
3. C. L. Hill and C. M. Prosser-McCartha, Coord. Chem. Rev., 1995, 143, 407–455.
4. T. Okuhara, N. Mizuno and M. Misono, Adv. Catal., 1996, 41, 113–252.
5. I. A. Weinstock, R. E. Schreiber and R. Neumann, Chem. Rev., 2018 DOI:10.1021/acs.chemrev.7b00444.
6. S.-S. Wang and G.-Y. Yang, Chem. Rev., 2015, 115, 4893–4962.
7. R. Neumann and A. M. Khenkin, Chem. Commun., 2006, 2529–2538.
8. R. Neumann, Inorg. Chem., 2010, 49, 3594–3601.
9. R. Neumann, Adv. Inorg. Chem., 2017, 69, 67–90.
10. H. Goldberg, I. Kaminker, D. Goldfarb and R. Neumann, Inorg. Chem., 2009, 48, 7947–7952.
11. I. Kaminker, H. Goldberg, R. Neumann and D. Goldfarb, Chem. – Eur. J., 2010, 16, 10014–10020.
12. I. Efremenko and R. Neumann, J. Am. Chem. Soc., 2012, 134, 20669–20680.
13. B. B. Sarma, R. Carmieli, A. Collauto, I. Efremenko, J. M. L. Martin and R. Neumann, ACS Catal., 2016, 6, 6403–6407.
14. D. Barats, G. Leitus, R. Popovitz-Biro, L. J. W. Shimon and R. Neumann, Angew. Chem., Int. Ed., 2008, 47, 9908–9912.
15. Y. V. Geletii, C. L. Hill, R. H. Atalla and I. A. Weinstock, J. Am. Chem. Soc., 2006, 128, 17033–17042.
16. O. Snir, Y. Wang, M. E. Tuckerman, Y. V. Geletii and I. A. Weinstock, J. Am. Chem. Soc., 2010, 132, 11678–11691.
17. O. Snir, Y. Wang and I. A. Weinstock, Isr. J. Chem., 2011, 51, 247–259.
18. M. Sadakane and E. Steckhan, Chem. Rev., 1998, 98, 219–237.
19. R. Neumann and M. Levin, J. Am. Chem. Soc., 1992, 114, 7278–7286.
20. C. D. Duncan and C. L. Hill, J. Am. Chem. Soc., 1997, 119, 243–244.
21. J. H. Grate, J. Mol. Catal., 1996, 114, 93–101.
22. E. G. Zhizhina, V. F. Odyakov, M. V. Simonova and K. I. Matveev, Kinet. Catal., 2005, 46, 354–363.
23. S. Sahu and D. P. Goldberg, J. Am. Chem. Soc., 2016, 138, 11410–11428.
24. S. Hong, Y. Lee, K. Ray and W. Nam, Coord. Chem. Rev., 2017, 334, 25–42.
25. P. M. Wood, Biochem. J., 1988, 253, 287–289.
26. S. Hammes-Schiffer, Acc. Chem. Res., 2001, 34, 273–281.
27. S. P. Neville, O. M. Kirkby, N. Kaltsoyannis, G. A. Worth and H. H. Fielding, Nat. Commun., 2016, 7, 11357.
28. G. G. Hammes, Thermodynamics and Kinetics for the Biological Sciences, John Wiley & Sons, Inc., USA and Canada, 2000.
29. C. Song and J. Zhang, PEM Fuel Cell Electrocatalysts and Catalyst Layers, Springer-Verlag, London, 2008, p. 88.
30. M. Setvin, U. Aschauer, J. Hulva, T. Simschitz, B. Daniel, M. Schmid, A. Selloni and U. Diebold, J. Am. Chem. Soc., 2016, 138, 9565–9571.
31. A. F. Cozzolino, D. Tofan, C. C. Cummins, M. Temprado, T. D. Palluccio, E. V. Rybak-Akimova, S. Majumdar, X. Cai, B. Captain and C. D. Hoff, J. Am. Chem. Soc., 2012, 134, 18249–18252.
32. P. L. Holland, Dalton Trans., 2010, 39, 5415–5425.
33. R. Poli and J. M. Harvey, Chem. Soc. Rev., 2003, 32, 1–8.
34. S. Kozuch and S. Shaik, J. Am. Chem. Soc., 2006, 128, 3355–3365.
35. S. Kozuch and J. M. L. Martin, ChemPhysChem, 2011, 12, 1413–1418.
36. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
37. G. A. Tsigdinos and C. J. Hallada, Inorg. Chem., 1968, 7, 437–441.
38. D. T. Sawyer, A. Sobkowiak and L. L. Roberts Jr., Electrochemistry for Chemists, Wiley, New York, 2nd edn, 1995, p. 505.
39. Q. Li, C. Batchelor-McAuley, N. C. Lawrence, R. S. Hartshorne and R. G. Compton, J. Electroanal. Chem., 2013, 688, 328–335.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Rev. E01, Gaussian, Inc., Wallingford, CT, 2012, http://www.gaussian.com.
41. W. Kohn and L. J. Sham, Phys. Rev. [Sect.] A, 1965, 140, 1133–1138.
42. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1970, p. 230.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 . Erratum, Phys. Rev. Lett., 1997, 78, 1396.
44. F. Jensen, J. Chem. Phys., 2001, 115, 9113–9125.
45. F. Jensen, J. Chem. Phys., 2002, 116, 7372–7379.
46. F. Jensen, J. Chem. Phys., 2013, 138, 014107.
47. M. Dolg, in Modern Methods and Algorithms of Quantum Chemistry, ed. J. Grotendorst, Jülich, 2000, vol. 1, pp. 479–508.
48. J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408–3420.
49. B. I. Dunlap, J. Chem. Phys., 1983, 78, 3140–3142.
50. B. I. Dunlap, THEOCHEM, 2000, 529, 37–40.
51. A. B. Nadykto, H. Dua and F. Yu, Vib. Spectrosc., 2007, 44, 286–296.
52. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
53. F. Jensen, J. Chem. Phys., 2002, 117, 9234–9240.
54. F. Jensen, J. Chem. Phys., 2003, 118, 2459–2463.
55. M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54.
56. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
57. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 112, 1995–2001.
58. S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104.
59. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
60. S. Grimme, DFTD3 website, viahttp://www.thch.uni-bonn.de.
61. B. Brauer, M. K. Kesharwani, S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2016, 18, 20905–20925.
62. W. T. G. Johnson, M. B. Sullivan and C. J. Cramer, Int. J. Quantum Chem., 2001, 85, 492–508.

---

Footnotes

† JMLM is the Baroness Thatcher Professor of Chemistry. RN is the Rebecca and Israel Sieff Professor of Organic Chemistry.

‡ Electronic supplementary information (ESI) available: Additional experimental kinetic data and computational data. See DOI: 10.1039/c7cp08610e

---