Open Access Article
Open Access ArticleStructure–composition trends in multicomponent borosilicate-based glasses deduced from molecular dynamics simulations with improved B–O and P–O force fields†
Baltzar
Stevensson
 ,
Yang
Yu
,
Yang
Yu
 and
Mattias
Edén
and
Mattias
Edén
 *
*
Physical Chemistry Division, Department of Materials and Environmental Chemistry, Stockholm University, SE-106 91 Stockholm, Sweden. E-mail: mattias.eden@mmk.su.se
First published on 7th February 2018
Abstract
We present a comprehensive molecular dynamics (MD) simulation study of composition–structure trends in a set of 25 glasses of widely spanning compositions from the following four systems of increasing complexity: Na2O–B2O3, Na2O–B2O3–SiO2, Na2O–CaO–SiO2–P2O5, and Na2O–CaO–B2O3–SiO2–P2O5. The simulations involved new B–O and P–O potential parameters developed within the polarizable shell-model framework, thereby combining the beneficial features of an overall high accuracy and excellent transferability among different glass systems and compositions: this was confirmed by the good accordance with experimental data on the relative BO3/BO4 populations in borate and boro(phospho)silicate networks, as well as with the orthophosphate fractions in bioactive (boro)phosphosilicate glasses, which is believed to strongly influence their bone-bonding properties. The bearing of the simulated melt-cooling rate on the borate/phosphate speciations is discussed. Each local {BO3, BO4, SiO4, PO4} coordination environment remained independent of the precise set of co-existing network formers, while all trends observed in bond-lengths/angles mainly reflected the glass-network polymerization, i.e., the relative amounts of bridging oxygen (BO) and non-bridging oxygen (NBO) species. The structural roles of the Na+/Ca2+ cations were also probed, targeting their local coordination environments and their relative preferences to associate with the various borate, silicate, and phosphate moieties. We evaluate and discuss the common classification of alkali/alkaline-earth metal ions as charge-compensators of either BO4 tetrahedra or NBO anions in borosilicate glasses, also encompassing the less explored NBO-rich regime: the Na+/Ca2+ cations mainly associate with BO/NBO species of SiO4/BO3 groups, with significant relative Na–BO4 contacts only observed in B-rich glass networks devoid of NBO species, whereas NBO-rich glass networks also reveal substantial amounts of NBO-bearing BO4 tetrahedra.
1 Introduction
Underlying the exploitation of glass for numerous purposes—ranging from everyday products to advanced industrial applications—is the well-controlled tuning of the desirable physical and chemical properties often attainable by a straightforward variation of the oxide precursor contents. This tailoring is greatly assisted by a detailed insight into the underlying composition–structure relations dictating the targeted glass properties. Yet, the amorphous nature yields distributions of the experimental observables, which limits the experimental probing and thereby also the structural insight, notably so at the medium-range scale (0.3–1 nm). The limited detailed structural understanding hampers a rational glass design for establishing composition–property trends, usually necessitating empirical “trial-and-error” procedures.Here we consider oxide-based glasses involving at least one of the network formers B, Si, and P, which encompass all primary formers but Al, thereby accounting for large groups of glasses of importance to chemistry, physics, as well as to materials and earth Sciences. The glass network-forming species are interlinked by covalent –O– bridges.1,2 The oxygen speciation is dominated either by such bridging oxygen (BO) atoms or by non-bridging oxygen (NBO) ions, which coordinate two (O[2]) and one (O[1]) network formers, respectively. The most frequent cation coordination number is four, as commonly adopted by B (BO4; B[4] coordination) and exclusively by Si (SiO4) and P (PO4).1,2 However, the small B atom often forms triangular BO3 groups (B[3] coordinations), as for instance encountered in vitreous B2O3.1–3
Electropositive cations (e.g., Na+ and Ca2+) are often referred to as glass-network modifiers, because they depolymerize the networks by arranging BO → NBO conversions.1,2 The modifiers mainly balance the negative charges of NBO ions and other anionic species, such as [BO4]− and phosphate groups present in B and P bearing glasses; notably, a commonly adopted (albeit simplified) structural description of borate/borosilicate glasses assumes that the M+/M2+ cations act predominantly either as NBO-associated “modifiers” or as “compensators” of the [BO4]− tetrahedra, as most frequently discussed for Na2O–B2O3–SiO2 glasses.4–10 Herein, we examine the relevance of this rather categorical classification in various B-based glass systems, also targeting the less investigated scenario of NBO-rich networks.
Concerning the experimentally derived structural insight from glasses involving B, Si, and/or P as network formers, diffraction techniques offer average cation–oxygen distances and bond-angle distributions (BADs),11–18 while spectroscopic methods—particularly magic-angle spinning (MAS) nuclear magnetic resonance (NMR)—provide accurate relative populations of the BO3 and BO4 coordinations (denoted by x[3]B and x[4]B, respectively) in B-bearing glasses.2,4–8,19–33 In phosphosilicate-based glasses, the distributions of co-existing {QnP} and {QnSi} tetrahedra with varying number n of BO atoms at the respective PO4 and SiO4 tetrahedra are often attainable by 31P/29Si MAS NMR,2,30,32–36 whereas 17O NMR informs about the BO/NBO speciation in oxide glasses.2,21,22,37,38 Solid-state NMR may also unveil the medium-range glass structure, such as providing connectivities/proximities and spatial distributions among the various network formers,2,28,31,39–44 but sophisticated and time-consuming experimentation is required that remains sparsely exploited for multicomponent glasses as compared with routine 11B/29Si/31P MAS NMR applications.
Given the limited accessible experimental data on several structural features of glasses, atomistic molecular dynamics (MD) simulations offer an alternative probing up to the nanometer scale,10,34,36,42–62 where a complete set of structural parameters is available from one sole glass model. Yet, the predictive power of classical MD simulations depends critically on the precise choice of force fields to model the local cation–oxygen interactions, which ultimately also control the medium-range organization of atoms. For instance, the temperature dependent BO3 ⇄ BO4 equilibrium in melts shifts to the right during melt-cooling, thereby elevating the BO4 content in the glass structure relative to the melt;8–10,23,24,26 this feature coupled with a strong composition dependence of the borate speciation compromises the accuracy of modeled {BO3, BO4} populations in B-bearing glasses. These problems were mitigated by invoking glass-composition dependent B–O potential parameters,52–54 however at the expense of system-dependent force fields with limited transferability.
Force fields accounting for polarization effects are known to enhance the modeling of both short and medium range structures of B2O3, encompassing boroxol-ring formation46,63–65 and the presence of BO4 groups at extreme pressures.66 However, thus far only two such force-field options exist for B-based multicomponent glasses.10,44 Here we present the derivation and assessments of new B–O and P–O pair-potentials utilized by us in a recent structural report on borophosphosilicate (BPS) glasses.44 They were developed within the polarizable shell-model potential introduced by Sanders et al.45 for the modeling of SiO2, which was subsequently extended to Na2O–CaO–SiO2–P2O5 glasses.55–57 The shell model employs full formal cation charges, which facilitates its implementation in widely spanning classes of multicomponent glasses. The high predictive abilities of our proposed force fields are demonstrated by validations on crystalline B/P-bearing structures (see the ESI†), as well as by the structural probing of glasses from the Na2O–B2O3, Na2O–B2O3–SiO2, Na2O–CaO–SiO2–P2O5, and Na2O–CaO–B2O3–SiO2–P2O5 systems.
Phosphorus participates only to a limited extent in the Na2O–CaO–(B2O3)–SiO2–P2O5 glass networks targeted herein that belong to the group of bioactive glasses (BGs) with applications to bone grafting and tissue engineering.67,68 Their bone-bonding properties correlate qualitatively with the extent of hydroxyapatite [Ca5(PO4)3OH] mineralization observed in vitro, which is believed to mainly depend on the amount of ortho-phosphate (Q0P) anions in the glass along with its silicate network connectivity;69–73 the latter is denoted by ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO and represents the average number of BO atoms per SiO4 tetrahedron.73 Silicate-based BGs manifest comparatively fragmented glass networks conforming to 2.0 ≤
SiBO and represents the average number of BO atoms per SiO4 tetrahedron.73 Silicate-based BGs manifest comparatively fragmented glass networks conforming to 2.0 ≤ ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO ≤ 2.6,73 while featuring sufficient amounts of Na+/Ca2+ cations to (potentially) charge-balance all phosphate species as Q0P moieties. Notwithstanding that 31P MAS NMR confirms that Q0P tetrahedra dominate the phosphate speciations (>85%), there are also non-negligible contributions from Q1P groups (signifying one P–O–Si bridge36,39–42,56,57), whereas higher-polymerization QnP (n ≥ 2) species are essentially absent.36,41 Unfortunately, all force fields utilized thus far in classical MD simulations of BGs give relatively poor predictions of the {QnP} populations, where the orthophosphate fraction is consistently underestimated relative to experiments,34,36,42 even when employing the likely best P–O potential available.57 Here we demonstrate that refinement of those parameters significantly improves the MD-derived {QnP} speciations in phosphosilicate glass models throughout the composition range relevant for BGs.
SiBO ≤ 2.6,73 while featuring sufficient amounts of Na+/Ca2+ cations to (potentially) charge-balance all phosphate species as Q0P moieties. Notwithstanding that 31P MAS NMR confirms that Q0P tetrahedra dominate the phosphate speciations (>85%), there are also non-negligible contributions from Q1P groups (signifying one P–O–Si bridge36,39–42,56,57), whereas higher-polymerization QnP (n ≥ 2) species are essentially absent.36,41 Unfortunately, all force fields utilized thus far in classical MD simulations of BGs give relatively poor predictions of the {QnP} populations, where the orthophosphate fraction is consistently underestimated relative to experiments,34,36,42 even when employing the likely best P–O potential available.57 Here we demonstrate that refinement of those parameters significantly improves the MD-derived {QnP} speciations in phosphosilicate glass models throughout the composition range relevant for BGs.
This article is organized as follows: Section 2 introduces the glass systems/samples and common notation, while the MD simulation procedures and force-field developments are described in Section 3. Sections 4 and 5 contrast the MD-derived borate and phosphate speciations, respectively, against experimental results, including their dependence on the choice of melt-cooling rate in the simulation. Section 6 discusses the local coordination environments of the network formers F = {B[3], B[4], Si, P}, including the F–O distances and intra/interpolyhedral bond angles, as well as the relative propensities for F–NBO associations. Section 7 discusses the structural roles of the Na+/Ca2+ cations, encompassing their local coordination environments and their relative preferences to associate with the various NBO-bearing silicate, borate, and phosphate moieties, with a particular focus on quantifying the extents of “modifier/compensator” roles from a wider perspective than that normally adopted. Section 8 summarizes the main findings of our study.
2 Glass samples
Table 1 compiles our set of 25 modeled glasses, encompassing members from the Na2O–B2O3 (NB), Na2O–B2O3–SiO2 (NBS), Na2O–CaO–SiO2–P2O5 (NCPS), and Na2O–CaO–B2O3–SiO2–P2O5 (NCBPS) systems, where each capital letter in the acronyms specifies the respective element of the glass-network modifier {Na, Ca} or former {B, P, Si}. We reserve the symbol “x” for fractions; for instance, the molar fraction of element E and oxide “EO” is denoted by xE and x(EO), respectively. All NC(B)PS glass members considered herein were prepared and characterized in our previous work.30,36,43,44 The borate/borosilicate glass compositions and their accompanying experimental data were obtained from the literature, as specified in Table 1 and Table S1 (ESI†).| Glass | Oxide equivalents (mol%) | BO4 fractionc | Na/Ca parametersd | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Na2O | CaO | B2O3 | SiO2 | P2O5 | x NBO | x [4]B(MD) | x [4]B(NMR) | ε (%) | Ref. |
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Na
Na
|
![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Ca
Ca
|
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Na–O) (pm) (Na–O) (pm) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Ca–O) (pm) (Ca–O) (pm) |
x(Na–O[1]) | x(Ca–O[1]) | |
a Glass compositions modeled by atomistic MD simulations, with the sample notation described in Section 2 and details about the MD simulations provided in Table S1 (ESI). The NCPS and NCBPS glass compositions were taken from Mathew et al.36,43 and Yu et al.,30,44 respectively, while the NBS compositions were adapted from ref. 5, 8 and 21–23.
b MD-derived NBO (O[1]) fraction out of all O species, with the remaining constituting BO: xNBO + xBO = 1.
c Fractional population x[4]B of B[4] coordinations obtained either by MD simulations or by 11B NMR from the as-indicated literature source. The relative {B[3], B[4]} populations {x[3]B, x[4]B} obey x[3]B + x[4]B = 1. ε is the (signed) relative deviation between the modeled and experimental results: 100{x[4]B(MD) − x[4]B(NMR)}/x[4]B(NMR).
d Average coordination number (![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) M), average M–O distance [ M), average M–O distance [![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (M–O)], and fraction of O[1] species [x(M–O[1])] present in the ensemble of {MOp} polyhedra for M = {Na, Ca}. Note that x(M–O[1]) + x(M–O[2]) = 1.
e The data listed in the upper and lower rows were obtained from slow and fast melt quenching, respectively.
f The NCPS[2.54] base composition was used to design the NCBPS(f) glass series by progressive SiO2 → B2O3 replacements.30,44
g Typical data uncertainties, estimated as the root-mean-square (rms) deviation from the average parameter value. The uncertainty of the NMR-derived x[4]B data is that reported by Yu et al.,44 which may be taken as representative also for the NB/NBS glasses (in the absence of stated data uncertainties in many of these reports).
h Based on the simulation/experimental uncertainties. (M–O)], and fraction of O[1] species [x(M–O[1])] present in the ensemble of {MOp} polyhedra for M = {Na, Ca}. Note that x(M–O[1]) + x(M–O[2]) = 1.
e The data listed in the upper and lower rows were obtained from slow and fast melt quenching, respectively.
f The NCPS[2.54] base composition was used to design the NCBPS(f) glass series by progressive SiO2 → B2O3 replacements.30,44
g Typical data uncertainties, estimated as the root-mean-square (rms) deviation from the average parameter value. The uncertainty of the NMR-derived x[4]B data is that reported by Yu et al.,44 which may be taken as representative also for the NB/NBS glasses (in the absence of stated data uncertainties in many of these reports).
h Based on the simulation/experimental uncertainties.
|
||||||||||||||||
| NB0.11 | 10.0 | 90.0 | 0.000 | 0.118 | 0.116 | 1.7 | 4 | 7.30 | 258.9 | 0.00 | ||||||
| NB0.20 | 17.0 | 83.0 | 0.000 | 0.214 | 0.225 | −4.9 | 4 | 7.23 | 258.8 | 0.00 | ||||||
| NB0.25 | 20.0 | 80.0 | 0.007 | 0.331 | 0.320 | 3.4 | 27 | 6.99 | 258.7 | 0.02 | ||||||
| NB0.50 | 33.3 | 66.7 | 0.050 | 0.420 | 0.430 | −2.3 | 4 | 6.91 | 257.6 | 0.09 | ||||||
| NB0.67 | 40.0 | 60.0 | 0.139 | 0.420 | 0.438 | −4.1 | 33 | 6.56 | 255.9 | 0.22 | ||||||
| NB1.00 | 50.0 | 50.0 | 0.337 | 0.331 | 6.14 | 253.3 | 0.45 | |||||||||
| NB1.30 | 56.5 | 43.5 | 0.495 | 0.238 | 6.00 | 252.0 | 0.60 | |||||||||
| NBS2–0.25(33) | 7.7 | 30.8 | 61.5 | 0.005 | 0.240 | 0.230 | 4.3 | 28 | 6.21 | 259.1 | 0.02 | |||||
| NBS2–0.50(33) | 14.3 | 28.6 | 57.1 | 0.020 | 0.433 | 0.450 | −3.8 | 4 | 6.42 | 258.5 | 0.06 | |||||
| NBS2–0.75(33) | 20.0 | 26.7 | 53.3 | 0.050 | 0.563 | 0.581 | −3.1 | 21 | 6.54 | 258.3 | 0.12 | |||||
| NBS2–2.50(33) | 45.4 | 18.2 | 36.4 | 0.445 | 0.385 | 0.350 | 10.0 | 5 | 5.78 | 251.8 | 0.61 | |||||
| NBS0.5–0.50(67) | 25.0 | 50.0 | 25.0 | 0.033 | 0.435 | 0.420 | 3.6 | 19 | 6.83 | 258.4 | 0.07 | |||||
| NBS5.10–1.31(16) | 17.7 | 13.5 | 68.8 | 0.097 | 0.615 | 0.830 | −25.9 | 8 | 6.04 | 256.9 | 0.24 | |||||
| NBS4–4.00(20) | 44.5 | 11.0 | 44.5 | 0.484 | 0.367 | 0.380 | −3.4 | 23 | 5.63 | 251.1 | 0.66 | |||||
| 0.330 | 11.2 | |||||||||||||||
| NCBPS(0)f | 24.1 | 23.3 | 48.6 | 4.0 | 0.625 | 5.84 | 5.91 | 252.1 | 246.2 | 0.74 | 0.91 | |||||
| NCBPS(10) | 24.1 | 23.3 | 4.9 | 43.7 | 4.0 | 0.584 | 0.403 | 0.388 | 3.9 | 30 | 5.95 | 6.03 | 252.4 | 247.1 | 0.70 | 0.87 |
| NCBPS(20) | 24.1 | 23.3 | 9.7 | 38.9 | 4.0 | 0.546 | 0.392 | 0.424 | −7.5 | 30 | 6.09 | 6.16 | 253.0 | 248.4 | 0.65 | 0.84 |
| NCBPS(30) | 24.1 | 23.3 | 14.6 | 34.0 | 4.0 | 0.504 | 0.431 | 0.432 | −0.2 | 30 | 6.24 | 6.19 | 253.7 | 248.7 | 0.60 | 0.80 |
| NCBPS(50) | 24.1 | 23.3 | 24.3 | 24.3 | 4.0 | 0.438 | 0.420 | 0.433 | −3.0 | 30 | 6.37 | 6.43 | 254.2 | 251.0 | 0.52 | 0.73 |
| NCBPS(80) | 24.1 | 23.3 | 38.9 | 9.7 | 4.0 | 0.348 | 0.419 | 0.419 | 0.0 | 44 | 6.61 | 6.64 | 255.5 | 253.1 | 0.40 | 0.63 |
| NCPS[2.11] | 24.6 | 26.7 | 46.1 | 2.6 | 0.688 | 5.87 | 5.96 | 251.6 | 246.1 | 0.77 | 0.91 | |||||
| NCPS[2.30] | 24.2 | 26.4 | 45.4 | 4.0 | 0.677 | 5.94 | 6.00 | 251.8 | 246.6 | 0.77 | 0.91 | |||||
| NCPS[2.54]f | 24.1 | 23.3 | 48.6 | 4.0 | 0.625 | 5.84 | 5.91 | 252.1 | 246.2 | 0.74 | 0.91 | |||||
| NCPS[2.74] | 20.2 | 22.2 | 55.0 | 2.6 | 0.544 | 5.82 | 5.85 | 252.9 | 246.4 | 0.67 | 0.88 | |||||
| NCPS[2.93] | 17.9 | 23.3 | 54.8 | 4.0 | 0.529 | 5.89 | 5.94 | 253.3 | 247.4 | 0.67 | 0.88 | |||||
| σ | 0.001 | 0.007 | 0.01 | 2.0h | 44 | 0.02 | 0.02 | 0.1 | 0.2 | 0.01 | 0.01 | |||||
The nomenclature of the Na-based borate [NBR] and borosilicate [NBSK–R(f)] glass members adopts the composition parametrization RNa2O–B2O3–KSiO2 of Yun–Dell–Bray–Xiao (YDBX)4,5 with R = x(Na2O)/x(B2O3) and K = x(SiO2)/x(B2O3). The YDBX structural model for borate/borosilicate glasses is introduced briefly in Section 4, with details provided in ref. 4 and 5. The NBR series invokes an increasing Na2O content (R) at K = 0. To sample a reasonably wide composition range with a small number of glasses, the NBS set encompasses 4 compositions with K = 2 and increasing R, together with 3 glasses of distinct {K, R} pairs.
The NCPS[![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO] phosphosilicate glasses are labelled by their silicate network connectivity (
SiBO] phosphosilicate glasses are labelled by their silicate network connectivity (![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO), owing to its direct relevance for the bioactivity.69,70,73 The NCBPS glass series was designed from the NCPS[2.54] base glass by replacing SiO2 by B2O3 at unaltered Na2O and CaO contents and a fixed sum x(SiO2) + x(B2O3).30,44 Consequently, the NCPS[2.54] and NCBPS(0) compositions are identical. To assist comparisons between the borosilicate and BPS compositions, the value f in each NCBPS(f) and NBK-R(f) label represents the percentage of B2O3 out of the total B2O3 and SiO2 contents: f = 100x(B2O3)/[x(SiO2) + x(B2O3)]. Note that besides comprising Ca, most NC(B)PS glass networks are markedly more fragmented than their NB(S) counterparts, as encoded by the NBO fraction out of the total O speciation in the structure: xNBO = xNBO/(xNBO + xBO), where xNBO + xBO = 1.
SiBO), owing to its direct relevance for the bioactivity.69,70,73 The NCBPS glass series was designed from the NCPS[2.54] base glass by replacing SiO2 by B2O3 at unaltered Na2O and CaO contents and a fixed sum x(SiO2) + x(B2O3).30,44 Consequently, the NCPS[2.54] and NCBPS(0) compositions are identical. To assist comparisons between the borosilicate and BPS compositions, the value f in each NCBPS(f) and NBK-R(f) label represents the percentage of B2O3 out of the total B2O3 and SiO2 contents: f = 100x(B2O3)/[x(SiO2) + x(B2O3)]. Note that besides comprising Ca, most NC(B)PS glass networks are markedly more fragmented than their NB(S) counterparts, as encoded by the NBO fraction out of the total O speciation in the structure: xNBO = xNBO/(xNBO + xBO), where xNBO + xBO = 1.
3 Computational methods and force-field developments
3.1 Molecular dynamics simulations
All glass models were generated by atomistic MD simulations using the DLPOLY4.08 program,74,75 utilizing NVT ensembles in a cubic box with periodic boundary conditions, with the box size and the number of atoms selected to match the experimental glass composition and density. The borate and borosilicate glass models comprised ≈3500 atoms, whereas the P-doped NC(B)PS counterparts involved 6000–7000 atoms to ensure sufficient statistics of their minor P speciations (≤4 mol% P2O5). Here we only provide the common simulation procedures and parameters (which were also employed for the force-field developments); the details are given in Table S1 (ESI†).Each melt-quench protocol started from a random atom configuration that was equilibrated for 100 ps at 3500 K, whereupon the temperature was reduced by 100 K every 10 ps (10 K ps−1 nominal cooling rate) to 300 K. Then followed another equilibration for 200 ps, from which the last 150 ps were averaged to yield the structural data. This procedure was completed 2–4 times (with different initial atom configurations for each glass composition), from which the average value and uncertainty of each reported structural parameter were derived. The equations of motion were integrated in steps of 0.2 fs using the velocity Verlet integrator, while the temperature was controlled using a gentle stochastic thermostat with a 1.0 ps time constant and a Langevin friction constant of 1.0 ps−1. These simulation conditions (e.g., system sizes and equilibration stages) provide well-converged and reliable structural parameters,36,58 whereas the effects from the choice of cooling rate are examined in Sections 4.1 and 5.3.
All computations utilized a polarizable shell-model potential,45,55,57 where each cation carries its full formal charge,45 but the O2− species are represented by core (OC) and shell (OS) portions with charges zC = +0.8482e and zS = −2.8482e, respectively (zC + zS = −2), and corresponding masses mC = 15.7994u and mS = 0.2000u, where e is the elementary charge and “u” is the atomic mass unit. The core–shell units are connected by a harmonic potential with the force constant 74.92 eV Å−2.45 The interaction energy of two atom/ion species α and β at a distance rαβ was parametrized by the following extended Buckingham potential,
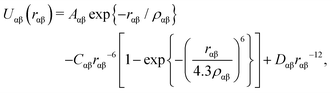 | (1) |
| α–β | Pair potentiala | Ref. | |||
|---|---|---|---|---|---|
| A αβ (keV) | ρ αβ (Å) | C αβ (eV Å6) | D αβ (eV Å12) | ||
a The pair potential involves a modified Buckingham term; see eqn (1). Full formal charges were employed for all cations, whereas the O2− ions are represented by core (OC) and shell (OS) parts.
b These parameters were first utilized in our recent report on BPS glass structures.44
c The three-body potential is represented by a truncated harmonic function 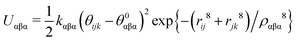 , which was used in our recent work36,42,43 and involves a modified functional of that reported by Tilocca et al.57 It was evaluated out to r = 250 pm.75 , which was used in our recent work36,42,43 and involves a modified functional of that reported by Tilocca et al.57 It was evaluated out to r = 250 pm.75
|
|||||
| Na–OS | 56.465 | 0.1939 | 0 | 0 | 55 |
| Ca–OS | 2.152 | 0.3092 | 0.099 | 0 | 55 |
| Si–OS | 1.284 | 0.3205 | 10.662 | 0 | 45 |
| B–OS | 0.472 | 0.3350 | 0 | 5.4 | 44 |
| P–OS | 1.750 | 0.2900 | 0 | 0 | 44 |
| OS–OS | 22.764 | 0.1490 | 27.880 | 0 | 45 |
| OC–OS | 0 | 0 | 0 | 0.1 | 36 |
The average coordination number of E (![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) E) corresponds to the (mean) number of O atoms in its first coordination shell; it was determined by integrating the pair distribution function [PDF; gE–O(r)] out to its first minimum,47 which throughout all models corresponded to cutoff radii of 205 pm for {B, Si, P} and 312 pm for {Na, Ca}. Noteworthily, a minor variation (±20 pm) around each of these “most suitable” cutoff radii had insignificant bearing on the resulting
E) corresponds to the (mean) number of O atoms in its first coordination shell; it was determined by integrating the pair distribution function [PDF; gE–O(r)] out to its first minimum,47 which throughout all models corresponded to cutoff radii of 205 pm for {B, Si, P} and 312 pm for {Na, Ca}. Noteworthily, a minor variation (±20 pm) around each of these “most suitable” cutoff radii had insignificant bearing on the resulting ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) E value. Note that as opposed to the “most probable E–O distance” obtained from the maximum of the PDF, we report the average E–O distance (“bond length”) throughout, denoted by
E value. Note that as opposed to the “most probable E–O distance” obtained from the maximum of the PDF, we report the average E–O distance (“bond length”) throughout, denoted by ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (E–O).
(E–O).
3.2 P–O force field optimizations
The new P–O parameters resulted by empirically refining those of Tilocca57 to reduce the discrepancies of the MD-generated fractional populations {xnP} of the {QnP} species relative to experiments, while preserving the already accurate modeling of local structural features of the PO4 tetrahedron.As explained in Section 5, the MD-generated BO-bearing phosphate population x1P is consistently overestimated at the expense of x0P. The P–NBO affinity may be increased by reducing the “softness” parameter ρ in eqn (1), which in practice was accomplished by locating the {A, ρ} pair that maximized x0P in models of the NCPS[2.93] glass. The {A, ρ} values of Table 2 resulted from a mesh of ρ-values, with the accompanying parameter A obtained from the constraint of keeping the modeled P–O[1] bond-length ≈154 pm for all {A, ρ} pairs. Further evaluations of NC(B)PS glasses verified a global improvement of the modeled {xnP} data, regardless of the precise glass composition and/or network polymerization degree (Section 5).
3.3 B–O force field optimizations
As opposed to the P–O parameters that resulted by adjusting those of ref. 57, the B–O parameters were developed from scratch. This is to our knowledge the first B–O interatomic potential option developed within the shell-model framework. Notably, the Si–O and P–O potentials invoke three-body terms (see Table 2) for preserving the tetrahedral geometry,45,57,75 whereas the B–O force field should operate in their absence to permit conversions between triangular and tetrahedral geometries for an accurate modeling of the borate speciation. An increase (decrease) of the “softness” parameter ρ promotes a larger relative BO4 (BO3) population.To avoid unrealistically short B–O (or more precisely B–OS) distances from shell model MD simulations of the small and “soft” B atom, it was necessary to invoke a non-zero repulsive parameter (D) together with the {A, ρ, C} entities in eqn (1). After verifying that the parameter C had insignificant bearing on the simulation outcomes, we proceeded with C ≡ 0. Each value of the {A, ρ, D} triplet was deduced sequentially by the following three-step protocol:
(1) A {ρ, D} grid was generated over the ranges 0.2 ≤ ρ ≤ 0.4 and 0 ≤ D ≤ 20. For each {ρ, D} pair, the parameter A was obtained by energy minimizations on crystalline borates (B2O3; CaB2O4; NaBO2; Na3CaB4O10), whose structures feature different {x[3]B, x[4]B} contributions. These optimizations were performed with the GULP program76 and the procedure outlined in the ESI,† except that all lattice parameters were fixed in the present calculations, while the atom positions were allowed to vary freely in the presence of the force fields.
(2) For each value of ρ, D was selected from the {A, ρ, D} triplet that minimized the energy in stage (1).
(3) The remaining parameter ρ was subsequently deduced from MD-generated models of the NCBPS(50) glass to best match its NMR-derived {x[3]B, x[4]B} fractions (Table 1).
Further assessments on B-bearing crystalline phases (see the ESI†) and glasses (Section 4) confirmed that the as-obtained B–O force field offers accurate borate speciations, thereby evidencing a very good transferability among different glass systems and compositions.
4 Borate speciations in multicomponent glasses
Here we evaluate the predictive power of the new B–O potential to quantitatively reproduce the fractional populations {x[3]B, x[4]B} of {BO3, BO4} groups in models of B-bearing glasses of increasing complexity from the Na2O–B2O3, Na2O–B2O3–SiO2, and Na2O–CaO–B2O3–SiO2–P2O5 systems (see Table 1). Note that x[4]B is often denoted as “N4” in the literature. Fig. 1 plots the x[4]B results obtained either by MD simulations or by 11B MAS NMR experiments against the parameter R.4,5 The NMR data were reproduced from various sources (see the caption of Fig. 1), with each value closest to the respective simulation outcome indicated by a red circle.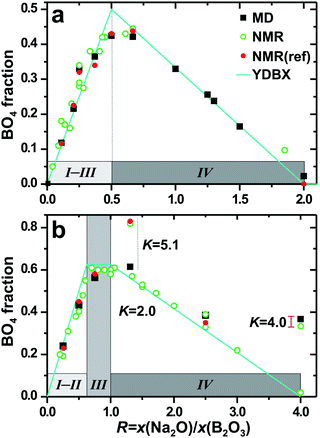 | ||
| Fig. 1 Fractional populations (x[4]B) of BO4 groups obtained either by MD simulations (squares) or by NMR experiments (circles) and plotted against R = x(Na2O)/x(B2O3) for (a) Na2O–B2O3 and (b) Na2O–B2O3–SiO2 glasses. The cyan solid lines represent x[4]B data predicted by the Yun–Dell–Bray–Xiao model, whereas the gray rectangles indicate its associated regions “I–IV”.4,5 The NBS glasses involve distinct values of K = x(SiO2)/x(B2O3), as identified in (b), whereas all NB glasses correspond to K = 0. The experimental data were selected from various literature sources; for borates: ref. 4, 27, 29, 33, 38, and 81; for borosilicates: ref. 4–6, 8, 20–23, 28, and 32. Several independent literature reports are available for some glass compositions: each solid circle marks the most representative NMR-derived value [“NMR(ref)”], which is compared with the MD-generated data in Table 1. The red bar associated with the NBS4–4(20) glass depicts the range of NMR-derived BO4 fractions obtained from glasses prepared with distinct melt-cooling rates.23 Here and elsewhere: data uncertainties within/around the symbol sizes are not displayed. | ||
For increasing Na2O content of the NB/NBS glass, Fig. 1 reproduces the well-known trend of an initial BO3 → BO4 conversion up to the R-value for which x[4]B is maximized, x[4]B(max) = Rmax, which according to the YDBX model occurs at Rmax = 0.5 and Rmax = (K/8 + 1)/2 for the NB and NBS systems, respectively.4,5 In Fig. 1, the YDBX predictions are depicted by lines in cyan color. Note that the relative BO4 population grows concurrently with the SiO2 content of the borosilicate glass, encoded by the parameter K = x(SiO2)/x(B2O3), and that x[4]B(max) is consistently higher than the corresponding borate analog (K = 0).4,5 When the Na2O content (R) of an NB glass is increased further, BO4 groups progressively convert into NBO-bearing BO3 moieties (Fig. 1a), which marks the onset of NBO formation.4,5 In contrast, x[4]B remains close to x[4]B(max) throughout “region III” of the NBS system (Fig. 1b): according to the YDBX model, only Si–NBO contacts exist in structures conforming to region III, while both SiO4 and BO3 groups (but not BO4) accommodate NBO species in regime IV.4,5 While the MD-generated xNBO values of Table 1 accord overall well with the YDBX prediction (not shown), minor NBO populations occur already for R < Rmax in both NB and NBS glasses, as also reported previously.10,19,20,37,51–53
Fig. 1 and Table 1 evidence an excellent accordance between the modeled and NMR-derived borate speciations, with the respective x[4]B values typically agreeing within the experimental/modeled data uncertainties, and well within the spread of NMR estimates originating from distinct studies of a given glass composition; see Fig. 1. Across all 18 B-based glasses compared (also encompassing the NCBPS system) in Table 1, the modeled BO4 fraction typically reproduces the experimental counterpart within 95%. The largest discrepancies of the simulated x[4]B data generally result for the Si-richest NBS/NCBPS glasses (f ≲ 20%), with the NBS5.10–1.31(16) glass model featuring the globally largest relative difference (26%). The borate speciations of the NCBPS glasses were evaluated further in ref. 44 for an expanded glass ensemble.
We conclude that despite non-negligible discrepancies of the {x[3]B, x[4]B} values relative to experiments observed for a few Si-rich NBS/NCBPS glasses (f ≲ 20%), our B–O potential provides overall excellent predictions of the {BO3, BO4} speciations in both borate and boro(phospho)silicate glasses over wide composition ranges: the predictive power typically matches that observed from system-dedicated force fields involving glass-composition dependent B–O potential parameters to enhance the performance.51–54 The present force field also appears to provide at least as accurate predictions as that recently introduced by Pacaud et al. for NBS glasses,10 which also involves constant B–O parameters that consider polarization effects. Assessments of five Na2O–B2O3–SiO2 glasses with variable compositions10 (yet across a narrower span than the present NBS glasses) revealed a 0–26% spread of relative deviations between the simulated and NMR-derived BO4 populations, with average and median deviations of 11% and 8.5%, respectively.10
4.1 Cooling-rate trends
The temperature-dependent borate speciation of the melt induces a strong relationship between the cooling-rate and the {x[3]B, x[4]B} fractions of the resulting glass structure,9,10,23,24,26 particularly considering the ∼10 orders of magnitude more rapid simulated quenching relative to the experimental glass production. To gauge the melt-cooling behavior for our present simulation conditions and B–O potential, we performed calculations with variable quench rates (q) for the NBS2–0.25(33), NBS2–0.75(33), and NCBPS(30) glasses, whose {x[4]B} results are shown in Fig. 2. The precise cooling-rate responses are clearly composition-dependent, but all glasses manifest a general trend of elevated BO4 populations for decreasing q, as expected.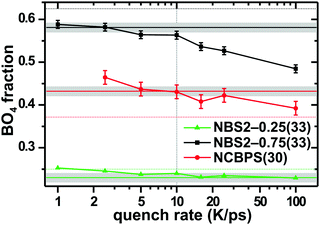 | ||
| Fig. 2 Cooling-rate (q) dependence of the MD-generated relative BO4 fraction for the as-indicated NBS and NCBPS glasses. The vertical line marks the rate q = 10 K ps−1 employed in all other simulations and corresponding to the {x[4]B} data listed in Table 1. Each of the three solid horizontal lines marks the NMR-derived experimental value, with the corresponding grey area indicating the experimental uncertainty (±σ), whereas the dotted horizontal lines show the predictions from the YDBX model.4,5 | ||
The NBS2–0.75 composition reveals the largest variation between the highest cooling rate (100 K ps−1) and that of 10 K ps−1 utilized in all other simulations herein. Yet, when q is decreased further, the x[4]B value converges to the experimental result within its ±σ uncertainty (Fig. 2). Moreover, it is gratifying that the BO4 population of the NBS2–0.25 counterpart remains close to the experimental value throughout the entire evaluated range 1 ≤ q/(K ps−1) ≤ 100. The NCBPS(30) composition reveals an intermediate behavior of a seemingly continuous decrease of the BO4 population when the cooling rate varies from 2 K ps−1 to 100 K ps−1, while the B-richer NCBPS(50) composition manifests much lower variations (see Fig. S1, ESI†).
Notwithstanding the composition-dependent effects, we conclude that usage of q = 10 K ps−1—for which the B–O potential parameters were also optimized—combines reasonable computation times with accurately modeled borate speciations.
5 Phosphate speciations in (boro)phosphosilicate glasses
5.1 Bioactive phosphosilicate glasses
Given the beneficial properties of phosphate incorporation into Na2O–CaO–SiO2 glasses for their in vitro apatite formation,71–73,77 assessments of composition–structure–bioactivity trends by MD modeling require accurate predictions of the {QnP} speciation over the network-connectivity span 2.0 ≲![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO ≲ 3.0 and particularly for glasses across the range 2.1 ≤
SiBO ≲ 3.0 and particularly for glasses across the range 2.1 ≤ ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO ≤ 2.6 with ≤6 mol% P2O5 that is relevant for all attainable bioactive glass compositions.73 For this regime, the Q0P fractional population (x0P) decreases for increasing glass network polymerization, but is independent of its P content.36 However, current force fields used in classical MD simulations cannot accurately reproduce the markedly stronger propensity for P–NBO contacts relative to Si–NBO: this leads to overestimated Q1P (and Q2P) populations at the expense of the orthophosphate counterpart that is experimentally evidenced to dominate the phosphate speciations in all NCPS glasses with sufficiently large Na+/Ca2+ reservoirs for balancing all negative charges of the Q0P tetrahedra.36
SiBO ≤ 2.6 with ≤6 mol% P2O5 that is relevant for all attainable bioactive glass compositions.73 For this regime, the Q0P fractional population (x0P) decreases for increasing glass network polymerization, but is independent of its P content.36 However, current force fields used in classical MD simulations cannot accurately reproduce the markedly stronger propensity for P–NBO contacts relative to Si–NBO: this leads to overestimated Q1P (and Q2P) populations at the expense of the orthophosphate counterpart that is experimentally evidenced to dominate the phosphate speciations in all NCPS glasses with sufficiently large Na+/Ca2+ reservoirs for balancing all negative charges of the Q0P tetrahedra.36
For glasses with variable silicate network connectivities, Fig. 3a contrasts the orthophosphate fraction predicted from MD simulations with that estimated by 31P MAS NMR in ref. 36. We first consider the widely studied BG composition 24.6Na2O–26.7CaO–46.1SiO2–2.6P2O5 of Hench, “45S5”,67 which features ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO = 2.11 and an NMR-derived phosphate speciation comprising 96 ± 1% of Q0P groups, while Q1P accounts for the remaining, i.e., {x0P, x1P} = {0.96, 0.04}.36 MD simulations with the new P–O force field offer an excellent prediction (x0P = 0.93 ± 0.015; circle in Fig. 3a), which translates into a 3% relative discrepancy, which is almost within ±σ of the experimental/simulation data uncertainties (and well within ±2σ). In contrast, a markedly larger deviation (11%) resulted when using the P–O parameters of ref. 57 in an otherwise identical computation (x0P = 0.85 ± 0.015; solid triangle in Fig. 3a). These values may be contrasted with other shell-model MD simulations of the 45S5 glass utilizing the P–O force field of ref. 57 and a melt-cooling rate of 10 K ps−1, yielding x0P values of 0.65 (ref. 57), 0.73 (ref. 34), 0.80 (ref. 61), and 0.82 (ref. 62), while calculations employing rigid-ion potentials generally give markedly worse estimates of x0P ≈ 0.5.59,62 The relatively large spread in simulation outcomes when using the same P–O force-field parameters partially stems from system-size variations, where x0P < 0.80 generally resulted from (too) small ensembles comprising <2000 atoms in the simulation box. However, other subtle factors may also contribute, as discussed below.
SiBO = 2.11 and an NMR-derived phosphate speciation comprising 96 ± 1% of Q0P groups, while Q1P accounts for the remaining, i.e., {x0P, x1P} = {0.96, 0.04}.36 MD simulations with the new P–O force field offer an excellent prediction (x0P = 0.93 ± 0.015; circle in Fig. 3a), which translates into a 3% relative discrepancy, which is almost within ±σ of the experimental/simulation data uncertainties (and well within ±2σ). In contrast, a markedly larger deviation (11%) resulted when using the P–O parameters of ref. 57 in an otherwise identical computation (x0P = 0.85 ± 0.015; solid triangle in Fig. 3a). These values may be contrasted with other shell-model MD simulations of the 45S5 glass utilizing the P–O force field of ref. 57 and a melt-cooling rate of 10 K ps−1, yielding x0P values of 0.65 (ref. 57), 0.73 (ref. 34), 0.80 (ref. 61), and 0.82 (ref. 62), while calculations employing rigid-ion potentials generally give markedly worse estimates of x0P ≈ 0.5.59,62 The relatively large spread in simulation outcomes when using the same P–O force-field parameters partially stems from system-size variations, where x0P < 0.80 generally resulted from (too) small ensembles comprising <2000 atoms in the simulation box. However, other subtle factors may also contribute, as discussed below.
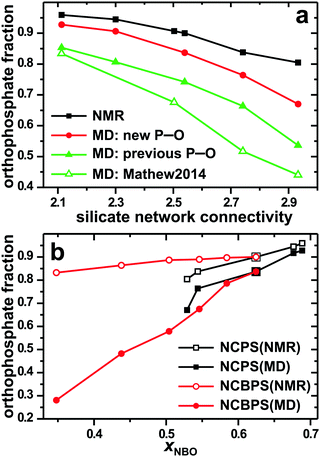 | ||
Fig. 3 Orthophosphate fractions obtained by MD simulations or NMR experiments30,44 for Na2O–CaO–SiO2–P2O5 glasses with variable network condensation degrees; the data are plotted against the (a) silicate network connectivity (![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO), or the (b) NBO fraction out of all O species (xNBO). The plot in (b) also includes the results from the NCBPS glasses (reproduced from ref. 44). All modeled data in (b), as well as those labeled “new P–O” in (a), resulted from the P–O force field herein. The data with solid/open triangles were obtained by employing the P–O potential parameters of ref. 57 with otherwise identical simulation conditions (solid triangles; “previous P–O”), or with the conditions of Mathew et al.36 (open triangles). The experimental and simulation uncertainties are σ ≈ 0.01 and σ ≈ 0.025, respectively. Except for the (new) data on NCPS[2.30], the experimental results from the NCPS and NCBPS glasses were reproduced from Mathew et al.36 and Yu et al.,30,44 respectively. SiBO), or the (b) NBO fraction out of all O species (xNBO). The plot in (b) also includes the results from the NCBPS glasses (reproduced from ref. 44). All modeled data in (b), as well as those labeled “new P–O” in (a), resulted from the P–O force field herein. The data with solid/open triangles were obtained by employing the P–O potential parameters of ref. 57 with otherwise identical simulation conditions (solid triangles; “previous P–O”), or with the conditions of Mathew et al.36 (open triangles). The experimental and simulation uncertainties are σ ≈ 0.01 and σ ≈ 0.025, respectively. Except for the (new) data on NCPS[2.30], the experimental results from the NCPS and NCBPS glasses were reproduced from Mathew et al.36 and Yu et al.,30,44 respectively. | ||
For increasing silicate network connectivity, Fig. 3a reveals progressively larger deviations between the modeled and experimental {QnP} speciations that implies substantial discrepancies for the most condensed NCPS glass networks with ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO ≥ 2.7. Yet, it is gratifying that significantly better predictions result with the new P–O potential throughout the
SiBO ≥ 2.7. Yet, it is gratifying that significantly better predictions result with the new P–O potential throughout the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO-range considered in Fig. 3a. For the NCPS[2.93] glass with an experimental orthophosphate fraction of 0.81, MD-derived counterparts of 0.54 and 0.67 were observed with the “previous”57 and new P–O force fields, respectively, which correspond to relative deviations of 33% and 17% to the experiment and an error reduction by ≈50% for the new force field.
SiBO-range considered in Fig. 3a. For the NCPS[2.93] glass with an experimental orthophosphate fraction of 0.81, MD-derived counterparts of 0.54 and 0.67 were observed with the “previous”57 and new P–O force fields, respectively, which correspond to relative deviations of 33% and 17% to the experiment and an error reduction by ≈50% for the new force field.
For sufficiently large atom (≳5000) ensembles and melt-cooling rates ≲10 K ps−1, the converged simulation outcome would be expected to depend predominantly on the choice of force-field parameters. However, other factors may also affect the results, as illustrated by the two data-sets represented by solid/open triangles in Fig. 3a: both were obtained using the same P–O potential parameters (see ref. 57), where the {x0P} results shown by solid triangles employed identical simulation conditions as those described in Section 3.1, while the obviously different data set labeled “Mathew2014” was obtained under identical conditions,36 except for employing a Berendsen thermostat and an older version (3.10.0) of the DLPOLY program. Further evaluations (not shown) suggested that the distinct DLPOLY versions accounted for most of the large discrepancies between the two data sets, which are far outside of the statistical uncertainties, and almost as large as between the “new” and “previous”57 P–O force fields in Fig. 3a.
5.2 Borophosphosilicate glasses
The significant formation of QnP moieties with n > 0 in the glass models stems from difficulties of P–O force fields to reproduce the very strong P–NBO affinity in dense phosphosilicate networks (i.e., with low NBO contents) at practically accessible melt-cooling rates of ≳1 K ps−1. This is illustrated by Fig. 3b, which plots the orthophosphate population against the NBO fraction of Na2O–CaO–(B2O3)–SiO2–P2O5 glasses. The equimolar B2O3-for-SiO2 substitution in the NCBPS glass design (Section 2) is accompanied by a significant network condensation for increasing B2O3 content toward the limiting Na2O–CaO–B2O3–P2O5 composition,44 because the number of network-forming atoms doubles (1Si → 2B) while the corresponding number of O atoms only grows by 1.5 (2O → 3O).For the most fragmented glass networks associated with xNBO ≳ 0.55, Fig. 3b manifests modest deviations between the experimental and modeled x0P values, as well as similar results between the NCPS and NCBPS glasses. However, as the NCBPS networks repolymerize (i.e., xNBO is decreased), the modeled Q0P populations diminish markedly, while the experimental counterparts alter marginally. The comparatively larger discrepancies between the NMR/MD-derived {x0P} data observed for the NCBPS glasses relative to their NCPS counterparts for xNBO ≈ 0.55 are attributed to the additional competition for NBO accommodation from a third network former (boron), which accentuates the underestimation of the P–NBO contacts; see ref. 44 and Section 6.1.
We conclude that relative to previous options, our new P–O force field greatly improves the modeled phosphate populations across the ranges 2.0 ≤ ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO ≤ 2.9 and x(P2O5) ≤ 0.06 that encompass the entire region of the Na2O–CaO–SiO2–P2O5 system relevant for rationalizing structure–composition–bioactivity trends. Yet, despite that the force field also offers substantial improvements for NCBPS glasses, non-negligible deviations between experiments and modeled {xnP} data remain that reflect limitations of (current) pair-potentials in classical MD simulations to accurately model the relative affinities among distinct glass-network formers to accommodate the BO/NBO species.
SiBO ≤ 2.9 and x(P2O5) ≤ 0.06 that encompass the entire region of the Na2O–CaO–SiO2–P2O5 system relevant for rationalizing structure–composition–bioactivity trends. Yet, despite that the force field also offers substantial improvements for NCBPS glasses, non-negligible deviations between experiments and modeled {xnP} data remain that reflect limitations of (current) pair-potentials in classical MD simulations to accurately model the relative affinities among distinct glass-network formers to accommodate the BO/NBO species.
5.3 Cooling-rate trends
Analogous with the cooling-rate dependence of the borate speciation, the underestimated Q0P populations observed in MD simulations stem partially from the orders-of-magnitude faster melt quenching necessitated in the calculations compared with the most rapid cooling attainable experimentally. Tilocca58 examined the dependence of the modeled {QnP} speciation of the 45S5 glass composition on the quench rate by using the P–O potential parameters of ref. 57, inferring that a limiting/converged value of x0P ≈ 0.10 is expected for quench-rates ≲2 K ps−1. Notably, this is more than twice that (x0P = 0.04) of the hitherto sole experimental (non-zero) estimate36 (note that ref. 58 involved comparisons with the experimental result x0P = 0.08 reported from a Na-free 45S5 analog40). The results herein demonstrate that MD-derived phosphate speciations closer to experiments are available by instead improving the P–O interatomic potential parameters while keeping the more attractive melt-cooling rate ≈10 K ps−1 that allows for much faster computations.We evaluated variable quench-rate MD simulations for the more difficult NCBPS scenario, where the improved P–O force field still yields markedly underestimated Q0P populations. Fig. S1 (ESI†) reveals the strongest increase in the orthophosphate fraction when the quench-rate is reduced from 100 K ps−1 to 16 K ps−1. The growth of x0P proceeds in the regime 2.5 ≤ q/(K ps−1) ≤ 16, but to a lower extent, suggesting that modest improvements are expected for the prohibitively time-consuming simulations associated with q < 1 K ps−1.
6 Local environments of the network formers
6.1 NBO distribution among network formers
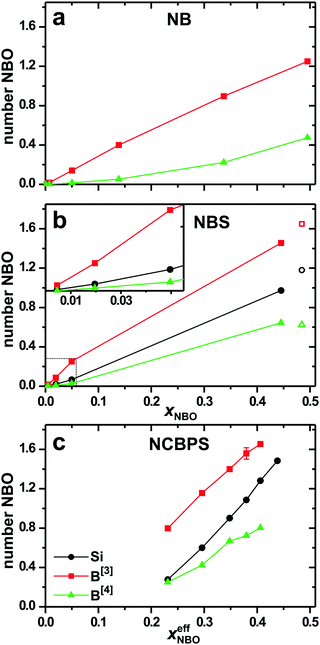
Yu et al.44 discussed the relative affinity of each network former {B[3], B[4], Si, P} to coordinate NBO in NCBPS glasses, mainly concluding that the propensity for NBO-accommodation decreases along the series P[4] ≫ B[3] > Si > B[4]. Here we examine these NBO-partitioning trends among the network formers further by also considering glasses from the NB and NBS systems, none of which comprise P, whose very substantial NBO affinity (with an average of 3.0–3.8 NBO ions per tetrahedron) consumes ≈30% of the entire NBO reservoir in the NCBPS glasses even at the modest amount of 4 mol% P2O5.44Fig. 4 plots the average number of NBO ions accommodated by each F = {B[3], B[4], Si} species against xNBO, in the NCBPS scenario employing the NBO fraction effectively available for B and Si (xeffNBO), i.e., after subtracting the P-associated NBO portion. The previously concluded relative NBO affinities among the various network formers44 also hold in the less complex NB and NBS systems: notwithstanding that only three O positions are available at the BO3 triangles, their NBO accommodation is higher than that of SiO4 throughout all glass compositions, including regions “I–III” (see Section 4), which is at odds with the YDBX prediction.4,5 Yet, similar observations were made in previous modeling studies of NBS glasses,10,51–53 also concerning the (unexpected) presence of B[4]–NBO contacts.10,51 Indeed, Fig. 4 reveals an average number of 0.25–0.8 NBO ions at the BO4 tetrahedra in the NCBPS networks, but also non-negligible B[4]–NBO contacts in the NB(S) glasses with 0.3 < xNBO < 0.5, in contrast with their assumed (near) absence in “conventional” borosilicate glass models5,25,78 across the xNBO range considered herein.
When compared at similar NBO contents, there is an overall increase in the number of NBO ions at each F species when progressing along the NB → NBS → NCBPS glass systems (even when disregarding the NBO consumption by P in the NCBPS models). Typically, an NBS/NCBPS glass network with xSi/xB ≈ 1 and xNBO ≈ 0.5 comprises primarily BO3 groups with 1 and 2 NBO ions, comparable amounts of BO4 tetrahedra with 0 and 1 NBO ions, while Q3Si groups constitute ≈50% of the silicate speciation, together with similar Q4Si and Q2Si populations.
6.2 F–O distances
Fig. 5(a, b) shows representative pair distribution functions associated with each network former F = {B[3], B[4], Si, P} in NB, NBS, NCPS, and NCBPS glasses with comparable network polymerization (xNBO ≈ 0.5). Since both NBO (O[1]) and BO (O[2]) species are present in the glass networks, each PDF shown in the top panel of Fig. 5 has contributions from the F–O[1] and F–O[2] component plotted in the mid/bottom panels, with the average F–O distance,![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O), being the weighted average over the two
(F–O), being the weighted average over the two ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[1]) and
(F–O[1]) and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[2]) components, according to the BO/NBO distribution in the first coordination sphere of F.
(F–O[2]) components, according to the BO/NBO distribution in the first coordination sphere of F.
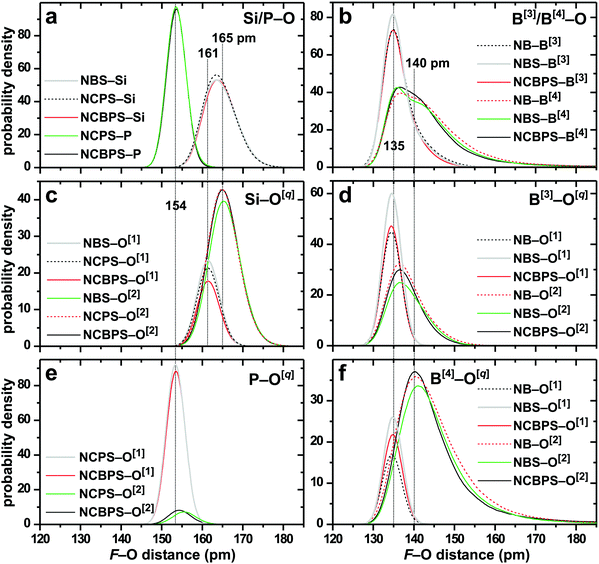 | ||
| Fig. 5 MD-derived pair distribution functions (PDFs) involving O and each network-former F = {B[3], B[4], Si, P} in the NB1.3, NBS2–2.5(33), NCPS[2.93], and NCBPS(30) glasses (see legends), which were selected to yield comparable NBO fractions xNBO = {0.50, 0.45, 0.53, 0.50}. The PDFs involve the (a, b) total F–O distributions, as well as the (c–f) underlying F–O[1] and F–O[2] component distributions. Dotted vertical lines mark the various PDF maxima, specified by the distance in pm, while Table 3 lists the accompanying bond lengths. | ||
Owing to the high field-strength of each network-forming cation, it tightly controls its first coordination shell, which remains essentially unperturbed by the neighboring F sites. Indeed, provided that the BO/NBO speciation is constant (xNBO is fixed), each average distance ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O),
(F–O), ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[1]), and
(F–O[1]), and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[2]) is nearly identical for a given F = {P, Si, B[3], B[4]} species both across and among the glass systems; see Table 3. This is expected from the very similar PDF curves in Fig. 5. The average F–O[1] distance amounts to ≈154 pm for P, 161–162 pm for Si, while those of B[3] and B[4] are almost equal (≈134–135 pm). For each network former, the F–O[1] distance distribution is narrower and its associated bond-length is slightly shorter relative to the F–O[2] counterparts, with the typical
(F–O[2]) is nearly identical for a given F = {P, Si, B[3], B[4]} species both across and among the glass systems; see Table 3. This is expected from the very similar PDF curves in Fig. 5. The average F–O[1] distance amounts to ≈154 pm for P, 161–162 pm for Si, while those of B[3] and B[4] are almost equal (≈134–135 pm). For each network former, the F–O[1] distance distribution is narrower and its associated bond-length is slightly shorter relative to the F–O[2] counterparts, with the typical ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[2]) −
(F–O[2]) − ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[1]) difference being ≈1 pm for P, ≈4 pm for Si and B[3], but significantly larger for B[4] (10–12 pm). These trends match the sequence of decreasing cation field-strength [CFS; ion charge divided by
(F–O[1]) difference being ≈1 pm for P, ≈4 pm for Si and B[3], but significantly larger for B[4] (10–12 pm). These trends match the sequence of decreasing cation field-strength [CFS; ion charge divided by ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[q])2]: P > B[3] ≳ Si > B[4].
(F–O[q])2]: P > B[3] ≳ Si > B[4].
| Glass | x NBO | P–O | Si–O | B–O | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P–O | P–O[1] | P–O[2] | Si–O | Si–O[1] | Si–O[2] | B–O | B[3]–O | B[3]–O[1] | B[3]–O[2] | B[4]–O | B[4]–O[1] | B[4]–O[2] | ||
| a Average F–O[1] and F–O[2] distances in pm, as well as the F–O counterpart representative for all O species coordinated by each network former F = {P, Si, B[3], B[4]}. Each average distance was obtained by scanning over all FOp polyhedra in the glass model, only accounting for O species within 205 pm from F. b Typical data uncertainties, estimated as the rms deviation from the average parameter value. | ||||||||||||||
| NB0.11 | 0.000 | 136.1 | 134.9 | 134.9 | 142.6 | 142.6 | ||||||||
| NB0.20 | 0.000 | 137.1 | 135.1 | 135.1 | 142.6 | 142.6 | ||||||||
| NB0.25 | 0.007 | 138.4 | 135.4 | 133.9 | 135.4 | 142.9 | 134.1 | 142.9 | ||||||
| NB0.50 | 0.050 | 139.5 | 135.7 | 134.0 | 135.8 | 143.4 | 134.2 | 143.4 | ||||||
| NB0.67 | 0.139 | 139.9 | 136.1 | 134.2 | 136.4 | 143.9 | 134.5 | 144.0 | ||||||
| NB1.00 | 0.337 | 139.9 | 136.7 | 134.4 | 137.7 | 144.6 | 134.6 | 145.2 | ||||||
| NB1.30 | 0.495 | 139.6 | 137.0 | 134.6 | 138.7 | 145.7 | 134.7 | 147.2 | ||||||
| NBS2–0.25(33) | 0.005 | 163.3 | 159.6 | 163.3 | 136.8 | 134.5 | 133.6 | 134.5 | 142.3 | 142.3 | ||||
| NBS2–0.50(33) | 0.020 | 163.7 | 160.1 | 163.8 | 138.6 | 134.9 | 133.8 | 134.9 | 142.3 | 134.5 | 142.3 | |||
| NBS2–0.75(33) | 0.050 | 164.1 | 160.4 | 164.1 | 139.9 | 135.4 | 134.0 | 135.5 | 142.5 | 134.6 | 142.6 | |||
| NBS2–2.50(33) | 0.445 | 164.8 | 161.6 | 165.9 | 140.5 | 136.9 | 134.7 | 138.9 | 144.9 | 135.0 | 146.8 | |||
| NBS0.5–0.50(67) | 0.033 | 164.3 | 160.3 | 164.3 | 139.2 | 135.4 | 133.9 | 135.5 | 142.9 | 134.2 | 142.9 | |||
| NBS5.10–3.31(16) | 0.097 | 163.9 | 160.3 | 164.1 | 140.1 | 135.5 | 133.9 | 135.8 | 142.3 | 134.9 | 142.5 | |||
| NBS4–4.00(20) | 0.484 | 164.8 | 161.7 | 166.1 | 140.2 | 137.0 | 134.7 | 139.8 | 144.4 | 135.0 | 146.2 | |||
| NCBPS(0) | 0.625 | 153.7 | 153.6 | 155.6 | 164.7 | 162.1 | 166.2 | |||||||
| NCBPS(10) | 0.584 | 153.7 | 153.6 | 155.2 | 164.7 | 161.9 | 166.0 | 140.6 | 136.7 | 134.7 | 139.1 | 145.0 | 135.1 | 147.4 |
| NCBPS(20) | 0.546 | 153.7 | 153.6 | 154.8 | 164.7 | 161.7 | 165.8 | 140.6 | 136.7 | 134.6 | 138.9 | 145.1 | 135.0 | 147.3 |
| NCBPS(30) | 0.504 | 153.7 | 153.6 | 154.6 | 164.7 | 161.7 | 165.6 | 140.9 | 136.6 | 134.6 | 138.3 | 145.1 | 134.9 | 147.2 |
| NCBPS(50) | 0.438 | 153.7 | 153.6 | 154.6 | 164.8 | 161.4 | 165.4 | 140.6 | 136.6 | 134.4 | 137.9 | 144.7 | 134.8 | 145.9 |
| NCBPS(80) | 0.348 | 153.6 | 153.5 | 154.2 | 164.9 | 161.2 | 165.1 | 140.4 | 136.6 | 134.2 | 137.1 | 144.6 | 134.6 | 145.3 |
| NCPS[2.11] | 0.688 | 153.7 | 153.7 | 155.7 | 165.0 | 162.7 | 167.0 | |||||||
| NCPS[2.30] | 0.677 | 153.7 | 153.7 | 155.7 | 164.9 | 162.4 | 167.0 | |||||||
| NCPS[2.54] | 0.625 | 153.7 | 153.6 | 155.6 | 164.7 | 162.1 | 166.2 | |||||||
| NCPS[2.74] | 0.544 | 153.7 | 153.6 | 155.8 | 164.6 | 161.8 | 165.9 | |||||||
| NCPS[2.93] | 0.529 | 153.7 | 153.5 | 155.8 | 164.4 | 161.6 | 165.5 | |||||||
| σ | 0.001 | 0.02 | 0.02 | 0.2 | 0.03 | 0.06 | 0.04 | 0.07 | 0.03 | 0.03 | 0.07 | 0.08 | 0.08 | 0.1 |
We next consider the composition dependence of the F–O/O[1]/O[2] bond lengths across the set of models from each glass system. Regardless of the glass network composition, the highest-CFS P5+ cation manifests an essentially constant distance of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (P–O[1]) ≈ 153.6 pm and a very weakly varying P–O[2] mean distance spanning 155.0 ± 0.8 pm. The P–O bond-length of 153.7 pm accords well with the diffraction-derived counterpart (155 ± 2 pm) for the Q0P groups in the 45S5 BG.18 Somewhat larger (yet minor) variations are observed within the {
(P–O[1]) ≈ 153.6 pm and a very weakly varying P–O[2] mean distance spanning 155.0 ± 0.8 pm. The P–O bond-length of 153.7 pm accords well with the diffraction-derived counterpart (155 ± 2 pm) for the Q0P groups in the 45S5 BG.18 Somewhat larger (yet minor) variations are observed within the {![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[1])} and {
(F–O[1])} and {![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[2])} distance-sets for Si, B[3], and B[4] (that manifest the same trends): the precise BO/NBO speciation of the glass accounts for most variations,12,35,49,60 with both F–O[1] and F–O[2] distances increasing concurrently with xNBO (see Table 3).
(F–O[2])} distance-sets for Si, B[3], and B[4] (that manifest the same trends): the precise BO/NBO speciation of the glass accounts for most variations,12,35,49,60 with both F–O[1] and F–O[2] distances increasing concurrently with xNBO (see Table 3).
Table 3 reveals that the trend of increasing F–O[1]/O[2] bond lengths (for Si, B[3], and B[4]) offsets the expected shortening of the F–O counterpart for increasing xNBO (and accompanying larger contributions from the shorter F–O[1] distances): the bond-length merely either remains essentially constant or increases slightly, such as the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Si–O) lengthening observed across the NCPS series. Notably, diffraction studies have also observed a Si–O distance-lengthening for increasing xNBO.12,79 Whereas experimental reference data are sparse even for simple binary silicate/borate glasses, we conclude that our modeled Si–O distances (163–165 pm) are typically 2–3 pm longer than diffraction-derived results from SiO2, binary silicate glasses, and the 45S5 NCPS composition.11–14,18 Moreover, it is gratifying that the MD-derived B–O and B[3]–O bond-lengths of 139.5 pm and 135.7 pm match very well the experimental counterparts of 139.5 ± 1 pm and 137 ± 1 ppm for the NB0.50 glass composition,15 while a slightly larger deviation is observed between the modeled and experimental B[4]–O distances of 143.4 pm and 147 ± 1 ppm, respectively. Noteworthily, the results of Table 3 reveal for each glass composition a 7–8 pm longer B[4]–O average distance than B[3]–O, in good agreement with previous findings by experiments and MD simulations.10,15,53,54
(Si–O) lengthening observed across the NCPS series. Notably, diffraction studies have also observed a Si–O distance-lengthening for increasing xNBO.12,79 Whereas experimental reference data are sparse even for simple binary silicate/borate glasses, we conclude that our modeled Si–O distances (163–165 pm) are typically 2–3 pm longer than diffraction-derived results from SiO2, binary silicate glasses, and the 45S5 NCPS composition.11–14,18 Moreover, it is gratifying that the MD-derived B–O and B[3]–O bond-lengths of 139.5 pm and 135.7 pm match very well the experimental counterparts of 139.5 ± 1 pm and 137 ± 1 ppm for the NB0.50 glass composition,15 while a slightly larger deviation is observed between the modeled and experimental B[4]–O distances of 143.4 pm and 147 ± 1 ppm, respectively. Noteworthily, the results of Table 3 reveal for each glass composition a 7–8 pm longer B[4]–O average distance than B[3]–O, in good agreement with previous findings by experiments and MD simulations.10,15,53,54
For all non-negligible F–O[2]–F′ linkages, we also evaluated the average distances between the F–F′ species present in neighboring polyhedra, which tend to decrease in the following order:
| Si–Si(308–311) > Si–P(297–303) > B[4]–P(290–297) > Si–B[4](276–282) ≳ Si–B[3](275–278) > B[4]–B[4](251–258) ≈ B[3]–B[4](251–258) > B[3]–B[3](243–248), | (2) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F–O[2]) and
(F–O[2]) and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (F′–O[2]) components in Table 3.
(F′–O[2]) components in Table 3.
6.3 Bond-angle distributions
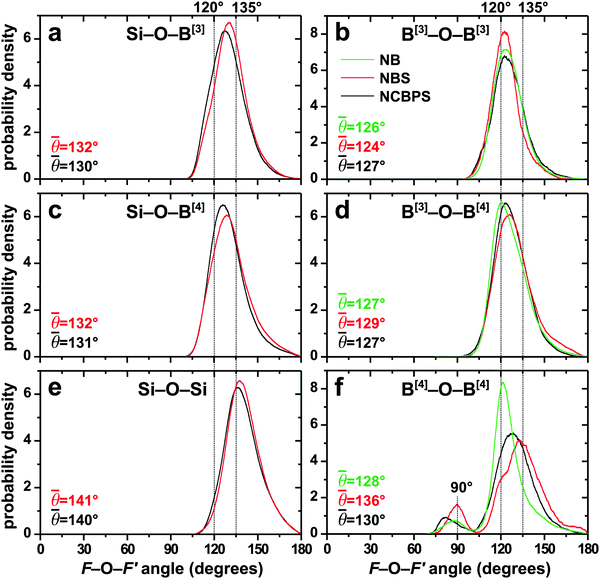
As for the F–O distances, the O–F–O intrapolyhedral bond-angle distributions (BADs) plotted in Fig. S2 (ESI†) for the {BO4, BO3, SiO4, PO4} groups of the NB1.3, NBS2–2.5(33), NCPS[2.93], and NCBPS(30) glass networks confirm that each coordination geometry remains invariant despite the presence of multiple network formers in the glass: narrow distributions are observed for all polyhedra, albeit with slightly broader distributions for the BO4 and BO3 moieties. Hence, each Si/P/B[3]/B[4] network former manifests well-defined coordination polyhedra with essentially fixed average O–F–O intratetrahedral angles of 109.4° for PO4, 109.3° for SiO4, and 109.1° ± 0.15° for BO4, while the planar BO3 groups exhibit the mean angle 119.7° ± 0.1°. These values agree well with both experimental11,16,17 and modeled10,52,60 bond angles in (boro)silicate glasses. The local geometries are independent of the precise glass composition (within 0.3°), which is unsurprising for the Si–O and P–O force fields that exploit three-body terms for maintaining a strict tetrahedral geometry, but the new B–O counterpart apparently accomplishes this task even without such precautions (see Section 3.3).We next consider the interpolyhedral bond-angle distributions of the F–O–F′ linkages involving {Si, B[3], B[4]} in the B/Si-bearing glasses. Table S3 (ESI†) compiles the average angles ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (F–O–F′), and Fig. 6 plots the BAD functions for a selection of glasses with comparable network polymerization (xNBO ≈ 0.5). The Si–O–Si BAD function is shifted to higher bond angles than all other {F, F′} pairs, as also reflected by the large value of
(F–O–F′), and Fig. 6 plots the BAD functions for a selection of glasses with comparable network polymerization (xNBO ≈ 0.5). The Si–O–Si BAD function is shifted to higher bond angles than all other {F, F′} pairs, as also reflected by the large value of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (Si–O–Si) ≈ 140° (Fig. 6e), whereas the other linkages exhibit similar mean angles
(Si–O–Si) ≈ 140° (Fig. 6e), whereas the other linkages exhibit similar mean angles ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (F–O–F′) in the range 124°–136°; see Table S3 (ESI†) and Fig. 6.
(F–O–F′) in the range 124°–136°; see Table S3 (ESI†) and Fig. 6.
The ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (F–O–F′) values of Table S3 (ESI†) reflect the well-known trend of decreasing bond angles for increasing NBO content of the glass,2,24,49,60 with the Si–O–Si/B[3] angles showing the largest variations (within ≈10°) across a given glass series. Naturally, the fragmented NCPS networks that accompany the high NBO contents manifest relatively low
(F–O–F′) values of Table S3 (ESI†) reflect the well-known trend of decreasing bond angles for increasing NBO content of the glass,2,24,49,60 with the Si–O–Si/B[3] angles showing the largest variations (within ≈10°) across a given glass series. Naturally, the fragmented NCPS networks that accompany the high NBO contents manifest relatively low ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (Si–O–Si) angles compared to SiO2, where the most recent studies confine
(Si–O–Si) angles compared to SiO2, where the most recent studies confine ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (Si–O–Si) ≈ 144°–147°.2 Experimental data on multi-component glasses are very sparse, but an NMR/DFT study reported
(Si–O–Si) ≈ 144°–147°.2 Experimental data on multi-component glasses are very sparse, but an NMR/DFT study reported ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) (Si–O–Si) ≈ 133° for a Na2O–SiO2 glass with xNBO = 0.58,35 which may be contrasted with the values ≈139° observed from our NCPS models with comparable NBO contents (Table S3, ESI†). The bond-angle dependence on xNBO partially accounts for the seemingly larger deviations observed among the glasses for the B[4]–O–B[4] pair in Fig. 6f, along with higher uncertainties of the BAD function for these comparatively rare interconnectivities (Section 6.1). Also noteworthy is the small peak ≈90° observed solely for the θ(B[4]–O–B[4]) distribution of each glass, which reflects a minor fraction of edge-shared BO4 tetrahedra.
(Si–O–Si) ≈ 133° for a Na2O–SiO2 glass with xNBO = 0.58,35 which may be contrasted with the values ≈139° observed from our NCPS models with comparable NBO contents (Table S3, ESI†). The bond-angle dependence on xNBO partially accounts for the seemingly larger deviations observed among the glasses for the B[4]–O–B[4] pair in Fig. 6f, along with higher uncertainties of the BAD function for these comparatively rare interconnectivities (Section 6.1). Also noteworthy is the small peak ≈90° observed solely for the θ(B[4]–O–B[4]) distribution of each glass, which reflects a minor fraction of edge-shared BO4 tetrahedra.
7 Structural roles of Na and Ca
7.1 Local Na and Ca environments
Table 1 lists the MD-derived average coordination numbers for Na (![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Na) and Ca (
Na) and Ca (![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Ca) in each glass structure. The phosphosilicate glasses reveal very similar values of ≈5.9 for both
Ca) in each glass structure. The phosphosilicate glasses reveal very similar values of ≈5.9 for both ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Na and
Na and ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Ca, as discussed by Mathew et al.43 All B-based glasses manifest higher mean Na/Ca coordination numbers, both growing for increasing B content or decreasing xNBO. However, the {xB, xNBO} parameters are usually coupled by the glass design (see Table 1): for instance, the decrease in xNBO is most likely mainly responsible for the reduced {
Ca, as discussed by Mathew et al.43 All B-based glasses manifest higher mean Na/Ca coordination numbers, both growing for increasing B content or decreasing xNBO. However, the {xB, xNBO} parameters are usually coupled by the glass design (see Table 1): for instance, the decrease in xNBO is most likely mainly responsible for the reduced {![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Na,
Na, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Ca} values when x(B2O3) grows along the NCBPS series. Variable NBO contents presumably also underlie similar
Ca} values when x(B2O3) grows along the NCBPS series. Variable NBO contents presumably also underlie similar ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Na trends reported earlier for NBS and NCBPS glasses for increasing amount of B2O3.50,54 At a fixed B content,
Na trends reported earlier for NBS and NCBPS glasses for increasing amount of B2O3.50,54 At a fixed B content, ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) Na also increases concomitantly with the BO4 population, which is particularly evident for the most polymerized borate/borosilicate networks with xNBO ≲ 0.05 in Table 1.
Na also increases concomitantly with the BO4 population, which is particularly evident for the most polymerized borate/borosilicate networks with xNBO ≲ 0.05 in Table 1.
Depending on the precise glass composition, the underlying {M[p]} ensembles may comprise coordination numbers 4 ≤ p ≤ 9 (see Table S4, ESI†), but the distribution-width σM(p) ≈ 1 for both Na and Ca constrains only three polyhedral types to dominate in each structure: MO5, MO6, and MO7, where MO6 and MO7 are most abundant when ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) M ≈ 6 and
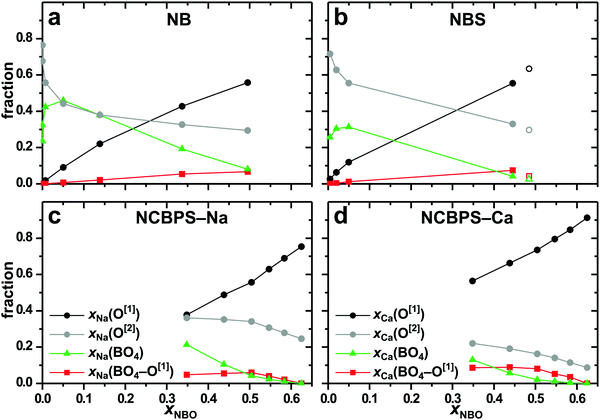
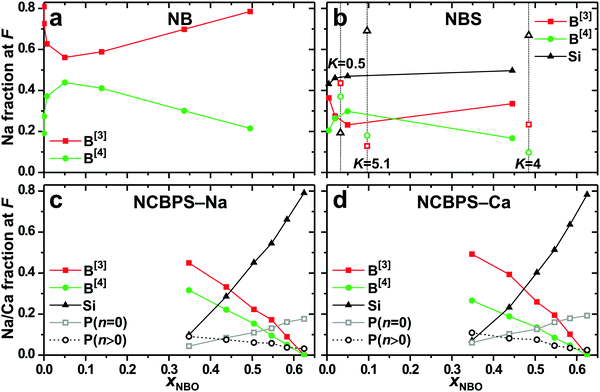
M ≈ 6 and ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) M ≈ 7, respectively. Noteworthily, all cations coordinate both O[1] and O[2] species. Yet, there is a strong propensity for NBO-accommodation at the NaOp and CaOp polyhedra,34,43,48,57 as evident from their associated x(Na–O[1]) and x(Ca–O[1]) data listed in Table 1 that represents the NBO fraction coordinated by the respective {NaOp} and {CaOp} ensemble. These Na/Ca–O[1] fractions are consistently higher than xNBO, notably so for the higher-CFS Ca2+ ion, whose coordination shells involve 63–91% of NBO contacts in the NC(B)PS glass models, whereas the corresponding range for the fraction of Na–O[1] bonds is 35–69%. The strong M–O[1] bonding preference has bearing on several other structural features discussed below.
M ≈ 7, respectively. Noteworthily, all cations coordinate both O[1] and O[2] species. Yet, there is a strong propensity for NBO-accommodation at the NaOp and CaOp polyhedra,34,43,48,57 as evident from their associated x(Na–O[1]) and x(Ca–O[1]) data listed in Table 1 that represents the NBO fraction coordinated by the respective {NaOp} and {CaOp} ensemble. These Na/Ca–O[1] fractions are consistently higher than xNBO, notably so for the higher-CFS Ca2+ ion, whose coordination shells involve 63–91% of NBO contacts in the NC(B)PS glass models, whereas the corresponding range for the fraction of Na–O[1] bonds is 35–69%. The strong M–O[1] bonding preference has bearing on several other structural features discussed below.
We next consider the Na–O and Ca–O average distances plotted against xNBO in Fig. 7, which also includes the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (M–O[1]) and
(M–O[1]) and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (M–O[2]) data for M = {Na, Ca}. Selected PDFs are depicted in Fig. S3 (ESI†). For both cations, the M–O[1] bond lengths are consistently shorter than M–O[2]. Yet, whereas the mean Ca–O[1] distance is shorter than that of Na–O[1] (by ≈5 pm) for a given glass composition, the situation is reversed for the O[2] contacts, where Ca manifests (on the average) ≈12 pm longer distances than Na: throughout all NC(B)PS glasses, well-confined values of
(M–O[2]) data for M = {Na, Ca}. Selected PDFs are depicted in Fig. S3 (ESI†). For both cations, the M–O[1] bond lengths are consistently shorter than M–O[2]. Yet, whereas the mean Ca–O[1] distance is shorter than that of Na–O[1] (by ≈5 pm) for a given glass composition, the situation is reversed for the O[2] contacts, where Ca manifests (on the average) ≈12 pm longer distances than Na: throughout all NC(B)PS glasses, well-confined values of ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Na–O[1]) ≈ 248 pm and
(Na–O[1]) ≈ 248 pm and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Ca–O[1]) ≈ 243 pm are observed, whereas the respective
(Ca–O[1]) ≈ 243 pm are observed, whereas the respective ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (M–O[2]) distance-spreads are larger, amounting to 260–266 pm for Na and 270–281 pm for Ca. However, notwithstanding that the various glass systems reveal similar spans of {
(M–O[2]) distance-spreads are larger, amounting to 260–266 pm for Na and 270–281 pm for Ca. However, notwithstanding that the various glass systems reveal similar spans of {![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Na–O[2])}, the Na–O[1] bond-length tends to increase concurrently with xNBO in the NB and NBS systems, corresponding to the range 238–246 pm in Fig. 7b.
(Na–O[2])}, the Na–O[1] bond-length tends to increase concurrently with xNBO in the NB and NBS systems, corresponding to the range 238–246 pm in Fig. 7b.
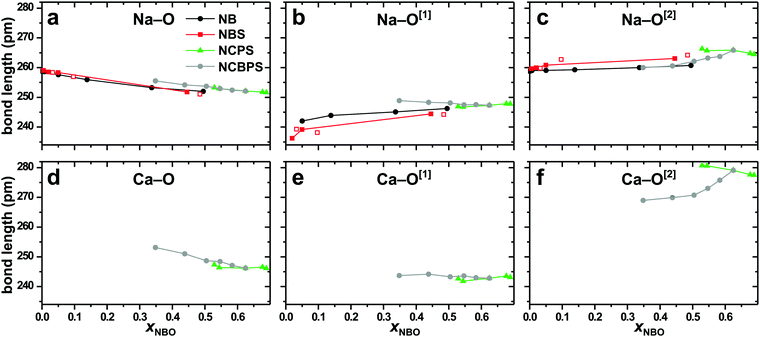 | ||
| Fig. 7 Average M–O distances plotted against xNBO for (a–c) Na and (d–f) Ca to each as-indicated O/O[1]/O[2] species and glass system; see the legend in (a). The solid and open symbols in (a–c) represent data for NBS glasses with K = 2 and K ≠ 2, respectively. The span of the vertical plot-range (48 pm) is around 50% of the full Na–O and Ca–O distance-spreads; see Fig. S3 (ESI†) for a selection of PDFs. | ||
The net M–O bond lengths plotted in Fig. 7(a, d) evidence overall slightly shorter ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Ca–O) values (246–253 pm) compared to
(Ca–O) values (246–253 pm) compared to ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (Na–O), the latter spanning 252–255 pm for the mixed-cation NC(B)PS glasses and 251–259 pm across all Na-bearing glasses. The average distances tend to shorten when xNBO is increased, as expected from the concurrently growing number of contributing shorter M–O[1] bonds (relative to M–O[2]) and the preference for Na, and particularly Ca, to coordinate NBO rather than BO species (in contrast with the results for the F–O distances; see Section 6.2). These trends also accord with the well-known decrease in
(Na–O), the latter spanning 252–255 pm for the mixed-cation NC(B)PS glasses and 251–259 pm across all Na-bearing glasses. The average distances tend to shorten when xNBO is increased, as expected from the concurrently growing number of contributing shorter M–O[1] bonds (relative to M–O[2]) and the preference for Na, and particularly Ca, to coordinate NBO rather than BO species (in contrast with the results for the F–O distances; see Section 6.2). These trends also accord with the well-known decrease in ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (M–O) for a concomitant reduction in
(M–O) for a concomitant reduction in ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) M. Note that we report the average Na–O (and Ca–O) distance, as opposed to the “most probable” counterpart observed at the PDF maximum, which appears to be most frequently reported for the “bond length” in the literature (see for instance ref. 13, 15, 48, 54, 57, 60, and 61). Our modeled M–O distances agree well with both—meaning that the PDF maxima around 235–240 pm and 230–235 pm of the respective Na–O and Ca–O PDFs in Fig. S3 (ESI†) accord with those of ref. 18, 48, 54, 57, 60 and 61, while the respective average distances also agree well with literature data.34,35
M. Note that we report the average Na–O (and Ca–O) distance, as opposed to the “most probable” counterpart observed at the PDF maximum, which appears to be most frequently reported for the “bond length” in the literature (see for instance ref. 13, 15, 48, 54, 57, 60, and 61). Our modeled M–O distances agree well with both—meaning that the PDF maxima around 235–240 pm and 230–235 pm of the respective Na–O and Ca–O PDFs in Fig. S3 (ESI†) accord with those of ref. 18, 48, 54, 57, 60 and 61, while the respective average distances also agree well with literature data.34,35
7.2 Modifier or compensator roles of Na+/Ca2+?
The commonly assumed roles of the M+/M2+ cations as either NBO-associated “network modifiers” or “charge compensators” of [BO4]− tetrahedra in B-based glasses4–7,9,10 provide an intuitive and conceptually appealing qualitative structural model. Yet, experimental assessments of the alkali/alkaline-earth partitioning among the various anionic moieties are sparse and qualitative.80,81 Inarguably, the M+/M2+ cations drive BO3 → BO4 conversions (Section 4.1) and indeed associate with [BO4]− tetrahedra, as proposed by the YDBX model4,5 and also by earlier descriptions of borate/borosilicate glasses.3,78 However, the categorical “modifier”/“compensator” view is oversimplified in (at least) two aspects: (i) despite that SiO4 and BO3 groups devoid of NBO ions are formally uncharged, their BO atoms are well-known to participate in the M+/M2+ coordination shells, as discussed above. (ii) A minor but xNBO-dependent fraction of the BO4 ensemble involves B[4]–O[1] contacts44 (see Fig. 4), whose associated M+/M2+ cations feature a dual compensator/modifier role.For every glass model, we assessed the partitioning of each M = {Na, Ca} species among the following four structural fragments, where M may act as (A) a “modifier”, encompassing all M–O[1] contacts but those involving BO4 groups with at least one B[4]–O[1] bond, or as (B) a “compensator” of BO4 moieties devoid of NBO; M may also associate with (C) NBO-bearing borate tetrahedra, or (D) BO species associated with the BO3 and SiO4 moieties (but excluding BO4). The relative contributions, {xM(O[1]), xM(BO4), xM(BO4–O[1]), xM(O[2])}, associated with the corresponding structural scenarios A–D were determined by scanning over the {MOp} ensemble, and assigning each of the p O sites at the MOp moiety to its relevant category A–D (weighted by 1/p, such that summation over all M–O contacts in the structure only counts each M site once).
First considering Na, Fig. 8a–c illustrates the dependence of the xNa(O[1]), xNa(O[2]), xNa(BO4), and xNa(BO4–O[1]) fractions on the NBO content in each B-bearing glass. These fractions are foremost dictated by the network polymerization degree and secondly by the relative Si/B contents, which for the NB/NBS glasses are parametrized by R and K, respectively (Table 1). All glass systems manifest the following gross trends:
(i) The Na ensemble mainly partitions between scenarios A and D, i.e., Na coordinates O[1] and O[2] species, respectively, implying that the xNa(O[1]) and xNa(O[2]) fractions typically dominate over all others in glasses with high (xNBO ≳ 0.35) and low (xNBO ≲ 0.35) NBO contents, respectively.
(ii) The “charge-compensator” role of Na is comparatively minor throughout: xNa(BO4) naturally correlates with the number of BO4 moieties in the glass (i.e., with the product xBx[4]B), meaning that high values of xNa(BO4) ≳ 0.2 are only observed for B-rich and highly polymerized glass networks adhering to the YDBX regimes I–III, for which x[4]B is large;4,5 see Section 4. However, even when xNa(BO4) is nearly maximized, the number of Na–O[2] contacts involving BO3/SiO4 groups generally outnumbers those of Na–BO4. Similar fractions of xNa(BO4) ≈ xNa(O[2]) are only observed for NB glasses with 0.5 ≲ R ≲ 0.7 (Fig. 8a), whereas xNa(BO4) is consistently lower than xNa(O[2]) for any borosilicate glass: the dependence of xNa(BO4) on the relative B/Si content (i.e., the parameter K) may be gauged by contrasting the higher xNa(BO4) values observed from the borate glasses (K = 0) in Fig. 8a with the (lower) counterparts from the NBS glasses with K = 2 in Fig. 8b. Moreover, the fraction of Na–O[1] contacts grows rapidly when xNBO is increased, such that Na+ ions coordinate both O[1] (scenario A) and O[2] (scenario D) species to a higher extent than associating with BO4 groups. This feature is particularly evident for the NCBPS glasses with xNBO ≳ 0.5 (Fig. 8c), but also applies for all NB(S) networks conforming to the YDBX region IV.
(iii) The minor but non-negligible number of B[4]–O[1] contacts (see Section 6.1 and ref. 44) implies that few Na+ species assume the dual modifier/compensator role (i.e., scenario C) throughout all glass structures, where typically xNa(BO4–O[1]) < 0.05. Yet, the number of B[4]–O[1] contacts grows concurrently with each of xNBO and xBx[4]B: naturally, the largest xNa(BO4–O[1]) values are encountered in NBO-rich networks that simultaneously exhibit high BO4 populations, such as in all NCBPS structures, as well as in the NB1.30 and NBS2–2.50(33) glasses [xNa(BO4–O[1]) ≈ 0.07]; see Fig. 8a–c.
All qualitative trends in the Na+ partitioning among the four scenarios A–D also apply to the divalent Ca2+ cation in the mixed-modifier NCBPS glasses (Fig. 8d), with the primary distinction of further emphasized Ca–O[1] contacts (see Section 7.1) at the expense of Ca–O[2] and Ca–BO4. Consequently, for a fixed glass composition, the xCa(O[1])–xCa(O[2]) difference observed in Fig. 8d is markedly larger than the xNa(O[1])–xNa(O[2]) counterpart of Fig. 8c. Moreover, in all highly fragmented glass networks (xNBO ≳ 0.45), Fig. 4c reveals that ≈50% of all BO4 tetrahedra accommodate at least one NBO ion, which rationalizes why both Na/Ca populations of case Cexceed that of B, i.e., why xM(BO4–O[1]) > xM(BO4); see Fig. 8(c and d).
We wish to underscore two aspects: first, our analysis based on the total number of M–O contacts of the {MOp} ensemble highlights the oversimplification of the “compensator/modifier” roles, where particularly the ignored M–O[2] contacts are substantial. Second, we also considered NBO-rich borate/borosilicate glass networks, which have received much less attention in the literature. However, once excluding the M–O[2] contacts from the statistics and focussing on highly polymerized NB(S) glasses, it is evident from Fig. 8(a, b) that the “compensator” portion of the {Na+} ensemble dominates its “modifier” counterpart in NB structures with xNBO ≲ 0.2 and in NBS2–R networks with xNBO ≲ 0.15, as confirmed experimentally for NB glasses.81 Notably, the relative “compensator/modifier” contributions then accord well with similar inferences from NBS glass models by Pacaud et al.,10 which were obtained by a different approach.
7.3 Partitioning of Na+ and Ca2+ among the network formers
We next move the spotlight onto the partitioning of the {Na+} and {Ca2+} ensembles around each network former, F = {B[3], B[4], Si, Q0P, Qn>0P}, where “Qn>0P” comprises all BO-bearing phosphate groups (mainly involving Q1P). These fractional populations are denoted by xNa(F) and xCa(F), respectively. This Na/Ca partitioning is complementary to that examined in Section 7.2 in that all M–O[1] contacts, which were previously split into xM(O[1]) and xM(BO4–O[1]), are considered for all NBO-associated FOp polyhedra, which involve primarily SiO4, BO3, and (to a lesser extent) BO4. Also, no distinction is made between BO4 groups with/without NBO ions, whose relative M contacts are grouped together into xM(B[4]).Fig. 9a–c plots each fraction xNa(F) against xNBO in the NB, NBS, and NCBPS glass networks. In the binary Na2O–B2O3 system (Fig. 9a), Na is shared exclusively between B[3] and B[4] coordinations, where xNa(B[4]) initially grows at the expense of xNa(B[3]) for increasing Na2O content, as anticipated (Section 4). The Na–B[3] (Na–B[4]) associations are lowest (highest) when the BO4 population is maximized (Fig. 9a), but xNa(B[3]) remains larger than xNa(B[4]) throughout all glass compositions, as expected from the results of Section 7.2. Fig. 9b reveals the same qualitative trends of the Na–B[3]/B[4] contacts in the NBS glasses, but now a significant portion of the Na+ cations also associate with Si, with the partitioning among each silicate (SiO4) and borate (BO3 and BO4) ensemble roughly given by the xSi/xB ratio, as evident by contrasting the results from glasses with distinct values of K. A nearly proportional partitioning of Na among Si and B also holds for the NCBPS networks (Fig. 9c), but a non-negligible fraction of the {Na+} reservoir now resides around the phosphate groups (despite their modest content). Fig. 9d manifests the same gross trends of the Ca partitioning as that of Na, with the main distinction that the Ca–BO3 associations are comparatively more abundant at the expense of Ca–SiO4 and Ca–BO4. The relatively larger number of Na–BO4 contacts stems from the sole B[4]–BO bonding at most BO4 tetrahedra, combined with the better charge-matching of Na+–[BO4]− than Ca2+–[BO4]−.
The trends in the various {xM(F)} fractions may be rationalized from the relative amount of each {B[3], B[4], Si, P} network species coupled with its propensity to associate with Na+/Ca2+, which depends primarily on the net negative charge of each FOp moiety. The relative preference for each Na/Ca–F contact was assessed by calculating PM(F) = xM(F)/xF, which is larger than unity for a preferential association of M with F: the higher the PM(F)-value, the stronger the preference. While the set of precise {PM(F)} values depends on the glass composition, notably so on xNBO, the following general trends apply (data not shown): (i) PM(Q0P) ≫ PM(Qn>0P) > PM(F) for F = {B[3], B[4], Si}. If disregarding the strong preference for Na–PO4 (and particularly) Ca–PO4 associations, the following observations are noteworthy in the NB(S) systems: (ii) There is a prominent preference for Na–B[4] contacts in highly polymerized networks (xNBO ≲ 0.05), as reflected in PNa(B[4]) values in the range 1.2–1.8, while PNa(B[3]) ≈ 1 and 0.86 ≲ PNa(Si) ≲ 1, meaning that there are fewer Na–Si contacts than predicted by a statistical distribution of Na around the {QnSi} moieties. (iii) Yet, the PNa(B[4]) values diminish rapidly for increasing NBO content of the network, with PNa(B[4]) remaining lower than both PNa(B[3]) and PNa(Si) whenever xNBO > 0.1. Altogether, these features rationalize why the “BO4 compensator” portion of the {Na+} reservoir is only significant in highly polymerized NB(S) glass networks (see Section 7.2).
7.4 Relative propensities for Na/Ca–F contacts in BPS glasses
We finally consider the relative propensities for Na+ and Ca2+ to associate with each network-forming species in the NCBPS glasses. This aspect was discussed in detail for (B-free) NCPS glasses by Mathew et al.,43 to which we refer for details. The key property behind all trends—also underlying those discussed in Sections 7.2 and 7.3—is the attraction strength between the positive Na+/Ca2+ cations and the negatively charged {FOp} network species, with more (less) charged FOp moieties exhibiting stronger (weaker) contacts with both Na+ and Ca2+, but where the preference for Ca2+–FOp associations grows with the number of NBO sites at FOp, as follows:(i) FOp moieties devoid of NBO ions prefer coordination of Na+ rather than Ca2+, meaning that a larger number of Na+ cations are present in the second coordination shell of F than that suggested by a statistical distribution and the xNa/xCa ratio. (ii) FOp polyhedra with one NBO ion exhibit an essentially statistical Na+/Ca2+ distribution according to the xNa/xCa ratio. (iii) All network groups featuring at least two NBO species strongly prefer to associate with Ca2+.
We remind that these trends are qualitative and the details depend on both xNBO and the precise speciation of all FOp polyhedra in the glass network. Two exceptions are noteworthy: first, BO4 tetrahedra with one NBO species manifest only a very weak preference for Ca coordination, despite that their net negative charge is equivalent to a BO3/SiO4 group coordinating two NBO ions. Second, the Q1P groups in the NCBPS glasses prefer coordinating Ca over Na, in contrast with the pronounced Na–Q1P preference observed in the NCPS counterparts, as discussed in ref. 43.
8 Concluding remarks
We have explored the short-range structural features of multi-component glasses with increasing complexity, ranging from the B-based Na2O–B2O3 and Na2O–B2O3–SiO2 systems that involve Na as the sole modifier, to the more complex Na/Ca-bearing four-component Na2O–CaO–SiO2–P2O5 and five-component Na2O–CaO–B2O3–SiO2–P2O5 systems, where the BPS glasses involve a large number of co-existing network-associated {BO3, BO4, QnSi, QnP} polyhedra. This is to our knowledge the first MD simulation report providing comparisons among four distinct glass systems (comprising up to three network formers) and involving samples together spanning a large range of compositions within each system.Despite the complexities, we demonstrated that accurate glass models are available by employing established shell-model Si–O/Na–O/Ca–O potentials,45,55,57 but new B–O and improved P–O force fields, validated against experimental data with overall gratifying results: (i) the modeled/experimental {x[3]B, x[4]B} fractions accorded very well, typically with <5% relative deviations, and with <10% discrepancies for all but one of 18 evaluated B-bearing glasses. (ii) The new P–O potential offers significantly improved predictions of the orthophosphate population in bioactive Na2O–CaO–SiO2–P2O5 glasses across the entire (relevant) network polymerization range 2.0 ≤ ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) SiBO ≤ 2.9, with relative deviations of 3–17% to experiments. Yet, the discrepancies grow rapidly for more condensed glass networks, such as for B-rich NCBPS glasses. (iii) Na/Ca–O and Si/B/P–O average distances, as well as intra/inter-polyhedral bond angles, agreed well with literature data. Last but not least, further successful validations of the B–O and P–O force fields against experimental constraints on the medium-range structures of NCBPS glasses are provided in ref. 44.
SiBO ≤ 2.9, with relative deviations of 3–17% to experiments. Yet, the discrepancies grow rapidly for more condensed glass networks, such as for B-rich NCBPS glasses. (iii) Na/Ca–O and Si/B/P–O average distances, as well as intra/inter-polyhedral bond angles, agreed well with literature data. Last but not least, further successful validations of the B–O and P–O force fields against experimental constraints on the medium-range structures of NCBPS glasses are provided in ref. 44.
Owing to the high field-strength of each F = {B[3], B[4], Si, P} network-forming cation, its local coordination environments remain essentially unperturbed, regardless of the presence of other network formers in the glass structure. Indeed, all of the minor alterations of F–O/O[1]/O[2] bond-lengths and F–O–F′ interpolyhedral bond angles observed among the glasses are readily attributed to variations of the precise BO/NBO speciation rather than the particular glass system considered.
Concerning the local {NaOp} and {CaOp} environments, 5, 6, and 7 coordinations dominate each distribution, which shifts towards higher coordination numbers for decreasing NBO content of the glass. Across the entire ensemble of 25 modeled glass compositions, Na revealed average coordination numbers between 5.8 and 7.2, whereas the span for Ca was 5.8–6.6 in the Ca-bearing NC(B)PS glasses. While NBO ions dominate both coordination shells of Na+ and Ca2+, the preference for Ca2+–NBO contacts is stronger. These features have bearing on the partitioning of each {NaOp} and {CaOp} ensemble among the various silicate, borate, and phosphate groups. The relative Na–F and Ca–F associations depend primarily on the net negative charge of the FOp polyhedron, with those devoid of NBO species manifesting a preference for Na+ in the mixed-modifier NCBPS glasses, while the modifiers are statistically distributed around FOp groups with one F–NBO bond, and those featuring more than one F–NBO contact prefer to associate with Ca2+. Moreover, the pronounced Na/Ca–NBO preference implies that the portion of each {Na+} and {Ca2+} reservoir that charge-balances the [BO4]− tetrahedra is only significant in B-rich borate/boro(phospho)silicate glass networks with low NBO contents, while the cations predominantly act as “modifiers” in all glasses with non-negligible NBO contents. Yet, even when the Na–BO4 associations are maximal in a boro(phospho)silicate glass, they are nevertheless outnumbered by the contacts between Na and the BO sites of SiO4/BO3 groups. Moreover, out of all Na+/Ca2+–BO4 associations in NBO-rich glass networks, a substantial fraction represents NBO-bearing borate tetrahedra.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Swedish Research Council (VR-NT 2014-4667) and the Carl Trygger Foundation (CTS 16:123), with computer resources provided by the Swedish National Infrastructure for Computing (SNIC at NSC; project 2016-1-493).References
- G. N. Greaves and S. Sen, Adv. Phys., 2007, 56, 1–166 CrossRef CAS.
- M. Edén, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2012, 108, 177–221 RSC.
- A. C. Wright, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2010, 51, 1–39 CAS.
- Y. H. Yun and P. J. Bray, J. Non-Cryst. Solids, 1978, 27, 363–380 CrossRef CAS.
- W. J. Dell, P. J. Bray and S. Z. Xiao, J. Non-Cryst. Solids, 1983, 58, 1–16 CrossRef CAS.
- A. Grandjean, M. Malki, V. Montouillout, F. Debruycker and D. Massiot, J. Non-Cryst. Solids, 2008, 354, 1664–1670 CrossRef CAS.
- D. Manara, A. Grandjean and D. R. Neuville, Am. Mineral., 2009, 94, 777–784 CrossRef CAS.
- X. Wu, R. E. Youngman and R. Dieckmann, J. Non-Cryst. Solids, 2013, 378, 168–176 CrossRef CAS.
- F. Michel, L. Cormier, P. Lombard, B. Beuneu, L. Galoisy and G. Calas, J. Non-Cryst. Solids, 2013, 379, 169–176 CrossRef CAS.
- F. Pacaud, J.-M. Delaye, T. Charpentier, L. Cormier and M. Salanne, J. Chem. Phys., 2017, 147, 161711 CrossRef PubMed.
- R. L. Mozzi and B. E. Warren, J. Appl. Crystallogr., 1969, 2, 164–172 CrossRef CAS.
- M. Misawa, D. L. Price and K. Suzuki, J. Non-Cryst. Solids, 1980, 37, 85–97 CrossRef CAS.
- G. N. Greaves, A. Fontaine, P. Lagarde, D. Raoux and S. J. Gurman, Nature, 1981, 293, 611–616 CrossRef CAS.
- D. I. Grimley, A. C. Wright and R. N. Sinclair, J. Non-Cryst. Solids, 1990, 119, 49–64 CrossRef CAS.
- J. Swenson, L. Börjesson and W. S. Howells, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9310–9319 CrossRef CAS.
- R. L. Mozzi and B. E. Warren, J. Appl. Crystallogr., 1970, 3, 251–257 CrossRef CAS.
- H. F. Poulsen, J. Neuefiend, H.-B. Neumann, J. R. Schneider and M. D. Zeidler, J. Non-Cryst. Solids, 1995, 188, 63–74 CrossRef CAS.
- R. A. Martin, H. L. Twyman, G. J. Rees, E. R. Barney, R. M. Moss, J. M. Smith, R. G. Hill, G. Chibin, T. Charpentier, M. E. Smith, J. V. Hanna and R. J. Newport, J. Mater. Chem., 2012, 41, 2212–2223 Search PubMed.
- G. El-Damrawi and W. Müller-Warmuth, J. Non-Cryst. Solids, 1992, 146, 137–144 CrossRef CAS.
- R. Martens and W. Müller-Warmuth, J. Non-Cryst. Solids, 2000, 265, 167–175 CrossRef CAS.
- L.-S. Du and J. F. Stebbins, J. Non-Cryst. Solids, 2003, 315, 239–255 CrossRef CAS.
- L.-S. Du and J. F. Stebbins, J. Phys. Chem. B, 2003, 107, 10063–10076 CrossRef CAS.
- S. Sen, Z. Xu and J. F. Stebbins, J. Non-Cryst. Solids, 1998, 226, 29–40 CrossRef CAS.
- F. Angeli, O. Villain, S. Schuller, T. Charpentier, D. de Ligny, L. Bressel and L. Wondraczek, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054110 CrossRef.
- M. M. Smedskjaer, J. C. Mauro, R. E. Youngman, C. L. Hogue, M. Potuzak and Y. Yue, J. Phys. Chem. B, 2011, 115, 12930–12946 CrossRef CAS PubMed.
- J. Wu and J. F. Stebbins, J. Am. Ceram. Soc., 2014, 97, 2794–2801 CrossRef CAS.
- J. D. Epping, H. Eckert, A. W. Imre and H. Mehrer, J. Non-Cryst. Solids, 2005, 351, 3521–3529 CrossRef CAS.
- S. Wegner, L. van Wüllen and G. Tricot, Solid State Sci., 2010, 12, 428–439 CrossRef CAS.
- Y. Kim and K. Morita, J. Non-Cryst. Solids, 2017, 471, 187–194 CrossRef CAS.
- Y. Yu and M. Edén, RSC Adv., 2016, 6, 101288–101303 RSC.
- G. Tricot, Phys. Chem. Chem. Phys., 2016, 18, 26764–26770 RSC.
- T. Nanba, M. Nishimura and Y. Miura, Geochim. Cosmochim. Acta, 2004, 68, 5103–5111 CrossRef CAS.
- D. Zielniok, C. Cramer and H. Eckert, Chem. Mater., 2007, 19, 3162–3170 CrossRef CAS.
- A. Pedone, T. Charpentier, G. Malavasi and M. M. Menziani, Chem. Mater., 2010, 22, 5644–5652 CrossRef CAS.
- F. Angeli, O. Villain, S. Schuller, S. Ispas and T. Charpentier, Geochim. Cosmochim. Acta, 2011, 75, 2453–2469 CrossRef CAS.
- R. Mathew, B. Stevensson, A. Tilocca and M. Edén, J. Phys. Chem. B, 2014, 118, 833–844 CrossRef CAS PubMed.
- P. Zhao, S. Kroeker and J. F. Stebbins, J. Non-Cryst. Solids, 2000, 276, 122–131 CrossRef CAS.
- J. F. Stebbins, P. Zhao and S. Kroeker, Solid State Nucl. Magn. Reson., 2000, 16, 9–19 CrossRef CAS PubMed.
- E. Leonova, I. Izquierdo-Barba, D. Arcos, A. López-Noriega, N. Hedin, M. Vallet-Regí and M. Edén, J. Phys. Chem. C, 2008, 112, 5552–5562 CAS.
- F. Fayon, C. Duée, T. Poumeyrol, M. Allix and D. Massiot, J. Phys. Chem. C, 2013, 117, 2283–2288 CAS.
- R. Mathew, C. Turdean-Ionescu, B. Stevensson, I. Izquierdo-Barba, A. García, D. Arcos, M. Vallet-Regí and M. Edén, Chem. Mater., 2013, 25, 1877–1885 CrossRef CAS.
- B. Stevensson, R. Mathew and M. Edén, J. Phys. Chem. B, 2014, 118, 8863–8876 CrossRef CAS PubMed.
- R. Mathew, B. Stevensson and M. Edén, J. Phys. Chem. B, 2015, 119, 5701–5715 CrossRef CAS PubMed.
- Y. Yu, B. Stevensson and M. Edén, J. Phys. Chem. B, 2017, 121, 9737–9752 CrossRef CAS PubMed.
- M. J. Sanders, M. Leslie and C. R. A. Catlow, J. Chem. Soc., Chem. Commun., 1984, 1271–1273 RSC.
- Q. Xu, K. Kawamura and T. Yokokawa, J. Non-Cryst. Solids, 1988, 104, 261–272 CrossRef CAS.
- X. Yuan and A. N. Cormack, J. Non-Cryst. Solids, 2001, 283, 69–87 CrossRef CAS.
- A. N. Cormack and J. Du, J. Non-Cryst. Solids, 2001, 293-295, 283–289 CrossRef CAS.
- J. Du and A. N. Cormack, J. Non-Cryst. Solids, 2004, 349, 66–79 CrossRef CAS.
- F. Gou, G. N. Greaves, W. Smith and R. Winter, J. Non-Cryst. Solids, 2001, 293–295, 539–546 CrossRef CAS.
- M. Barlet, A. Kerrache, J.-M. Delaye and C. L. Rountree, J. Non-Cryst. Solids, 2013, 382, 32–44 CrossRef CAS.
- L.-H. Kieu, J.-M. Delaye, L. Cormier and C. Stolz, J. Non-Cryst. Solids, 2011, 357, 3313–3321 CrossRef CAS.
- H. Inoue, A. Masuno and Y. Watanabe, J. Phys. Chem. B, 2012, 116, 12325–12331 CrossRef CAS PubMed.
- X. Lu, L. Deng, P.-H. Kuo, M. Ren, I. Buterbaugh and J. Du, J. Mater. Sci., 2017, 52, 8793–8811 CrossRef CAS.
- A. Tilocca, N. H. de Leeuw and A. N. Cormack, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104209 CrossRef.
- A. Tilocca and A. N. Cormack, J. Phys. Chem. B, 2007, 111, 14256–14264 CrossRef CAS PubMed.
- A. Tilocca, A. N. Cormack and N. H. de Leeuw, Chem. Mater., 2007, 19, 95–103 CrossRef CAS.
- A. Tilocca, J. Chem. Phys., 2013, 139, 114501 CrossRef PubMed.
- Y. Xiang and J. Du, Chem. Mater., 2011, 23, 2703–2717 CrossRef CAS.
- A. Pedone, G. Malavasi, M. C. Menziani, A. N. Cormack and U. Segre, J. Phys. Chem. B, 2006, 110, 11780–11795 CrossRef CAS PubMed.
- A. Pedone, G. Malavasi and M. Menziani, J. Phys. Chem. C, 2009, 113, 15723–15730 CAS.
- A. Tilocca, J. Chem. Phys., 2008, 129, 084504 CrossRef PubMed.
- J. K. Maranas, Y. Chen, D. K. Stillinger and F. H. Stillinger, J. Chem. Phys., 2001, 115, 6578–6589 CrossRef CAS.
- O. L. G. Alderman, G. Ferlat, A. Baroni, M. Salanne, M. Micoulat, C. J. Benmore, A. Lin, A. Tamalonis and J. K. R. Weber, J. Phys.: Condens. Matter, 2015, 27, 455104 CrossRef CAS PubMed.
- G. Ferlat, The B2O3 Case, in Molecular Dynamics Simulations of Disordered Materials, Springer International Publishing, 2015 Search PubMed.
- A. Zeidler, K. Wezka, D. A. J. Whittaker, P. S. Salmon, A. Baroni, S. Klotz, H. E. Fischer, M. C. Wilding, C. L. Bull, M. G. Tucker, M. Salanne, G. Ferlat and M. Micoulat, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 024206 CrossRef.
- L. L. Hench, J. Am. Ceram. Soc., 1991, 74, 1487–1510 CrossRef CAS.
- J. R. Jones, Acta Biomater., 2013, 9, 4457–4486 CrossRef CAS PubMed.
- Z. Strnad, Biomaterials, 1992, 13, 317–321 CrossRef CAS PubMed.
- R. Hill, J. Mater. Sci. Lett., 1996, 15, 1122–1125 CrossRef CAS.
- M. D. O'Donnell, S. J. Watts, R. V. Law and R. G. Hill, J. Non-Cryst. Solids, 2008, 354, 3554–3560 CrossRef.
- M. D. O'Donnell, S. J. Watts, R. G. Hill and R. V. Law, J. Mater. Sci.: Mater. Med., 2009, 20, 1611–1618 CrossRef PubMed.
- M. Edén, J. Non-Cryst. Solids, 2011, 357, 1595–1602 CrossRef.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- I. Lebecq, F. Désanglois, A. Leriche and C. Follet-Houttemane, J. Biomed. Mater. Res., 2007, 83A, 156–168 CrossRef CAS PubMed.
- T. Abe, J. Am. Ceram. Soc., 1952, 35, 284–299 CrossRef CAS.
- A. C. Wright, A. G. Clare, B. Bachra, R. N. Sinclair, A. C. Hannon and B. Vessal, Trans. Am. Crystallogr. Assoc., 1991, 27, 239–254 CAS.
- E. Ratai, M. Janssen and H. Eckert, Solid State Ionics, 1998, 105, 25–37 CrossRef CAS.
- J. D. Epping, W. Strojek and H. Eckert, Phys. Chem. Chem. Phys., 2005, 7, 2384–2389 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp08593a |
| This journal is © the Owner Societies 2018 |