On the prediction of core level binding energies in molecules, surfaces and solids
Abstract
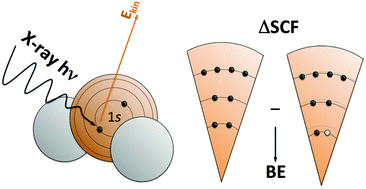
Core level binding energies, directly measured by X-ray photoelectron spectroscopy (XPS), provide unique information regarding the chemical environment of atoms in a given system. However, interpretation of XPS in extended systems may not be straightforward and requires assistance from theory. The different state-of-the-art theoretical methods commonly used to approach core level binding energies and their shifts with respect to a given reference are reviewed and critically assessed with special emphasis on recently developed theoretical methods and with a focus on future applications in materials and surface sciences.
- This article is part of the themed collections: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases, PCCP Perspectives and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...