Dihydrogen vs. hydrogen bonding in the solvation of ammonia borane by tetrahydrofuran and liquid ammonia

Abstract

The solvation structures of two systems rich in hydrogen and dihydrogen bonding interactions have been studied in detail experimentally through neutron diffraction with hydrogen/deuterium isotopic substitution. The results were analysed by an atomistic Monte Carlo simulation employing refinement to the experimental scattering data. The systems studied were the hydrogen storage material ammonia borane (NH₃BH₃, AB) dissolved in tetrahydrofuran (THF), and liquid ammonia (NH₃), the latter in which AB shows unusually high solubility (260 g AB per 100 g NH₃) and potential regeneration properties. The full orientational and positional manner in which AB–AB, AB–THF and AB–NH₃ pairs interact with each other were successfully deciphered from the wide Q-range total neutron scattering data. This provided an unprecedented level of detail into such highly (di)hydrogen bonding solute–solvent interactions. In particular this allowed insight into the way in which H–B acts as a hydrogen bond acceptor. The (di)hydrogen bonding was naturally determined to dictate the intermolecular interactions, at times negating the otherwise expected tendency for polar molecules to align themselves with anti-parallel dipole moments. Several causes for the extreme solubility of AB in ammonia were determined, including the ability of ammonia to (di)hydrogen bond to both ends of the AB molecule and the small size of the ammonia molecule relative to AB and THF. The AB B–H to ammonia H dihydrogen bond was found to dominate the intermolecular interactions, occurring almost three times more often than any other hydrogen or dihydrogen bond in the system. The favourability of this interaction was seen on the bulk scale by a large decrease in AB clustering in ammonia compared to in the dihydrogen bond-less THF.

---

1 Introduction

A classic example of an important intermolecular interaction is the hydrogen bond.¹ This follows the pattern X–H⋯Y, where the donor atom X, being more electronegative than hydrogen, causes said hydrogen to possess a partial positive charge. The acceptor, Y, is an atom capable of stabilising this charge, usually taking the form of an atom with a free lone or non-bonding pair of electrons, commonly a nitrogen or oxygen. Hydrogen bonds are common, and influence the properties of molecules as small as water, up to those as large and complex as proteins and DNA.

A somewhat rarer type of intermolecular interaction is dihydrogen bonding. This is quite similar to regular hydrogen bonding in terms of the donor, but the difference lies in that the acceptor is no longer a single atom. A dihydrogen bond instead follows the pattern X–H⋯H–Y, where the H bound to Y possesses a partial negative charge, caused normally by the relatively lower electronegativity of Y. This leads to a weak electrostatic attraction between the two hydrogens involved. Dihydrogen bonds have been observed within transition metal hydrides, playing a role in processes such as proton transfer and H₂ evolution.² Dihydrogen bonding has also frequently been observed in main group hydrides, especially those containing boron, where they have been shown to enable stereochemical control of reactions like reduction.^3,4

Amine-boranes are a family of compounds known to be rich in dihydrogen bonding, owing to the hydridic and protonic natures of the hydrogens bound to boron and nitrogen respectively. Ammonia borane (NH₃BH₃, AB) is the simplest amine-borane, and studies of the solid-state structure of AB, both theoretical and experimental, are numerous.^5–9 In AB, the dihydrogen bonds were distinguished from other intermolecular interactions (such as van der Waals forces) and classified as a type of hydrogen bond using “atoms in molecules” theory.¹⁰ The H_N⋯H_B dihydrogen bond is responsible for many of the properties of AB, including the high melting point (110–114 °C, cf. the isoelectronic ethane −182.8 °C).¹¹

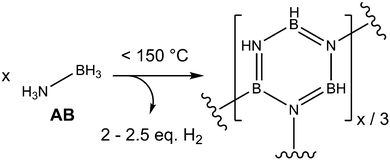
AB has received wide-spread attention due to its potential as an air-stable and safe hydrogen storage material. AB contains 19.6 wt% hydrogen, approximately 13–16 wt% (2–2.5 eq. H₂ per AB) of which can be extracted by heating to mild temperatures (<150 °C) (Fig. 1). The dihydrogen bonds have to be overcome in order for the material to melt, which occurs simultaneously with the onset of hydrogen release.¹¹ In addition to these intermolecular interactions, homopolar H_B⋯H_B interactions have been theorised to exist during the dehydrogenation process, due to an isotopic substitution experiment (which observed, for example, D₂ on dehydrogenation of NH₃BD₃).¹²

Fig. 1 The thermal dehydrogenation of AB leads to a multitude of unsaturated cyclic products.

A factor holding back the use of AB is in the difficulty of recycling the waste material post-dehydrogenation. This waste consists of a variety of partially hydrogenated hexagonal boron nitride-like products. Many attempts have been made to efficiently regenerate AB waste.^13–17 A promising one-pot route involves treating the waste with hydrazine in liquid ammonia, which was shown to regenerate an AB waste surrogate successfully in 24 hours at 40 °C.¹⁴ A further curiosity in terms of treating AB waste surrogates with liquid ammonia was demonstrated by Davis et al., who showed that some Lewis bases (specifically, pyridine and ammonia) were able to scavenge some of the residual high energy B–H bonds in the waste and rearrange them to form BH₃. If the Lewis base used was ammonia, this led to direct regeneration of some of the waste back into AB.¹⁸ AB also has an extremely high solubility in ammonia (260 g AB per 100 g NH₃ at 298 K, cf. 25 g AB per 100 g tetrahydrofuran).¹¹ This behaviour raises the question of how AB interacts with ammonia in solution, and has implications for future attempts at the regeneration of AB waste.

While there have been studies into the dynamics of dihydrogen bonding using IR and NMR spectroscopy, there has not yet to our knowledge been a detailed empirical analysis of the full structural and orientational way in which dihydrogen bonding occurs in solution.^19,20 Solvation as studied through neutron diffraction is a wide-ranging and active subject with applications in many fields ranging from physical chemistry to biochemistry.^21–27 In addition to the AB–ammonia interactions, a more fundamental interest in the nature of solvation in such a (di)hydrogen bond-rich environment sparks our study of these systems. Insight into the AB–AB intermolecular interactions is a further goal for this work. Due to the concurrent release of hydrogen when AB melts, the interactions within molten AB cannot be directly studied; a concentrated solution of AB in liquid ammonia, especially considering the structural similarities, is probably the best analogue for studying such a system.

In this paper the solvation structure of AB in both liquid ammonia and tetrahydrofuran (THF), another common solvent, has been investigated through the use of neutron diffraction. Empirical Potential Structure Refinement (EPSR) was used to analyse the results, and build up a simulation box that could be interrogated to determine the spatial and orientational solvent–solute interactions.^28–30 Isotopic substitution of both the solvent and solute hydrogens for deuterium was performed to obtain additional, complementary constraints for the data refinement process. The results were compared with those from solid state diffraction and ab initio calculations of dimers, providing important insight into the distribution of dihydrogen bonding structures in the liquid state. A description of the theory behind the neutron diffraction experiments and the EPSR procedure is provided in the ESI.†

2 Results and discussion

The neutron scattering experiments were performed on 7 samples for AB in THF and 3 samples for AB in NH₃ (details in Experimental section). Table 1 shows the seed parameters used for the EPSR simulations, with the atom nomenclature shown in Fig. 2. The Lennard-Jones parameters for AB were adapted from the CHARMM parameters for methylamine used in Chen et al., as parameters for AB do not exist to our knowledge.³¹ It is important to mention that the seed potentials are only a starting point, and differences in structural behaviour induced in the simulation would be compensated for by the refinement. The AB charges were sourced from a Mulliken analysis of AB itself.³² For ammonia, the nitrogen parameters were taken from Gao et al., with the hydrogen values adjusted to match the AB N–Hs.³³ Finally, the THF parameters were taken from the OPLS all-atom force field.^34–38

Table 1 EPSR seed parameters used in the simulations

Atom label	Epsilon/kJ mol^−1	Sigma/Å	Charge/e
N	0.25104	3.5458	−0.9100
B	0.33472	3.5458	−0.2900
HN	0.04184	1.5591	0.4500
HB	0.16736	2.2451	−0.0500
NA	0.87900	3.3600	−1.0260
HA	0.04184	1.5591	0.3420
O1	0.58576	2.9000	−0.4000
C1	0.27614	2.5000	0.1400
C2	0.27614	2.5000	−0.1200
HC1	0.12552	2.5000	0.0300
HC2	0.12552	2.5000	0.0600

---

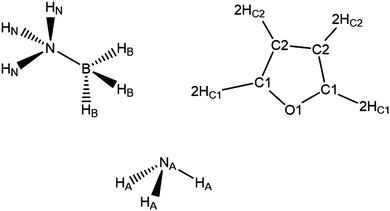Fig. 2 Atom labels used throughout the analysis of the EPSR simulations of AB dissolved in THF and liquid ammonia.

The normalised structure factors for the AB in THF and AB in ammonia experiments are shown in Fig. 3 and 4 respectively, together with the simulated EPSR fits. Scattering for Q < 2 Å⁻¹ is dominated by the intermolecular interactions, weighted by each atom's neutron scattering length and concentration. The opposite occurs at high Q, with the intramolecular interactions dominant. The EPSR fits are of good quality, with the deviations at Q < 0.5 Å⁻¹ caused most likely by errors in the inelasticity correction, which would explain the larger magnitude in hydrogen (rather than deuterium) rich samples.^39,40

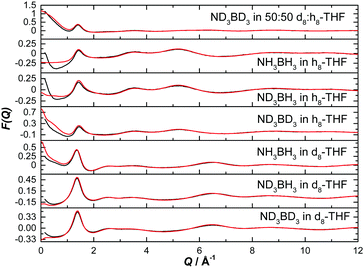Fig. 3 Diffraction pattern (black) and EPSR fitted structure factor (red) for various isotope combinations of ammonia borane dissolved in THF.

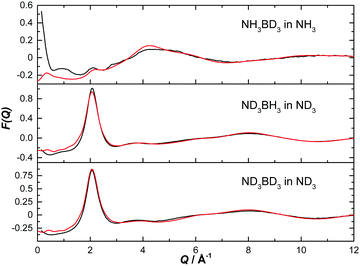Fig. 4 Diffraction pattern (black) and EPSR fitted structure factor (red) for various isotope combinations of ammonia borane dissolved in ammonia.

The Fourier transformation of the total structure factors produces the total radial distribution functions, shown in Fig. S1 and S2 (ESI†). These show that the intramolecular bond lengths are modelled accurately in our simulations.

More specific structural information can be obtained by looking at the partial radial distribution functions (g(r), RDF) for atom pairs of interest in our systems.

2.1 Ammonia borane–ammonia borane interactions

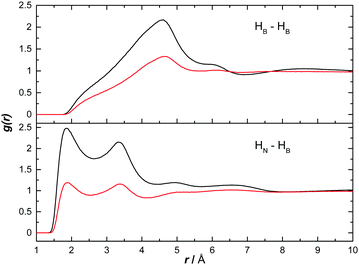
We have used the output of the EPSR simulations to study both hetero- and homopolar interactions between AB molecules. Given the likelihood for AB–AB interactions to be less rigid in solution than in the solid state (and arguably more similar to melted/dehydrogenating AB), this allows an understanding of the interactions suggested to exist during dehydrogenation.¹²

Fig. 5 shows the partial RDF for heteropolar H_N⋯H_B and homopolar H_B⋯H_B interactions. The sharp peak at 1.85 Å in the heteropolar function suggests the presence of strong dihydrogen bonding between AB molecules. This distance is smaller than the sum of the van der Waals radii for two hydrogen atoms (2.4 Å) and characteristic of, though slightly shorter than, the dihydrogen bonding present in the solid state (2.02 Å).^11,20 This structural motif appears in both ammonia and THF. In ammonia however, the magnitude of the peak is much lower suggesting AB–AB interactions are less numerous (both graphs were normalised to the bulk concentration of AB). The second peaks at 3.4 Å are not due to a second coordination shell, but the non-bonding H_Bs on the same AB molecule responsible for the 1.85 Å peak.

Fig. 5 Partial radial distribution functions for AB–AB correlations via heteropolar H_N⋯H_B and homopolar H_B⋯H_B interactions. The red line corresponds to the EPSR simulation of AB dissolved in ammonia and the black line that of AB dissolved in THF.

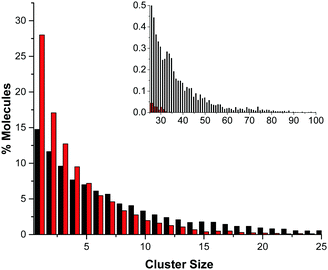
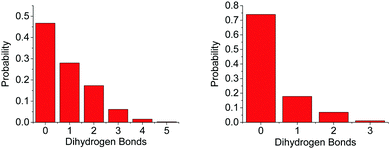
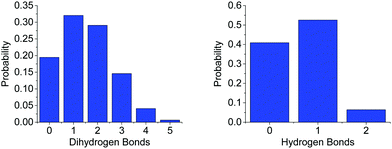
The difference in the number of AB–AB interactions between the two solvents can further be seen in an analysis of the AB–AB clustering (a cluster defined as having an H_N⋯H_B distance of 2.7 Å or less) present in the solutions, shown in Fig. 6. Overall 86% of the AB molecules in THF were in a cluster of size two or more, compared to 72% in liquid ammonia. This lower overall clustering in ammonia also manifested as a tendency towards smaller clusters, with the largest involving about 20 AB molecules. In THF however, larger clusters were often observed containing over 30 AB molecules. Each H_N on average dihydrogen bonds to 0.701 H_Bs in THF, compared to only 0.438 in ammonia. This was determined from the average coordination numbers obtained by integrating the partial radial distribution functions. The results are shown in Table 2. More detailed probability distributions of the dihydrogen bonding in the first coordination shell (<2.7 Å) are shown in Fig. 7. These show that although the average coordination number is less than one, situations where multiple H_Ns are dihydrogen bonded to each H_B are not uncommon, more so in THF than in liquid ammonia, reflecting the increased clustering.

Fig. 6 Cluster size distribution for AB–AB clusters in THF (black) and liquid ammonia (red). Clusters were defined as having an H_N⋯H_B distance of less than or equal to 2.7 Å, showing that long-range AB–AB interactions are more common in THF than ammonia. The inset shows the much larger range in cluster size present in THF.

Table 2 First coordination shell numbers for AB–AB interactions, as well as for AB–solvent interactions, for EPSR derived systems of AB dissolved in THF and liquid ammonia. Coordination distances were defined by the location of the first minimum in the partial radial distribution functions

Atom pair	Range/Å	Average coordination number
HN⋯HB	2.7	0.701 (AB–THF)
HN⋯HB	2.7	0.438 (AB–NH3)
HN⋯O1	2.7	0.361
O1⋯HN	2.7	0.282
HN⋯NA	2.7	0.798
NA⋯HN	2.7	0.258
HB⋯HA	2.5	1.905
HA⋯HB	2.5	0.206

---

Fig. 7 Probability distributions of the number of H_Ns in dihydrogen bonding distance (<2.7 Å) to an H_B, in the models of AB dissolved in THF (left) and liquid ammonia (right). These again highlight the greater AB–AB interaction in THF.

The lower clustering in ammonia suggests that AB–ammonia interactions are relatively favourable compared to AB–THF. This may be linked to the ability of ammonia to partially break down the polymeric structure of the waste material, redistributing the residual B–H bonds to form AB as mentioned before.¹⁸ This is a process that would be promoted by stronger AB–solvent interactions, and is not observed in THF.

In Fig. 5, the peak signifying homopolar H_B⋯H_B interactions does not appear until 4.5 Å. This long range suggests that there are no direct correlations in these solutions. The density observed in these functions at this distance is likely instead due to the heteropolar interactions. This suggests that the presence of D₂ during the dehydrogenation of NH₃BD₃, as observed by Wolstenholme et al., was more likely to be a result of hydrogen scrambling than homopolar coordination.¹²

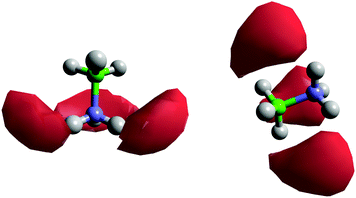
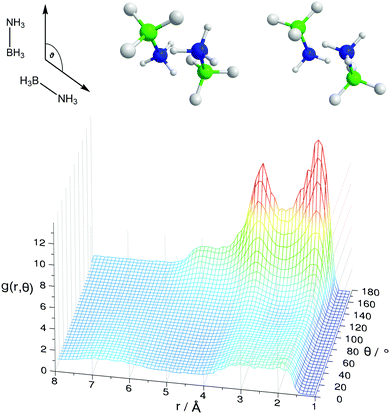
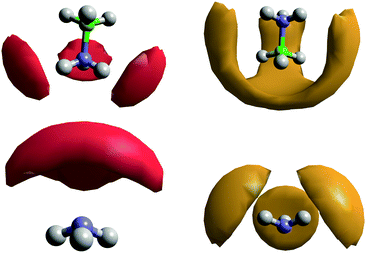
Fig. 8 shows the spatial density functions (SDF) showing where neighbouring AB molecule density is located around a central AB in ammonia (similar SDFs are seen in THF). The density is broadly located side-on to the central AB rather than end-on, and adopts the three-fold symmetry expected for intermolecular interactions primarily based on the hydrogen bonding sites. Fig. 9 shows the angular RDF for the AB–AB interactions, with θ corresponding to the angle between the AB dipole moments. The distance r is that between H_N and an H_B. The function shown is for AB dissolved in THF, the same function calculated in liquid ammonia (Fig. S3, ESI†) showed the same features. This implies that the only difference caused by the solvent is in the number of AB–AB interactions rather than the structure. A strong bias towards anti-parallel dipole moments is observed. The side-on configuration shown in Fig. 9 is the only configuration where (heteropolar) dihydrogen bonding and anti-parallel dipole moments can occur together. The second peak, at 3.5 Å, is assigned to the distance between H_N and the other H_Bs on the dihydrogen bonding AB.

Fig. 8 Spatial density functions for AB–AB interactions via H_N⋯H_B dihydrogen bonds, for AB dissolved in liquid ammonia. The density shows the 20% most likely positions for the neighbouring molecule's (left) H_Bs and (right) H_Ns in the first coordination shell, defined as having a distance of 2.0–4.0 Å between the centre of the three-fold symmetric hydrogens and the neighbouring molecule's heteropolar hydrogen. The blue atom is the AB nitrogen and the green the boron.

Fig. 9 Angular radial distribution function for AB–AB pairs in THF, showing the anti-parallel nature of the AB dipoles. The angle θ is defined above, along with AB–AB orientations that satisfies the graph as well as the spatial density functions. The distance is that between H_N and an H_B. The blue atom is the AB nitrogen and green the AB boron.

In the angular RDF in Fig. S4 (ESI†) with θ equal to the angle between the N–H bonds, a preference for both a parallel and anti-parallel orientation of the N–H bonds is seen. The resulting AB–AB pairs fulfilling all of the above criteria are shown in Fig. 9. The N–H_N bonds point towards the B–H_B bonds, rather than directly at the H_Bs. This structure, observed before in theoretical studies of dimers, has been suggested to be favourable by allowing the protonic hydrogen to get nearer to the relatively negative boron atom.⁴¹ As a result, it was proposed that the σ-bond itself was the acceptor in the dihydrogen bond rather than just the hydridic hydrogen.²⁰ This may also explain how multiple dihydrogen bonds can form with a particular H_B, as H_Ns can bond from many angles surrounding the σ bond rather than from only pointing directly at the H_B (regular hydrogen bonds typically being linear, see Section 2.4).

In considering the H_N density in Fig. 8 near to the nitrogen end of AB, we note that there is no close-range H_N⋯H_N homopolar correlation either, the peak in the partial RDF appearing at approximately 4.2 Å (Fig. S6, ESI†).

2.2 Ammonia borane–tetrahydrofuran interactions

The H to O partial RDFs for AB dissolved in THF are shown in Fig. 10. Only H_N shows strong interactions to O1 with two contacts at 2.05 and 3.44 Å respectively. The first is attributed to a direct H_N⋯O1 hydrogen bond while the second peak is due to a longer range interaction between the oxygen and another H_N on the same nitrogen. As expected, given the hydridic nature of H_B, the H_B⋯O1 RDF shows only a much longer range interaction, indicated by a broad peak centred at 4.83 Å.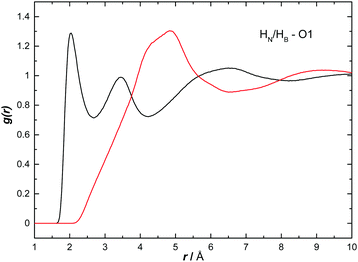

Fig. 10 Partial radial distribution functions for H_N (black) and H_B (red) to O1, calculated from the EPSR fitted system, for AB dissolved in THF.

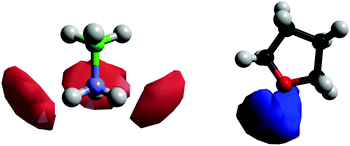
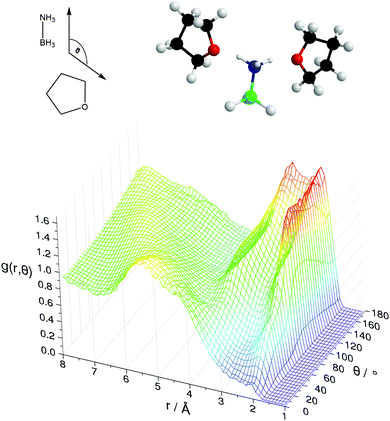
Fig. 11 shows the SDFs plotting the regions of highest probability density around the AB and THF in which the other molecule is located. These show that the density is centred around the hydrogen bonding sites O1 and H_N. Fig. 12 shows the angular RDF, where the angle θ is that between the AB and THF dipoles, and the distance r is that between H_N and O1. A roughly equal, high probability is seen for orientations with θ between 90 and 180°. Together with the SDFs and other angular RDFs (Fig. S7–S9, ESI†), we can determine that THF occupies a range around the nitrogen end of AB, with O1 always pointing at H_N. This can involve a disruption of the usual tendency for pairs to align with anti-parallel dipole moments, which speaks to the strength of the hydrogen bonding interactions. It could also be a result of the increased degree of disorder present in liquid samples.

Fig. 11 Spatial density functions showing the location of the 20% most likely positions for molecules in the first coordination shell (2.0–3.6 Å) around AB and THF. The red density is the position of the THF O1s and the blue density the AB H_Ns. The blue AB atom is the AB nitrogen.

Fig. 12 Angular radial distribution function for AB–THF interactions, illustrating the hydrogen bonding between H_N and O1. θ is the angle between the AB and THF dipole moments. The distance is calculated between H_N and O1. AB–THF orientations that fit these peaks and the spatial density functions are shown above.

On average, each H_N coordinates to 0.361 O1s, suggesting it is about twice as likely for an AB (via H_N) to bond to another AB (0.701) than to a THF molecule. A more detailed distribution of the AB–THF coordination is shown in Fig. 13, which also shows that it is much less likely for each H_N to be within hydrogen bonding distance of more than one O1, than with multiple H_Bs (Fig. 7). Looking at the distribution of H_Ns around O1s also reveals that the THF oxygen can be within hydrogen bonding range of two H_Ns at once, suggesting that both of the oxygen non-bonding electron pairs could be involved in hydrogen bonding at the same time.

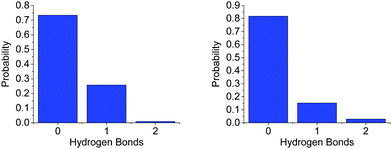Fig. 13 Probability distribution of (left) the number of O1s in hydrogen bonding distance (<2.7 Å) to each H_N and (right) the number of H_Ns around O1, for the model of AB dissolved in THF.

2.3 Ammonia borane–ammonia interactions

Fig. 14 shows the AB H to ammonia N_A and H_A partial RDFs. H_A predominantly interacts with H_B, as can be seen by the defined peak at 1.98 Å. This is a slightly longer dihydrogen bond than the corresponding bond between two ABs (H_N⋯H_B, 1.9 Å), suggesting it may be weaker. H_N, however, does not seem to dihydrogen bond directly with H_A, the ‘shoulder’ peak at 2.7 Å instead likely due to AB bonded via the H_B, as was observed in Ricci et al.⁴² The opposite was determined for bonding to N_A, with H_N showing a clear peak at 2.19 Å. H_B however does not show any bonding to N_A before the first peak at 2.88 Å, likely again caused by bonding to the other end of AB. The extra dihydrogen bonding interactions observed between AB and ammonia, and not present in THF, are likely responsible for the large difference in solubilities.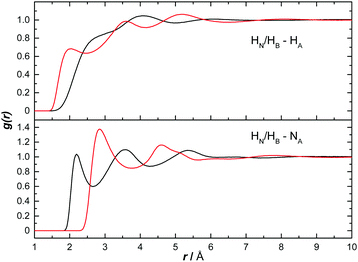

Fig. 14 Partial radial distribution functions for H_N (black) and H_B (red) to H_A as well as to N_A, calculated from the EPSR fitted system, for AB dissolved in liquid ammonia.

The average first shell (<2.5 Å) coordination number of N_A around H_N, and of H_A around H_B is 0.798, and 1.905 respectively. The latter is remarkably high, possibly due to the large number of H_As in the system compared to N_As. Something of note though in comparing to THF, is the effective doubling of the average coordination number of O1 around H_N (0.361) in regards to N_A. While it is likely this is at least partly due to the higher concentration of AB in ammonia, the smaller size of the ammonia molecule may also make it less sterically unfavourable for multiple H_Ns on an AB to be coordinated. Fig. 15 shows the more detailed analysis of the coordination, which reveals just how frequently H_B⋯H_A dihydrogen bonds occur. As many as five H_As were observed to be within dihydrogen bonding distance of one H_B, eclipsing the coordination observed in THF. The coordination is also weighted more towards one or two bonds rather than zero as was observed in the AB–AB coordination in THF.

Fig. 15 Probability distributions of the number of (left) H_As within dihydrogen bonding range (<2.5 Å) of H_Bs and (right) the number of N_As in the same distance of H_N, for AB dissolved in liquid ammonia.

The SDFs for AB–ammonia pairs are shown in Fig. 16. The density around AB largely mirrors that seen in the previous pairs, a three-fold symmetrical pattern of density around the H_Ns, and between the H_Bs. In this case, the lobes of density between the H_Bs also extend down to meet end-on to the boron atom, unlike in the AB–AB pair. This could reflect the extreme prevalence of H_B⋯H_A dihydrogen bonds, and the smaller size of the ammonia molecule relative to AB enabling it to bond from positions where the larger AB could not. This large volume of probability density may also be the reason that a coordination number as high as 5 can be observed, albeit very rarely. The location of the probability density being between the H_Bs rather than pointing at them again highlights that it is the B–H_B σ bond that is acting as the dihydrogen bond acceptor.

Fig. 16 Spatial density functions showing the location of the 20% most likely positions for ammonia or AB molecules in the first coordination shell around the other, for the model solution of AB (20 wt%) in ammonia. The red density shows the H_N to N_A pair in a range of 2.2–3.5 Å, while the orange density shows the H_B to H_A pair in a range of 2.2–4.2 Å.

The angular RDFs were split into those calculated based on H_N⋯N_A, and H_B⋯H_A interactions. These are shown in Fig. S10 and S11 (ESI†) respectively. Orientations that satisfy the ARDFs and the SDFs, are shown in Fig. 17. The additional angular RDFs needed to narrow down the most probable orientations are shown in Fig. S12 and S13 (ESI†).

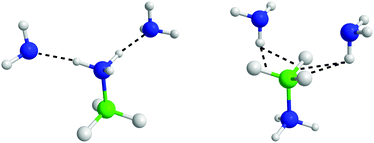Fig. 17 AB–ammonia orientations that satisfy the spatial density functions and angular radial distribution functions.

2.4 Directionality of dihydrogen bonding in solution

The hydrogen and dihydrogen bonding angles X–H⋯Y observed throughout the simulations, where X is the hydrogen bond donor and Y the acceptor, were determined with the resulting probability distributions shown in Fig. 18. All the interactions are predominantly linear, matching what would be expected for hydrogen bonds.¹ The dihydrogen bonds however, show wider peaks than the regular hydrogen bonds, indicating more flexibility. This could reflect a slightly weaker bond, or be a product of the larger number of these interactions forcing some to adopt a less ideal orientation. The other angles XH⋯Y–A, where A is an atom covalently bound to Y, were also determined and shown in Fig. 19. The peaks are much wider for these angles, reflecting less rigidity. The H_N⋯H_B–B angle however predominantly appears at 90°. This is due to the dihydrogen bond acceptor formally being the H_B–B σ bond rather than just the hydridic hydrogen, as was seen in the SDF (Fig. 8). For the H_A⋯H_B–B dihydrogen bond, a slightly larger angle of 110° is seen. This may be due to H_N having a slightly more positive charge than H_A, and therefore experiencing a stronger attraction to the electron density in the σ bond.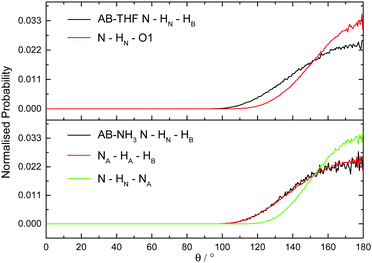

Fig. 18 Normalised probability distributions for the angle X–H⋯YA, where X is the hydrogen bond donor and Y the acceptor, in (top) AB dissolved in THF and (bottom) AB dissolved in liquid ammonia.

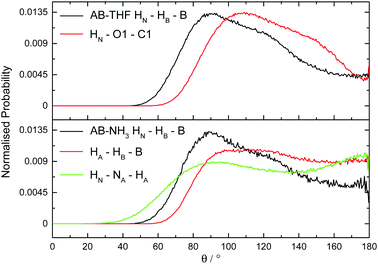Fig. 19 Normalized probability distributions for the angle A–Y⋯HX, where Y is the hydrogen bond acceptor and X the donor, in (top) AB dissolved in THF and (bottom) AB dissolved in liquid ammonia.

Analysing the angles of the (di)hydrogen bonds also enables us to distinguish these from other intermolecular interactions (such as van der Waals forces). Fig. S14 (ESI†) shows the angular distribution for the non-(di)hydrogen bonding B–H_B⋯H_B. The distribution is very flat, with the reduction in probability at <120° likely due to steric reasons. This is very different to what we see in the (di)hydrogen bonds, which all seem to show directionality.

2.5 Comparison of ammonia borane–ammonia results to a theoretical approach

After observing that (di)hydrogen bonding to both ends of the AB molecule by ammonia was occurring, the possibility was raised that a single ammonia could bond to both ends of the same AB. Indeed in theoretical studies run on systems of AB dissolved in ammonia by Kar and Scheiner, their fully relaxed AB–NH₃ dimer (Fig. 20) showed H_N⋯N_A hydrogen bonding as well as H_A dihydrogen bonding to two H_Bs.⁴³ Looking for pairs where (di)hydrogen bonding occurs on both ends of an AB molecule to one NH₃ in our empirically refined simulation showed that this occurred 32% of the time (out of all bonding pairs). Dihydrogen bonding was determined by the atom pairs satisfying distance constraints of <2.7 Å for H_N⋯N_A and <2.5 Å for H_B⋯H_A. These constraints were chosen to include the full breadth of the corresponding peak in the partial RDFs. Angular constraints were not included as any orientation which involves bonding to both sides of the AB would be radically different to what we saw in the prior analysis. Searching specifically for the bonding pattern in the theoretically optimised dimer (one H_A dihydrogen bonding to two H_Bs, and N_A hydrogen bonding to one H_N), showed it as present only 4.2% of the time. The average geometric parameters were also quite different (H_N⋯N_A lit. 1.993 Å, exp. 2.455 Å; H_A⋯H_B lit. 2.495 Å, exp. 2.155 Å; N–H_N⋯N_A lit. 150.4°, exp. 130.3°; H_A⋯H_B–B lit. 88.6°, exp. 86.9°).⁴³ The closest match was the last angle, which the authors claimed to show energy minima at 100 and 180°; in this work we see broad corresponding probability peaks at about 90 and 180° (Fig. 19). The broadness of the peaks and the relatively small differences between experimental and theoretical results reflects the disordered nature of the liquid samples. The theoretical model also only had to minimise the energy of two molecules, while in the liquid multiple interactions had to be globally minimised. The chelate effect would suggest that solvation structures where one ammonia bonds to both ends of AB would be favoured, considering the increase in entropy gained from displacing other ammonia molecules. Nevertheless the probabilities were quite low, this may be because such orientations diverge from the most favourable angles (Fig. S10 and S11, ESI†); the multiply bonded pairs have H_A–N_A running parallel to the AB dipole rather than anti-parallel.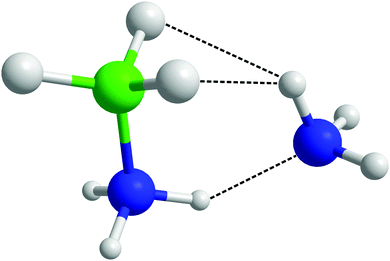

Fig. 20 Theoretically optimised AB–ammonia dimer in which bonding to both sides of the AB molecule from one ammonia is observed.⁴³

3 Conclusions

The solvation structure of AB by THF and liquid ammonia has been determined via refinement of a Monte Carlo simulation to neutron diffraction data, constrained by complementary data sets of isotopically substituted samples. The large capacity of AB to hydrogen bond was found to dominate the solute–solvent interactions. In THF, hydrogen bonding via the oxygen was usually observed to happen only once per THF, with instances where both non-bonding electron pairs were involved occurring five times less frequently. The low number of hydrogen bonds formed with THF, along with the larger and more rigid size relative to another AB, caused AB–AB contacts to be favoured over AB–THF. This manifested as a noticeable increase in AB clustering.

The extreme solubility of AB in liquid ammonia could then be seen in the sheer number of (di)hydrogen bonds formed on average between AB and ammonia. The first shell coordination number of N_A around H_N was more than double that of the THF oxygen around H_N. This could be due to the increased availability of the nitrogen lone pair compared to the oxygen non-bonding electron pairs. The H_B⋯H_A dihydrogen bond in particular was prevalent, with a coordination number roughly 2.5 times greater than even N_A around H_N. This also came with a relative decrease in AB clustering.

The structure of the dihydrogen bonding between AB and either ammonia or another AB in solution was determined to be very directional, with the N–H_N/A⋯H_B angle centred around 180°. This was still slightly less rigid than regular hydrogen bonds. The frequency of these interactions was attributed to the preference for a 90° H_N/A⋯H_B–B angle, which enabled the bonding to occur from a much larger volume of space surrounding each H_B. This may also be the reason for the lower rigidity of N–H_N/A⋯H_B, as some distortion of the linearity to point towards the B–H_B σ bond would be expected.

The fact that ammonia can hydrogen bond to both ends of the AB molecule undoubtedly leads to an increased solubility of AB compared to in THF. In comparing to AB–AB contacts however, which can also occur on both ends of the molecule, AB–ammonia contacts were still preferred. We determined this could be due to the smaller size of the ammonia molecule opening up new volumes of space in which hydrogen bonding could occur from. This was mainly observed in an end-on position next to the AB boron.

It is the combination of these factors that cause the high solubility of AB in liquid ammonia. An interesting test would be to study in a similar way the solvation structure of AB in water, as water also has a small size and could bond to both ends of AB. The solubility in water (33.6 g AB per 100 g solvent) however is more similar to that in THF (25 g AB) than ammonia (260 g AB).¹¹ This could perhaps place more weight on the availability of the lone pair as well as the number of hydrogens involved in terms of factors contributing to solubility. It could also be possible that the three-fold symmetry of the ammonia is complementary to the AB symmetry, and enables a larger degree of dihydrogen bonding between the two.

In terms of implications towards AB regeneration, the sheer favourability in ammonia of the H_B⋯H_A dihydrogen bonds may be the reason for the observed B–H bond redistribution in AB waste treated with ammonia.¹⁸ Typically, the reduction of BX₃ (X = O, S, or halide) to BH₃ is the highest energy step in regeneration. In ammonia however, the formation of BH₃ would be stabilised by the numerous dihydrogen bonds formed with the H_As, making the reduction more facile. Ammonia can also stabilise the formation of AB via interacting with the other end of the molecule through a regular hydrogen bond. This is the only interaction possible in other coordinating solvents like THF and other ethers, which lack the multitude of partially positive hydrogens ammonia has and therefore cannot stabilise BH₃. An example of a different solvent that does is water, but that raises issues in terms of incompatibility with reducing agents like sodium borohydride, that ammonia does not have. This explains the relative success of regeneration processes in ammonia, and suggests that any energetically efficient regeneration would be wise to use it as a solvent.

4 Experimental

¹¹B enriched ammonia borane was synthesised following the procedure described in Ramachandran and Gagare.⁴⁴¹¹B enriched sodium borohydride and borodeuteride were sourced from Katchem, ammonium sulfate from Alfa Aesar, and the THF from Sigma-Aldrich. Deuteration of the nitrogen hydrogens was achieved by dissolving in D₂O and removing the solvent under reduced pressure three times. All the chemicals were used as received without further purification. For the neutron scattering experiments, the THF and ammonia were both sourced from Sigma-Aldrich and again used without further purification.

The neutron scattering experiments were run on the Small Angle Neutron Diffractometer for Amorphous and Liquid Samples (SANDALS) beamline at the spallation neutron source ISIS, at the Rutherford Appleton Laboratory, Didcot, UK.⁴⁵ The neutron diffraction patterns of ND₃BD₃, NH₃BH₃ and ND₃BH₃ were measured dissolved in THF and THF-d₈, as well as ND₃BD₃ in a mixture of 50 : 50 THF : THF-d₈. The ND₃BD₃ in THF-d₈ sample was 12 wt% AB, with the other samples in the same mole ratio. For the ammonia experiments, less combinations were possible due to exchanging of the ammonia protons with the AB N–Hs. ND₃BD₃ and ND₃BH₃ were dissolved and measured in ND₃ along with NH₃BD₃ in NH₃. The ND₃BD₃ in ND₃ sample was 20 wt% AB, with the other samples in the same mole ratio.

The samples in THF were prepared under an inert atmosphere before being sealed in a cell made of a null-scattering titanium/zirconium alloy. The cell had a flat-plate geometry facing the neutron beam to reduce multiple scattering and absorption.³⁹ The diffraction pattern was measured at room temperature, monitored by a thermocouple, and the length of each experiment was approximately 8 hours. The samples in ammonia were measured in the same cell at 220 K, with the ammonia being condensed directly into the cell. The data correction method followed was that implemented by the Gudrun program.⁴⁶ This involved taking a background measurement of the empty instrument, the empty sample cell, and an incoherently scattering vanadium slab. Gudrun was also used to correct for the inelastic self-scattering using ‘top-hat’ deconvolution and an iterative method before the analysis by EPSR.^40,47 Analysis of the final simulation box after EPSR was performed using the dlputils software.⁴⁸

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the EPSRC (EP/L504889/1) and Cella Energy for funding, as well as the ISIS Neutron Scattering Facility for beamtime allocations RB1610270 and RB1610293 on SANDALS. We also thank Prof. Alan Soper for assistance with the THF EPSR simulation.

References

1. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1619–1636.
2. N. V. Belkova, L. M. Epstein, O. A. Filippov and E. S. Shubina, Chem. Rev., 2016, 116, 8545–8587.
3. S. C. Gatling and J. E. Jackson, J. Am. Chem. Soc., 1999, 121, 8655–8656.
4. X. Chen, J.-C. Zhao and S. G. Shore, Acc. Chem. Res., 2013, 46, 2666–2675.
5. D. G. Allis, M. E. Kosmowski and B. S. Hudson, J. Am. Chem. Soc., 2004, 126, 7756–7757.
6. W. J. Shaw, M. Bowden, A. Karkamkar, C. J. Howard, D. J. Heldebrant, N. J. Hess, J. C. Linehan and T. Autrey, Energy Environ. Sci., 2010, 3, 796.
7. S. M. Kathmann, C. J. Mundy, G. K. Schenter, T. Autrey, P. C. Aeberhard, B. David, M. O. Jones and T. Ramirez-Cuesta, J. Phys. Chem. C, 2012, 116, 5926–5931.
8. K. M. Dreux, L. E. McNamara, J. T. Kelly, A. M. Wright, N. I. Hammer and G. S. Tschumper, J. Phys. Chem. A, 2017, 121, 5884–5893.
9. K. P. Vijayalakshmi and C. H. Suresh, J. Phys. Chem. A, 2017, 121, 2704–2714.
10. P. L. A. Popelier, J. Phys. Chem. A, 1998, 102, 1873–1878.
11. F. H. Stephens, V. Pons and R. Tom Baker, Dalton Trans., 2007, 2613.
12. D. J. Wolstenholme, K. T. Traboulsee, Y. Hua, L. A. Calhoun and G. S. McGrady, Chem. Commun., 2012, 48, 2597.
13. A. D. Sutton, B. L. Davis, K. X. Bhattacharyya, B. D. Ellis, J. C. Gordon and P. P. Power, Chem. Commun., 2010, 46, 148–149.
14. A. D. Sutton, A. K. Burrell, D. A. Dixon, E. B. Garner, J. C. Gordon, T. Nakagawa, K. C. Ott, J. P. Robinson and M. Vasiliu, Science, 2011, 331, 1426–1429.
15. C. Reller and F. O. R. L. Mertens, Angew. Chem., Int. Ed., 2012, 51, 11731–11735.
16. Y. Tan, L. Zhang, X. Chen and X. Yu, Dalton Trans., 2015, 44, 753–757.
17. O. T. Summerscales and J. C. Gordon, Dalton Trans., 2013, 42, 10075.
18. B. L. Davis, B. D. Rekken, R. Michalczyk, E. B. Garner, III, D. A. Dixon, H. Kalviri, R. T. Baker and D. L. Thorn, Chem. Commun., 2013, 49, 9095.
19. C. H. Giammanco, P. L. Kramer and M. D. Fayer, J. Phys. Chem. B, 2015, 119, 3546–3559.
20. R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980.
21. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2013, 52, 4623–4627.
22. R. Hayes, S. A. Bernard, S. Imberti, G. G. Warr and R. Atkin, J. Phys. Chem. C, 2014, 118, 21215–21225.
23. R. J. Gillams, J. V. Busto, S. Busch, F. M. Goñi, C. D. Lorenz and S. E. McLain, J. Phys. Chem. B, 2015, 119, 128–139.
24. A. J. Johnston, Y. R. Zhang, S. Busch, L. C. Pardo, S. Imberti and S. E. McLain, J. Phys. Chem. B, 2015, 119, 5979–5987.
25. H. J. Jiang, S. Imberti, R. Atkin and G. G. Warr, J. Phys. Chem. B, 2017, 121, 6610–6617.
26. D. T. Bowron and K. J. Edler, Langmuir, 2017, 33, 262–271.
27. M. Falkowska, D. T. Bowron, H. G. Manyar, C. Hardacre and T. G. A. Youngs, ChemPhysChem, 2016, 17, 2043–2055.
28. A. Soper, Chem. Phys., 1996, 202, 295–306.
29. A. Soper, Mol. Phys., 2001, 99, 1503–1516.
30. A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204.
31. I. J. Chen, D. Yin and A. D. MacKerell, J. Comput. Chem., 2002, 23, 199–213.
32. B. Zhong, L. Song, X. X. Huang, L. Xia and G. Wen, Phys. Scr., 2012, 86, 015606.
33. J. Gao, X. Xia and T. F. George, J. Phys. Chem., 1993, 97, 9241–9247.
34. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
35. R. C. Rizzo and W. L. Jorgensen, J. Am. Chem. Soc., 1999, 121, 4827–4836.
36. M. L. P. Price, D. Ostrovsky and W. L. Jorgensen, J. Comput. Chem., 2001, 22, 1340–1352.
37. E. K. Watkins and W. L. Jorgensen, J. Phys. Chem. A, 2001, 105, 4118–4125.
38. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
39. T. F. Headen, C. A. Howard, N. T. Skipper, M. A. Wilkinson, D. T. Bowron and A. K. Soper, J. Am. Chem. Soc., 2010, 132, 5735–5742.
40. A. Soper, Mol. Phys., 2009, 107, 1667–1684.
41. T. Richardson, S. de Gala, R. H. Crabtree and P. E. M. Siegbahn, J. Am. Chem. Soc., 1995, 117, 12875–12876.
42. M. A. Ricci, M. Nardone, F. P. Ricci, C. Andreani and A. K. Soper, J. Chem. Phys., 1995, 102, 7650–7655.
43. T. Kar and S. Scheiner, J. Chem. Phys., 2003, 119, 1473–1482.
44. P. V. Ramachandran and P. D. Gagare, Inorg. Chem., 2007, 46, 7810–7817.
45. C. Benmore and A. Soper, The SANDALS Manual, 1998.
46. A. K. Soper, GudrunN and GudrunX Manual, 2012.
47. A. K. Soper, ISRN Phys. Chem., 2013, 2013, 1–67.
48. T. G. A. Youngs, dlputils: Calculate Properties from Molecular Dynamics Trajectories, accessed July 2017, https://www.projectaten.com/dlputils.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp08220g

---