Electronic structure of dipeptides in the gas-phase and as an adsorbed monolayer†
Abstract
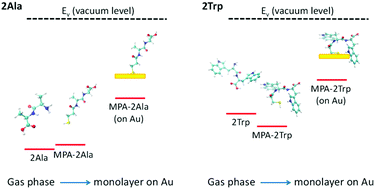
Peptide-based molecular electronic devices are promising due to the large diversity and unique electronic properties of biomolecules. These electronic properties can change considerably with peptide structure, allowing diverse design possibilities. In this work, we explore the effect of the side-chain of the peptide on its electronic properties, by using both experimental and computational tools to detect the electronic energy levels of two model peptides. The peptides include 2Ala and 2Trp as well as their 3-mercaptopropionic acid linker which is used to form monolayers on an Au surface. Specifically, we compare experimental ultraviolet photoemission spectroscopy measurements with density functional theory based computational results. By analyzing differences in frontier energy levels and molecular orbitals between peptides in gas-phase and in a monolayer on gold, we find that the electronic properties of the peptide side-chain are maintained during binding of the peptide to the gold substrate. This indicates that the energy barrier for the peptide electron transport can be tuned by the amino acid compositions, which suggests a route for structural design of peptide-based electronic devices.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...