Study of the electronic structure of electron accepting cyano-films: TCNQversusTCNE

Abstract

In this article, we perform systematic research on the electronic structure of two closely related organic electron acceptor molecules (TCNQ and TCNE), which are of technological interest due to their outstanding electronic properties. These studies have been performed from the experimental point of view by the use electron spectroscopies (XPS and UPS) and supported theoretically by the use of ab-initio DFT calculations. The cross-check between both molecules allows us to identify the characteristic electronic features of each part of the molecules and their contribution to the final electronic structure. We can describe the nature of the band gap of these materials, and we relate this with the appearance of the shake-up features in the core level spectra. A band bending and energy gap reduction of the aforementioned electronic structure in contact with a metal surface are seen in the experimental results as well in the theoretical calculations. This behavior implies that the TCNQ thin film accepts electrons from the metal substrate becoming a Schottky n-junction.

---

I. Introduction

7,7,8,8-tetracyano-p-quinodimethane (TCNQ) and other related organic donor–acceptor compounds have been the scope of a large number of studies over the last two decades. This interest arises from the very unusual electronic, optical, and magnetic properties exhibited by some of these materials.¹ The large plethora of enhanced electrical properties can be illustrated in quasi one-dimensional donor–acceptor charge-transfer systems incorporating TCNQ. Their properties can go from a Mott–Hubbard metal–insulator transition^2–4 or Peierls metal–insulator transition⁵ to possible Fröhlich-type superconductivity behavior.⁶ Their properties make them suitable for their use in many technological applications ranging from superconductivity to organic electronics, organic batteries,⁷ as materials for direct injection sensitized solar cells^8,9 or as candidates for spintronic devices. However, a clear prerequisite in the understanding of these materials’ properties is the determination of the electronic structure of the pure solid-films. Thus, detailed information on the electronic structure of TCNQ and related molecules is especially valuable in light of efforts to control the growth of films with given properties.¹³

A large number of surface spectroscopy techniques have been used to study the electronic structure of TCNQ (core-level photoemission spectroscopy,¹⁴ valence-band photoelectron spectroscopy,¹⁵ electron transmission spectroscopy¹⁶) and its anionic state^17–19 showing a large dispersion depending on the preparation method and, therefore, in the properties of the system. Thus, a systematic study that could lead to a complete description of the electronic structure of the TCNQ films that allows its spectroscopic features to be correlated to its electronic behavior is still lacking.

On the other hand, many studies of the electronic levels of TCNQ have been performed with a theoretical approach. They can be placed into three classes: ab initio,^20,21 semiempirical,^22,23 and Xα.²⁴ Although there are some previous studies that relate the electronic structure of these compounds with their electronic properties,^10–12 there is still a lack of a deep and complete correlation between their calculated electronic state and the different electronic singularities observed in these compounds. Our aim is to carry out a systematic experimental study supported by ab initio theoretical calculations in order to lead to a complete description of the electronic behavior of this acceptor organic system that could allow us not only to describe these properties but also to predict their singularities.

A similar molecule, tetracyanoethylene (TCNE), also forms a variety of donor–acceptor complexes and has been employed extensively in the study of electron-transfer phenomena. Because TCNE is somewhat smaller and simpler than TCNQ (see Fig. 1), it provides a useful case for proving our calculations and conclusions for the TCNQ case.

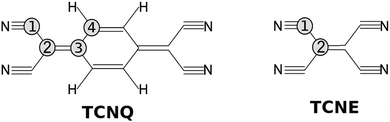Fig. 1 Molecular structure of; (left) TCNQ with four carbon atoms in different chemical environments and (right) TCNE with two carbon atom environments.

We have undertaken a systematic study of the electronic properties of TCNQ films on a metal substrate. For that purpose, we have studied the TCNQ film growth on a metal surface increasing the film thickness step-by-step and monitoring the changes in the electronic structure. Surface analysis techniques such as X-ray Photoelectron Spectroscopy (XPS), Ultraviolet Photoelectron Spectroscopy (UPS) and Inverse Photo-Emission (IPES) give access to the Fermi level and the electronic structure of a material. We have compared these results and those present in the literature to our theoretical results. We have made a cross-check of these properties with those obtained for TCNE films, in order to undoubtedly confirm our results and conclusions. The ab initio approach is the most suitable for comparing the theoretical results to the surface spectroscopy results. The ab initio calculations are, however, very expensive and storage limited, so it is difficult to perform them or to extend them to larger systems, as in the case of TCNQ. Here, we use first principles theoretical calculations performed in the context of Density Functional Theory^25,26 using the SIESTA^27,28 code, which has largely demonstrated its performance for such large molecular solids.

The origin of the UPS spectra features has been given by means of the theoretical calculations, making a correlation between each peak with its corresponding molecular orbitals. The assignment of the band gap with the molecular orbitals (HOMO, LUMO) can explain the presence of shake-up features in the core level photoemission spectra. Our study shows that a band bending of the electron bands of the TCNQ film at the metal interface is needed in order to explain all the different electronic properties observed. All these issues can play a crucial role in the properties of these materials for the production of organic electronic devices.

II. Method section

II.1. Experimental method

TCNQ (7,7,8,8-tetracyanoquinodimethane) powder from Sigma Aldrich was used in the experiment. The TCNQ films were deposited on a Cu(001) single crystal under Ultra High Vacuum (UHV) conditions (base pressure 2 × 10⁻¹⁰ mbar) maintaining the substrate at −50 °C by means of a nitrogen liquid circuit. We prepared the Cu(001) single crystal by “in situ” Ar⁺ sputtering and flash-annealing cycles under UHV conditions. As a result of this, a sharp diffraction pattern could be observed for the copper substrate, including copper surface diffraction rods giving a measure of the substrate quality. TCNQ was deposited by thermal evaporation from glass crucibles at a pressure of 1 × 10⁻⁸ mbar, which corresponded to a crucible temperature of 65 °C. Under these conditions the growth rate for TCNQ was measured to be 0.2 ML per min (Mono-Layer per min). Samples of different thickness were grown, but here we mainly show the results for a very thick film (17.1 ML).

The electronic properties were studied with a hemispherical energy analyzer (SPHERA-U7) and using a monochromatic Al Kα line source (hν = 1486.7 eV) for the X-ray Photoelectron Spectroscopy (XPS) studies and an ultraviolet He discharge lamp for the valence band measurements (Ultra-violet Photoelectron Spectroscopy, UPS). Both He I (hν = 21.2 eV) and He II (hν = 40.8 eV) lines were used for the UPS measurements. The analyzer pass energy was set to 20 eV for the XPS measurements to have a resolution of 0.6 eV, whereas for UPS, the pass energy was set to 5 eV corresponding to a resolution of 0.1 eV. All the core levels energies are calibrated with the Cu 2p_3/2 peak of the clean substrate (binding energy of 932.3 eV) and the UPS spectra to the Fermi edge of the clean Cu substrate. The TCNQ film measurements are compared to those obtained for the TCNE (tetracyanoethylene) films grown under the same experimental conditions here described. In Fig. 1, we show a sketch of both molecules.

The TCNQ structure was characterized by means of “in situ” surface X-ray diffraction at the W1.1 beamline at the Hasylab synchrotron at Desy. The experimental setup has a six circle goniometer to allow a diffraction geometry with fixed incoming beam angle onto the crystal surface and an UHV evaporation chamber with a large beryllium window (transparent to X-rays) to allow simultaneous X-ray diffraction (XRD) measurements during the film growth.²⁹ The X-ray diffraction studies (not shown here) show that under the used growth conditions, the TCNQ film preserves a C2/c monoclinic structure, with a = 8.906 Å, b = 7.060 Å, c = 16.395 Å and β = 98.54° cell parameters.³⁰ The TCNQ film shows a preferential orientation with respect to the substrate. The film has a TCNQ (020) orientation, with the TCNQ molecules being stacked perpendicular to the substrate direction. But the C-ring of the TCNQ molecules does not lay completely parallel to the substrate surface.²⁹TCNE shows a P21/n monoclinic structure with a unit cell with a = 7.4890 Å, b = 6.2045 Å, c = 69911 Å and β = 97.235° being in complete agreement with the structure given by Chaplot et al.³¹

II.2. Theoretical method

In order to study the geometrical and electronic structure of TCNQ film, we use first principles density functional^25,26 calculations using the SIESTA code,^27,28 which uses localized orbitals as base functions.³² We use a double ξ basis set (in some instances, the results are checked by increasing the basis with polarized orbitals), non-local norm conserving pseudopotentials and for the exchange correlation functional, we use the generalized gradient approximation (GGA)³³ including van der Waals interaction as implemented by Roman-Perez and Soler³⁴ with the functional developed by Dion et al.³⁵ In some cases, the results are compared with those obtained with the functional originally developed by Berland and Hyldgaard.³⁶ The results depend quantitatively on the van der Waals implementation but qualitatively, they are very similar (see below). The calculations are performed with stringent criteria in the electronic structure convergence (down to 10⁻⁵ in the density matrix), 2D Brillouin zone sampling (up to 600 k-points), real space grid (energy cut-off of 400 Ry) and equilibrium geometry (residual forces lower than 2 × 10⁻² eV Å⁻¹). Due to the rapid variation of the density of states at the Fermi level, we used a polynomial smearing method.³⁷ Concerning the basis set used, it should be indicated that we could not get a good and stable density matrix and geometrical structure using the default SIESTA basis. We, instead, used a different cut-off for the basis set. For instance, in the case of carbon, we used 4.298 Bohr and 5.120 Bohr cut-off for l = 0 and l = 1, respectively, instead of the default values of 4.088 Bohr and 4.870 Bohr. In addition, we used an energy shift of 300 meV. We believe that a complete description of the electronic properties and structure of TCNQ using a localized basis set is by itself an interesting, and difficult, piece of research that, by the way, we are continuing to study.

Concerning the Mesh-Cutoff used (400 Ry), it is probably too large. We tried 200 and 300 Ry with very similar results. However, considering the rather sparse TCNQ structure, the small atoms involved, and the difficulties in obtaining an equilibrium structure, we decided to keep the value of 400 Ry in the calculations to avoid any “eggbox” effect. The calculated results were compared with the experimental valence band photoemission measurements.

The structure has been optimized in preliminary calculations for the isolated molecules, slabs for one layer, two layers, three layers and the full bulk structure. As the obtained results were similar to those found in the literature, for the final electronic structure calculations, the experimental lattice parameters were used.

A double cross-check between the experimental X-ray diffraction structure and the theoretical optimized structure has been made for both molecular solids. The optimized TCNQ molecular bond distances are comparable to those calculated by Long et al.³⁰ within a maximum divergence of 1.2% with respect to the literature. The molecular packing is driven by N⋯N and CN⋯NC van der Waals dispersion interactions leading to an interleaving herringbone packing motif similar to that observed for benzene and aromatic fused-ring systems with the cell lattice previously given. The calculated molecular TCNQ inter-plane distance along the b-axis direction is 3.536 Å and perpendicular to the TCNQ ring direction, it is 3.23 Å due to the herringbone angle of 48.2°, which is comparable to those data given by Long et al. (interplane distance of 3.45 Å and herringbone angle of 48°).³⁰ The perpendicular distance is also in agreement with the statistical studies of all TCNQ and MTCNQ compounds that gives an average distance of 3.3 Å,³⁸ indicating that the stacking is caused by the same driving forces.

The theoretical optimized TCNE structure also completely agrees with the diffraction structure shown in the literature.³¹ The remarkable point is that the TCNE C-bridge bond (bond between two C labeled as 2 in Fig. 1) is more similar in distance to the C-ring bond than to the C-bridge bond of TCNQ (TCNQ: C4–C4 bond and C2–C3 bond, respectively).

III. Results and discussion

III.1. XPS measurements

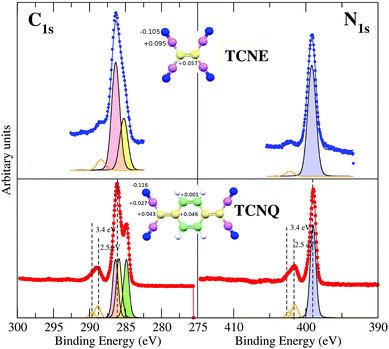
The XPS spectra of TCNQ have been measured with High Resolution (monochromatized Al Kα). The C1s and the N1s results are shown in Fig. 2.

Fig. 2 (left) C1s and (right) N1s XPS spectra of the TCNQ (bottom) and TCNE (top) thick films (17 ML) grown on Cu(001). The points show the high resolution spectra (red: TCNQ and blue: TCNE) and the lines show their corresponding low resolution spectra (orange: TCNQ and violet: TCNE). The yellow line shows the high resolution powder XPS spectra of a powder TCNQ sample, which has an intermediate shape between them.

The right lower panel of Fig. 2 shows the N1s core level spectra of TCNQ taken under low (orange line) and high (red points and line) energy resolution conditions. It may be noted that the low resolution spectrum is quite similar to those published by Grobman et al.³⁹ and Lindquist et al.¹⁴ The N1s TCNQ spectrum is characterized by a unique main peak at a binding energy of 399.1 eV, which is similar to the literature value (399.2 eV³⁹ and 399.7 eV¹⁴). A single peak agrees with an identical chemical environment for the four N of the TCNQ molecule (Fig. 1).

The N1s spectrum also has a broad satellite peak placed at 2.6 eV higher binding energy with respect to the main peak that has been associated in the literature to shake-ups. This peak has an intensity of 22% of the main peak, which is reasonable (usually, the intensity is 20% maximum with respect to the main peak). A detailed inspection of this peak lets us note that it is clearly asymmetric, indicating that it is not a single peak but due to two peak contributions (with an intensity of 15% and 7%, respectively). Both satellite shake-up peaks should be associated with the unique N1s XPS main peak of TCNQ. The shake-up phenomenon is an energy loss of the photoelectron due to other electron excitations to higher-lying bound states. It is related to a local intramolecular electronic excitation process but preserves the spatial localization.⁴⁰ Thus, there are two electron excitations across the band gap in the semiconducting TCNQ spatially related to the cyano-N atoms. Although this shake-up phenomenon assignation is well known in the literature, the origin of the electronic state transitions has not been clearly determined.

The left lower panel of Fig. 2 shows the C1s core level spectra of TCNQ taken under low (orange line) and high (red points and line) energy resolution conditions. The low resolution spectra are also similar to the corresponding C1s spectra published by Lindquist et al.¹⁴ However, the presence of two main peaks is clearer in the C1s high resolution spectrum given here (red points) than can be expected for carbon atoms present in more than one type of chemical environment in this compound. The TCNQ molecules have four different carbon environments (see Fig. 1), but only two peak contributions can be clearly distinguished in the spectrum. These two peaks are placed at 286.0 eV and 284.8 eV of binding energy. The intensity ratio between these two peaks is 2 : 1. The corresponding carbon chemical environment for each peak remains still not well established in the literature. In order to shine a light on this peak assignation, we have compared the TCNQ C1s spectra with the equivalent for TCNE. TCNE is chemically similar but a simpler molecule than TCNQ (Fig. 1). It has two types of chemical environments of C similar to TCNQ (labeled as 1 and 2) and two types of chemical environments absent (related to the C-ring and labeled as 3 and 4). The ratio is 4 C-cyano (label-1) versus 2 C-bridge (label-2). Thus, by comparing the two C1s high resolution spectra it seems that the higher binding energy main peak (the most intense one) is related to the cyano group carbon (type-1).

The TCNQ C1s spectrum (similarly to the already discussed N1s) has also shown a broad shake-up peak at higher binding energy. This shake-up also has an asymmetric shape (like the N1s shake-up) and it has shifted 2.6 eV with respect to the more intense main peak. The shake-up asymmetry is due to the presence of two components in the satellite peak. It can be noted that TCNE also has shake-up satellites in both the C1s and N1s XPS spectra. Although in this case, the shake-ups are less intense and thereby only observable in the high resolution XPS spectra.

In order to unequivocally assign the carbon peak origin in TCNQ and to define the transitions implicated in the TCNQ molecule photoemission shake-ups, we have undertaken theoretical calculations for those TCNQ and TCNE compound solids. The theoretical calculations show different carbon chemical environments in the TCNQ molecule when using the calculated Voronoi charge localization.⁴¹ The calculated charges are displayed in the inset of Fig. 3. There are two carbons that are clearly different; the C-cyano (type 1 in Fig. 1) that has a local positive charge and the C-ring (type 4) that has a local negative charge. Type 2 and 3, which from now we will call a C-bridge, have an intermediate charge and its value is very close between them. When we compare these results to the calculated Voronoi charge for the TCNE molecule case, it is clear than in the latter case, it has only the C-cyano (local positive charge) and C-bridge (local negative charge).

Fig. 3 Analysis of the components for the C1s (left panel) and N1s (right panel) XPS spectra of both TCNQ (bottom) and TCNE (upper). Each component has been colored considering their atomic contribution. This correlation has been made considering the calculated local Voroni atomic charge. The calculated charge localized in each atom is given in the structure sketch here shown. Orange lines show the components for the satellite shakeups that appear in the TCNQ and TCNE films.

These different C-environments can be used to explain the XPS spectra. There is no doubt in the N1s spectra peak fitting and assignation because there is a unique N chemical environment and a unique XPS main peak in both cases (TCNE and TCNQ). The C1s XPS spectrum of TCNE has two main peaks. A more intense peak placed at higher binding energy has an intensity ratio of 4 : 2 with respect to the less intense one. Considering the TCNE chemical formula and the calculated local charge (inset in Fig. 3), the highest binding energy C1s main peak corresponds to C-cyano atoms (the most positive charged carbon). These chemical shifts are in the direction predicted for the photoemission core level shift as a function of the local oxidation state.⁴²

The C1s spectrum of TCNQ has different contributions. Three different C-chemical environments can be distinguished with respect to their local charge. There are 4 C-cyano atoms (carbons with the intermediate positive local charge) and 4 C-ring atoms (the carbons with most negative local charge). Between both, there are the C-bridge atoms (type 2 and type 3) with the most local positive charge, which is very similar between them (there are 2 + 2 of these). Fig. 3 shows the fit considering the different environments described and their relative intensity (4 : 4 : 4). In any case, it is clear that the 4 C-ring atoms contribute to the well resolved peak at lower binding energy while the peak at higher binding energy is composed of the rest of the C atoms in two components that cannot be resolved. The binding energies of the peaks are in agreement with the expected core level shifts.⁴²

Orange lines in Fig. 3 show the fit for the shake-up satellites. The shake-up peak asymmetry is due to two contributions, 2.47 eV and 3.43 eV for the N1s and 2.56 eV and 3.36 eV with respect to the main peak for the C1s spectra of the TCNQ film. Considering that the shake-up comes from an electron transition between an occupied to an unoccupied band, the lowest satellite to peak energy distance ∼2.5 eV must be higher or at least equal to the TCNQ band gap. In the case of TCNE, the shake-up satellite cannot have such a detailed fit due to its lower intensity. It seems that the origin of the shake-up is the same in both organic films.

We have also observed a peak shift in the C1s and N1s XPS spectra toward lower binding energies by increasing the TCNQ film thickness. This effect has already been pointed out by other authors;⁴³ although the origin of such a phenomenon still remains unclear, some authors attribute this energy shift to the interplane π–π interactions. We have some evidence that this is not the origin of this effect.

III.2. UPS measurements

Fig. 4 shows the measured He–I photoelectron spectrum of TCNQ film (right panel). The lack of electron emission at the Fermi level indicates the insulator character of the solid TCNQ. This is compared with the TCNE solid spectrum measured under the same experimental conditions (left panel). These spectra are compared with the equivalent ones for the gaseous phase measured by Ikemoto et al.¹⁵

Fig. 4 Bottom panels: UPS spectra of the gas phase of TCNQ (orange on the left panel) and TCNE (violet on the right panel) as shown in the literature.⁹ These spectra are compared with their corresponding spectra for the very thick film measured by us (red and blue for TCNQ and TCNE, respectively). The UPS spectra have been shifted in energy taking into account the measured working function and the calculated polarization for each. Upper panels: DOS calculations.

The TCNQ gaseous data presented in the literature are shown in an energy scale referring to the vacuum zero. The TCNQ solid UPS spectrum measured by us is given in energy with respect to the metal Fermi level, which is measured with respect to the copper Fermi level (vertical solid lines). Thus, in order to put this in absolute energy with respect to zero, we need to correct it by using the TCNQ solid work-function. This work-function is experimentally derived from subtracting the cut-off photoemission energy (the edge placed at the highest absolute binding energy of the UPS spectra) with respect to the photon energy (21.22 eV for the used He–I excitation photon energy). The measured work-function is respectively 5.3 eV for TCNQ and 6.7 eV for TCNE. The value measured for TCNQ is comparable to other values given in the literature (Φ_TCNQ = 5.01 eV⁴⁴).

Furthermore, the TCNQ solid spectrum, after the aforementioned work function correction, shows a first peak at 8.6 eV, which is comparable to the values given in the literature (8.53 eV⁴⁵ and 8.0 eV³⁹). However, these values are different to the first peak of TCNQ gas (9.7 eV).¹⁵ This difference has been explained in the literature by the presence of a surface dipole in the solid. The presence of a surface dipole is well-established in the molecular system case. Thus, Lipari et al.⁴⁵ show that it is more appropriate to define the polarization energy as the shift required to bring the gas- and solid-phase peaks into coincidence. Thus, in our case, the difference between the first peak energy (8.6 eV) and the energy for the first peak of the gas-phase given by Ikemoto et al.¹⁵ (9.7 eV) is 1.1 eV, which is equal within the error bar to that obtained for Lipari et al.⁴⁵ (P = 1.13 eV) and close to that calculated by Sato et al.⁴⁶ (1.4 eV).

In the case of TCNE, the first peak appears (once it has been corrected by the work function) at 10.3 eV and the value given by Ikemoto et al. for the gas-phase is 11.9 eV.¹⁵ Thus, the polarization energy given by the necessary energy shift for overlaying the gas and solid phase UPS spectra is 1.6 eV. This value is within the usual energy range known for organic molecules, which can go from 0.9 eV to 3.0 eV.⁴⁶

After these energy corrections, it can be appreciated that both the gas-phase and the solid-phase UPS spectra of TCNQ are comparable except for a difference in the peak width. This indicates weak van der Waals forces between rigid molecules in the TCNQ solid.⁴⁷ In the case of TCNE, there are some more differences between the gas and the solid, however, the TCNE solid spectrum has a lower quality, in spite of having preserved the same experimental conditions. There is some electron density close to the Fermi edge indicating that the TCNE film can be lightly polluted.

The TCNQ UPS spectrum has two discrete peaks before the broad main peak and the TCNE has only one. It seems (by comparing their molecule structure) that one of these peaks could be related to the C-ring orbitals. However, the peak assignation of the UPS spectra still remains unknown. Thus, we have undertaken an analysis of the spectra by comparing with the theoretical DOS calculation (solid black line in Fig. 4). The high coincidence of the calculated density of state with the measured UPS spectra for both molecules can be observed. Even if the calculated peak intensity is in very good agreement with the UPS. However, both TCNQ and TCNE seem to have a contraction in the energy of the Density of State width of approx. 20%. We have checked the origin of this divergence and it seems that it could be due to the basis used in the ab initio method and not due to an error in the intramolecular distances.

We have shown that we are able to describe the occupied electronic state of both the TCNQ and the TCNE films. However, to further test the calculation validity as a step prior to seeing if they can be used to make some predictions in the films’ electronic behavior, we have also studied the unoccupied electronic state. In Fig. 5, we compare the energy corrected occupied DOS to the measured UPS spectra for TCNQ (black solid line versus red filled points) and the calculated unoccupied DOS to the inverse photoemission measurements shown in the literature⁴⁸ (black dashed line versus the magenta holed points).

Fig. 5 UPS (left panel) and C1s XPS (right panel) spectra of TCNQ. We have compared the spectra measured for a very thick film (17.1 ML in red) with that measured for a very thin one (1.8 ML in orange). The inverse photoemission spectrum⁴⁰ has been included to show the experimental state of the empty TCNQ bands. The calculated band structure is shown by a continuous black line for the occupied bands and dashed black lines for the unoccupied ones. The first peak at positive values in thick black line corresponds to the HOMO while the first peak in dashed black line corresponds to the LUMO orbitals. In the right panel, we have included as an inset the dependence of the XPS peak position versus the film thickness.

The TCNQ inverse photoemission spectrum is characterized by the presence of an isolated peak previous to a more continuous signal that resembles the isolated LUMO-peak that appears in our calculations. However, if the zero of both UPS and inverse photoemission experiment is the same, the HOMO to LUMO difference is ∼4.0 eV (see Fig. 3) but the calculated HOMO to LUMO distance is 1.8 eV. This huge difference between them can be due either to an underestimation of the TCNQ band gap in our calculations (error in the calculated gap) or to a difference in the energy scale between the UPS and inverse photoemission experiments (error in the estimated experimental gap) or both. Considering that the shake-up comes from an occupied to an unoccupied band electron transition, the lowest relative energy shake-up signal (∼2.5 eV) should be equal to or higher than the HOMO–LUMO band gap. Joel S. Miller et al.⁴⁹ calculated a band gap value of 2.5 eV by means of DFT calculations using the B3LYP functional for one isolate TCNQ molecule. Thus, the most plausible cause of this energy shift is mainly due to a difference in the zero of our UPS measurement due to a sample charge because of the isolator character of TCNQ (despite the use of a charge compensator during the UPS measurement). The high film thickness (17.1 ML) hides the substrate Cu-metal peak, which is usually used as an absolute energy reference in very thin films, making it impossible to neglect a certain sample charge during the measurement. Thus, we have shifted the zero of the UPS spectra in such a way that the HOMO to LUMO gap (the last UPS peak with respect to the first inverse photoemission peak) has a gap equal to the value given by the shake-up signal (2.5 eV) (see Fig. 6). Although the band gap is not exactly the same as that of the excitation energy because there is relaxation of the excited state that should be considered, we can, in a first approach, compare them. Our calculated HOMO to LUMO distance is 1.8 eV, which is close to this measured shake-up energy, considering the well-known underestimation in the solid gap calculations in our method.

Fig. 6 A sketch of the band structure of the TCNQ film on Cu(001). Only the TCNQ π-bands closer to the Fermi level are shown in order to have a clearer sketch. In a very thick film, TCNQ has the LUMO near to its Fermi level. In the vicinity of the metal substrate (very thin film), there is a band bending driving the TCNQ LUMO below the metal Fermi level. In this situation, the TCNQ LUMO is partially occupied by metal electrons. The TCNQ band gap decreases slightly at the metal interface. The metal interface extends up to the three first TCNQ layers.

Both our calculation and the experimental inverse photoemission show a LUMO band near the metal Fermi level. Thus, it can be partially occupied when it is close enough to a metal. The UPS spectra of the very thin TCNQ film (1.8 ML) over Cu(001) metal shows a small peak at 1.2 eV below the Fermi level (orange points in Fig. 5). Note the difficulty in identifying the peak due to the presence of a high intensity Cu-substrate d-band close to this region. Feyer et al.⁵⁰ also showed the appearance of a peak in TCNQ very thin films over Ag(001) or Cu(001) substrates at 0.95 eV and 1.20 eV, respectively. The UPS spectra of this very thin film shifts by ∼1.2 eV with respect to the very thick one (pink arrows in Fig. 5). Taking into account this spectral shift, this new peak is placed at the position estimated for the LUMO position. Thus, this appearing peak is related to a partial occupation of the TCNQ film LUMO.

The appearance of this peak is also associated with the disappearance of the shake-up peaks in both C1s and N1s XPS spectra. This behavior enhances two facts: the TCNQ LUMO level becomes below the metal Fermi level in very thin films and the shake-up phenomenon is related to the TCNQ LUMO band. This new peak (at 1.2 eV below the metal Fermi level) has an energy distance of 1.9 eV to the TCNQ HOMO, which is slightly lower than the gap of 2.5 eV of the very thick TCNQ film. There is a band gap distance reduction of ∼0.6 eV when the TCNQ solid suffers a charge transfer from the metal substrate. Our calculation reproduces this band gap reduction when the TCNQ is charged.

The shake-up disappearing and the TCNQ LUMO occupation relationship are confirmed in the MTCNQ compounds. It has been shown in the literature that when a metal–TCNQ compound is formed, the XPS spectra of C1s and N1s have no shake-up satellite. This is due to the transfer of charge from the metal to TCNQ since the TCNQ LUMO is partial/totally occupied.⁵¹

The inset in Fig. 5 shows the C1s position versus the film thickness. The substrate to TCNQ film electron transfer is accompanied by an XPS peak shift toward higher binding energies in both C1s and N1s spectra. This progressive XPS peak shift is indicative of a band bending in the TCNQ–film interface. The evolution of the peak position versus the film thickness gives a band bending of approx. 0.8 eV in the TCNQ film. This band bending value is comparable to the UPS spectrum shift in the very thin film with respect to the very thick one, being 1.2 eV. There is a good agreement between both measurements considering the low number of points in the XPS thickness dependence figure. The dependence of the XPS signal on the film thickness also allows the band bending extent to be estimated as the first three TCNQ layers.

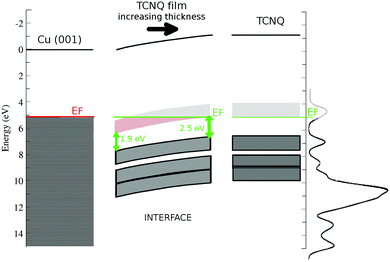
Fig. 6 shows a sketch of the band structure of the TCNQ film/Cu(001) interface made with the already discussed points. The used work functions are 5.1 eV for Cu(001)⁵² and 5.3 eV for the TCNQ film. We have also included the polarization previously calculated here for the TCNQ film (1.1 eV). It shows the band bending of TCNQ to be close to the metal interface already discussed. The proximity of the TCNQ LUMO band to the metal Fermi level allows a substrate to film electron transfer. It also shows the reduction of the TCNQ band gap at low film thickness, the band gap is 2.5 eV in very thick TCNQ films.

Thus, we have shown the quality of the theoretical calculations in both occupied and unoccupied states. In order to describe the different contributions to the UPS spectra, we have studied separately the different atomic contributions to the total DOS (see Fig. 7). In both TCNQ and TCNE, UPS spectra are characterized by the presence of a very intense broad peak (at ∼5 eV below the Fermi level). The partial density of state indicates that this intensity comes mainly from the cyano-group σ-bond (blue line is N and pink is C-cyano), justifying its presence in both samples. A difference between both samples is that TCNQ has two isolated peaks and TCNE has only one at energies closer to the Fermi level with respect to these main peaks. The partial density of state in the TCNQ indicates that one of these two peaks (indexed as 2) is mainly related to the C-ring π-bond (green line). The same case occurs for the TCNQ peak of ∼7.8 eV. These peaks do not appear in the TCNE solid due to the absence of a C-ring in its molecule. Thus, our calculation not only reproduces the experimental UPS spectra of both TCNQ and TCNE but can also explain their relative coincidences and differences. Our theoretical calculation of the density of states agrees to a high extent with the experimental data for both solids.

Fig. 7 Top: The partial atomic contribution to the total density of state (DOS) is shown. The color code used for the atoms contribution is the same as that already described (blue: N-cyano, pink: C-cyano, green: C-ring and yellow: C-bridge). The DOS is compared to the experimental UPS spectra of the molecule film. In the case of TCNE, we have also included the UPS for the gas phase due to the lower resolution measured for the film one. Bottom: We show a sketch of the atomic contribution to each band for those electronic bands closest to the Fermi level. The green and pink lines show the molecule symmetry planes perpendicular to the molecule-ring plane.

III.3. The origin of the shake-ups

Bearing in mind the aforementioned DOS decomposition, it is possible to describe the origin of the shake-ups. The shake-up are peaks resulting from the electron's loss of energy as it leaves during the ionization process with associated promotion of valence band electrons to either an excited state or continuum. The shake-up, or shake-off, process involves a monopole transition, the ion itself being a monopole. Thus, it must match the selection rules for monopole transitions, which are: D_l = 0, D_s = 0 and, therefore, D_j = 0 for the electron involved. This means that only a change in n can occur in both shake-up or shake-off processes. Furthermore, the highest shake-up and shake-off probabilities are for valence electrons. Thus, in order to relate the origin of the shake-ups, we have studied the partial atomic density contribution to the total DOS (Fig. 7).

We have already seen that the XPS shake-up satellite has two contributions (Fig. 3), which are placed at ∼2.5 eV and ∼3.4 eV with respect to the main XPS peaks (also the highest binding energy ones) in both C1s and N1s spectra. By comparing the N1s and C1s satellite for the TCNQ film, it can be observed that both are quite similar in shape but also in distance with respect to only the C1s main peak component. Thus, although the C1s XPS spectrum has two components, the observed shake-up satellite seems to be associated only with the main one. That means that the lower binding energy component, which we have shown to be related to the C-ring, has no clear shake-up signal associated with it. However, we cannot discard completely its presence because this can be hidden in the C1s main peak signal.

We have already shown that both components of the shake-up satellite are related to the LUMO band because they disappear when the LUMO band is partially occupied. It must be noted that the LUMO band of the thick TCNQ film is very close to its Fermi level, this fact being a clue for the apparition of shake-ups.

Using only the symmetry criteria for the monopole transition (inversion center in LUMO, HOMO−1 and HOMO−2, long molecular symmetry plane in LUMO, HOMO and HOMO−2 and short molecular symmetry plane in HOMO and HOMO−1), only the HOMO−2 to LUMO monopole transition should be allowed. However, some authors have shown in the literature that this rule is not preserved or can be broken for molecule cases.⁴⁰ Thus, we are going to consider all these possible transitions in spite of the symmetry transition rule. All the shown bands (HOMO−1, HOMO−2, HOMO and LUMO) have a π_z-character, thus the bond character will be preserved in their transition. This is a minimal requirement for the shake-up transitions.

Although both bands (HOMO and LUMO) have contributions from all the TCNQ atoms, the C-cyano (type-1, pink line) has the lowest contribution. Then, although the HOMO to LUMO transition does not preserve the symmetry, it preserves the atomic spatial localization. The calculated difference in energy between these two bands is 1.8 eV, which is in very good agreement with the first component of the shake-up satellite (2.5 eV).

The second shake-up component is at ∼3.4 eV with respect to the main XPS peak. This must also be related to an electron transition toward the LUMO level because it also disappears when substrate to TCNQ film doping occurs. The HOMO−1 band has a unique C-ring contribution (type-4 and green line) and the HOMO−2 has mainly atomic contributions from the C-bridge and N-cyano. The calculated energy difference is 3.0 eV between HOMO−1 to LUMO and 3.7 eV between HOMO−2 to LUMO. By comparing the experimental and theoretical spectra, we can infer that both the HOMO−1 and HOMO−2 bands contribute in the second UPS peak (with respect to the Fermi level) as in other theoretical calculations shown in the literature.⁴⁵ The experimental energy difference of this UPS peak with the first inverse photoemission peak is ∼3.4 eV (see Fig. 5), which agrees with the second shake-up component. Because the HOMO−1 band is only related to C-ring atoms, the HOMO−1 to LUMO transition should appear as a shake-up associated with the least intense and lower binding energy C1s peak and not with respect to the main peak. No clear shake-up intensity is observed at ∼3.4 eV with respect to the C-ring XPS peak. This may be due to the absence of this transition or because its own XPS signal and shake-up intensity, which are present in this region, make its observation difficult. The calculated energy distance between HOMO−2 and LUMO (3.7 eV) agrees well with the fitted second shake-up component, and this transition preserves the symmetry and the atomic spatial localization.

We have shown that the observed shake-up satellites come from the HOMO to LUMO and HOMO−2 to LUMO transitions and they are mainly associated with the C1s main peak, the symmetry transition rule for the monopole transition not being fulfilled. Other parameters must influence the shake-up appearance rules. The spatial atomic localization and the preserving of the bond character in the transition seem to be a rule that is fulfilled in our case. The HOMO−1 to LUMO transition cannot be completely discarded but it seems not to be present. In this case, this can be due to the absence of an electron in the C-cyano and C-bridge atoms in the HOMO−1 but that contributes largely in the LUMO. Thus, if a C-ring electron promotes to the LUMO level, the electron should be localized in a band with contributions of almost all the TCNQ molecule atoms, resulting in a loss of its spatial localization.

The presence of shake-up satellites in TCNE is therefore justified because of the presence of a LUMO band very close to the Fermi level. Their lower intensity is related to a unique transition from the HOMO (unique isolated peak below the Fermi level in UPS) to the isolated LUMO level at just above the Fermi level. The difference in this case should be ∼3.0 eV.

IV. Conclusions

We have performed a comparative study of the electronic structure of TCNQ and TCNE. We have unequivocally assigned the contribution of the C and N atoms of TCNQ and TCNE in the XPS spectra. The N1s XPS core level is characterized by a single peak, as it corresponds to a single N-atom chemical environment in both solids. The C1s spectrum is more complex as it corresponds to the presence of different chemical environments present in the molecules. Two contributions are needed in the TCNE case and three for the TCNQ. In the TCNQ case, we have shown that the C-ring contributes at lower binding energy of the spectrum while the C-cyano and the C-bridge carbons contribute to a single component at higher binding energy.

We have described the TCNQ and TCNE Density Of States. The final experimental electronic structure agrees well with the theoretical results. Furthermore, the energy alignment of the TCNQ electronic structure at the TCNQ/Cu(001) interface has been studied in detail. TCNQ is an insulator but it has an empty electron band nearby the Fermi level. This fact means that the TCNQ thin film accepts electrons from the metal substrate that are injected into this empty band, becoming a Schottky n-junction. This injecting ohmic junction can be used as a low resistance stable contact in organic semiconductor devices as an interface between the semiconductor and metal wires or control electrodes.

As a result of the aforementioned charge injection from the substrate, there is a band bending at the interface. This result is confirmed by the photoemission data (core levels and valence band) and gave as result a deep understanding of the level alignment at the interface with the copper substrate. The band bending is observed in the C1s and N1s core levels as well as in the UPS data for different coverages of TCNQ. From the core levels, a band bending of 0.8 ± 0.1 eV has been deduced. This result is in agreement with the observed TCNQ feature shifts for the UPS spectra of sub-monolayer coverage of TCNQ on Cu(001) (1.1 eV). The interface region width can be estimated as 3.1 ML. Moreover, a shift of the TCNQ LUMO position at the interface has been observed, reducing the TCNQ band gap from 2.5 eV in the bulk to 1.9 eV at the interface. Our theoretical calculations are consistent with this band-gap reduction originated in the charge injection in the LUMO at the interface.

The band structure is able to explain the electronic experimental measurements. Thus, it is compatible with the UPS and the inverse photoemission results. The theoretical calculations allow us to know the contribution of the TCNQ atoms to the different UPS features. This allows us both to perfectly describe the difference in the UPS spectra between TCNQ and TCNE, and to describe the origin of the shake-up signal measured in the XPS spectra in both solids. In such a way, the contribution of the different HOMO–LUMO transitions in the shake-up features has been analyzed in detail, for the TCNQ case, depending on the symmetry and local atomic density of state of the involved states in the frame of the monopole transitions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Spanish MICyT under grants No. FIS2016-74893-P and MAT2013-47869-C4-3-P. Authors would like to thank Prof. Dr Felix Yndurain for the theoretical calculations here shown and the further fruitful discussions. Parts of this research were carried out at the light source MAX-lab IV and Hasylab at DESY member of the Helmholtz Association (HGF). We would like to thank Dr O. Seeck his for assistance in using beamline W1.

References

1. R. Foster, Organic Charge-Transfer Complexes, Academic, London, 1969.
2. A. J. Epstein, S. Etemad, A. F. Garito and A. J. Heeger, Phys. Rev. B: Solid State, 1972, 5, 952–977.
3. L. B. Coleman, J. J. Cohen, D. J. Sandman, F. G. Yamagishi, A. F. Garito and A. J. Heeger, Solid State Commun., 1973, 12, 1125–1132.
4. J. Ferraris, D. O. Cowan, V. Walatka, Jr. and J. H. Perlstein, J. Am. Chem. Soc., 1973, 95, 948–949.
5. M. J. Rice and S. Strassler, Solid State Commun., 1973, 13, 125–128.
6. H. Frolich, Proc. R. Soc. A, 1954, 223, 296–305; J. Bardeen, Solid State Commun., 1973, 13, 357–359; D. Allender, J. W. Bray and J. Bardeen, Phys. Rev. B: Solid State, 1974, 9, 119–129.
7. B. V. Ratnakumar, S. Di Stefano, R. M. Willianms, G. Nagasubramanian and C. P. Bankston, J. Appl. Electrochem., 1990, 20, 357–364.
8. R. Jono, J. Fujisawa, H. Segawa and K. Yamashita, J. Phys. Chem. Lett., 2011, 2, 1167–1170.
9. S. Manzhos, R. Jono, K. Yamashita, J. Fujisawa, M. Nagata and H. Segawa, J. Phys. Chem. C, 2011, 115, 21487–21493.
10. R. Precht, R. Hausbrand and W. Jaegermann, Phys. Chem. Chem. Phys., 2015, 17, 6588–6596.
11. Y. Chen and S. Manzhos, Phys. Chem. Chem. Phys., 2016, 18, 8874–8880.
12. Y. Chen and S. Manzhos, Phys. Chem. Chem. Phys., 2016, 18, 1470–1477.
13. S. Masuda, H. Hayashi, Y. Harada and S. Kato, Chem. Phys. Lett., 1991, 180, 279–282.
14. J. M. Lindquistt and J. C. Hemminger, J. Phys. Chem., 1988, 92-6, 1394–1396.
15. I. Ikemoto, K. Samizo, T. Fujikawa, K. Ishii, T. Ohtaand and H. Kuroda, Chem. Lett., 1974, 785–790.
16. P. D. Burrow, A. E. Howard, A. R. Johnston and K. D. Jordan, J. Phys. Chem., 1992, 96, 7570–7578.
17. C. E. Klots, R. N. Compton and V. F. Raaen, J. Chem. Phys., 1974, 60, 1177–1178; R. N. Compton and C. D. Cooper, J. Chem. Phys., 1997, 66, 4325–4329.
18. E. C. M. Chen and W. E. Wentworth, J. Chem. Phys., 1975, 63, 3183–3191.
19. E. A. Brinkman, E. Gunter, O. Schaefer and J. I. Brauman, J. Chem. Phys., 1994, 100, 1840–1848; E. A. Brinkman, E. Gunter and J. I. Brauman, J. Chem. Phys., 1991, 95, 6185–6187.
20. H. T. Jonkman, G. A. Van der Velde and W. C. Nieuwpoort, Chem. Phys. Lett., 1974, 25, 62–65.
21. H. Johansen, Int. J. Quantum Chem., 1975, 9, 459–471.
22. M. Ratner, J. R. Sabin and E. E. Ball, Mol. Phys., 1973, 26, 1177–1184.
23. T. Ladik, A. Karpfen, G. Stollhoff and P. Fulde, Chem. Phys., 1975, 7, 267–277.
24. F. Herman and I. P. Batra, Phys. Rev. Lett., 1974, 33, 94–97; F. Herman and I. P. Batra, Nuovo Cimento B, 1974, 23, 282–291; F. Herman, A. R. Williams and K. J. Johnson, J. Chem. Phys., 1974, 61, 3508–3522.
25. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
26. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
27. P. Ordejon, E. Artacho and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, R10441–R10444.
28. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
29. M. J. Capitan, C. Navio, J. I. Beltran, R. Otero and J. Alvarez, J. Phys. Chem. C, 2016, 120, 26889–26898.
30. R. E. Long, R. A. Sparks and K. N. Trueblood, Acta Crystallogr., 1965, 18, 932–939.
31. S. L. Chaplot, R. Chakravarthy, W. I. F. David and J. Tomkinson, J. Phys.: Condens. Matter, 1991, 3, 9271–9278.
32. O. F. Sankey and D. J. Niklewski, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3979–3995.
33. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
34. G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102.
35. R. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
36. K. Berland and P. Hyldgaard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035412.
37. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
38. J. Huang, S. Kingsburyand and M. Kertesz, Phys. Chem. Chem. Phys., 2008, 10, 2625–2635.
39. W. D. Grobman, R. A. Pollak, D. E. Eastman, E. T. Maas and B. A. Scott, Phys. Rev. Lett., 1974, 32, 534–537.
40. T. A. Carlson, in Photoionization and Other Probes of Many – Electron Interactions, ed. F. Wuilleumier, Springer, US, 1976, NATO Advanced Study Institutes Series, (vol. 18, Chapter: Multiple Excitation in Free Molecules, pp. 343–353).
41. C. F. Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2003, 25, 189–210.
42. C. C. Chusuei and D. W. Goodman, Encyclopedia of physical science and technology, in X-ray Photoelectron Spectroscopy, ed. R. A. Meyers, 2003, vol. 17, p. 921.
43. C. Wackerlin, C. Iacovita, D. Chylarecka, P. Fesser, T. A. Jung and N. Ballav, Chem. Commun., 2012, 47, 9146–9148.
44. A. K. Neufeld, A. M. Bond and C. F. Hogan, Chem. Mater., 2003, 15, 3573–3585.
45. N. O. Lipari, P. Nielsen, J. J. Ritsko, A. J. Epstein and D. J. Sandman, Phys. Rev. B: Solid State, 1976, 14–6, 2229–2238.
46. N. Sato, K. Seki and H. Inokuchi, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 1621–1633.
47. H. Inokuchi, K. Seki and N. Sato, Phys. Scr., 1987, T17, 93–103.
48. K. Kanai, K. Akaike, K. Koyasu, K. Sakai, T. Nishi, Y. Kamizuru, T. Nishi, Y. Ouchi and K. Seki, Appl. Phys. A: Mater. Sci. Process., 2009, 95, 309–313.
49. H.-L. Vo, J. L. Arthur, M. Capdevila-Cortada, S. H. Lapidus, P. W. Stephens, J. J. Novoa, A. M. Arif, R. K. Nagi, M. H. Bartl and J. S. Miller, J. Org. Chem., 2014, 79, 8189–8201.
50. V. Feyer, M. Graus, P. Nigge, G. Zamborlini, R. G. Acres, A. Schöll, F. Reinert and C. M. Schneider, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 125–131.
51. M. J. Capitán, J. Álvarez, C. Navío and R. Miranda, J. Phys.: Condens. Matter, 2016, 28–18, 185002.
52. J. Holzl and F. K. Schulte, Solid Surface Physics, ed. G. Hohler, Springer-Verlag, Berlin, 1979.

---

Footnote

† PACS: 71. Electronic structure of bulk materials, 71.20.-b Electron density of states and band structure of crystalline solids, 73.20.-r electron states at surfaces and interfaces. 73.61.-r electrical properties of specific thin films, 73.61.Ph polymers; organic compounds.

---