Thermally induced hopping model for long-range triplet excitation energy transfer in DNA

Abstract

We present a theoretical model for long-range triplet excitation energy transfer in DNA sequences of alternating adenine–thymine steps. It consists of thermally induced hops through thymine bases. Intrastrand hops between thymines separated by an AT step are preferred to interstrand hops between thymines in consecutive steps. Our multi-step mechanism is consistent with recent results (L. Antusch, N. Gass and H.-A. Wagenknecht, Angew. Chem., Int. Ed., 2017, 56, 1385–1389) describing a shallow dependence of triplet sensitized DNA damage relative to the distance between the sensitizer and the reacting thymine–thymine pair.

---

Introduction

Pyrimidine dimers are the major products of DNA photodamage by near UV light, and their mechanism of formation has been extensively studied.^1,2 Their formation can be triggered by direct light absorption from the nucleobases, in which case it is assumed to involve singlet excited states. Pyrimidine dimers can be also generated after photosensitization by endogenous or exogeneous chromophores.^3,4 In the benzophenone case, the sensitizer undergoes intersystem crossing after the excitation, and the mechanism involves triplet excited states.⁵ This reaction is of great interest because it can be used as a Trojan horse to induce photodamage.⁶ Importantly, the sensitizer is intercalated in DNA but does not have to be located near the reacting pyrimidine pair. It can be separated from the reaction site by several pairs of stacked bases, in which case there is triplet excitation energy transfer (TEET) between the sensitizer and the reactive pair through the stack. Therefore, TEET is an essential part of triplet photosensitized DNA damage, and understanding it is important to realize the potential of photosensitization.

The mechanism of TEET has been considered in a recent paper by Antusch et al.⁷ which provides the starting point for our work. These authors have studied the distance dependence of T 〈〉 T (T = thymine) formation after triplet sensitization in specially synthetized double-strand DNA oligonucleotides consisting of A–T (A = adenine) base pairs and a benzophenone sensitizer (4-methylbenzophenone 1, 4-methoxy-benzophenone 2 or 2-methoxyacetophenone 3) covalently linked to DNA as C-nucleoside. This design fixes the position of the sensitizer in the DNA strand, and the distance-dependence of T 〈〉 T formation is studied by varying the number of alternated A–T base pairs between the triplet sensitizer X and two adjacent T units (see Scheme 1). It results in distances between 3.4 and 30 Å. The TEET process is quantified by the amount of T 〈〉 T formed within the DNA models after irradiation. There is a shallow exponential dependence of the photoproduct yield on the distance between the photosensitizer and the T 〈〉 T product, where the yield is proportional to exp(−βR_DA) and the value of the decay parameter β lies between 0.13 and 0.34 Å⁻¹ for the three studied systems. On the basis of these findings, the authors exclude a Förster resonance energy transfer mechanism⁸ and postulate that the Dexter-exchange mechanism⁹ is responsible for the long-range TEET.

Scheme 1

TEET has important common features with electron transfer (ET).^8,10,11 In particular, the rate of ET between donor and acceptor decreases exponentially with the intermolecular distance. It has been established experimentally that two main mechanisms, single-step (coherent) and multi-step (hopping) between guanine (G) bases, determine the hole transfer in DNA. A breakpoint between the two mechanisms occurs after 3–4 bases,^12,13i.e. the super-exchange interaction can mediate charge transfer only over short distances up to 3–4 bases.^14,15 The resulting mechanism is called thermally induced hopping (TIH) and has been used successfully to explain long-range charge transfer in DNA,^16,17 but until now it has not been considered to describe TEET. Here we provide a description of the TEET mechanism as a TIH between the T bases. The relative rates of individual steps are estimated from couplings calculated ab initio. Our results suggest that for the studied sequences, hops between T bases on the same strand separated by an A base are preferred to hops between T bases in consecutive steps lying on opposite strands.

Computational details

The inter-base couplings have been estimated from time-dependent density functional theory calculations for ideal B-DNA nucleobase stacks. Cartesian coordinates are provided in the ESI.† The calculations were carried out with the ω-B97XD functional¹⁸ and the def2svp basis set, using the E01 version of the Gaussian09 program,¹⁹ and the triplet excited states were calculated with the Tamm–Dancoff approximation.²⁰ The analysis of the excited states^21,22 and calculation of the electronic couplings^23,24 were performed using spin-free transition densities, with a local program.²⁵ Absolute TEET rates for the stack capped with the sensitizer 1 were obtained with Marcus theory.^26,27 The estimated reorganization energy is 0.60 eV.²⁸ The free energy difference for TEET between T bases and between T and 1 is approximated to zero, in line with experimental data that suggest that the free energy difference between benzophenone derivatives and T in DNA is about zero.²⁹ The system of kinetic equations is solved analytically with a matrix inversion approach.³⁰

Results and discussion

The proposed TIH scheme to estimate the photodimer yield in modified DNA oligomers is presented in Scheme 2.

Scheme 2

Our scheme assumes that the triplet exciton is localized on single T bases, in line with theoretical estimations.²⁸ The triplet excited photosensitizer, ³X, is formed after irradiation of the oligomer and intersystem crossing. The triplet exciton decays to the ground state with the rate k_dec,X or is injected irreversibly to a neighbouring T with the rate k_X. This step requires strong coupling between the sensitizer and the nearest T to be efficient, since non-covalently bound additives yield less than 1% T 〈〉 T dimerization yield. After the injection step, we consider two possible hop types to reach the dimerization site: interstrand hops with a rate k_inter, where the exciton migrates to the T base of the next step lying on the opposite strand, and intrastrand hops with a rate k_intra to the T base on the same strand located two steps away.

Scheme 2 illustrates the case where the sensitizer and the dimerization site are separated by two alternating A–T pairs (n = 1 in Scheme 1). Because of the twisted helical structure and the different relative positions of the bases in the stack, the two interstrand hopping rates are different. For larger separations (n ≤ 5), our kinetic scheme includes all interstrand hops between neighboring steps and all intrastrand hops over two steps. We assume that the hops can take place backwards at the same rate than forwards. At each site, the hops also compete with parallel decay channels that have the overall rate k_dec,T. These channels include non-radiative decay to the ground state found experimentally.⁷ We refer to the manifold of possible products as T⁰. The final step is the irreversible dimerization reaction with the rate k_dim. Note that our scheme does not account for the nick between the two dimerizing bases in the experimental system because we assume that the final step is irreversible.

While the actual rates of dimerization depend on the absolute rates of the individual steps, the quantum yield of T 〈〉 T in our scheme depends on the relative values of k_intra, k_inter, k_inter′ and k_dec,T. The relation between k_intra, k_inter and k_inter′ has been estimated from the calculated electronic couplings for an ideal (TAT)·(ATA) arrangement (see computational details). The calculated intrastrand coupling in Scheme 2 is 0.420 × 10⁻³ eV, and the interstrand couplings are 0.950 × 10⁻⁵ and 0.175 × 10⁻⁵ eV. Considering that the free energy for TEET between different T bases is equal to zero, the rates are proportional to the square of the coupling. Assuming these relations between the intra- and interstrand hopping rates, the quantum yield in our scheme depends on a single parameter γ, the ratio of ³T decay to intrastrand hopping rate (k_dec,T/k_intra). For given values of γ, the product yields can be obtained for different separations, i.e. different values of n in Scheme 1, by solving the system of kinetic equations (see Computational details). The decay parameter β is obtained fitting the relative yields as an exponential function of the distance.

The results obtained solving the kinetic scheme for different values of γ are presented in Table 1 and Fig. 1. The decay attenuation factor β depends on the relative probability of competing reactions (the side processes versus hopping) and increases with γ. For γ between 0.4 and 2.0, β ranges from 0.085 to 0.192 Å⁻¹. The fit for γ = 1.0 is presented in Fig. 1. We obtain excellent agreement with the experimental decay parameter of 0.13 Å⁻¹ for sensitizer 1.

Table 1 Relative T 〈〉 T yields and fitted decay parameter β as a function of γ

γ	n = 0	n = 1	n = 2	n = 3	n = 4	β [Å^−1]
0.4	1.000	0.627	0.357	0.195	0.105	0.085
0.6	1.000	0.545	0.267	0.127	0.060	0.106
0.8	1.000	0.483	0.210	0.089	0.037	0.123
1.0	1.000	0.434	0.170	0.065	0.025	0.138
1.5	1.000	0.347	0.111	0.035	0.011	0.167
2.0	1.000	0.290	0.078	0.021	0.006	0.192

---

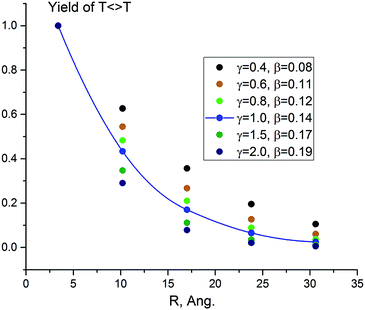Fig. 1 Computed photodimerization yield predicted by the TIH kinetic model (Scheme 2) for γ = 0.4–2.0 and different number of separating bases (n = 0–4). The line is the exponential fit of the data for γ = 1.0, with β = 0.14 Å⁻¹.

As an alternative to our TIH mechanism, we have considered the possibility of single-step TEET from the triplet donor (the sensitizer X) to the final acceptor (the first T unit of the dimerizing TT pair) involving super-exchange mediated by the (AT) pairs separating donor and acceptor. However, this seems not consistent with the experimental results. According to the common notion,^8,10,11 TEET is controlled by short-range electronic interactions between donor and acceptor. In many systems, TEET coupling is clearly dominated by the orbital interaction term, which is directly related to hole and electron transfer (HT and ET) between the donor and acceptor sites.⁸ It implies simultaneous super-exchange interaction between the HOMOs of donor and acceptor, as well as between their LUMOs, which leads to β_TEET ≈ β_HT + β_ET.⁸ Given that for super-exchange HT and ET in DNA, β_HT ≈ β_ET ≥ 0.7 Å⁻¹, we estimate β_TEET ≥ 1.4 Å⁻¹, which is much bigger than the β values of 0.13 and 0.17 Å⁻¹ reported for systems 1 and 3.⁷ In principle, a single-step Dexter mechanism could be reconciled with small β values assuming significant delocalization of triplet excitations over several bases. However, theoretical analysis of TEET in DNA²⁸ shows that triplet excited states in DNA are strongly localized on single bases. Direct coupling seems also unlikely, since for π-stacked organic molecules such as the nucleobases, β is found to be larger than 3 Å⁻¹.^8,31

To confirm these ideas about the single-step TEET and provide further support for the TIH mechanism, we have investigated an (AT)₂·(TA)₂ double-stranded stack of ideal conformation capped by a molecule of sensitizer 1 (see Fig. 2). For this model, the coupling between 1 and T over 0, 2 and 4 separating base pairs (corresponding to n = 0, 1 and 2 in Scheme 1) is V₀ = 0.54 meV, V₁ = 0.22 × 10⁻² and V₂ = 0.12 × 10⁻³ meV, and the estimated absolute rates for TEET (see computational details) are k₀ = 0.18 × 10⁸ s⁻¹, k₁ = 0.30 × 10³ s⁻¹ and k₂ = 0.91 s⁻¹. k₀ is a numerical estimate for k_X in our kinetic scheme (see Scheme 2). The results indicate that direct triplet exciton injection from 1 to the neighboring T base is greatly preferred against single-step TEET over 2 or more base pairs, in line with our mechanistic scheme. As an additional test, we have included single-step TEET in our kinetic model, and the results are indistinguishable from the ones obtained when this path is not included. This confirms that the single-step contribution to the TEET can be neglected compared to TIH.

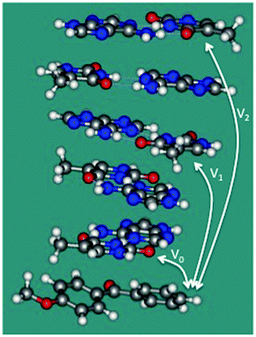Fig. 2 Double-stranded stack capped by a molecule of 1 used to estimate the couplings between the sensitizer and T bases separated by 0, 2, and 4 base steps (V₀, V₁ and V₂, respectively).

An important feature of our mechanism is that intrastrand coupling between T bases separated by A is much stronger (by about 2 orders of magnitude) than interstrand TT coupling between adjacent base pairs. Considering that the TEET rate is proportional to the square of the coupling, it can be inferred from the coupling values mentioned above that the main TEET path will involve intrastrand hopping mediated by A. Morevoer, the central AT pair plays an important role in mediation of the electronic interaction. If it is not included in the calculation, the intrastrand TT coupling becomes vanishingly small, 0.154 × 10⁻⁸ eV. However, the predominance of intrastrand over interstrand hops in the DNA oligomers studied here needs to be confirmed by calculations that consider the dynamic fluctuations of the DNA structure.

Conclusions

TEET in DNA fragments containing alternating AT pairs most likely follows a triplet–triplet hopping mechanism involving T bases, where every hop is mediated by Dexter-type coupling. This model is analogous to the well established TIH model for charge transfer in DNA strands and is based on the current physical view of TEET in molecular systems. The calculated couplings for an ideal B-DNA-like structure also suggest that in the present system, intrastrand steps over one separating A base, mediated by superexchange coupling, are preferred compared to interstrand hops between consecutive steps. This result needs to be confirmed by calculations accounting for structural fluctuations.

Our model is in good agreement with the observed exponential distance dependence, which is determined by the competition between the hops and side reactions. The model also suggests that the exponential decay factors derived from experiment can be used as an indirect measure of the parameter γ, that describes the role of side processes competing with the formation of the photoproduct T 〈〉 T.

Further insight into the TIH process could be provided, for instance, by experiments including sequence variations, i.e. substituting A–T pairs by C–G pairs. This would also help to elucidate whether superexchange TEET steps over a few bases can occur with different sequences than the one studied in ref. 7. For instance, it seems plausible that intrastrand hops mediated by an intermediate base will also occur when A is substituted by G.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Ministerio de Economía y Competitividad (MINECO), Spain (project CTQ2015-69363-P), the Departament d’Innovació, Universitats i Empresa (DIUE), Generalitat de Catalunya (Project 2014SGR1202) is gratefully acknowledged.

References

1. R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593.
2. T. Douki, A. Reynaud-Angelin, J. Cadet and E. Sage, Biochemistry, 2003, 42, 9221–9226.
3. B. Epe, Photochem. Photobiol. Sci., 2012, 11, 98–106.
4. E. Dumont and A. Monari, Front. Chem., 2015, 3, 43.
5. M. C. Cuquerella, V. Lhiaubet-Vallet, J. Cadet and M. A. Miranda, Acc. Chem. Res., 2012, 45, 1558–1570.
6. V. Vendrell-Criado, G. M. Rodríguez-Muñiz, M. C. Cuquerella, V. Lhiaubet-Vallet and M. A. Miranda, Angew. Chem., Int. Ed., 2013, 52, 6476–6479.
7. L. Antusch, N. Gass and H.-A. Wagenknecht, Angew. Chem., Int. Ed., 2017, 56, 1385–1389.
8. G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87.
9. D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850.
10. R. D. Harcourt, G. D. Scholes and K. P. Ghiggino, J. Chem. Phys., 1994, 101, 10521–10525.
11. N. J. Turro; V. Ramamurthy and J. C. Scaiano, Modern Molecular Photochemistry of Organic Molecules, University Science Books, Sausalito, Ca., USA, 2010.
12. B. Giese, S. Wessely, M. Spormann, U. Lindemann, E. Meggers and M. E. Michel-Beyerle, Angew. Chem., Int. Ed., 1999, 38, 996–998.
13. F. D. Lewis, H. Zhu, P. Daublain, B. Cohen and M. R. Wasielewski, Angew. Chem., Int. Ed., 2006, 45, 7982–7985.
14. H.-A. Wagenknecht, Nat. Prod. Rep., 2006, 23, 973–1006.
15. Charge Transfer in DNA: From Mechanism to Application, ed. H.-A. Wagenknecht, Wiley-VCH, Weinheim, Germany, 2005.
16. Y. A. Berlin, A. L. Burin and M. A. Ratner, J. Am. Chem. Soc., 2001, 123, 260–268.
17. M. Bixon and J. Jortner, J. Am. Chem. Soc., 2001, 123, 12556–12567.
18. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Revision E.01. Gaussian, Inc., Wallingford, CT, 2013.
20. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291.
21. A. V. Luzanov and O. A. Zhikol, Int. J. Quantum Chem., 2010, 110, 902–924.
22. F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 034106.
23. A. A. Voityuk, J. Chem. Phys., 2014, 140, 244117.
24. Z. Q. You and C. P. Hsu, J. Chem. Phys., 2010, 133, 074105.
25. A. A. Voityuk, Ecoupling v. 7.2, Girona, 2017.
26. R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322.
27. J. E. Subotnik, J. Vura-Weis, A. J. Sodt and M. A. Ratner, J. Phys. Chem. A, 2010, 114, 8665–8675.
28. C. Curutchet and A. A. Voityuk, Angew. Chem., Int. Ed., 2011, 50, 1820–1822.
29. F. Bosca, V. Lhiaubet-Vallet, M. C. Cuquerella, J. V. Castell and M. A. Miranda, J. Am. Chem. Soc., 2006, 128, 6318–6319.
30. A. Bar-Haim and J. Klafter, J. Chem. Phys., 1998, 109, 5187–5193.
31. C. Curutchet and A. A. Voityuk, J. Phys. Chem. C, 2012, 116, 22179–22185.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of structures. See DOI: 10.1039/c7cp07811k

---