Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Neutron diffraction and gravimetric study of the manganese nitriding reaction under ammonia decomposition conditions†
Thomas J.
Wood
 *a,
Joshua W.
Makepeace
*a,
Joshua W.
Makepeace
 ab and
William I. F.
David
*ab
ab and
William I. F.
David
*ab
aISIS Facility, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, OX11 0QX, UK. E-mail: thomas.wood@stfc.ac.uk; bill.david@stfc.ac.uk
bInorganic Chemistry Laboratory, University of Oxford, Oxford, OX1 3QR, UK
First published on 15th March 2018
Abstract
Manganese and its nitrides have recently been shown to co-catalyse the ammonia decomposition reaction. The nitriding reaction of manganese under ammonia decomposition conditions is studied in situ simultaneously by thermogravimetric analysis and neutron diffraction. Combining these complementary measurements has yielded information on the rate of manganese nitriding as well as the elucidation of a gamut of different manganese nitride phases. The neutron diffraction background was shown to be related to the extent of the ammonia decomposition and therefore the gas composition. From this and the sample mass, implications about the rate-limiting steps for nitriding by ammonia and nitriding by nitrogen are discussed.
Introduction
As a feedstock for fertilisers, ammonia is one of the most globally significant synthetic chemicals industrially with approximately 170 megatonnes produced per year via the Haber–Bosch process.1 Ammonia also has excellent potential as a clean chemical energy store2–4 since only water and nitrogen gas are produced on reaction with oxygen (either via combustion5 or in a fuel cell6–8). Other desirable properties include a specific energy of 5.2–6.2 kW h kg−1 (depending on whether water is produced as gas or liquid) and straightforward storage as a liquid at 10 bar and room temperature. In order to realise the potential of ammonia as an energy vector, advances both in the technology and understanding of the ammonia decomposition reaction are required, as this reaction is necessary to use ammonia in low temperature fuel cells and desirable for combustion engines.9 A large fraction of the studies performed on the ammonia decomposition reaction thus far have been with the motivation of studying the more currently relevant ammonia synthesis reaction.Transition metal catalysts, such as ruthenium, nickel and iron, are the most active with regards to ammonia decomposition.10,11 Recently, however, light metal amides and imides have also been found to decompose ammonia with performances comparable to ruthenium.12–14 There is some evidence that the use of transition metal nitride as co-catalysts with light metal amides and imides enhances the catalytic reaction, where manganese nitride is the best performer.15–17 Manganese nitrides have also been used in the reverse reaction—ammonia synthesis—as a looping catalyst.18
There exist few studies for the ammonia decomposition reaction over manganese and its nitrides, largely because it is relatively inactive without the presence of a light metal amide or imide.19 However, it is established that, given sufficiently high temperatures (above 500 °C), manganese will react with either ammonia or nitrogen (one of the products of ammonia decomposition) to form manganese nitrides.20 The structures of these various manganese nitride phases are well established, especially through the use of neutron diffraction to determine the magnetic structures as well as the nitrogen ordering.21–24
In this study, simultaneous in situ thermogravimetric analysis and neutron diffraction are employed to investigate the nitriding of manganese under ammonia decomposition conditions. Information gained on the quantity of phases present, as well as the rate-limiting steps of the nitriding reactions by ammonia or by nitrogen, is applied to the ammonia decomposition reaction using manganese (nitride) co-catalysts.
Experimental
In situ neutron diffraction measurements were performed at the POLARIS diffractometer, ISIS Pulsed Neutron and Muon Source, UK using the Intelligent Gravimetric Analyser for Neutrons (IGAn, Hiden Isochema). The experimental procedure largely followed that for iron nitriding under ammonia decomposition conditions reported previously.25 This entailed the weighing out of around 730 mg of manganese powder (99.3%, ∼325 mesh, Alfa Aesar) into a quartz bucket under inert atmosphere (to prevent any oxidation). The bucket was then hung from a fine tungsten wire connected to a balance. A stainless steel reaction chamber surrounded the sample and the entire setup was lowered into the neutron beam. Furnace elements were located above and below the quartz bucket and a thermocouple was also positioned above. The pressure was controlled by an inlet and outlet valve such that gas did not flow through the system, but any local changes in pressure (e.g. release of gas by sample) were adjusted for. A schematic of the setup is shown in the ESI.†Two experiments were run with manganese powder under ammonia (99.98%, SIP Analytical). First, the sample was heated to 250 °C at 4 °C min−1 and then to 420 °C at 1.4 °C min−1, where it dwelled for ∼15 h. Secondly, a fresh sample was heated to 480 °C at 3.7 °C min−1 (with a short interval of cooling when the neutron beam was unavailable), where it dwelled for ∼10 h before cooling at 2 °C min−1 to 420 °C and dwelling for a further ∼2.5 h. The ammonia atmosphere was evacuated and refreshed periodically for both experiments in order to remove nitrogen and hydrogen products from the ammonia decomposition reaction.
Neutron diffraction data were analysed by Rietveld analysis using TOPAS v5 (Bruker AXS). The banks of detectors used for fitting the data were the backscattering bank (up to 2.62 Å), the bank at 90° (up to 4.1 Å) and the low angle bank at 50° (up to 7.0 Å). Steel peaks were fitted by Pawley analysis using two different Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases corresponding to the reactor walls at neutron beam entry and exit points. Similarly, small peaks pertaining to the thermocouple were fitted to an Im
m phases corresponding to the reactor walls at neutron beam entry and exit points. Similarly, small peaks pertaining to the thermocouple were fitted to an Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m NiCr phase. A previously collected silica scattering pattern was used as a scalable background to fit the scattering from the quartz bucket in conjunction with a Chebyshev polynomial function. Multiple datasets were refined using a batch process from a seed dataset, which had all phases present.
m NiCr phase. A previously collected silica scattering pattern was used as a scalable background to fit the scattering from the quartz bucket in conjunction with a Chebyshev polynomial function. Multiple datasets were refined using a batch process from a seed dataset, which had all phases present.
Results & discussion
Nitride phases present
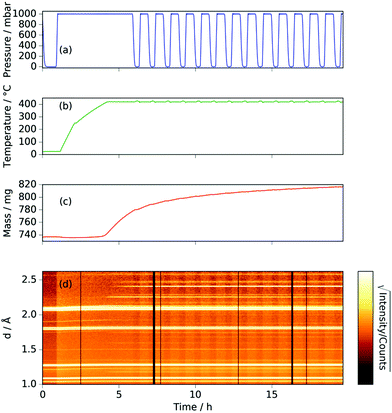
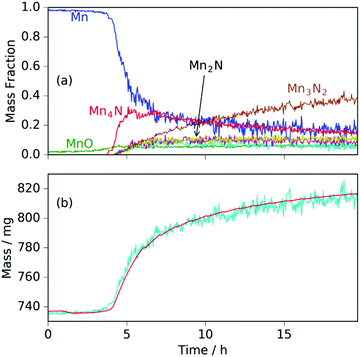
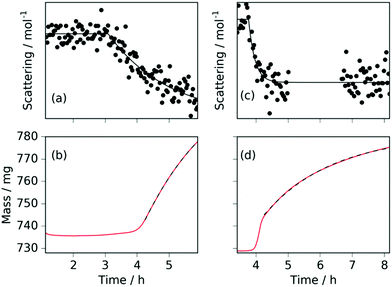
The neutron diffraction and sample mass data, along with the temperature and pressure, for the sample run at 420 °C are shown in Fig. 1. Pairs of steel peaks (corresponding to neutron beam entry and exit points) at 1.1 Å (311), 1.3 Å (220), 1.8 Å (200) and 2.1 Å (111) were the most prominent features. Initially, besides the steel peaks, there were manganese peaks at 2.10 Å (330)/(411) (this peak is initially a shoulder to the steel (111) peak), 1.90 Å (332), 1.75 Å (510)/(431) and 1.21 Å (721)/(633)/(552) along with the MnO(111) peak at 2.52 Å. After reaching 400 °C under ammonia the manganese peaks diminished and were replaced by manganese nitride phases including Mn4N (which appeared first with peaks at 1.18 Å (311), 1.59 Å (211), 1.75 Å (210), and 2.25 Å (111)), followed by Mn2N phases (with peaks at 2.17 Å, 2.29 Å and 2.47 Å) and Mn3N2 (which appeared concurrently to Mn2N with major peaks at 1.23 Å (181) and 2.41 Å (031)/(130)), Fig. 2(a).When the expected sample mass (calculated from the Rietveld analysis-obtained manganese nitride mass fractions) is compared with the actual mass gain (measured gravimetrically), there is excellent agreement over the course of the experiment, Fig. 2(b).
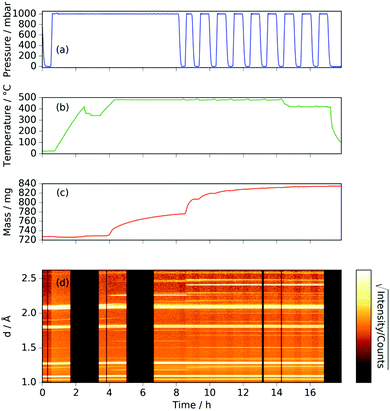
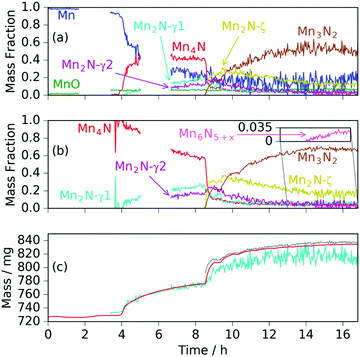
Heating a fresh manganese sample under ammonia to 480 °C showed similar results to those at 420 °C, in that the manganese peaks began to diminish at ∼400 °C and were replaced by Mn4N peaks followed by Mn2N phases, then Mn3N2 and finally Mn6N5+x (up to 3 wt%), Fig. 3 and 4. There are, however, some significant differences from the 420 °C experiment that include a greater degree of nitriding. This is shown by the appearance of Mn6N5+x after 13 h and a larger overall sample mass gain. It can also be seen that the sample mass gain is stepped in correlation with the ammonia evacuation–repressurization cycles (Fig. 3(a) and (c)).
Similarly to the 420 °C sample, below 8.5 h, the calculated sample mass from the Rietveld analysis agrees well with the gravimetrically measured sample mass, but above 8.5 h there is a significant underestimate. This can be explained by the Rietveld analysis overestimating the remaining elemental manganese fraction. There are a number of reasons for this: first, manganese itself has a much smaller (in absolute magnitude) coherent scattering length than nitrogen (−3.73 fm and 9.36 fm respectively); secondly, the largest Mn peak (the (330)/(411) peak at 2.10 Å) appeared as a shoulder of the largest steel peak and as such, there can be significant uncertainties when the manganese fraction is small. These manganese fraction uncertainties are shown by the noise of the manganese fraction trace after 8.5 h, Fig. 4(a). When the manganese (and manganese oxide) fractions are removed, the normalized manganese nitride phase fractions exhibit significantly reduced noise, such that even the evacuation–repressurization cycles can be seen as steps in the Mn3N2 fraction, Fig. 4(b). Moreover, the calculated sample mass above time = 8.5 h is significantly closer to the gravimetric value when the Mn fraction is assumed to be zero. After cooling to 420 °C, there was no significant change in the rate of mass increase, but the decrease of Mn2N levelled out.
Another significant difference between the two experiments is the fraction and composition of the Mn2N phases present denoted ζ in the Mn–N phase diagram (where Mn, Mn4N, Mn3N2 and Mn6N5+x are denoted α, ε, η and θ respectively).21 Leineweber et al. found that these Mn2N ζ phases had commonality in the hexagonal close packed ordering of the manganese atoms, but differed in the nitrogen ordering.23 Here we have borrowed the notation of γ to denote disordered nitrogen occupancy (space group P63/mmc) and ζ to denote orthorhombic ordering of the Fe2N type (other nitrogen orderings were not observed), Fig. 5.
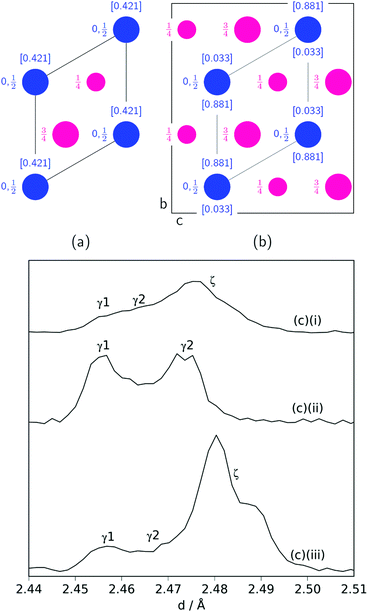 | ||
| Fig. 5 Nitrogen (blue) ordering within a hexagonal manganese (magenta) array for: (a) the disordered P63/mmc unit cell (ab plane shown) denoted γ; (b) the orthorhombic Pbcn unit cell (bc plane shown) denoted ζ. For both, the nitrogen occupancies are in square brackets and are taken from ref. 22. (c) Mn2N peak profiles (γ (100) reflection and ζ (021) and (002) reflections) for: (i) sample at 420 °C; (ii): sample at 480 °C (between time = 6.6 h and 8.5 h); (iii) sample at 480 °C (after time = 8.5 h). | ||
During the experiment run at 420 °C the γ and ζ Mn2N phases began to appear at the same time (from time = 4.2 h) and can be most simply fitted to two γ Mn2N phases and one ζ Mn2N phase, Fig. 5(c). This latter phase is easily discernible from the former phases by a (110) superstructure peak at 3.567 Å, which appeared in the 90° and 55° detector banks (see ESI†). It can be seen at 420 °C (Fig. 5(c)(i)) that the assignment of two γ phases is arbitrary and there is probably a solid solution between the γ end member nitrogen occupancy values. The low signal-to-noise ratio in the neutron diffraction data collected during these experiments (because of the relatively low mass fractions of these phases) did not allow these nitrogen occupancy values to be fit without a high degree of uncertainty, but it is assumed that an increase in the lattice parameters corresponds to an increase in nitrogen occupancy. At 480 °C, initially there was no ζ Mn2N phase present (this appeared on the first ammonia evacuation–repressurization cycle) and the γ phases separated into two end members (denoted γ1 and γ2), Fig. 5(c)(ii). When this sample was exposed to fresh ammonia, then the γ phases diminished significantly and the ζ phase began to appear, Fig. 5(c)(iii). These observations are consistent with the ζ phase being associated with a larger nitrogen occupancy, as previously observed.22
Possible nitriding mechanisms
Inspection of the neutron diffraction data in Fig. 1 and 3 show a significant difference in the height of the background dependent on the pressure of the system, where the background significantly increased upon the introduction of NH3 gas.25 This is due to the large incoherent scattering cross section of hydrogen, which is the major contributor to the background. Since the volume of the system is constant, the number of gas moles in the IGAn vessel is a function of pressure and temperature (according, to a good approximation, to the ideal gas equation, n = pV/RT). Integrating the background for the 90° bank for the 2.63–2.74 Å and 3.10–3.45 Å regions (where no Bragg peaks are expected) gives a measure of the changes in incoherent scattering. The following corrections were performed for the integrated background data: (i) the initial background (due to incoherent scattering from the manganese and steel walls as well as coherent and incoherent scattering from the silica bucket) was taken away; (ii) incoherent scattering from any nitrogen gained by the sample was taken away (by comparing the difference between the elemental manganese and the nitride manganese under vacuum); (iii) dividing the background data by p/T transformed the data into incoherent scattering per gas mole (i.e. removing the effects of pressure and temperature). For the experiment at 420 °C, the incoherent scattering per gas mole value was constant up to ∼3 h before decreasing steadily up to ∼6 h, Fig. 6(a). This decrease in scattering per gas mole is associated with either the manganese nitriding reaction: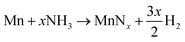 | (1) |
| 2NH3 → N2 + 3H2 | (2) |
Comparison of the incoherent scattering for this experiment with the sample mass shows that the ammonia begins to decompose (at ∼350 °C) before the manganese significantly increases in mass (at ∼400 °C), Fig. 6(a) and (b). This decrease in incoherent scattering was fitted to an exponential decay function (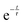 ), where τ = 1.9(6) h. Once the sample has reached a constant temperature of 420 °C, the sample mass gain can be well fitted to an exponential saturation function of the form
), where τ = 1.9(6) h. Once the sample has reached a constant temperature of 420 °C, the sample mass gain can be well fitted to an exponential saturation function of the form 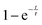 , where τ = 2.446(3) h. This can be related to the Kolmogorov–Johnson–Mehl–Avrami expression (which describes phase transformations), where
, where τ = 2.446(3) h. This can be related to the Kolmogorov–Johnson–Mehl–Avrami expression (which describes phase transformations), where 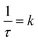 , the rate constant, and the exponent of t = 1; this may be indicative of a two-dimensional growth via a diffusional reaction process, with all nucleation sites present at the beginning of the reaction.26,27 This relationship between sample mass means that the nitriding reaction (eqn (1)) must be first order with respect to one of the reactants (either ammonia or manganese). Although the incoherent scattering per gas mole decrease is fitted to an exponential decay function, the noise in the data means that the ammonia decrease may follow a more complicated form. Indeed, for ammonia decomposition over most transition metal catalysts (including iron) the rate is dependent on both the ammonia and the hydrogen partial pressures (the Temkin–Pyzhev mechanism28).29 If this is the case here and the rate-limiting step of reaction (1) is dependent on the partial pressure of ammonia, the sample mass increase would be expected to be a more complex form than a simple exponential. If however, the rate-limiting step is first-order dependent on the ratio of elemental manganese to nitrided manganese, then this would fit with a simple exponential decrease in the manganese. Therefore the two possibilities that remain are: (i) the manganese nitriding reaction is first order with respect to the partial pressure of ammonia and the ammonia itself is decomposing via a tungsten-type mechanism (where N–H bond scission is the rate limiting step)29 or (ii) the manganese nitriding reaction is first order with respect to the ratio of elemental manganese to nitrided manganese.
, the rate constant, and the exponent of t = 1; this may be indicative of a two-dimensional growth via a diffusional reaction process, with all nucleation sites present at the beginning of the reaction.26,27 This relationship between sample mass means that the nitriding reaction (eqn (1)) must be first order with respect to one of the reactants (either ammonia or manganese). Although the incoherent scattering per gas mole decrease is fitted to an exponential decay function, the noise in the data means that the ammonia decrease may follow a more complicated form. Indeed, for ammonia decomposition over most transition metal catalysts (including iron) the rate is dependent on both the ammonia and the hydrogen partial pressures (the Temkin–Pyzhev mechanism28).29 If this is the case here and the rate-limiting step of reaction (1) is dependent on the partial pressure of ammonia, the sample mass increase would be expected to be a more complex form than a simple exponential. If however, the rate-limiting step is first-order dependent on the ratio of elemental manganese to nitrided manganese, then this would fit with a simple exponential decrease in the manganese. Therefore the two possibilities that remain are: (i) the manganese nitriding reaction is first order with respect to the partial pressure of ammonia and the ammonia itself is decomposing via a tungsten-type mechanism (where N–H bond scission is the rate limiting step)29 or (ii) the manganese nitriding reaction is first order with respect to the ratio of elemental manganese to nitrided manganese.
Further light can be shed on these reactions by examining the background incoherent scattering per gas mole and the sample mass gain for the sample at 480 °C before the first ammonia evacuation–repressurization cycle, Fig. 6(c) and (d). It can be seen from the incoherent scattering data that the ammonia decomposition reaction proceeds more quickly at higher temperatures—the time constants for the exponential fits in Fig. 6(a) and (c) are 1.9(6) h and 0.20(4) h respectively. As in the 420 °C case, the manganese nitriding starts at around 400 °C, but by ∼4.2 h there is a significant slowing in the rate of sample mass gain. However, the sample mass keeps increasing despite the fact that there is very little ammonia present. This increase in sample mass can (similarly to the 420 °C case) again be well fitted to an exponential saturation function of the form 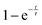 , where τ = 2.125(4) h. These considerations imply that the nitriding of the manganese occurs directly from nitrogen gas rather than via ammonia since there is very little present in the system beyond time = 4.2 h. This reaction would be of the form:
, where τ = 2.125(4) h. These considerations imply that the nitriding of the manganese occurs directly from nitrogen gas rather than via ammonia since there is very little present in the system beyond time = 4.2 h. This reaction would be of the form:
| 2Mn + xN2 → 2MnNx | (3) |
The nitriding reactions via ammonia (reaction (1)) and nitrogen (reaction (3)) are expected to proceed via a series of steps involving gas molecule adsorption, bond cleavage of either N–H or N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds to form N(ads) species on the manganese surface, followed by the dissolution of the adsorbed nitrogen atoms into the bulk lattice to form MnNx species. In the case of reaction (1), there would also be the recombination of H(ads) species and desorption to form H2, but this would not be expected to be rate limiting given that H2 readily forms from H(ads) on transition metal surfaces at these temperatures.30,31Reaction (1) can therefore be split into the following (generalized) reactions:
N bonds to form N(ads) species on the manganese surface, followed by the dissolution of the adsorbed nitrogen atoms into the bulk lattice to form MnNx species. In the case of reaction (1), there would also be the recombination of H(ads) species and desorption to form H2, but this would not be expected to be rate limiting given that H2 readily forms from H(ads) on transition metal surfaces at these temperatures.30,31Reaction (1) can therefore be split into the following (generalized) reactions:
| NH3(g) → NH3(ads) | (4) |
| NH3(ads) → N(ads) + 3H(ads) | (5) |
| Mn(s) + xN(ads) → MnNx(s) | (6) |
| 2H(ads) → H2(g) | (7) |
| N2(g) → N2(ads) | (8) |
| N2(ads) → 2N(ads) | (9) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond scission (reaction (9)) is rate limiting in the case of reaction (3). In both cases the chemisorption requires active sites on the manganese surface, where it is likely that there is a difference in active site density between elemental manganese and nitrided manganese. A significant number of extra experiments would be required to confirm these are definitely the rate-limiting steps (especially given that the presence of different manganese nitride phases has not been considered). However, the scenario where reaction (9) is the rate-limiting step for reaction (3) is consistent with the rate-limiting step observed for ammonia synthesis where N
N bond scission (reaction (9)) is rate limiting in the case of reaction (3). In both cases the chemisorption requires active sites on the manganese surface, where it is likely that there is a difference in active site density between elemental manganese and nitrided manganese. A significant number of extra experiments would be required to confirm these are definitely the rate-limiting steps (especially given that the presence of different manganese nitride phases has not been considered). However, the scenario where reaction (9) is the rate-limiting step for reaction (3) is consistent with the rate-limiting step observed for ammonia synthesis where N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond cleavage is slow32 and with the very slow degree of nitriding shown once the majority of manganese is (at least partially) nitrided at 480 °C.
N bond cleavage is slow32 and with the very slow degree of nitriding shown once the majority of manganese is (at least partially) nitrided at 480 °C.
Implications for use of manganese nitrides as ammonia decomposition catalysts
The results presented have implications for using manganese and manganese nitrides as supports/co-catalysts for ammonia decomposition. It has been reported that the combination of Mn6N5+x and lithium imide (Li2NH) results in a larger rate of ammonia decomposition than for either of the separate parts.15 There are a number of possibilities why this may be the case: (i) the lithium acts as a promoter to the manganese (nitride)-mediated ammonia decomposition; (ii) the manganese (nitride) catalyses the rate-limiting step in the lithium imide-mediated ammonia decomposition; (iii) the ammonia decomposition proceeds via an intermediate to which both manganese (nitride) and lithium imide contribute. Differentiating between these possibilities is not straightforward. Regardless of the mechanism of ammonia decomposition, however, greater understanding of how manganese nitrides and the propensity of manganese (nitride) surfaces to adsorb nitrogen is valuable information in elucidating these mechanisms. Different partial pressures of ammonia (and therefore nitrogen and hydrogen) in the system lead to differing rates of nitriding, which must be taken into consideration when using manganese nitride as an ammonia decomposition co-catalyst. The method of bypassing this variability is to use the end member MnN (Mn6N5+x where x is 1), but there is no evidence that this is the optimum phase for ammonia decomposition. Indeed previous studies of ammonia decomposition over manganese nitrides found that moving from lower to higher temperatures (the turning point being 440 °C) resulted in higher activation energies for ammonia decomposition, which was suggested to be due to different nitride species.19 If this relationship holds when lithium imide is a co-catalyst, then a lower degree of nitriding may be beneficial for the ammonia decomposition rate, in which case, the results shown here suggest that minimizing the partial pressure of ammonia (such that nitriding proceeds as slowly as possible) would be optimal.Conclusions
The nitriding reaction of manganese under ammonia decomposition conditions yields a variety of manganese nitride phases including at least two nitrogen-disordered P63/mmc (γ1 and γ2) Mn2N phases and one nitrogen-ordered Pbcn (ζ) Mn2N phase. The simultaneous gravimetric and neutron diffraction measurements agreed with each other and provided complementary information on nitriding rate and phase identification respectively. Further information on the gas composition (i.e. the extent of ammonia decomposition) gained from the incoherent background scattering of the diffraction data showed that the nitriding reaction proceeded by reaction of manganese with either ammonia or nitrogen gas. In the former case, the most probable rate-limiting step was inferred to be N–H bond scission on the surface of the manganese, whereas for the latter the scission of the nitrogen–nitrogen triple bond was most likely rate-limiting.Funding sources
This work was financially supported by an EPSRC grant “Fuel Cell Technologies for an Ammonia Economy”, EP/M014371/1. JWM would like to thank St John's College, University of Oxford for financial support.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge the technical assistance of Paul McIntyre, Adam Sears, James Taylor and Ronald Smith for technical assistance as well as Alan Soper for provision of neutron scattering data for silica.References
- “Nitrogen (Fixed)-Ammonia”, U.S. Geological Survey, Mineral Commodity Summaries, 2017.
- L. Green, Jr., Int. J. Hydrogen Energy, 1982, 7, 355–359 CrossRef
.
- A. Klerke, C. H. Christensen, J. K. Nørskov and T. Vegge, J. Mater. Chem., 2008, 18, 2304–2310 RSC
.
- F. Schüth, R. Palkovits, R. Schlögl and D. S. Su, Energy Environ. Sci., 2012, 5, 6278–6289 Search PubMed
.
-
R. Michikawauchi and Y. Ito, US Pat., 8240277, 2012 Search PubMed
.
- K. Kordesch, V. Hacker, J. Gsellmann, M. Cifrain, G. Faleschini, P. Enzinger, R. Fankhauser, M. Ortner, M. Muhr and R. R. Aronsson, J. Power Sources, 2000, 86, 162–165 CrossRef CAS
.
- J. C. Ganley, J. Power Sources, 2008, 178, 44–47 CrossRef CAS
.
-
M. J. Grieve and G. B. Fisher, US Pat., 8034499, 2011 Search PubMed
.
- M. Comotti and S. Frigo, Int. J. Hydrogen Energy, 2015, 40, 10673–10686 CrossRef CAS
.
- S. R. Logan and C. Kemball, Trans. Faraday Soc., 1960, 56, 144–153 RSC
.
- K. S. Love and P. H. Emmett, J. Am. Chem. Soc., 1941, 63, 3297–3308 CrossRef CAS
.
- W. I. F. David, J. W. Makepeace, S. K. Callear, H. M. A. Hunter, J. D. Taylor, T. J. Wood and M. O. Jones, J. Am. Chem. Soc., 2014, 136, 13082–13085 CrossRef CAS PubMed
.
- J. W. Makepeace, T. J. Wood, H. M. A. Hunter, M. O. Jones and W. I. F. David, Chem. Sci., 2015, 6, 3805–3815 RSC
.
- J. W. Makepeace, H. M. A. Hunter, T. J. Wood, R. I. Smith, C. A. Murray and W. I. F. David, Faraday Discuss., 2016, 188, 525–544 RSC
.
- J. Guo, P. Wang, G. Wu, A. Wu, D. Hu, Z. Xiong, J. Wang, P. Yu, F. Chang, Z. Chen and P. Chen, Angew. Chem., Int. Ed., 2015, 54, 2950–2954 CrossRef CAS PubMed
.
- J. Guo, F. Chang, P. Wang, D. Hu, P. Yu, G. Wu, Z. Xiong and P. Chen, ACS Catal., 2015, 5, 2708–2713 CrossRef CAS
.
- P. Yu, J. Guo, L. Liu, P. Wang, G. Wu, F. Chang and P. Chen, ChemSusChem, 2016, 9, 364–369 CrossRef CAS PubMed
.
- R. Michalsky, A. M. Avram, B. A. Peterson, P. H. Pfromm and A. A. Peterson, Chem. Sci., 2015, 6, 3965–3974 RSC
.
- C. R. Lotz and F. Sebba, Trans. Faraday Soc., 1957, 53, 1246–1252 RSC
.
- M. D. Lyutaya and A. B. Goncharuk, Powder Metall. Met. Ceram., 1977, 16, 208–212 CrossRef
.
- N. A. Gokcen, Bull. Alloy Phase Diagrams, 1990, 11, 33 CrossRef CAS
.
- A. Leineweber, R. Niewa, H. Jacobs and W. Kockelmann, J. Mater. Chem., 2000, 10, 2827–2834 RSC
.
- A. Leineweber, H. N. Jacobs and W. Kockelmann, J. Alloys Compd., 2004, 368, 229–247 CrossRef CAS
.
- A. Leineweber, H. Jacobs, W. Kockelmannn, S. Hull and D. Hinz-Hübner, J. Alloys Compd., 2004, 384, 1–5 CrossRef CAS
.
- T. J. Wood, J. W. Makepeace and W. I. F. David, Phys. Chem. Chem. Phys., 2017, 19, 27859–27865 RSC
.
- M. Avrami, J. Chem. Phys., 1940, 8, 212 CrossRef CAS
.
- A. D. Fortes, E. Suard, M.-H. Lemée-Cailleau, C. J. Pickard and R. J. Needs, J. Chem. Phys., 2009, 131, 154503 CrossRef PubMed
.
- M. I. Temkin and V. Pyzhev, Acta Physicochim. URSS, 1940, 12, 327–356 CAS
.
- K. Tamaru, Acc. Chem. Res., 1988, 21, 88–94 CrossRef CAS
.
- F. Bozso, G. Ertl, M. Grunze and M. Weiss, Appl. Surf. Sci., 1977, 1, 103–119 CrossRef CAS
.
- G. Ertl and M. Huber, J. Catal., 1980, 61, 537–539 CrossRef CAS
.
- G. Ertl, S. B. Lee and M. Weiss, Surf. Sci., 1982, 114, 515–526 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp07613d |
| This journal is © the Owner Societies 2018 |