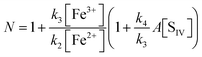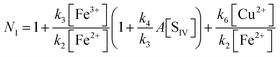The oxidation of sulfur(IV) by reaction with iron(III): a critical review and data analysis
Received
9th November 2017
, Accepted 9th January 2018
First published on 15th January 2018
Abstract
The dependences on ionic strength of the hydrolysis constants of Fe3+ and of the first dissociation constant of sulfurous acid are briefly reviewed. The data are needed to derive from apparent stability constants reported in the literature the stability constants for the three iron–sulfito complexes defined by the equilibria (c1) FeOH2+ + HSO3− = FeSO3+ + H2O, (c2) FeSO3+ + HSO3− = Fe(SO3)2− + H+, (c3a) Fe(SO3)2− + HSO3− = Fe(SO3)3H2−, where Kc1 = 1982 ± 518 dm3 mol−1, Kc2 = 0.72 ± 0.08, Kc3a = 189 ± 9 dm3 mol−1 (ionic strength μ = 0.1 mol dm−3). The rapid formation of these complexes is followed by a slower decomposition leading to the formation of SO3− radicals; the associated rate coefficients are k1 = 0.19 s−1, k1a ≈ 0.04 s−1, and k1b ≈ 0.08 s−1, respectively. The subsequent reaction leads to dithionate and sulfate as products. Overall rates and product yields from a variety of studies of the slow reaction are found to be consistent with a mechanism, in which the production of dithionate occurs mainly by the reaction of SO3− with FeSO3+ and that of sulfate by the reaction of SO3− with FeOH2+ and/or Fe3+. The role of copper as a catalyst is also analyzed. Rate coefficients for individual reactions are estimated from the data at low pH (μ = 1.0 mol dm−3) under conditions where the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is prevalent. They are extrapolated to lower ionic strengths for an analysis of the data obtained at higher pH to explore conditions when reactions of the higher complexes become important. The overall rate and the product yields of the reaction depend critically on the pH, the initial ratio of S(IV) to Fe(III) and the ionic strength of the solution.
1-complex is prevalent. They are extrapolated to lower ionic strengths for an analysis of the data obtained at higher pH to explore conditions when reactions of the higher complexes become important. The overall rate and the product yields of the reaction depend critically on the pH, the initial ratio of S(IV) to Fe(III) and the ionic strength of the solution.
Introduction
Iron belongs to a group of transition metals that are known to catalyze the oxidation of S(IV) in aqueous solution.1 Such reactions are of interest especially in the atmospheric sciences because they are predicted to occur in the aqueous phase of clouds and fogs, where they would contribute to the removal of SO2 from the atmosphere.1–3 Thus, it is not surprising that the Fe(III)-catalyzed oxidation of S(IV) in aerated aqueous solutions has been studied in much detail.1 A consistent chemical mechanism was developed,4,5 which incorporates a chain reaction carried by sulfuroxy radicals, and rate coefficients are available for most of the individual reactions involved.6–8 But Fe(III) is known to oxidize S(IV) also in the absence of oxygen. Far fewer studies have dealt with this process,9–16 and no consensus has been reached regarding the relevant mechanism. This reaction in de-aerated solutions is the subject of the present critical analysis.
There is agreement that the reaction is initiated by the formation of one or more iron–sulfito complexes. The presence of such complexes is indicated by the appearance, and the subsequent fading, of a reddish brown color when a solution containing Fe(III) is mixed with another solution containing S(IV). Stopped flow spectrophotometry has been used to follow the formation and decay of the complexes.14–17 Measurements at short reaction times suggest the existence of three complexes resulting from the successive addition to Fe(III) of S(IV) as ligand.17,19,20 Absorbance changes due to the variation of S(IV) concentrations have been exploited to derive apparent stability constants for the complexes under various experimental conditions.14,17–19 Unfortunately, the results have never been subjected to a detailed analysis, so that the true stability constants are still not available. The slower subsequent reaction, which leads to Fe(II), S(V) and S(VI) as products, has been studied by product analysis under conditions when the reaction is sufficiently slow.9–14 In reviewing these publications I have found that the modification of a simple reaction mechanism first proposed by Higginson and Marshall9 can explain most if not all of the experimental results.
Fundamental to an analysis of all experimental data is a knowledge of the speciation of Fe(III) and S(IV) resulting from the hydrolysis of Fe3+ and SO2aq, respectively, and their dependence on pH and ionic strength. This makes it necessary to review briefly the hydrolysis constants of iron, and the first dissociation constant of sulfurous acid. Whereas the ionic strength dependences of the iron hydrolysis constants are quite well known, that of the dissociation constant of sulfurous acid appears to have not been well defined in the literature so that it needs to be re-examined. Following these preliminaries the data available for the apparent stability constants of the Fe(III)–S(IV) complexes are reviewed, the true stability constants are derived, and rate coefficients of their formation are discussed. The results are then used in the subsequent analysis of the experimental data reported for the slower reaction, which follows the decomposition of the complexes. In addition to making use of functional relationships in evaluating the experimental data, computer simulations were carried out aiming to reproduce the experimental data.
Iron(III) in aqueous solution
Trivalent iron, Fe3+, undergoes hydrolysis in aqueous solution whereby FeOH2+, Fe(OH)2+, and Fe2(OH)24+ are formed as products. The sum of all species and the total concentration will be designated Fe(III) and [FeIII]tot, respectively. The relative concentrations of the different species are determined by equilibria that depend on the pH, the ionic strength and the total concentration. In acidic solutions the solubility of Fe(III) decreases with increasing pH; the final hydrolysis product Fe(OH)3 is the least soluble. Precipitation sets in at pH > 4, even at low concentrations, so that experimental studies of Fe(III) are restricted to the more acidic pH regime. At pH 2–3 the major species are Fe3+ and FeOH2+. The extent of dimer formation can be minimized by keeping [FeIII]tot below 1 mmol dm−3. Under such conditions the dominant equilibrium is| | | Fe3+ + H2O = FeOH2+ + H+ | (h1) |
| Kh1 = [FeOH2+][H+]/[Fe3+] |
The H2O molecule causing the hydrolysis is taken from the hydration sphere of Fe3+. In the following, the hydration sphere will be neglected, however. Fig. 1 shows Kh1 as a function of ionic strength at 25 °C. Points are values obtained from spectrophotometric measurements – conducted mainly at 340 nm wavelength – and the solid line represents the best fit to the extended Debye–Hückel equation
| | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kh1 = log Kh1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh1 − 2.04μ½/(1 + 2.4μ½) − 0.01μ, 0Kh1 − 2.04μ½/(1 + 2.4μ½) − 0.01μ, | (1) |
where log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh1
0Kh1 = −2.174 is obtained by extrapolation. The numerical parameters in this equation were originally suggested by Milburn and Vosburgh,
21 whose measurements covered ionic strengths up to
μ = 3.0. While spectrophotometry has been the favored measurement technique, potentiometric titration has also been applied, based on measuring simultaneously the hydrogen ion concentration and the Fe
3+/Fe
2+ redox potential. By means of computer-assisted analyses of the titration curves, Byrne
et al.30 and Stefanson
28 have obtained results in perfect agreement with those of Milburn and Vosburgh.
21
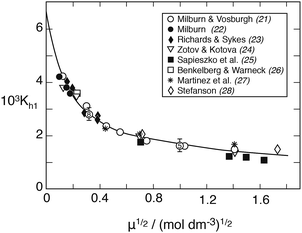 |
| | Fig. 1 The first hydrolysis constant of Fe(III) versus the root of ionic strength in NaClO4 medium at 25 °C derived from spectrophotometric measurements. To avoid crowding, the points at μ½ = 0.316 and 1.0 are shown as averages: the former includes 8 values from the authors listed plus Knight and Sylva,29 the latter includes five values. The solid line is calculated from eqn (1). | |
Whereas the dependence on ionic strength of the first hydrolysis constant is well documented, measurements of the second hydrolysis constant are still sparse. The equilibrium may be written in two ways:
| | | Fe3+ + 2H2O = Fe(OH)2+ + 2H+ | (h2) |
| | | FeOH2+ + H2O = Fe(OH)2+ + H+ | (h2a) |
| Kh2 = [Fe(OH)2+][H+]2/[Fe3+] |
| Kh2a = [Fe(OH)2+][H+]/[FeOH2+] |
Both equilibrium constants are related in that Kh2a = Kh2/Kh1. The first expression is prevalent in the literature, however. Early attempts to determine the equilibrium constant by means of potentiometric titration25,31,32 gave results that scattered over a wide range. Then Byrne et al.30 critically reviewed the data and concluded that potentiometric titration is not sufficiently sensitive and unsuitable for the determination of Kh2. On the other hand, more recent optical absorption studies over an extended range of pH have revealed a spectrum that was assigned,28,33,34 to Fe(OH)2+. This made the determination of Kh2 by means of spectrophotometry possible. Stefansson28 has summarized the available data and suggested an ionic strength dependence
| | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kh2 = log Kh2 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh2 − 3.06μ½/(1 + 1.58μ½) 0Kh2 − 3.06μ½/(1 + 1.58μ½) | (2) |
where log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh2
0Kh2 = −5.76 ± 0.06 was again obtained by extrapolation. This value, as well as that in the denominator of the second term, is still uncertain because of an insufficient number of data available at low ionic strengths.
The equilibrium constant of the Fe2(OH)24+ complex may also be defined in two ways:
| | | Fe3+ + 2H2O = Fe2(OH)24+ + 2H+ | (h3) |
| | | FeOH2+ + FeOH2+ = Fe2(OH)24+ | (h3a) |
| Kh3 = [Fe2(OH)24+][H+]2/[Fe3+] |
| Kh3a = [Fe2(OH)24+]/[FeOH2+]2 |
The first of these is preferred because it is nearly independent of ionic strength, whereas the second varies strongly with it. According to Stefansson28
| | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kh3 = log Kh3 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh3 + 0.022/μ½ 0Kh3 + 0.022/μ½ | (3) |
where log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh3
0Kh3 = −2.92.
Fig. 2 shows the distribution of Fe(
III) species
versus the pH for [Fe
III]
tot = 0.5 mmol dm
−3. Under these conditions the dimer contributes mostly in the pH region 3.0–3.5, but when [Fe
III]
tot ≤ 0.1 mmol dm
−3 the contribution of Fe
2(OH)
24+ can be neglected, while the distribution of the other species remains essentially unaffected.
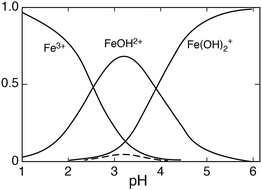 |
| | Fig. 2 The distribution of Fe(III) hydrolysis species as a function of pH, [FeIII] = 0.5 mmol dm−3, μ = 0.1; the broken line represents Fe2(OH)24+. | |
Sulfur(IV) in aqueous solution
When sulfur dioxide reacts with water, H2SO3, HSO3− and SO32− are formed as products. The sum of these species and their total concentration are designated S(IV) and [SIV]tot, respectively. Relative concentrations are determined by the two equilibria:
| Kd1 = [HSO3−][H+]/[SO2aq] |
| Kd2 = [SO32−][H+]/[HSO3−] |
Here, SO2aq denotes the sum of physically dissolved SO2 in water and sulfurous acid proper. The former displays a typical feature in the near ultraviolet absorption spectrum, whereas the latter cannot be so identified. Values of the two equilibrium constants at 25 °C and zero ionic strength (very dilute solution) are:350Kd1 = 1.39 × 10−2, 0Kd2 = 6.72 × 10−8 (mol dm−3). In the acidic pH range considered here the second dissociation process is essentially negligible. Regarding the first dissociation constant a greater number of studies have sought to determine 0Kd1, as reviewed by Goldberg and Parker,35 whereas the dependence on ionic strength appears to have been of lesser interest. The few reliable data are summarized in Fig. 3, which shows a plot of pKd1 = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd1 as a function of μ½ at 25 °C. The only systematic studies are those of Huss and Eckert,36 who used spectrophotometry and collected 33 data points at low ionic strength, and of Millero et al.,37 who employed potentiometric titration with a focus on high ionic strengths. The two data points of Sekine et al.38 were obtained as a byproduct of studying the distribution of S(IV) between carbon tetrachloride and water by means of iodometry. They agree well with the other data. The single point due to Devèze and Rumpf39 is included because these authors also used spectrophotometric measurements. This technique appears to be most reliable. The older data of Frydman et al.40 obtained for μ = 1.0 and μ = 3.5 mol dm−3 by potentiometric titration fall outside the range of the other data by a wide margin and are not shown. The solid line in Fig. 3 represents the best fit to the experimental data by the extended Debye–Hückel equation:
Kd1 as a function of μ½ at 25 °C. The only systematic studies are those of Huss and Eckert,36 who used spectrophotometry and collected 33 data points at low ionic strength, and of Millero et al.,37 who employed potentiometric titration with a focus on high ionic strengths. The two data points of Sekine et al.38 were obtained as a byproduct of studying the distribution of S(IV) between carbon tetrachloride and water by means of iodometry. They agree well with the other data. The single point due to Devèze and Rumpf39 is included because these authors also used spectrophotometric measurements. This technique appears to be most reliable. The older data of Frydman et al.40 obtained for μ = 1.0 and μ = 3.5 mol dm−3 by potentiometric titration fall outside the range of the other data by a wide margin and are not shown. The solid line in Fig. 3 represents the best fit to the experimental data by the extended Debye–Hückel equation:| | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd1 = log Kd1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kd1 + 1.02μ½/(1 + 1.3μ½) − 0.215μ 0Kd1 + 1.02μ½/(1 + 1.3μ½) − 0.215μ | (4) |
where log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kd1 = log
0Kd1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0139 = −1.85698 was kept fixed and the other two parameters were determined by a least square curve fitting program. The factor 1.3 in the denominator of the second term on the right is consistent with the value 1.64, which Huss and Eckert36 had adopted by analogy with other 1–1 electrolytes of comparable size. By extrapolating the Debye–Hückel equation to μ = 0 they had found 0Kd1 = 0.0138 ± 0.0004, in excellent agreement with 0Kd1 = 0.0139 ± 0.0002 obtained from conductivity measurements.
0.0139 = −1.85698 was kept fixed and the other two parameters were determined by a least square curve fitting program. The factor 1.3 in the denominator of the second term on the right is consistent with the value 1.64, which Huss and Eckert36 had adopted by analogy with other 1–1 electrolytes of comparable size. By extrapolating the Debye–Hückel equation to μ = 0 they had found 0Kd1 = 0.0138 ± 0.0004, in excellent agreement with 0Kd1 = 0.0139 ± 0.0002 obtained from conductivity measurements.
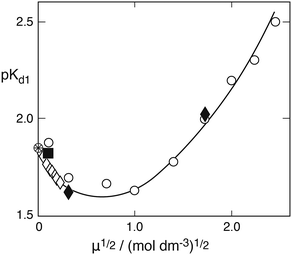 |
| | Fig. 3 The pK = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd1 of the first dissociation constant of sulfurous acid versus the root of ionic strength: open diamonds (Huss and Eckert36); filled diamonds (Sekine et al.38); open points (Millero et al.37); square (Devèze and Rumpf39). The solid line was calculated from eqn (4). Kd1 of the first dissociation constant of sulfurous acid versus the root of ionic strength: open diamonds (Huss and Eckert36); filled diamonds (Sekine et al.38); open points (Millero et al.37); square (Devèze and Rumpf39). The solid line was calculated from eqn (4). | |
Iron(III)–sulfito complexes
The interaction of S(IV) with Fe(III) leads to the formation of addition complexes that feature absorption spectra in the wavelength region 300–600 nm, partly overlapping the absorption spectra of FeOH2+ and Fe(OH)2+. The complexes are formed rapidly, whereas the subsequent reactions proceed more slowly, so that complex formation is best studied by means of stopped-flow techniques within a millisecond time frame. The early photometric titration experiments of Danilczuk and Swinarski20 had indicated the existence of three complexes formed by the stepwise addition of S(IV) to Fe(III) in the pH range 2–3, but the results of Conklin and Hoffmann14 and of Betterton18 subsequently provided evidence for the formation of only one complex. The existence of three complexes was ultimately confirmed by Kraft and van Eldik17 and by Prinsloo et al.,19 who employed rapid-scan spectrometry to follow the formation of the complexes as a function of time. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex was found to form very rapidly after mixing the reagents (in the mmol dm−3 concentration range), the formation of the 1
1-complex was found to form very rapidly after mixing the reagents (in the mmol dm−3 concentration range), the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex was completed within 10–50 ms, and the reaction to form the 1
2-complex was completed within 10–50 ms, and the reaction to form the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex took up to 200 ms to be completed. Conklin and Hoffmann14 had used a fixed reaction time of 10 ms; Betterton18 used a reaction time of 160 ms. The time frame in the latter study would have meant that at least the 1
3-complex took up to 200 ms to be completed. Conklin and Hoffmann14 had used a fixed reaction time of 10 ms; Betterton18 used a reaction time of 160 ms. The time frame in the latter study would have meant that at least the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the 1
1 and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes were present. This led to uncertainties in the data interpretation. Kraft and van Eldik17 had suggested that the 1
2-complexes were present. This led to uncertainties in the data interpretation. Kraft and van Eldik17 had suggested that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex can exist in two isomeric forms, but the data of Prinsloo et al.19 did not provide further support for the idea. The following analysis will focus on the results of the last authors because they reported the most comprehensive data set.
2-complex can exist in two isomeric forms, but the data of Prinsloo et al.19 did not provide further support for the idea. The following analysis will focus on the results of the last authors because they reported the most comprehensive data set.
Prinsloo et al.19 defined the reaction system in terms of the following equilibria
| | | FeOH2+ + HSO3− = FeSO3+ + H2O | (c1) |
| | | FeSO3+ + HSO3− = Fe(SO3)2− + H+ | (c2) |
| | | Fe(SO3)2− + HSO3− = Fe(SO3)33− + H+ | (c3) |
| Kc1 = [FeSO3+]/[FeOH2+][HSO3−] |
| Kc2 = [Fe(SO3)2−][H+]/[FeSO3+][HSO3−] |
| Kc3 = [Fe(SO3)33−][H+]/[Fe(SO3)2−][HSO3−] |
The authors did not present equilibrium constants in this form, however. Instead they reported apparent equilibrium constants defined by the equations
| Kc1app = [FeSO3+]/[FeIII][SIV] |
| Kc2app = [Fe(SO3)2−]/[FeSO3+][SIV] |
| Kc3app = [Fe(SO3)33−]/[Fe(SO3)2−]/[SIV] |
Here, [Fe
III] and [S
IV] represent the equilibrium concentrations of the sums of the free Fe(
III) and S(
IV) species, respectively. The relations between the true equilibrium constants and the apparent ones will be considered further below. Prinsloo
et al.19 had assumed the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2- and 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
3-complexes to be fully dissociated, but this need not be the case. In fact, it will be shown that in the pH range explored the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
3-complex occurs primarily in the form Fe(SO
3)
3H
2−. Other authors
9,11,12,14,16 have considered Fe
3+ to be involved in the formation of the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1-complex, and they have written
reaction (c1) in the form
| Fe3+ + HSO3− = FeSO3+ + H+ |
| | | Kc1a = [FeSO3+][H+]/[Fe3+][HSO3−] | (c1a) |
Yet this reaction is equivalent to the equilibrium (c1) because of the simultaneous equilibrium between Fe3+ and FeOH2+, so that Kc1a = Kc1Kh1. The possibility that SO32− is the reacting sulfur species rather than HSO3− is rather remote at pH < 3. It might become more important when the pH is raised to values exceeding pH 4.
Prinsloo et al.19 as well as other authors14,18 have applied the technique of Newton and Arcand41 to determine apparent equilibrium constants from the experimental data. The method is based on the equation
| | | A = A∞ − (1/K)(A − A0)/[SIV]n | (5) |
obtained by eliminating [Fe
III]/[Fe
III]
tot from the fundamental equations that describe the equilibria involved and the total absorbance. It is assumed that only one complex exists and that the equilibrium is fully established. The total concentration of iron is held constant, the concentration [S
IV] is varied, and the absorbance
A is measured;
A0 is the absorbance in the absence of S(
IV),
A∞ is the absorbance the solution would acquire if all Fe(
III) were incorporated in the complex. The equilibrium constant
K is found from the reciprocal of the slope of the line obtained by plotting
A vs. (
A −
A0)/[S
IV]
n. Newton and Arcand
41 had introduced the exponent
n = 1, 2 or 3 to make allowance for the prompt formation of a complex carrying the corresponding number of ligands. This case does not apply here, because the successive addition of S(
IV) to form complexes with more than one ligand will yield a straight line at low [S
IV], when
n = 1, with deviations from linearity at higher [S
IV] concentrations when additional complexes with different absorption coefficients are formed. It is important to note that [S
IV] represents the actual equilibrium concentration of S(
IV), which is initially not known but can be calculated once
K is established. It is customary to set [S
IV] ≈ [S
IV]
tot, but this approximation is approached only when [S
IV]
tot ≫ [Fe
III]
tot.
Plots of A versus (A − A0)/[SIV]tot for the 50–100 ms time frame reported by Kraft and van Eldik17 showed two intercepting linear portions (hockey-stick shape) that were interpreted as being due to the successive formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes. Betterton18 had raised doubts about this interpretation because his data did not show a change in the slope. Prinsloo et al.19 then restudied the absorption changes as a function of [SIV]tot, again by means of rapid-scan spectrometry. They largely confirmed the earlier results of Kraft and van Eldik17 and derived apparent stability constants for the complexes at pH 2.5 and pH 3, which they found to be essentially independent of wavelength in the region 390–470 nm (as required). The formation of the 1
2-complexes. Betterton18 had raised doubts about this interpretation because his data did not show a change in the slope. Prinsloo et al.19 then restudied the absorption changes as a function of [SIV]tot, again by means of rapid-scan spectrometry. They largely confirmed the earlier results of Kraft and van Eldik17 and derived apparent stability constants for the complexes at pH 2.5 and pH 3, which they found to be essentially independent of wavelength in the region 390–470 nm (as required). The formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes was studied at a reaction time of about 50 ms, that of the 1
2-complexes was studied at a reaction time of about 50 ms, that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex at later times. The values reported at pH 2.5 and 3.0 (T = 25 °C, μ = 0.1 mol dm−3) are: Kc1app = 425 ± 18 and 861 ± 120, respectively, as well as Kc2app = 231 ± 16 and 604 ± 52, Kc3app = 158 ± 18 and 190 ± 25 (units: mol, dm3).
3-complex at later times. The values reported at pH 2.5 and 3.0 (T = 25 °C, μ = 0.1 mol dm−3) are: Kc1app = 425 ± 18 and 861 ± 120, respectively, as well as Kc2app = 231 ± 16 and 604 ± 52, Kc3app = 158 ± 18 and 190 ± 25 (units: mol, dm3).
Corrections are still required because the equilibrium concentrations [SIV] < [SIV]tot. At short reaction times, when only the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes are present, the relevant mass balance equations are
2-complexes are present, the relevant mass balance equations are
| | | [SIV]tot = [SIV] + Kc1app[FeIII][SIV] + 2Kc1appKc2app[FeIII][SIV]2 | (6a) |
| | | [FeIII]tot = [FeIII](1 + Kc1app[SIV] + Kc1appKc2app[SIV]2) | (6b) |
The elimination of [FeIII] leads to a cubic equation for [SIV], which is conveniently solved by iteration techniques. Prinsloo et al.19 have applied [FeIII]tot = 1 mmol dm−3 and [SIV]tot = 1–20 mmol dm−3. Under these conditions it is found that at low concentrations of [SIV]tot the ratio [SIV]/[SIV]tot ≈ 0.6 at pH 2.5, and ∼0.5 at pH 3. At higher concentrations [SIV]/[SIV]tot approaches unity. The ratios depend little on the exact choice of Kc1app and Kc2app. It will be clear that corrections are required when the value of the first equilibrium constant is sought, whereas the equilibrium constants of the two higher complexes are much less thus affected. Estimates for the corrected Kc1app values may be obtained by applying the calculated correction factors directly to the reported Kc1app. This results in values of 773 ± 33 at pH 2.5 and 1722 ± 240 at pH 3.
Prinsloo et al.19 also presented (in their Fig. 2) measured absorbances A at λ = 390 nm as a function of [SIV]tot that can be used together with estimated values of A0 to prepare new Newton–Arcand plots based on the calculated [SIV] concentrations. The upper part of Fig. 4 shows the measured absorbance curves,19 while the lower part presents the corresponding Newton–Arcand plots at pH 2 and pH 2.5. Both demonstrate the hockey-stick shape, which indicates the increasing influence of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex when [SIV]tot is raised. The Kc1app values obtained from the initial slopes are 320 ± 26 at pH 2 and 787 ± 216 at pH 2.5. Data for pH 3 are not shown, because the number of data points defining the initial rise of absorbance is insufficient to allow a reasonably reliable evaluation. An estimate obtained from the first two points is Kc1app ≈ 2230, which is much higher than, and clearly inconsistent with, the approximate value 1722 ± 240 obtained above. However, the value reported by Prinsloo et al.19 at λ = 390 nm, Kc1app = 916 ± 113, is also higher than the average obtained from data at all wavelengths. The values for Kc2app obtained at pH 2.5 and pH 3 were only slightly different from those given above,19 the differences falling within the range of the experimental error.
2-complex when [SIV]tot is raised. The Kc1app values obtained from the initial slopes are 320 ± 26 at pH 2 and 787 ± 216 at pH 2.5. Data for pH 3 are not shown, because the number of data points defining the initial rise of absorbance is insufficient to allow a reasonably reliable evaluation. An estimate obtained from the first two points is Kc1app ≈ 2230, which is much higher than, and clearly inconsistent with, the approximate value 1722 ± 240 obtained above. However, the value reported by Prinsloo et al.19 at λ = 390 nm, Kc1app = 916 ± 113, is also higher than the average obtained from data at all wavelengths. The values for Kc2app obtained at pH 2.5 and pH 3 were only slightly different from those given above,19 the differences falling within the range of the experimental error.
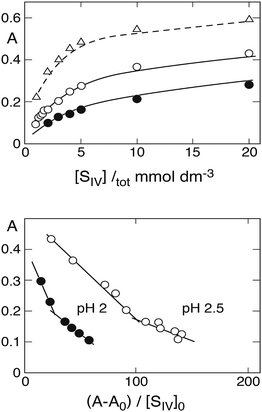 |
| | Fig. 4 Top: Rise of absorbance at 390 nm with increasing S(IV) concentration (Prinsloo et al.19), points pH 2, circles pH 2.5, triangles pH 3. Lines are calculated in the first two cases with ε(FeSO3+) = 270, ε(Fe(SO3)2−) = 400, ε(Fe(SO3)3H2−) = 450 (dm3 mol−1 cm−1); different values are needed to reproduce the absorbance curve at pH 3 (broken line, see text). Bottom: Newton–Arcand plots of the absorbance data at pH 2 and 2.5. | |
In order to determine the true stability constants from the apparent ones, reference is made to the definitions of the equilibrium constants Kc1–Kc3 and Kc1app–Kc3app. Thus, one finds for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex
1-complex
| | | [FeSO3+] = Kc1[FeOH2+][HSO3−] = Kc1app[FeIII][SIV] = Kc1app([Fe3+] + [FeOH2+])([SO2aq] + [HSO3−] + [SO32−]) | (7) |
From the equilibria involving the reactants and the associated equilibrium constants Kh1 = 2.87 × 10−3; Kd1 = 2.24 × 10−2; Kd2 = 1.5 × 10−7 (at μ = 0.1 and 25 °C) it follows that
| | | Kc1 = Kc1app(1 + [H+]/Kh1)(1 + [H+]/Kd1 + Kd2/[H+]) | (7a) |
The individual values of Kc1 calculated from the apparent stability constants derived at pH 2 and pH 2.5 are 2075 ± 167 and 1889 ± 518 dm3 mol−1. The average is 1982 ± 518 dm3 mol−1, where the statistical uncertainty is that of the reported measurements. The value at pH 3 derived from the corrected overall average, 1722 ± 240, would be Kc1 = 2426 ± 338, which is at the upper end of the error range. The value will not be used, because at pH 3 other iron–sulfito complexes may contribute to the observed absorbances (vide infra). The corrected value estimated from the overall average given by Prinsloo et al.19 at pH 2.5 is Kc1 = 1855 ± 80, which agrees well with that derived here from the data at 390 nm.
The equilibrium constant for the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex is,
2-complex is,
| | | Kc2 = Kc2app[H+](1 + [H+]/Kd1 + Kd2/[H+]) = 0.733 ± 0.102 | (8) |
This value is the average of the individual results 0.834 ± 0.058 at pH 2.5 and 0.631 ± 0.054 at pH 3. Here, the statistical uncertainty is that of the averaging process. The experimental error range is larger.
Finally, the equilibrium between the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes is considered. In this case, the observed Kc3app values show only a slight dependence on pH, indicating that the 1
3-complexes is considered. In this case, the observed Kc3app values show only a slight dependence on pH, indicating that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex remains nearly fully protonated in the (admittedly narrow) pH range covered. Accordingly, reaction (c3) should be written
3-complex remains nearly fully protonated in the (admittedly narrow) pH range covered. Accordingly, reaction (c3) should be written
| | | Fe(SO3)2− + HSO3− = Fe(SO3)3H2− | (c3a) |
| Kc3a = [Fe(SO3)3H2−]/[Fe(SO3)2−][HSO3−] |
The corresponding equilibrium constant is
| | | Kc3a = Kc3app(1 + [H+]/Kd1 + Kd2/[H+]) = 189 ± 9 dm3 mol−1 | (9) |
The value on the right is the average of the two results 180 ± 21 and 198 ± 26 obtained at pH 2.5 and pH 3, respectively. Here, the experimental error range is again greater than the statistical uncertainty of the averaging process.
It must be kept in mind that these results refer to an ionic strength μ = 0.1. The Debye–Hückel theory predicts log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc1 = log
Kc1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kc1 − 2.04μ½/(1 + aμ½), log
0Kc1 − 2.04μ½/(1 + aμ½), log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc2 ≈ log
Kc2 ≈ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kc2 (no significant ionic strength dependence), and log Kc3a = log
0Kc2 (no significant ionic strength dependence), and log Kc3a = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kc3a + 1.02μ½/(1 + βμ½). The factors a and β in the denominators of the second terms must be estimated. Regarding the equilibrium constant Kc1 Lente and Fabian16 have found Kc1a = Kc1Kh1 = 1.35 ± 0.15 at μ = 1.0 mol dm−3; which is equivalent to Kc1 = 825 ± 92 at this ionic strength. The corresponding value of a in the extended Debye–Hückel equation would be a ≈ 1.5. The value of Kc3a increases with increasing ionic strength, but the effect is not very pronounced, and it is neglected in calculating equilibrium distributions of the Fe(III) species.
0Kc3a + 1.02μ½/(1 + βμ½). The factors a and β in the denominators of the second terms must be estimated. Regarding the equilibrium constant Kc1 Lente and Fabian16 have found Kc1a = Kc1Kh1 = 1.35 ± 0.15 at μ = 1.0 mol dm−3; which is equivalent to Kc1 = 825 ± 92 at this ionic strength. The corresponding value of a in the extended Debye–Hückel equation would be a ≈ 1.5. The value of Kc3a increases with increasing ionic strength, but the effect is not very pronounced, and it is neglected in calculating equilibrium distributions of the Fe(III) species.
In order to compare the above results with those obtained by Conklin and Hoffmann14 and by Betterton18 it is necessary to calculate the relative distribution among the three complexes at the reaction times used by these authors. Rate coefficients for the formation of the complexes that are required for the calculations will be discussed in the next section. Here, only the results of such calculations are used.42 The experimental conditions applied by Conklin and Hoffmann14 were: pH 2.1, [FeIII]tot = 0.56 mmol dm−3, [SIV]tot = 0.5–45 mmol dm−3, μ = 0.4 mol dm−3, Δt = 10 ms. The calculated distribution of the complexes under these conditions shows that the first complex dominates only at very low S(IV) concentrations where the scatter of the measured absorbances would have obscured the initial slope determined by Kc1app. The bulk of the data refer to the second complex. In this region the contribution of the first complex remains nearly constant and the contribution of the third complex can be ignored. Measurements made at two wavelengths (350 and 450 nm) gave apparent K-values of 57.2 and 76.4, respectively, with an average of Kc2app = 66.8 ± 10.4 dm3 mol−1. When the correction factor of eqn (8) is applied, one obtains the true equilibrium constant Kc2 = 0.694 ± 0.11, which is in excellent agreement with the value calculated above from the data of Prinsloo et al.19 Thus, the three values can be combined to derive an overall average Kc2 = 0.72 ± 0.08.
Betterton18 has explored the change with pH of the apparent equilibrium constant under experimental conditions quite similar to those of Conklin and Hoffmann.14 The major difference was the longer reaction time (Δt = 160 ms) spent between mixing the reagents and observing the products in the optical cuvette. The measured Kapp was found to increase as the pH was raised from 1 to 3 whence a plateau was reached. This observation is in accord with the notion that the formation of the complexes proceeds via FeOH2+ and HSO3− as the active reactants, since the concentrations of both species increase with increasing pH. The calculated time dependence for the formation of the complexes indicates that at pH 1 where the concentrations of the reactants are small, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is still dominant after 160 ms reaction time, even at high S(IV) concentrations. This condition applies also at pH 1.25 over most of the [SIV] concentration range. Thus, the K-values reported by Betterton18 at low pH can be identified with Kc1app. At pH 1 ([FeIII]tot = 1.25 × 10−4 mol dm−3, μ = 0.5) the average of the reported K-values is Kc1app = 8.3 ± 3.7 (3 wavelengths), and at pH 1.25 ([FeIII]tot = 5.0 × 10−4 mol dm−3, μ = 0.2) the average is Kc1app = 11.4 ± 1.6 (6 wavelengths). Calculations for these experimental conditions show that [SIV] ≈ [SIV]tot so that corrections for [SIV] are not required. The true equilibrium constants, defined by eqn (7a), are then calculated to be Kc1 = 2143 ± 952 dm−3 mol−1 at pH 1, Kc1 = 913 ± 128 dm−3 mol−1 at pH 1.25. These values must be corrected for the ionic strength effect in order that they can be compared with the results of Prinsloo et al.,19 which were obtained at μ = 0.1. The corrected Kc1 values are estimated to be 3781 ± 1678 and 1151 ± 161 dm3 mol−1 at pH 1 and 1.25, respectively. The values bracket that derived from the data of Prinsloo et al.,19 but it is not obvious, why they diverge so much from each other.
1-complex is still dominant after 160 ms reaction time, even at high S(IV) concentrations. This condition applies also at pH 1.25 over most of the [SIV] concentration range. Thus, the K-values reported by Betterton18 at low pH can be identified with Kc1app. At pH 1 ([FeIII]tot = 1.25 × 10−4 mol dm−3, μ = 0.5) the average of the reported K-values is Kc1app = 8.3 ± 3.7 (3 wavelengths), and at pH 1.25 ([FeIII]tot = 5.0 × 10−4 mol dm−3, μ = 0.2) the average is Kc1app = 11.4 ± 1.6 (6 wavelengths). Calculations for these experimental conditions show that [SIV] ≈ [SIV]tot so that corrections for [SIV] are not required. The true equilibrium constants, defined by eqn (7a), are then calculated to be Kc1 = 2143 ± 952 dm−3 mol−1 at pH 1, Kc1 = 913 ± 128 dm−3 mol−1 at pH 1.25. These values must be corrected for the ionic strength effect in order that they can be compared with the results of Prinsloo et al.,19 which were obtained at μ = 0.1. The corrected Kc1 values are estimated to be 3781 ± 1678 and 1151 ± 161 dm3 mol−1 at pH 1 and 1.25, respectively. The values bracket that derived from the data of Prinsloo et al.,19 but it is not obvious, why they diverge so much from each other.
The Kapp-values reported by Betterton18 at pH 2 compare quite favorably with those of Conklin and Hoffmann14 at pH 2.1. Therefore, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex appears to be primarily involved. Rather similar results were obtained with [FeIII]tot = 2.5 × 10−4 and 5.0 × 10−4 mol dm−3. The average of 8 individual values obtained at 5 different wavelengths is 82.0 ± 11.2. The corresponding true equilibrium constant calculated with the help of eqn (8) is Kc2 = 1.15 ± 0.16. This result is higher than that derived above from the data of the other authors,14,19 but the calculated time dependence for complex formation shows that at the longer reaction time used by Betterton18 the contribution of the 1
2-complex appears to be primarily involved. Rather similar results were obtained with [FeIII]tot = 2.5 × 10−4 and 5.0 × 10−4 mol dm−3. The average of 8 individual values obtained at 5 different wavelengths is 82.0 ± 11.2. The corresponding true equilibrium constant calculated with the help of eqn (8) is Kc2 = 1.15 ± 0.16. This result is higher than that derived above from the data of the other authors,14,19 but the calculated time dependence for complex formation shows that at the longer reaction time used by Betterton18 the contribution of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex cannot be fully ignored. At concentrations [SIV]tot ≥ 10 mmol dm−3 the 1
3-complex cannot be fully ignored. At concentrations [SIV]tot ≥ 10 mmol dm−3 the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex becomes the dominant species, requiring appropriate corrections. The overall conclusion is that the results obtained by Betterton18 for this pH regime agree reasonably well with the other data discussed above. In the pH range 2–3, however, all three complexes are simultaneously present at similar concentrations, which makes it difficult to interpret the Newton–Arcand plots in a simple manner even if straight lines are observed. Note that nearly straight lines would be obtained if the 1
3-complex becomes the dominant species, requiring appropriate corrections. The overall conclusion is that the results obtained by Betterton18 for this pH regime agree reasonably well with the other data discussed above. In the pH range 2–3, however, all three complexes are simultaneously present at similar concentrations, which makes it difficult to interpret the Newton–Arcand plots in a simple manner even if straight lines are observed. Note that nearly straight lines would be obtained if the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes featured absorption coefficients of similar magnitude. From the preceding discussion it will be clear that much of the difficulty experienced in disentangling the three equilibria from simple absorbance measurements is due to the complexity of the system and the necessity of finding suitable experimental conditions for the task.
3-complexes featured absorption coefficients of similar magnitude. From the preceding discussion it will be clear that much of the difficulty experienced in disentangling the three equilibria from simple absorbance measurements is due to the complexity of the system and the necessity of finding suitable experimental conditions for the task.
The stability constants derived above for the Fe(III)–S(IV) complexes may be summarized as follows: Kc1 = 1982 ± 518 dm3 mol−1 (μ = 0.1), Kc1 = 825 ± 92 dm3 mol−1 (μ = 1.0), Kc2 = 0.72 ± 0.08 (μ = 0.1), Kc3a = 189 ± 9 dm3 mol−1 (μ = 0.1). These values will be employed further below when discussing the slow reaction following the formation of Fe(III)–S(IV) complexes.
Rates of formation of iron–sulfito-complexes
Kraft and van Eldik17 presented apparent rate coefficients for the formation of the second and third complexes. The formation of the first complex was too fast to be studied by stopped-flow spectrometry (kc1f > 103 s−1). Betterton18 used a pulse-accelerated flow technique to estimate the second order rate constant for the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex. He reported kc1f = 4.0 × 106 dm3 mol−1 s−1 at pH 2. This result when combined with the equilibrium constant derived above suggests kc1f = 4.0 × 106, kc1r = 2.08 × 103 for the rate coefficients of the forward and reverse reactions. Kraft and van Eldik17 used a stopped-flow instrument with a short mixing time (∼0.2 ms) to measure rate constants for the formation of the complex appearing within the 1–10 ms time frame (denoted step I). Experimental conditions were: [FeIII]tot = 2 mmol dm−3, pH 2.5, μ = 0.1, and [SIV]tot was varied between 10 and 60 mmol dm−3. The high concentrations of S(IV) combined with the time frame used make it fairly certain that the 1
1-complex. He reported kc1f = 4.0 × 106 dm3 mol−1 s−1 at pH 2. This result when combined with the equilibrium constant derived above suggests kc1f = 4.0 × 106, kc1r = 2.08 × 103 for the rate coefficients of the forward and reverse reactions. Kraft and van Eldik17 used a stopped-flow instrument with a short mixing time (∼0.2 ms) to measure rate constants for the formation of the complex appearing within the 1–10 ms time frame (denoted step I). Experimental conditions were: [FeIII]tot = 2 mmol dm−3, pH 2.5, μ = 0.1, and [SIV]tot was varied between 10 and 60 mmol dm−3. The high concentrations of S(IV) combined with the time frame used make it fairly certain that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex was observed. The rate constant was found to vary linearly with [SIV]tot (their Fig. 6a). From the slope of the straight line one obtains kc2app = 5.2 × 103 dm3 mol−1 s−1. A correction is needed to take into account that the reactive species is HSO3−. The appropriate correction factor (1 + [H+]/Kd1 + Kd2/[H+]) leads to kc2f = 5.9 × 103 dm3 mol−1 s−1. The rate coefficient for the reverse reaction step is calculated to be kc2r = kc2f/Kc2 = 8.24 × 103 dm3 mol−1 s−1. The formation of the 1
2-complex was observed. The rate constant was found to vary linearly with [SIV]tot (their Fig. 6a). From the slope of the straight line one obtains kc2app = 5.2 × 103 dm3 mol−1 s−1. A correction is needed to take into account that the reactive species is HSO3−. The appropriate correction factor (1 + [H+]/Kd1 + Kd2/[H+]) leads to kc2f = 5.9 × 103 dm3 mol−1 s−1. The rate coefficient for the reverse reaction step is calculated to be kc2r = kc2f/Kc2 = 8.24 × 103 dm3 mol−1 s−1. The formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex proceeds subsequent to that of the 1
3-complex proceeds subsequent to that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex. Kraft and van Eldik17 found that it can be conveniently followed by means of stopped-flow spectrometry within the time frame 50–200 ms (step II). The experimental conditions were [FeIII]tot = 0.5 mmol dm−3, pH 2.5, [SIV]tot = 5–50 mmol dm−3, μ = 0.1. Rate coefficients were measured as a function of [SIV] at two wavelengths (390 and 450 nm). From the slopes of the straight lines obtained in plots of kc3appvs. [SIV] (their Fig. 8 and 9) one obtains kc3app = 3.3 × 103 dm3 mol−1 s−1. The correction needed to take into account that HSO3− is the true reactant raises the value to kc3af = 3.8 × 103 dm3 mol−1 s−1. The corresponding rate coefficient for the reverse reaction step then is kc3ar = kc3af/Kc3a = 20.1 s−1.
2-complex. Kraft and van Eldik17 found that it can be conveniently followed by means of stopped-flow spectrometry within the time frame 50–200 ms (step II). The experimental conditions were [FeIII]tot = 0.5 mmol dm−3, pH 2.5, [SIV]tot = 5–50 mmol dm−3, μ = 0.1. Rate coefficients were measured as a function of [SIV] at two wavelengths (390 and 450 nm). From the slopes of the straight lines obtained in plots of kc3appvs. [SIV] (their Fig. 8 and 9) one obtains kc3app = 3.3 × 103 dm3 mol−1 s−1. The correction needed to take into account that HSO3− is the true reactant raises the value to kc3af = 3.8 × 103 dm3 mol−1 s−1. The corresponding rate coefficient for the reverse reaction step then is kc3ar = kc3af/Kc3a = 20.1 s−1.
These data were used to explore the successive formation of the three complexes and the overall development of the system as a function of time. Fig. 5 shows, as an example, the development calculated with [FeIII] = 1 mmol dm−3, [SIV]tot = 10 mmol dm−3, pH 2.5. The equilibrium between FeOH2+ and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is reached at times shorter than 1 ms. Full equilibrium between all three complexes is reached about 250 ms after mixing the reagents.
1-complex is reached at times shorter than 1 ms. Full equilibrium between all three complexes is reached about 250 ms after mixing the reagents.
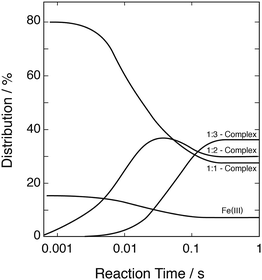 |
| | Fig. 5 Evolution with time of the distribution of the Fe(III)–S(IV) complexes; initial concentrations: [FeIII]tot = 1 mmol dm−3, [SIV]tot = 10 mmol dm−3, pH 2.5. | |
Absorption coefficients
As a consistency check the rate coefficients and equilibrium constants derived above may be used to calculate absorbance curves for comparison with the experimental results reported at λ = 390 nm19 as a function of [SIV]tot at three different pH (2.0, 2.5 and 3.0). The reaction time was 50–100 ms, [FeIII]tot = 1 mmol dm−3 (μ = 0.1). Molar absorption coefficients required for the calculation can in principle be estimated from the Newton–Arcand plots by extrapolating the observed straight lines back to the ordinate, where A → A∞. The method can also be applied when two complexes are successively formed, provided the straight lines observed are clearly separated. This implies that the absorption coefficients of the two complexes have distinctly different values. Prinsloo et al.19 have estimated absorption coefficients (their Table 1), but these refer to Fe(III) and S(IV) as reactants and should be considered order of magnitude values. An alternative method is to calculate the relative distributions of the individual complexes under the experimental conditions applied and adjust the individual values of the absorption coefficients until the observed absorbance curve is reproduced. As absorption coefficients are constants, the values should not change when the pH is varied.
Table 1 Reaction mechanism for the oxidation of S(IV) by Fe(III) in the absence of oxygen under conditions of low pH (μ = 1.0)a
|
Reference numbers are shown in parentheses. Units of equilibrium constants and rate coefficients are in mol, dm3, s.
Present data.
Adjusted from 1.2 × 107 at μ = 0.07.
[H+] = 0.255 mol dm−3.
[H+] = 0.1 mol dm−3.
|
| (h1) |
Fe3+ (+H2O) = FeOH2+ + H+ |
K
h1 = 1.64 × 10−3 (ref. 21) |
| (d1) |
SO2aq = HSO3− + H+ |
K
d1 = 2.35 × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
| (d3) |
HSO4− = SO42− + H+ |
K
d3 = 7.94 × 10−2 (ref. 45) |
| (c4) |
Fe3+ + SO42− = FeSO4+ |
K
c4 = 1.38 × 102 (ref. 46) |
| (c1) |
FeOH2+ + HSO3− = FeSO3+ + H+ |
K
c1 = 8.25 × 102 (ref. 16) |
| (1) |
FeSO3+ → Fe2+ + SO3− |
k
1 = 0.19 (ref. 16) |
| (2) |
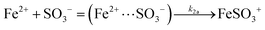
|
k
2 = 3.0 × 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c (ref. 47) c (ref. 47) |
| (3a) |
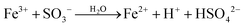
|
k
3/k2 = 0.016b,d |
| (3b) |
FeOH2+ + SO3− → Fe2+ + HSO4− |
k
3 = k3a + k3bKh1/[H+] |
| (4) |
FeSO3+ + SO3− → Fe2+ + S2O62− |
k
4/k3 ≈ 45b,e |
| (5a) |
SO3− + SO3− → S2O62− |
2k5 = 1.0 × 109 (ref. 5) |
| (5b) |
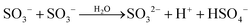
|
k
5a/k5 = 0.37 (ref. 8) |
| (6) |
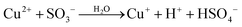
|
k
6/k2 = 0.27b |
| (7) |
Cu+ + FeOH2+ → Cu2+ + Fe2+ + OH− |
k
7 = 3.0 × 107 (ref. 48 and 49) |
Fig. 4 includes calculated absorbance curves for comparison with the measurements. The absorption coefficient of Fe3+ at 390 nm is essentially zero, and that of the first hydrolysis product is ε(FeOH2+) ≈ 60 dm3 mol−1 cm−1.19,28,33 Absorption coefficients that were found to provide good agreement between calculated and observed absorbances at both pH 2.0 and 2.5 are ε(FeSO3+) = 270, ε(Fe(SO3)2−) = 400, ε(Fe(SO3)3H2−) = 450 (dm3 mol−1 cm−1). Fig. 4 indicates the extent of the agreement. These absorption coefficients, however, cannot reproduce the absorbance curve at pH 3.0. To obtain a good fit in this case would require ε(FeSO3+) = 500, ε(Fe(SO3)2−) = 400, ε(Fe(SO3)3H2−) = 650 (dm3 mol−1 cm−1). Fig. 4 shows the result by the broken line. The discrepancy suggests that at pH 3 the reaction mixture contains one or more additional absorbers.
At pH 3 one enters into a pH regime where the Fe(III) hydrolysis product Fe(OH)2+ increases in importance, and the dimer Fe2(OH)24+ must also be taken into account (see Fig. 2). The distribution of Fe(III) species at pH 3 with [FeIII]tot = 1 mmol dm−3 is [Fe3+] = 22%, [FeOH2+] = 64%, [Fe(OH)2+] = 7.5%, and [Fe2(OH)24+] = 6.5%. The dimer has been shown by Lente and Fabian16 to react with HSO3− to form the Fe2OHSO33+ complex; Fe(OH)2+ is also expected to react with HSO3−; both FeOHSO3 and FeSO3+ are possible products. The equilibrium constant between Fe2OHSO33+ and its precursors is K21 = 2344,16 and the rate of formation is rapid. The absorption coefficient of the complex at λ = 450 nm is ε(Fe2OHSO33+) = 500 dm3 mol−1 cm−1; at 390 nm it would be at least twice as large. When this complex is taken into account, the initial rise of the calculated absorbance curve, setting ε(FeSO3+) = 270 dm3 mol−1 cm−1, agrees much better with that observed experimentally,19 but it does not entirely alleviate the discrepancy between calculated and observed absorbances at high concentrations of S(IV). The necessity of taking into account additional equilibria demonstrates the growing complexity of the system. Further studies are needed to identify the additional reactions active in the region pH ≥ 3. One of the consequences of the presence of other iron–sulfito complexes and their contribution to the total absorbance is their interference in the determination of Kc1app by means of Newton–Arcand plots. These additional complexes presumably are responsible for the comparably high value of Kc1 obtained at pH 3 from the measured absorbances at λ = 390 nm.
Reactions following the formation of iron–sulfito complexes
The ultimate products resulting from the interaction of Fe(III) with S(IV) in the absence of oxygen are Fe(II), sulfate and dithionate. The majority of studies of the slow reaction were carried out at pH ∼ 1 (and μ ≈ 1 mol dm−3) where FeSO3+ is the dominant iron–sulfito complex. Kuzminykh and Bomshtein43 and Higginson and Marshall9 both found that the yield of dithionate increases with rising [SIV]/[FeIII] ratio, and that the addition of Fe(II) causes the rate of the reaction to decline, whereas the addition of Cu(II) accelerates it. By analogy with other one-equivalent oxidizing reagents, Higginson and Marshall9 proposed a simple reaction mechanism involving the SO3− radical as an intermediate. In this mechanism the reaction of SO3− with Fe2+ reverses the decomposition of FeSO3+, thereby reducing the overall reaction rate, whereas the reaction with Fe3+ scavenges SO3− radicals and promotes the decomposition of FeSO3+. The effect of Cu2+ is to catalyze the last process. We note in passing that Cu(II) also interacts with S(IV) to form an addition complex, which is prone to decompose.44 In acidic solutions, however, the reaction is slow (in contrast to alkaline solutions); hence its neglect is justified.
Pollard et al.10 first demonstrated that the rate of the reaction between Fe(III) and S(IV) (without additives) decreases with time due to the rise of the concentration of Fe(II) formed as a product. They also found the rate of dithionate production to approach one half of that for the consumption of Fe(III) when [S(IV)]0/[Fe(III)]0 > 0.5; but most importantly, they found that the reaction 2SO3− → S2O62−, which Higginson and Marshall had assumed to be the source of dithionate, is incompatible with the observed dependence of the rate of dithionate formation on the initial reactant concentrations. Accordingly another reaction must serve as a source of dithionate. In the present study it was found that the reaction SO3− + FeSO3+ → Fe2+ + S2O62− agrees with most of the experimental data. The reaction 2SO3− → S2O62− will occur as well, but it is unimportant in this system. Table 1 shows the complete reaction mechanism that was used here to analyze the experimental data available in the literature. All the equilibria are established rapidly, and they are essentially maintained during the subsequent reaction. For the purpose of computer simulations the following forward or reverse rate coefficients were taken from the literature and combined with the established equilibrium constants (μ = 1.0 mol dm−3): kh1f = 2.0 × 107,50kd1r = 2.0 × 108,51kd3r = 1.0 × 1011,51kc4f = 6.3 × 103,50kc1f = 4.0 × 106.18 Rate coefficients for some of the reactions following the formation of the complexes are known; appropriate references are indicated in Table 1. The analysis will begin with the results of Carlyle and Zeck,12 as they have reported the most extensive data set. The conclusions reached will then provide a basis for discussing the results of the other authors.
Analysis of the data of Carlyle and Zeck
In their study the course of the overall reaction was followed by monitoring the optical absorption of the Fe(III) complex at wavelengths in the region 320–443 nm as a proxy for Fe(III). In all experiments the temperature was 25 °C and the ionic strength was μ = 1.0 mol dm−3. Rate measurements were done mostly with Fe(II) in excess of Fe(III) while maintaining [SIV] > [FeIII]. The main series of experiments were carried out by setting [H+] = 0.043 or [H+] = 0.129 (mol dm−3).
With the notation [FeIII] = [Fe3+] + [FeOH2+] + [FeSO3+] = [Fe3+]{(1 + Kh1/[H+]) + A[SIV]}, and making use of the steady state assumption d[SO3−]/dt ≈ 0, one obtains the following equation for the [FeIII] loss rate
| | 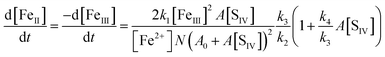 | (10) |
Here,
A0 = 1 +
Kh1/[H
+] and
A =
Kc1a/[H
+](1 + [H
+]/
Kd1), with
Kc1a =
Kc1Kh1. The principal parameters determining the reaction rate are
k1A and the ratios
k3/
k2 and
k4/
k3. The factor
N in the denominator of
eqn (10) is
It turns out that N ≈ 1 so long as [Fe2+] > [Fe3+]. The rate coefficient k3 replaces the individual rate coefficients of reactions (3a) and (3b) in Table 1 as it is not possible to separate the two processes here:
| | | k3 = k3a + k3bKh1/[H+] | (11) |
The above eqn (10) agrees well with the empirical rate law found by Carlyle and Zeck,12 in particular with the second order behavior of [FeIII], the increase of the rate with a[SIV] + b[SIV]2, and the dependence on the reciprocal of [Fe2+]. The good agreement supports the applied reaction mechanism and suggests that the rate data reported can be used to estimate the ratio of the rate coefficients k4/k3. For this purpose eqn (10) is rearranged in the form
| | | R = kobs[Fe2+]0(A0 + A[SIV])2/A[SIV] = 2(k1k3/k2)(1 + (k4/k3)A[SIV]) | (10a) |
where
kobs = d[Fe
III]/[Fe
III]
2d
t is the empirical rate coefficient. The quantities
kobs, [Fe
2+]
0 and [S
IV]
0, given by Carlyle and Zeck
12 for each experiment (their Table 2), were used to calculate
R. If the assumptions made are applicable, a plot of
R versus A[S
IV] should yield a straight line with the slope being determined by (
k4/
k3) and the intercept with the ordinate representing 2(
k1k3/
k2). This relation is indeed observed as
Fig. 6a illustrates.
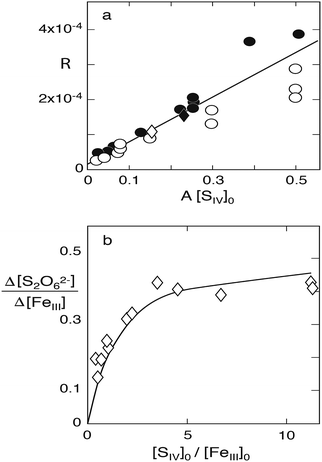 |
| | Fig. 6 Reaction of S(IV) with Fe(III) in the absence of oxygen. (a) Plot of R versus A[SIV] to test the validity of eqn (10), experimental data of Carlyle and Zeck:12 points [H+] = 0.043, circles [H+] = 0.129, open diamond [H+] = 0.086, filled diamond, [H+] = 0.03 (mol dm−3); only data points below A[SIV] = 0.3 were used in calculating the linear regression line shown. (b) Dithionate formation at [H+] = 0.1 mol dm−3: points represent the measured ratio [S2O62−]∞/[FeIII]0; the solid line was calculated with k4/k3 = 45. | |
Some of the experiments in this series were carried out with rather high concentrations of S(IV) compared to those of Fe(III), causing the presence of higher Fe(III)–S(IV) complexes in addition to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex. Computer calculations of the equilibria established between the three complexes indicated that the higher complexes begin to interfere when [HSO3−]/[FeIII] > ∼50, that is [SIV]/[FeIII] ≈ 150, when [H+] = 0.043 M, and [SIV]/[FeIII] ≈ 300 when [H+] = 0.129 M. Since the above eqn (10) is based on the assumption that only the 1
1-complex. Computer calculations of the equilibria established between the three complexes indicated that the higher complexes begin to interfere when [HSO3−]/[FeIII] > ∼50, that is [SIV]/[FeIII] ≈ 150, when [H+] = 0.043 M, and [SIV]/[FeIII] ≈ 300 when [H+] = 0.129 M. Since the above eqn (10) is based on the assumption that only the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is present the results of those experiments that did not satisfy this condition were not used. This removes 8 data points from a total set of 25. The remaining data were subjected to a linear regression treatment that resulted in a slope of (6.7 ± 0.4) × 10−4 s−1 and an intercept with the ordinate of (1.6 ± 1.2) × 10−5 s−1. According to eqn (10a) the slope and the intercept are equivalent to 2(k1k3/k2)(k4/k3) and 2(k1k3/k2), respectively. Their ratio is k4/k3 = 42 with a large margin of error due to the uncertainty associated with the value of the intercept.
1-complex is present the results of those experiments that did not satisfy this condition were not used. This removes 8 data points from a total set of 25. The remaining data were subjected to a linear regression treatment that resulted in a slope of (6.7 ± 0.4) × 10−4 s−1 and an intercept with the ordinate of (1.6 ± 1.2) × 10−5 s−1. According to eqn (10a) the slope and the intercept are equivalent to 2(k1k3/k2)(k4/k3) and 2(k1k3/k2), respectively. Their ratio is k4/k3 = 42 with a large margin of error due to the uncertainty associated with the value of the intercept.
These data do not allow a determination of the value of k3/k2, because the second order rate coefficients kobs reported are not calibrated. The data can only describe the influence of important parameters on the reaction rate. In contrast to the exponential behavior of first order reactions, the decay of a reactant undergoing a second order reaction follows the rate law 1/x = 1/x0 + kobst. Due to experimental difficulties Carlyle and Zeck12 could not determine x0, and for kobst much larger than 1/x0 the initial signature of x0 is lost. However, the value of k3/k2 can be estimated from other data discussed further below, in which the rise of Fe(II) was observed as a function of time.
Carlyle and Zeck12 have also measured, in separate experiments, the yield of dithionate under various conditions (their Table 1). In this study the concentration of Fe(III) was raised to [FeIII]0 ≈ 0.01 mol dm−3 compared to [FeIII]0 ≈ (3–5) × 10−4 mol dm−3 in the reaction rate measurements; [SIV]0/[FeIII]0 ranged from 0.4 to 11, approximately, and the hydrogen ion concentration was [H+] = 0.1 in most cases. Only these data are considered here. The extent of dithionate production predicted by the reaction system shown in Table 1 was explored by computer simulations and the yields obtained were compared with those determined experimentally. The experimental data are for [SV]∞ = 2[S2O62−]∞, that is, the reaction was assumed to have gone to completion, but the time periods between starting the reaction and the final product analysis were not given. The computer calculations showed that for reasonable values of k3/k2 (vide infra) the reaction is essentially complete after 24 h, but even after 12 h the amount of dithionate formed is already close to the final value. The calculations confirmed the prediction that the rate of dithionate formation slows down as the reaction proceeds, because the consumption of S(IV) lowers the concentration of the FeSO3+ complex as well. This effect diminishes with increasing excess of S(IV) over Fe(III).
According to the stoichiometric equations associated with the reaction mechanism in Table 1
| | | −Δ[FeIII] = Δ[FeII] = 2Δ[SO42−] + 2Δ[S2O62−] | (12a) |
| | | −Δ[SIV] = Δ[SO42−] + 2Δ[S2O62−] | (12b) |
the rate of Fe(
III) consumption is twice that of the production of sulfate plus dithionate so that the ratio [S
2O
62−]
∞/[Fe
II]
∞ < 0.5. With [S
IV] in excess, [Fe
II]
∞ ≈ [Fe
III]
0. Thus, one may compare, as Carlyle and Zeck have done, [S
2O
62−]
∞/[Fe
III]
0 with the initial [S
IV]
0/[Fe
III]
0 concentration ratio. In those cases where [Fe
III]
0 > [S
IV]
0 the consumption of [S
IV] at the end of the reaction will be complete, hence one can calculate the corresponding Δ[Fe
III] from the above equations.
Fig. 6b shows that [S
2O
62−]
∞/Δ[Fe
III]
∞ rises with increasing [S
IV]
0/[Fe
III]
0 ratio as expected. The results of computer calculations were largely found to agree with the measurements. The best fit to the measurements, resulting in an average deviation of 5%, was obtained with
k4/
k3 = 45. The solid line in
Fig. 6b, which represents the calculated values, indicates the extent of agreement reached. Thereby it is demonstrated that the data reported by Carlyle and Zeck for the Fe(
III)–S(
IV) reaction system are self-consistent and agree with the adopted reaction mechanism in essentially all respects.
Comparison with other studies
A direct comparison of the results of Carlyle and Zeck12 with those of other studies is not possible, not only because of the widely varying experimental conditions employed, but also because the data are not presented in a uniform manner. However, initial reaction rates and the production of dithionate were measured in most studies. Therefore, computer simulations were mostly used to determine how far the results are consistent with each other.
Karraker11 sought to suppress the formation of dithionate by working with iron in large excess over S(IV). In some experiments Fe(II) was added. The ionic strength was adjusted to μ ≈ 1.0 mol dm−3, and the hydrogen ion concentration was set to [H+] = 0.255 except in three cases (0.51, 0.63, 1.0). The rise of [Fe2+] with time was measured and the half-rise time was determined. Assuming dithionate formation to be negligible, the stoichiometry is simplified to Δ[Fe2+] = −Δ[FeIII] = −2Δ[SIV]. This allows one to replace in equation eqn (10): −d[FeIII]/dt by −2d[SIV]/dt, and [Fe2+] by [Fe2+]0 + 2([SIV]0–[SIV]), respectively. As [FeIII] stays nearly constant, the resulting expression can be integrated to yield
| | | ([Fe2+]0 + 2([SIV]0 + (k3/k2)[FeIII]0))ln([SIV]/[SIV]0 + 2([SIV]0–[SIV])) = −k1(k3/k2)A[FeIII]02Δt | (13a) |
where
A =
Kc1a/[H
+](1 + [H
+]/
Kd1) as before. Karraker considered the last term on the left to be negligible. By setting ln([S
IV]/[S
IV]
0) = −0.693 for Δ
t = Δ
t½ and rearranging
eqn (13a), he derived an equation of the form
| | | [FeIII]0Δt½ = 0.693{(1/k1A) + (k2/k3k1A)([Fe2+]0 + 2[SIV]0)/[FeIII]0} | (13b) |
which is predicted to yield a straight line when the measured half-life times are plotted
versus ([Fe
2+]
0 + 2[S
IV]
0). Karraker
11 used data from 10 runs with [Fe
III]
0 = 0.0653 and [H
+] = 0.255 mol dm
−3 and reported the prediction to be verified, but he did not show the associated plot. A plot of the quantity [Fe
III]
0Δ
t½/0.693
versus ([Fe
2+]
0 + 2[S
IV]
0)/[Fe
III]
0 is shown in
Fig. 7a. Here, all the data for [H
+] = 0.255 mol dm
−3 are used, including 3 data points where [Fe
III]
0 differs from 0.0653. Most of the data are seen to fall on a straight line, confirming Karraker's claim. The linear regression line shown leads to an intercept with the ordinate of 0.191 min, that is
k1Kc1a = 0.26 ± 0.07 s
−1, while the slope of the straight line gives
k2/
k3 = 21.8 ± 1.3. These values agree with those reported by Karraker:
k1A/[H
+] = 1.35 min
−1,
i.e. k1Kc1a = 0.26 s
−1, and
k2/
k3 = 22. Note that
k1Kc1a = 0.26 is in close agreement with the value 0.256 ± 0.03 s
−1 found by Lente and Fabian
16 from direct measurements. This agreement lends credence to Karraker's data and his method of analysis.
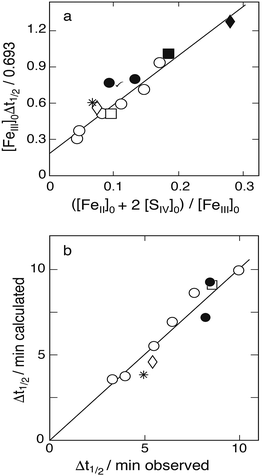 |
| | Fig. 7 (a) Plot of [FeIII]0Δt½versus ([Fe2+]0 + 2[SIV]0)/[FeIII]0 to test the applicability of eqn (13b) in evaluating the data of Karraker;11 initial concentrations (mmol dm−3): [SIV]0: 1.35–5.53, [FeIII]0: circles 65.3, asterisk 89.0, open diamond 75.0, open square 13.1; [Fe2+] added: points 0.9, solid square 4.93, solid diamond 11.4. The linear regression line excludes the marked point. (b) Comparison of calculated and measured reaction half-life times. The straight line is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 relation obtained with k1/k2 = 61.4. 1 relation obtained with k1/k2 = 61.4. | |
The ratio k2/k3 ≈ 22 can only be a coarse estimate, however, because dropping the term 2([SIV]0–[SIV]) in eqn (13a) is not really justified. Although this term may be taken into account when evaluating the equation, it was considered more appropriate to determine k2/k3 by means of computer simulations. The procedure was to find the best fit between calculated and measured half-life times by varying k2/k3 in a narrow range. The calculations made use of k4/k3 = 42 determined from the data of Carlyle and Zeck.12 This gave [S2O62−]/[SVI] ratios rising with the [SIV]0 concentration as expected but still staying in the low percentage range. The best fit between calculated and measured half-life times for k1Kc1a = 0.256 s−1 was obtained with k2/k3 = 61.4 ± 3.0. Fig. 7b shows the agreement that is reached. The average deviation of the points from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line is about 3%. Fig. 7b includes all the data with [H+] = 0.255, except the two points obtained when [Fe2+]0 > [SIV]0 as they are off-scale. In this case the calculated half-life times are 17 and 31.7 min, whereas the measured values were 10.2 and 13.7 min, respectively. It appears that when larger amounts of Fe(II) are added the measurement of half-life times become less precise. The three data points at different hydrogen ion concentrations were already discarded by Karraker; they do not fit into any scheme.
1 line is about 3%. Fig. 7b includes all the data with [H+] = 0.255, except the two points obtained when [Fe2+]0 > [SIV]0 as they are off-scale. In this case the calculated half-life times are 17 and 31.7 min, whereas the measured values were 10.2 and 13.7 min, respectively. It appears that when larger amounts of Fe(II) are added the measurement of half-life times become less precise. The three data points at different hydrogen ion concentrations were already discarded by Karraker; they do not fit into any scheme.
Higginson and Marshall9 and Pollard et al.,10 in contrast to other investigators, have used in their experiments hydrogen sulfate and sulfuric acid, respectively, to adjust the hydrogen ion concentration. The consequence is that most of the Fe(III) is bound to SO42− in the strong FeSO4+ complex, leaving only a few percent of Fe(III) available as free Fe3+ and FeOH2+. If the FeSO4+ complex is chemically inactive, it will merely provide a reservoir of free [FeIII], but the reaction rate will be strongly reduced in comparison to the situation when sulfate is not initially present. Taking the FeSO4+ complex to be chemically inert, computer simulations reproduced the results of Higginson and Marshall9 only approximately, when the ratio k2/k3 = 61.4 was used in the calculations. In these experiments the hydrogen ion concentration was [H+] ≈ 0.08 mol dm−3, the ionic strength was μ = 2.0 mol dm−3, and Fe(II) was added. Pollard et al.10 did not control the ionic strength, but at the high concentrations used in the experiments it was found to stay approximately constant at μ ≈ 0.9 mol dm−3. When Fe(II) was added, the ionic strength rose to μ ≈ 1.7 mol dm−3. The hydrogen ion concentration was [H+] ≈ 0.5 mol dm−3. Both groups of investigators presented their results as rates (Δ[FeII]/Δt and Δ[S2O62−]/Δt) during the initial stage of the reaction, but Pollard et al.10 have in one case explored the course of the reaction over a period of 24 h. They treated the reaction as bimolecular and plotted the logarithm of the ratio of the reactant loss rates versus time. Fig. 8 compares their measurements with computer simulations. The solid line was obtained with k2/k3 = 61.4 and this value could also reproduce their other rate data, thus providing some support for the value of k2/k3 derived above.
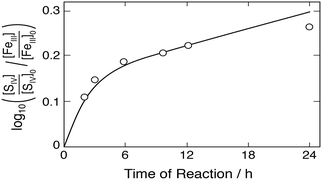 |
| | Fig. 8 Rate of the Fe(III)–S(IV) reaction (assumed to be bimolecular) as a function of time according to Pollard et al.10 Points represent measurements, the solid line was calculated. Initial concentrations (mol dm−3): [FeIII]0 = 0.2, [SIV]0 = 0.0468, [H+] = 0.5; derived initial concentrations due to the presence of sulfates [FeSO4+] = 0.186, [Fe3+] = 0.0136, [HSO4−] = 0.809, [SO42−] = 0.09. | |
With regard to dithionate one should note that the mechanism in Table 1 predicts the relative production rate Δ[S2O62−]/Δ[Fe2+] to depend primarily on A[SIV], because this factor determines the concentration of the FeSO3+ complex. As A involves the equilibrium constants Kc1, Kh1 and Kd1 in addition to the hydrogen ion concentration, the ionic strength dependence of the equilibrium constants as well as differences in [H+] must be taken into account when comparing the ratio Δ[S2O62−]/Δ[Fe] observed in the different studies. Fig. 9 compares this ratio as a function of A[SIV]. While the data of Higginson and Marshall9 and of Carlyle and Zeck12 are approximately in agreement, much higher relative dithionate production rates were obtained by Pollard et al.10 and by Dasgupta et al.13 The latter authors, in fact, found dithionate to be the exclusive S(IV) oxidation product. The incongruity of the data is perturbing, but may have its origin in analytical difficulties. The classical analytical procedure that most authors have used, involves the oxidation of dithionate to sulfate by dichromate. The oxidant is added in excess, and the surplus is then determined by back-titration. This procedure requires the prior removal of all interfering substances (metal ions, sulfite, etc.). Carlyle and Zeck12 have measured dichromate by spectrophotometry, which is more accurate than titration, whereas Dasgupta et al.13 have used HNO3 as oxidant and determined the amount of sulfate produced. This method is the least reliable, because it rests on the prior removal of sulfate produced during the reaction. In view of the good agreement of the results obtained by Carlyle and Zeck12 with the proposed reaction mechanism, and the agreement of their rate data with dithionate production rates, their results are presently the most convincing. But the comparison shows that the extent of dithionate production in this reaction is not settled and should be reexamined with modern analytical techniques such as ion chromatography.
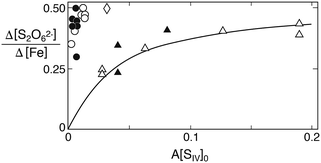 |
| | Fig. 9 Relative rate of dithionate production as a function of A[SIV]0. Comparison of results obtained in different studies: circles A = 0.136, points (Fe(II) added) A = 0.078 (Pollard et al.10); diamond, A = 6.22 (Dasgupta et al.13); filled triangles, A = 2.04 (Higginson and Marshall9); open triangles, A = 2.57 (Carlyle and Zeck12). The solid line was calculated with k4/k3 = 45. | |
The role of copper as a catalyst
The addition of copper to the solution reduces the rate of dithionate formation. This effect is only weakly apparent in the results of Higginson and Marshall9 due to the scatter of the data, but the results of Carlyle and Zeck12 show it quite clearly. A concentration of Cu(II) similar to that of Fe(III) reduces the rate of dithionate production to about one third of that in the absence of copper. In the mechanism proposed by Higginson and Marshall9 the effect arises from the role of copper as an efficient SO3− radical scavenger. Dithionate production rates measured by Carlyle and Zeck12 included two experiments, in which copper was added. The measured decrease of dithionate production could be adequately reproduced by computer simulations when the rate coefficient for the reaction of SO3− with Cu(II) was assumed to be about ten times greater than that with Fe(III), that is k6/k3 ≈ 10. Carlyle and Zeck have conducted an extensive series of experiments to explore the influence of copper on the rate of the Fe(III)–S(IV) reaction. The majority of the experiments were carried out with S(IV) in excess over Fe(III), with [Fe2+] > 10[Fe3+], and with [H+] set to 0.03, 0.043, or 0.086 mol dm−3. The results of these runs were subjected to a detailed analysis.
As Table 1 indicates, the reaction with SO3− converts Cu(II) to Cu(I), which then reacts (more rapidly) with Fe(III) to restore Cu(II). The second reaction has been studied by means of pulse radiolysis48,49 and was found to proceed primarily via the FeOH2+ complex. If these two reactions are the only ones involving copper, the concentration of Cu(I) will be kept in a steady state with Cu(II), that is [Cu+]/[Cu2+] = k6[SO3−]/k7[FeOH2+]. This relation can be used together with the steady state assumption d[SO3−]/dt ≈ 0 to modify eqn (10) so as to include the additional reactions of copper. The kinetic equation thus obtained is
| | 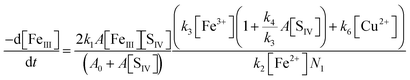 | (10b) |
Here the factor
N in the denominator of
eqn (10) is replaced by
As before, under conditions when [F2+] > [Fe3+], the second term in N1 becomes much smaller than unity. The further analysis showed that except for very low concentrations of copper, the third term is also smaller than the fourth, k6[Cu2+]/k2[Fe2+], so that eqn (10b) reduces to
| | 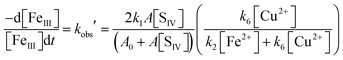 | (10c) |
This equation agrees with the empirical rate law reported by Carlyle and Zeck12 except for a term quadratic in [Cu2+] in the denominator of their expression. It is interesting to note that in contrast to the second order rate behavior observed when copper is absent (eqn (10)), the rate law changes to one of first order in the presence of copper. The change is evident from the data of Carlyle and Zeck as well as from a comparison of eqn (10) and (10c). It may be taken to provide a further confirmation of the adopted mechanism. For the purpose of analysis it is convenient to rearrange the equation as follows
| | 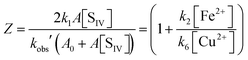 | (10d) |
In this form the equation predicts that a plot of Z versus the ratio [Fe2+]/[Cu2+] should yield a straight line with the slope being determined by (k2/k6). Fig. 10 shows the corresponding plot. Here, the results of 22 experiments were used for which the above-mentioned conditions apply. While a linear relationship is clearly observed, it is also evident that a crowding of data points occurs in the region near the origin. This effect arises from the high concentration of copper used in 13 of the experiments. Despite the uneven distribution, a linear regression analysis shows the data to fall on a straight line with remarkably little variance. The line intersects the ordinate at 1.04 ± 0.17, and the slope is k2/k6 = 3.7 ± 0.3.
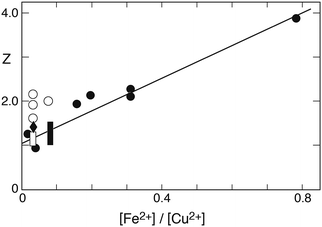 |
| | Fig. 10 Plot of Z = 2k0A[SIV]/kobs′(A0 + A[SIV]) versus the concentration ratio [Fe2+]/[Cu2+] to test the applicability of eqn (10c) in evaluating the data of Carlyle and Zeck;12 initial concentrations (mmol dm−3): [Fe3+]0 0.3 or 0.5, [SIV]0 0.844–51.6, [Fe2+]0 3.37, predominantly, μ = 1.0; points [H+] = 0.043, diamond [H+] = 0.03, open box (5 values) [H+] = 0.086 (mol dm−3). The open points were deleted in deriving the linear regression line. | |
Rate coefficients
The foregoing results suggest that apart from the chosen initial conditions, the rate of the reaction is defined by the rate coefficient k1 for the decomposition of the FeSO3+ complex, and by the ratios of rate coefficients k2/k3, k4/k3, and k2/k6. To determine the individual rate coefficients requires separate measurements. Only one such study appears to exist. Buxton et al.47 have studied reaction (2) by means of the pulse radiolysis technique and found the reaction to proceed via an intermediate complex, which is in fast equilibrium with the reactants SO3− and Fe2+. The pre-equilibrium constant was determined to be K2 = 278, and the rate coefficient for the forward reaction k2a = 3.05 × 104 s−1 at 20 °C. The overall rate coefficient then is k2 = 8.5 × 106 dm3 mol−1 s−1. The value at 25 °C can be estimated by means of the activation energy, 46.6 kJ mol−1, measured over the temperature range 20–30 °C: k2 = 1.2 × 107 dm3 mol−1 s−1. Unfortunately, the value refers to an ionic strength of μ = 0.07 rather than μ = 1.0 mol dm−3 as required here. All reactions between ions in aqueous solution are known to depend on the ionic strength.52 It is customary to express this dependence by the modified Brønsted–Bjerrum relation log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = log
k = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0k + 1.02zAzBμ½/(1 + μ½), where zA and zB are the electric charges of the reactants A and B. Several reactions in the sulfur–oxygen system have been found to obey this relation.6,53 In the case of reaction (2) the product zAzB = −2, leading to an estimate of k2 = 3.0 × 106 dm3 mol−1 s−1 at μ = 1. This value, when used in conjunction with k2/k3 = 61.4, provides k3 = 4.9 × 104 dm3 mol−1 s−1. In addition, the combination with the ratios k3/k4 = 42 and k6/k2 = 0.27 leads to k4 = 2.1 × 106 and k6 = 8.1 × 105 dm3 mol−1 s−1. These values must be considered estimates, and confirmation by direct measurements will be needed.
0k + 1.02zAzBμ½/(1 + μ½), where zA and zB are the electric charges of the reactants A and B. Several reactions in the sulfur–oxygen system have been found to obey this relation.6,53 In the case of reaction (2) the product zAzB = −2, leading to an estimate of k2 = 3.0 × 106 dm3 mol−1 s−1 at μ = 1. This value, when used in conjunction with k2/k3 = 61.4, provides k3 = 4.9 × 104 dm3 mol−1 s−1. In addition, the combination with the ratios k3/k4 = 42 and k6/k2 = 0.27 leads to k4 = 2.1 × 106 and k6 = 8.1 × 105 dm3 mol−1 s−1. These values must be considered estimates, and confirmation by direct measurements will be needed.
According to eqn (11) the overall rate coefficient k3 is a pH-dependent average of k3a and k3b. If the reaction of SO3− with Fe3+ were dominant, the value derived above for k3 would refer to k3a. Alternatively, if the reaction proceeded via FeOH2+, k3 ≈ k3bKh1/[H+]. In this case k3b ≈ 7.6 × 106 dm3 mol−1 s−1 at μ = 1.0. The experimental data,10–12 especially those of Carlyle and Zeck in Fig. 6a, show little influence of the pH. This would suggest k3 = k3a. But the data points are rather scattered so that they do not allow a clear choice between the two alternatives. On the other hand, the results discussed further below, obtained at higher pH, indicate that reaction (3b) is important. In analyzing these data both possibilities will be considered, but the issue clearly is not resolved and will require further scrutiny.
Results from studies at higher pH
The preceding discussion referred to data obtained at low pH under conditions where the FeSO3+ complex is dominant and higher complexes can be neglected. When the pH is raised, this condition no longer holds and the presence of the higher Fe(III)–S(IV) complexes must be taken into account. At higher pH the reaction also proceeds much more rapidly so that it cannot be studied by conventional techniques. Thus, Conklin and Hoffmann14 and Kraft and van Eldik15 have used spectrophotometry to follow the decay of the complexes with time, whereas Millero et al.54 applied micro-molar concentrations of Fe(III) and S(IV) to extend the time scale of observation to 80 min. The latter authors unfortunately worked with seawater or concentrated NaCl solutions as solvents, which led to the formation of various other Fe(III) complexes in addition to those between iron and sulfite, This makes the system difficult to interpret. In fact, the observed rate coefficients were by orders of magnitude greater than those found in other studies.
The presence of higher Fe(III)–S(IV) complexes requires an extension of the reaction mechanism in Table 1 because similar to FeSO3+ these complexes may also decompose and react with SO3− radicals. For the purpose of discussion the additional reactions may be defined as follows:
| | | Fe(SO3)2− → Fe2+ + SO32− + SO3− | (1a) |
| | | Fe(SO3)3H2− → Fe2+ + SO32− + HSO3− + SO3− | (1b) |
| | | Fe(SO3)2− + SO3− → Fe2+ + S2O62− + SO32− | (4a) |
| | | Fe(SO3)3H2− + SO3− → Fe2+ + S2O62− + HSO3− + SO32− | (4b) |
The reaction rate will be determined by an equation similar to eqn (10), where now [FeIII] = [Fe3+] + [FeOH2+] + [FeSO3+] + [Fe(SO3)2−] + [Fe(SO3)3H2−] and k1 and k4 must be replaced by the weighted total rate coefficients k1tot = k1f1 + k1af2 + k1bf3 and k4tot = k4f1 + k4af2 + k4bf3, respectively, where the fi denote the corresponding fractions of the three iron–sulfito complexes. Since the relative abundance of the three complexes is a function of the pH, the product distribution and the reaction rate are expected to vary accordingly. Although appropriate measurements should, in principle, provide information on the participation of each complex in the overall reaction, the available data are fragmentary, and measurements of the product distributions are almost totally lacking.
Conklin and Hoffmann14 have studied the reaction at pH 2 and μ = 1.0 mol dm−3 in the presence of formic acid. They used spectrophotometry at λ = 350 nm to monitor the decay of the absorbance resulting from the sum of Fe(III) species. Formic acid forms a complex with Fe(III), which ties up a considerable fraction of Fe(III) so that the concentration of free Fe(III) and the reaction rate are markedly reduced compared to values in the absence of formic acid. Hence, the time period of the decay extends for hours rather than seconds or minutes as in the absence of formic acid. According to Biruš et al.50 the formation of the FeOOCH2+ complex proceeds via FeOH2+ and HCOOH as reactants, but the only reliable value for the stability constant, Kcfa = 1.26 × 103 dm3 mol−1, reported by Perrin32 at μ = 1.0 and 25 °C, refers to the formation from Fe3+ and HCOO−:
| | | FeOH2+ + HCOOH = FeOOCH2+ + H2O | (cf) |
| | | Fe3+ + HCOO− = FeOOCH2+ | (cfa) |
| Kcf = [FeOOCH2+]/[FeOH2+][HCOOH] |
| Kcfa = [FeOOCH2+]/[Fe3+][HCOO−] |
Both equilibrium constants are related in that Kcf = KcfaKd4/Kh1. Here, Kd4 = 2.95 × 10−4 mol dm−3 is the dissociation constant of formic acid at μ = 1.0.55 Accordingly, Kcf = 2.2 × 102 dm3 mol−1. Rate coefficients for the formation and decomposition of the complex as estimated by Moorhead and Sutin56 are 2.5 × 103 dm3 mol−1 s−1 and 11 s−1, respectively. The values are large enough to guarantee that the equilibrium between free Fe(III) and the FeOOCH2+ complex is maintained during the Fe(III)–S(IV) reaction.
Fig. 11 shows two of the absorbance decay curves observed by Conklin and Hoffmann.14 Computer calculations were carried out with the aim to reproduce these decay curves. Absorption coefficients required in the calculations were estimated from the absorbance data given by the authors at λ = 350 nm as a function of [SIV] (their Fig. 3a). These data were evaluated by calculating the changes in the distribution of Fe(III)–S(IV) complexes under the particular conditions applied in these experiments, and the estimated absorption coefficients were adjusted until agreement was reached between calculated and observed absorbances. The coefficients derived are ε(FeSO3+) ≈ 290, ε(Fe(SO3)2−) ≈ 740, ε(Fe(SO3)3H2−) ≈ 750 dm3 mol−1 cm−1; ε(FeOH2+) = 630 and ε(FeSO4+) = 576 at λ = 350 nm are known from previously work.26 The absorbances calculated with these data for the distributions of Fe(III) species at the start of the reaction under the experimental conditions used in Fig. 11 did not quite reproduce the observed initial values. However, the FeOOCH2+ complex is known to be photochemically active,57,58 and it is expected to contribute to the total absorbance at wavelengths near 350 nm. An absorption coefficient of ε(FeOOCH2+) ≈ 170 was found to close the gap and to bring calculated and observed initial absorbances into agreement. This value is similar in magnitude to that estimated by Baxendale and Bridge57 at λ = 365 nm: ε(FeOOCH2+) ≈ 100 dm3 mol−1 cm−1.
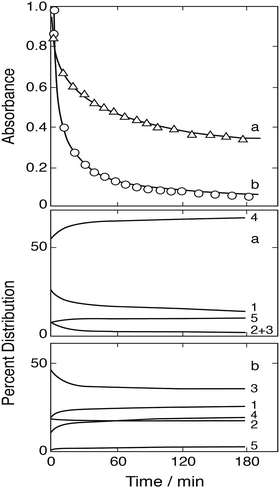 |
| | Fig. 11 Fe(III)–S(IV) reaction in the presence of 1 mol dm−3 of formic acid, pH 2, μ = 1.0 (Conklin and Hoffmann14). Upper frame: Points are measurements of the absorbance due to Fe(III) species at 350 nm; (a) [FeIII]0 = [SIV]0 = 5 mmol dm−3, (b) [FeIII]0 = 4 and [SIV]0 = 20 mmol dm−3; the solid lines were calculated (see text for details). Lower frames: Change with time of the associated equilibrium distributions of Fe(III) species (exclusive of FeOOCH2+), (1) FeSO3+, (2) Fe(SO3)2−, (3) FeH(SO3)32−, (4) Fe3+, (5) FeOH2+. | |
The experimental data shown in Fig. 11 refer to two initial concentrations: (a) [FeIII]0 = [SIV]0 = 5 mmol dm−3, and (b) [FeIII]0 = 4 and [SIV]0 = 20 mmol dm−3. The calculated equilibrium distributions indicate that in the first case about 95% of total iron is bound to the FeOOCH2+ complex, in the second case it is about 84%. These fractions do not greatly vary during the reaction. The distributions of the remaining Fe(III) species and their changes as the reaction proceeds are indicated in the two lower frames of Fig. 11. In the first case the FeSO3+ complex is dominant, in the second case (Fe(SO3)3H2−) is more abundant. It was expected that the simple mechanism in Table 1 would suffice to reproduce the decay of absorbance in the first case, while in the second case the mechanism would have to be extended to include reactions of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex. The computer calculations first showed that the experimental data can be reproduced only by assuming that reaction (3b) is the main channel of reaction (3) with k3b = 7.6 × 106 dm3 mol−1 s−1 (at μ = 1.0 mol dm−3). But in contrast to expectation the calculations also showed that the basic mechanism of Table 1 is adequate to reproduce both sets of experimental data. The results are shown in Fig. 11 by the solid lines. The assumption of even a minimal contribution by the decomposition of the 1
3-complex. The computer calculations first showed that the experimental data can be reproduced only by assuming that reaction (3b) is the main channel of reaction (3) with k3b = 7.6 × 106 dm3 mol−1 s−1 (at μ = 1.0 mol dm−3). But in contrast to expectation the calculations also showed that the basic mechanism of Table 1 is adequate to reproduce both sets of experimental data. The results are shown in Fig. 11 by the solid lines. The assumption of even a minimal contribution by the decomposition of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex only worsened the agreement between calculated and experimental data in that the initial decay rate became too rapid. The rate coefficient for the decomposition was estimated to be k1b < 0.01 s−1. These results suggest that under the experimental conditions chosen the 1
3-complex only worsened the agreement between calculated and experimental data in that the initial decay rate became too rapid. The rate coefficient for the decomposition was estimated to be k1b < 0.01 s−1. These results suggest that under the experimental conditions chosen the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex does not significantly participate in the reaction.
3-complex does not significantly participate in the reaction.
The experimental data in Fig. 11 were also subjected to tests for first and/or second order reaction behavior. A first order decay was found to occur only in the very initial stage of the reaction. There follows a transition period, which is apparent in Fig. 11 by an adjustment of the distributions of Fe(III) species, until after about 20 min the decay of absorbance shows second order behavior. Conklin and Hoffmann14 had tried to fit the observed decay curves by a rate expression with two consecutive exponential terms. This procedure provides only a coarse description of the experimental data, and it is in conflict with the present mechanism and its steady state description in eqn (10).
Kraft and van Eldik15 have analyzed absorbance decay curves obtained at λ = 390 nm, μ = 0.1 mol dm−3 under various experimental conditions. They described decay curves only in general terms,17 but did not present the original data. Following Conklin and Hoffmann, they interpreted the observed kinetic behavior as that of two consecutive reactions and reported apparent first order rate coefficients, one for the initial, and the second for a later stage of the reaction (stages III and IV in their notation). The preceding discussion has shown, however, that the true origin of the observed kinetic behavior is that of a shift from first to second order and not, for example, the decomposition of complexes occurring in parallel at different rates. Accordingly, only the first of the two apparent rate coefficients can be useful, whereas the second defies a meaningful analysis. No details were given about how the rate coefficients were determined. The authors state that a standard least-square fitting program was used17 in the data evaluation, but the time periods for the averaging process were not specified.
Computer calculations were performed with the aim to reproduce the apparent first order rate coefficients reported for the initial section of the decay curve. As the measured quantity is the absorbance A, the apparent rate coefficients are defined as k = −dA/Adt or, in integrated form, k = (1/Δt)ln(A1/A2) with Δt = t2 − t1. Both expressions were explored, with little difference in the results (Δt = 1 s). Fig. 5 had shown that the various Fe(III) species come to equilibrium at t ≈ 0.2 s and this sets a lower limit to t1. The decomposition of iron–sulfito complexes begins before the equilibrium is fully achieved. All results show that the reaction can be truly of first order only at very short reaction times. Due to the rapidity of the reaction sufficient Fe2+ develops early in the process to activate the back-reaction SO3− + Fe2+ → FeSO3+ whereupon the reaction rate decreases. This is evident also during the time period available to calculate apparent first order rate coefficients. Here, the time period was confined to the range 0.5–4 s. At longer times the values obtained are markedly lowered while the calculated standard deviation of the averages increases.
Absorption coefficients at λ = 390 nm for the three complexes and ε(FeOH2+) were derived earlier (see under Absorption coefficients), and ε(FeSO4+) ≈ 100 dm3 mol−1 cm−1 was obtained by extrapolation of published data;26 the contribution by Fe3+ to the absorbance can be neglected. The calculations made use of the reaction rate coefficients derived in the preceding section. They were adjusted to the difference in ionic strength (μ = 0.1), which leads to k1 = 0.19 s−1, k2 = 1.0 × 107, k3a ≤ 3.0 × 105, k3b ≤ 2.6 × 107, k4 ≈ 4.0 × 106 (dm3 mol−1 s−1). Additional rate coefficients for reactions involving the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes were then introduced on a trial basis as needed to bring observed and calculated data to agreement.
3-complexes were then introduced on a trial basis as needed to bring observed and calculated data to agreement.
Kraft and van Eldik15 reported results for three series of experiments. Two series were performed at pH 2.5: (a) [SIV]0 = 1.25 mmol dm−3 was kept constant and [FeIII]0 was varied between 0.25 and 6.0 mmol dm−3; (b) [FeIII]0 = 0.5 mmol dm−3 was kept constant and [SIV]0 was varied between 0.1 and 3.0 mmol dm−3; (c) in the third series [FeIII]0 = 0.5 and [SIV]0 = 20 mmol dm−3 were kept constant and the pH was varied between 1.3 and 2.9. The results of series (a) show that the apparent first order rate coefficient initially decreases with increasing Fe(III) until, when [FeIII]0 ≥ 2.0 mmol dm−3, an essentially constant value is reached, with a reported average kapp = (0.054 ± 0.04) s−1 in the range [FeIII]0 = 2–6 mmol dm−3. In this region the FeSO3+ complex is dominant and contributions of the two higher complexes can be neglected. Calculations of the apparent first order rate coefficient were performed for two limiting cases of k3, setting either k3a = 3.0 × 105 and k3b = 0 or k3b = 2.6 × 107 and k3a = 0 (dm3 mol−1 s−1). Average kapp values obtained for [FeIII]0 = 2, 4, and 6 mmol dm−3 were 0.067 ± 0.013 s−1 in the first case, and 0.090 ± 0.012 s−1 in the second (9 data points each). The former result is closer to the value reported than the latter, suggesting that reaction (3b) is not the sole channel of reaction (3).
The upper frame of Fig. 12 shows apparent initial first order rate coefficients obtained when [SIV]0 was varied and [FeIII]0 was kept constant.15 The rate coefficient first rises with increasing [SIV]0 and then approaches a constant value of kapp ≈ 0.135 s−1. The lower frame of the figure shows the corresponding change in the calculated distribution of Fe(III) species. As the S(IV) concentration is raised, the distribution shifts from FeSO3+ to Fe(SO3)3H2− as the major species. The observation that the apparent rate coefficient still remains at a high value is a clear indication that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex is subject to decomposition and that it participates in the reaction. Computer calculations were performed in attempts to reproduce the observed variation in the kapp values. The solid line shown in the upper part of Fig. 12 was obtained with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.08 s−1 for the decomposition of the 1
3-complex is subject to decomposition and that it participates in the reaction. Computer calculations were performed in attempts to reproduce the observed variation in the kapp values. The solid line shown in the upper part of Fig. 12 was obtained with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.08 s−1 for the decomposition of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1
3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex. The initial rise curve was better represented with k3b = 2.6 × 107 dm3 mol−1 s−1 rather than with k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0 (shown by the broken line). The experimental data indicate a slight overshoot at [SIV]0 ≈ 5 mmol dm−3, which could be reproduced, if the value chosen for k4 were raised by 50%. Fig. 13 shows the variation of the apparent initial first order rate coefficients with the pH and, in the lower part of the figure, the change in the equilibrium distribution of Fe(III) species. The distribution shifts from FeSO3+ to Fe(SO3)3H2− as the pH is raised, indicating again that the higher complexes participate in the overall reaction. Computer calculations performed in attempts to reproduce the observed variation in the kapp values showed that in this case the results differed little with the choice of k3 (either k3b = 2.6 × 107 or k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0). The solid line shown in the upper part of Fig. 13 was calculated with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.06 s−1 for the decomposition of the 1
3-complex. The initial rise curve was better represented with k3b = 2.6 × 107 dm3 mol−1 s−1 rather than with k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0 (shown by the broken line). The experimental data indicate a slight overshoot at [SIV]0 ≈ 5 mmol dm−3, which could be reproduced, if the value chosen for k4 were raised by 50%. Fig. 13 shows the variation of the apparent initial first order rate coefficients with the pH and, in the lower part of the figure, the change in the equilibrium distribution of Fe(III) species. The distribution shifts from FeSO3+ to Fe(SO3)3H2− as the pH is raised, indicating again that the higher complexes participate in the overall reaction. Computer calculations performed in attempts to reproduce the observed variation in the kapp values showed that in this case the results differed little with the choice of k3 (either k3b = 2.6 × 107 or k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0). The solid line shown in the upper part of Fig. 13 was calculated with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.06 s−1 for the decomposition of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1
3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex. These values are quite similar to those found applicable in the preceding case when the pH was kept constant and [SIV]0 was varied. Above pH 2.5 it was not possible to obtain a good fit between calculated and observed kapp values.
3-complex. These values are quite similar to those found applicable in the preceding case when the pH was kept constant and [SIV]0 was varied. Above pH 2.5 it was not possible to obtain a good fit between calculated and observed kapp values.
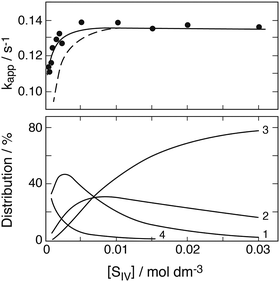 |
| | Fig. 12 Upper frame: Apparent initial first order rate coefficient as a function of [SIV]0, [FeIII]0 = 0.5 mmol dm−3, pH 2.5, μ = 0.1; points are measurements (Kraft and van Eldik15), the solid line represents computer-based calculations with k3b = 2.6 × 107 dm3 mol−1 s−1 (see text for details), the broken line results with k3a = 3.0 × 105 dm3 mol−1 s−1, k3b = 0. Lower frame: Equilibrium distributions of Fe(III) species at the beginning of the reaction: (1) FeSO3+, (2) Fe(SO3)2−, (3) Fe(SO3)3H2−, (4) FeOH2+ ≈ Fe3+. | |
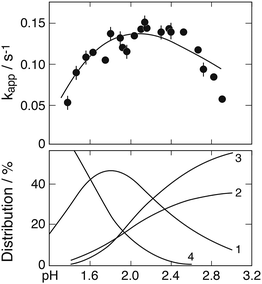 |
| | Fig. 13 Upper frame: Apparent initial first order rate coefficient as a function of pH, [FeIII]0 = 0.5, [SIV]0 = 10 mmol dm−3, μ = 0.1; points are measurements (Kraft and van Eldik15), the line represents computer-based calculations (see text for details). Lower frame: Equilibrium distributions of Fe(III) species at the beginning of the reaction: (1) FeSO3+, (2) Fe(SO3)2−, (3) Fe(SO3)3H2−, (4) Fe3+. | |
The overall result of the computer simulations is the recognition that all three complexes undergo decomposition, but the decomposition rates for the two higher complexes are markedly lower than that for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex (k1a ≈ 0.04 s−1 and k1b ≈ 0.08 s−1 compared to k1 = 0.19 s−1). This conclusion obviously disagrees with that derived above in evaluating the data of Conklin and Hoffmann,14 which had indicated that the 1
1-complex (k1a ≈ 0.04 s−1 and k1b ≈ 0.08 s−1 compared to k1 = 0.19 s−1). This conclusion obviously disagrees with that derived above in evaluating the data of Conklin and Hoffmann,14 which had indicated that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 iron–sulfito complexes do not significantly participate in the reaction. The major difference in the applied experimental conditions, apart from the presence of formic acid in the latter case, is the difference in ionic strength (μ = 0.1 versus μ = 1.0). This may have a bearing on the reaction rate coefficients, but it should not affect the decomposition rates.
3 iron–sulfito complexes do not significantly participate in the reaction. The major difference in the applied experimental conditions, apart from the presence of formic acid in the latter case, is the difference in ionic strength (μ = 0.1 versus μ = 1.0). This may have a bearing on the reaction rate coefficients, but it should not affect the decomposition rates.
Kraft and van Eldik15 have also used ion chromatography to determine the yields of sulfate and dithionate after a reaction time of 5 min and 40 min, respectively. The initial concentration of iron was [FeIII]0 = 0.5 mmol dm−3, [SIV]0 was varied from 0.5 to 5.0 mmol dm−3. The average pH was 3.47 (range 3.30–3.56). The ionic strength was not controlled but it is estimated to approximate to μ ≈ 0.006. These data are needed to calculate the equilibrium constants involved and to determine the equilibrium distribution of the Fe(III) species. At pH 3.5 the contribution of Fe3+ to the sum of Fe(III) hydrolysis products is almost negligible, but that of Fe(OH)2+ cannot be ignored as Fig. 2 showed. Fe(OH)2+ is expected to react with HSO3− in a similar way as Fe(OH)2+ to form an Fe(III)–S(IV) complex, but this reaction has not yet been explored and no definite knowledge exists about the nature of the complex. Both FeOHSO3 and FeSO3+ may be formed. In order to allow an analysis of the product yields it will be assumed that Fe(OH)2+ reacts like Fe(OH)2+ so that both species can be combined. The upper part of Fig. 14 shows the yields of dithionate reported by Kraft and van Eldik15 as a function of [SIV]0, the lower part shows the calculated distribution of Fe(III) species. The rise of dithionate yield with increasing [SIV]0 is accompanied by a rise in the relative concentrations of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes, whereas that of the sum of Fe(OH)2+ and Fe(OH)2+ decreases.
3-complexes, whereas that of the sum of Fe(OH)2+ and Fe(OH)2+ decreases.
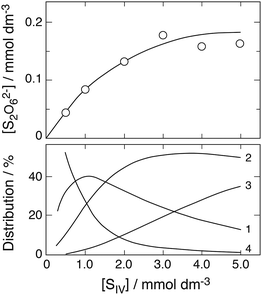 |
| | Fig. 14 Upper frame: Points show the measured yield of dithionate (Kraft and van Eldik15) as a function of [SIV]0 ([FeIII]0 = 0.5 mmol dm−3), the solid line shows results of computer calculation based on the competition of reactions (3b) and (4). Lower frame: Equilibrium distribution of Fe(III) species at the beginning of the reaction (1) FeSO3+, (2) Fe(SO3)2−, (3) Fe(SO3)3H2−, (4) sum of FeOH2+ and Fe(OH)2+. | |
In contrast to the experimentally observed rise in the yield of dithionate with increasing [SIV]0 Kraft and van Eldik found the yield of sulfate to stay nearly constant,15 decreasing slightly from 0.33 to 0.26 mmol dm−3. If the results for sulfate were correct, the sum of both product yields would significantly exceed the limit of 0.25 mmol dm−3 mandated by the reaction mechanism (cf.eqn (10a)). It appears, therefore, that the data for sulfate are spoiled by the presence of an impurity introduced with one of the solutions used to make up the reaction mixture. The occurrence of dithionate as an impurity is rather unlikely so that the measured concentrations of dithionate are taken to provide true yields.
In the foregoing, the reaction of SO3− radicals with the FeSO3+ complex was shown to be the only source of dithionate, but the extended reaction mechanism would allow this product to be formed also in reactions of SO3− radicals with one of the two higher complexes. This possibility was explored by means of computer simulations. The individual rate coefficients used in this case were obtained by an appropriate adjustment to the lower ionic strength μ = 0.006 in these experiments. It was confirmed that at low [SIV] concentrations, where FeSO3+ contributes significantly to the mix of Fe(III) species, reaction (4) remains the most important source of dithionate. The rise of the dithionate yield with increasing [SIV]0 must then be due to a competing reaction (leading to sulfate). Reaction (3a) will be unimportant at pH 3.4 because the concentration [Fe3+] is too small, but reaction (3b) fills the need if the rate coefficient is k3b ≈ 3.0 × 107 dm3 mol−1 s−1. The value corresponds approximately to that obtained by extrapolation of the ionic strength to μ = 0.006. The equivalent reaction (3c) of SO3− with Fe(OH)2+ need not be invoked. A complete set of computer calculations then reveals that reactions (3b) and (4) suffice to reproduce the observed dithionate yields over the whole range of S(IV) concentrations. The solid line in the upper part of Fig. 14 indicates the extent of agreement reached between observed and calculated yields.
This result does not preclude the participation of higher complexes in the production of dithionate, provided sulfate or another product is formed in a parallel reaction. Trial calculations showed that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex is less likely a source of dithionate than the 1
2-complex is less likely a source of dithionate than the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex, which gains prominence at the high end of the S(IV) concentration range. The addition of reaction (4b) with a rate coefficient of k4b ≈ 1.2 × 107 dm3 mol−1 s−1 would also provide good agreement with the measured dithionate yields, provided the reaction consisted of two channels, one leading to dithionate with a yield of 65%, the other one leading to sulfate with a yield of 35%. This partitioning determines the plateau of the dithionate concentration at high S(IV) concentrations. It will be clear that the limited data on dithionate formation reported by Kraft and van Eldik15 cannot give definitive answers on all possible routes to dithionate production. However, the recognition that reaction (3b) is more likely in this mechanism than (3a) would be in accord with the conclusions reached in the preceding discussion of the apparent initial first order rate coefficients determined by the authors.
3-complex, which gains prominence at the high end of the S(IV) concentration range. The addition of reaction (4b) with a rate coefficient of k4b ≈ 1.2 × 107 dm3 mol−1 s−1 would also provide good agreement with the measured dithionate yields, provided the reaction consisted of two channels, one leading to dithionate with a yield of 65%, the other one leading to sulfate with a yield of 35%. This partitioning determines the plateau of the dithionate concentration at high S(IV) concentrations. It will be clear that the limited data on dithionate formation reported by Kraft and van Eldik15 cannot give definitive answers on all possible routes to dithionate production. However, the recognition that reaction (3b) is more likely in this mechanism than (3a) would be in accord with the conclusions reached in the preceding discussion of the apparent initial first order rate coefficients determined by the authors.
Conclusions
Three iron–sulfito complexes are formed by the successive addition of HSO3− to FeOH2+. These processes occur rapidly. The subsequent slow reaction is due to the decomposition of the complexes and the formation of SO3− radicals. The decomposition of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex has been documented, the disintegration of the 1
1-complex has been documented, the disintegration of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and the 1
2- and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes are found to be slower. The mechanism in Table 1 is consistent with most of the data reported for experimental conditions under which the FeSO3+ complex is the most abundant intermediate (pH < 2, [SIV]/[FeIII] < 200). However, yields of dithionate reported by different authors diverge significantly, presumably because the classical analytical methods formerly in use were inadequate. Although it was possible to estimate rate coefficients of the reactions involved, the true values will have to be determined in future studies. One of the problems that will require closer attention is the ionic strength dependence of the stability constants of the complexes as well as that of the rate coefficients of the individual reactions.
3-complexes are found to be slower. The mechanism in Table 1 is consistent with most of the data reported for experimental conditions under which the FeSO3+ complex is the most abundant intermediate (pH < 2, [SIV]/[FeIII] < 200). However, yields of dithionate reported by different authors diverge significantly, presumably because the classical analytical methods formerly in use were inadequate. Although it was possible to estimate rate coefficients of the reactions involved, the true values will have to be determined in future studies. One of the problems that will require closer attention is the ionic strength dependence of the stability constants of the complexes as well as that of the rate coefficients of the individual reactions.
Finally it important to note that the decomposition of the iron–sulfito complexes discussed in this study initiates the oxidation of S(IV) also in the presence of oxygen so that the same stability constants and decomposition rates of the complexes will be applicable. But in that case the SO3− radicals are converted to SO5− radicals and the subsequent mechanism takes a different course.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
Open Access funding provided by the Max Planck Society.
References
- C. Brandt and R. van Eldik, Chem. Rev., 1995, 95, 119–190 CrossRef CAS and literature cited therein.
-
P. Warneck, Chemistry of the Natural Atmosphere, 2nd edn, Academic Press, San Diego, 2000, pp. 507–510 Search PubMed.
- E. Harris, B. Sinha, D. van Pinxteren, A. Tilgner, K. W. Fomba, J. Schneider, A. Roth, T. Gnauk, B. Fahlbusch, S. Mertes, T. Lee, J. Collett, S. Foley, S. Borrmann, P. Hoppe and H. Herrmann, Science, 2013, 340, 727–730 CrossRef CAS PubMed.
- K. Bal Reddy and R. van Eldik, Atmos. Environ., 1992, 26A, 661–665 CrossRef.
- J. Ziajka, F. Beer and P. Warneck, Atmos. Environ., 1994, 28, 2549–2552 CrossRef CAS.
- G. V. Buxton, S. McGowan, G. A. Salmon, J. E. Williams and N. D. Wood, Atmos. Environ., 1996, 30, 2483–2493 CrossRef CAS.
- G. V. Buxton, T. N. Malone and G. A. Salmon, J. Chem. Soc., Faraday Trans., 1996, 92, 1287–1289 RSC.
- M. Fischer and P. Warneck, J. Phys. Chem., 1996, 100, 15111–15117 CrossRef CAS.
- W. C. E. Higginson and J. W. Marshall, J. Chem. Soc., 1957, 447–458 RSC.
- F. H. Pollard, P. Hanson and G. Nickless, J. Chromatogr., 1961, 5, 68–73 CrossRef CAS.
- D. G. Karraker, J. Phys. Chem., 1963, 67, 871–874 CrossRef CAS.
- D. W. Carlyle and O. F. Zeck, Inorg. Chem., 1973, 12, 2978–2983 CrossRef CAS.
- P. K. Dasgupta, P. A. Mitchell and P. W. West, Atmos. Environ., 1979, 13, 775–782 CrossRef CAS.
- M. H. Conklin and M. R. Hoffmann, Environ. Sci. Technol., 1988, 22, 899–907 CrossRef CAS PubMed.
- J. Kraft and R. van Eldik, Inorg. Chem., 1989, 28, 2306–2312 CrossRef CAS.
- G. Lente and I. Fábián, J. Chem. Soc., Dalton Trans., 2002, 778–784 RSC.
- J. Kraft and R. van Eldik, Inorg. Chem., 1989, 28, 2297–2305 CrossRef CAS.
- E. A. Betterton, J. Atmos. Chem., 1993, 17, 307–324 CrossRef CAS.
- F. Prinsloo, C. Brandt, V. Lepentsiotis, J. Pienaar and R. van Eldik, Inorg. Chem., 1997, 36, 119–121 CrossRef CAS.
- E. Danilczuk and A. Swinarski, Rocz. Chem., 1961, 35, 1563–1572 CAS.
- R. M. Milburn and W. C. Vosburgh, J. Am. Chem. Soc., 1955, 77, 1352–1355 CrossRef CAS.
- R. M. Milburn, J. Am. Chem. Soc., 1957, 79, 537–540 CrossRef CAS.
- D. H. Richards and K. W. Sykes, J. Chem. Soc., 1960, 3626–3633 RSC.
- A. V. Zotov and Z. Y. Kotova, Geokhimiya, 1979, 285–290 CAS.
- R. S. Sapieszko, R. C. Patel and E. Matijević, J. Phys. Chem., 1977, 77, 1061–1068 CrossRef.
- H.-J. Benkelberg and P. Warneck, J. Phys. Chem., 1995, 99, 5214–5221 CrossRef CAS.
- P. Martinez, R. van Eldik and H. Kelm, Ber. Bunsenges. Phys. Chem., 1985, 89, 81–86 CrossRef CAS , the data were reanalyzed.
- A. Stefansson, Environ. Sci. Technol., 2007, 41, 6117–6123 CrossRef CAS PubMed.
- R. J. Knight and R. N. Sylva, J. Inorg. Nucl. Chem., 1975, 37, 779–783 CrossRef CAS.
- R. H. Byrne, Y.-R. Luo and R. W. Young, Mar. Chem., 2000, 70, 23–35 CrossRef CAS.
- B. O. A. Hedström, Archiv. Kemi., 1952, 6, 1–16 Search PubMed.
- D. D. Perrin, J. Chem. Soc., 1959, 1710–1717 RSC.
- L. Lopes, L. de Laat and B. Legube, Inorg. Chem., 2002, 41, 2505–2517 CrossRef CAS PubMed.
- W. N. Perera and G. Hefter, Inorg. Chem., 2003, 42, 5917–5923 CrossRef CAS PubMed.
- R. N. Goldberg and V. B. Parker, J. Res. Natl. Bur. Stand., 1985, 90, 341–358 CrossRef CAS.
- A. Huss and C. A. Eckert, J. Phys. Chem., 1977, 81, 2268–2270 CrossRef CAS.
- F. J. Millero, J. P. Hershey, G. Johnson and J.-Z. Zhang, J. Atmos. Chem., 1989, 8, 377–389 CrossRef CAS.
- T. Sekine, I. Hidehiko, M. Sakairi, F. Shimada and M. Inarida, Bull. Chem. Soc. Jpn., 1968, 41, 1–7 CrossRef CAS.
- D. Devèze and P. C. Rumpf, C. R. Acad. Sci. Paris, 1964, 258, 6135–6138 Search PubMed.
- M. Frydman, G. Nilsson, T. Rengemo and L. G. Sillen, Acta Chem. Scand., 1958, 12, 878–884 CrossRef CAS.
- T. W. Newton and G. M. Arcand, J. Am. Chem. Soc., 1953, 75, 2449–2453 CrossRef CAS.
- Use was made of the computer program of A. R. Curtis, W. P. Sweetenham, Facsimile, UK Atomic Energy Authority, AERE Report R-12805, Harwell, 1987.
- I. N. Kuzminykh and T. B. Bomshtein, Zh. Prikl. Khim., 1953, 26, 3–8 CAS.
- M. H. Conklin and M. R. Hoffmann, Environ. Sci. Technol., 1988, 22, 883–891 CrossRef CAS PubMed.
-
R. M. Smith and A. E. Martell, Critical Stability Constants Inorganic Complexes, Plenum Press, New York, 1976, vol. 4, p. 79 Search PubMed.
- R. L. S. Willix, Trans. Faraday Soc., 1963, 59, 1315–1324 RSC.
- G. V. Buxton, S. Barlow, S. McGowan, G. A. Salmon and J. E. Williams, Phys. Chem. Chem. Phys., 1999, 1, 3111–3115 RSC.
- E. Bjergbakke, Nukleonika, 1979, 24, 825–845 CAS.
- E. Bjergbakke, K. Sehested and O. L. Rasmussen, Radiat. Res., 1979, 66, 433–442 CrossRef.
- M. Biruš, N. Kujundžić and M. Pribanić, Prog. React. Kinet., 1993, 18, 171–271 Search PubMed.
- M. Eigen, W. Kruse, G. Maass and L. DeMaeyer, Prog. React. Kinet., 1964, 2, 285–318 CAS.
-
M. J. Pilling and P. W. Seakins, Reaction Kinetics, Oxford University Press, 1996, pp. 156–158 Search PubMed.
-
P. Warneck, Aqueous Solution Chemistry, in Low-Temperature Chemistry in the Atmosphere, ed. G. K. Moortgat, A. J. Barnes, G. Le Bras, J. R. Sodeau, NATO ASI Series I, Springer-Verlag, Berlin, 1994, vol. 21, pp. 175–196 Search PubMed.
- F. J. Millero, M. Gonzales-Davila and J. M. Santana-Casiano, J. Geophys. Res., 1995, 100, 7235–7244 CrossRef CAS.
-
A. E. Martell and R. M. Smith, Critical Stability Constants, Other Organic Ligands, Plenum Press, New York, 1976, vol. 3, p. 1 Search PubMed.
- E. G. Moorhead and N. Sutin, Inorg. Chem., 1966, 5, 1866–1871 CrossRef CAS.
- J. H. Baxendale and N. K. Bridge, J. Phys. Chem., 1955, 59, 783–788 CrossRef CAS.
- H. B. Abrahamson, A. B. Rezvani and J. G. Brushmiller, Inorg. Chim. Acta, 1994, 226, 117–127 CrossRef CAS.
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is prevalent. They are extrapolated to lower ionic strengths for an analysis of the data obtained at higher pH to explore conditions when reactions of the higher complexes become important. The overall rate and the product yields of the reaction depend critically on the pH, the initial ratio of S(IV) to Fe(III) and the ionic strength of the solution.
1-complex is prevalent. They are extrapolated to lower ionic strengths for an analysis of the data obtained at higher pH to explore conditions when reactions of the higher complexes become important. The overall rate and the product yields of the reaction depend critically on the pH, the initial ratio of S(IV) to Fe(III) and the ionic strength of the solution.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kh1 = log
Kh1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh1 − 2.04μ½/(1 + 2.4μ½) − 0.01μ,
0Kh1 − 2.04μ½/(1 + 2.4μ½) − 0.01μ,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh1 = −2.174 is obtained by extrapolation. The numerical parameters in this equation were originally suggested by Milburn and Vosburgh,21 whose measurements covered ionic strengths up to μ = 3.0. While spectrophotometry has been the favored measurement technique, potentiometric titration has also been applied, based on measuring simultaneously the hydrogen ion concentration and the Fe3+/Fe2+ redox potential. By means of computer-assisted analyses of the titration curves, Byrne et al.30 and Stefanson28 have obtained results in perfect agreement with those of Milburn and Vosburgh.21
0Kh1 = −2.174 is obtained by extrapolation. The numerical parameters in this equation were originally suggested by Milburn and Vosburgh,21 whose measurements covered ionic strengths up to μ = 3.0. While spectrophotometry has been the favored measurement technique, potentiometric titration has also been applied, based on measuring simultaneously the hydrogen ion concentration and the Fe3+/Fe2+ redox potential. By means of computer-assisted analyses of the titration curves, Byrne et al.30 and Stefanson28 have obtained results in perfect agreement with those of Milburn and Vosburgh.21

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kh2 = log
Kh2 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh2 − 3.06μ½/(1 + 1.58μ½)
0Kh2 − 3.06μ½/(1 + 1.58μ½)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh2 = −5.76 ± 0.06 was again obtained by extrapolation. This value, as well as that in the denominator of the second term, is still uncertain because of an insufficient number of data available at low ionic strengths.
0Kh2 = −5.76 ± 0.06 was again obtained by extrapolation. This value, as well as that in the denominator of the second term, is still uncertain because of an insufficient number of data available at low ionic strengths.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kh3 = log
Kh3 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh3 + 0.022/μ½
0Kh3 + 0.022/μ½![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kh3 = −2.92. Fig. 2 shows the distribution of Fe(III) species versus the pH for [FeIII]tot = 0.5 mmol dm−3. Under these conditions the dimer contributes mostly in the pH region 3.0–3.5, but when [FeIII]tot ≤ 0.1 mmol dm−3 the contribution of Fe2(OH)24+ can be neglected, while the distribution of the other species remains essentially unaffected.
0Kh3 = −2.92. Fig. 2 shows the distribution of Fe(III) species versus the pH for [FeIII]tot = 0.5 mmol dm−3. Under these conditions the dimer contributes mostly in the pH region 3.0–3.5, but when [FeIII]tot ≤ 0.1 mmol dm−3 the contribution of Fe2(OH)24+ can be neglected, while the distribution of the other species remains essentially unaffected.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd1 as a function of μ½ at 25 °C. The only systematic studies are those of Huss and Eckert,36 who used spectrophotometry and collected 33 data points at low ionic strength, and of Millero et al.,37 who employed potentiometric titration with a focus on high ionic strengths. The two data points of Sekine et al.38 were obtained as a byproduct of studying the distribution of S(IV) between carbon tetrachloride and water by means of iodometry. They agree well with the other data. The single point due to Devèze and Rumpf39 is included because these authors also used spectrophotometric measurements. This technique appears to be most reliable. The older data of Frydman et al.40 obtained for μ = 1.0 and μ = 3.5 mol dm−3 by potentiometric titration fall outside the range of the other data by a wide margin and are not shown. The solid line in Fig. 3 represents the best fit to the experimental data by the extended Debye–Hückel equation:
Kd1 as a function of μ½ at 25 °C. The only systematic studies are those of Huss and Eckert,36 who used spectrophotometry and collected 33 data points at low ionic strength, and of Millero et al.,37 who employed potentiometric titration with a focus on high ionic strengths. The two data points of Sekine et al.38 were obtained as a byproduct of studying the distribution of S(IV) between carbon tetrachloride and water by means of iodometry. They agree well with the other data. The single point due to Devèze and Rumpf39 is included because these authors also used spectrophotometric measurements. This technique appears to be most reliable. The older data of Frydman et al.40 obtained for μ = 1.0 and μ = 3.5 mol dm−3 by potentiometric titration fall outside the range of the other data by a wide margin and are not shown. The solid line in Fig. 3 represents the best fit to the experimental data by the extended Debye–Hückel equation:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd1 = log
Kd1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kd1 + 1.02μ½/(1 + 1.3μ½) − 0.215μ
0Kd1 + 1.02μ½/(1 + 1.3μ½) − 0.215μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kd1 = log
0Kd1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0139 = −1.85698 was kept fixed and the other two parameters were determined by a least square curve fitting program. The factor 1.3 in the denominator of the second term on the right is consistent with the value 1.64, which Huss and Eckert36 had adopted by analogy with other 1–1 electrolytes of comparable size. By extrapolating the Debye–Hückel equation to μ = 0 they had found 0Kd1 = 0.0138 ± 0.0004, in excellent agreement with 0Kd1 = 0.0139 ± 0.0002 obtained from conductivity measurements.
0.0139 = −1.85698 was kept fixed and the other two parameters were determined by a least square curve fitting program. The factor 1.3 in the denominator of the second term on the right is consistent with the value 1.64, which Huss and Eckert36 had adopted by analogy with other 1–1 electrolytes of comparable size. By extrapolating the Debye–Hückel equation to μ = 0 they had found 0Kd1 = 0.0138 ± 0.0004, in excellent agreement with 0Kd1 = 0.0139 ± 0.0002 obtained from conductivity measurements.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd1 of the first dissociation constant of sulfurous acid versus the root of ionic strength: open diamonds (Huss and Eckert36); filled diamonds (Sekine et al.38); open points (Millero et al.37); square (Devèze and Rumpf39). The solid line was calculated from eqn (4).
Kd1 of the first dissociation constant of sulfurous acid versus the root of ionic strength: open diamonds (Huss and Eckert36); filled diamonds (Sekine et al.38); open points (Millero et al.37); square (Devèze and Rumpf39). The solid line was calculated from eqn (4).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex was found to form very rapidly after mixing the reagents (in the mmol dm−3 concentration range), the formation of the 1
1-complex was found to form very rapidly after mixing the reagents (in the mmol dm−3 concentration range), the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex was completed within 10–50 ms, and the reaction to form the 1
2-complex was completed within 10–50 ms, and the reaction to form the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex took up to 200 ms to be completed. Conklin and Hoffmann14 had used a fixed reaction time of 10 ms; Betterton18 used a reaction time of 160 ms. The time frame in the latter study would have meant that at least the 1
3-complex took up to 200 ms to be completed. Conklin and Hoffmann14 had used a fixed reaction time of 10 ms; Betterton18 used a reaction time of 160 ms. The time frame in the latter study would have meant that at least the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the 1
1 and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes were present. This led to uncertainties in the data interpretation. Kraft and van Eldik17 had suggested that the 1
2-complexes were present. This led to uncertainties in the data interpretation. Kraft and van Eldik17 had suggested that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex can exist in two isomeric forms, but the data of Prinsloo et al.19 did not provide further support for the idea. The following analysis will focus on the results of the last authors because they reported the most comprehensive data set.
2-complex can exist in two isomeric forms, but the data of Prinsloo et al.19 did not provide further support for the idea. The following analysis will focus on the results of the last authors because they reported the most comprehensive data set.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes to be fully dissociated, but this need not be the case. In fact, it will be shown that in the pH range explored the 1
3-complexes to be fully dissociated, but this need not be the case. In fact, it will be shown that in the pH range explored the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex occurs primarily in the form Fe(SO3)3H2−. Other authors9,11,12,14,16 have considered Fe3+ to be involved in the formation of the 1
3-complex occurs primarily in the form Fe(SO3)3H2−. Other authors9,11,12,14,16 have considered Fe3+ to be involved in the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex, and they have written reaction (c1) in the form
1-complex, and they have written reaction (c1) in the form![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes. Betterton18 had raised doubts about this interpretation because his data did not show a change in the slope. Prinsloo et al.19 then restudied the absorption changes as a function of [SIV]tot, again by means of rapid-scan spectrometry. They largely confirmed the earlier results of Kraft and van Eldik17 and derived apparent stability constants for the complexes at pH 2.5 and pH 3, which they found to be essentially independent of wavelength in the region 390–470 nm (as required). The formation of the 1
2-complexes. Betterton18 had raised doubts about this interpretation because his data did not show a change in the slope. Prinsloo et al.19 then restudied the absorption changes as a function of [SIV]tot, again by means of rapid-scan spectrometry. They largely confirmed the earlier results of Kraft and van Eldik17 and derived apparent stability constants for the complexes at pH 2.5 and pH 3, which they found to be essentially independent of wavelength in the region 390–470 nm (as required). The formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes was studied at a reaction time of about 50 ms, that of the 1
2-complexes was studied at a reaction time of about 50 ms, that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex at later times. The values reported at pH 2.5 and 3.0 (T = 25 °C, μ = 0.1 mol dm−3) are: Kc1app = 425 ± 18 and 861 ± 120, respectively, as well as Kc2app = 231 ± 16 and 604 ± 52, Kc3app = 158 ± 18 and 190 ± 25 (units: mol, dm3).
3-complex at later times. The values reported at pH 2.5 and 3.0 (T = 25 °C, μ = 0.1 mol dm−3) are: Kc1app = 425 ± 18 and 861 ± 120, respectively, as well as Kc2app = 231 ± 16 and 604 ± 52, Kc3app = 158 ± 18 and 190 ± 25 (units: mol, dm3).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complexes are present, the relevant mass balance equations are
2-complexes are present, the relevant mass balance equations are![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex when [SIV]tot is raised. The Kc1app values obtained from the initial slopes are 320 ± 26 at pH 2 and 787 ± 216 at pH 2.5. Data for pH 3 are not shown, because the number of data points defining the initial rise of absorbance is insufficient to allow a reasonably reliable evaluation. An estimate obtained from the first two points is Kc1app ≈ 2230, which is much higher than, and clearly inconsistent with, the approximate value 1722 ± 240 obtained above. However, the value reported by Prinsloo et al.19 at λ = 390 nm, Kc1app = 916 ± 113, is also higher than the average obtained from data at all wavelengths. The values for Kc2app obtained at pH 2.5 and pH 3 were only slightly different from those given above,19 the differences falling within the range of the experimental error.
2-complex when [SIV]tot is raised. The Kc1app values obtained from the initial slopes are 320 ± 26 at pH 2 and 787 ± 216 at pH 2.5. Data for pH 3 are not shown, because the number of data points defining the initial rise of absorbance is insufficient to allow a reasonably reliable evaluation. An estimate obtained from the first two points is Kc1app ≈ 2230, which is much higher than, and clearly inconsistent with, the approximate value 1722 ± 240 obtained above. However, the value reported by Prinsloo et al.19 at λ = 390 nm, Kc1app = 916 ± 113, is also higher than the average obtained from data at all wavelengths. The values for Kc2app obtained at pH 2.5 and pH 3 were only slightly different from those given above,19 the differences falling within the range of the experimental error.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex
1-complex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex is,
2-complex is,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes is considered. In this case, the observed Kc3app values show only a slight dependence on pH, indicating that the 1
3-complexes is considered. In this case, the observed Kc3app values show only a slight dependence on pH, indicating that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex remains nearly fully protonated in the (admittedly narrow) pH range covered. Accordingly, reaction (c3) should be written
3-complex remains nearly fully protonated in the (admittedly narrow) pH range covered. Accordingly, reaction (c3) should be written![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc1 = log
Kc1 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kc1 − 2.04μ½/(1 + aμ½), log
0Kc1 − 2.04μ½/(1 + aμ½), log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc2 ≈ log
Kc2 ≈ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kc2 (no significant ionic strength dependence), and log Kc3a = log
0Kc2 (no significant ionic strength dependence), and log Kc3a = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0Kc3a + 1.02μ½/(1 + βμ½). The factors a and β in the denominators of the second terms must be estimated. Regarding the equilibrium constant Kc1 Lente and Fabian16 have found Kc1a = Kc1Kh1 = 1.35 ± 0.15 at μ = 1.0 mol dm−3; which is equivalent to Kc1 = 825 ± 92 at this ionic strength. The corresponding value of a in the extended Debye–Hückel equation would be a ≈ 1.5. The value of Kc3a increases with increasing ionic strength, but the effect is not very pronounced, and it is neglected in calculating equilibrium distributions of the Fe(III) species.
0Kc3a + 1.02μ½/(1 + βμ½). The factors a and β in the denominators of the second terms must be estimated. Regarding the equilibrium constant Kc1 Lente and Fabian16 have found Kc1a = Kc1Kh1 = 1.35 ± 0.15 at μ = 1.0 mol dm−3; which is equivalent to Kc1 = 825 ± 92 at this ionic strength. The corresponding value of a in the extended Debye–Hückel equation would be a ≈ 1.5. The value of Kc3a increases with increasing ionic strength, but the effect is not very pronounced, and it is neglected in calculating equilibrium distributions of the Fe(III) species.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is still dominant after 160 ms reaction time, even at high S(IV) concentrations. This condition applies also at pH 1.25 over most of the [SIV] concentration range. Thus, the K-values reported by Betterton18 at low pH can be identified with Kc1app. At pH 1 ([FeIII]tot = 1.25 × 10−4 mol dm−3, μ = 0.5) the average of the reported K-values is Kc1app = 8.3 ± 3.7 (3 wavelengths), and at pH 1.25 ([FeIII]tot = 5.0 × 10−4 mol dm−3, μ = 0.2) the average is Kc1app = 11.4 ± 1.6 (6 wavelengths). Calculations for these experimental conditions show that [SIV] ≈ [SIV]tot so that corrections for [SIV] are not required. The true equilibrium constants, defined by eqn (7a), are then calculated to be Kc1 = 2143 ± 952 dm−3 mol−1 at pH 1, Kc1 = 913 ± 128 dm−3 mol−1 at pH 1.25. These values must be corrected for the ionic strength effect in order that they can be compared with the results of Prinsloo et al.,19 which were obtained at μ = 0.1. The corrected Kc1 values are estimated to be 3781 ± 1678 and 1151 ± 161 dm3 mol−1 at pH 1 and 1.25, respectively. The values bracket that derived from the data of Prinsloo et al.,19 but it is not obvious, why they diverge so much from each other.
1-complex is still dominant after 160 ms reaction time, even at high S(IV) concentrations. This condition applies also at pH 1.25 over most of the [SIV] concentration range. Thus, the K-values reported by Betterton18 at low pH can be identified with Kc1app. At pH 1 ([FeIII]tot = 1.25 × 10−4 mol dm−3, μ = 0.5) the average of the reported K-values is Kc1app = 8.3 ± 3.7 (3 wavelengths), and at pH 1.25 ([FeIII]tot = 5.0 × 10−4 mol dm−3, μ = 0.2) the average is Kc1app = 11.4 ± 1.6 (6 wavelengths). Calculations for these experimental conditions show that [SIV] ≈ [SIV]tot so that corrections for [SIV] are not required. The true equilibrium constants, defined by eqn (7a), are then calculated to be Kc1 = 2143 ± 952 dm−3 mol−1 at pH 1, Kc1 = 913 ± 128 dm−3 mol−1 at pH 1.25. These values must be corrected for the ionic strength effect in order that they can be compared with the results of Prinsloo et al.,19 which were obtained at μ = 0.1. The corrected Kc1 values are estimated to be 3781 ± 1678 and 1151 ± 161 dm3 mol−1 at pH 1 and 1.25, respectively. The values bracket that derived from the data of Prinsloo et al.,19 but it is not obvious, why they diverge so much from each other.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex appears to be primarily involved. Rather similar results were obtained with [FeIII]tot = 2.5 × 10−4 and 5.0 × 10−4 mol dm−3. The average of 8 individual values obtained at 5 different wavelengths is 82.0 ± 11.2. The corresponding true equilibrium constant calculated with the help of eqn (8) is Kc2 = 1.15 ± 0.16. This result is higher than that derived above from the data of the other authors,14,19 but the calculated time dependence for complex formation shows that at the longer reaction time used by Betterton18 the contribution of the 1
2-complex appears to be primarily involved. Rather similar results were obtained with [FeIII]tot = 2.5 × 10−4 and 5.0 × 10−4 mol dm−3. The average of 8 individual values obtained at 5 different wavelengths is 82.0 ± 11.2. The corresponding true equilibrium constant calculated with the help of eqn (8) is Kc2 = 1.15 ± 0.16. This result is higher than that derived above from the data of the other authors,14,19 but the calculated time dependence for complex formation shows that at the longer reaction time used by Betterton18 the contribution of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex cannot be fully ignored. At concentrations [SIV]tot ≥ 10 mmol dm−3 the 1
3-complex cannot be fully ignored. At concentrations [SIV]tot ≥ 10 mmol dm−3 the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex becomes the dominant species, requiring appropriate corrections. The overall conclusion is that the results obtained by Betterton18 for this pH regime agree reasonably well with the other data discussed above. In the pH range 2–3, however, all three complexes are simultaneously present at similar concentrations, which makes it difficult to interpret the Newton–Arcand plots in a simple manner even if straight lines are observed. Note that nearly straight lines would be obtained if the 1
3-complex becomes the dominant species, requiring appropriate corrections. The overall conclusion is that the results obtained by Betterton18 for this pH regime agree reasonably well with the other data discussed above. In the pH range 2–3, however, all three complexes are simultaneously present at similar concentrations, which makes it difficult to interpret the Newton–Arcand plots in a simple manner even if straight lines are observed. Note that nearly straight lines would be obtained if the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes featured absorption coefficients of similar magnitude. From the preceding discussion it will be clear that much of the difficulty experienced in disentangling the three equilibria from simple absorbance measurements is due to the complexity of the system and the necessity of finding suitable experimental conditions for the task.
3-complexes featured absorption coefficients of similar magnitude. From the preceding discussion it will be clear that much of the difficulty experienced in disentangling the three equilibria from simple absorbance measurements is due to the complexity of the system and the necessity of finding suitable experimental conditions for the task.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex. He reported kc1f = 4.0 × 106 dm3 mol−1 s−1 at pH 2. This result when combined with the equilibrium constant derived above suggests kc1f = 4.0 × 106, kc1r = 2.08 × 103 for the rate coefficients of the forward and reverse reactions. Kraft and van Eldik17 used a stopped-flow instrument with a short mixing time (∼0.2 ms) to measure rate constants for the formation of the complex appearing within the 1–10 ms time frame (denoted step I). Experimental conditions were: [FeIII]tot = 2 mmol dm−3, pH 2.5, μ = 0.1, and [SIV]tot was varied between 10 and 60 mmol dm−3. The high concentrations of S(IV) combined with the time frame used make it fairly certain that the 1
1-complex. He reported kc1f = 4.0 × 106 dm3 mol−1 s−1 at pH 2. This result when combined with the equilibrium constant derived above suggests kc1f = 4.0 × 106, kc1r = 2.08 × 103 for the rate coefficients of the forward and reverse reactions. Kraft and van Eldik17 used a stopped-flow instrument with a short mixing time (∼0.2 ms) to measure rate constants for the formation of the complex appearing within the 1–10 ms time frame (denoted step I). Experimental conditions were: [FeIII]tot = 2 mmol dm−3, pH 2.5, μ = 0.1, and [SIV]tot was varied between 10 and 60 mmol dm−3. The high concentrations of S(IV) combined with the time frame used make it fairly certain that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex was observed. The rate constant was found to vary linearly with [SIV]tot (their Fig. 6a). From the slope of the straight line one obtains kc2app = 5.2 × 103 dm3 mol−1 s−1. A correction is needed to take into account that the reactive species is HSO3−. The appropriate correction factor (1 + [H+]/Kd1 + Kd2/[H+]) leads to kc2f = 5.9 × 103 dm3 mol−1 s−1. The rate coefficient for the reverse reaction step is calculated to be kc2r = kc2f/Kc2 = 8.24 × 103 dm3 mol−1 s−1. The formation of the 1
2-complex was observed. The rate constant was found to vary linearly with [SIV]tot (their Fig. 6a). From the slope of the straight line one obtains kc2app = 5.2 × 103 dm3 mol−1 s−1. A correction is needed to take into account that the reactive species is HSO3−. The appropriate correction factor (1 + [H+]/Kd1 + Kd2/[H+]) leads to kc2f = 5.9 × 103 dm3 mol−1 s−1. The rate coefficient for the reverse reaction step is calculated to be kc2r = kc2f/Kc2 = 8.24 × 103 dm3 mol−1 s−1. The formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex proceeds subsequent to that of the 1
3-complex proceeds subsequent to that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex. Kraft and van Eldik17 found that it can be conveniently followed by means of stopped-flow spectrometry within the time frame 50–200 ms (step II). The experimental conditions were [FeIII]tot = 0.5 mmol dm−3, pH 2.5, [SIV]tot = 5–50 mmol dm−3, μ = 0.1. Rate coefficients were measured as a function of [SIV] at two wavelengths (390 and 450 nm). From the slopes of the straight lines obtained in plots of kc3appvs. [SIV] (their Fig. 8 and 9) one obtains kc3app = 3.3 × 103 dm3 mol−1 s−1. The correction needed to take into account that HSO3− is the true reactant raises the value to kc3af = 3.8 × 103 dm3 mol−1 s−1. The corresponding rate coefficient for the reverse reaction step then is kc3ar = kc3af/Kc3a = 20.1 s−1.
2-complex. Kraft and van Eldik17 found that it can be conveniently followed by means of stopped-flow spectrometry within the time frame 50–200 ms (step II). The experimental conditions were [FeIII]tot = 0.5 mmol dm−3, pH 2.5, [SIV]tot = 5–50 mmol dm−3, μ = 0.1. Rate coefficients were measured as a function of [SIV] at two wavelengths (390 and 450 nm). From the slopes of the straight lines obtained in plots of kc3appvs. [SIV] (their Fig. 8 and 9) one obtains kc3app = 3.3 × 103 dm3 mol−1 s−1. The correction needed to take into account that HSO3− is the true reactant raises the value to kc3af = 3.8 × 103 dm3 mol−1 s−1. The corresponding rate coefficient for the reverse reaction step then is kc3ar = kc3af/Kc3a = 20.1 s−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is reached at times shorter than 1 ms. Full equilibrium between all three complexes is reached about 250 ms after mixing the reagents.
1-complex is reached at times shorter than 1 ms. Full equilibrium between all three complexes is reached about 250 ms after mixing the reagents.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b
b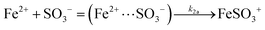
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c (ref. 47)
c (ref. 47)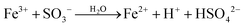
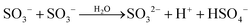
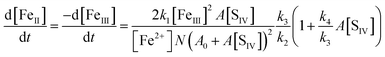

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex. Computer calculations of the equilibria established between the three complexes indicated that the higher complexes begin to interfere when [HSO3−]/[FeIII] > ∼50, that is [SIV]/[FeIII] ≈ 150, when [H+] = 0.043 M, and [SIV]/[FeIII] ≈ 300 when [H+] = 0.129 M. Since the above eqn (10) is based on the assumption that only the 1
1-complex. Computer calculations of the equilibria established between the three complexes indicated that the higher complexes begin to interfere when [HSO3−]/[FeIII] > ∼50, that is [SIV]/[FeIII] ≈ 150, when [H+] = 0.043 M, and [SIV]/[FeIII] ≈ 300 when [H+] = 0.129 M. Since the above eqn (10) is based on the assumption that only the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex is present the results of those experiments that did not satisfy this condition were not used. This removes 8 data points from a total set of 25. The remaining data were subjected to a linear regression treatment that resulted in a slope of (6.7 ± 0.4) × 10−4 s−1 and an intercept with the ordinate of (1.6 ± 1.2) × 10−5 s−1. According to eqn (10a) the slope and the intercept are equivalent to 2(k1k3/k2)(k4/k3) and 2(k1k3/k2), respectively. Their ratio is k4/k3 = 42 with a large margin of error due to the uncertainty associated with the value of the intercept.
1-complex is present the results of those experiments that did not satisfy this condition were not used. This removes 8 data points from a total set of 25. The remaining data were subjected to a linear regression treatment that resulted in a slope of (6.7 ± 0.4) × 10−4 s−1 and an intercept with the ordinate of (1.6 ± 1.2) × 10−5 s−1. According to eqn (10a) the slope and the intercept are equivalent to 2(k1k3/k2)(k4/k3) and 2(k1k3/k2), respectively. Their ratio is k4/k3 = 42 with a large margin of error due to the uncertainty associated with the value of the intercept.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 relation obtained with k1/k2 = 61.4.
1 relation obtained with k1/k2 = 61.4.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line is about 3%. Fig. 7b includes all the data with [H+] = 0.255, except the two points obtained when [Fe2+]0 > [SIV]0 as they are off-scale. In this case the calculated half-life times are 17 and 31.7 min, whereas the measured values were 10.2 and 13.7 min, respectively. It appears that when larger amounts of Fe(II) are added the measurement of half-life times become less precise. The three data points at different hydrogen ion concentrations were already discarded by Karraker; they do not fit into any scheme.
1 line is about 3%. Fig. 7b includes all the data with [H+] = 0.255, except the two points obtained when [Fe2+]0 > [SIV]0 as they are off-scale. In this case the calculated half-life times are 17 and 31.7 min, whereas the measured values were 10.2 and 13.7 min, respectively. It appears that when larger amounts of Fe(II) are added the measurement of half-life times become less precise. The three data points at different hydrogen ion concentrations were already discarded by Karraker; they do not fit into any scheme.

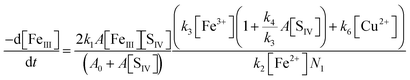
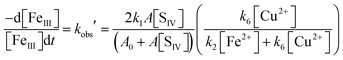
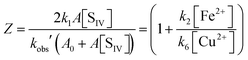

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = log
k = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0k + 1.02zAzBμ½/(1 + μ½), where zA and zB are the electric charges of the reactants A and B. Several reactions in the sulfur–oxygen system have been found to obey this relation.6,53 In the case of reaction (2) the product zAzB = −2, leading to an estimate of k2 = 3.0 × 106 dm3 mol−1 s−1 at μ = 1. This value, when used in conjunction with k2/k3 = 61.4, provides k3 = 4.9 × 104 dm3 mol−1 s−1. In addition, the combination with the ratios k3/k4 = 42 and k6/k2 = 0.27 leads to k4 = 2.1 × 106 and k6 = 8.1 × 105 dm3 mol−1 s−1. These values must be considered estimates, and confirmation by direct measurements will be needed.
0k + 1.02zAzBμ½/(1 + μ½), where zA and zB are the electric charges of the reactants A and B. Several reactions in the sulfur–oxygen system have been found to obey this relation.6,53 In the case of reaction (2) the product zAzB = −2, leading to an estimate of k2 = 3.0 × 106 dm3 mol−1 s−1 at μ = 1. This value, when used in conjunction with k2/k3 = 61.4, provides k3 = 4.9 × 104 dm3 mol−1 s−1. In addition, the combination with the ratios k3/k4 = 42 and k6/k2 = 0.27 leads to k4 = 2.1 × 106 and k6 = 8.1 × 105 dm3 mol−1 s−1. These values must be considered estimates, and confirmation by direct measurements will be needed.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex. The computer calculations first showed that the experimental data can be reproduced only by assuming that reaction (3b) is the main channel of reaction (3) with k3b = 7.6 × 106 dm3 mol−1 s−1 (at μ = 1.0 mol dm−3). But in contrast to expectation the calculations also showed that the basic mechanism of Table 1 is adequate to reproduce both sets of experimental data. The results are shown in Fig. 11 by the solid lines. The assumption of even a minimal contribution by the decomposition of the 1
3-complex. The computer calculations first showed that the experimental data can be reproduced only by assuming that reaction (3b) is the main channel of reaction (3) with k3b = 7.6 × 106 dm3 mol−1 s−1 (at μ = 1.0 mol dm−3). But in contrast to expectation the calculations also showed that the basic mechanism of Table 1 is adequate to reproduce both sets of experimental data. The results are shown in Fig. 11 by the solid lines. The assumption of even a minimal contribution by the decomposition of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex only worsened the agreement between calculated and experimental data in that the initial decay rate became too rapid. The rate coefficient for the decomposition was estimated to be k1b < 0.01 s−1. These results suggest that under the experimental conditions chosen the 1
3-complex only worsened the agreement between calculated and experimental data in that the initial decay rate became too rapid. The rate coefficient for the decomposition was estimated to be k1b < 0.01 s−1. These results suggest that under the experimental conditions chosen the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex does not significantly participate in the reaction.
3-complex does not significantly participate in the reaction.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes were then introduced on a trial basis as needed to bring observed and calculated data to agreement.
3-complexes were then introduced on a trial basis as needed to bring observed and calculated data to agreement.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex is subject to decomposition and that it participates in the reaction. Computer calculations were performed in attempts to reproduce the observed variation in the kapp values. The solid line shown in the upper part of Fig. 12 was obtained with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.08 s−1 for the decomposition of the 1
3-complex is subject to decomposition and that it participates in the reaction. Computer calculations were performed in attempts to reproduce the observed variation in the kapp values. The solid line shown in the upper part of Fig. 12 was obtained with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.08 s−1 for the decomposition of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1
3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex. The initial rise curve was better represented with k3b = 2.6 × 107 dm3 mol−1 s−1 rather than with k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0 (shown by the broken line). The experimental data indicate a slight overshoot at [SIV]0 ≈ 5 mmol dm−3, which could be reproduced, if the value chosen for k4 were raised by 50%. Fig. 13 shows the variation of the apparent initial first order rate coefficients with the pH and, in the lower part of the figure, the change in the equilibrium distribution of Fe(III) species. The distribution shifts from FeSO3+ to Fe(SO3)3H2− as the pH is raised, indicating again that the higher complexes participate in the overall reaction. Computer calculations performed in attempts to reproduce the observed variation in the kapp values showed that in this case the results differed little with the choice of k3 (either k3b = 2.6 × 107 or k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0). The solid line shown in the upper part of Fig. 13 was calculated with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.06 s−1 for the decomposition of the 1
3-complex. The initial rise curve was better represented with k3b = 2.6 × 107 dm3 mol−1 s−1 rather than with k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0 (shown by the broken line). The experimental data indicate a slight overshoot at [SIV]0 ≈ 5 mmol dm−3, which could be reproduced, if the value chosen for k4 were raised by 50%. Fig. 13 shows the variation of the apparent initial first order rate coefficients with the pH and, in the lower part of the figure, the change in the equilibrium distribution of Fe(III) species. The distribution shifts from FeSO3+ to Fe(SO3)3H2− as the pH is raised, indicating again that the higher complexes participate in the overall reaction. Computer calculations performed in attempts to reproduce the observed variation in the kapp values showed that in this case the results differed little with the choice of k3 (either k3b = 2.6 × 107 or k3a = 3.0 × 105 dm3 mol−1 s−1 and k3b = 0). The solid line shown in the upper part of Fig. 13 was calculated with the rate coefficients given above and the assumption that k1a = 0.04 s−1, k1b = 0.06 s−1 for the decomposition of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1
3-complexes, respectively, and k4b = 1.2 × 107 dm3 mol−1 s−1 for the reaction of SO3− radicals with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex. These values are quite similar to those found applicable in the preceding case when the pH was kept constant and [SIV]0 was varied. Above pH 2.5 it was not possible to obtain a good fit between calculated and observed kapp values.
3-complex. These values are quite similar to those found applicable in the preceding case when the pH was kept constant and [SIV]0 was varied. Above pH 2.5 it was not possible to obtain a good fit between calculated and observed kapp values.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex (k1a ≈ 0.04 s−1 and k1b ≈ 0.08 s−1 compared to k1 = 0.19 s−1). This conclusion obviously disagrees with that derived above in evaluating the data of Conklin and Hoffmann,14 which had indicated that the 1
1-complex (k1a ≈ 0.04 s−1 and k1b ≈ 0.08 s−1 compared to k1 = 0.19 s−1). This conclusion obviously disagrees with that derived above in evaluating the data of Conklin and Hoffmann,14 which had indicated that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 iron–sulfito complexes do not significantly participate in the reaction. The major difference in the applied experimental conditions, apart from the presence of formic acid in the latter case, is the difference in ionic strength (μ = 0.1 versus μ = 1.0). This may have a bearing on the reaction rate coefficients, but it should not affect the decomposition rates.
3 iron–sulfito complexes do not significantly participate in the reaction. The major difference in the applied experimental conditions, apart from the presence of formic acid in the latter case, is the difference in ionic strength (μ = 0.1 versus μ = 1.0). This may have a bearing on the reaction rate coefficients, but it should not affect the decomposition rates.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and 1
2- and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes, whereas that of the sum of Fe(OH)2+ and Fe(OH)2+ decreases.
3-complexes, whereas that of the sum of Fe(OH)2+ and Fe(OH)2+ decreases.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-complex is less likely a source of dithionate than the 1
2-complex is less likely a source of dithionate than the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complex, which gains prominence at the high end of the S(IV) concentration range. The addition of reaction (4b) with a rate coefficient of k4b ≈ 1.2 × 107 dm3 mol−1 s−1 would also provide good agreement with the measured dithionate yields, provided the reaction consisted of two channels, one leading to dithionate with a yield of 65%, the other one leading to sulfate with a yield of 35%. This partitioning determines the plateau of the dithionate concentration at high S(IV) concentrations. It will be clear that the limited data on dithionate formation reported by Kraft and van Eldik15 cannot give definitive answers on all possible routes to dithionate production. However, the recognition that reaction (3b) is more likely in this mechanism than (3a) would be in accord with the conclusions reached in the preceding discussion of the apparent initial first order rate coefficients determined by the authors.
3-complex, which gains prominence at the high end of the S(IV) concentration range. The addition of reaction (4b) with a rate coefficient of k4b ≈ 1.2 × 107 dm3 mol−1 s−1 would also provide good agreement with the measured dithionate yields, provided the reaction consisted of two channels, one leading to dithionate with a yield of 65%, the other one leading to sulfate with a yield of 35%. This partitioning determines the plateau of the dithionate concentration at high S(IV) concentrations. It will be clear that the limited data on dithionate formation reported by Kraft and van Eldik15 cannot give definitive answers on all possible routes to dithionate production. However, the recognition that reaction (3b) is more likely in this mechanism than (3a) would be in accord with the conclusions reached in the preceding discussion of the apparent initial first order rate coefficients determined by the authors.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-complex has been documented, the disintegration of the 1
1-complex has been documented, the disintegration of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2- and the 1
2- and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-complexes are found to be slower. The mechanism in Table 1 is consistent with most of the data reported for experimental conditions under which the FeSO3+ complex is the most abundant intermediate (pH < 2, [SIV]/[FeIII] < 200). However, yields of dithionate reported by different authors diverge significantly, presumably because the classical analytical methods formerly in use were inadequate. Although it was possible to estimate rate coefficients of the reactions involved, the true values will have to be determined in future studies. One of the problems that will require closer attention is the ionic strength dependence of the stability constants of the complexes as well as that of the rate coefficients of the individual reactions.
3-complexes are found to be slower. The mechanism in Table 1 is consistent with most of the data reported for experimental conditions under which the FeSO3+ complex is the most abundant intermediate (pH < 2, [SIV]/[FeIII] < 200). However, yields of dithionate reported by different authors diverge significantly, presumably because the classical analytical methods formerly in use were inadequate. Although it was possible to estimate rate coefficients of the reactions involved, the true values will have to be determined in future studies. One of the problems that will require closer attention is the ionic strength dependence of the stability constants of the complexes as well as that of the rate coefficients of the individual reactions.