Why does the Y326I mutant of monoamine oxidase B decompose an endogenous amphetamine at a slower rate than the wild type enzyme? Reaction step elucidated by multiscale molecular simulations

Abstract

This work investigates the Y326I point mutation effect on the kinetics of oxidative deamination of phenylethylamine (PEA) catalyzed by the monoamine oxidase B (MAO B) enzyme. PEA is a neuromodulator capable of affecting the plasticity of the brain and is responsible for the mood enhancing effect caused by physical exercise. Due to a similar functionality, PEA is often regarded as an endogenous amphetamine. The rate limiting step of the deamination was simulated at the multiscale level, employing the Empirical Valence Bond approach for the quantum treatment of the involved valence states, whereas the environment (solvated protein) was represented with a classical force field. A comparison of the reaction free energy profiles delivered by simulation of the reaction in the wild type MAO B and its Y326I mutant yields an increase in the barrier by 1.06 kcal mol⁻¹ upon mutation, corresponding to a roughly 6-fold decrease in the reaction rate. This is in excellent agreement with the experimental kinetic studies. Inspection of simulation trajectories reveals possible sources of the point mutation effect, namely vanishing favorable electrostatic interactions between PEA and a Tyr326 side chain and an increased amount of water molecules at the active site due to the replacement of tyrosine by a less spacious isoleucine residue, thereby increasing the dielectric shielding of the catalytic environment provided by the enzyme.

---

1. Introduction

The action of monoamine oxidase enzymes (MAOs) in the central nervous system has been a source of profound experimental and theoretical research due to their high relevance in the metabolism of neurotransmitters and therewith associated neurological disorders and neurodegenerative diseases.^1–4 MAOs are flavoenzymes, catalyzing the oxidative transformation of monoamines and thereby regulating the level of neurotransmitters and neuromodulators in the central nervous system. Deficient or elevated activity of MAOs is a potential source of various neuropsychiatric disorders associated with excessive or insufficient amounts of neurotransmitters, such as depression, autism and aggressive behavior.^1,2,5,6 In addition, the action of MAOs represents an inherent source of oxidative stress, leading to the damage and death of neurons, which can culminate in neurodegenerative diseases such as Parkinson's or Alzheimer's disease.^7–9

MAO enzymes exist in two forms, A and B (MAO A, MAO B), which share about 70% of the sequence identity,¹⁰ but differ in substrate specificity.^2,11 However, both MAO A and MAO B share a wide array of common substrates. It has been accepted that the catalytic step of amine oxidation includes the cleavage of a C–H bond at the methylene group vicinal to the amino group, i.e., the α-C–H bond, accompanied by the hydrogen transfer to the flavin adenine dinucleotide (FAD) prosthetic group covalently bound to the cysteine residue.¹² While full consensus on the mechanism of this step has not yet been reached,^13–17 there is growing evidence that it proceeds via the direct hydride transfer mechanism, as recently demonstrated by quantum calculations using cluster and QM/MM models^18–20 and at least implicitly validated by computational treatments based on this mechanism.^21–27 The assumed reaction scheme is displayed in Fig. 1.

Fig. 1 Scheme of the rate limiting step of phenylethylamine oxidation catalyzed by MAOs and proceeding via the hydride transfer mechanism.

Enzyme point mutations, i.e. replacement of a given amino acid residue in the sequence by another residue, represent a mechanism that provides everlasting changes of biomolecules and their functionalities, contributing to biological evolution. In the context of enzyme research, point mutations are a powerful tool for the understanding of the selectivity and specificity of enzymes at an atomic level. Because of the two isoforms, MAO enzymes are particularly appealing for research based on point mutations.^28–32 It has been shown that point mutations at several equivalent positions in the sequence effectively reverse the substrate and inhibitor specificity between MAO A and B.¹¹ Perhaps the most crucial residues in this regard are isoleucine 335 in MAO A and the equivalent tyrosine 326 residue in MAO B. It has been found that the I335Y mutation of MAO A causes the enzyme to act like MAO B in terms of specificity, and vice versa for the reciprocal Y326I mutation of MAO B.¹¹

In this work we scrutinize the Y326I point mutation effect in MAO B for the decomposition of phenylethylamine (PEA). PEA is a biogenic monoamine present in the central nervous system. Although it is chemically similar to monoaminergic neurotransmitters such as dopamine, serotonin or noradrenaline, it primarily functions as a neuromodulator rather than an excitatory neurotransmitter. PEA per se does not activate dopamine receptors. Rather than being absorbed by a presynaptic neuron, PEA spends a significant amount of time in the cerebrospinal fluid, and is thus capable of reaching and influencing neurons over long distances, without requiring any synaptic contacts between them. It has been found that PEA is released in significant quantities during physical exercise, producing a considerable mood enhancing effect, known as “runner's high”.³³ Due to the effects similar to those of amphetamine, i.e. blocking the dopamine transporter and hence increasing the dopamine level at the synaptic gap, PEA is often regarded as an endogenous amphetamine.^34–36 Additionally, it has been suggested that an increased level of PEA is associated with schizophrenia.^37,38

Similarly to neurotransmitters, PEA is an endogenous substrate of both MAO A and B. In neurons, it is estimated that PEA has a half-life of about 30 seconds.^39,40 Due to its stability – unlike dopamine^41,42 PEA is not prone to autooxidation – it is a popular research substrate of MAO enzymes.^{11,31,43–45} Additionally, several ring-substituted analogs of PEA are available, facilitating the research of kinetic and mechanistic aspects by exploiting the electronic structure effects of the substituents.^45–47 For the same reason, another popular research substrate of MAOs is benzylamine which differs from PEA only in that its amino alkyl chain is shorter by one methylene group.^{13,44,48–51} However, unlike PEA, benzylamine is not endogenous and has not been reported to exhibit neurological effects.

In efforts to acquire an understanding of the functions of enzymes at an atomic level, molecular simulation represents an indispensable tool capable of accurately predicting various properties and providing unique insight into the structure and chemistry of enzymes. Since biological macromolecules are in general too complex for analytical treatment, multiscale simulation is the method of choice for gaining insight into enzyme catalysis. Previous computational studies of MAO enzymes utilized multiscale techniques in various forms.^17,24 Among the most promising multiscale protocols, the empirical valence bond (EVB) methodology is a cost-efficient computational approach specially tuned for the simulation of chemical reactions in a complex environment, such as enzyme active sites.^52–54 EVB combines the quantum treatment of empirical valence states – typically reactants and products of a chemical reaction of interest – and classical representation of the surroundings. Because of the simplicity of the quantum part the computational formalism is noticeably less demanding than most of the ‘traditional’ multiscale QM/MM protocols which typically quantize electronic structure. Consequently, EVB allows for substantial thermal averaging needed for convergent free energy profiles. The reliability of EVB has been demonstrated by a variety of studies of enzymatic reactions.^53,55–59 Technically, EVB can be classified as a QM/MM method, with peculiar character of the quantum part.

Recently, we investigated various aspects of the metabolism of monoamines and catalytic effects of MAOs, by using the EVB methodology in the first place. The issues addressed in our studies include a comparison of preorganized electrostatics between MAO A and B,²⁶ pK_a calculations of selected residues near the active site,^26,60 selectivity between MAO A and B for the decomposition of adrenaline,⁶¹ H/D kinetic isotope effects associated with nuclear quantum effects⁶² and various simulations of point mutation effects.^21,22 We demonstrated that EVB reliably predicts the change of free energy barrier and the corresponding rate constant for various mutants of both MAO A and B, and for various substrates.

In essence, this work augments our recent I335Y point mutation study of MAO A for PEA oxidation,²¹ by treating the reciprocal point mutation Y326I in MAO B for the same reaction. According to the kinetic measurements, the Y326I mutation results in a slight decrease in the reaction rate relatively to the wild type (WT) enzyme – the rate constant of 98.4 min⁻¹ in WT MAO B drops to 27.3 min⁻¹ in the Y326I mutant.¹¹ This corresponds to the barrier elevation from 17.29 to 18.05 kcal mol⁻¹ upon mutation. Interestingly, the observed increase in the barrier does not follow the reciprocity between MAO A and MAO B found at the level of substrate and inhibitor specificity on I335Y/Y326I mutation. If reciprocity also existed at the catalytic level, the I335Y mutation of MAO A would result in a lower barrier, since it has been found that PEA oxidation in MAO B is faster than that in MAO A;¹¹ rather than that, the mutation of both MAO A and B increases the barrier.¹¹ Since physical interpretation of the I335Y point mutation effect on the kinetics of MAO A has been devised in terms of the change in local polarity near the mutated residue,²¹ this could potentially suggest that the reciprocal Y326I mutation of MAO B decreases rather than increases the barrier, provided that the local polarity at the mutated position plays the same role in MAO A and B. The challenge remains whether the EVB simulation can account for the differences between MAO A and MAO B that prevent the isoenzymes from being fully reciprocal on the aforementioned mutations.

A special feature of EVB is that the formalism uses empirical parameters related to the quantum coupling between the valence states of reactants and products. These parameters must be acquired empirically by calibration, requiring simulation of a reference reaction – a reaction of the same mechanism for which thermodynamic and kinetic parameters are known – to be performed in advance. While the most popular form of the reference reaction is either in the gas phase or in aqueous solution, the choice is arbitrary because of transferability of the EVB parameters between media.⁵³ Accordingly, in this work we used the PEA decomposition in WT MAO B as reference and subsequently applied the calibrated parameters for the same reaction in the mutated enzyme. In such a way we minimized the difference between the models and circumvented the issue of conformational flexibility of the reacting moiety.⁶³ In addition, such a selection of the reference reaction minimizes the impact of deprotonation free energy of PEA. Namely, under physiological conditions PEA predominantly exists in the protonated (R–NH₃⁺) form, whereas it undergoes the reaction as a neutral (R–NH₂) molecule. We recently demonstrated that the reaction rate for the protonated adrenaline substrate is extremely low.⁶⁴ In order to make the computed barrier fully comparable with experimental data, the barrier should be corrected for the free energy of deprotonation of PEA, because the experimental measurement includes this correction by definition. This requires that the pK_a value of PEA be estimated within the active site of MAO B, which is all but a trivial task.⁶⁵ However, the assumption that the pK_a value of PEA does not change much upon mutation appears to be reasonable, hence the deprotonation corrections are canceled out in the present treatment. Our recent study demonstrating that the pK_a value of dopamine is effectively unchanged when moving the molecule from an aqueous environment to the MAO B active site supports this reasoning.⁶⁰

In this work we calculated the reaction profiles for wild type MAO B and the Y326I mutant by using multiscale simulation based on empirical valence bond description of the reactive subsystem and molecular mechanics description of the enzyme and solvent. Full dimensionality of the enzyme was considered. An increased activation free energy was found for the mutant, giving rise to a slower reaction, which is in good agreement with the experiment. The results contribute to an improved understanding of the chemical processes involved in the metabolism of neurotransmitters.

2. Simulation details

Simulations of the rate limiting step of PEA oxidation by WT MAO B and its Y326I mutant were based on the EVB methodology in conjunction with the free energy perturbation (FEP) sampling technique,^66,67 as implemented in the Q v. 5.06 program package.⁶⁸ A model of solvated MAO B was built on the basis of the crystal structure acquired from the Protein Data Bank (code 1GOS)⁶⁹ and included a spherical simulation cell with a radius of 30 Å, centered at the reacting nitrogen atom of the flavin prosthetic group; the cell was filled with water molecules (Fig. 2). Simulations utilized the OPLS-AA empirical force field^70–72 tuned for both the reactant and product valence states and proceeded as sequences of molecular dynamics (MD) simulations in which the system parameters were gradually converted from reactants to products. The typical length of MD simulations was 5.1 nanoseconds, which corresponds to 51 FEP steps of 100 picoseconds. All simulations were performed in batches of 10 independent runs (replicas) generated from the same starting structure by randomizing initial velocities. Prior to reaction simulations the system was equilibrated to 300 K by approximately 2 nanoseconds of restrained MD during which the restraints were gradually removed, ultimately keeping a minimal amount of restraints necessary for smooth free energy profiles, as discussed in our earlier studies.^21,63

Fig. 2 A spherical simulation cell of solvated MAO B with the reacting PEA molecule and the FAD prosthetic group.

The applied EVB approach relies on a two-state Hamiltonian expressed as a 2 × 2 matrix with the diagonal elements representing the classical Hamiltonians of the valence states of reactants and products, respectively, whereas the off-diagonal term corresponds to the coupling between the states and has to be determined empirically. The other empirical parameter not included in the original Hamiltonian is the relative shift between the states representing their difference in heat of formation. Both the coupling term and the relative shift are obtained by calibration, a standard procedure of EVB simulations. Calibration includes a simulation of a reference reaction for which the barrier and free energy are known in advance (either determined experimentally or computed by first-principles methods). The coupling term and the relative shift are fitted such that the barrier and reaction energy delivered from the simulation match the reference values. As mentioned in the previous section, the tunable EVB parameters were presently calibrated for the simulations of the reaction in the WT enzyme such that the experimental barrier of 17.29 kcal mol⁻¹ was reproduced, and then subsequently used for the calculation of free energy profiles in the mutated enzyme. The calibrated values of the coupling term and the relative shift are 63.92 and 112.67 kcal mol⁻¹, respectively. The reader is referred to ref. 21 for further details about the simulations. A thorough review of the EVB protocol can be found in ref. 53.

The main output of the present simulations are the free energy profiles from which the activation barrier was deduced (as average over the 10 replicas). Because the reaction in WT MAO B was used as reference, simulation in the WT enzyme by definition reproduces the experimental barrier of 17.29 kcal mol⁻¹; the change in the barrier when passing from WT to the mutated enzyme was obtained from simulation of the reaction in Y326I MAO B. The corresponding change in the reaction rate constant (k) was obtained by the Eyring–Polanyi equation: , where ΔG^‡ is the free energy barrier, T is the absolute temperature and k_B and h are the Boltzmann and Planck constant, respectively. Physical origins of the changed rate upon mutation were attempted to be deduced by inspection of the simulation trajectories. Visualization and analysis of trajectories were carried out by using the VMD program package.⁷³ The active site of WT and Y326I MAO B is displayed in Fig. 3.

Fig. 3 Active site of MAO B with the PEA substrate and the FAD prosthetic group in ball-and-stick representation together with the residue at position 326 (Tyr in the wild type enzyme and Ile in the mutant).

3. Results and discussion

Reaction free energy profiles in the WT enzyme and in the Y326I mutant are displayed in Fig. 4. Activation barriers and reaction free energies over the 10 simulation replicas are summarized in Table 1.

Fig. 4 Reaction free energy profiles for the wild type MAO B and its Y326I mutant with average barriers. Note that in both cases ten profiles were computed corresponding to ten simulation replicas.

Table 1 Activation barriers (ΔG^‡) and reaction free energies (ΔG_R) (in kcal mol⁻¹) calculated for 10 simulation replicas of WT MAO B and its Y326I mutant. Note that the datasets for the WT enzyme and mutant are independent of one another

Replica	WT MAO B		Y326I MAO B
	ΔG^‡	ΔGR	ΔG^‡	ΔGR
1	17.59	−0.71	20.24	1.40
2	16.22	−2.91	18.51	0.27
3	16.30	−1.82	16.16	−2.50
4	17.17	0.33	18.66	−0.27
5	17.04	−0.56	18.17	−0.22
6	18.08	−3.39	18.31	−2.41
7	17.27	−1.22	18.46	1.17
8	18.44	1.12	18.37	−2.02
9	16.75	−0.86	18.13	−3.31
10	18.02	0.01	18.51	0.84
Average	17.29	−1.00	18.35	−0.71

---

The most illustrative output of the present simulations is the increase in the free energy barrier for the rate limiting step of PEA oxidation for MAO B by 1.06 kcal mol⁻¹ on the Y326I point mutation. While in both cases the profiles exhibit slight differences between individual replicas, the increase is significant. The increased barrier corresponds to an about 6-fold decrease in the reaction rate. Remarkably, the computed increase in the barrier of 1.06 kcal mol⁻¹ (from 17.29 to 18.35 kcal mol⁻¹) is in very good agreement with the experimental kinetic measurements in which the observed decrease in the reaction rate upon mutation converts into a barrier increase of 0.76 kcal mol⁻¹. Therefore, the simulation can accurately predict the point mutation effect, as was the case with the related I335Y mutation in the MAO A enzyme,²¹ and in several point mutations of residue Tyr444 in MAO A for noradrenaline decomposition.²² The barriers and reaction free energies slightly vary over the 10 replicas (Table 1), but the increase of the barrier upon mutation is evident. The average reaction free energy for the WT enzyme is −1.00 kcal mol⁻¹ whereas for the Y326I mutant is −0.71 kcal mol⁻¹. The difference is virtually insignificant, but is consistent with the postulate that in the case of two similar organic reactions the more exothermic one has a lower barrier. However, since no experimental data are available for this particular parameter, this is of little (if any) interpretative value, especially because the barrier appears to be almost insensitive to relatively large variations of the reaction free energy.²¹

It should also be noted that the deviation between profiles is perceivably larger for products than for the transition state (Fig. 4 and Table 1) because the profiles have been shifted to a common origin at the minimum corresponding to the state of reactants. In fact, most of the deviations are built up in the transition state region (from slightly before to slightly after the TS), hence the deviations at the product well are about twice as large as atop the barrier. This feature is common to our EVB simulations and has been recently attributed to the poorer statistics in the transition state region.⁶³

It has been reported that the Tyr326 residue in MAO B and the equivalently positioned Ile335 residue in MAO A is crucial for the specificity of both isoenzymes. Namely, on Y326I mutation MAO B becomes similar to MAO A in terms of specificity for various substrates and inhibitors, and vice versa for the reciprocal I335Y mutant of MAO A.¹¹ While computational assessment of substrate specificity is for various reasons beyond the scope of this work, we found it interesting that the ‘reciprocity’ between MAO B and MAO A is not sustained (neither experimentally nor from simulations) in the case of reaction rates for the same substrate. In the present case the reaction rate of PEA decomposition decreases on the Y326I mutation of MAO B, but it also decreases for MAO A on the I335Y mutation.²¹ In terms of reaction rates, the aforementioned reciprocal mutations do not effectively turn MAO A into MAO B and vice versa. However, the fact that the reaction rate drops upon mutation in both the isoenzymes is in agreement with the view that enzymes are evolutionarily optimized so that any deliberate mutation of either enzyme is quite unlikely to further enhance its activity that has been tuned over millions of years of evolution. Therefore it can be reasonably assumed that a laboratory-induced mutation will most likely decrease the catalytic performance of the enzyme, as is presently the case. Apart from the chemical step, the point mutation also influences the stability of the Michaelis complex and affinities of MAO reversible inhibitors. The latter issue is crucial for drug design. However, the binding issue is to a large extent independent of the reactivity and deserves special assessment. Significant experimental and computational efforts have been initiated in this direction. For instance, it has been demonstrated experimentally⁷⁴ and computationally⁷⁵ that Y326 is one of the gating residues in MAO B and has a predominant role in influencing the binding of the substrates. Nevertheless, regardless of its effect on the catalytic step, a particular mutation might result in either increasing or decreasing the efficiency of binding, because binding is separated from the catalytic efficiency.

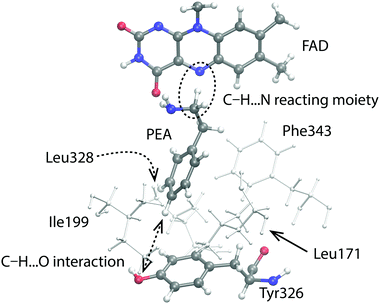
In our related study of the I335Y point mutation of MAO A for PEA decomposition, inspection of simulation trajectories revealed possible sources of the barrier change due to mutation. The observed increase in the barrier can be reasonably explained by the increased local polarity caused by the replacement of Ile335 by Tyr.²¹ In the present case however, mutation decreases the local polarity (replacement of Tyr326 by Ile), and no major structural changes that could be attributed to the decreased polarity are observed in the trajectories. Specifically, the conformational alignment between PEA and Phe343 phenyl rings which changed significantly in the case of MAO A I335Y mutation²¹ is virtually unchanged in the present case. On the other hand, the interaction between Tyr326 and PEA aromatic rings in the WT enzyme has a significant face-to-edge character (Fig. 5). As demonstrated previously,²¹ this type of interaction stabilizes the transition state to a larger extent than reactants, contributing to the lowering of the barrier. Since this interaction is lost upon mutation, it offers a plausible explanation for the observed increase of the barrier. Alongside with that, the OH group of Tyr326 acts as a proton acceptor of the ring hydrogen atoms of PEA, mainly at the p-position relative to the ethylamino group, facilitating the formation of a weak C–H⋯O interaction (quasi hydrogen bond; see Fig. 5). Analysis of the trajectory shows that the C⋯O distance varies between 4.5 and 5.0 Å. This interaction also contributes to the lowering of the reaction barrier, and is lost upon mutation. Moreover, an inspection of distances between the reactive C atom of PEA and the C_α atoms of the surrounding hydrophobic residues (Leu171, Ile199 and Leu328; see Fig. 5) reveals a slight shift of these residues away from PEA (by up to 0.5 Å for Ile199) upon mutation, giving more space for water molecules around the active site of the mutant. Indeed, a small increase in the number of water molecules in a radius of 7 Å from the reacting alpha-carbon of the PEA molecule could be observed upon mutation, i.e. more water molecules appear to be present in the vicinity of the reacting moiety in the mutated enzyme. The analysis was made for each of the 10 simulation replicas. For the WT enzyme, the number of water molecules varies between 4.99 and 5.95 over the 10 replicas, whereas for the Y326 mutant it is between 5.64 and 6.26 water molecules. Accordingly, the increased amount of water contributes to the increased shielding of catalytic electrostatic interactions provided by the enzyme, thereby the reaction environment becoming more similar to the aqueous solution, which results in the increased barrier. However, this evidence is not fully consistent because the count of water molecules depends on the origin and size of the sphere in which the water molecules are counted; results may differ with different origin and sphere radius. Also, the possible explanation – that the smaller size of Ile (relative to Tyr) in the mutated enzyme allows more water molecules to enter the active site – is counter-intuitive to the argument that the hydrophobic Ile residue eventually repels water molecules from its surroundings.

Fig. 5 Active site of wild type MAO B with surrounding aromatic and hydrophobic residues, with indicated reacting moiety and specific C–H⋯O interaction between the 326 phenylethylamine substrate and the Tyr326 residue. Note that this interaction vanishes upon mutation Tyr326Ile. For further information see the text.

The changed electrostatics caused by the Y326I point mutation is reflected in an increased donor⋯acceptor distance in the C–H⋯N reacting moiety. The average C⋯N distance increases from 3.03 to 3.06 Å upon mutation, an effect hindering hydride transfer which is fully consistent with the increased barrier. An alternative yet quite generalized explanation of the observed point mutation effect is that the increased barrier is due to entropic factors and/or a large number of small enthalpic contributions originating from barely detectable structural changes. However, a detailed assessment of such effects is far from being trivial and is beyond the scope of the present investigation.

4. Conclusions

We have elucidated the effect of Y326I point mutation in MAO B on the rate of decomposition of PEA, an endogenous amphetamine, by using multiscale EVB simulations. In full agreement with experimental observations,¹¹ the point mutation slows down the catalyzed reaction by a factor of six, which corresponds to a 1.06 kcal mol⁻¹ increase in the free energy barrier. An inspection of trajectories shows evidence that the increased barrier is caused by the disappearance of electrostatic interactions between the PEA substrate and the Tyr326 residue. These interactions stabilize the transition state to a greater extent than the state of reactants, and hence their disappearance contributes to the elevation of the barrier. In addition, a slightly larger amount of water molecules is present near the reacting moiety in the mutant, which shields the catalytic effect of the enzyme. Another possible explanation is that the point mutation effect is due to entropic effects or to several small contributions not detectable by simulations.

The present work addresses the effects that alter the performance of an enzyme by barrier changes of up to a few k_BT units, corresponding to a few times changed reaction rates. These changes may be crucial for life and death of an organism, but in terms of catalytic power of enzymes they are regarded as very subtle. In most cases the achievable precision of such simulations is about 0.5 kcal mol⁻¹. Nevertheless, the methodology appears to correctly predict the sign and magnitude of the changed performance of MAO B for PEA decomposition to almost quantitative precision; it has reportedly been successful in predicting every single MAO point mutation effect considered so far.^21,22 This implies that the hydride transfer mechanism²⁰ assumed in our studies is correct, although separate studies are required in order to directly validate the mechanism in the full-scale enzymatic environment.

The so far successful assessment of point mutation effects is promising in the context of precision medicine where the genome variations may contribute to the performance of enzymes and therewith associated diseases or disorders. Patients with a point mutation of Y326I will have six times slower decomposition of PEA, giving rise to considerably increased PEA levels. The increased PEA levels will be reflected in the blocked dopamine transporters, and dopamine levels in the synaptic gap will be increased. One may speculate that long lasting physical activities such as running that produce additional PEA levels will result in increased addiction to sport activities for patients with this mutation. Less active MAO B is expected to cause a lower dopamine decomposition rate giving rise to decreased production of hydrogen peroxide and a lower extent of neurodegeneration.⁷⁶ In reality the expression levels of enzymes and transporters may be changed and dopaminergic synapse requires macroscopic description at the level of a system of differential equations. The corresponding methodology has been developed and is ready to be used.⁷⁷

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work benefited from the program group funding of the Slovenian Research Agency (P1-0012) and was carried out in collaboration with the Gimnazija Vič high school. The coauthor Domen Pregeljc, a student of Gimnazija Vič, contested with a research project based on the present work at two international research olympiads (both in 2017): ISWEEEP, Houston, TX, United States; and GENIUS, Oswego, NY, United States, winning silver and gold medal, respectively. All the authors thank Mrs Alenka Mozer, chemistry teacher at the Gimnazija Vič, for providing excellent mentorship and for coordinating the project to fit into the scope of the contests.

References

1. H. G. Brunner, M. Nelen, X. O. Breakefield, H. H. Ropers and B. A. Vanoost, Science, 1993, 262, 578–580.
2. J. C. Shih, K. Chen and M. J. Ridd, Annu. Rev. Neurosci., 1999, 22, 197–217.
3. M. Bortolato, K. Chen and J. C. Shih, Adv. Drug Delivery Rev., 2008, 60, 1527–1533.
4. R. R. Ramsay, Prog. Neuro-Psychopharmacol., 2016, 69, 81–89.
5. N. Pivac, J. Knezevic, D. Kozaric-Kovacic, M. Dezeljin, M. Mustapic, D. Rak, T. Matijevic, J. Pavelic and D. Muck-Seler, J. Affective Disord., 2007, 103, 131–138.
6. M. Bortolato, S. C. Godar, L. Alzghoul, J. L. Zhang, R. D. Darling, K. L. Simpson, V. Bini, K. Chen, C. L. Wellman, R. C. S. Lin and J. C. Shih, Int. J. Neuropsychopharmacol., 2013, 16, 869–888.
7. S. Gandhi and A. Y. Abramov, Oxid. Med. Cell. Longevity, 2012, 428010.
8. M. Naoi, W. Maruyama, Y. Akao, H. Yi and Y. Yamaoka, J. Neural Transm., Suppl., 2006, 67–77.
9. M. Naoi, W. Maruyama, K. Inaba-Hasegawa and Y. Akao, Int. Rev. Neurobiol., 2011, 100, 85–106.
10. A. W. J. Bach, N. C. Lan, D. L. Johnson, C. W. Abell, M. E. Bembenek, S. W. Kwan, P. H. Seeburg and J. C. Shih, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 4934–4938.
11. R. M. Geha, I. Rebrin, K. Chen and J. C. Shih, J. Biol. Chem., 2001, 276, 9877–9882.
12. J. P. Klinman and R. G. Matthews, J. Am. Chem. Soc., 1985, 107, 1058–1060.
13. J. R. Miller and D. E. Edmondson, Biochemistry, 1999, 38, 13670–13683.
14. R. B. Silverman, Acc. Chem. Res., 1995, 28, 335–342.
15. K. A. Kurtz, M. A. Rishavy, W. W. Cleland and P. F. Fitzpatrick, J. Am. Chem. Soc., 2000, 122, 12896–12897.
16. P. F. Fitzpatrick, Arch. Biochem. Biophys., 2010, 493, 13–25.
17. E. Abad, R. K. Zenn and J. Kastner, J. Phys. Chem. B, 2013, 117, 14238–14246.
18. V. E. Atalay and S. S. Erdem, Comput. Biol. Chem., 2013, 47, 181–191.
19. G. Zapata-Torres, A. Fierro, G. Barriga-Gonzalez, J. C. Salgado and C. Celis-Barros, J. Chem. Inf. Model., 2015, 55, 1349–1360.
20. R. Vianello, M. Repic and J. Mavri, Eur. J. Org. Chem., 2012, 7057–7065.
21. G. Oanca, M. Purg, J. Mavri, J. C. Shih and J. Stare, Phys. Chem. Chem. Phys., 2016, 18, 13346–13356.
22. M. Poberznik, M. Purg, M. Repic, J. Mavri and R. Vianello, J. Phys. Chem. B, 2016, 120, 11419–11427.
23. M. Repič, R. Vianello, M. Purg, F. Duarte, P. Bauer, S. C. L. Kamerlin and J. Mavri, Proteins, 2014, 82, 3347–3355.
24. M. A. Akyuz and S. S. Erdem, J. Neural Transm., 2013, 120, 937–945.
25. G. Oanca, J. Stare, R. Vianello and J. Mavri, Eur. J. Pharmacol., 2017, 817, 46–50.
26. M. Repič, M. Purg, R. Vianello and J. Mavri, J. Phys. Chem. B, 2014, 118, 4326–4332.
27. M. Repic, R. Vianello, M. Purg, F. Duarte, P. Bauer, S. C. L. Kamerlin and J. Mavri, Proteins, 2014, 82, 3347–3355.
28. A. M. Cesura, J. Gottowik, H. W. Lahm, G. Lang, R. Imhof, P. Malherbe, U. Rothlisberger and M. DaPrada, Eur. J. Biochem., 1996, 236, 996–1002.
29. J. Gottowik, A. M. Cesura, P. Malherbe, G. Lang and M. Daprada, FEBS Lett., 1993, 317, 152–156.
30. J. Gottowik, P. Malherbe, G. Lang, M. Daprada and A. M. Cesura, Eur. J. Biochem., 1995, 230, 934–942.
31. R. M. Geha, K. Chen and J. C. Shih, J. Neurochem., 2000, 75, 1304–1309.
32. Y. Tsugeno, I. Hirashiki, F. Ogata and A. Ito, J. Biochem., 1995, 118, 974–980.
33. A. Szabo, E. Billett and J. Turner, Br. J. Sports Med., 2001, 35, 342–343.
34. P. A. J. Janssen, O. E. Leysen, A. A. H. P. Megens and F. H. L. Awouters, Int. J. Neuropsychopharmacol., 1999, 2, 229–240.
35. E. M. Parker and L. X. Cubeddu, J. Pharmacol. Exp. Ther., 1988, 245, 199–210.
36. H. C. Sabelli and J. I. Javaid, J. Neuropsychiatry Clin. Neurosci., 1995, 7, 6–14.
37. M. E. Wolf and A. D. Mosnaim, Gen. Pharmacol., 1983, 14, 385–390.
38. R. L. Oreilly and B. A. Davis, Prog. Neuro-Psychopharmacol., 1994, 18, 63–75.
39. M. D. Berry, J. Neurochem., 2004, 90, 257–271.
40. K. J. Broadley, Pharmacol. Ther., 2010, 125, 363–375.
41. E. Herlinger, R. F. Jameson and W. Linert, J. Chem. Soc., Perkin Trans. 2, 1995, 259–263.
42. A. Hermida-Ameijeiras, E. Mendez-Alvarez, S. Sanchez-Iglesias, C. Sanmartin-Suarez and R. Soto-Otero, Neurochem. Int., 2004, 45, 103–116.
43. R. K. Zenn, E. Abad and J. Kastner, J. Phys. Chem. B, 2015, 119, 3678–3686.
44. A. K. Tan and R. R. Ramsay, Biochemistry, 1993, 32, 2137–2143.
45. R. Nandigama and D. Edmondson, Biochemistry, 2000, 39, 15258–15265.
46. A. Fierro, D. E. Edmondson, C. Celis-Barros, M. Rebolledo-Fuentes and G. Zapata-Torres, PLoS One, 2016, 11, e0154989.
47. M. A. Akyuz, S. S. Erdem and D. E. Edmondson, J. Neural Transm., 2007, 114, 693–698.
48. M. C. Walker and D. E. Edmondson, Biochemistry, 1994, 33, 7088–7098.
49. J. Wang and D. E. Edmondson, Biochemistry, 2011, 50, 7710–7717.
50. S. MacMillar, D. E. Edmondson and O. Matsson, J. Am. Chem. Soc., 2011, 133, 12319–12321.
51. R. Orru, M. Aldeco and D. E. Edmondson, J. Neural Transm., 2013, 120, 847–851.
52. A. Warshel and R. M. Weiss, J. Am. Chem. Soc., 1980, 102, 6218–6226.
53. J. Aqvist and A. Warshel, Chem. Rev., 1993, 93, 2523–2544.
54. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
55. M. H. M. Olsson, J. Mavri and A. Warshel, Philos. Trans. R. Soc., B, 2006, 361, 1417–1432.
56. A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. B. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235.
57. A. J. Adamczyk, J. Cao, S. C. L. Kamerlin and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 14115–14120.
58. A. V. Pisliakov, J. Cao, S. C. L. Kamerlin and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17359–17364.
59. I. Feierberg, V. Luzhkov and J. Aqvist, J. Biol. Chem., 2000, 275, 22657–22662.
60. R. Borštnar, M. Repič, S. C. L. Kamerlin, R. Vianello and J. Mavri, J. Chem. Theory Comput., 2012, 8, 3864–3870.
61. G. Oanca, J. Stare and J. Mavri, Proteins, 2017, 85, 2170–2178.
62. J. Mavri, R. A. Matute, Z. T. Chu and R. Vianello, J. Phys. Chem. B, 2016, 120, 3488–3492.
63. J. Stare, RSC Adv., 2017, 8740–8754.
64. G. Oanca, J. Stare and J. Mavri, Proteins, 2017, 85, 2170–2178.
65. Y. Y. Sham, Z. T. Chu and A. Warshel, J. Phys. Chem. B, 1997, 101, 4458–4472.
66. R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426.
67. P. Kollman, Chem. Rev., 1993, 93, 2395–2417.
68. J. Marelius, K. Kolmodin, I. Feierberg and J. Aqvist, J. Mol. Graphics Modell., 1998, 16, 213–225.
69. C. Binda, P. Newton-Vinson, F. Hubalek, D. E. Edmondson and A. Mattevi, Nat. Struct. Biol., 2002, 9, 22–26.
70. W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
71. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
72. M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509.
73. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
74. E. M. Milczek, C. Binda, S. Rovida, A. Mattevi and D. E. Edmondson, FEBS J., 2011, 278, 4860–4869.
75. A. Marsavelski and R. Vianello, Chem. – Eur. J., 2017, 23, 2915–2925.
76. M. Pavlin, M. Repic, R. Vianello and J. Mavri, Mol. Neurobiol., 2016, 53, 3400–3415.
77. J. A. Best, H. F. Nijhout and M. C. Reed, Theor. Biol. Med. Modell., 2009, 6, 21.

---