 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Process-morphology scaling relations quantify self-organization in capillary densified nanofiber arrays†
Ashley L.
Kaiser‡
 a,
Itai Y.
Stein‡
a,
Itai Y.
Stein‡
 *b,
Kehang
Cui
*b,
Kehang
Cui
 c and
Brian L.
Wardle
c and
Brian L.
Wardle
 *b
*b
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
bDepartment of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: iys@alum.mit.edu; wardle@mit.edu
cDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 2nd January 2018
Abstract
Capillary-mediated densification is an inexpensive and versatile approach to tune the application-specific properties and packing morphology of bulk nanofiber (NF) arrays, such as aligned carbon nanotubes. While NF length governs elasto-capillary self-assembly, the geometry of cellular patterns formed by capillary densified NFs cannot be precisely predicted by existing theories. This originates from the recently quantified orders of magnitude lower than expected NF array effective axial elastic modulus (E), and here we show via parametric experimentation and modeling that E determines the width, area, and wall thickness of the resulting cellular pattern. Both experiments and models show that further tuning of the cellular pattern is possible by altering the NF–substrate adhesion strength, which could enable the broad use of this facile approach to predictably pattern NF arrays for high value applications.
The potential for meter-scale bulk manufacturing and unique anisotropic physical properties of one-dimensional nanostructures, such as nanowires, nanotubes, and nanofibers (NFs), motivates their use in industrial applications, such as electrical interconnects,1–4 energy harvesting and storage,4–8 sensors and actuators,9–12 and structural reinforcement.13–15 However, the low packing density and inherent stochastic nature of these NFs when synthesized by scalable approaches, such as chemical vapor deposition, leads to observed properties that are orders of magnitude lower than expected.16–18 This could be substantially overcome by densification approaches such as capillary-mediated densification, which is a versatile and scalable approach that has been utilized to increase the packing density and form intricate three-dimensional nano-architectures out of aligned NF systems.19–22 But since NFs self-organize into two-dimensional cellular structures of unpredictable shapes and sizes when this approach is applied to bulk NF arrays ≳100 μm tall,20–22 models that predict cellular network formation are needed. Here, we develop process-morphology scaling relations that quantify and accurately predict the self-organization of an exemplary system of NFs, aligned carbon nanotube (CNT) arrays, into cellular patterns, and show that the effective elastic modulus scaling of the cell wall with its height governs the wall thickness, width, and area of the resulting cells.
Intrinsic and scale-dependent properties of CNTs has made them a primary choice for studying NF array behavior, and previous work on aligned CNTs has shown that their morphology can be tuned to form complex three-dimensional shapes and patterns via capillary-mediated densification.20–22 By utilizing densification approaches, previous studies have shown that CNT architectures with excellent electrical, thermal, and mechanical properties that approach those predicted by early theoretical models can be synthesized, with the potential for mass production.23–26 Although targeted densification can be achieved via various creative approaches, e.g. plasma exposure27 and low pressure sealing,28 elasto-capillary self-assembly is the most widely utilized technique due to its simplicity and compatibility with scalable manufacturing approaches.20–22 See Fig. 1 for an overview of capillary densification in aligned CNTs. While the CNT length governs the force balance during elasto-capillary self-assembly,29–31 where longer CNTs self-organize into larger cells (see Fig. 1b), accurately predicting the geometry of the CNT cellular patterns given a starting NF array morphology (e.g. CNT length) is not currently possible. This originates from the large variability in previously reported CNT cell sizes (see Fig. 1c) and (as will be shown herein) non-representative assumptions of the CNT array elastic response,32–39 which led to a linear scaling law in ref. 32 that leaves several previous observations unexplained. In this report, we use extensive quantification of the CNT cellular network to model the mechanical behavior of CNTs during elasto-capillary self-assembly, and to develop representative scaling relations that accurately predict the evolution of the CNT cell geometry with the height of the initial CNT array.
 | ||
Fig. 1 Capillary-mediated densification of aligned carbon nanotube (CNT) arrays into 2D cellular networks. (a) Illustrations and scanning electron microscopy (SEM) images demonstrating the formation of cells from CNT arrays. (b) Side view illustrations and top view SEM images of CNT cell networks showing that the height (h) of CNT arrays governs the width (w) and wall thickness (t) of the resulting CNT cell, all other factors being the same. (c) Previously reported w of CNT cells made from CNTs with diameters Dcnt ∼ 5–15 nm to 15–60 nm (●, and  , respectively),32–39 and the linear scaling relation proposed in ref. 32. , respectively),32–39 and the linear scaling relation proposed in ref. 32. | ||
Aligned CNT arrays were grown in a 22 mm internal diameter quartz tube furnace at atmospheric pressure via a previously described thermal catalytic chemical vapor deposition process with ethylene as the carbon source and 600 ppm of water vapor added to the inert gas.40–42 The CNTs were grown on 1 cm × 1 cm Si substrates via a base-growth mechanism on a catalytic layer composed of 1 nm Fe on 10 nm Al2O3 deposited via electron beam physical vapor deposition.43–45 The CNTs self-assemble into aligned arrays that were ∼10–300 μm tall, and were composed of multiwalled CNTs with an average outer diameter of ∼8 nm (3–7 walls with ∼5 nm inner diameter and intrinsic CNT density of ≈1.6 g cm−3),42,45–47 inter-CNT spacing of ∼60–80 nm,48–50 and Vf of ∼1% CNTs.42 To test the impact of CNT adhesion to the growth substrate, a subset of aligned CNTs was heat treated for 40 min at 740 °C under 200 sccm of helium flow, which leads to samples that we call cemented CNTs (→c-CNTs) which are compared to baseline samples that we call not cemented CNTs (→nc-CNTs), i.e. nc-CNTs do not undergo thermal post-processing. The cementation post-processing conditions used here originate from a recent study that investigated the tensile force required to remove CNTs from the growth substrate after post-processing for a variety of times and environments at 740 °C (the CNT growth temperature). A maximum of ∼4× increase in the CNT-growth substrate adhesion force is reported when compared to the untreated CNTs (i.e. nc-CNTs) for samples heat treated in an He ambient for 40 min (additional analysis of these findings is the subject of an upcoming publication).51 The cementation processing utilized here is similar to other post-growth CNT–substrate adhesion tuning techniques that were investigated in previous studies,22,52,53 which found that allowing the CNTs to cool in a hydrocarbon ambient increased their adhesion to the growth substrate, and that the CNT–substrate bonding could be weakened via etching of the CNT–catalyst interface, e.g. using H2O vapor.52 The current approach is distinct in its effect and purpose of further increasing the CNT–substrate adhesion. After growth (and cementation processing for c-CNTs), all CNT array samples were then exposed to a previously developed O2 plasma treatment,31 and then densified via a previously reported paper-soaking technique,54 which leads to slower wetting and thereby less CNT delamination and damage than direct immersion techniques,21 using two different solvents (acetone and ethanol). After capillary densification, the cell wall thickness (t) was measured via scanning electron microscopy (Zeiss Merlin, 5 mm working distance, 5 kV accelerating voltage). Cell area (A) and circularity (O) were estimated from optical microscope (Carl Zeiss Axiotech 30 HD) images via ImageJ (see Section S1 in the ESI† for details),55 and the cell width (w) was evaluated as a one-dimensional approximation via . See Fig. 2 for exemplary histograms of t, w, and A. To determine the arithmetic means (Λ), the raw t datasets were analyzed via Gaussian distributions, while the raw w and A datasets were analyzed via log-normal distributions. Log-normal distributions were used for the raw w and A data because they originate from the time evolution of a Gaussian distribution, i.e. the inter-CNT spacing,16,49,50 without producing new elements, which was postulated to give rise to log-normal statistics in the long-time limit.56–58 The h dependence of t, w, and A was then investigated by averaging Λ from 2–4 samples, and this is presented in Fig. 3 and Tables S2, S3 in Section S3 of the ESI.†
. See Fig. 2 for exemplary histograms of t, w, and A. To determine the arithmetic means (Λ), the raw t datasets were analyzed via Gaussian distributions, while the raw w and A datasets were analyzed via log-normal distributions. Log-normal distributions were used for the raw w and A data because they originate from the time evolution of a Gaussian distribution, i.e. the inter-CNT spacing,16,49,50 without producing new elements, which was postulated to give rise to log-normal statistics in the long-time limit.56–58 The h dependence of t, w, and A was then investigated by averaging Λ from 2–4 samples, and this is presented in Fig. 3 and Tables S2, S3 in Section S3 of the ESI.†
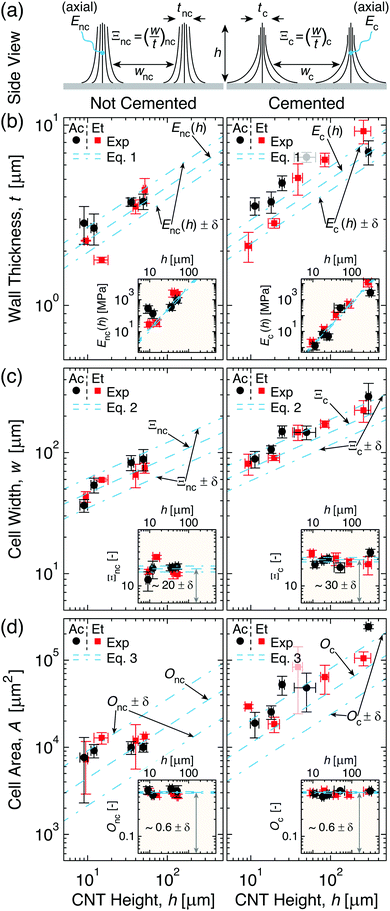 | ||
| Fig. 3 Cell geometry evolution with CNT height (h) for non-cemented (nc, left) and cemented (c, right) CNTs densified via acetone and ethanol (→Ac and Et). (a) Illustrations of different effective wall elastic moduli (E) and densification factors (Ξ) giving rise to thicknesses and widths (t and w) of cells formed from nc- and c-CNTs (→Enc, Ξnc, tnc, wnc and Ec, Ξc, tc, wc, respectively). (b) Plot showing that ∂Ec/∂h < ∂Enc/∂h leads to faster t scaling with h (eqn (1), see inset) for c-CNTs. (c) Plot illustrating that w scales faster with h (eqn (2), see inset) for c-CNTs because Ξc > Ξnc. (d) Plot demonstrating that while cell area (A) scales faster with h (eqn (3), see inset) for c-CNTs, cell circularity (→Onc and Oc) is constant. | ||
As Fig. 2a illustrates, the post-processing cementation that creates c-CNTs significantly impacts the self-organization of CNTs into a network of two-dimensional cells. This difference between the cells formed by c-CNTs and those formed by nc-CNTs can be explained by examining the impact of CNT–substrate adhesion on CNT elastic behavior. Although cementation increases CNT–substrate adhesion via several mechanisms, this diminished CNT mobility reduces the amount of CNT–CNT junctions that can form in the CNT axial direction as the array self-assembles into CNT walls, i.e. when the CNTs are deflected perpendicular to their axial direction to form the CNT bundles that comprise the cell walls. Since the torsion deformation mechanism was previously found to contribute >90% of the effective compliance of CNT architectures comprised of weakly interacting CNTs such as those herein,16 formation of additional CNT–CNT junctions is a mechanism by which the CNTs could collectively reinforce one another and thereby resist deforming via torsion. However, because cementation lowers the mobility of CNTs local to the substrate during the capillary-mediated self-assembly process, their ability to entangle with one another in three-dimensional space is likely hindered, which means that the number of CNT–CNT junctions that could be formed along the CNT length in c-CNTs is lower than that of nc-CNTs for a given two-dimensional packing fraction. This effect could be exacerbated by the larger gradient in two-dimensional packing fraction along the length of c-CNTs (see Fig. 2a for illustration) due to lower CNT base mobility when compared to nc-CNTs that can more freely slide and pack. Such a difference in the collective reinforcement efficacy of CNTs with higher substrate adhesion forces implies that the cementation processing would lead c-CNT walls to be less stiff than nc-CNT walls at a comparable t, since c-CNTs would need to achieve a higher three-dimensional volume fraction to reach a similar number of CNT–CNT junctions. Since the capillary forces will be unchanged, this reduction in the wall stiffness as a result of cementation means that, to maintain the force balance, c-CNTs will need to form larger effective bundles. When this is coupled with the diminished CNT mobility perpendicular to their axial direction (due to cementation mediated enhanced substrate adhesion forces), c-CNTs are therefore expected to form larger CNT cells with thicker walls than the cells formed by nc-CNTs. Experimental results support this prediction, as illustrated in histograms of the cell area (A), width (w), and wall thickness (t) for nc- and c-CNTs with h ∼ 35 μm in Fig. 2b. As seen in Fig. 2b, the evaluated Λ for c-CNTs is significantly larger than for nc-CNTs for t (∼6.4 μm vs. ∼4.0 μm), w (∼140 μm vs. ∼97 μm), and A (∼7.0 × 104 μm2vs. ∼1.3 × 104 μm2), consistent with enhanced substrate adhesion diminishing the CNT cell wall's mechanical reinforcement efficacy. To better understand how cementation affects the mechanics that underpin the formation of CNT cellular networks, models that tie CNT cell geometry to h are discussed next.
To model the capillary-mediated self-organization process of CNT arrays, we assume a one-dimensional point of view for simplicity (as illustrated in Fig. 2a). In this framework, the t for the cell walls can be estimated by starting with the previously derived maximum capillary formed bundle size,20,59,60 in addition to the recently characterized CNT array morphology,47–49 which yields the following form:
 | (1) |
| w ≈ tΞ | (2) |
| A ≈ O(ζw)2 | (3) |
As Fig. 3 illustrates, t (Fig. 3b), w (Fig. 3c), and A (Fig. 3d) monotonically increase with h for both nc- and c-CNTs (see Fig. 3a for schematic illustrating the two different cell wall geometries, and Section S3 in the ESI† for the raw data). Since acetone and ethanol have very similar values of γ, but very different partial pressures at ambient conditions, Fig. 3 shows that the solvent evaporation rate does not significantly alter the patterns formed since CNTs densified by both acetone and ethanol yield very similar cellular networks. To better understand the effect of cementation on the t scaling with h, E was estimated (viaeqn (1)) for cell walls comprised of nc- and c-CNTs (see Fig. 3b inset). As Fig. 3b inset illustrates, E scaling with h can be estimated as E ∝ α(h)ω where αnc ≈ 0.030 ± 0.006 ∝ 10 × αc and ωnc = ωc ≈ 8/3. This leads to ∂Enc/∂h > ∂Ec/∂h, which corresponds to tnc < tc at constant h (e.g.Fig. 2b), and is consistent with the previous discussion of lower CNT mobility reducing the effective cell wall stiffness. Additionally, because c-CNTs are harder to delaminate, Fig. 3b indicates that cellular pattern formation is possible at h > 300 μm for c-CNTs, which is significantly larger than the maximum h ∼ 60 μm at which nc-CNTs delaminate from the substrate (and subsequently collapse) due to capillary forces. To elucidate how altering the CNT substrate adhesion influences CNT densification in the cell walls, Ξ was approximated using eqn (2) for CNT cells formed from nc- and c-CNTs (see Fig. 3c inset). As Fig. 3c inset illustrates, Ξnc < Ξc (i.e. 20 ± 2 vs. 30 ± 3), which leads to wnc < wc at comparable values of h. Ξc leads to a CNT volume fraction in the cell walls of ∼30–40%, which is very similar to the maximum packing fraction estimated for similar CNTs (∼40 vol% CNTs).62 This indicates that the densification of c-CNTs is well described by a one-dimensional mechanism similar to how the scaling of the effective indentation modulus of CNT arrays was modeled.62 However, because Ξnc is significantly lower than Ξc, densification in nc-CNTs may not be purely one-dimensional in nature, since nc-CNTs are able to more freely translate and re-orient themselves with respect to their neighbors, requiring further consideration of two-dimensional interactions.
To further investigate two-dimensional densification effects, O for nc- and c-CNTs was approximated using eqn (3) (see Fig. 3d inset). As the inset of Fig. 3d demonstrates, O is surprisingly found to be of similar magnitude for both nc- and c-CNTs (i.e. Onc ≈ 0.60 ± 0.04 and Oc ≈ 0.58 ± 0.02), which indicates crack initiation and propagation in the CNT arrays, and leads to formation of anisotropic cells with aspect ratios ∼3.5 ± 0.3 (see Section S2 in the ESI† for details), that is likely dependent on spatial variations in number density and tortuosity of the CNTs that originate from the CNT growth process.63–66 These results indicate that although the one-dimensional simplifications used here can capture the underlying physical mechanisms that govern cell formation, and thereby yield predictions that agree well with the experimental data presented in Fig. 3, further work that quantifies and simulates topological inhomogeneities present within the CNT arrays is needed to better model CNT cellular network formation in two-dimensions. Note that experimental quantification of such features in as-grown NF arrays is quite challenging.
In summary, the impact of carbon nanotube (CNT) length on capillary-mediated self-assembly of aligned CNT arrays into two-dimensional cellular networks was quantified under conditions that varied the densification solvent and CNT array height, and scaling relations that accurately predict geometry of the resulting CNT cells are presented. The experimental results indicate that CNT cell width, area, and wall thickness increase monotonically as a function of the CNT array height (h). Additionally, by modifying the CNT substrate adhesion force through a post-processing step termed cementation, we find that CNT cells can be made at larger h, since CNT junction interactions are diminished, and that cells formed from cemented CNTs (c-CNTs) counterintuitively exhibit larger width, area, and wall thicknesses compared to their non-cemented CNT (nc-CNT) counterparts at constant h. Modeling illustrates that this originates from how the effective axial elastic modulus (E) of CNTs increases with packing density, and that by reducing CNT mobility, cementation reduces the effective array stiffness of the c-CNTs vs. the baseline nc-CNT arrays. Also, modeling indicates that the densification of c-CNTs is approximately one-dimensional in nature, while nc-CNT densification might experience two-dimensional effects. Investigation of CNT cell aspect ratio and circularity shows no statistically significant difference between c-CNTs and nc-CNTs, illustrating that further work building on recent advances in two-dimensional meso-scale simulation of self-organization of such nano-systems due to capillary forces is needed.67–69 Additionally, since cementation modifies the cellular pattern formation by altering the CNT substrate adhesion force (Fa), but data that could allow the characterization and modeling of the physics and/or chemical mechanisms that gives rise to the observed enhancement in Fa (e.g. CNT–CNT, CNT–catalyst, catalyst–substrate or combination thereof) is not currently available, additional work is required to quantify and predict how Fa scales with processing conditions. Once Fa and two-dimensional densification effects can be precisely described and modeled, capillary-mediated densification could be used to inexpensively, quickly, and accurately design bulk nanofiber systems with tuned topologies that could enable next-generation processors, batteries, and lightweight structures.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was partially supported by Airbus, ANSYS, Embraer, Lockheed Martin, Saab AB, Saertex, and TohoTenax through MIT's Nano-Engineered Composite Aerospace STructures (NECST) Consortium, and partially supported by the National Aeronautics and Space Administration (NASA) Space Technology Research Institute (STRI) for Ultra-Strong Composites by Computational Design (US-COMP), grant number NNX17AJ32G. The authors thank Dr S. Kim (MIT) and Prof. A. J. Hart (MIT) for help with O2 plasma treatment, D. Lidston (MIT) for help with cementation processing, and the members of necstlab at MIT for technical support and advice. This work made use of the MIT Materials Research Laboratory (MRL) Shared Experimental Facilities, supported in part by the MRSEC Program of the National Science Foundation under award number DMR-1419807, and was carried out in part through the use of MIT's Microsystems Technology Laboratories.References
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- M. M. Shulaker, G. Hills, N. Patil, H. Wei, H.-Y. Chen, H.-S. P. Wong and S. Mitra, Nature, 2013, 501, 526–530 CrossRef CAS PubMed.
- M. M. Shulaker, G. Hills, R. S. Park, R. T. Howe, K. Saraswat, H.-S. P. Wong and S. Mitra, Nature, 2017, 547, 74–78 CrossRef CAS PubMed.
- W. Wu, Nanoscale, 2017, 9, 7342–7372 RSC.
- H. Sun, Y. Zhang, J. Zhang, X. Sun and H. Peng, Nat. Rev. Mater., 2017, 2, 17023 CrossRef CAS.
- J. Ni and Y. Li, Adv. Energy Mater., 2016, 6, 1600278 CrossRef.
- L. Mai, X. Tian, X. Xu, L. Chang and L. Xu, Chem. Rev., 2014, 114, 11828–11862 CrossRef CAS PubMed.
- K. Cui, T. Chiba, S. Omiya, T. Thurakitseree, P. Zhao, S. Fujii, H. Kataura, E. Einarsson, S. Chiashi and S. Maruyama, J. Phys. Chem. Lett., 2013, 4, 2571–2576 CrossRef CAS.
- J. Zhang, X. Liu, G. Neri and N. Pinna, Adv. Mater., 2016, 28, 795–831 CrossRef CAS PubMed.
- J. F. Fennell, S. F. Liu, J. M. Azzarelli, J. G. Weis, S. Rochat, K. A. Mirica, J. B. Ravnsbæk and T. M. Swager, Angew. Chem., Int. Ed., 2016, 55, 1266–1281 CrossRef CAS PubMed.
- G. V. Stoychev and L. Ionov, ACS Appl. Mater. Interfaces, 2016, 8, 24281–24294 CAS.
- L. Kong and W. Chen, Adv. Mater., 2014, 26, 1025–1043 CrossRef CAS PubMed.
- S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, Macromolecules, 2017, 50, 714–731 CrossRef CAS.
- A. K. Naskar, J. K. Keum and R. G. Boeman, Nat. Nanotechnol., 2016, 11, 1026–1030 CrossRef CAS PubMed.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed.
- I. Y. Stein, D. J. Lewis and B. L. Wardle, Nanoscale, 2015, 7, 19426–19431 RSC.
- B. Natarajan, N. Lachman, T. Lam, D. Jacobs, C. Long, M. Zhao, B. L. Wardle, R. Sharma and J. A. Liddle, ACS Nano, 2015, 9, 6050–6058 CrossRef PubMed.
- I. Y. Stein and B. L. Wardle, Nanotechnology, 2016, 27, 035701 CrossRef PubMed.
- Z. Hu, C. Uzun, Z. Dong, W. Li, A. A. Bernussi and G. Kumar, Appl. Phys. Lett., 2017, 111, 023107 CrossRef.
- S. H. Tawfick, J. Bico and S. Barcelo, MRS Bull., 2016, 41, 108–114 CrossRef CAS.
- M. De Volder and A. J. Hart, Angew. Chem., Int. Ed., 2013, 52, 2412–2425 CrossRef CAS PubMed.
- M. De Volder, S. H. Tawfick, S. J. Park, D. Copic, Z. Zhao, W. Lu and A. J. Hart, Adv. Mater., 2010, 22, 4384–4389 CrossRef CAS PubMed.
- L. Zhang, G. Zhang, C. Liu and S. Fan, Nano Lett., 2012, 12, 4848–4852 CrossRef CAS PubMed.
- J. Di, X. Wang, Y. Xing, Y. Zhang, X. Zhang, W. Lu, Q. Li and Y. T. Zhu, Small, 2014, 10, 4606–4625 CrossRef CAS PubMed.
- Q. Liu, M. Li, Y. Gu, Y. Zhang, S. Wang, Q. Li and Z. Zhang, Nanoscale, 2014, 6, 4338–4344 RSC.
- Y. Wang, M. Li, Y. Gu, X. Zhang, S. Wang, Q. Li and Z. Zhang, Nanoscale, 2015, 7, 3060–3066 RSC.
- W. Wang, I. Ruiz, K. Ahmed, H. H. Bay, A. S. George, J. Wang, J. Butler, M. Ozkan and C. S. Ozkan, Small, 2014, 10, 3389–3396 CrossRef CAS PubMed.
- T. Wang, K. Jeppson and J. Liu, Carbon, 2010, 48, 3795–3801 CrossRef CAS.
- S. Tawfick, Z. Zhao, M. Maschmann, A. Brieland-Shoultz, M. De Volder, J. W. Baur, W. Lu and A. J. Hart, Langmuir, 2013, 29, 5190–5198 CrossRef CAS PubMed.
- S. Tawfick, M. De Volder and A. J. Hart, Langmuir, 2011, 27, 6389–6394 CrossRef CAS PubMed.
- M. F. L. D. Volder, S. J. Park, S. H. Tawfick, D. O. Vidaud and A. J. Hart, J. Micromech. Microeng., 2011, 21, 045033 CrossRef.
- N. Chakrapani, B. Wei, A. Carrillo, P. M. Ajayan and R. S. Kane, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 4009–4012 CrossRef CAS PubMed.
- S. Kaur, S. Sahoo, P. Ajayan and R. Kane, Adv. Mater., 2007, 19, 2984–2987 CrossRef CAS.
- H. Liu, S. Li, J. Zhai, H. Li, Q. Zheng, L. Jiang and D. Zhu, Angew. Chem., Int. Ed., 2004, 43, 1146–1149 CrossRef CAS PubMed.
- Q. Li, R. DePaula, X. Zhang, L. Zheng, P. N. Arendt, F. M. Mueller, Y. T. Zhu and Y. Tu, Nanotechnology, 2006, 17, 4533 CrossRef CAS PubMed.
- M. A. Correa-Duarte, N. Wagner, J. Rojas-Chapana, C. Morsczeck, M. Thie and M. Giersig, Nano Lett., 2004, 4, 2233–2236 CrossRef CAS.
- K. Zhang, T. Li, L. Ling, H. Lu, L. Tang, C. Li, L. Wang and Y. Yao, Carbon, 2017, 114, 435–440 CrossRef CAS.
- A. Qiu and D. F. Bahr, Carbon, 2013, 55, 335–342 CrossRef CAS.
- L. F. Dumée, K. Sears, J. A. Schütz, N. Finn, M. Duke, S. Mudie, N. Kirby and S. Gray, J. Colloid Interface Sci., 2013, 407, 556–560 CrossRef PubMed.
- J. Lee, I. Y. Stein, S. S. Kessler and B. L. Wardle, ACS Appl. Mater. Interfaces, 2015, 7, 8900–8905 CAS.
- I. Y. Stein, A. L. Kaiser, A. J. Constable, L. Acauan and B. L. Wardle, J. Mater. Sci., 2017, 52, 13799–13811 CrossRef CAS.
- J. Lee, I. Y. Stein, M. E. Devoe, D. J. Lewis, N. Lachman, S. S. Kessler, S. T. Buschhorn and B. L. Wardle, Appl. Phys. Lett., 2015, 106, 053110 CrossRef.
- A. J. Hart and A. H. Slocum, J. Phys. Chem. B, 2006, 110, 8250–8257 CrossRef CAS PubMed.
- D. Handlin, I. Y. Stein, R. Guzman de Villoria, H. Cebeci, E. M. Parsons, S. Socrate, S. Scotti and B. L. Wardle, J. Appl. Phys., 2013, 114, 224310 CrossRef.
- I. Y. Stein and B. L. Wardle, Carbon, 2014, 68, 807–813 CrossRef CAS.
- N. Lachman, I. Y. Stein, A. Ugur, D. L. Lidston, K. K. Gleason and B. L. Wardle, Nanotechnology, 2017, 28, 24LT01 CrossRef PubMed.
- I. Y. Stein, N. Lachman, M. E. Devoe and B. L. Wardle, ACS Nano, 2014, 8, 4591–4599 CrossRef CAS PubMed.
- I. Y. Stein and B. L. Wardle, Phys. Chem. Chem. Phys., 2013, 15, 4033–4040 RSC.
- I. Y. Stein and B. L. Wardle, Phys. Chem. Chem. Phys., 2016, 18, 694–699 RSC.
- H. K. Mutha, Y. Lu, I. Y. Stein, H. J. Cho, M. E. Suss, T. Laoui, C. V. Thompson, B. L. Wardle and E. N. Wang, Nanotechnology, 2017, 28, 05LT01 CrossRef PubMed.
- D. L. Lidston, MSc thesis, Massachusetts Institute of Technology, 2017.
- C. L. Pint, Y.-Q. Xu, M. Pasquali and R. H. Hauge, ACS Nano, 2008, 2, 1871–1878 CrossRef CAS PubMed.
- M. Bedewy, J. Mater. Res., 2017, 32, 153–165 CrossRef CAS.
- D. Jiang, T. Wang, S. Chen, L. Ye and J. Liu, Microelectron. Eng., 2013, 103, 177–180 CrossRef CAS.
- C. A. Amadei, I. Y. Stein, G. J. Silverberg, B. L. Wardle and C. D. Vecitis, Nanoscale, 2016, 8, 6783–6791 RSC.
- M. Y. Choi, H. Choi, J.-Y. Fortin and J. Choi, Europhys. Lett., 2009, 85, 30006 CrossRef.
- S. Goh, H. W. Kwon, M. Y. Choi and J.-Y. Fortin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061115 CrossRef PubMed.
- S. Goh, H. W. Kwon and M. Y. Choi, J. Phys. A: Math. Theor., 2014, 47, 225101 CrossRef.
- F. Chiodi, B. Roman and J. Bico, Europhys. Lett., 2010, 90, 44006 CrossRef.
- C. Py, R. Bastien, J. Bico, B. Roman and A. Boudaoud, Europhys. Lett., 2007, 77, 44005 CrossRef.
- J. Qiu, J. Terrones, J. J. Vilatela, M. E. Vickers, J. A. Elliott and A. H. Windle, ACS Nano, 2013, 7, 8412–8422 CrossRef CAS PubMed.
- H. Cebeci, I. Y. Stein and B. L. Wardle, Appl. Phys. Lett., 2014, 104, 023117 CrossRef.
- M. R. Maschmann, Carbon, 2015, 86, 26–37 CrossRef CAS.
- V. Balakrishnan, M. Bedewy, E. R. Meshot, S. W. Pattinson, E. S. Polsen, F. Laye, D. N. Zakharov, E. A. Stach and A. J. Hart, ACS Nano, 2016, 10, 11496–11504 CrossRef CAS PubMed.
- E. R. Meshot, D. W. Zwissler, N. Bui, T. R. Kuykendall, C. Wang, A. Hexemer, K. J. J. Wu and F. Fornasiero, ACS Nano, 2017, 11, 5405–5416 CrossRef CAS PubMed.
- W. Shi, J. Li, E. S. Polsen, C. R. Oliver, Y. Zhao, E. R. Meshot, M. Barclay, D. H. Fairbrother, A. J. Hart and D. L. Plata, Nanoscale, 2017, 9, 5222–5233 RSC.
- H.-W. Pei, H. Liu, Z.-Y. Lu and Y.-L. Zhu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 020401 CrossRef PubMed.
- H.-W. Pei, H. Liu, Y.-L. Zhu and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2016, 18, 18767–18775 RSC.
- H.-W. Pei, X.-L. Liu, H. Liu, Y.-L. Zhu and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2017, 19, 4710–4718 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional data analysis details (Fig. S1); model derivation (eqn (S1)–(S9), Fig. S2, S3, and Table S1); and full data-sets (Tables S2 and S3). See DOI: 10.1039/c7cp06869g |
| ‡ These authors have contributed equally to this work. |
| This journal is © the Owner Societies 2018 |

