 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical investigation of the infrared spectrum of small polyynes†
Kirstin D.
Doney
 *a,
Dongfeng
Zhao
b,
John F.
Stanton
c and
Harold
Linnartz
a
*a,
Dongfeng
Zhao
b,
John F.
Stanton
c and
Harold
Linnartz
a
aSackler Laboratory for Astrophysics, Leiden Observatory, Leiden University, Leiden, The Netherlands. E-mail: doney@strw.leidenuniv.nl; Tel: +31 (0)71 527 8413
bCAS Center for Excellence in Quantum Information and Quantum Physics and Hefei National Laboratory for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei, Anhui, P. R. China
cDepartment of Chemistry, University of Florida, Gainesville, Florida, USA
First published on 3rd November 2017
Abstract
The full cubic and semidiagonal quartic force fields of acetylene (C2H2), diacetylene (C4H2), triacetylene (C6H2), and tetraacetylene (C8H2) are determined using CCSD(T) (coupled cluster theory with single and double excitations and augmented by a perturbative treatment of triple excitations) in combination with the atomic natural orbital (ANO) basis sets. Application of second-order vibrational perturbation theory (VPT2) results in vibrational frequencies that agree well with the known fundamental and combination band experimental frequencies of acetylene, diacetylene, and triacetylene (average discrepancies are less than 10 cm−1). Furthermore, the predicted ground state rotational constants (B0) and vibration–rotation interaction constants (αi) are shown to be consistent with known experimental values. New vibrational frequencies and rotational parameters from the presented theoretical predictions are given for triacetylene and tetraacetylene, which can be used to aid laboratory and astronomical spectroscopic searches for characteristic transitions of these molecules.
1 Introduction
Due to their reactive nature, unsaturated linear hydrocarbons, such as acetylene and polyynes (general structure HC2nH; X1Σg+), are prevalent in combustion chemistry,1–4 plasma processes,5,6 chemical synthesis,7–10 chemistry of planetary atmospheres,11–19 and interstellar gas-phase chemistry.20–25 They are of particular interest for astronomers, because they are believed to act as the ultraviolet (UV) shield in hydrocarbon-rich atmospheres,26–29 and in the formation and destruction of polycyclic aromatic hydrocarbons (PAHs),18,30–33 a major reservoir of carbon in the universe. In astronomical environments, the formation of long chain polyynes from acetylene is believed to occur through polymerization reactions,19,34,35| HC2nH + C2H → HC2n+2H + H, | (1a) |
| HC2H + C2nH → HC2n+2H + H, | (1b) |
| HC2nH+ + HC2H → HC2n+2H2+ + H, | (2a) |
| HC2n+2H2+ + e− → HC2n+2H + H. | (2b) |
Although long carbon chain molecules (e.g., HCn and HCnN for n ≤ 9)36–39 and small polyynes (HC2nH for n ≤ 3) have been detected in carbon-rich astronomical sources,20,21,39 tetraacetylene has yet to be observed. One limiting factor is that as centrosymmetric molecules, polyynes lack a permanent dipole moment, and cannot be detected by radioastronomy using pure rotational transitions, unlike, e.g., HCnN. Therefore, ro-vibrational spectra in the infrared (IR) region are the most important spectroscopic tools to detect polyynes both in the laboratory and in space. In particular, detection of acetylene, diacetylene, and triacetylene in planetary atmospheres and protoplanetary nebulae has been realized primarily through observation of the strongest perpendicular band (ν5, ν8, and ν11, respectively, at ∼13–17 μm) and the second strongest parallel band (ν4 + ν5, ν6 + ν8, and ν8 + ν11, respectively, at ∼8 μm).11,12,20,21 However, accurate line positions for tetraacetylene are lacking, from either laboratory or theoretical studies.
Extensive theoretical and experimental studies have been carried out for acetylene and diacetylene in the past few decades, including high-resolution spectroscopic studies of all the fundamental bands and a significant number of the combination bands,29,40–50 and high level ab initio calculations that take into account anharmonic effects.51–54 The combination of these studies shows that current quantum chemical theory, particularly coupled cluster theory with single and double excitations and augmented by a perturbative treatment of triple excitations (CCSD(T)),55 is able to accurately reproduce equilibrium geometries, experimental vibrational frequencies, vibration–rotation interaction constants (αi), and ground state rotational constants (B0).
Triacetylene and tetraacetylene are not as thoroughly studied, notably in terms of rotational information. While all of the fundamental vibrational modes of triacetylene have been measured, there is only rotational information for the IR active fundamental modes,56 and the strongest IR combination band (ν8 + ν11).57–61 However, theoretical studies of triacetylene do give rotational information for the remaining modes from CCSD(T) calculations of the vibration–rotation interaction constants62 and the equilibrium geometry.63 In addition, the harmonic frequencies of triacetylene were calculated using partial fourth-order many-body perturbation theory [SDQ-MBPT(4)].63 Conversely though, to the authors' knowledge, there is almost no rotational information for tetraacetylene. There has been only one low-resolution spectroscopic study of tetraacetylene, which measured three of the fundamentals (ν6, ν8, and ν14 at 3329.4, 2023.3, and 621.5 cm−1, respectively), and one combination band (ν10 + ν14 at 1229.7 cm−1), and gives an estimate for the electronic ground state rotational constant, B0.64 Unfortunately, the theoretical knowledge of tetraacetylene is equally limited, with only two studies of the equilibrium geometry (at the Hartree–Fock65 and B3LYP66 level of theory), and a calculation of the harmonic vibrational frequencies at the SVWN level of theory.64 While the two modes that are most useful for astronomical identification (ν14 and ν10 + ν14) were measured, the uncertainty associated with the line positions is too large to allow for an unambiguous assignment. Moreover, some high-resolution IR searches have been attempted,50,61,62,67 but so far no transitions have been assigned to tetraacetylene.
In this paper, we report the ab initio calculations for acetylene, diacetylene, triacetylene, and tetraacetylene. Due to the centrosymmetric nature of these molecules, observations in the laboratory and in space are most easily accomplished through their infrared spectra. As such, the properties computed and presented here are those related to that technique: fundamental vibrational frequencies, ground state rotational constants, and intramolecular interactions. The computational approach is calibrated using the well studied acetylene and diacetylene, and then extended to make predictions for triacetylene and tetraacetylene.
2 Computational methods
All calculations were carried out at the CCSD(T) level of theory, which with a sufficiently large basis set has been shown to accurately reproduce experimental values of semi-rigid molecules.52–55,68–72 Equilibrium geometries were determined using the large core-valence correlation-consistent quadruple-ζ basis set (cc-pCVQZ), which features [8s7p5d3f1g] (non-hydrogen atoms) and [4s3p2d1f] (hydrogen) of (15s9p5d3f1g) and (6s3p2d1f) primitive basis sets, respectively.73–75 All electron (AE)-CCSD(T)/cc-pCVQZ has been shown to give very accurate equilibrium geometries for unsaturated hydrocarbons.54,76–78 Optimizations were done using analytic energy derivatives,79 and were considered converged when the root-mean-square (RMS) gradient fell below 10−10 au.However, it is well known that correlation-consistent basis sets, such as cc-pCVQZ, tend to underestimate the vibrational frequencies of symmetric bending modes (πg) of conjugated molecules, e.g., polyynes, due to their susceptibility to an intramolecular variant of basis set superposition error (BSSE).54,80 It has been shown that one way to avoid this problem is to use basis sets with a large number of Gaussian primitives (particularly f-type), such as the atomic natural orbital (ANO) basis set (with the primitive basis set (13s8p6d4f2g) for non-hydrogen atoms and (8s6p4d2f) for hydrogen).52,81,82 The basis set has two common truncations: [4s3p2d1f] for non-hydrogen atoms and [4s2p1d] for hydrogen (hereafter known as ANO1), and [5s4p3d2f1g] (non-hydrogen atoms) and [4s3p2d1f] (hydrogen) (hereafter known as ANO2).74,75,81 In addition, only the valence electrons of carbon are considered in the correlation treatment, i.e., standard frozen-core (fc) calculations. (fc)-CCSD(T)/ANO1 has been shown to accurately reproduce experimental frequencies and intensities for small molecules.52,83,84 Using the (fc)-CCSD(T)/ANO1 optimized geometry, second-order vibrational perturbation (VPT2) theory calculations were determined from full cubic and the semidiagonal part of the quartic force fields obtained by numerical differentiation of analytic CCSD(T) second derivatives.70,85 All calculations were performed with the development version of the CFOUR program.86
3 Results and discussion
3.1 Equilibrium structure
The AE-CCSD(T)/cc-pCVQZ equilibrium geometries are shown in Fig. 1, with comparison to experimentally derived values (in italics) when known.53,87,88 The theoretical equilibrium bond lengths for acetylene, diacetylene, and triacetylene all agree within 0.5% of the structures determined from experimentally measured rotational constants. As the length of the carbon chain increases, the C–H bond lengths stay essentially the same, ∼1.062 Å, consistent with a sp-H type C–H bond. However, the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond lengths increase (particularly the internal C
C bond lengths increase (particularly the internal C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bonds), while the C–C bond lengths decrease, becoming closer to that typical of CC double bonds. This suggests that the π electrons become more delocalized over the internuclear axis, and the polyyne's configuration moves from a strict triple-single bond alternation to more of a consecutive double bond character of the CC bonds, making the overall structure more rigid as C2 units are added, an effect that also qualitatively acts to increase the biradical character of the molecule as the size grows.
C bonds), while the C–C bond lengths decrease, becoming closer to that typical of CC double bonds. This suggests that the π electrons become more delocalized over the internuclear axis, and the polyyne's configuration moves from a strict triple-single bond alternation to more of a consecutive double bond character of the CC bonds, making the overall structure more rigid as C2 units are added, an effect that also qualitatively acts to increase the biradical character of the molecule as the size grows.
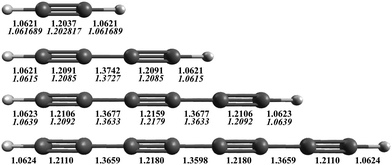 | ||
| Fig. 1 AE-CCSD(T)/cc-pCVQZ equilibrium geometries (Å) for HC2nH. Experimentally determined equilibrium bond lengths for acetylene,87 diacetylene,53 and triacetylene88 are given in italics below. | ||
The equilibrium rotational constants, Be, obtained from the AE-CCSD(T)/cc-pCVQZ equilibrium geometries are summarized in Table 1, and agree well with experimental ground state rotational constants (B0). As such, the equilibrium rotational constants suggest that the calculations predict the correct ground state geometry, because for linear molecules with more than three atoms the summation of vibration–rotation interaction constants (αi) is expected to be close to zero, and from
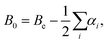 | (3) |
In addition, as seen for other carbon chains (e.g., HCn, HC2n+1N, and H2Cn)89 the centrifugal distortion constant (De) decreases with increasing molecular size, with a theoretical De = 1.6 × 10−6 cm−1 for acetylene, De = 1.5 × 10−8 cm−1 for diacetylene, De = 8.6 × 10−10 cm−1 for triacetylene, and De = 1.2 × 10−10 cm−1 for tetraacetylene. These values are consistent with those found experimentally for the respective vibrational ground states (Table 1). As noted by Thaddeus et al.89 this behavior of increasing stiffness with chain length is a distinguishing characteristic associated with bona fide chains.
3.2 Spectroscopic properties of acetylene and diacetylene
The quality of the present calculations is checked by comparison to the experimentally well studied acetylene and diacetylene. The harmonic and VPT2 fundamental frequencies of the fundamental and combination bands are given in Table 2 and 3 for acetylene and diacetylene, respectively, and experimental values are included for comparison. The (fc)-CCSD(T)/ANO1 VPT2 fundamental frequencies show good agreement with experimental values, with most observed–calculated deviations (o–c) being less than 5 cm−1 and all being less than 15 cm−1.| CCSD(T)/ANO1a | Experimental | ||
|---|---|---|---|
| ω | ν | ν | |
| a Intensities in km mol−1 are given in parentheses. | |||
| ν 1(σg+) | 3514.2(0) | 3375.2(0) | 3372.85141 |
| ν 2(σg+) | 2001.5(0) | 1964.8(0) | 1974.31741 |
| ν 3(σu+) | 3414.6(84.7) | 3285.9(74.8) | 3288.5807548 |
| ν 4(πg) | 600.5(0) | 600.6(0) | 612.87142 |
| ν 5(πu) | 752.3(90.5) | 734.7(91.7) | 730.33242 |
| ν 4 + ν5(σu+) | 1352.8 | 1329.2(10.8) | 1328.07442 |
| ν 2 + ν5(πu) | 2753.8 | 2698.3(0.1) | 2701.90743 |
| ν 3 + ν4(πu) | 4015.1 | 3878.5(0.5) | 3882.406041 |
| ν 1 + ν5(πu) | 4266.5 | 4098.9(0.5) | 4091.1732691 |
| ν 1 + ν3(σu+) | 6928.7 | 6551.9(2.0) | 6556.4640 |
| Anharmonic ZPE = 5760.1 | |||
| CCSD(T)/ANO1a | Experimental | ||
|---|---|---|---|
| ω | ν | ν | |
| a Intensities in km mol−1 are given in parentheses. | |||
| ν 1(σg+) | 3465.8(0) | 3332.5(0) | 3332.1547646 |
| ν 2(σg+) | 2240.2(0) | 2193.1(0) | 2188.928544 |
| ν 3(σg+) | 891.1(0) | 859.2(0) | 871.958244 |
| ν 4(σu+) | 3465.9(152.7) | 3333.1(135.5) | 3333.663450 |
| ν 5(σu+) | 2054.1(0.2) | 2016.9(0.5) | 2022.241544 |
| ν 6(πg) | 636.3(0) | 624.2(0) | 625.64350729 |
| ν 7(πg) | 479.8(0) | 476.9(0) | 482.707844 |
| ν 8(πu) | 636.3(78.7) | 624.1(78.8) | 628.04077629 |
| ν 9(πu) | 220.7(7.3) | 219.6(7.3) | 219.9771347 |
| 2ν9(σg+) | 441.4 | 438.5(0) | 438.4775747 |
| ν 7 + ν9(σu+) | 700.5 | 696.3(0.8) | 701.893929 |
| ν 6 + ν9(σu+) | 857.0 | 843.9(0.01) | 845.65551329 |
| ν 8 + ν9(σg+) | 857.0 | 843.9(0) | 848.36591829 |
| ν 7 + ν8(πu) | 1116.1 | 1103.1(0.6) | 111145 |
| ν 6 + ν8(σu+) | 1272.6 | 1244.7(21.8) | 1241.06082846 |
| 2ν6 + ν8(πu) | 1909.0 | 1864.6(0.0) | 1863.251244 |
| ν 2 + ν9(πu) | 2460.9 | 2410.0(0.04) | 2406.425144 |
| ν 5 + ν7(πu) | 2533.9 | 2489.0(0.01) | 2500.645844 |
| ν 5 + ν6(πu) | 2690.4 | 2637.0(0.04) | 2643.3232346 |
| ν 2 + ν8(πu) | 2876.6 | 2810.9(0.4) | 280545 |
| ν 1 + ν9(πu) | 3686.5 | 3551.6(0.1) | 3551.5615815946 |
| ν 1 + ν8(πu) | 4102.1 | 3946.9(0.7) | 393945 |
| ν 4 + ν6(πu) | 4102.3 | 3947.8(0.7) | |
| ν 2 + ν5(σu+) | 4294.3 | 4194.0(0.1) | |
| ν 4 + ν3(σu+) | 4357.0 | 4192.3(0.1) | |
| ν 1 + ν4(σu+) | 6931.7 | 6557.2(3.4) | 6565.47249 |
| Anharmonic ZPE = 7966.9 | |||
Based on previous studies of acetylene52 and diacetylene,53 the use of the ANO2 basis set was evaluated compared to the ANO1 basis set. For some of the vibrational modes, such as the ν4 mode of acetylene [612.88 cm−1 (observed)],42 Martin et al.52 showed that CCSD(T)/ANO2 can give a slightly better agreement (o–c value of ∼2 cm−1) compared to the ANO1 basis set (o–c value of ∼12 cm−1). However, the study by Thorwirth et al.53 showed that, for diacetylene, the average o–c value with CCSD(T)/ANO2 is comparable to that for the ANO1 basis set (∼6 cm−1 and ∼4 cm−1, respectively). Moreover, the time cost of (fc)-CCSD(T)/ANO2 calculations compared to (fc)-CCSD(T)/ANO1 far outweighs the minor frequency differences, and does not justify the higher computational cost of the ANO2 basis set in predicting the fundamental frequencies of longer polyynes.
The (fc)-CCSD(T)/ANO1 anharmonicity constants (xij, ESI†) also accurately account for the known combination bands of acetylene and diacetylene (Tables 2 and 3, respectively). All the combination bands are within 5 cm−1 of their observed values. For both acetylene and diacetylene, the ANO1 basis set is able to most accurately reproduce the C–H asymmetric stretch mode (ν3 and ν4, respectively). Significant is the agreement between the experimental and our predicted frequencies of ν6 + ν8 [1241.060828(38) cm−1 (observed)46 and 1244.7 cm−1 (theoretical)], and 2ν6 + ν8 [1863.2512(5) cm−1 (observed)44 and 1864.6 cm−1 (theoretical)] of diacetylene; both of which had only previously been calculated with CCSD(T)/cc-pCVQZ, and had o–c values greater than 20 cm−1.54 This suggests that the combination band VPT2 frequencies of polyynes determined using (fc)-CCSD(T)/ANO1 are accurate to aid identification of molecules, such as in astronomical surveys.
The vibration–rotation interaction constants (Table 4) are also determined in the course of the VPT2 calculation, and are in good agreement with both previous theoretical studies52,54 and experimentally determined values.29,44,46,50,51,54 Based on the vibration–rotation interaction constants, the ground state rotational constants (B0) were determined using the AE-CCSD(T)/cc-pCVQZ determined Be values (Table 1). For acetylene, B0 = 1.175319 cm−1, which is a 0.1% difference compared to the experimentally determined value of B0 = 1.17664632(18) cm−1.90 Diacetylene shows a similar 0.2% difference between the theoretical value of B0 = 0.146167 cm−1, and the experimentally determined value of B0 = 0.1464123(17) cm−1.50 The consistent accuracy of these values suggests that the method presented is clearly good enough to be extrapolated to and aid high-resolution infrared spectroscopic searches for the larger polyynes.
| Mode | HC2H (×103) | HC4H (×104) | HC6H (×105) | HC8H (×105) |
|---|---|---|---|---|
| a Deperturbed. | ||||
| α 1 | 6.853(6.904a)51 | 2.157(2.153)50 | 2.97 | 0.730 |
| α 2 | 6.007(6.181)51 | 6.608 | 15.20 | 4.91 |
| α 3 | 5.800(5.882a)51 | 3.123(3.110a)54 | 7.44 | 2.55 |
| α 4 | −1.464(−1.354)51 | 2.139(2.183)50 | 3.82 | 3.76 |
| α 5 | −2.134(−2.232)51 | 3.938(3.948)44 | 2.99(3.58)61 | 0.930 |
| α 6 | 0.730 | −0.700(−0.678)29 | 9.91(9.15)58 | 0.730 |
| α 7 | 4.06 | −2.703(−2.711)46 | 9.91 | 4.06 |
| α 8 | 2.33 | −0.647(−0.636)29 | −1.17(−1.071)58 | 2.33 |
| α 9 | 2.05 | −4.125(−4.183)46 | −5.83 | 2.05 |
| α 10 | −7.42(−7.88)58 | −0.295 | ||
| α 11 | −1.06(−1.06)57 | −1.95 | ||
| α 12 | −5.07 | −1.69 | ||
| α 13 | −8.47(−8.7207)59 | −2.26 | ||
| α 14 | −0.295 | |||
| α 15 | −0.163 | |||
| α 16 | −2.29 | |||
| α 17 | −2.80 | |||
3.3 Spectroscopic properties of triacetylene
The (fc)-CCSD(T)/ANO1 harmonic and VPT2 fundamental frequencies along with the experimental frequencies are given in Table 5. Comparison between theoretical VPT2 frequencies and experimental fundamentals measured with high-resolution techniques shows average o–c values that are smaller than those seen for acetylene or diacetylene (o–c ∼ 2 cm−1). For the known combination band, the (fc)-CCSD(T)/ANO1 anharmonicity constants (xij, ESI†) are able to reproduce the experimental value to within 5 cm−1, suggesting other combination band frequencies are of equal accuracy.| CCSD(T)/ANO1a | Experimental | ||
|---|---|---|---|
| ω | ν | ν | |
| a Intensities in km mol−1 are given in parentheses. | |||
| ν 1(σg+) | 3463.1(0) | 3330.4(0) | 331356 |
| ν 2(σg+) | 2284.0(0) | 2213.2(0) | 220156 |
| ν 3(σg+) | 2061.0(0) | 2023.2(0) | 201956 |
| ν 4(σg+) | 616.1(0) | 612.7(0) | 62556 |
| ν 5(σu+) | 3463.1(126.4) | 3329.5(175.0) | 3329.053361 |
| ν 6(σu+) | 2172.2(0.0) | 2130.4(0.1) | 2128.9163758 |
| ν 7(σu+) | 1169.6(1.7) | 1160.9(0.2) | 1115.059 |
| ν 8(πg) | 633.0(0) | 620.9(0) | 622.3857 |
| ν 9(πg) | 489.5(0) | 486.2(0) | 49156 |
| ν 10(πg) | 252.0(0) | 251.1(0) | 25856 |
| ν 11(πu) | 632.0(80.5) | 619.9(83.2) | 621.3401160 |
| ν 12(πu) | 444.7(1.0) | 441.8(1.0) | 443.559 |
| ν 13(πu) | 106.4(4.1) | 105.9(3.5) | 105.03861659 |
| ν 9 + ν13(σu+) | 595.9 | 591.7(0.8) | |
| ν 10 + ν12(σu+) | 696.7 | 691.8(1.8) | |
| ν 8 + ν12(σu+) | 1077.7 | 1063.5(0.3) | |
| ν 9 + ν11(σu+) | 1121.5 | 1107.1(0.7) | |
| ν 8 + ν11(σu+) | 1265.0 | 1237.4(31.4) | 1232.90429558 |
| ν 3 + ν7(σu+) | 3230.5 | 3182.8(0.1) | |
| ν 2 + ν7(σu+) | 3453.6 | 3362.2(2.5) | |
| 3ν7(σu+) | 3508.7 | 3498.7(0.01) | |
| ν 1 + ν13(πu) | 3569.5 | 3436.1(0.2) | |
| ν 5 + ν10(πu) | 3715.1 | 3583.7(0.1) | |
| ν 4 + ν5(σu+) | 4079.3 | 3945.8(0.1) | |
| ν 1 + ν11(πu) | 4095.2 | 3940.1(0.8) | |
| ν 5 + ν8(πu) | 4096.2 | 3943.9(0.8) | |
| ν 3 + ν6(σu+) | 4233.1 | 4141.1(0.1) | |
| ν 2 + ν6(σu+) | 4456.2 | 4334.7(0.1) | |
| ν 2 + ν5(σu+) | 5747.2 | 5548.4(0.2) | |
| ν 1 + ν5(σu+) | 6926.3 | 6555.1(4.6) | |
| Anharmonic ZPE = 10095.8 | |||
For the modes observed in low-resolution studies (e.g., ν1 and ν12), the agreement is still good with o–c values less than 20 cm−1. The notable exception is the internal C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C asymmetric stretch mode (ν7), which differs by 45 cm−1. Since no rotationally resolved data can be found for this band, it is possible that the band observed at 1115.0 cm−1
C asymmetric stretch mode (ν7), which differs by 45 cm−1. Since no rotationally resolved data can be found for this band, it is possible that the band observed at 1115.0 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59 was mis-assigned as the ν7 fundamental. A more likely assignment for this band is the ν9 + ν11 combination band, which has a predicted VPT2 frequency of 1107.1 cm−1, a calculated intensity of 0.7 km mol−1, and the same symmetry. Furthermore, the combination band is expected to be 3.5× more intense than the ν7 fundamental at 0.2 km mol−1, suggesting that ν9 + ν11 is more likely of the two to be observed. However, rotationally resolved measurements of this band are clearly needed to confirm this speculation.
59 was mis-assigned as the ν7 fundamental. A more likely assignment for this band is the ν9 + ν11 combination band, which has a predicted VPT2 frequency of 1107.1 cm−1, a calculated intensity of 0.7 km mol−1, and the same symmetry. Furthermore, the combination band is expected to be 3.5× more intense than the ν7 fundamental at 0.2 km mol−1, suggesting that ν9 + ν11 is more likely of the two to be observed. However, rotationally resolved measurements of this band are clearly needed to confirm this speculation.
We note that, a resonance between the ν5 fundamental and the ν2 + ν7 and 3ν7 combination bands must be addressed to achieve the very small (1 cm−1) o–c difference obtained for the C–H asymmetric stretch mode, ν5. The vibrational frequencies as a result of resonant interactions are calculated by a deperturbation-diagonalization technique followed by transformation of the deperturbed transition moments, as discussed in the work of Vázquez and Stanton and Matthews et al.85 This combination of Fermi and Darling–Dennison interactions shifts the ν5 predicted frequency from 3333.1 to 3329.5 cm−1, which is able to reproduce the experimentally observed frequency [3329.0533(2) cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61] with the same accuracy seen for diacetylene (o–c ∼ 0.5 cm−1). The combination bands involved are similarly shifted: ν2 + ν7 from 3329.5 to 3362.2 cm−1, and 3ν7 from 3526.7 to 3498.7 cm−1. Since the shift is most pronounced for the two combination bands, future experimental work to observe either of these bands is required to confirm this prediction.
61] with the same accuracy seen for diacetylene (o–c ∼ 0.5 cm−1). The combination bands involved are similarly shifted: ν2 + ν7 from 3329.5 to 3362.2 cm−1, and 3ν7 from 3526.7 to 3498.7 cm−1. Since the shift is most pronounced for the two combination bands, future experimental work to observe either of these bands is required to confirm this prediction.
The vibration–rotation interaction constants for triacetylene are given in Table 4, and are consistent with the previous CCSD(T)/cc-pCVQZ theoretical study62 and experimentally determined values.57–59,61 Consequently, the calculated ground state rotational constant B0 = 0.044092 cm−1 is within 0.2% of the experimentally observed B0 = 0.0441735(12) cm−1.61
3.4 Spectroscopic properties of tetraacetylene
The (fc)-CCSD(T)/ANO1 harmonic and VPT2 frequencies of the fundamental and combination bands for tetraacetylene are given in Table 6, and the (fc)-CCSD(T)/ANO1 anharmonicity constants (xij) are given in the ESI.† For the four experimentally observed bands, agreement of the observed and calculated frequencies is good at 7 cm−1, which is comparable to the uncertainty of the low resolution measurements. Furthermore, the ANO1 VPT2 frequencies are able to reproduce the experimental frequencies far better than the previous harmonic frequency calculations, which had o–c values of ∼20–100 cm−1.64 Of the predicted fundamental and combination bands, there are a number of bands that are found/predicted to have sufficient intensity and/or relatively unique frequency range that could offer viable target transitions to use to search for tetraacetylene in future laboratory or astronomical spectra. For example, in the IR the ν1 + ν6 at 6550.8 cm−1 or ν12 + ν15 at 871.9 cm−1 combination bands have both comparable predicted intensity to measured bands of di- and triacetylene, and have transitions in relatively clean regions of the spectrum. In terms of astronomical searches, the ν17 mode at 60.7 cm−1, offers a unique target transition, since its low frequency makes it accessible by far-IR observations, similar to the ν2 bending mode of C3.92| CCSD(T)/ANO1a | Experimental | ||
|---|---|---|---|
| ω | ν | ν | |
| a Intensities in km mol−1 are given in parentheses. | |||
| ν 1(σg+) | 3462.0(0) | 3330.5(0) | |
| ν 2(σg+) | 2263.2(0) | 2208.0(0) | |
| ν 3(σg+) | 2134.6(0) | 2094.2(0) | |
| ν 4(σg+) | 1296.4(0) | 1285.8(0) | |
| ν 5(σg+) | 470.0(0) | 455.3(0) | |
| ν 6(σu+) | 3461.6(223.1) | 3328.8(214.2) | 3329.464 |
| ν 7(σu+) | 2254.7(1.0) | 2227.6(0.5) | |
| ν 8(σu+) | 2064.3(0.3) | 2026.6(0.6) | 2023.364 |
| ν 9(σu+) | 911.6(3.2) | 922.4(2.0) | |
| ν 10(πg) | 632.4(0) | 620.0(0) | |
| ν 11(πg) | 489.3(0) | 486.0(0) | |
| ν 12(πg) | 422.3(0) | 419.5(0) | |
| ν 13(πg) | 158.8(0) | 157.9(0) | |
| ν 14(πu) | 632.6(79.6) | 619.7(79.9) | 621.564 |
| ν 15(πu) | 474.2(0.1) | 470.9(0.2) | |
| ν 16(πu) | 267.7(3.2) | 266.7(3.1) | |
| ν 17(πu) | 61.0(2.3) | 60.7(2.2) | |
| ν 11 + ν17(σu+) | 550.3 | 546.5(0.6) | |
| ν 13 + ν15(σu+) | 633.0 | 628.5(1.7) | |
| ν 12 + ν16(σu+) | 690.1 | 684.8(3.1) | |
| ν 12 + ν15(σu+) | 896.5 | 871.9(3.5) | |
| ν 11 + ν15(σu+) | 963.5 | 970.5(1.3) | |
| ν 10 + ν15(σu+) | 1106.6 | 1092.2(0.6) | |
| ν 10 + ν14(σu+) | 1265.1 | 1236.7(37.5) | 1229.764 |
| ν 2 + ν9(σu+) | 3174.8 | 3130.1(0.5) | |
| ν 4 + ν8(σu+) | 3360.7 | 3311.4(0.5) | |
| ν 6 + ν10(πu) | 4094.0 | 3939.1(0.8) | |
| ν 1 + ν14(πu) | 4094.6 | 3940.6(0.8) | |
| ν 1 + ν6(σu+) | 6923.6 | 6550.8(5.7) | |
| Anharmonic ZPE = 12218.2 | |||
Based on the results discussed for the other small polyynes, the theoretical vibration–rotation interaction constants given in Table 4 are sufficient to assist in identification of ro-vibrational bands of tetraacetylene. The αi results in a theoretical ground state rotational constant of B0 = 0.018844 cm−1 that agrees within errors with the experimentally determined value, B0 = 0.020(3) cm−1.64 Overall, for polyynes the difference between the experimental and calculated rotational constants (ΔB0) decreases from 0.001 to 0.00008 cm−1 as the chain length is increased, which is consistent with the trend seen for other carbon chain molecules (e.g., HCnN, HCn, CnO).93 Therefore, if the trend continues as expected then the ΔB0 for tetraacetylene is equal to or smaller than that seen for triacetylene, and the determined ground state rotational constant is a good approximation of the true value.
4 Conclusions
Accurate equilibrium geometries have been determined at the AE-CCSD(T)/cc-pCVQZ level of theory, and the full cubic and semidiagonal quartic force field have been determined at the (fc)-CCSD(T)/ANO1 level of theory for acetylene and the three smallest polyynes. No scaling or adjustments had to be included to match theoretical values with those determined by experiments. The resulting VPT2 fundamental vibrational frequencies and vibration–rotation interaction constants agree with known experimental values, showing about a 5 cm−1 deviation in frequencies for bands with high-resolution infrared information. For bands with only low-resolution data, the theoretical frequencies are able to confirm mode assignments or suggest a reassignment, as in the case of the observed band at 1115.0 cm−1 of triacetylene to the ν9 + ν11 combination band, which has previously been attributed to the ν7 fundamental. The provisional ab initio method used here is also able to accurately reproduce the observed frequencies of combination bands.The calculated fundamental frequencies for triacetylene and tetraacetylene give insight as to why tetraacetylene has not yet been observed in space. Observation of centrosymmetric molecules in astronomical environments is mainly through infrared detection of the high intensity bending modes; e.g., ν8 [628.040776(36) cm−1]29 and ν6 + ν8 [1241.060828(38) cm−1]46 of diacetylene, or ν11 [621.34011(42) cm−1]60 and ν8 + ν11 [1232.904295(74) cm−1]58 of triacetylene. However, the analogous modes for tetraacetylene are the ν14 [621.5(5) cm−1]64 and ν10 + ν14 [1229.7(5) cm−1],64 and are predicted to be significantly weaker in intensity due to lower column densities.34,35 Consequently, at these frequencies and resolutions of the previous infrared observations where polyynes were detected,20–22,24,25 the transitions of tetraacetylene are blended with those of triacetylene. Other bands of tetraacetylene would be more suitable for identification, such as ν1 + ν6, ν12 + ν15, or ν17 that are expected to be equally strong as bands already used to identify di- and triacetylene.
Overall, the resulting computed geometries lead to equilibrium rotational constants (Be), which when corrected for vibrational zero-point effects give ground state equilibrium constants (B0) that agree with experimental values (0.2%). Based on the small o–c values for acetylene, diacetylene, and triacetylene, we are confident that the fundamental frequencies and spectroscopic constants determined here offer an accurate guide for spectroscopic searches focused on detection of ro-vibrational bands of triacetylene and tetraacetylene. Such work is underway in our laboratory.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr D. J. Nesbitt for helpful discussions. We acknowledge the financial support of the Netherlands Organization for Scientific Research (NWO) through a VICI grant, and the Netherlands Research School for Astronomy (NOVA). D. Z. also acknowledges financial support from the National Key R&D Program of China (2017YFA0303502) and the Fundamental Research Funds for the Central Universities of China.References
- M. Frenklach, D. W. Clary, W. C. Gardiner and S. E. Stein, Symp. (Int.) Combust., [Proc.], 1985, 20, 887–901 CrossRef.
- I. Cherchneff, J. R. Barker and A. G. G. M. Tielens, Astrophys. J., 1992, 401, 269–287 CrossRef CAS.
- K.-H. Homann, Angew. Chem., Int. Ed., 1998, 37, 2434–2451 CrossRef.
- H. Richter, T. G. Benish, O. A. Mazyar, W. H. Green and J. B. Howard, Proc. Combust. Inst., 2000, 28, 2609–2618 CrossRef CAS.
- T. Fujii and M. Kareev, J. Appl. Phys., 2001, 89, 2543–2546 CrossRef CAS.
- H. Thejaswini, A. Majumdar, T. Tun and R. Hippler, Adv. Space Res., 2011, 48, 857–861 CrossRef CAS.
- H. Shirakawa, Rev. Mod. Phys., 2001, 73, 713–718 CrossRef CAS.
- X. Zhao, Y. Ando, Y. Liu, M. Jinno and T. Suzuki, Phys. Rev. Lett., 2003, 90, 187401 CrossRef PubMed.
- A. Milani, M. Tommasini, M. Del Zoppo, C. Castiglioni and G. Zerbi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 153418 CrossRef.
- T.-B. Ma, Y.-Z. Hu and H. Wang, J. Appl. Phys., 2008, 104, 064904 CrossRef.
- V. G. Kunde, A. C. Aikin, R. A. Hanel, D. E. Jennings, W. C. Maguire and R. E. Samuelson, Nature, 1981, 292, 686–688 CrossRef CAS.
- T. de Graauw, H. Feuchtgruber, B. Bezard, P. Drossart, T. Encrenaz, D. A. Beintema, M. Griffin, A. Heras, M. Kessler, K. Leech, E. Lellouch, P. Morris, P. R. Roelfsema, M. Roos-Serote, A. Salama, B. Vandenbussche, E. A. Valentijn, G. R. Davis and D. A. Naylor, Astron. Astrophys., 1997, 321, L13–L16 CAS.
- E. Wilson and S. Atreya, Planet. Space Sci., 2003, 51, 1017–1033 CrossRef CAS.
- V. G. Kunde, F. M. Flasar, D. E. Jennings, B. Bézard, D. F. Strobel, B. J. Conrath, C. A. Nixon, G. L. Bjoraker, P. N. Romani, R. K. Achterberg, A. A. Simon-Miller, P. Irwin, J. C. Brasunas, J. C. Pearl, M. D. Smith, G. S. Orton, P. J. Gierasch, L. J. Spilker, R. C. Carlson, A. A. Mamoutkine, S. B. Calcutt, P. L. Read, F. W. Taylor, T. Fouchet, P. Parrish, A. Barucci, R. Courtin, A. Coustenis, D. Gautier, E. Lellouch, A. Marten, R. Prangé, Y. Biraud, C. Ferrari, T. C. Owen, M. M. Abbas, R. E. Samuelson, F. Raulin, P. Ade, C. J. Césarsky, K. U. Grossman and A. Coradini, Science, 2004, 305, 1582–1587 CrossRef CAS PubMed.
- V. Vuitton, J.-F. Doussin, Y. Bénilan, F. Raulin and M.-C. Gazeau, Icarus, 2006, 185, 287–300 CrossRef CAS.
- M. Burgdorf, G. Orton, J. van Cleve, V. Meadows and J. Houck, Icarus, 2006, 184, 634–637 CrossRef CAS.
- V. S. Meadows, G. Orton, M. Line, M.-C. Liang, Y. L. Yung, J. Van Cleve and M. J. Burgdorf, Icarus, 2008, 197, 585–589 CrossRef CAS.
- J. H. Waite, D. T. Young, T. E. Cravens, A. J. Coates, F. J. Crary, B. Magee and J. Westlake, Science, 2007, 316, 870–875 CrossRef CAS PubMed.
- X. Gu, Y. S. Kim, R. I. Kaiser, A. M. Mebel, M. C. Liang and Y. L. Yung, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16078–16083 CrossRef CAS PubMed.
- J. Cernicharo, A. M. Heras, J. R. Pardo, A. G. G. M. Tielens, M. Guélin, E. Dartois, R. Neri and L. B. F. M. Waters, Astrophys. J., Lett., 2001, 546, L127–L130 CrossRef CAS.
- J. Cernicharo, A. M. Heras, A. G. G. M. Tielens, J. R. Pardo, F. Herpin, M. Guélin and L. B. F. M. Waters, Astrophys. J., Lett., 2001, 546, L123–L126 CrossRef CAS.
- J. Bernard-Salas, E. Peeters, G. C. Sloan, J. Cami, S. Guiles and J. R. Houck, Astrophys. J., Lett., 2006, 652, L29–L32 CrossRef CAS.
- V. Wakelam, I. W. M. Smith, E. Herbst, J. Troe, W. Geppert, H. Linnartz, K. Öberg, E. Roueff, M. Agúndez, P. Pernot, H. M. Cuppen, J. C. Loison and D. Talbi, Space Sci. Rev., 2010, 156, 13–72 CrossRef CAS.
- J. P. Fonfría, J. Cernicharo, M. J. Richter and J. H. Lacy, Astrophys. J., 2011, 728, 43 CrossRef.
- S. E. Malek, J. Cami and J. Bernard-Salas, Astrophys. J., 2012, 744, 16 CrossRef.
- R. E. Bandy, C. Lakshminarayan, R. K. Frost and T. S. Zwier, Science, 1992, 258, 1630–1633 CAS.
- R. E. Bandy, C. Lakshminarayan, R. K. Frost and T. S. Zwier, J. Chem. Phys., 1993, 98, 5362–5374 CrossRef CAS.
- R. K. Frost, G. S. Zavarin and T. S. Zwier, J. Phys. Chem., 1995, 99, 9408–9415 CrossRef CAS.
- L. Bizzocchi, F. Tamassia, C. D. Esposti, L. Fusina, E. Cané and L. Dore, Mol. Phys., 2011, 109, 2181–2190 CrossRef CAS.
- M. Frenklach and E. D. Feigelson, Astrophys. J., 1989, 341, 372–384 CrossRef CAS.
- S. P. Ekern, A. G. Marshall, J. Szczepanski and M. Vala, J. Phys. Chem. A, 1998, 102, 3498–3504 CrossRef CAS.
- A. Krestinin, Combust. Flame, 2000, 121, 513–524 CrossRef CAS.
- M. E. Kress, A. G. Tielens and M. Frenklach, Adv. Space Res., 2010, 46, 44–49 CrossRef CAS.
- P. M. Woods, T. J. Millar, E. Herbst and A. A. Zijlstra, Astron. Astrophys., 2003, 402, 189–199 CrossRef CAS.
- N. Sakai and S. Yamamoto, Chem. Rev., 2013, 113, 8981–9015 CrossRef CAS PubMed.
- J. Cernicharo and M. Guélin, Astron. Astrophys., 1996, 309, L27–L30 CAS.
- M. B. Bell, P. A. Feldman, M. J. Travers, M. C. McCarthy, C. A. Gottlieb and P. Thaddeus, Astrophys. J., Lett., 1997, 483, L61 CrossRef CAS.
- M. B. Bell, P. A. Feldman, J. K. G. Watson, M. C. McCarthy, M. J. Travers, C. A. Gottlieb and P. Thaddeus, Astrophys. J., 1999, 518, 740–747 CrossRef CAS.
- V. Vuitton, R. Yelle and M. McEwan, Icarus, 2007, 191, 722–742 CrossRef.
- E. K. Plyler, E. D. Tidwell and T. A. Wiggins, J. Opt. Soc. Am., 1963, 53, 589–593 CrossRef CAS.
- K. F. Palmer, M. E. Mickelson and K. N. Rao, J. Mol. Spectrosc., 1972, 44, 131–144 CrossRef CAS.
- J. Pliva, J. Mol. Spectrosc., 1972, 44, 165–182 CrossRef CAS.
- J. Pliva, J. Mol. Spectrosc., 1972, 44, 145–164 CrossRef.
- G. Guelachvili, A. Craig and D. Ramsay, J. Mol. Spectrosc., 1984, 105, 156–192 CrossRef CAS.
- N. L. Owen, C. H. Smith and G. A. Williams, J. Mol. Struct., 1987, 161, 33–53 CrossRef CAS.
- D. McNaughton and D. Bruget, J. Mol. Struct., 1992, 273, 11–25 CrossRef CAS.
- E. Arié and J. Johns, J. Mol. Spectrosc., 1992, 155, 195–204 CrossRef.
- J. Vanderauwera, D. Hurtmans, M. Carleer and M. Herman, J. Mol. Spectrosc., 1993, 157, 337–357 CrossRef CAS.
- J. E. Gambogi, R. Z. Pearson, X. Yang, K. K. Lehmann and G. Scoles, Chem. Phys., 1995, 190, 191–205 CrossRef CAS.
- D. Zhao, K. D. Doney and H. Linnartz, J. Mol. Spectrosc., 2014, 296, 1–8 CrossRef CAS.
- M. A. Temsamani and M. Herman, J. Chem. Phys., 1995, 102, 6371–6384 CrossRef CAS.
- J. M. L. Martin, T. J. Lee and P. R. Taylor, J. Chem. Phys., 1998, 108, 676–691 CrossRef CAS.
- S. Thorwirth, M. E. Harding, D. Muders and J. Gauss, J. Mol. Spectrosc., 2008, 251, 220–223 CrossRef CAS.
- A. C. Simmonett, H. F. Schaefer III and W. D. Allen, J. Chem. Phys., 2009, 130, 044301 CrossRef PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- E. Bjarnov, D. Christensen, O. Nielsen, E. Augdahl, E. Kloster-Jensen and A. Rogstad, Spectrochim. Acta, Part A, 1974, 30, 1255–1262 CrossRef.
- K. Matsumura, H. Kanamori, K. Kawaguchi, E. Hirota and T. Tanaka, J. Mol. Spectrosc., 1988, 131, 278–287 CrossRef CAS.
- D. McNaughton and D. Bruget, J. Mol. Spectrosc., 1991, 150, 620–634 CrossRef CAS.
- S. Haas, K. Yamada and G. Winnewisser, J. Mol. Spectrosc., 1994, 164, 445–455 CrossRef CAS.
- S. Haas, G. Winnewisser, K. Yamada, K. Matsumura and K. Kawaguchi, J. Mol. Spectrosc., 1994, 167, 176–190 CrossRef CAS.
- K. D. Doney, D. Zhao and H. Linnartz, J. Mol. Spectrosc., 2015, 316, 54–63 CrossRef CAS.
- C.-H. Chang, J. Agarwal, W. D. Allen and D. J. Nesbitt, J. Chem. Phys., 2016, 144, 074301 CrossRef PubMed.
- K. W. Sattelmeyer and J. F. Stanton, J. Am. Chem. Soc., 2000, 122, 8220–8227 CrossRef CAS.
- F. Shindo, Y. Bénilan, P. Chaquin, J.-C. Guillemin, A. Jolly and F. Raulin, J. Mol. Spectrosc., 2001, 210, 191–195 CrossRef CAS.
- J. L. Toto, T. T. Toto, C. P. de Melo, B. Kirtman and K. Robins, J. Chem. Phys., 1996, 104, 8586–8592 CrossRef CAS.
- R. I. Kaiser, B. J. Sun, H. M. Lin, A. H. H. Chang, A. M. Mebel, O. Kostko and M. Ahmed, Astrophys. J., 2010, 719, 1884 CrossRef CAS.
- D. Zhao, J. Guss, A. J. Walsh and H. Linnartz, Chem. Phys. Lett., 2013, 565, 132–137 CrossRef CAS.
- T. J. Lee and G. E. Scuseria, in Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy, ed. S. Langhoff, Kluwer Academic Publishers, Dordrecht, 1995 Search PubMed.
- R. J. Bartlett, in Modern Electronic Structure Theory, Part II, ed. D. R. Yarkony, World Scientific, Singapore, 1995 Search PubMed.
- J. Gauss and J. F. Stanton, Chem. Phys. Lett., 1997, 276, 70–77 CrossRef CAS.
- J. Gauss, in Encyclopedia of Computational Chemistry, ed. P. V. R. Schleyer, Wiley, New York, 1998 Search PubMed.
- L. McCaslin and J. F. Stanton, Mol. Phys., 2013, 111, 1492–1496 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- A. A. Auer and J. Gauss, Phys. Chem. Chem. Phys., 2001, 3, 3001–3005 RSC.
- K. L. Bak, J. Gauss, P. Jørgensen, J. Olsen, T. Helgaker and J. F. Stanton, J. Chem. Phys., 2001, 114, 6548–6556 CrossRef CAS.
- X. Zhang, A. T. Maccarone, M. R. Nimlos, S. Kato, V. M. Bierbaum, G. B. Ellison, B. Ruscic, A. C. Simmonett, W. D. Allen and H. F. Schaefer III, J. Chem. Phys., 2007, 126, 044312 CrossRef PubMed.
- J. F. Stanton and J. Gauss, Int. Rev. Phys. Chem., 2000, 19, 61–95 CrossRef CAS.
- E. D. Simandiras, J. E. Rice, T. J. Lee, R. D. Amos and N. C. Handy, J. Chem. Phys., 1988, 88, 3187–3195 CrossRef CAS.
- J. Almlöf and P. R. Taylor, J. Chem. Phys., 1987, 86, 4070–4077 CrossRef.
- C. W. Bauschlicher and P. R. Taylor, Theor. Chim. Acta, 1993, 86, 13–24 CrossRef CAS.
- J. M. L. Martin, P. R. Taylor and T. J. Lee, Chem. Phys. Lett., 1997, 275, 414–422 CrossRef CAS.
- J. Vázquez and J. F. Stanton, Mol. Phys., 2007, 105, 101–109 CrossRef.
- D. A. Matthews, J. Vázquez and J. F. Stanton, Mol. Phys., 2007, 105, 2659–2666 CrossRef CAS.
- Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package by J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, L. Cheng, O. Christiansen, F. Engel, R. Faber, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, F. Lipparini, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, 2017, see http://www.cfour.de.
- F. Tamassia, E. Cane, L. Fusina and G. Di Lonardo, Phys. Chem. Chem. Phys., 2016, 18, 1937–1944 RSC.
- R. Tay, G. F. Metha, F. Shanks and D. McNaughton, Struct. Chem., 1995, 6, 47–55 CrossRef CAS.
- P. Thaddeus, M. C. McCarthy, M. J. Travers, C. A. Gottlieb and W. Chen, Faraday Discuss., 1998, 109, 121–135 RSC.
- Y. Kabbadj, M. Herman, G. D. Lonardo, L. Fusina and J. Johns, J. Mol. Spectrosc., 1991, 150, 535–565 CrossRef CAS.
- R. D'Cunha, Y. Sarma, G. Guelachvili, R. Farrenq, Q. Kou, V. Devi, D. Benner and K. N. Rao, J. Mol. Spectrosc., 1991, 148, 213–225 CrossRef.
- J. Cernicharo, J. R. Goicoechea and E. Caux, Astrophys. J., Lett., 2000, 534, L199–L202 CrossRef CAS PubMed.
- E. E. Etim and E. Arunan, Astrophys. Space Sci., 2017, 362, 4 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06131e |
| This journal is © the Owner Societies 2018 |
