Structural stability and magnetic-exchange coupling in Mn-doped monolayer/bilayer MoS₂

Abstract

Ferromagnetic (FM) two-dimensional (2D) transition metal dichalcogenides (TMDs) have potential applications in modern electronics and spintronics and doping of TMDs with transition metals can enhance the magnetic characteristics. In this work, the structural stability, electronic states, and magnetic properties of Mn-doped monolayer/bilayer MoS₂ are studied systematically by first-principles calculations. Substitutional Mn dopants at the Mo sites are energetically favorable in both monolayer and bilayer MoS₂ under the S-rich condition which is common in the synthesis of MoS₂ nanosheets. Two Mn dopants participate in the FM interaction in monolayer MoS₂ and magnetic coupling of two Mn dopants via the double-exchange mechanism can be mediated by the nearest neighboring S. Magnetic coupling can be ascribed to the competition between the double-exchange, direct-exchange, and super-exchange interactions, which take place between two Mn dopants in bilayer MoS₂ with the Mn_iMn_Mo, Mn_iMn_S and Mn_Mo–Mn_Mo configurations. Our results reveal the geometrical dependence of magnetic-exchange coupling suggesting that Mn-doped monolayer/bilayer MoS₂ has large potential in spintronic devices.

---

1. Introduction

The discovery of graphene and its unique properties have stimulated extensive research in two-dimensional (2D) materials^1–4 and efforts have been made to fabricate high-quality 2D sheets to study the novel physical properties and design new devices.^5–9 However, the gapless feature of pristine graphene limits its integration into microelectronic and nanoelectronic devices.¹ On the other hand, many transition metal dichalcogenides (TMDs) possessing interesting semiconducting, metallic, superconducting, and magnetic properties have potential applications in photovoltaics,^10,11 optical detection,^12–14 photocatalysis,^15,16 field-effect transistors,^17,18 as well as lithium-ion batteries.^19–22 These compounds are composed of MX₂ (M = Mo, W, Nb, Re, Ta; X = S, Se, Te) layers with covalent bonding within the layers and weak van der Waals (vdW) bonding between layers enabling easy exfoliation. Semiconducting TMDs such as MoS₂ are potential candidates in next-generation electronic and optoelectronic devices.^23,24 Recently, a spin lifetime of 1 ns or longer exceeding that of graphene has been observed by polarization-resolved photoluminescence measurements.²⁵ The spin–orbit coupling and absence of inversion symmetry induce spin splitting at the valence band maximum thus suppressing spin relaxation and enhancing the spin lifetime.^26–28

In spintronics, attention has been paid to strategies that induce and manipulate the magnetic properties in semiconductors and stable magnetism in semiconducting 2D materials. Doping is a simple technique to produce stable magnetic properties in 2D materials.^29,30 Theoretical and experimental studies have been conducted to explore magnetism in MoS₂ nanosheets doped with transition metals.^31–34 For example, substitutional replacement of Mo with TM atoms (V, Mn, Fe, Co, Cu, Ni, Zn, Cd and Hg) can induce significant magnetism in monolayer MoS₂^35–38 if the dopants are separated from each other at a certain distance.³⁹ Substitutional replacement of Mo with Mn can even produce FM properties via the double-exchange mechanism.^37,38 Since this interaction is short-ranged, percolation is a key factor in controlling the long-range magnetic order.³⁷ Shu et al.⁴⁰ have observed FM coupling in Fe-doped monolayer MoS₂ through magnetic double-exchange coupling but antiferromagnetic (AFM) coupling in bilayer and multilayer samples by magnetic super-exchange coupling. The electronic states and magnetic properties can be manipulated by the ‘pizza’ and ‘sandwich’ configurations of Mn clusters in MoS₂ nanosheets⁴¹ thereby suggesting that the magnetism as well as magnetic-exchange coupling among dopants can be manipulated by altering the doping configuration and distribution, which are sensitive to the growth conditions and parameters such as the S/Mo ratio and temperature. Hence, the magnetic coupling behavior and effects of different doping configurations are interesting from the perspective of fundamental understanding and spintronic applications. In this work, based on first-principles calculations, the structural stability and magnetic exchange interactions in Mn-doped MoS₂ nanosheets are systematically studied and applications to spintronic devices are discussed thermodynamically and kinetically.

2. Computational method and model

The calculation is performed using the Vienna ab initio simulation package based on density functional theory.^42,43 The electron–ion core interaction is described by the projector augmented wave potentials⁴⁴ which are more accurate than the ultra-soft pseudo-potentials. The Perdew–Burke–Ernzerhof⁴⁵ formulation of the generalized gradient approximation is chosen to describe the exchange–correlation interaction. The DFT-D2 approach within the Grimme scheme is adopted to correct the contribution of the vdW interactions between different layers⁴⁶ and the cutoff energy for the plane waves is 400 eV. To avoid the interactions between dopants in neighboring unit cells, a 4 × 4 × 1 supercell of the MoS₂ primitive cell in which the separation between dopants is larger than 12 Å is adopted. A 15 Å vacuum layer is added in the out-of-plane direction to inhibit the interactions of neighboring layers. The Brillouin–zone integration is performed by using an 11 × 11 × 1 k-mesh according to the Monkhorst–Pack scheme and a Gaussian smearing broadening of 0.2 eV is introduced. A conjugate-gradient algorithm is implemented to relax the ions to the ground states with an energy convergence of 1.0 × 10⁻⁵ eV and force convergence of 0.02 eV Å⁻¹ on each ion, respectively. The supercells and magnetic moment distribution are visualized by the VESTA software.⁴⁷

In addition, the GGA functional fails to describe partially occupied 3d orbitals of transition metal elements. Therefore using a model of GGA with the correction of a Hubbard U term (GGA+U) to describe the 3d orbitals of impurity transition metal elements seems to be necessary.^36,40 However, several on site Hubbard U parameters have been tested for Mo (4d) orbitals, which yield almost the same results as the GGA calculations.^31,48 Similarly, Cheng et al. studied the magnetism of monolayer MoS₂ doped with Mn by using GGA+U, which agrees with that of the theoretical results within GGA. In order to obtain a reasonable U parameter, the role of U parameter in the range of 3–5 eV (U = 3, 3.5, 4, 4.5, and 5 eV) is investigated. Taking two Mn dopants substitutionally inserted into monolayer MoS₂ as a test example, we find that adjusting the U value does not change the magnetic moment (total and local magnetic moments) and FM characteristic upon comparing the result calculated with the GGA method (Fig. S1 in the ESI†). Thus, the GGA+U method is not considered to describe the Mn dopant in MoS₂ nanosheets in this work.

The thermodynamic stability of the Mn dopant in MoS₂ nanosheets is evaluated by calculating the formation energy (E_f) as shown in the following equation:

E_f = E_T − E_P − Δn_Moμ_Mo − Δn_Sμ_S − Δn_Mnμ_Mn, (1)

where E_T and E_P are the energies of the Mn-doped and perfect MoS₂ sheets, respectively, and μ_i and Δn_i are the chemical potential and difference of atomic species i (i = Mo, S, and Mn) in the Mn-doped and perfect MoS₂ sheets. μ_Mnμ_Mn and μ_Mo are the respective chemical potentials of a single Mn and Mo atom. The energy per atom of α-Mn is taken as μ_Mn.³⁸μ_Mo is defined within a range of values corresponding to Mo-rich or S-rich growth conditions. For the Mo-rich condition, μ_Mo is taken as the energy of a Mo atom within its stable fcc lattice. μ_Mo is determined from the difference in the energy between a diatomic S₂ molecule and one formula unit of MoS₂, corresponding to the S-rich condition. In order to maintain thermodynamic equilibrium of the crystalline phase (μ_Mo + 2μ_S = μ_MoS2), the value of μ_S should satisfy the requirement of μ_S(bulk) − ΔH_f < μ_S < μ_S(bulk), in which the upper (lower) limit corresponds to the S-rich (Mo-rich) condition and ΔH_f is the formation heat of MoS₂. The computed formation heat is 1.44 eV which is in good agreement with reported results.^40,49

3. Results and discussion

3.1 Mn dopant in monolayer MoS₂

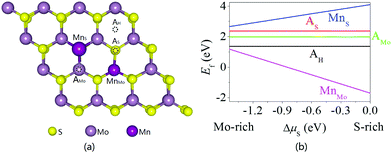
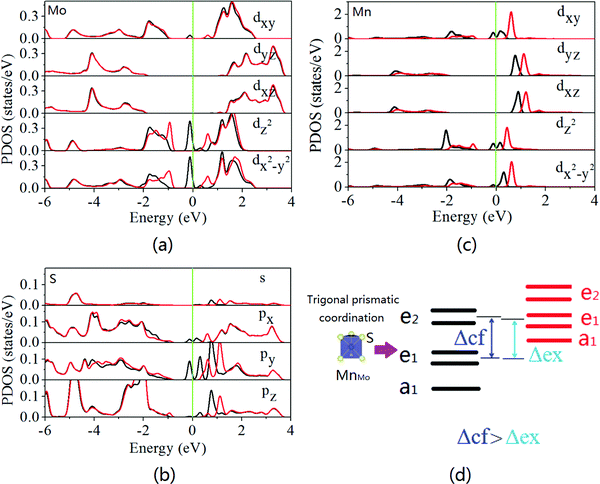
The structural stability and magnetic properties of the isolated Mn dopant in monolayer MoS₂ are first investigated. Five doping configurations are considered, that is, Mn adsorbed on top of the Mo, S or hollow sites (A_Mo, A_S, and A_H) and Mn replacing Mo or S (Mn_Mo and Mn_S) as schematically illustrated in Fig. 1a. Metal-doped MoS₂ has been synthesized^50,51 and Au on top of the S, Mo, and hollow sites of MoS₂ has been observed.⁵² Furthermore, Cr/V/Nb dopants directly substitute Mo atoms,^53,54 and Pt atoms are localized at S vacancies exhibiting dynamic hopping to the nearby surface layers.⁵⁵ Up to now, the position of Mn dopants in MoS₂ has been ambiguous. The formation energies of the five possible doping configurations as a function of the chemical potential difference for different S concentrations (Δμ_S = μ_S − μ_bulk) are calculated and shown in Fig. 1b. The formation energy of the Mn_Mo doping configuration is the lowest one and negative in most cases. In particular, under the S-rich growth condition, the formation energy of Mn_Mo doping in monolayer MoS₂ is −1.702 eV which is in good agreement with the reported value of −1.8 eV.⁴² Therefore, Mn dopants tend to replace Mo atoms in monolayer MoS₂ and it has been observed experimentally.^54,56

Fig. 1 (a) Atomic model and (b) formation energy of a single Mn dopant in monolayer MoS₂.

To understand the spin splitting, the electronic states of monolayer MoS₂ with the Mn_Mo doping configurations are calculated. The trigonal prismatic coordination of Mo atoms leads to degeneracy of the Mo 4d levels. The lowest energy band of the Mo d_z² orbital is fully occupied, the degenerate energy bands of the Mo d_xy and Mo d_x²−y² orbitals are unoccupied, and those of Mo d and Mo d_yz bands are the highest ones. Hybridization among the Mo d_z², Mo d_xy, Mo d_x²−y², and S 3p orbitals dominates the conduction and valence band edges of MoS₂.^23–27 As shown in Fig. 2, spin polarization occurs in monolayer MoS₂ with the Mn_Mo doping configuration leading to highly localized states in the band gap. The partial density of states (PDOS) suggests that the mid-gap states mainly arise from the d states of the Mn dopant and its neighboring spin-polarized 3d states of Mo atoms and 3p states of S atoms. Strong hybridization between the 3d states of Mn and 3p states of adjacent S atoms produces mid-gap states in the spin-up channel (Fig. 3b and c). Moreover, no band gap is observed from the spin-up channel, although a considerable band gap is kept in the spin-down channel, indicating the half-metallic feature of the Mn-doped monolayer MoS₂. Thus, it is expected to provide 100% spin polarization current and favorable spintronic applications. Some valence electrons (3d⁶4s¹) of the Mn dopant transfer to the nearest-neighboring S atoms and the residual valence electrons produce spin polarization and a magnetic moment of 1.035 μ_B (Table S1, ESI†). This is in good agreement with the previously reported value of ∼1 μ_B.³² The Mn 3d orbitals undergo crystal-field splitting (Δcf) and interatomic Hund's exchange splitting (Δex). The five Mn 3d states are split into three groups, anti-bonding states, e₁ (d_xy and d_x²−y²), e₂ (d_xz and d_yz), and a₁ (d_z²) due to the trigonal prismatic coordination of S atoms. As schematically shown in Fig. 3d, the energies of the spin-down states a₁ and e₁ are lower than those of the spin-up states e₂, suggesting Δcf > Δex.

Fig. 2 Total and partial density of states of Mn substituting Mo (Mn_Mo) in monolayer MoS₂. The black and red lines represent the spin-up and spin-down channels, respectively, and the Fermi level which is set at zero is indicated by the green line.

Fig. 3 Orbital decomposed density of states of Mn substituting Mo (Mn_Mo) in monolayer MoS₂: (a) Mo 4d states, (b) S 3s and 3p states, and (c) Mn 3d states. The Mo and S atoms are the nearest to the Mn dopant. The black and red lines represent the spin-up and spin-down channels, respectively. The Fermi level is set at zero and indicated by the green line. (d) Schematic plot of the splitting of Mn d orbitals due to crystal-field splitting (Δcf) and interatomic Hund's exchange (Δex).

The long-range ferromagnetism is mediated by the AFM coupling between the localized Mn 3d states and delocalized S 3p states in monolayer MoS₂.^37,38 It has been predicted that the Curie temperature of Mn-doped monolayer MoS₂ can reach room temperature if the Mn dopant concentration is 10–15%.³⁸ It has been demonstrated by experiments that an inert substrate (i.e., graphene) allows only 2 at% doping of Mn in MoS₂, otherwise it is difficult to retain the 2D morphology.^57,58 To further study the effects of the dopant concentration on magnetic-exchange coupling, two Mn dopants are substitutionally inserted into monolayer MoS₂ and the magnetic-exchange coupling is evaluated by comparing the energies of the FM and AFM states:

ΔE = E_FM − E_AFM, (2)

where E_FM and E_AFM are the energies of the Mn-doped MoS₂ in the FM and AFM states, respectively. The energy of the FM state is less than that of the AFM state when two Mn dopants are close to each other. That is, the FM state is preferred. The magnetic coupling interactions in Mn-doped monolayer MoS₂ are further examined by the spin density distribution (Fig. 4). When two Mn_Mo dopants are separated by a distance less than 16.53 Å (Fig. S2, ESI†), the Mn dopants are highly spin-polarized with the same spin-polarization direction and the nearest neighboring S atoms between two Mn dopants are AFM coupled with the S atoms (Fig. 4a–c). But it is different if the separation between two Mn dopants is increased to 22.05 Å and the energy of the FM state is equal to that of the AFM state (Fig. 4d). The results indicate long-range FM coupling of two Mn dopants in monolayer MoS₂.³⁸ The results are different from those of Co-doped monolayer MoS₂ that is nonmagnetic when the dopants are close to each other.⁵⁹ However, the system becomes magnetic with a magnetic moment of 6.00 μ_B if the two dopants are separated by 5.50 Å. Based on the mean-field approximation (MFA), the Curie temperature (T_C) is estimated from the energy difference between the FM and AFM states with the following equation:where k_B is the Boltzmann constant and n is the number of dopants in a supercell. The estimated T_C is 224 K and lower than room temperature and it is in good agreement with the reported value of ∼200 K obtained by Monte Carlo simulation.³⁷

Fig. 4 Spin-density isosurface distributions for FM and AFM configurations of Mn-doped monolayer MoS₂ with the 2Mn_Mo configuration in (a) 4 × 4, (b) 5 × 5, (c) 6 × 6, and (d) 7 × 7 supercells. The red and green isosurfaces represent the positive and negative spin densities, respectively. The isosurface value is 0.003 e Å⁻³.

3.2 Single Mn dopant in bilayer MoS₂

In 2D materials, surface doping is commonly implemented to manipulate the physical properties, but oxidization and migration may take place on these exposed atoms producing structural and functional instability. It may be overcome if the dopants can be fixed in the interlayer of bilayer MoS₂. The two stacking sequences, AA and AB, exist in bilayer MoS₂. In AA (AB) stacking, the Mo atoms in one layer are on top of the Mo (S) atoms in the other layer (Fig. S3, ESI†). The AB stacking configuration is more stable than the AA one, but both AA and AB stacking configurations are obtained by CVD.⁶⁰ Here, both are considered and two typical interlayer doping sites are considered: (1) dopant just above the hollow site of the hexagonal rings in bilayer MoS₂ (H) and (2) dopant directly under the S atom in the upper layer (S). As shown in Fig. 5a and c, for the Mn dopant at the H site in bilayer MoS₂ with the AA and AB stacking configurations (AA-H and AB-H), the Mn dopant is bonded to three S atoms in each sublayer. For the Mn dopant directly under the S atom in the upper layer of the AA stacking configuration (AA-S), the Mn dopant is bonded to one S atom in the upper sublayer and one S atom in the lower sublayer (Fig. 5b). For the Mn dopant directly under the S atom in the upper layer in the AB configuration (AB-S), the Mn dopant is bonded to one S atom in the upper sublayer and three S atoms in the lower sublayer (Fig. 5d). As shown in Table S2 (ESI†), for the Mn dopant in the AA-H (AA-S) stacking configuration, the interlayer distance decreases (increases) to 3.665 Å (3.872 Å) from the original value of 3.720 Å, whereas the interlayer distance in the AB stacking configuration is between 3.112 Å and 3.121 Å, which is close to the ideal interlayer distance of bilayer MoS₂ (3.110 Å). In the AA-S and AB-S configurations, the bond lengths between the Mn dopant and S atoms are between 2.113 Å and 2.220 Å, which is shorter than that of the covalent Mn–S bond (∼2.37 Å). However, in the AA-H and AB-H configurations, the bond lengths between the Mn dopant and S atoms increase to the range of 2.421–2.563 Å. The interlayer Mn dopant and S atoms of bilayer MoS₂ in all the configurations are covalent bonded. Fig. 6 shows the charge density difference of the Mn-doped bilayer MoS₂ with the AA and AB configurations. The electron density accumulates between the Mn dopants and adjacent S atoms characteristic of covalent bonding.

Fig. 5 Atomic models of a single Mn dopant in bilayer MoS₂ with the (a and b) AA and (c and d) AB stacking configurations.

Fig. 6 Charge density difference of a single Mn dopant in bilayer MoS₂ with the (a and b) AA and (c and d) AB stacking configurations. The red and turquoise isosurfaces represent the gain and depletion of charge density, respectively. The isosurface value is 0.005 e Å⁻³.

Owing to the different doping environments, the AA-H, AA-S, AB-H, and AB-S doping configurations exhibit completely distinct magnetic moments of 5.07 μ_B, 3.03 μ_B, 3.87 μ_B, and 3.00 μ_B, respectively. The overall magnetic moments can be ascribed to spin polarization of excess d electrons on the Mn dopant. Each Mn atom possesses 5 electrons in the 3d orbital. When Mn is doped at the H site in bilayer MoS₂ with both the AA and AB stacking configurations, the interaction between the Mn dopant and S is weak because of the larger bond length. Strong interactions between Mn and S are induced, accompanied by substantial electron transfer from the 4s to 3d states of the Mn dopant if Mn is doped at the S site in bilayer MoS₂ with the AA and AB stacking configurations. This reduces the unpaired electrons and magnetic moment.^40,61

To again investigate magnetic coupling of a single Mn dopant in bilayer MoS₂, the orbital decomposed density of states and splitting of Mn 3d orbitals are presented in Fig. 7. The magnetic moment is sensitive to the doping environment. In the AA-H doping configuration, the trigonal prismatic coordination of S atoms around the Mn dopant is similar to that of the Mn_Mo dopant in monolayer MoS₂, but the bond length between Mn and S atoms is larger and as a result, crystal-field splitting is reduced and Δcf < Δex (Fig. 7b). The magnetism is mainly due to spin polarization around the Mn atom (Fig. 7a and Table S2, ESI†). In spite of some differences in the electronic states, similar results are observed from the AA-S doping configuration (Fig. 7c and d). The octahedral and tetrahedral coordination of S atoms around the Mn dopant exist in the AB-H and AB-S doping configurations. The bond length between Mn and S atoms is equal and the antibonding states e₁ and e₂ have the same energy, so that crystal-field splitting disappears (Fig. 7e–h). Similar to the Mn doped bilayer MoS₂, the doping environment dependent electronic states of Cr, Fe, and Co in bilayer MoS₂ are also observed (Fig. S4–S6, ESI†).⁶¹

Fig. 7 Orbital decomposed density of states and splitting of 3d orbitals in a single Mn dopant in bilayer MoS₂ with the (a, b and c, d) AA and (e, f and g, h) AB stacking configurations.

3.3 Double Mn dopants in bilayer MoS₂

The structural and magnetic properties of the 4 × 4 supercell in bilayer MoS₂ are investigated by considering six doping configurations (Fig. 8a): (i) an intercalated Mn atom (Mn_i) and Mn_Mo dopant (Mn_iMn_Mo), (ii) an intercalated Mn atom (Mn_i) and Mn_S dopant (Mn_iMn_S), (iii) two intercalated Mn atoms (Mn_iMn_i), (iv) two Mn_Mo dopants in different sublayers (Mn_Mo–Mn_Mo), (v) two Mn_S dopants in different sublayers (Mn_S–Mn_S), and (vi) Mn_Mo and Mn_S dopants in different sublayers (Mn_Mo–Mn_S). Fig. 8b shows the formation energies of the six doping configurations as a function of chemical potentials. It can be seen that Mn_iMn_S is the most stable doping configuration under the Mo-rich condition (Δμ_S < −1.024 eV), but Mn_Mo–Mn_Mo becomes the most stable one in the S-rich regime (Δμ_S > −0.75 eV) and Mn_iMn_Mo and Mn_Mo–Mn_S are stable if Δμ_S is in the range between −1.024 and −0.812 eV. The doping configurations of Mn_iMn_i, and Mn_S–Mn_S are energetically unfavorable. Although experimental results demonstrate that S vacancies are energetically favorable in most cases,^49,62,63 Mn dopants prefer to substitutionally replace Mo under the S-rich condition and the Mn_Mo–Mn_Mo doping configurations can be obtained more easily. The results are different from the recently reported results in which the Fe_MoFe_i doping configuration is observed to be stable under the S-rich condition.⁴⁰

Fig. 8 (a) Atomic models and (b) formation energy of two Mn dopants in bilayer MoS₂.

The magnetic ground states of the stable doping configurations are evaluated according to eqn (2). The calculated ΔE values are −823, 42, −241 and 5 meV for the Mn_iMn_Mo, Mn_iMn_S, Mn_Mo–Mn_Mo, and Mn_Mo–Mn_S doping configurations, respectively. Consequently, the Mn_iMn_Mo and Mn_Mo–Mn_Mo doping configurations should exhibit the FM state, whereas the Mn_iMn_S and Mn_Mo–Mn_S doping configurations should have the AFM state. However, it is hard to obtain the Mn_iMn_Mo and Mn_MoMn_S doping configurations in bilayer MoS₂ due to the small stable region of the chemical potential. Fig. 9 shows the spin density (ρ↑–ρ↓) distribution in the bilayer MoS₂ with the Mn_iMn_Mo, Mn_iMn_S, Mn_Mo–Mn_Mo, and Mn_Mo–Mn_S doping configurations. In bilayer MoS₂ with the Mn_iMn_Mo doping configuration, the two Mn dopants exhibit double-exchange coupling and the same spin polarization direction. Moreover, the Mn dopants are AFM coupled with the nearest neighboring S atoms (Fig. 9a), which is similar to the case of monolayer MoS₂ with FM coupling. In bilayer MoS₂ with the Mn_iMn_S doping configuration, direct chemical bonding and exchange coupling take place between the two Mn dopants with opposite spin polarization resulting in the AFM state. Although two Mn dopants in bilayer MoS₂ with the Mn_Mo–Mn_S doping configuration also have the opposite polarization direction, the magnetic exchange coupling is different from that in bilayer MoS₂ with the Mn_iMn_S doping configuration, and super-exchange coupling takes place between the two Mn atoms with opposite spin polarization (Fig. 9d). Owing to AFM coupling between the Mn dopants, bilayer MoS₂ with the Mn_iMn_S and Mn_S–Mn_S doping configurations possesses negligible magnetism. Meanwhile, the opposite polarization of the Mn dopant and nearest neighboring Mo atoms or S atoms leads to AFM coupling. In bilayer MoS₂ with the Mn_Mo–Mn_Mo doping configuration, the distance between two Mn dopants is 6.788 Å which is so large that the interaction between them is weak and they are independent. Hence, the result is the same as that of the Mn-doped monolayer MoS₂. The estimated T_C of bilayer MoS₂ with the Mn_Mo–Mn_Mo doping configuration is 931 K and well above room temperature. Therefore, room-temperature ferromagnetism is expected from bilayer MoS₂ with different Mn doping configurations spurring potential application in spintronic devices.

Fig. 9 Spin-density isosurface distributions of two Mn dopants in bilayer MoS₂ with different doping configurations: (a) Mn_iMn_Mo, (b) Mn_iMn_S, (c) Mn_Mo–Mn_Mo, and (d) Mn_Mo–Mn_S. The red and green isosurfaces represent the positive and negative spin densities, respectively, and the isosurface value is 0.02 e Å⁻³.

The results indicate that the Mn_Mo doping configuration is energetically stable in the S-rich regime of the MoS₂ nanosheet, while the Mn_iMn_S doping configuration is more favorable in the S-deficient environment. The S-rich environment is generally adopted to synthesize MoS₂ nanosheets. Thus, the Mn_Mo doping configuration is energetically favorable in Mn-doped MoS₂ and similar behaviors occur in Fe-, Cr-, V-, and Nb-doped MoS₂ nanosheets.^52,53 For instance, in the Fe-doped MoS₂ layered crystals prepared by the chemical vapor transport method, the replacement of Mo by Fe takes place in the S-rich regime, while the replacement of S by Fe takes place under the Mo-rich condition.⁴⁰ However, Pt atoms are preferentially localized at S vacancies and usually hop to the nearby surface layers,⁵⁴ and Au atoms are preferentially on the top of S, Mo, and hollow sites of MoS₂.⁵¹ Additionally, Co adsorption on the Mo site was evidenced from the high angle annular dark field image, which is confirmed as the energetically favourable geometry by density functional theory calculations.

So far, a large number of theoretical studies have been done to explore the stable magnetism in TM-doped MoS₂ nanosheets. However, they mainly focused on studying the influences of a single dopant on the magnetic properties of MoS₂ nanosheets and the magnetic-exchange coupling among dopants is commonly ignored. In fact, the magnetic properties are sensitive to magnetic-exchange coupling among dopants in the host materials. Shu et al.⁴⁰ showed that the layer number is crucial in controlling the magnetic properties of Fe-doped MoS₂, that is, FM coupling occurs in Fe-doped monolayer MoS₂, but AFM coupling in Fe-doped bi- and trilayer MoS₂. The direct and mediated bonding interactions between the intercalated and substitutional Fe dopants follow the superexchange mechanism. As for Mn-doped MoS₂ nanosheets in this work, it is found that the doping sites are crucial in controlling the magnetic properties. Particularly, AFM coupling takes place in monolayer MoS₂ with Mn_Mo–Mn_S or Mn_iMn_S doping configurations, and otherwise, FM coupling occurs in the Mn_Mo–Mn_Mo or Mn_iMn_Mo doping configurations. Since the doping sites depend on the synthesis conditions, the precise control of doping sites is required to generate ferromagnetism.

4. Conclusion

The structural stability, electronic states, and magnetic properties of Mn-doped monolayer/bilayer MoS₂ are studied by first-principles calculations. The structural stability of Mn-doped MoS₂ depends on the chemical potential and layer number. In the S-rich environment, Mn replacement of Mo in monolayer MoS₂ (Mn_Mo) is stable but in the S-deficient environment, the Mn_iMn_S doping configuration is more favorable in bilayer MoS₂. Mn dopants lead to FM coupling in monolayer MoS₂ and magnetic coupling of Mn dopants via the double-exchange mechanism can be mediated by the nearest neighboring S. In bilayer MoS₂, the magnetic-exchange coupling is related to the competition between the double-exchange, direct-exchange, and super-exchange interactions. Specifically, in the Mn_iMn_Mo doping configuration, double-exchange coupling takes place between the two Mn dopants and it is the same as that of the Mn-doped monolayer MoS₂ with FM coupling. Although the two Mn dopants have opposite spin polarization, the magnetic-exchange mechanisms of the Mn_iMn_S and Mn_Mo–Mn_S doping configurations are different. The findings provide insights into the development of intrinsic diluted magnetic semiconductors based on 2D MoS₂ nanosheets.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was jointly supported by the National Natural Science Foundation of China (Grant No. 51471130, 51771144, 51501012), the Natural Science Foundation of Shaanxi Province (No. 2017JZ015), Fund of the State Key Laboratory of Solidification Processing in NWPU (SKLSP201708), Fundamental Research Funds for the Central Universities, City University of Hong Kong Applied Research Grant (ARG) No. 9667122, as well as City University of Hong Kong Strategic Research Grant (SRG) No. 7004644. This work was carried out at the HPCC Platform in Xian Jiaotong University.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, S. C. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197.
4. Y. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
5. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451.
6. C. Lee, Q. Li, W. Kalb, X.-Z. Liu, H. Berger, R. W. Carpick and J. Hone, Science, 2010, 328, 76.
7. A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
8. A. K. Geim, Science, 2009, 324, 1530.
9. S. Park and R. S. Ruoff, Nat. Nanotechnol., 2009, 4, 217.
10. B. W. H. Baugher, H. O. H. Churchill, Y. Yang and P. J. Herrero, Nat. Nanotechnol., 2014, 9, 262.
11. A. Pospischil, M. M. Furchi and T. Mueller, Nat. Nanotechnol., 2014, 9, 257.
12. O. Lopez-Sanchez, D. Lembke, M. Kayci, A. Radenovic and A. Kis, Nat. Nanotechnol., 2013, 8, 497.
13. J. Xia, X. Huang, L. Z. Liu, M. Wang, L. Wang, B. Huang, D. D. Zhu, J. J. Li, C. Z. Gu and X. M. Meng, Nanoscale, 2014, 6, 8949.
14. W. Zhang, C. P. Chu, J. K. Huang, C. H. Chen, M. L. Tsai, Y. H. Chang, C. T. Liang, Y. Z. Chen, Y. L. Chueh and J. H. He, Sci. Rep., 2014, 4, 3826.
15. H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232.
16. A. B. Laursen, S. Kegnæs, S. Dahl and I. Chorkendorff, Energy Environ. Sci., 2012, 5, 5577.
17. B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147.
18. J. S. Ross, P. Klement, A. M. Jones, N. J. Ghimire, J. Yan, D. G. Mandrus, T. Taniguchi, K. Watanabe, K. Kitamura, W. Yao, H. C. David and X. D. Xu, Nat. Nanotechnol., 2014, 9, 268.
19. H. Hwang, H. Kim and J. Cho, Nano Lett., 2011, 11, 4826.
20. X. Zhao, C. M. Hayner, M. C. Kung and H. H. Kung, ACS Nano, 2011, 5, 8739.
21. J. Cabana, L. Monconduit, D. Larcher and M. R. Palacin, Adv. Mater., 2010, 22, E170.
22. M. Chhowalla, H. S. Shin, G. Eda, L. J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263.
23. H. S. Lee, S.-W. Min and S. Im, Nano Lett., 2012, 12, 3695.
24. R. S. Sundaram, M. Engel, A. Lombardo, R. Krupke, A. C. Ferrari, P. Avouris and M. Steiner, Nano Lett., 2013, 13, 1416.
25. K. F. Mak, K. L. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494.
26. D. Xiao, G. B. Liu, W. X. Feng, X. D. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802.
27. Z. Y. Zhu, Y. C. Cheng and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 153402.
28. Y. Ohno, R. Terauchi, T. Adachi, F. Matsukura and H. Ohno, Phys. Rev. Lett., 1999, 83, 4196.
29. Q. Chen, X. Ouyang, S. Yuan, R. Li and J. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 16835.
30. S. Y. Wang, T. S. Ko, C. C. Huang, D. Y. Lin and Y. S. Huang, Jpn. J. Appl. Phys., 2014, 53, 04EH07.
31. A. N. Andriotis and M. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125304.
32. W. S. Yun and J. D. Lee, Phys. Chem. Chem. Phys., 2014, 16, 8990.
33. H.-P. Komsa, N. Berseneva, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. X, 2014, 4, 031044.
34. M. Kan, S. Adhikari and Q. Sun, Phys. Chem. Chem. Phys., 2014, 16, 4990.
35. Q. Yue, S. Chang, S. Qin and J. Lin, Phys. Lett. A, 2013, 377, 1362.
36. Y. C. Chen, Z. Y. Zhu, W. B. Mi, Z. B. Guo and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 100401(R).
37. A. Ramasubramaniam and D. Naveh, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195201.
38. R. Mishra, W. Zhou, S. J. Pennycook, S. T. Pantelides and J.-C. Idrobo, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 144409.
39. Y. R. Wang, S. Li and J. B. Yi, Sci. Rep., 2016, 6, 24153.
40. H. B. Shu, P. F. Luo, P. Liang, D. Cao and X. S. Chen, ACS Appl. Mater. Interfaces, 2015, 7, 7534.
41. M. Zhang, Z. J. Huang, X. Wang, H. Y. Zhang, T. H. Li, Z. L. Wu, Y. H. Luo and W. Cao, Sci. Rep., 2016, 6, 19504.
42. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
43. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
44. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
46. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
47. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653.
48. Y. Wang, S. S. Wang, Y. H. Lu, J. Z. Jiang and S. Y. A. Yang, Nano Lett., 2016, 16, 4576.
49. W. Zhou, X. L. Zou, S. Najmaei, Z. Liu, Y. M. Shi, J. Kong, J. Luo, P. M. Ajayan, B. I. Yakobson and J.-C. Idrobo, Nano Lett., 2013, 13, 2615.
50. B. Li, L. Huang, M. Z. Zhong, N. J. Huo, Y. T. Li, S. X. Yang, C. Fan, J. H. Yang, W. P. Hu, Z. M. Wei and J. B. Li, ACS Nano, 2015, 9, 1257.
51. G. L. Liu, A. W. Robertson, M. M.-J. Li, W. C. H. Kuo, M. T. Darby, M. H. Muhieddine, Y. C. Lin, K. Suenaga, M. Stamatakis, J. H. Warner and S. C. E. Tsang, Nat. Chem., 2017, 9, 810.
52. Y. C. Lin, D. O. Dumcenco, H. P. Komsa, Y. Niimi, A. V. Krasheninnikov, Y. S. Huang and K. Suenaga, Adv. Mater., 2014, 26, 2857.
53. A. W. Robertson, Y. C. Lin, S. S. Wang, H. Sawada, C. S. Allen, Q. Chen, S. Lee, G. D. Lee, J. Lee, S. Han, E. Yoon, A. I. Kirkland, H. Kim, K. Suenaga and J. H. Warner, ACS Nano, 2016, 10, 10227.
54. J. Suh, T.-E. Park, D. Y. Lin, D. Fu, J. Park, H. J. Jung, Y. B. Chen, C. Ko, C. Jang, Y. H. Sun, R. Sinclair, J. Chang, S. Tongay and J. Q. Wu, Nano Lett., 2014, 14, 6976.
55. H. S. Li, S. S. Wang, H. Sawada, G. G. D. Han, T. Samuels, C. S. Allen, A. I. Kirkland, J. C. Grossman and J. H. Waener, ACS Nano, 2017, 11, 3392.
56. J. Gao, Y. D. Kim, L. B. Liang, J. C. Idrobo, P. Chow, J. W. Tan, B. C. Li, L. Li, B. G. Sumpter, T.-M. Lu, V. Meunier, J. Hone and N. Koratkar, Adv. Mater., 2016, 28, 9735.
57. K. H. Zhang, S. Feng, J. J. Wang, A. Azcatl, N. Lu, R. Addou, N. Wang, C. J. Zhou, J. Lerach, V. Bojan, M. J. Kim, L. Q. Chen, R. M. Wallace, M. Terrones, J. Zhu and J. A. Robinson, Nano Lett., 2015, 15, 6586.
58. H. Tan, W. Hu, C. Wang, C. Ma, H. L. Duan, W. S. Yan, L. Cai, P. Guo, Z. H. Sun, Q. H. Liu, L. Cai, P. Guo, Z. H. Sun, Q. H. Liu, X. S. Zheng, F. C. Hu and S. Q. Wei, Small, 2017, 340, 1701389.
59. Y. R. Wang, S. A. Li and J. B. Yi, Sci. Rep., 2016, 6, 24153.
60. J. X. Yan, J. Xia, X. L. Wang, L. Liu, J. L. Kuo, B. K. Tay, S. S. Chen, W. Zhou, Z. Liu and Z. X. Shen, Nano Lett., 2015, 15, 8155.
61. Z. Y. Huang, X. Y. Peng, H. Yang, C. Y. He, L. Xue, G. L. Hao, C. X. Zhang, W. L. Liu, X. Qi and J. X. Zhong, RSC Adv., 2013, 3, 12939.
62. A. M. Van der Zande, P. Y. Huang, D. A. Chenet, T. C. Berkelbach, Y. M. You, G.-H. Lee, T. F. Heinz, D. R. Reichman, D. A. Muller and J. C. Hone, Nat. Mater., 2013, 12, 554.
63. S. Najmaei, Z. Liu, W. Zhou, X. Zou, G. Shi, S. Lei, B. I. Yakobson, J.-C. Idrobo, P. M. Ajayan and J. Lou, Nat. Mater., 2013, 12, 754.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05988d

---