Exploring the solid state phase transition in DL-norvaline with terahertz spectroscopy†
Jens
Neu
 *,
Coleen T.
Nemes
*,
Coleen T.
Nemes
 ,
Kevin P.
Regan
,
Kevin P.
Regan
 ,
Michael R. C.
Williams‡
and
Charles A.
Schmuttenmaer
,
Michael R. C.
Williams‡
and
Charles A.
Schmuttenmaer
 *
*
Department of Chemistry, Yale University, PO Box 208107, 225 Prospect St., New Haven, CT 06520-8107, USA. E-mail: jens.neu@yale.edu; charles.schmuttenmaer@yale.edu
First published on 29th November 2017
Abstract
DL-Norvaline is a molecular crystal at room temperature and it undergoes a phase transition when cooled below 190 K. This phase transition is believed to be Martensitic, thus making it of particular interest for molecular machines. In this paper we investigate this phase transition by measuring its terahertz (THz) spectrum over a range of temperatures. Temperature-dependent THz time-domain spectroscopy (THz-TDS) measurements reveal that the transition temperature (Tβ→α) is 190 K. The influence of nucleation seeds was analyzed by determining the Tβ→α of molecular crystals with varying grain size. Grains of 5 μm or less result in a lower transition temperature (Tβ→α = 180 K) compared to larger grains of 125–250 μm (Tβ→α = 190 K). Additionally, we gain insight into the physical process of the phase transition via temperature-dependent THz-TDS spectra of doped and mixed molecular crystals. The addition of molecular dopants, which differ from DL-norvaline only at the end of the side chain which resides in the hydrophobic layers of the crystal, decreases Tβ→α. This is consistent with a solid–solid phase transition in which the unit cell shifts along this hydrophobic layer, and it leads us to believe that the phase transition in DL-norvaline is Martensitic in nature.
1 Introduction and motivation
Most of the proteinogenic amino acids exhibit crystalline forms in the solid state. The same is also true for other non-proteinogenic α-amino acids such as norvaline (COOHCHNH2CH2CH2CH3). In many cases, multiple crystalline solid phases, each with a unique geometry and distinct physical properties, have been identified for a given material. Polymorphism occurs when different crystalline phases (polymorphs) of the same material are thermodynamically accessible.1–4 Previous studies have observed phase transitions between different polymorphs of various amino acids as a function of temperature or pressure.5–9 In other amino acids, multiple polymorphs have been found to exist at the same temperature and pressure.10–12 This is possible because specific crystallization conditions may favor the formation of metastable polymorphs, which are structures representing local, not global, thermodynamic free energy minima at a given temperature and pressure.Typically, solid–solid phase transitions in molecular crystals (i.e. from one polymorph to another) are understood to take place via a nucleation and growth mechanism.13–15 In this model, a small nucleus of a new crystalline phase is first formed at a defect site in the original lattice phase. The growth of the new phase proceeds as molecules from the original phase break out of their lattice position and find a place in the new lattice. This rearrangement is linked with a diffusion of molecules in the newly forming lattice. In general, there is no definite relationship between the orientation of the original lattice and the new lattice since the orientation of the new phase's initial nucleus is random or at least highly idiosyncratic.
In rare cases, the transition between two polymorphs is thought to take place via a concerted, diffusion-free mechanism, known as a Martensitic or displacive phase transition.16–19 The resulting process does not cause a randomized reorganization of the lattice, and therefore the lattice exhibits a memory effect.20 Molecular systems that undergo these concerted phase changes are of particular interest for the understanding and design of molecular machines.21 Unlike typical solid–solid phase transitions, the concerted motion of a displacive phase transition results in a net force on a microscopic length scale. Therefore, progress towards observing, tuning, or triggering these phase transitions has applications in nanoscale engineering.22,23
A standard method of studying solid–solid phase transitions is temperature-dependent X-ray diffraction, which provides essential information about a molecular crystal's time-averaged geometrical structure. However, since motion is the characteristic property of displacive phase transitions, it is naturally desirable to complement structural information with dynamical information. For this application, terahertz time-domain spectroscopy (THz-TDS),24–29 which allows detection of infrared-active vibrations in the low frequency far-infrared range (typically 10–200 cm−1, and 1 THz = 33.34 cm−1) is a promising tool. Most importantly, vibrations in this frequency range can be significantly intermolecular in character12,30 and are therefore extremely sensitive to the arrangement and orientation of molecules in the crystal lattice.11,31–33 As a result, THz-TDS measurements can easily distinguish among different polymorphs. Furthermore, an understanding of the specific vibrational motion of the molecules at these low frequencies may provide insight into the mechanism by which a concerted phase change occurs.
2 Experimental setup and sample preparation
2.1 Sample preparation
DL-Norvaline was purchased from Alfa Aesar (purity 98%) and used without further purification. The dopant amino acids, which are listed in the ESI† (Sigma Aldrich, purity 99%), were also used without further purification. 100 mL solutions containing pure DL-norvaline (1.7 g) and 12% per mole of the impurity were prepared. The mixtures slowly evaporated at 40 °C resulting in crystals with sub-millimeter dimensions. The crystallites were characterized with powder XRD at room temperature (Rigaku SmartLab X-ray Diffractometer, see ESI†). The crystallized materials were ball-milled for 3 min resulting in a homogeneous powder containing grains less than 5 μm in size.The samples used in this study are pressed pellets of a mixture of PTFE (Teflon, purchased from ChemCruz) and a small amount of amino acid (typically ≈25 mg amino acid in ≈1000 mg Teflon, see Table S1 in the ESI†). The amino acid crystallites are either pure DL-norvaline, or DL-norvaline crystallized from a mixed solution with the dopant. The mixtures were then pressed with an applied pressure of 11 kbar, and the resulting pellets have a diameter of 13 mm and were approximately d ≈ 3.3 mm thick. Reference samples of pure Teflon were pressed under the same conditions.
Teflon-mixed pellets have several advantages over pure amino acid pellets. Thicker samples can be prepared due to the low absorption of Teflon in the THz range. Thicker samples have the advantage of being less fragile and easier to handle, and they also allow one to remove etalon effects in the THz spectrum via truncation of the time-domain measurement. In addition, the fraction of amino acid in the Teflon host material can be optimized such that the absorption features are not saturated.
2.2 Experimental setup
Spectra were measured in a THz-TDS spectrometer as described in a previous publication.12 For temperature controlled measurements, the samples were mounted in a sample-in-vapor cryostat cooled with nitrogen gas, which allows measurements from room temperature down to 78 K. The cryostat was cooled in either 10 K or 5 K increments using an adjustable nitrogen flow and resistive-heaters. The sample was allowed to reach thermal equilibrium prior to each measurement. To avoid contamination of the sample, a temperature sensor was not placed directly on the sample, but rather above and below it. The average of both temperature sensors provides an accurate approximation of the sample's temperature (±0.5 K). THz-TDS measures the amplitude of the transmitted THz pulse rather than its intensity. Thus, Fourier transformation of the measured time domain traces provides information on both the spectral amplitude and phase of the measured electric field. Given phase and amplitude information of the THz pulse, the real (n′) and imaginary (n′′) parts of the complex-valued refractive index can be obtained directly.| t(ω) = t12(ω)·p2(ω)·t21(ω) | (1) |
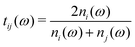 is the Fresnel amplitude transmission coefficient from medium i to medium j, p2 = eik0dn2 is the propagation operator through the sample (medium 2) where k0 = (ω/c) is the wave-vector in vacuum, and d the sample thickness. In the present case, the THz pulse enters the sample from air (n1 = 1), propagates through the sample, and then exits at the sample–air interface. The pellets are d > 3 mm thick, which corresponds to more than 30 ps for the doubly-reflected pulse to emerge. Therefore, a measurement time duration of 28 ps was chosen in order to avoid multiple pulses, and thus eliminate etalon effects in the complex transmission function.
is the Fresnel amplitude transmission coefficient from medium i to medium j, p2 = eik0dn2 is the propagation operator through the sample (medium 2) where k0 = (ω/c) is the wave-vector in vacuum, and d the sample thickness. In the present case, the THz pulse enters the sample from air (n1 = 1), propagates through the sample, and then exits at the sample–air interface. The pellets are d > 3 mm thick, which corresponds to more than 30 ps for the doubly-reflected pulse to emerge. Therefore, a measurement time duration of 28 ps was chosen in order to avoid multiple pulses, and thus eliminate etalon effects in the complex transmission function.
The measured transmission through the sample is complex-valued and can therefore be separated into an amplitude and phase term. This allows us to rewrite eqn (1) as:
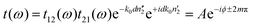 | (2) |
Effective medium theory is used to calculate the index for the amino acid. The well-known Bruggeman equation36 relates the measured permittivity of a mixture (εm) to the permittivity of the two components (εh for Teflon host, and εi for amino acid inclusions):
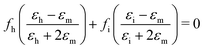 | (3) |
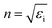 , and the absorption coefficient is determined from the imaginary part:
, and the absorption coefficient is determined from the imaginary part: 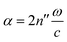 .
.
2.3 DFT calculations of DL-norvaline
Calculations of the optimized structure and vibrational modes of DL-norvaline were carried out using the SIESTA DFT software package (3.2 revision 462). We employed the vdW-DF-cx functional,37 which is based on a generalized gradient approximation (GGA) level exchange–correlation functional, which also accounts for van der Waals forces using the Lundqvist–Langreth nonlocal density–density interaction framework.38 Typical GGA or meta-GGA exchange–correlation functionals are capable of modeling only local or semi-local forces, and this is inadequate for modeling a system with regions dominated by hydrophobic interactions, and therefore van der Waals (dispersion) forces, such as DL-norvaline. These DFT calculations incorporate vdW-DF functionals that do not require empirical correction terms. In particular, the vDW-DF-cx functional aims to be nonempirical and to use the vdW-DF scheme to calculate both correlation and exchange terms in a self-consistent way.37SIESTA uses periodic boundary conditions, and the basis set consists of numerical atomic orbitals. We used a triple-zeta, doubly polarized (TZDP) basis set. Minimum energy structures were obtained by optimizing the initial coordinates and lattice cell parameters obtained by XRD measurements of single crystals.39 The atomic positions and unit cell parameters were simultaneously optimized to minimize interatomic forces and unit cell stress. Details of calculating vibrational frequencies and IR intensities have been previously reported.12 Briefly, harmonic modes were calculated using the force-constant matrix40 determined by displacing each atom 0.02 Å in each direction along the Cartesian axes. For IR intensities, the Berry phase approach was used to calculate macroscopic polarization,41 which was then used to calculate the Born effective charge tensor of each atom.40 The Born effective charge tensor of each atom was then used to calculate the IR intensity of each mode.12,41
3 Experimental results
3.1 Pure DL-norvaline
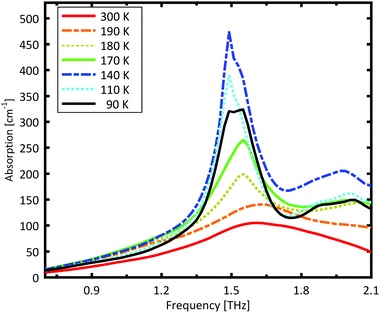
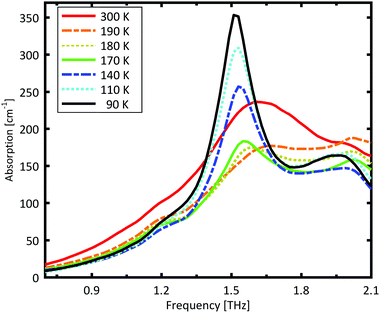
A Teflon/DL-norvaline pellet was cooled in 10 K increments. At selected temperatures, the transmission though the sample pellet was measured along with the transmission through an identical aperture without a sample (the reference). The absorption spectra, calculated from these measurements, are plotted in Fig. 1. For temperatures higher than 180 K, the samples show a broad, weak absorption with a central-frequency of 1.65 THz and full width at half maximum (FWHM) of about 0.8 THz. The THz transmission spectrum changes fundamentally as the sample is cooled from 190 K to 180 K. A strong and narrow peak emerges at 1.55 THz with a FWHM of 0.26 THz. THz measurements are sensitive to collective vibrational and rotational/librational modes in the crystal lattice. In general, these modes are narrower and more pronounced at lower temperatures.31 The distinct change in the absorption mode seen here, and in particular the red-shift of the peak with decreasing temperature, cannot be explained merely by thermal shrinkage of the lattice. Such a significant change in the transmission spectrum can only be explained by a similarly significant change of the lattice, which is a solid–solid phase transition that occurs between 190 K and 180 K and has also been observed in single crystal XRD measurements.39The absorption spectrum continues to change as the temperature is decreased from 180 K to 140 K. The absorption strength increases, and the characteristic feature becomes narrower. For temperatures below 140 K, however, the absorption decreases with decreasing temperature, and this also cannot be explained by a simple contraction of the lattice. Although the change in the absorption spectrum is more subtle than that between 190 K and 180 K, it indicates a second solid–solid phase transition. The phase transition between 190 K and 180 K is reversible, but the one starting at around 140 K is irreversible. This is in agreement with delamination in DL-norvaline observed at these lower temperatures.39
3.2 Comparison of calculated and measured THz spectra
The frequencies and IR intensities at 0 K were calculated after optimizing the atomic coordinates determined crystallographically at −90 °C (183 K).39 In accordance with previous studies42 the D and L enantiomers alternate along the c axis, and are identical along the a and b axes.39 For the low temperature α phase, norvaline molecules adopt two conformations, denoted A and B, where A had an abundance of 51.5%.39 The side chain can adopt trans and gauche conformations upon rotation around the Cα–Cβ and Cβ–Cγ bonds. The A conformer of the α phase is trans, gauche+, and the B conformer is trans, trans.39 The reported single crystal X-ray diffraction data (CCSD zzzodu02) does not determine which molecule in the unit cell is the A conformer and which is B.39Fig. 2 shows the optimized geometry of a 4-molecule unit cell where A–B neighbors are along the a axis, A–A and B–B neighbors are along the c axis, and A–A and B–B neighbors are along the b axis. We denote each type of unit cell by the sequence of conformer type in positions 1–2–3–4. For example, Fig. 2 displays the AABB unit cell. We note that the structural optimization does not result in conformational changes of the molecules. Unit cell calculations included all six possible conformer configurations with a 50% abundance of each conformer: AABB, BBAA, ABBA, BAAB, ABAB, and BABA. The results of these calculation are presented in Table 1.
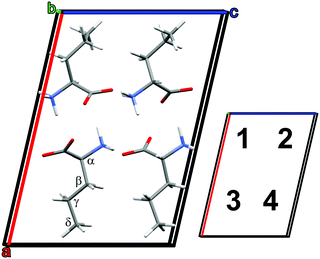 | ||
| Fig. 2 Optimized DL-norvaline unit cell with conformer configuration AABB. Molecules in positions 1 and 3 are L, and those in positions 2 and 4 are D. | ||
| Geometry/label | zzzodu01 | AABB | BBAA | ABBA | BAAB | ABAB | BABA |
|---|---|---|---|---|---|---|---|
| a [Å] | 14.21 | 14.27 | 14.27 | 14.54 | 14.53 | 13.91 | 13.91 |
| b [Å] | 4.76 | 4.86 | 4.86 | 4.88 | 4.88 | 4.87 | 4.87 |
| c [Å] | 9.86 | 9.84 | 9.84 | 9.80 | 9.80 | 8.82 | 9.82 |
| α [°] | 90 | 90 | 90 | 89.66 | 90.35 | 90 | 90 |
| β [°] | 102.85 | 102.93 | 102.95 | 102.83 | 102.83 | 102.22 | 102.17 |
| γ [°] | 90 | 90 | 90 | 92.55 | 87.53 | 90 | 90 |
| Volume [Å3] | 649.81 | 665 | 665.41 | 677.19 | 676.90 | 650.42 | 650.41 |
| Energy [eV] | −8360.06 | −8360.06 | −8360.03 | −8360.03 | −8360.16 | −8360.16 |
The initially monoclinic symmetry of the unit cell is broken during the optimization of the ABBA and BAAB configurations, and their minimum energy calculated structures are triclinic. Furthermore, these configurations deviate strongly from the previously reported geometry. The a axis is significantly longer in the calculation than in previously reported crystallographic data. Therefore, we conclude that these two conformer combinations are less likely. The remaining four unit cells (ABAB, BABA, AABB, BBAA) all optimized to axes length within ±2% of the reported crystallographic dimensions. This slight discrepancy between the calculation and previous crystallographic results is to be expected, because the crystallographic structure is determined at 183 K, while the calculation is at 0 K. The final unit cell energy of the ABAB conformer is the lowest, hence the most favorable. However, the energetic difference of 0.13 eV (3.0 kcal mol−1) is not large enough to rule out the remaining three unit cells.
The IR spectrum for all six unit cells is calculated and plotted in the ESI† (Fig. S1 and S2). The calculated spectra all exhibit a resonance around 1.5 THz, in agreement with our experimental results. To better understand the effect of conformer configuration on the calculated spectrum, we performed a mode character analysis, in which intermolecular and intramolecular contributions of each mode are quantified.31 As seen in the Fig. S3 (ESI†), modes across different conformer configurations can be grouped according to similar frequency, intensity, and mode character. The intense peaks in the 1.4 THz to 1.75 THz range are mostly rotational/librational in character (blue and green squares), while those in the 2.0 THz to 2.4 THz range have equal contributions from rotational/librational and intramolecular motions with almost no translational character (yellow squares). In general, greater similarities are observed for conformer configurations with similar optimized unit cell parameters, for example AABB and BBAA.
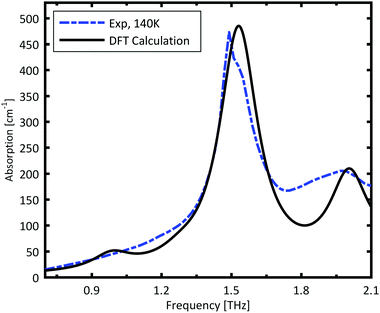
The spectrum calculated for the ABAB conformer combination, is plotted in Fig. 3. The calculated resonances are convoluted with a Lorentzian function with FWHM of 0.2 THz to mimic the experimental line width. The strong peak is very well reproduced by the calculations. The broad minor peak close to 2 THz is also reasonably well reproduced.
3.3 Grain size dependence
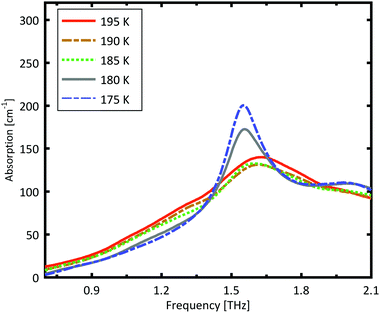
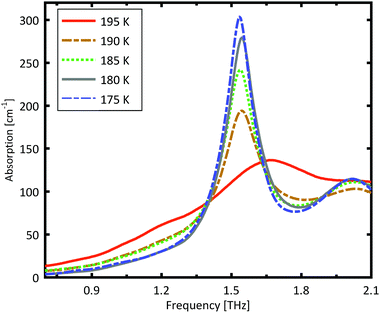
A more detailed investigation of the phase change between 190 K and 180 K can be performed by measuring the phase transition of DL-norvaline/Teflon pellets with differing DL-norvaline grain sizes. If we assume that the defect and impurity density is independent of grain size, smaller grains will contain fewer defects and impurities. These impurities and defects act as nucleation points for phase transitions. This holds true for both the nucleation and growth as well as Martensitic mechanisms of phase transitions.17,43,44 A larger total number of impurities/defects will disturb the ideal lattice to a greater extent, and the energy barrier for a phase transition will be lower.We measured THz spectra of samples with two different grain sizes to investigate this. The first sample contained crystals that were ball-milled for 3 min to produce grains smaller than s = 5 μm in diameter. For the second sample, the grains where ground using a mortar and pestle and sorted by size using a micro sieve. Grain diameters of this second sample ranged from 125 μm to 250 μm.
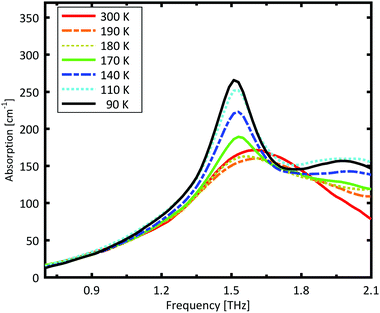
The results for the ball-milled sample are plotted in Fig. 4. A temperature step size of 5 K ± 0.5 K was chosen to more accurately determine the phase transition temperature. When the sample was cooled from 185 K to 180 K, the absorption profile changed abruptly. Measurements performed on the larger grains are plotted in Fig. 5. A clear change in the spectrum is visible when the sample is cooled from 195 K to 190 K, which is 10 K higher than for the micro-grain sample in Fig. 4. The only difference in these samples is their grain size, and therefore the total number of imperfections and defects per grain. The larger grains have an about 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times larger volume, and under the assumption of a constant imperfection density, the probability of having an imperfection is 50
000 times larger volume, and under the assumption of a constant imperfection density, the probability of having an imperfection is 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times higher. The resulting 10 K difference in phase transition temperature suggests that these imperfections are important as starting points for the phase transition, which is in agreement with a Martinsitic phase transition mechanism, but does not rule out nucleation and growth.
000 times higher. The resulting 10 K difference in phase transition temperature suggests that these imperfections are important as starting points for the phase transition, which is in agreement with a Martinsitic phase transition mechanism, but does not rule out nucleation and growth.
A comparison of the two different grain sizes also reveals that the high temperature absorption coefficient of both samples is α = 145 ± 15 cm−1, however the low temperature absorption at 175 K is different. It is α = 210 ± 15 cm−1 for the small grain size, while it is α = 310 ± 15 cm−1 for the larger ones. This indicates that possibly not all grains in the micro granular sample have converted to the low temperature phase, even through 175 K is more than 15 K colder than the phase transition temperature measured for the larger grains.
3.4 Mixed amino acid crystals
A more detailed understanding of the origin of the resonant absorption and the phase transition can be gained by measuring doped DL-norvaline crystals. The molecular dopants have similar geometries and chemical properties as the host material. A concentration of 12 mol% dopants in solution was chosen. This high concentration ensures that enough material for the crystallization process is present to form not only doped crystals but also mixed crystals.45 In general, three different types of crystal can result from this mixing. The first case is that the two amino acids form two pure crystals that are commingled. The PXRD of this crystal would be a simple linear combination of the pure amino acids. This case has not be detected. The second case would be a formation of a doped crystal, that is, where 12% of the original lattice molecules are replaced by the dopant. The third case would be the formation of a different type of mixed crystal that has regions of pure DL-norvaline crystals and other regions of crystals formed by 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 or 75
50 or 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 mixtures in the unit cell.
25 mixtures in the unit cell.
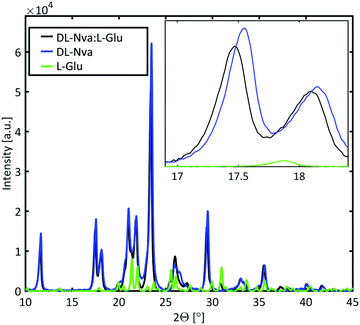
Powder X-ray diffraction (PXRD) measurements were performed to determine whether the dopant is incorporated in the host lattice or forms a mixed crystal. The PXRD spectra of DL-norvaline, L-glutamic acid, and DL-norvaline doped with L-glutamic acid, are plotted in Fig. 6. The intensity of the peaks for the pure crystals are weighted with their molar concentration. If the crystal consists of regions of pure DL-norvaline and regions of pure dopant, the corresponding PXRD spectrum would be a simple linear combination of these individual spectra. A small shift of the features would correspond to the doped case,46 while new features, existing in neither the dopant nor in DL-norvaline, can be explained by the formation of a new lattice. This new lattice case is referred to as mixed crystals.
The PXRD spectrum of the crystal in Fig. 6 features similar to those of the pure material spectrum. These features are shifted to slightly smaller angles and therefore we conclude that the lattice is slightly larger than the lattice of the pure material. This result is consistent with a doped crystal in which the dopant material occupies some of the lattice positions of the pure materials by replacing them.46 This behavior was observed for DL-norvaline doped with DL-norleucine, L-glutamic acid, and L-phenylglycine (see ESI,† Fig. S5). On the other hand, the PXRD spectra for DL-norvaline mixed with equal amounts of L-phenylglycine and D-phenylglycine, and L-asparagine have additional features that are neither in the pure dopant spectra nor in the pure DL-norvaline spectra (see ESI,† Fig. S6). These new features are explained by a fraction of the sample is a mixture that forms a new lattice which is different from the lattice of the pure DL-norvaline. Therefore, these crystals are referred to as mixed crystals to distinguish them from the doped crystals.
In combination with the PXRD results, we conclude that the dopant molecules are incorporated in the original lattice and do not significantly change the resonance frequency. However, the dopant influences the phase transition temperature, which is reduced to 170 K. The dopant provides additional lattice defects, acting as seeds for a crystallization in the nucleation and growth mechanism, and therefore, the phase transition temperature is expected to be higher. The fact that the phase transition occurs at a lower temperature is consistent with it being Martensitic. In this transition, the unit cell slides along the b axis, by half a unit cell length.39 This sliding is a collective, quasi-simultaneous movement of all molecules in the layer. The -R group in L-glutamic acid terminates with a carboxylic acid, but is a methyl group in DL-norvaline. This carboxylic acid group is located in the plane at which the collective displacement takes place, and will locally change the energy profile and thereby hinder this sliding process. The larger potential barriers due to the dopants result in a lower onset temperature.
As discussed with the L-glutamic acid doped case, the molecular structure for L-phenylglycine is similar to DL-norvaline, except for the phenyl ring at the end of the –R group which is located at the sliding interface. As in the case for L-glutamic acid, the additional disturbance along this plane, increases the energy barrier and decreases the phase transition temperature.
4 Conclusions
DL-Norvaline forms a layered crystal and is suspected to undergo a Martensitic phase transition when cooled.39 This phase transition has been studied with temperature-dependent THz spectroscopy. When the pure DL-norvaline is cooled below 180 K a significant change in the absorption spectrum is measured which is associated with a phase-transition. A better understanding of the mechanism for this phase transition is gained by measuring different crystal sizes since larger crystals have a higher probability for containing impurities. These impurities act as seeds for phase transitions, and therefore larger crystals undergo the phase transition at higher temperatures. For grains with an average size between 125 and 250 μm, the transition temperature was 190 K, while it is 180 K for grains of 5 μm or less. This effect is consistent with Martensitic transistions.The phase transition mechanism was studied in more detail by doping DL-norvaline crystals with similar amino acids. These dopants reduced the phase transition temperature by 10 K, although one would expect the additional defect sites caused by the dopants should increase the transition temperature. This is a strong indicator for a Martensitic phase transition, because the suspected transition can be described as a sliding of neighboring unit cells. The dopants used are identical to DL-norvaline, except for the end of the -R group which is found at the hydrophobic layer where the sliding occurs. The dopants locally increase the energy barrier for the sliding process which requires a lower temperature for the Martensitic transition.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the National Science Foundation (NSF) under grant number: NSF CHE - CSDMA 1465085. KR and CN acknowledge financial support by the U.S. Department of Energy Office of Science, Office of Basic Energy Sciences, under award no. DE-FG02-07ER15909.References
- W. C. McCrone, in Physics and Chemistry of the Organic Solid State, ed. D. Fox, M. M. Labes and A. Weissberger, Interscience Publishers, 1965, vol. 2, pp. 725–767 Search PubMed.
- J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, New York, 2002, vol. 14 Search PubMed.
- A. Gavezzotti, J. Pharm. Sci., 2007, 96, 2232–2241 CrossRef CAS PubMed.
- A. D. Bond, Curr. Opin. Solid State Mater. Sci., 2009, 13, 91–97 CrossRef CAS.
- E. V. Boldyreva, H. Sowa, Y. V. Seryotkin, T. N. Drebushchak, H. Ahsbahs, V. Chernyshev and V. Dmitriev, Chem. Phys. Lett., 2006, 429, 474–478 CrossRef CAS.
- A. S. Sabino, G. P. De Sousa, C. Luz-Lima, P. T. C. Freire, F. E. A. Melo and J. M. Filho, Solid State Commun., 2009, 149, 1553–1556 CrossRef CAS.
- V. S. Minkov, A. S. Krylov, E. V. Boldyreva, S. V. Goryainov, S. N. Bizyaev and A. N. Vtyurin, J. Phys. Chem. B, 2008, 112, 8851–8854 CrossRef CAS PubMed.
- V. S. Minkov, N. A. Tumanov, R. Q. Cabrera and E. V. Boldyreva, CrystEngComm, 2010, 12, 2551–2560 RSC.
- E. A. Belo, J. A. Lima Jr., P. T. C. Freire, F. E. A. Melo, J. M. Filho, H. N. Bordallo and A. Polian, Vib. Spectrosc., 2010, 54, 107–111 CrossRef CAS.
- H. N. Bordallo, E. V. Boldyreva, A. Buchsteiner, M. M. Koza and S. Landsgesell, J. Phys. Chem. B, 2008, 112, 8748–8759 CrossRef CAS PubMed.
- A. B. True, K. Schroeck, T. A. French and C. A. Schmuttenmaer, J. Infrared, Millimeter, Terahertz Waves, 2011, 32, 691–698 CrossRef CAS.
- M. R. C. Williams, D. J. Aschaffenburg, B. K. Ofori-Okai and C. A. Schmuttenmaer, J. Phys. Chem. B, 2013, 117, 10444–10461 CrossRef CAS PubMed.
- Y. V. Mnyukh, Mol. Cryst. Liq. Cryst., 1979, 52, 505–521 CAS.
- J. D. Dunitz, Pure Appl. Chem., 1991, 63, 177–185 CrossRef CAS.
- F. H. Herbstein, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 341–383 Search PubMed.
- S. C. Tuble, J. Anwar and J. D. Gale, J. Am. Chem. Soc., 2004, 126, 396–405 CrossRef CAS PubMed.
- J. Anwar, S. C. Tuble and J. Kendrick, J. Am. Chem. Soc., 2007, 129, 2542–2547 CrossRef CAS PubMed.
- D. Zahn and J. Anwar, RSC Adv., 2013, 3, 12810 RSC.
- J. A. van den Ende and H. M. Cuppen, Cryst. Growth Des., 2014, 14, 3343–3351 CAS.
- J. Mohd Jani, M. Leary, A. Subic and M. A. Gibson, Mater. Des., 2014, 56, 1078–1113 CrossRef CAS.
- K. Bhattacharya and R. D. James, Science, 2005, 307, 53–54 CrossRef CAS PubMed.
- J. S. Juan, M. L. No and C. A. Schuh, Nat. Nanotechnol., 2009, 4, 415–419 CrossRef PubMed.
- K. Kinbara and T. Aida, Chem. Rev., 2005, 105, 1377–1400 CrossRef CAS PubMed.
- M. van Exter and D. Grischkowsky, Appl. Phys. Lett., 1990, 56, 1694–1696 CrossRef CAS.
- J. Neu, R. Beigang and M. Rahm, Appl. Phys. Lett., 2013, 103, 041109 CrossRef.
- J. A. Zeitler, P. F. Taday, D. A. Newnham, M. Pepper, K. C. Gordon and T. Rades, J. Pharm. Pharmacol., 2007, 59, 209–223 CrossRef CAS PubMed.
- J. Neu and M. Rahm, Opt. Express, 2015, 23, 12900–12909 CrossRef CAS PubMed.
- D. Grischkowsky, S. Keiding, M. van Exter and C. Fattinger, J. Opt. Soc. Am. B, 1990, 7, 2006–2015 CrossRef CAS.
- J. Neu, B. Krolla, O. Paul, B. Reinhard, R. Beigang and M. Rahm, Opt. Express, 2010, 18, 27748–27757 CrossRef CAS PubMed.
- P. U. Jepsen and S. J. Clark, Chem. Phys. Lett., 2007, 442, 275–280 CrossRef CAS.
- M. R. C. Williams, A. B. True, A. F. Izmaylov, T. A. French, K. Schroeck and C. A. Schmuttenmaer, Phys. Chem. Chem. Phys., 2011, 13, 11719–11730 RSC.
- M. D. King, W. D. Buchanan and T. M. Korter, J. Pharm. Sci., 2011, 100, 1116–1129 CrossRef CAS PubMed.
- A. M. Fedor, D. G. Allis and T. M. Korter, Vib. Spectrosc., 2009, 49, 124–132 CrossRef CAS.
- S. J. Orfanidis, Electromagnetic Waves and Antennas, Rutgers University, 2006 Search PubMed.
- This assumes that there is no phase shift at the interfaces. This is a valid assumption because this additional phase is roughly 1000 times smaller than that from propagation through the sample, as explained in detail in the ESI† of this paper.
- T. Choy, Effective Medium Theory: Principles and Applications, Clarendon Press, 1999 Search PubMed.
- K. Berland and P. Hyldgaard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035412 CrossRef.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- C. H. Görbitz, J. Phys. Chem. B, 2011, 115, 2447–2453 CrossRef PubMed.
- D. Fernández-Torre, R. Escribano, T. Archer, J. M. Pruneda and E. Artacho, J. Phys. Chem. A, 2004, 108, 10535–10541 CrossRef.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651–1654 CrossRef CAS.
- P. Chatzigeorgiou, N. Papakonstantopoulos, N. Tagaroulia, E. Pollatos, P. Xynogalas and K. Viras, J. Phys. Chem. B, 2010, 114, 1294–1300 CrossRef CAS PubMed.
- W. Cao, J. A. Krumhansl and R. J. Gooding, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 11319–11327 CrossRef.
- A. A. Boulbitch and P. Tolédano, Phys. Rev. Lett., 1998, 81, 838–841 CrossRef CAS.
- J. C. Givand, A. S. Teja and R. W. Rousseau, AIChE J., 2001, 47, 2705–2712 CrossRef CAS.
- H. C. Koolman and R. W. Rousseau, AIChE J., 1996, 42, 147–153 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05479c |
| ‡ Present address: Center for Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. |
| This journal is © the Owner Societies 2018 |