Structural dynamics upon photoexcitation-induced charge transfer in a dicopper(I)–disulfide complex

Abstract

The structural dynamics of charge-transfer states of nitrogen-ligated copper complexes has been extensively investigated in recent years following the development of pump–probe X-ray techniques. In this study we extend this approach towards copper complexes with sulfur coordination and investigate the influence of charge transfer states on the structure of a dicopper(I) complex with coordination by bridging disulfide ligands and additionally tetramethylguanidine units [Cu^I₂(NSSN)₂]²⁺. In order to directly observe and refine the photoinduced structural changes in the solvated complex we applied picosecond pump–probe X-ray absorption spectroscopy (XAS) and wide-angle X-ray scattering (WAXS). Additionally, the ultrafast evolution of the electronic excited states was monitored by femtosecond transient absorption spectroscopy in the UV-Vis probe range. DFT calculations were used to predict molecular geometries and electronic structures of the ground and metal-to-ligand charge transfer states with singlet and triplet spin multiplicities, i.e. S₀, ¹MLCT and ³MLCT, respectively. Combining these techniques we elucidate the electronic and structural dynamics of the solvated complex upon photoexcitation to the MLCT states. In particular, femtosecond optical transient spectroscopy reveals three distinct timescales of 650 fs, 10 ps and >100 ps, which were assigned as internal conversion to the ground state (S_n → S₀), intersystem crossing ¹MLCT → ³MLCT, and subsequent relaxation of the triplet to the ground state, respectively. Experimental data collected using both X-ray techniques are in agreement with the DFT-predicted structure for the triplet state, where coordination bond lengths change and one of the S–S bridges is cleaved, causing the movement of two halves of the molecule relative to each other. Extended X-ray absorption fine structure spectroscopy resolves changes in Cu–ligand bond lengths with precision on the order of 0.01 Å, whereas WAXS is sensitive to changes in the global shape related to relative movement of parts of the molecule. The results presented herein widen the knowledge on the electronic and structural dynamics of photoexcited copper–sulfur complexes and demonstrate the potential of combining the pump–probe X-ray absorption and scattering for studies on photoinduced structural dynamics in copper-based coordination complexes.

---

1 Introduction

In the chemistry of life copper plays an important role being a core part of many essential metalloenzymes.¹ Among copper active sites the mononuclear blue Cu site and the binuclear Cu_A site participate in electron transfer processes with unusually high rates.^1,2 It was suggested that copper–sulfur interactions play a crucial role in their function, where the polarisable nature of sulfur serves in tuning electronic properties and reactivity.^1,3 In the past few decades there have been many efforts in the field of bioinorganic chemistry for synthesising and characterising complexes which could serve as model compounds for these enzymes.^4–14 In order to understand the mechanism of their function, orbital structures of many copper enzymes and their model complexes were analysed both experimentally and theoretically.^15–18 Charge transfer that occurs during the catalytic cycle of a copper enzyme can be modelled by optical excitation of the metal-to-ligand or ligand-to-metal charge transfer states in a mimetic copper complex. Structural changes that accompany such photoinduced charge transfer typically occur on nanosecond timescales or faster and can thus be monitored almost exclusively by pump–probe time-resolved techniques. Hard X-ray methods, such as picosecond time-resolved K-edge X-ray absorption spectroscopy (TR-XAS) and time-resolved wide-angle X-ray scattering (TR-WAXS), are directly sensitive to the structures of excited states also in the case of dilute solutions. These techniques are still under development mainly driven by rapid progress of synchrotron sources, optical and X-ray lasers and data acquisition technologies.^19–24 It is noteworthy that copper compounds were among the first systems investigated by these techniques. In particular Cu–bisphenantroline complexes have served as model compounds for X-ray as well as UV-Vis time-resolved spectroscopic studies.^25–32 It was shown that upon photoexcitation with visible light the metal-to-ligand charge transfer (MLCT) transition occurs and the oxidation state of copper formally changes from +1 to +2. Such an alteration of the electronic configuration of copper – from closed-shell 3d¹⁰ to 3d⁹ – gives rise to significant structural changes of the complex. The excited state is subject to pseudo-Jahn–Teller distortion,^33–35 and the flattening of the complex from Cu(I)-preferred pseudotetrahedral geometry in the direction of the formal Cu(II) square-planar arrangement occurs on sub-ps timescale. Another characteristic feature of copper complexes is relatively slow (in comparison with other transition metal complexes, such as Fe, Ru, Cr³⁶) intersystem crossing (ISC) to the triplet state ³MLCT that in some cases competes with visible fluorescence due to the relaxation of ¹MLCT to the ground state.³⁷ From ³MLCT both non-radiative and emissive decays are possible, depending on the electronic structure of the particular complex due to different ligand substituents, the degree of flattening, and on the solvent. It was observed that in many Cu complexes the phosphorescence lifetime is shortened in donating solvents, and there is dispute in the literature concerning the coordination of the solvent molecule to the flattened excited state.^26,27,38 Some recent TR-XAS experiments and molecular dynamic simulations on the model complex suggest the lack of complexation and rationalise the lifetime shortening by a decrease in ³MLCT energy and ISC yield in donating solvents.²⁹ The copper complex investigated in this work bears certain similarities to Cu–bisphenantrolines, such as copper coordination by sp²-nitrogens. At the same time additional coordination by sulfur causes specific interactions influencing the excited state structure. In particular in the context of structural responses to electronic excitations within biologically relevant Cu/N/S systems, coordinated disulfide groups offer ideal conditions as electrons sink due to their empty antibonding sigma orbitals. What is more, many biorelevant and functional materials contain two or more copper atoms in a molecule. In particular, some dicopper complexes demonstrate attractive photoemissive properties making them a promising material for organic light-emitting diodes (OLEDs).³⁹ However, to the best of our knowledge, no ultrafast studies on dicopper complexes have been reported. Both factors, Cu–S interaction and the presence of two metal atoms in the complex, make this study an interesting contribution to the emerging field of structural dynamics studies and to the knowledge of biologically-relevant ET-coupled structural changes.

2 Experimental section

2.1 Materials

The investigated compound [Cu₂(TMGphS-SphTMG)₂]X₂ (X = OTf, PF₆, TMG: tetramethylguanidine) was synthesised as described in ref. 14. The details of characterisation by X-ray single crystal diffraction, elemental analysis, UV-Vis and IR spectroscopy, SQUID and cyclic voltammetry are also presented therein. Due to the presence of basic guanidine nitrogens and the labile Cu–S bonding, the choice of solvents suitable for handling the complex is limited to solvents that are polar, aprotic and non-coordinating. Following these criteria, 1,2-difluorobenzene (DFB) and dichloromethane (DCM) were chosen for the experiments. The compound is also stable at high concentrations in acetonitrile (ACN) and demonstrates better radiation damage stability in this solvent, which was also used for the experiments. Grades of the used solvents were: acetonitrile (ACN) from Carl Roth, 99.98%, Ultra LC-MS, for luminescence and TA; from Sigma-Aldrich, anhydrous, 99.8%, for TR-XAS; dichloromethane (DCM), HPLC grade, non-stabilised, from Carl Roth (stored under an inert atmosphere), for luminescence and TA; 1,2-difluorobenzene (DFB), 98%, from Thermo Fisher Scientific, Acros Organics and ChemPur, for TR-XAS and TR-WAXS. All solvents were used as purchased.

2.2 Steady-state absorption and emission

UV-Vis steady state absorption spectra were measured using a Shimadzu UV-3600 spectrophotometer. The luminescence experiments were performed using an Ocean Optics 65 000 spectrometer as well as using a home-built time-correlated single-photon counting setup.⁴⁰ The complex was excited with light pulses in the range of 360–410 nm. However, it does not show any measurable luminescence at 400–900 nm at room temperature in solution, so no more experimental details are given.

2.3 UV-Vis transient absorption (TA)

The TA measurements were performed in the ELI-Beamlines facility in Dolní Břežany, Czech Republic. The TA setup was based on an amplified Ti:sapphire laser, which was used to generate the pump and probe pulses. The 400 nm pump pulses at 1 kHz had a total energy of about 2.5 μJ and a diameter of about 0.4 mm at the sample position. White light continuum pulses used as a probe were generated in a CaF₂ rotating plate and had a spectral range of 340–750 nm. The probe and pump beams were focused and overlapped on the quartz sample cell with 1 mm path length. Several scans were averaged and for the background removal the data recorded before excitation were subtracted from all the spectra. The instrumental response function of ∼120 fs was estimated measuring the stimulated Raman amplification signal from the solvent. All experimental data were corrected for the group velocity dispersion (GVD), and global decay analysis was used to obtain the time constants. The measurements were done on [Cu₂(NSSN)₂](OTf)₂ and [Cu₂(NSSN)₂](PF₆)₂ in three solvents: dichloromethane, acetonitrile and 1,2-difluorobenzene. The studied compounds were dissolved at a concentration of 4–6 × 10⁻⁴ M corresponding to an OD of ∼0.4–0.6 at the pump wavelength. UV-Vis steady state spectra of the compound were registered before and after the measurements to control the integrity of the sample. More detailed technical description of the experimental setup is given in ESI.†

2.4 Steady state X-ray absorption spectroscopy (XAS)

Two steady-state XAS data sets were acquired: [Cu₂(NSSN)₂](OTf)₂ as a solid and as a solution in acetonitrile. The XAS experiments of the solid [Cu₂(NSSN)₂](OTf)₂ at the Cu K-edge (8979 eV) were performed at the XAS beamline of the synchrotron ANKA (Ångstrømquelle Karlsruhe) in Karlsruhe (Germany) at ambient temperature. The spectra were collected in transmission mode with a maximum beam current of 180 mA by application of a Si(111) double crystal monochromator. The sample was diluted with boron nitride and a Cu foil was measured simultaneously downstream for energy calibration. The Cu K-edge XAS spectra of the 10 mM solution of [Cu₂(NSSN)₂](OTf)₂ in acetonitrile were measured at the European synchrotron radiation facility (ESRF) beamline BM23 in Grenoble (France) with a maximum beam current of 200 mA at ambient temperature using a Si(111) double crystal monochromator. Due to the low concentration of copper, experiments were carried out in fluorescence geometry. To enable energy calibration and to exclude energy drifts of the beamline, a Cu foil spectrum was registered directly before and after the sample measurements. Energy calibration was carried out by referencing the first inflection point of the Cu foil spectrum to 8979 eV.

2.5 Time-resolved (100 ps) X-ray absorption spectroscopy (TR-XAS)

The TR-XAS measurements were performed at the beamline P11 of Petra III synchrotron in Hamburg, Germany. The setup is described in detail in ref. 23. The measurements were performed on 5 mM [Cu₂(NSSN)₂](PF₆)₂ ACN and 5 mM [Cu₂(NSSN)₂](OTf)₂ DFB solutions. Different solvents were used in order to compare the behaviour of the complex in a coordinating and a non-coordinating solvent. However, due to S/N problems the DFB XAS data could not be analysed further and therefore no further experimental details are reported. The X-ray beam for the experiment was monochromatised to energy resolution of dE/E = 1.3 × 10⁻⁴ with the Si(111) crystal and focused to 10 μm using two Kirkpatrick–Baez (KB) mirror systems. The excitation was performed using the 343 nm third harmonic of the pulsed fs laser PHAROS from Light Conversion. The laser was operated with a frequency of 65 kHz which corresponds to half of the Petra III roundtrip frequency. The sample was delivered using a cylindrical 300 μm liquid jet; laser pulse energy was 3 μJ; the spot size on the jet was ∼300 μm (adjusted to the jet diameter). The detection was done in fluorescence mode using an avalanche photo diode (APD) installed perpendicular to the X-ray beam. The normalisation was performed with the second APD which collected the X-rays scattered from a Co foil placed several cm after the jet. The absorption by copper at the energies above the absorption edge at the given concentration and jet thickness was negligible (∼0.3%) and allowed us to work in this geometry. UV-Vis steady state spectra of the compound were registered before and after the measurements to control the integrity of the sample.

2.6 Time-resolved (100 ps) wide-angle X-ray scattering (TR-WAXS)

The TR-WAXS measurements were performed at beamline ID09 of the ESRF synchrotron, Grenoble, France. The description of the pump–probe setup at beamline ID09b is given elsewhere.^41,42 The sample was prepared as a 4 mM solution of [Cu₂(NSSN)₂](OTf)₂ in DFB. The sample solution was delivered via a 300 μm flat sheet jet from a sapphire nozzle providing a flow speed of approximately 3 m s⁻¹ to ensure the complete sample exchange between consecutive pump–probe events at a repetition rate of 1 kHz of the experiment. The solution was regularly refilled with a new solvent to compensate for evaporation. Excitation was performed using the 400 nm frequency doubled output of the Ti:sapphire amplified system (Legend Elite, Coherent Inc.) with a frequency of 1 kHz and a pulse length (FWHM) of ∼1 ps. To avoid non-linear absorption and saturation effects the laser pulse energy was set to a low value of 20 μJ. Single X-ray pulses (∼100 ps FWHM, 18 keV, 3% bandwidth “pink” beam) generated from the U17 undulator were selected using a mechanical chopper system to reduce the repetition rate to 1 kHz. The size of the laser spot on the sample was measured using a pinhole and was determined to be 120 × 150 μm (h × v). The size of the X-ray beam was 90 × 60 μm (h × v). The scattered X-rays were collected using a Rayonix MX170-HS CCD detector with 3840 × 3840 pixels in 2 × 2-pixel binning. The detector was placed 38 mm behind the liquid jet. A cylindrical tungsten beamstop of 1.5 mm diameter was used to block the direct beam in front of the detector. The 2D scattering images upon 1.5 s exposure were collected for 18 different time delays between the laser and X-ray pulses in the range from −300 ps to 1 μs. After every three images a reference image was taken at a nominal delay of −3 ns corresponding to the non-excited sample. In total about 3500 images were acquired which results in approximately 150 repetitions for each pump–probe delay. The scattering contribution of the DFB solvent to the total difference scattering signal was additionally measured in a separate TR-WAXS measurement with the same setup using the solution of an azobenzene dye (4-[(4-bromophenyl)diazenyl]-N,N-diethylaniline, CAS 22700-62-5) as proposed in ref. 43.

Cu Kα emission was recorded using a 1 m diameter Rowland-circle spectrometer arranged in the horizontal plane with a Si(111) analyzer crystal ((444) reflection) and a silicon drift detector with a multichannel analyser to additionally suppress the elastic background. A He-filled tank was installed in the path of emitted X-rays to avoid absorption and scattering by air. The measurements were performed by scanning the analyser Bragg angle near 79° in order to span the energy range of the Cu Kα₁ peak (∼8048 eV). In total 35 scans were performed; certain spectral points were sampled 51 times.

2.7 DFT calculations

Density functional theory (DFT) calculations were carried out using the implementation of gaussian 09.⁴⁴ The most frequently used hybrid functional B3LYP^45–47 and a more recent meta hybrid functional TPSSh⁴⁸ were applied to calculate the geometrical and electronic structures of the ground state and the lowest charge-transfer triplet state T₁ (³MLCT). Excitations and geometrically relaxed singlet excited states were addressed using time dependent (TD)-DFT⁴⁹ and a computationally feasible cc-pVDZ⁵⁰ basis set. More precisely, the calculations were performed by solving the Casida equations within every step of a structural relaxation of the specific excited-state.⁵¹ For the evaluation of excitation spectra triple-ζ basis def2-TVZP^52,53 was applied. Both basis sets included polarisation functions. Additionally, the influence of different solvents⁵⁴ was examined using a continuum solvent model.⁵⁵ Vibrational frequencies were checked for the ground state to ensure a true minimum. These concepts have been shown to result in reliable excited-state properties for the system within the copper-sulfur or related copper-oxygen chemistry.^18,56

3 Results and discussion

3.1 Molecular and electronic structure

3.1.1 Ground state. The binuclear Cu(I) complex under study is the cation [Cu₂(TMGphS-SphTMG)₂]²⁺ (further referred to as Cu₂(NSSN)₂). Its molecular structure was already obtained by a crystallographic study as discussed in detail in ref. 14. Briefly, it consists of two copper atoms, which are connected by two disulfide bridges to form a six-membered ring in a twisted conformation as shown in Fig. 1. Two sulfur atoms take part in the formation of a tetrahedral coordination polyhedron together with two nitrogen atoms from tetramethylguanidine ligands (TMG). TMG has strong donor properties and strong basicity and is a part of various ligand systems.^57,58 The ground-state structure of the molecule has D₂ symmetry. The compound was synthesised with two counter-anions – OTf⁻ and PF₆⁻.

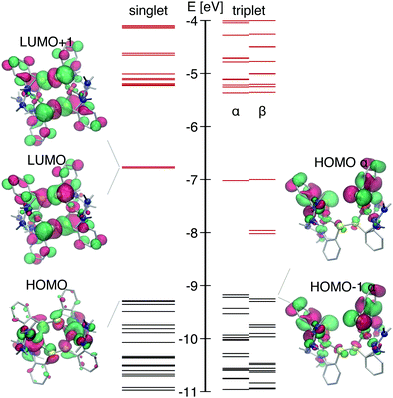
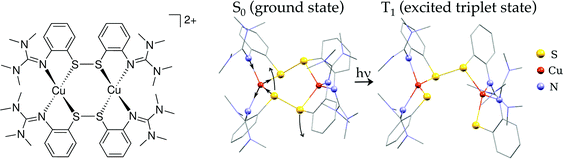Fig. 1 Left: Scheme of [Cu₂(NSSN)₂]²⁺; right: calculated geometries of the ground state and ³MLCT (lowest triplet state). Hydrogen atoms are omitted for visual clarity.

The critical parts of the complex for its photoreactivity are Cu–N and Cu–S bonds. N_TMG shows sp² hybridisation, like N_py, and the Cu–N_TMG distance determined from X-ray diffraction (av. 2.02 Å) is close to Cu–N_py coordination (2.01–2.07 Å)^26,59 and shorter than typical for Cu(I)–NR₃ (2.16(9) Å).⁶⁰ Several examples reporting complexes existing in both Cu(I) and Cu(II) forms^26,58,60 all have a shorter Cu–N bond length for Cu(II) than for Cu(I). The same trend is observed when Cu(II) is created by photoexcitation of Cu(I).²⁶ For Cu(I)–disulfide coordination the Cu–S distance was reported to be within 2.20–2.37 Å.^7,59,61 Our complex with 2.28–2.30 Å falls in this range. Cu(II) complexes tend to have 4+1 or 4+2 coordination with axial bonds elongated or shortened due to pseudo-Jahn–Teller distortion.³³ For Cu(II)–disulfide bonds in axial coordination the span of covered Cu–S bond lengths is 2.68 Å to 3.28 Å in ref. 62–66. For a Cu(II)–disulfide linkage with a rare case of seemingly equal six Cu–ligand bonds⁶⁷ Cu–S is within 2.46–2.57 Å, which is longer than that characteristic of Cu(I)–disulfide. However, for Cu(II) with equatorially bound radical disulfide (S₂⁻˙) a much shorter distance of 2.27 Å was reported.⁶⁸ For several complexes of Cu(I) and Cu(II) with the same aliphatic thiolate NS₃ ligands Cu(I)–S bonds were reported to be 2.26 Å, whereas Cu(II)–S – was 2.37–2.38 Å.⁶⁰ This broad variance in Cu(II)–S distances makes it difficult to predict the direction of the Cu–S bond length change upon photoexcitation.

The DFT-calculated structures of the ground state show good agreement with the crystallographic data in terms of intraligand distances (see Table 1); however, the calculated Cu–ligand bond lengths are consistently longer. Xc-functional and basis set combination TPSSh/def2-TZVP results in a better match to the crystallographic distances compared to B3LYP/cc-pVDZ. Including the solvent in the calculation (DFB) results in a slight shortening of Cu–ligand distances (less than 0.01 Å) and in a better match in the UV part of the spectrum (ESI,† Fig. S1). Since TPSSh/def2-TZVP is more suitable for TM complexes and shows a better match with the crystallographic data, these calculation results were further used for data modelling.

Table 1 Comparison of crystallographic data and calculation results for selected bond lengths for Cu₂(NSSN)₂. S₀ and T₁ are calculated using the TPSSH functional. For crystallographic bond lengths the average of all corresponding bond lengths in the molecule with their standard deviations is given. The last column contains the structural changes of the respective bonds upon excitation to the triplet state

Bond	Crystallography, Å	DFT(TPSSh/def2-TVZP)
		S0, Å	dR(T1–S0), Å
Cu–N	2.021 ± 0.010	2.070	−0.040, 0.008
Cu–S	2.288 ± 0.011	2.315	−0.079, 0.035
S–S	2.126, 2.137	2.180	0.029, 3.063
Cu–Cu	3.941	4.133	0.662
S–Cph	1.778 ± 0.012	1.764
N–Cph	1.386 ± 0.013	1.398
N–CTMG	1.349 ± 0.006	1.334
Cph–Cph	1.411 ± 0.010	1.416

---

The DFT-calculated singlet GS electronic structure is shown in Fig. 2. This complex has two close-lying LUMO orbitals with strong S-p contribution (σ* of two disulfide bridges) that are significantly lower in energy than LUMO+2 and further orbitals. Both orbitals have a large anti-bonding character equally distributed over both S–S bridges. They mainly differ by the character of Cu-3d contribution: for the LUMO it has the d_xy shape, whereas for LUMO+1 − d_z². Transitions from the HOMO and the HOMO−n with strong Cu 3d contribution occur to the LUMO and the LUMO+1 and account for a broad absorption band centered at 415 nm with ε ∼ 10⁴ M⁻¹ cm⁻¹. The electron is excited from an orbital located on both copper atoms, thus creating a formally Cu₂^1.5+ state. Further in the UV region there are strong absorption bands due to intraligand transitions as well as MLCT Cu → N (ESI,† Fig. S1).

Fig. 2 Molecule orbital spectra of S₀ (left) and T₁ (right) in their equilibrium structures, respectively. Occupied states are depicted in black, unoccupied – red.

3.1.2 Excited state. As a benchmark study the calculations of the possible excited state singlet structures were performed for all significant excitation channels in the MLCT range, resulting in 13 excited state structures. The calculated structures originating from different excitation channels significantly differ from each other structurally and energetically. All the structures have in common strong S–S bond elongation for one or both S–S bonds, since the electron is excited to an antibonding orbital localised on the disulfide bridges.

With the temporal resolution of the transient synchrotron-based experiments (70–100 ps) we expect that we will only observe the complex after it underwent ISC to the triplet state as it normally happens for copper complexes on a faster time-scale (<30 ps).^31,34,69 The structural parameters of the calculated lowest triplet state T₁ are summarised in Table 1. The orbital spectra of T₁ are compared to the singlet S₀ in Fig. 2. Single occupation of one antibonding disulfide σ* leads to the S–S bond breaking, causing the movement of two halves of the molecule relative to each other and increase of the Cu–S–S–Cu torsion angle from 67° to 99° (see Fig. 1). The other S–S bond is slightly elongated, and there are symmetric changes in coordination bond lengths on both copper atoms. In comparison with Cu–bisphenantroline complexes²⁹ quite small flattening of the coordination polyhedron occurs – the angle between ligand chelate planes changes from 89° to 75° on both copper atoms.

Interestingly, the cleavage of the disulfide bridge for Cu₂(NSSN)₂ can be achieved not only via photoexcitation, but also chemically by addition of chloride ions.¹⁴ In the resulting Cu₂(NS)₂Cl₂ complex both copper atoms have the oxidation state of +2, and S–S is cleaved creating two thiolate bridges.

3.2 Optical transient absorption

In order to obtain an insight into the ultrafast processes in the photoexcited complex, femtosecond transient absorption experiments were carried out upon excitation at 400 nm. Time-resolved spectra were recorded in the spectral range 350–670 nm and timescale 0–1 ns in DFB, ACN and DCM. Typical transient absorption spectra of Cu₂(NSSN)₂(PF₆)₂ in DFB at different times following excitation are depicted in Fig. 3. Quite similar transient absorption spectra were obtained for other solutions. The corresponding time constants are similar within the experimental error and are gathered in the ESI,† in Table S4.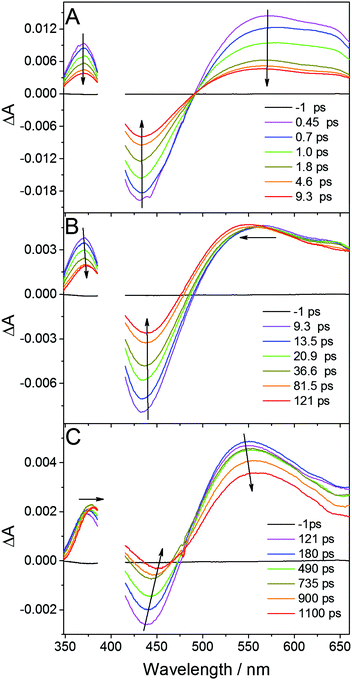

Fig. 3 Transient absorption spectra of Cu(NSSN)₂(PF₆)₂ in DFB recorded at different time delays after femtosecond excitation at 400 nm.

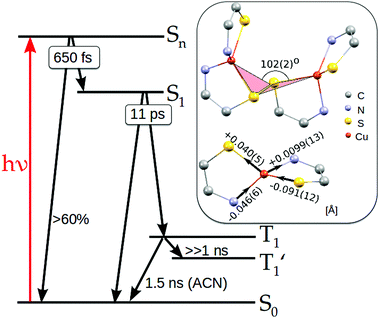
Femtosecond excitation leads to the formation of a spectrum composed of three characteristic bands (spectrum at 0.45 ps, Fig. 3A). The negative band around 430 nm is located in the region of the ground state ¹MLCT absorption (compare Fig. S1, ESI†) and is attributed to the ground state bleaching (GSB), whereas the positive band with the maximum at 370 nm as well as featureless broad absorption extending above 500 nm are ascribed to excited state absorption (ESA). Regarding DFT calculations and the experimental ground state absorption spectrum of the studied complex (see above), the excitation at 400 nm corresponds to the one of the higher singlet excited state S_n. Global fit analysis (see Fig. S20 in ESI†) of the time dependent spectral evolution reveals the existence of three steps (Fig. 3) characterised by three different time constants. During the first few picoseconds all the bands decrease simultaneously (Fig. 3A) by about 60% in intensity without significant shifts and shape variations revealing ultrafast deexcitation to the ground state with a time constant of about 650 fs. Since no emission was observed for the studied complex, this decay is attributed to non-radiative internal conversion (IC). It shows that the conformation in the higher excited singlet states has strong coupling with the ground state of the complex. The remaining excited species evolve with a time constant of 10.6 ps exhibiting the blueshift of the broad ESA band with a concomitant redshift and a decrease in the intensity of GSB and the second ESA band (see Fig. 3B). Such a time constant of about 10 ps was reported as intersystem crossing (ISC) to the triplet ³MLCT state in various homoleptic and heteroleptic copper complexes.^34,37,70,71 The further spectral evolution exhibits a redshift and a decrease of intensity with a time constant >100 ps. This step can be ascribed to the beginning of further structural changes in the triplet state and radiationless decay to the ground state as designated in TR-XAS and TR-WAXS experiments reported below. The limited accuracy for this decay time constant is due to the limited pump–probe time delay (∼1 ns) accessible in our experiments which cannot be extended to the whole kinetics. Apart from IC and ISC, vibrational relaxation in the excited state and ground states can contribute to the observed signal. This phenomenon can take place in quite wide timescales (100 fs to 100 ps) depending on the complex structure and on the solvent. For TM complexes IC, VR and rearrangement of the solvation sphere are typically convoluted and only the average time constant for all these processes is observed.⁷² In order to disentangle the individual ultrafast processes the set of additional purposeful experiments would have to be performed.

The performed transient absorption experiment allows us, by judging from the relevant timescales, to conclude on the arrival of the excited complex to its triplet state (ISC). Thus, with the temporal resolution of the TR-XAS and WAXS measurements reported here we could only observe the triplet excited state. This information is important for narrowing down the set of candidate structures provided by DFT to only triplets to be considered as the starting structure for optimization.

3.3 Ground state EXAFS

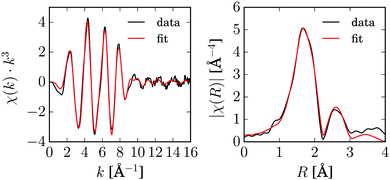
Before the pump–probe experiments were performed, steady-state X-ray absorption spectra of [Cu₂(NSSN)₂](OTf)₂ were measured in the solid state and in a 10 mM solution in acetonitrile. The EXAFS spectra of both look almost identical, which confirms that the complex is intact at this concentration in the acetonitrile solution and there are no or only negligible influences of coordinating acetonitrile molecules visible (ESI,† Fig. S2). Since the spectrum of the solid [Cu₂(NSSN)₂](OTf)₂ has better data quality, the EXAFS analysis was carried out based on these data. The data and the fit are shown in Fig. 4. Data reduction was performed in Athena,⁷³ EXAFS fitting was done in horae Artemis,⁷³ using Feff85L.⁷⁴ The crystallographic structure was used as the model, fitting was done in k-space for k = 3–16 Å⁻¹. Only non-structural parameters (S₀², E₀, “Debye–Waller” factors σ²) were fitted, since the crystallographic structure was used to construct excited state models. The list of scattering paths and the fitting parameters are given in the ESI,† in Table S1. The fit and the extracted parameters (“Debye–Waller factors” σ² and amplitude reduction factor S₀²) were further used for the fitting of TR-EXAFS data.

Fig. 4 EXAFS spectra and best fit in k- and R-space of [Cu₂(NSSN)₂](OTf)₂ (solid).

In order to assure the validity of this analysis, fitting including structural parameters was performed for both solid and liquid samples as reported in the ESI.† Two different software packages (Artemis and ExCurve⁷⁵) and approaches to data modeling (3D structure and shell-by-shell adding atoms) were used. The Cu–S and Cu–N distances obtained using two software packages are in agreement with each other and match the crystallographic distances within their uncertainties.

3.4 Pump–probe XAS

In order to observe the structural changes occurring upon photoexcitation, pump–probe XAS experiments were carried out. Fig. 5 shows the edge region of the Cu K-edge absorption spectrum of the complex. The edge position (maximum of the first derivative at 8981.1 eV) and shape (shoulder at 8985.5 eV, assigned as 1s → 4p transition) correspond to four-coordinated Cu(I).^76,77 Upon photoexcitation with 343 nm light pulses strong changes are observed in the XANES spectrum. The transient signal, shown in Fig. 5, has a double minimum corresponding to the disappearance of two edge shoulders due to the edge shift to higher energies for Cu(II). This fact was used to estimate the excited state fraction (vide infra). At the same time a small positive preedge feature emerges at 8978 eV which in the literature is assigned to the 1s → 3d(+4p) transition which is characteristic of Cu(II) with non-centrosymmetric coordination.^77–79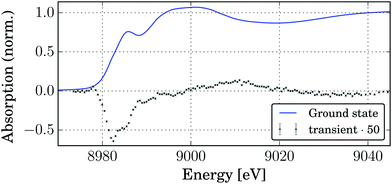

Fig. 5 XANES spectrum of the ground state (solid Cu₂(NSSN)₂(OTf)₂) and the transient spectrum at a delay of 80 ps (5 mM solution in acetonitrile).

The laser-pumped spectrum has contributions of both ground and excited state spectra. In order to extract the ES spectrum, the knowledge of the relative contribution of the excited state spectrum (excited state fraction f) is necessary. In order to estimate it the edge shape for the GS spectrum was modelled as a sum of an error function and two pseudo-Voigt peaks centered at 8982.4 eV and 8985.4 eV (see the ESI,† Fig. S7). We expect that the transition at a lower energy (8982.4 eV) should not be present for a Cu²⁺ compound. However, since upon photoexcitation only one electron is transfered per two copper atoms, the electron density loss is divided between them, and a more realistic estimation is that a 50% decrease in the intensity of the edge peak at 8982.4 eV would correspond to the excited state spectrum. This condition is satisfied for f = 0.074, which is a lower-border estimation for f. For more details refer to the ESI.†

3.4.1 Transient EXAFS. The transient signal in the XANES part of the spectrum is much stronger than in the EXAFS. However, quantitative modelling of XANES may be difficult, and for EXAFS the theory for quantitative structural analysis is established. In our experiments the data quality allowed us to perform analysis of the transient XAS in the EXAFS energy range. The analysis is based on comparing in the energy space the experimental transient Δχ_exp(E) with a series of simulated transient EXAFS spectra calculated as

Δχ_calc.(E) = f·(χ^ES(E^ES₀) −χ^GS(E^GS₀)), (1)

as applied in ref. 80 and 81. S₀² and “Debye–Waller factors” σ² retrieved from the GS fit are used to calculate χ^ES(k), which is recalculated into the energy space with the energy E^ES₀ corresponding to k = 0. The precise value of E^ES₀ is not known, and the chemical shift dE = E^ES₀ − E^GS₀ is one of the fitting parameters. The chemical shift is caused by the change of the electronic density on copper upon the MLCT transition. Since the structural changes in the triplet state are symmetric on both copper atoms, we expect that they have the same chemical shift. For some Cu(N₄) complexes this shift (estimated from the shift of the K-edge in XANES spectra on the half of the edge jump) was found to be 3–3.5 eV.^29,58 Due to high covalency of Cu–S bonds and loss of one electron per two copper atoms, the chemical shift for Cu₂(NSSN)₂ should be smaller than that observed for Cu(N₄) complexes. In the fitting procedure dE was varied from −1 eV to 5 eV with 0.1 eV steps. Another parameter that has to be fitted is the ES fraction f. We estimated its lower border value to be f = 0.074. However, the presence of two copper sites makes it difficult to predict the edge position and shape of the ES spectrum, and f was varied as an independent parameter from 3% to 20% with 0.5% steps. As demonstrated above, the crystallographic structure reproduces the static EXAFS measurement of the GS much closer than the DFT-calculated structure for both the solid powder and the solvated sample. Therefore, the crystallographic structure was used as the GS model for the analysis of the time-resolved data hereafter. Accordingly, the DFT-predicted structure of the ES is also expected to be different from the experimental one. Therefore, the initial model for the excited triplet state, T^cr₁, was constructed from the GS crystallographic structure by applying the following relative transformations to the respective inter-atomic distances. That is, the Cu–N and Cu–S bond lengths of the crystallographic GS structure were modified by the same relative amount as they change between the DFT-predicted structures of the ground and the triplet T₁ states, as illustrated in Fig. 1. We note that the ligands of the molecule can be separated into four structurally equal parts, each including TMG, phenyl and one sulfur of the disulfide bridge. For each copper the set of scattering paths significantly contributing to the EXAFS signal entirely belongs to such ligand parts with the exception of the two sulfur atoms at r = 3.4–3.7 Å and the second copper at r = 3.9 Å. For the construction of the candidate ES structures these four ligand parts were moved independently as fixed units. In the first step each ligand unit was moved in the Cu–S–N plane along the Cu–N vector to a certain Cu–N distance. In the second step the ligand was rotated in the same plane around the coordinating N-atom until the necessary Cu–S distance was reached. The structural modifications were performed on both copper atoms independently, without changing the Cu–Cu distance. The structure obtained this way was denoted as T^cr₁. In order to perform the structural refinement, additional ES structures were constructed along the transformation path S^cr₀ → T^cr₁ with the configurational coordinate Q changing from 0.5 to 1.5 representing the relative bond length changes such that the structure of the T^cr₁ state corresponds to Q = 1.0. The S–S bond cleavage in the triplet state is accompanied by movement of two halves of the molecule relative to each other. As a result the distance from copper to atoms belonging to the other half of the molecule grows, as well as the variance in the distance. Therefore the contributions of scattering paths Cu–Cu and one of Cu–S (at r = 3.4–3.7 Å) were removed from the excited state. With these prerequisites χ(k) was then calculated for both copper atoms in the ES with the amplitude reduction factor S₀² = 0.5. For each parameter set (Q, dE) χ(k) was recalculated into χ(E). The theoretical transient for a set of ES fractions f was then calculated according to eqn (1), and the χ_red² estimator was used as a measure of agreement between the calculation and the experiment as reported in the ESI.† The fitting results are presented in Fig. 6.

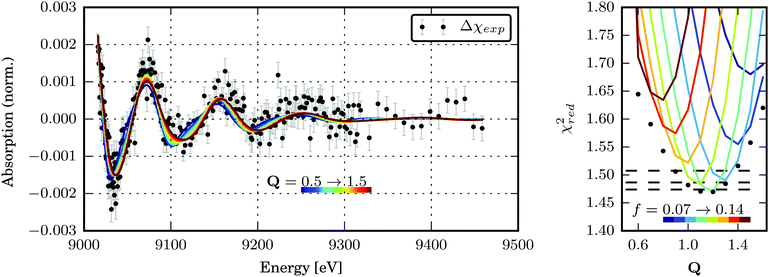Fig. 6 (a) Best transient EXAFS fits for structures along the S^cr₀ → T^cr₁ transformation path Q. The best-fit parameters are given in Table S3 in the ESI.† (b) χ_red² as a function of the T^cr₁ structure for dE = 1.4 eV and different excited state fractions of 7–14%. The global minima of χ_red² for each structure are marked with black dots. The dashed black lines denote the confidence levels of 68.3, 95.5 and 99.7% calculated with fixed optimal values of f and dE. The confidence region for (Q, dE, f) parameter space is shown in the ESI,† Fig. S10.

The global minimum of χ_red² is found for Q = 1.17^+0.13_−0.17, dE = 1.4^+0.2_−0.4 eV and f = 10^+3.5₋₁%. (The errorbars cover the 68.3% confidence interval.) It corresponds to the following bond length changes: Cu–N = −0.046(6) and +0.0099(13) Å, Cu–S = +0.040(5) and −0.091(12) Å (see Fig. 8). It should be noted that a very small error bar on one of the Cu–N bond lengths (0.0013 Å) stems from our fitting model (the only structural degree of freedom is Q) and does not directly reflect sensitivity of the method. Sensitivity of EXAFS to distances to the first shell atoms can be on the order of 0.01 Å. The strongest change in the bond length happens to Cu–S_cleaved: it shrinks to unusually short for a Cu–S bond length of 2.19 Å. However, a similarly short Cu–S bond (2.22 Å) is observed in the compound Cu₂(NS)₂Cl₂ obtained from Cu₂NSSN₂ by chloride-induced reductive cleavage of the S–S bond.¹⁴ The values for the excited state fraction and the energy shift are in good agreement with the expectations.

According to the DFT predictions, the overall molecular structure in the triplet state is greatly perturbed compared to the GS since one of the S–S bridges is broken. In the solution phase therefore the two equal parts of the complex around the Cu atoms may significantly move with respect to each other. EXAFS is an element specific photoelectron technique with a limitation of structural sensitivity up to distances of 3–4 Å for molecules with low symmetry structures like Cu₂(NSSN)₂. For this complex the Cu–Cu distance is 3.9 Å in the ground state and increases in the excited state. Thus the Cu–Cu distance or large relative movements of the two parts of the Cu₂(NSSN)₂ molecule cannot be reliably probed via transient EXAFS only. On the other hand, the elastic scattering technique like WAXS provides a global probe of the overall structure capable of detecting large structural deformations involving long inter-atomic distances.

3.5 Time-resolved Wide-angle X-ray Scattering (TR-WAXS)

The time-resolved wide-angle X-ray scattering (TR-WAXS) method has been successfully applied to many systems in solution photochemistry over the past decade.^22,42,82,83 The difference scattering between the laser-excited and the ground state samples contains contributions from changes in the solute structure, from rearrangements of the solvation shell and from changes in the thermodynamic state of the surrounding solvent, i.e. variations in temperature and density. The technique essentially serves as a global structural probe covering various length-scales of changing inter-atomic distances during laser-induced reactions and thus provides information complementary to the “local” element-specific X-ray absorption spectroscopy. Compared to EXAFS, the global sensitivity of WAXS offers information also on variation of large distances. A TR-WAXS experiment was carried out on Cu₂(NSSN)₂(OTf)₂ solution in DFB as described in the experimental section. The difference scattering signal as a function of momentum transfer q at 100 ps delay is shown in Fig. 7. The momentum transfer is represented as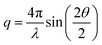 , where λ is the X-ray wavelength and 2θ is the scattering angle. Unlike XAS, the elastic X-ray scattering technique has no element selectivity and therefore is generally sensitive to all interatomic distances present in solution. Within the chosen analysis framework the laser-induced response of the solvent bulk is obtained empirically within a reference measurement as reported in the experimental part while the changes in the solute–solvent interatomic distances, or the solvent cage term, are neglected. The TR-WAXS signal component originating from the structural changes in the solute molecule was modelled using a set of candidate structures of the triplet ES and the crystallographic structure for the GS. However, the refinement of the configurational coordinate Q alone, as applied for the transient EXAFS data, is insufficient for accurate description of the solute scattering signals since changes in the overall structure of the complex have to be considered and not just in the first coordination shell of Cu as imposed by varying Q. In this respect for the Cu₂(NSSN)₂ complex it is essential to account for changes in relative positions of the two halves of the molecule around each copper. For each structure used in the transient EXAFS analysis, i.e. for a set of Q values along the S^cr₀ → T^cr₁ path, one of the S–S bonds in the complex was used as a rotation axis of the two isostructural entities of the molecule relative to each other (see Fig. 1). Such modification is motivated by the structural trend of the DFT prediction for the triplet state. In this way the second structural parameter, the Cu–S–S–Cu torsion angle ϕ, is added to the refinement procedure of the TR-WAXS data. The range for ϕ variation is chosen from 52° to 144°, limited by the GS value and the arising steric hindrance of further ligand movement within the molecule, respectively. The goodness of the fit was judged by the values of the χ_red² estimator. For detailed description of the signal modelling and data fitting procedures refer to the ESI.†χ_red² as a function of the structural parameters demonstrates a strong dependence on the Cu–S–S–Cu torsion angle ϕ (see the ESI,† Fig. S14 and S15b). The minimum of χ_red² is found at ϕ = 102° ± 2°, as compared to 99° predicted by DFT (see Fig. 8). On the other hand, the χ_red² estimator does not exhibit any significant dependence on the configurational coordinate, Q (ESI,† Fig. S15a). This is explained by small relative changes in the Cu–ligand bond lengths with varying Q (see Table 1). The largest change upon the coordination bond refinement for Q = 0.5–1.5 occurs on one of the Cu–S bonds and amounts to about 0.08 Å or ∼3% of the absolute bond length. In contrast, the relative rotation of two parts of molecules, i.e. variation of ϕ, causes changes of some interatomic distances by several Å. According to the Debye equation, the elastic scattering is most sensitive to inter-atomic distances between the heaviest atoms in the molecule.⁸² The sensitivity roughly scales as multiplication of the two atomic numbers. Therefore, changing the Cu–Cu distance gives the strongest contribution to the difference scattering. Moreover, since this distance is relatively long (compared to the Cu–ligand distances) the limited q-range of the experiment will accommodate a larger number of structural oscillations of the scattering signal greatly increasing the fit confidence and selectivity to the Cu–Cu distance compared to the shorter Cu–ligand distances. A quantitative illustration of the changes in the interatomic distances between Cu and ligand atoms upon different structural refinement is given in the ESI,† in Fig. S18 and S19. The effect of these particular changes in the atomic position on the calculated difference scattering from the solute, ΔS(q)_solute, demonstrates the contrasting sensitivity of the χ_red² to variations in ϕ and Q (see the ESI,† Fig. S17). The configurational coordinate, Q, has a weak influence on ΔS(q)_solute affecting mostly the signal amplitude, whereas changes in the torsion angle, ϕ, cause strong modifications in the overall signal shape.

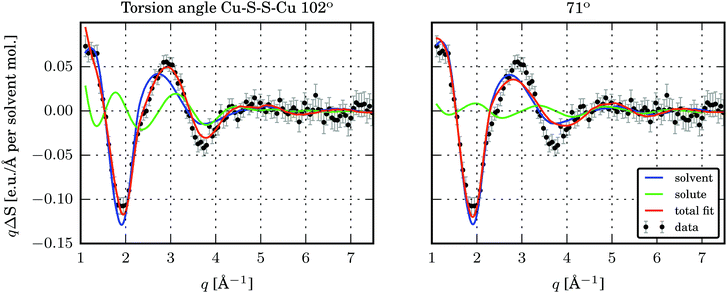Fig. 7 S(q) and best fits for two structures with different torsion angles Cu–S–S–Cu. Left: Torsion angle 102°, in the global minimum of χ_red². Right: Torsion angle 71°.

Fig. 8 Schematic representation of the states involved in the photocycle of Cu₂(NSSN)₂ derived from the results of transient optical and X-ray measurements. The right panel illustrates main structural changes associated with the T₁ triplet state formation as extracted from the time-resolved X-ray experiments. The bottom structure shows the changes in copper–ligand bond lengths in Å compared to the ground state structure extracted from the TR-EXAFS analysis. The top structure shows the torsion angle Cu–S–S–Cu coupled to the rotation between the two halves of Cu₂(NSSN)₂ around the S–S bond extracted from the TR-WAXS analysis.

Comparing the two fits in Fig. 7 it appears that for the given experimental conditions the structural sensitivity is most pronounced in the q-range of 2.5–4.5 Å⁻¹. At lower q values the solvent response dominates the signal, and starting from the q = 4.5 Å⁻¹ no oscillations can be distinguished within the noise. Further optimisation of the experimental conditions towards using solvents with weaker heating response and maximising the excited state fraction may help in enhancing the structural sensitivity of the method providing higher confidence in refinement of the ES structure. Moreover, achieving a better signal-to-noise ratio at higher q, where contributions of solute and solvent have comparable amplitudes, would further improve the structural resolution.

3.6 Lifetimes of the excited state from the time-resolved XAS and WAXS experiments

The transient spectra for both TR-XAS and TR-WAXS experiments were registered for a set of pump–probe delays. From these measurements the lifetime of the triplet excited state could be extracted. For TR-XAS the transient signal at 8982.3 eV (the biggest amplitude of the signal) was registered at delays up to 6 ns. For TR-WAXS the excited state fraction was extracted from fitting the data at pump–probe delays from 100 ps to 20 ns. Only the optimised structure of the solute ES was used in the fit, since there was no indication of the solute-related signal shape evolution within the range of delays, as shown in the ESI,† in Fig. S16. Both kinetic traces are shown in Fig. S13 in the ESI.† The data sets were fitted using a model of exponential decay to a constant offset, convolved with the Gaussian X-ray probe pulse, as described in the ESI.† TR-XAS data yield τ₁ = 1.53 ± 0.04 ns lifetime for ACN solution. The lifetime in DFB, obtained from TR-WAXS, is 2.9 ± 0.7 ns. This observation is in agreement with the general trend that lifetimes of excited states of molecules in a more polar and coordinating solvent (ACN) are shorter.²⁹ However, with the low precision of determination of the lifetime in DFB, as well as different experimental conditions for two solvents, it is difficult to make reliable conclusions about the solvent effect. In the literature about Cu–bisphenantroline complexes the question of solvent coordination in the excited state is widely discussed.^29,31 The driving force for exciplex formation is flattening of coordination polyhedron and preference of Cu(II) for the 5- and 6-coordinated states. TR-EXAFS and TA measurements were performed in a coordinating solvent, acetonitrile, which potentially could form an exciplex with the excited state of Cu₂(NSSN)₂. However, DFT predicts only small flattening of the copper coordination polyhedron—from 89° to 75° (angle between ligand chelate planes). It does not seem to be feasible that a solvent molecule could coordinate copper in this geometry. However, we have not addressed this question in more detail.

3.7 Summary and discussion of the photoexcitation cycle

Based on the results presented above, we elucidate the main steps in the photocycle and structural dynamics of solvated Cu₂(NSSN)₂, as shortly summarised below and in Fig. 8.

The main MLCT absorption band in the UV-Vis spectrum (3d(Cu) → σ*(S–S)) shows a maximum at 410–420 nm. As evident from the UV-Vis transient absorption spectra, after exciting this MLCT transition with 400 nm photons at least 60% of the excited molecules undergo fast radiationless deexcitation to the ground state with ∼650 fs time constant. This ultrafast decay competes with transitions to the lowest singlet state S₁. The remaining fraction of the excited species undergoes further evolution with a lifetime of 11 ps which we assign as ISC to the triplet state ³MLCT. In this state DFT predicts strong structural changes, which were followed by the 100 ps time-resolved synchrotron-based experiments, TR-XAS and TR-WAXS. The combination of these techniques gives access to different structural degrees of freedom of the excited state of the Cu₂(NSSN)₂ complex. In particular, TR-EXAFS yields the following Cu–ligand distance changes (symmetric on both copper atoms): Cu–N = −0.046(6) and +0.0099(13) Å, Cu–S = +0.040(5) and −0.091(12) Å as shown in Fig. 8. The energy shift dE = 1.4^+0.2_−0.4 eV and excited state fraction f = 10.0^+3.5_−1.0% are in agreement with estimations (0 < dE ≤ 3 eV, f ≥ 7%). The TR-WAXS fit was not sensitive to the refinement of the coordination bond lengths in the excited state. However, it showed strong sensitivity to the value of the torsion angle Cu–S–S–Cu coupled to the relative movement of the two halves of the molecule, which was beyond the sensitivity of TR-EXAFS data. This angle was found to be 102° ± 2° as shown in Fig. 8 (compared to 99° predicted by DFT). Thus, TR-XAS and TR-WAXS applied in this work complemented each other and allowed us to evaluate the most relevant structural changes occurring in the photoexcited state. For a solution at room temperature, the T₁ → S₀ transition follows the non-radiative pathway, therefore its lifetime could not be measured in a luminescence experiment and was extracted from both X-ray experiments in different solvents. The solution of Cu₂(NSSN)₂ in ACN (TR-XAS) demonstrates a lifetime of 1.53 ± 0.04 ns, while DFB solution yields a lifetime of 2.9 ± 0.7 ns (TR-WAXS), as shown in Fig. S13 in the ESI.† The fact that the resulting lifetimes are quite similar, as well as small flattening of the coordination polyhedron predicted by DFT, do not support the assumption of solvent coordination in the excited state. However, the long-lived component of the excited state transients extracted from both XAS and WAXS for the two solvents indicates the formation of another metastable state, T₁′, that could be associated with partial intercalation of solvent molecules in the space between the two halves of the solute in its triplet state. In order to better address this question, a TA experiment in the ns regime (laser flash photolysis) could be performed under the same experimental conditions for different solvents. It should be noted that the performed experiments are not directly sensitive to the S–S bonding. In order to probe the cleavage and recombination of this bond directly, it could be interesting to perform a TR-XAS experiment on the sulfur K-edge as recently reported in ref. 84 and85.

4 Conclusions

In this work we studied the effect of the photoinduced metal-to-ligand charge transfer on the local environment of copper and the global shape of the molecule in a dicopper complex with disulfide and guanidine ligands Cu₂(NSSN)₂. Photoexcitation in the blue part of the visible spectrum populates an antibonding orbital of the disulfide bridge, causing S–S bond cleavage, which is reversible since the complex remains bound via the second disulfide bridge. The long-term air and radiation stability makes Cu₂(NSSN)₂ a good model to study S–S bond cleavage and recombination. At the same time, photoexcitation of a MLCT band models electron transfer from metal to ligands, which is relevant for the biological function of certain Cu–S enzymes. In particular for Cu₂(NSSN)₂ the charge transfer causes conversion from disulfide to thiolate coordination. Disulfide–thiolate interconversion is frequent in nature where it is found as one of the mechanisms of formation of the tertiary structure of proteins and protection of cells from oxidative stress.⁸⁶ For this copper model system the disulfide–thiolate conversion can be achieved by both population of the antibonding orbital of the S–S bridge via photoexcitation and by chemical reaction with chloride ions.¹⁴

This work demonstrates that combining time-resolved X-ray absorption spectroscopy and wide-angle X-ray scattering has great potential for studies of photoinduced changes in molecular systems in solution. This is one of the first studies where these two structurally-sensitive methods are applied together to investigate the photochemistry of a dinuclear copper complex providing insight into different structural aspects of the excited state.

Author contributions

M. N., M. Rüb. and G. H. designed the experiment. D. K., A. B., M. N., and N. K. performed the WAXS experiments; D. K. analysed the data. M. Reb, M. K., S. E., and M. N. performed the TA experiments; M. Reb. analysed the data. B. D., M. Bied., B. G.-L., M. N., and S. E. performed the TR-XAS experiments; M. N. analysed the data. M. Rohr. performed the DFT calculations. R. S., M. Bauer and M. N. acquired static XAS; M. N. and R. S. analysed the data. A. N. and J. O. synthesised the sample. M. N., D. K., M. Reb., M. Rohr., A. B., C. B. and M. Rüb. wrote the paper. All authors contributed to the interpretation of the results and the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors would like to thank Alke Meents, Dennis Goeries as well as Anja Burkhardt and other staff of beamline P11 for their support during TR-XAS measurements. The authors would like to acknowledge Sebastian Schulz, Peter Zalden, Christina Bömer and beamline scientist Michael Wulff for the support of TR-WAXS measurements at ID09b, as well as Olivier Mathon and the beamline staff of BM23 for the support of the static XAS measurements. M. N. thanks Vadim Murzin and Wolfgang Caliebe for supporting XAS measurements at beamline P64 of Petra III and Tadesse Abebaw Assefa for discussions of TR-EXAFS data analysis. M. Bauer thanks the synchrotron ANKA for provision of beamtime and Stefan Mangold for assistance during the experiment. Most of the plots were prepared using matplotlib.⁸⁷ DFT calculations were performed by using grants of the Paderborn Center for Parallel Computing PC² and the Höchstleistungs-Rechenzentrum Stuttgart. The authors acknowledge the financial support by DFG FOR1405 “BioCTDyn” and by the Federal Ministry of Education and Research of Germany (BMBF) in the framework of “Erforschung kondensierter Materie”. M. Reb., S. E., M. K. and J. A. thank ELI Extreme Light Infrastructure Phase 2 (CZ.02.1.01/0.0/0.0/15_008/0000162) and ELIBIO (CZ.02.1.01/0.0/0.0/15_003/0000447) from the European Regional Development Fund for financial support. J. A. additionally thanks the Ministry of Education, Youth and Sports as part of targeted support from the National Programme of Sustainability II with registration number LQ1606, the Röntgen Ångström Cluster and Chalmers Area of Advance, Material science.

References

1. E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659–3853.
2. C. Belle, W. Rammal and J. L. Pierre, J. Inorg. Biochem., 2005, 99, 1929–1936.
3. M. H. M. Olsson, U. Ryde, B. O. Roos and K. Pierloot, J. Biol. Inorg. Chem., 1998, 3, 109–125.
4. R. P. Houser, J. A. Halfen, V. G. Young Jr., N. J. Blackburn and W. B. Tolman, J. Am. Chem. Soc., 1995, 117, 10745–10746.
5. R. P. Houser, V. G. Young and W. B. Tolman, J. Am. Chem. Soc., 1996, 118, 2101–2102.
6. N. D. J. Branscombe, A. J. Blake, A. Marin-Becerra, W.-S. Li, S. Parsons, L. Ruiz-Ramirez and M. Schröder, Chem. Commun., 1996, 2573–2574.
7. S. Itoh, M. Nagagawa and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 4087–4088.
8. Y. Ueno, Y. Tachi and S. Itoh, J. Am. Chem. Soc., 2002, 124, 12428–12429.
9. A. I. Uraev, I. S. Vasilchenko, V. N. Ikorskii, T. A. Shestakova, A. S. Burlov, K. A. Lyssenko, V. G. Vlasenko, T. A. Kuz'menko, L. N. Divaeva, I. V. Pirog, G. S. Borodkin, I. E. Uflyand, M. Y. Antipin, V. I. Ovcharenko, A. D. Garnovskii and V. I. Minkin, Mendeleev Commun., 2005, 15, 133–135.
10. W. Rammal, C. Belle, C. Béguin, C. Duboc, C. Philouze, J.-L. Pierre, L. L. Pape, S. Bertaina, E. Saint-Aman and S. Torelli, Inorg. Chem., 2006, 45, 10355–10362.
11. N. Roy, S. Sproules, E. Bothe, T. Weyhermüller and K. Wieghardt, Eur. J. Inorg. Chem., 2009, 2655–2663.
12. M. Gennari, J. Pécaut, S. DeBeer George, F. Neese, M.-N. Collomb and C. Duboc, Angew. Chem., Int. Ed., 2011, 50, 5662–5666.
13. A. Neuba, U. Flörke, W. Meyer-Klaucke, M. Salomone-Stagni, E. Bill, E. Bothe, P. Höfer and G. Henkel, Angew. Chem., Int. Ed. Engl., 2011, 50, 4503–4507.
14. A. Neuba, R. Haase, W. Meyer-Klaucke, U. Flörke and G. Henkel, Angew. Chem., Int. Ed. Engl., 2012, 51, 1714–1718.
15. E. I. Solomon, R. K. Szilagyi, S. Debeer George and L. Basumallick, Chem. Rev., 2004, 104, 419–458.
16. R. Sarangi, S. DeBeer George, D. J. Rudd, R. K. Szilagyi, X. Ribas, C. Rovira, M. Almeida, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 2316–2326.
17. A. Jesser, M. Rohrmüller, W. G. Schmidt and S. Herres-Pawlis, J. Comput. Chem., 2014, 35, 1–17.
18. M. Witte, U. Gerstmann, A. Neuba, G. Henkel and W. G. Schmidt, J. Comput. Chem., 2016, 37, 1005–1018.
19. L. X. Chen, Science, 2001, 292, 262–264.
20. M. Saes, C. Bressler, R. Abela, D. Grolimund, S. L. Johnson, P. A. Heimann and M. Chergui, Phys. Rev. Lett., 2003, 90, 047403.
21. W. Gawelda, C. Bressler, M. Saes, M. Kaiser, A. Tarnovsky, D. Grolimund, S. L. Johnson, R. Abela and M. Chergui, Phys. Scr., 2005, T115, 102–106.
22. H. Ihee, M. Wulff, J. Kim and S.-i. Adachi, Int. Rev. Phys. Chem., 2010, 29, 453–520.
23. D. Goeries, B. Dicke, P. Roedig, N. Stübe, J. Meyer, A. Galler, W. Gawelda, A. Britz, P. Geßler, H. Sotoudi Namin, A. Beckmann, M. Schlie, M. Warmer, M. Naumova, C. Bressler, M. Rübhausen, E. Weckert and A. Meents, Rev. Sci. Instrum., 2016, 87, 053116.
24. A. Britz, T. A. Assefa, A. Galler, W. Gawelda, M. Diez, P. Zalden, D. Khakhulin, B. Fernandes, P. Gessler, H. S. Namin, A. Beckmann, M. Harder, H. Yavas and C. Bressler, J. Synchrotron Radiat., 2016, 23, 1409–1423.
25. L. X. Chen, G. Jennings, T. Liu, D. J. Gosztola, J. P. Hessler, D. V. Scaltrito and G. J. Meyer, J. Am. Chem. Soc., 2002, 124, 10861–10867.
26. L. X. Chen, G. B. Shaw, I. Novozhilova, T. Liu, G. Jennings, K. Attenkofer, G. J. Meyer and P. Coppens, J. Am. Chem. Soc., 2003, 125, 7022–7034.
27. G. Smolentsev, A. V. Soldatov and L. X. Chen, J. Phys. Chem. A, 2008, 112, 5363–5367.
28. J. V. Lockard, S. Kabehie, J. I. Zink, G. Smolentsev, A. Soldatov and L. X. Chen, J. Phys. Chem. B, 2010, 114, 14521–14527.
29. T. J. Penfold, S. Karlsson, G. Capano, F. A. Lima, J. Rittmann, M. Reinhard, M. Rittmann-Frank, O. Braem, E. Baranoff, R. Abela, I. Tavernell, U. Rothlisberger, C. J. Milne and M. Chergui, J. Phys. Chem. A, 2013, 117, 4591–4601.
30. G. Capano, M. Chergui, U. Rothlisberger, I. Tavernelli and T. J. Penfold, J. Phys. Chem. A, 2014, 118, 9861–9869.
31. M. W. Mara, K. A. Fransted and L. X. Chen, Coord. Chem. Rev., 2015, 282-283, 2–18.
32. G. Capano, C. J. Milne, M. Chergui, U. Rothlisberger, I. Tavernelli and T. J. Penfold, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 214001.
33. I. B. Bersuker, Electronic structure and properties of transition metal compounds: introduction to the theory, 2010.
34. M. Iwamura, S. Takeuchi and T. Tahara, J. Am. Chem. Soc., 2007, 129, 5248–5256.
35. L. Hua, M. Iwamura, S. Takeuchi and T. Tahara, Phys. Chem. Chem. Phys., 2015, 17, 2067–2077.
36. L. S. Forster, Coord. Chem. Rev., 2006, 250, 2023–2033.
37. Z. A. Siddique, Y. Yamamoto, T. Ohno and K. Nozaki, Inorg. Chem., 2003, 42, 6366–6378.
38. K. A. Fransted, N. E. Jackson, R. Zong, M. W. Mara, J. Huang, M. R. Harpham, M. L. Shelby, R. P. Thummel and L. X. Chen, J. Phys. Chem. A, 2014, 118, 10497–10506.
39. D. M. Zink, D. Volz, T. Baumann, M. Mydlak, H. Flügge, J. Friedrichs, M. Nieger and S. Bräse, Chem. Mater., 2013, 25, 4471–4486.
40. B. Grimm-Lebsanft, PhD thesis, Hamburg University, 2016.
41. M. Wulff, A. Plech, L. Eybert, R. Randler, F. Schotte and P. Anfinrud, Faraday Discuss., 2002, 122, 13–26.
42. H. Ihee, Science, 2005, 309, 1223–1227.
43. K. S. Kjær, T. B. van Driel, J. Kehres, K. Haldrup, D. Khakhulin, K. Bechgaard, M. Cammarata, M. Wulff, T. J. Sørensen and M. M. Nielsen, Phys. Chem. Chem. Phys., 2013, 15, 15003–15016.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, 2009.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
46. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
47. A. D. Becke, J. Comput. Chem., 1999, 20, 63–69.
48. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
49. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
50. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
51. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
52. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
53. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
54. G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107.
55. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
56. M. Rohrmüller, A. Hoffmann, C. Thierfelder, S. Herres-Pawlis and W. G. Schmidt, J. Comput. Chem., 2015, 36, 1672–1685.
57. A. Neuba, M. Rohrmüller, R. Hölscher, W. G. Schmidt and G. Henkel, Inorg. Chim. Acta, 2015, 430, 225–238.
58. A. Hoffmann, S. Binder, A. Jesser, R. Haase, U. Flörke, M. Gnida, M. Salomone Stagni, W. Meyer-Klaucke, B. Lebsanft, L. E. Grünig, S. Schneider, M. Hashemi, A. Goos, A. Wetzel, M. Rübhausen and S. Herres-Pawlis, Angew. Chem., Int. Ed. Engl., 2014, 53, 299–304.
59. L. G. Warner, T. O. R. Ottersen and K. Seff, Inorg. Chem., 1974, 8, 2819–2826.
60. E. A. Ambundo, M.-V. Deydier, A. J. Grall, N. Aguera-Vega, L. T. Dressel, T. H. Cooper, M. J. Heeg, L. A. Ochrymowycz and D. B. Rorabacher, Inorg. Chem., 1999, 38, 4233–4242.
61. T. Ohta, T. Tachiyama, K. Yoshizawa, T. Yamabe, T. Uchida and T. Kitagawa, Inorg. Chem., 2000, 39, 4358–4369.
62. J. A. Thich, D. Mastropaolo, J. Potenza and H. J. Schugar, J. Am. Chem. Soc., 1974, 96, 726–731.
63. K. Miyoshi, Y. Sugiura, K. Ishizu, Y. Iitaka and H. Nakamura, J. Am. Chem. Soc., 1980, 102, 6130–6136.
64. M. L. Brader, E. W. Ainscough, E. N. Baker, A. M. Brodie and D. A. Lewandoski, J. Chem. Soc., Dalton Trans., 1990, 2089–2094.
65. J. Niclos-Gutiérrez, E. Abarca-Garcia, B. Viossat, D. Nguyen-Huy, A. Busnot and J. F. Hemidy, Acta Crystallogr., 1993, C49, 19–22.
66. J. M. González-Pérez, D. Choquesillo-Lazarte, A. Domínguez-Martín, E. Vílchez-Rodríguez, I. Pérez-Toro, A. Castiñeiras, O. K. Arriortua, M. E. García-Rubiño, A. Matilla-Hernández and J. Niclós-Gutiérrez, Inorg. Chim. Acta, 2016, 452, 258–267.
67. S. Fox, R. T. Stibrany, J. A. Potenza, S. Knapp and H. J. Schugar, Inorg. Chem., 2000, 39, 4950–4961.
68. J. T. York, E. C. Brown and W. B. Tolman, Angew. Chem., Int. Ed., 2005, 44, 7745–7748.
69. L. Bergmann, G. J. Hedley, T. Baumann, S. Bräse and I. D. W. Samuel, Sci. Adv., 2016, 2, e1500889.
70. M. Iwamura, H. Watanabe, K. Ishii, S. Takeuchi and T. Tahara, J. Am. Chem. Soc., 2011, 133, 7728–7736.
71. M. Sandroni, A. Maufroy, M. Rebarz, Y. Pellegrin, E. Blart, C. Ruckebusch, O. Poizat, M. Sliwa and F. Odobel, J. Phys. Chem. C, 2014, 118, 28388–28400.
72. A. Vlček Jr., Coord. Chem. Rev., 2000, 200–202, 933–977.
73. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
74. A. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565–7576.
75. N. Binsted, EXCURV98: CCLRC Daresbury Laboratory Computer Program, CCLRC Daresbury Laboratory, Warrington, UK, 1998.
76. L. S. Kau, D. J. Spira-Solomon, J. E. Penner-Hahn, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1987, 109, 6433–6442.
77. R. K. Hocking and E. I. Solomon, Struct. Bonding, 2012, 142, 155–184.
78. M. Sano, S. Komorita and H. Yamatera, Inorg. Chem., 1992, 31, 459–463.
79. Molecular Electronic Structures of Transition Metal Complexes I, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer, 2012.
80. W. Gawelda, V.-T. Pham, R. M. van der Veen, D. Grolimund, R. Abela, M. Chergui and C. Bressler, J. Chem. Phys., 2009, 130, 124520.
81. R. van der Veen, C. Milne, A. El Nahhas, F. Lima, V.-T. Pham, J. Best, J. Weinstein, C. Borca, R. Abela, C. Bressler and M. Chergui, Angew. Chem., Int. Ed., 2009, 48, 2711–2714.
82. M. Christensen, K. Haldrup, K. Bechgaard, R. Feidenhans'l, Q. Kong, M. Cammarata, M. L. Russo, M. Wulff, N. Harrit and M. M. Nielsen, J. Am. Chem. Soc., 2009, 131, 502–508.
83. J. H. Lee, M. Wulff, S. Bratos, J. Petersen, L. Guerin, J.-C. Leicknam, M. Cammarata, Q. Kong, J. Kim, K. B. Møller and H. Ihee, J. Am. Chem. Soc., 2013, 135, 3255–3261.
84. M. Ochmann, I. von Ahnen, A. A. Cordones, A. Hussain, J. H. Lee, K. Hong, K. Adamczyk, O. Vendrell, T. K. Kim, R. W. Schoenlein and N. Huse, J. Am. Chem. Soc., 2017, 139, 4797–4804.
85. B. E. V. Kuiken, M. R. Ross, M. L. Strader, A. A. Cordones, H. Cho, J. H. Lee, R. W. Schoenlein and M. Khalil, Struct. Dyn., 2017, 4, 044021.
86. R. C. Fahey, in Biologically Important Thiol-Disulfide Reactions and the Role of Cyst(E)Ine in Proteins: an Evolutionary Perspective, ed. M. Friedman, Springer US, Boston, MA, 1977, pp. 1–30.
87. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.

---

Footnotes

† Electronic supplementary information (ESI) available: Comparison of the DFT-calculated and experimental UV-Vis absorption spectra; details of the ground state EXAFS fitting; estimation of the excited state fraction in the different pump-probe experiments; TR-EXAFS data extraction and analysis; TR-WAXS: data analysis and sensitivity of the calculated transient scattering signal to the refinement of structural parameters; technical description of the setup for transient absorption in UV-Vis; comparative kinetic behavior of the sample in different solvents. See DOI: 10.1039/c7cp04880g

‡ These authors contributed equally to this work.

§ Present address: Max-Planck Institut für Kohlenforschung, 45470 Mülheim an der Ruhr, Germany.

---