Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Competitive DNA binding of Ru(bpy)2dppz2+ enantiomers studied with isothermal titration calorimetry (ITC) using a direct and general binding isotherm algorithm†
Anna K. F.
Mårtensson
 and
Per
Lincoln
*
and
Per
Lincoln
*
Department of Chemistry and Chemical Engineering, Chalmers University of Technology, SE-41296 Gothenburg, Sweden. E-mail: lincoln@chalmers.se
First published on 13th December 2017
Abstract
While isothermal titration calorimetry (ITC) is widely used and sometimes referred to as the “gold standard” for quantitative measurements of biomolecular interactions, its usage has so far been limited to the analysis of the binding to isolated, non-cooperative binding sites. Studies on more complicated systems, where the binding sites interact, causing either cooperativity or anti-cooperativity between neighboring bound ligands, are rare, probably due to the complexity of the methods currently available. Here we have developed a simple algorithm not limited by the complexity of a binding system, meaning that it can be implemented by anyone, from analyzing systems of simple, isolated binding sites to complicated interactive multiple-site systems. We demonstrate here that even complicated competitive binding calorimetric isotherms can be properly analyzed, provided that ligand–ligand interactions are taken into account. As a practical example, the competitive binding interactions between the two enantiomers of Ru(bpy)2dppz2+ (Ru-bpy) and poly(dAdT)2 (AT-DNA) are analyzed using our new algorithm, which provided an excellent global fit for the ITC experimental data.
Introduction
When studying the binding interactions between a ligand and a macromolecule, isothermal titration calorimetry (ITC) has many advantages. It is a powerful, high-precision tool that is often referred to as the “gold standard” for quantitative measurements of biomolecular interactions, and the only direct thermodynamic method that enables full thermodynamic characterization (stoichiometry, association constant, enthalpy and entropy of binding) of the interaction after a single titration experiment. However, the currently available analysis software is generally limited to the analysis of multiple binding systems with isolated (i.e. non-interactive) binding sites, and cannot adequately take into account cooperative or anti-cooperative interactions inherent in the binding of large ligands to DNA.1In our previous ITC studies on ruthenium complexes intercalating into DNA, a generalized McGhee–von Hippel binding isotherm algorithm was utilized to account for binding site interactions.2,3 However, the algorithm employed4 in our earlier work involves two nested iterations: the inner iteration for solving the secular equations, the outer for solving the mass-balance equations. This algorithm has never got a wide-spread use, not unlikely due to its complexity and limited efficiency. Moreover, it is limited to describe interactions between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding site
1 binding site![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand equilibria.
ligand equilibria.
Here we present a much improved and simplified algorithm, which iterates the mass balance equations directly with just 14 lines of the MATLAB code (see the ESI†). The new method is very general, and is no longer limited to just the nearest-neighbor interactions between bound ligands, since higher than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding site
1 binding site![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand equilibria can be treated just as easy. While this method can be utilized for modelling ligand binding to any type of linear biopolymers (such as actin, myosin or tubulin), we anticipate that the most frequent usage would be for studying the binding affinity of ligands to the closely spaced binding sites of DNA.
ligand equilibria can be treated just as easy. While this method can be utilized for modelling ligand binding to any type of linear biopolymers (such as actin, myosin or tubulin), we anticipate that the most frequent usage would be for studying the binding affinity of ligands to the closely spaced binding sites of DNA.
The intercalation ability of ligands to DNA is commonly determined by ethidium bromide displacement assays.5–8 This method was scrutinized in a recent study, using ITC as an alternative non-label method.9 However, the study focused on whether ethidium bromide displacement ability could automatically be interpreted as the intercalation potential of small molecules, not addressing the issue with ligand–ligand interactions. Most often, ITC experiments included in competitive binding studies are limited to the determination of thermodynamic parameters, ignoring ligand–ligand interactions. There are a few notable examples of ITC data analysis methods that are capable of adequately analysing more complex ligand–macromolecule systems. One such example is the AFFINImeter software (S4SD), which is capable of the global fitting of non-standard binding models, such as competing ligands to a multiple site receptor. However, while several case studies are available exemplifying the resourcefulness of the method,10 a binding system of a repetitive one-dimensional lattice of closely spaced binding sites (e.g. DNA) is not included. Perhaps for that reason, nearest-neighbor cooperativity is not addressed either. In addition, Buurma and Haq have developed a general software package, denoted IC-ITC, capable of analysing ITC data with a model including two independent binding sites and taking ligand self-aggregation into account.11
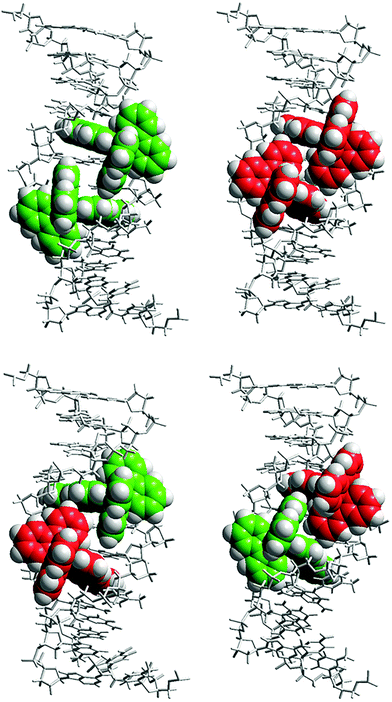
To exemplify the practical usage of our algorithm, we have conducted a series of competitive ITC experiments titrating enantiopure Ru(bpy)2dppz2+ (Ru-bpy; bpy = 2,2′-bipyridine; dppz = dipyrido[3,2-a:2′,3′-c]phenazine) into a solution of poly(dAdT)2 (AT-DNA). Ru-bpy is an intercalating Ru(II) polypyridyl complex with a strong binding affinity to DNA (and a slight preference towards A–T base pairs). The complex has an octahedral coordination geometry resulting in two possible configurations, a right-handed (Δ) and a left-handed (Λ) propeller-like structure (Fig. 1).
It is well-established that it is the dppz moiety that intercalates between the base pairs of the DNA helix using both spectroscopic and biophysical methods as well as using X-ray crystallography.12–20 However, while the intercalating properties of Ru(II) polypyridyl complexes are certainly important, it is becoming more and more apparent that the molecular structure of the ancillary ligands has a strong influence on the binding characteristics of a complex,21–25 including complex–complex interactions.2,3,26 It has often been neglected to take into account the cooperative and anti-cooperative behaviour of DNA-bound dppz-based Ru-centred structures when analysing the complex-DNA interactions.
Only recently have high-resolution structures and calorimetric studies emerged that have revealed nearest-neighbor interactions as a possible explanation to the complicated thermodynamic profiles of these complexes.2,3,16–19,26,27 The non-classical ITC curves previously reported for Ru(L)2dppz2+ complexes (L = bpy or phen (phen = 1,10-phenanthroline)) have been attributed to an additional enthalpy contribution from neighboring complexes on the DNA as saturation of binding sites increases.2,3 DNA, being a right-handed helical structure, would assumingly interact differently with the Δ and Λ-enantiomers of tri-bidentate complexes, and previous results obtained using calorimetry do indeed indicate the Δ-form of both Ru-bpy and Ru-phen to have a stronger binding affinity towards DNA.2,14
Analysis of a single enantiomer – DNA ITC titration with a simple neighbor interaction lattice model requires 3 binding parameters (the intrinsic binding constant K, the cooperativity parameter yaa and n, the number of basepairs covered by the bound ligand) and two enthalpy parameters (the intrinsic binding enthalpy  and ligand–ligand interaction enthalpy
and ligand–ligand interaction enthalpy 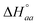 ), thus determining the thermodynamic characteristics of Δ- and ΛRu-bpy binding requires (6 + 4) fitting parameters.3 By augmenting the dataset with two continued titrations, in which one enantiomer is titrated into DNA saturated with the opposite enantiomer, the consistency of the model can be scrutinized by performing a global analysis of all 4 titrations with only two additional fitting parameters (yab and
), thus determining the thermodynamic characteristics of Δ- and ΛRu-bpy binding requires (6 + 4) fitting parameters.3 By augmenting the dataset with two continued titrations, in which one enantiomer is titrated into DNA saturated with the opposite enantiomer, the consistency of the model can be scrutinized by performing a global analysis of all 4 titrations with only two additional fitting parameters (yab and  ).
).
Recently, Mikek et al. showed that the non-classical ITC curves, which arise upon titration of a 25-bp DNA oligomer duplex with ruthenium dppz complexes, can be excellently fitted with a two independent site binding model with 4 binding parameters (K1, K2, f1 and f2) and 2 enthalpy parameters ( and
and  ) per titration.28 Since the binding site fractions f1 and f2 were found to be reasonably similar for both enantiomers, one could envisage that a global analysis with the two independent site model on the augmented data set could provide an alternative interpretation to the lattice based models.
) per titration.28 Since the binding site fractions f1 and f2 were found to be reasonably similar for both enantiomers, one could envisage that a global analysis with the two independent site model on the augmented data set could provide an alternative interpretation to the lattice based models.
Our previous ITC studies on binding of Ru(L)2dppz2+ complexes to poly(dAdT)2 have modeled the DNA as a homo-polymer of identical intercalation pockets.2,3 Crystallographic studies from the Cardin group have convincingly shown that the Λ-enantiomer of Ru(L)2dppz2+ type complexes strongly prefers 5′-TA-3′ to 5′-AT-3′.17 Thus, it is further of considerable interest to investigate a more realistic binding model, in which the two alternating intercalation pockets of poly(dAdT)2 are explicitly accounted for.
Experimental
Materials and sample preparation
All experiments were performed in an aqueous buffer solution (pH = 7.0) containing 150 mM NaCl and 1 mM cacodylate (dimethylarsinic acid sodium salt). A stock solution of poly(dAdT)2 (AT-DNA) (∼5 mM nucleotides) was prepared by dissolving the sodium salt (Sigma-Aldrich) in buffer. Stock solutions of the complexes (∼1 mM) were prepared by dissolving the chloride salts in buffer. Concentrations were determined spectrophotometrically using extinction coefficients: ε260 = 6600 M−1 cm−1 per nucleotide for AT-DNA, and ε444 = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 M−1 cm−1 for Ru(bpy)2dppz2+. For ITC measurements the DNA solution was dialyzed against pure buffer for at least 48 hours at 8 °C. Ruthenium complex solutions of appropriate concentrations were prepared by dilution of the stock solutions in the dialysate. The dialysis membrane used had a molecular weight cut-off of 3.5–5 kDa (Spectra-Por® Float-A-Lyzer® G2, Sigma-Aldrich).
100 M−1 cm−1 for Ru(bpy)2dppz2+. For ITC measurements the DNA solution was dialyzed against pure buffer for at least 48 hours at 8 °C. Ruthenium complex solutions of appropriate concentrations were prepared by dilution of the stock solutions in the dialysate. The dialysis membrane used had a molecular weight cut-off of 3.5–5 kDa (Spectra-Por® Float-A-Lyzer® G2, Sigma-Aldrich).
Enantiopure Δ- and Λ-[Ru(bpy)2dppz]Cl2 used in this study were prepared as previously reported.20
Other chemicals were purchased from Sigma-Aldrich and used without purification.
Absorption spectra were measured on a Varian Cary 4000 UV/vis spectrophotometer (path length = 1 cm).
Isothermal titration calorimetry
Isothermal titration calorimetry (ITC) is a high-precision tool where the heat produced or absorbed upon addition of the complex to a DNA solution enables direct assessment of the binding free energy by integrating the power required to maintain the reference and sample cells at the same temperature. The experimental raw data consist of a series of heat flow peaks, and each peak corresponds to one injection of complex. These heat flow spikes are integrated with respect to time, which gives the total heat exchanged per mole injectant plotted against the ratio [Ru]/[base pairs].Calorimetric data were obtained using an ITC200 isothermal titration calorimeter (Microcal) controlled by Origin 7.0 software. The ITC profiles of the Δ and Λ enantiomers of Ru-bpy were obtained by a single injection of 1 μl followed by 19 sequential titrations in 2 μl aliquot injections of complex from a syringe stock solution (∼470 μM) into the sample cell (206 μl) loaded with AT-DNA in 150 mM NaCl aqueous solution (∼300 μM nucleotides). This was subsequently followed by an additional 20 sequential additions (single injection of 1 μl followed by 19 injections of 2 μl aliquots) of the opposite enantiomer into the sample cell now loaded with AT-DNA saturated by the first complex. All ITC experiments were performed at 25 °C. The injection spacing was 180 s, the syringe rotation was 750 rpm, and there was an initial delay of 120 s prior to the first injection. The concentration ranges used for the complex and DNA were set to span mixing ratios of [Ru]/[base pairs] from 0.08 to 0.6 for the first titration and from 0.7 to 1.4 for the second titration. The primary ITC data were corrected for the heat of complex dilution by subtracting the average heat per injection of the complex titrated into buffer. There was negligible heat arising from DNA dilution. The raw ITC data peaks were automatically integrated using the Origin 7.0 software. For improved accuracy of the integration, the integration range for each heat peak was narrowed to include ∼2/3 of the original range, thus reducing the background noise from the baseline.
Results
Derivation of the general binding isotherm algorithm
The problem of modelling binding equilibria between a set of ligands and an infinite one-dimensional lattice of identical binding site units is advantageously treated with the statistical thermodynamics of linear hetero-polymers, which can conveniently be cast into matrix equations. The binding site unit itself can be defined to consist of one or several polymer sub-units, and may provide one or several distinct ligand binding sites. The mathematical equivalence between the partition function and Markov chain formalisms have been demonstrated earlier,4 and although we here will use a variant of the elegant formulation by Chen of the ligand binding problem using the former formalism,29 the derivation uses the probabilistic Markov chain approach, implicit in the classical paper by McGhee and von Hippel.30In the most general case, at equilibrium with L different ligands A (A = 1,…L), the initial homo-polymer of bare binding-site units has been converted into a hetero-polymer with N + 1 different types of elementary units i (i = 0, 1…N), where the unit 0 is the bare binding site unit, and the other N elementary units i are composed of ni consecutive binding site units and 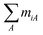 ligands. We denote ni the length, and miA the stoichiometric coefficient with respect to the ligand A, of the elementary unit i. At equilibrium, each elementary unit is further characterized by its binding density θi and its binding potential xi. The probability that a randomly chosen binding site unit is in the elementary unit i is given by niθi, and the binding densities thus give the total concentration of the bound ligand A:
ligands. We denote ni the length, and miA the stoichiometric coefficient with respect to the ligand A, of the elementary unit i. At equilibrium, each elementary unit is further characterized by its binding density θi and its binding potential xi. The probability that a randomly chosen binding site unit is in the elementary unit i is given by niθi, and the binding densities thus give the total concentration of the bound ligand A:
 | (1) |
The binding potential is a function of the intrinsic binding constant Ki (the equilibrium constant for the formation of elementary unit i from free ligands and ni consecutive bare binding site units in the absence of interactions with neighbor units) and the free ligand concentrations Afree:
 | (2) |
The interactions between neighboring elementary units are given by a set of non-negative cooperativity constants yij that are elements of the cooperativity matrix Y = [yij], i, j = 0, 1,…N. The product of the cooperativity constant yij and the intrinsic binding constants Ki and Kj gives the equilibrium constant Kij for formation of the two consecutive units i and j from free ligands and ni + nj consecutive bare binding sites in the absence of other neighbor interactions:
| Kij =KiKjyij | (3) |
Defining matrix M = [miA] and column vectors x = [xi], θ = [θi], k = [Ki], cf = [Afree] and cb = [Abound] (i = 1,…N; A = 1,…L), eqn (1) and (2) can be expressed in matrix notation:
| cb = B0MTθ | (4) |
x = exp[ln(k) + M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) ln(cf)] ln(cf)] | (5) |
Given that an N by N non-singular transformation matrix T can be constructed such that the product TM has only 0 and 1 as elements, with exactly one 1 in each row but no zero columns; N mass balance equations can be set up:
| TMc0 = exp(T[ln(x) − ln(k)]) + B0TMMTθ | (6) |
In order to solve eqn (6), the relation between x, θ and Y has to be made explicit. Given any positive N vector r, Y can be transformed into a stochastic matrix P with the constant row sum of 1:
| P = D(s)YD([1; r]) | (7) |
| si = (yi0 + yTir)−1, i = 0, 1,…N | (8) |
| pij = siyijrj | (9) |
Following the probabilistic approach of McGhee and von Hippel, the binding potential xi can, in the absence of neighbor interactions, be equated to the quotient between the probability of finding the elementary unit i, preceded by the elementary unit a and followed by the unit b, and the probability of finding a and b enclosing ni consecutive bare binding site units:
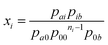 | (10) |
 | (11) |
| xi = siris0−ni | (12) |
For any primitive stochastic matrix, the constant N + 1 vector e = [1] is the right-hand eigenvector corresponding to the dominant eigenvalue 1:
| Pe = e | (13) |
| fTP = fT | (14) |
| fT[1; n] = 1 | (15) |
| fT = [(1 − θTn) θT] | (16) |
 | (17) |
| θT = PT01V−1, V = (I + npT01 − P11) | (18) |
Given cooperativity parameters in matrix Y and elementary unit lengths in column vector n, the vectors of binding potentials x and binding densities θ are thus functions of an N-vector r > 0 through eqn (7), (8), (12) and (18). Given intrinsic binding constants k, stoichiometric coefficients M, total ligand concentrations c0 and total binding site concentration B0, the mass balance eqn (6) can be rearranged to
| q = exp(T[ln(x) − ln(k)]) + TM (B0MTθ − c0) | (19) |
 | (20) |
 | (21) |
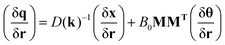 | (22) |
 | (23) |
 | (24) |
 | (25) |
 | (26) |
 | (27) |
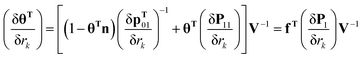 | (28) |
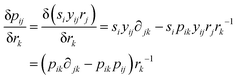 | (29) |
Insertion of eqn (29) in fT(δP1/δrk) gives
 | (30) |
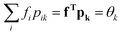 . Assembling the rows of eqn (30) into a matrix and transposing gives with eqn (28):
. Assembling the rows of eqn (30) into a matrix and transposing gives with eqn (28): | (31) |
Isothermal titration calorimetry and model fitting
Fig. 2 shows raw ITC data of titration of AT-DNA with the enantiomers ΔRu-bpy and ΛRu-bpy. To the left, the ligand is titrated into AT-DNA only. In accordance with our previous results, further injections with the same enantiomer (not shown) gave only very small, constant heat values, indicating full saturation of the DNA.2,3 However, when proceeding the titration by injecting the opposite enantiomer (Fig. 2, right) substantial enthalpy changes are observed, indicating that both enantiomers can displace each other on the DNA.In the global fitting of these ITC isotherms, a data point i in the ITC isotherm is assumed to be a sum of intrinsic and neighbor interaction binding enthalpies:
 | (32) |
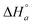 is the standard enthalpy change for the formation of elementary unit a from free ligands and binding sites in the absence of interactions with neighbor units and
is the standard enthalpy change for the formation of elementary unit a from free ligands and binding sites in the absence of interactions with neighbor units and 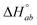 is the standard enthalpy change of the interaction between neighbor elementary units a and b. ΔHbaseline is a small constant, and is an approximation for various enthalpy contributions not included in the model and not corrected for by the subtraction of the heat of dilution. Examples of such possible contributions could be the different environment in the counter-ion distribution around the DNA compared to in buffer or weak association of the ruthenium complex cations with the saturated, but still negatively charged DNA.
is the standard enthalpy change of the interaction between neighbor elementary units a and b. ΔHbaseline is a small constant, and is an approximation for various enthalpy contributions not included in the model and not corrected for by the subtraction of the heat of dilution. Examples of such possible contributions could be the different environment in the counter-ion distribution around the DNA compared to in buffer or weak association of the ruthenium complex cations with the saturated, but still negatively charged DNA.
For the titration data point i, Δa(i), the change in the concentration (per mole of the injected ligand) of the elementary unit a from the preceding point i − 1, is calculated as B0(i)θa(i) − dfB0(i − 1)θa(i − 1), and the change in concentration (per mole of injected ligand) of nearest-neighbors Δab(i) is calculated as B0(i)θa(i)pab(i) − dfB0(i − 1)θa(i − 1)pab(i − 1), where, at data point i, B0(i) is the total concentration of binding site units divided with the mole amount of the injected ligand, and pab(i) is the conditional probability that ligand a is directly followed by ligand b on the DNA lattice. The dilution factor df is calculated as 1 − Vadd/Vcell. The ΔH° values were determined by a least-square projection of the column matrix with all the ITC data on the space spanned by the Δb and Δab columns, and 4 constant columns corresponding to the 4 baselines. The elements of the constant columns were 1 for the corresponding titration and zero elsewhere. The simulated ITC curves were then calculated with eqn (32) and the RMSD goodness-of-fit determined as the Euclidian norm of the difference between the measured and simulated data matrices, divided by the square root of the number of data points (here 76). To facilitate comparison with other ITC studies, we here report nRMSD values, i.e. RMSD normalized by division with the mean of the absolute values of the data (the mean value being 3.316 kJ per mol injectant for this data set). The MATLAB program ITCalgorithmModelX (as shown in the ESI†) performs this calculation, and was used with the non-linear optimization MATLAB routine fminsearch to find the parameter values for the best global fit to the experimental ITC data.
We have considered 5 models, which are schematically depicted as lattice models in Fig. 3. Models 1–3 consider both intrinsic 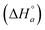 and neighbor interaction
and neighbor interaction 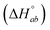 reaction enthalpies. Model 1 is the classical model, which takes the lattice subunit to be one base pair and thus assumes all intercalation pockets on the DNA to be equal. The binding site coverage vector n is allowed to vary in the fit, but is expected to take a value close to 2, i.e. nearest-neighbor exclusion, as observed for binding of most intercalators to DNA. Models 2 and 3 take the lattice subunit to be 2 base pairs (and n close to 1); in model 2 the subunit is assumed to bind Δ or Λ only in one way, modelling a strict TA (or AT) selectivity for both enantiomers. In model 3, this selectivity is relaxed for Δ which is assumed to be able to bind in either of the intercalation pockets 1 or 2 of the lattice subunit, while Λ only binds in pocket 1. Nearest-neighbor exclusion is followed since Λ1 or Δ1 cannot be directly followed by Δ2 (see Fig. 3). Models 4 and 5 assume two binding modes for each enantiomer, and consider only intrinsic reaction enthalpies
reaction enthalpies. Model 1 is the classical model, which takes the lattice subunit to be one base pair and thus assumes all intercalation pockets on the DNA to be equal. The binding site coverage vector n is allowed to vary in the fit, but is expected to take a value close to 2, i.e. nearest-neighbor exclusion, as observed for binding of most intercalators to DNA. Models 2 and 3 take the lattice subunit to be 2 base pairs (and n close to 1); in model 2 the subunit is assumed to bind Δ or Λ only in one way, modelling a strict TA (or AT) selectivity for both enantiomers. In model 3, this selectivity is relaxed for Δ which is assumed to be able to bind in either of the intercalation pockets 1 or 2 of the lattice subunit, while Λ only binds in pocket 1. Nearest-neighbor exclusion is followed since Λ1 or Δ1 cannot be directly followed by Δ2 (see Fig. 3). Models 4 and 5 assume two binding modes for each enantiomer, and consider only intrinsic reaction enthalpies  . In model 4, the two binding modes are modelled as two independent binding sites, for which the fraction of the total concentration of base pairs is a freely adjustable parameter, i.e. no lattice model is involved. It is possible to construct a mathematically equivalent lattice model in the case the fractions of the two binding sites have the same value, as shown for model 4* in Fig. 3. The lattice subunit contains here 4 base pairs, all yij = 1, and a third type of elementary unit with two bound ligands is required, for which the intrinsic binding constant K3 = K1K2. Model 4* gives numerically identical results to model 4 with only one value of the fraction parameter, but relaxing the independence of the two binding sites (by allowing the intrinsic binding constant of each of the 8 elementary units to vary independently) did only marginally improve the bad global fit. Although the location of the bound ligand(s) within the lattice subunit is arbitrary, Fig. 3 indicates a possible physical interpretation, where the two distinct sites of model 4* are assigned to intercalation from minor and major groove, respectively. Thus, model 4* can be interpreted as only permitting alternating minor and major groove intercalation for consecutive sequences of bound ligands. To simplify this idea, in model 5 two binding modes are defined, which must alternate in consecutive sequences, which hence only interact (yij ≠ 1) for different mode neighbors. The best fit of this model was obtained when the lattice subunit was defined to be one base pair, as depicted in Fig. 3.
. In model 4, the two binding modes are modelled as two independent binding sites, for which the fraction of the total concentration of base pairs is a freely adjustable parameter, i.e. no lattice model is involved. It is possible to construct a mathematically equivalent lattice model in the case the fractions of the two binding sites have the same value, as shown for model 4* in Fig. 3. The lattice subunit contains here 4 base pairs, all yij = 1, and a third type of elementary unit with two bound ligands is required, for which the intrinsic binding constant K3 = K1K2. Model 4* gives numerically identical results to model 4 with only one value of the fraction parameter, but relaxing the independence of the two binding sites (by allowing the intrinsic binding constant of each of the 8 elementary units to vary independently) did only marginally improve the bad global fit. Although the location of the bound ligand(s) within the lattice subunit is arbitrary, Fig. 3 indicates a possible physical interpretation, where the two distinct sites of model 4* are assigned to intercalation from minor and major groove, respectively. Thus, model 4* can be interpreted as only permitting alternating minor and major groove intercalation for consecutive sequences of bound ligands. To simplify this idea, in model 5 two binding modes are defined, which must alternate in consecutive sequences, which hence only interact (yij ≠ 1) for different mode neighbors. The best fit of this model was obtained when the lattice subunit was defined to be one base pair, as depicted in Fig. 3.
 | ||
| Fig. 3 Schematic illustration summarizing the 5 proposed lattice models of the DNA-ligand binding interactions. | ||
For each of the models, the number of fitting parameters (binding parameters, and for model 3 also the number of enthalpy parameters) was also gradually reduced from the full model by symmetry considerations or by assuming non-cooperativity. An overview of the goodness-of-fit of the different models is given in Fig. 4, which plots the relative RMSD of calculated and experimental ITC-data against the total number of fitting parameters. If non-cooperative binding is assumed for models 1–3 and 5 (all non-zero yij are set to 1), the RMSD increases by a factor of 2–5 compared to the best fit, as seen to the left in Fig. 4. While the non-interacting site model 4 makes a descent fit (nRMSD = 3.50%) when the fractions of site 1 and site 2 are allowed to have different values in all four different titrations (to the right in Fig. 4), restraining the 8 fractions of the global fit to take fewer different values makes the RMSD increase by a factor of about 2 (see Fig. S1 in the ESI†). On the other hand, for model 3 (total number of fitting parameters 9 + 7 = 16), which gives the lowest RMSD of all the models investigated here (nRMSD = 2.45%), the RMSD is only slightly increased (15%) if the binding and enthalpy parameters of Δ are constrained to be the same for the two base pair steps (total number of fitting parameters 7 + 5 = 12). Furthermore, for (7 + 5) parameter models 1–3, the best fit value of the yΔΔ cooperativity parameter was found to be close to one, and defining yΔΔ = 1 (i.e. fitting only 6 + 5 parameters) increased the RMSD by less than 0.5%. Fig. 5 shows the excellent fit of the (6 + 5) parameter model 3 to the integrated peaks of the raw data in Fig. 2. Model 5 performs almost as well as model 3, but since it requires a larger number of binding parameters for a comparable RMSD, the best fit values of these are not further considered here.
 | ||
| Fig. 4 Relative RMSD plotted against the total number of fitting parameters comparing the goodness-of-fit for all 5 models. | ||
An estimate for the sensitivity of the fitting parameters to changes in the model can be obtained from Table 1, which gives the values of the binding and enthalpy parameters, as well as the nRMSD, for the global fit of (6 + 5) parameter models 1–3. All three fits showed only small baseline enthalpy values, given in Table S1 in the ESI†.
| Model | Δ | Λ | ΔΔ | ΛΛ | ΔΛ | nΔ | nΛ | nRMSDb (%) | rRMSDc | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a RMSD decreases less than 0.5% if yΔΔ is allowed to vary: best fit values 1.22 (1), 1.28 (2), 1.09 (3). b nRMSD: RMSD normalized by division with the mean of the absolute values of the ITC data. c rRMSD (relative RMSD): RMSD divided by the RMSD of the (9 + 7) parameter fit of model 3 (nRMSD 2.45%). d K/106 M−1. e ΔH°/kJ mol−1. f Enclosed in parentheses; nRMSD and rRMSD of the non-cooperative (4 + 5) parameter fit. g Models 2 and 3 define the lattice subunit to be 2 base pairs, hence for comparison with model 1 the n values should be multiplied by 2. | |||||||||||
| 1 | K | 0.604 | 0.075 | y | 1 | 6.75 | 5.62 | 2.28 | 2.53 | 4.04 | 1.65 |

|
3.43 | 5.05 |

|
−6.83 | −17.68 | −15.23 | (10.3) | (4.18)f | |||
| 2 | K | 0.919 | 0.256 | y | 1 | 2.67 | 2.88 | 1.18g | 1.25 | 4.48 | 1.83 |
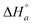
|
4.77 | 3.89 |
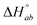
|
−5.87 | −15.17 | −14.14 | (7.72) | (3.14) | |||
| 3 | K | 0.700 | 0.081 | y | 1 | 5.23 | 6.17 | 1.13 | 1.30 | 2.83 | 1.15 |

|
3.29 | 8.33 |

|
−6.59 | −19.61 | −15.37 | (10.0) | (4.11) | |||
Table 2 gives standard thermodynamic values from the (6 + 5) parameter fit of model 3. Given the 9-fold difference in the intrinsic binding constant, the almost identical corresponding ΔS°-values of Δ and Λ are striking, suggesting that the affinity difference is of purely enthalpic origin. However, the similarity in calculated entropy changes is better regarded as coincidental and provisional, since any small model-dependent change in the ΔH°-values would partition the free energy difference differently between enthalpy and entropy contributions.
| Equilibrium constant | ΔG°/kJ mol−1 | ΔH°/kJ mol−1 | ΔS°/J K−1 mol−1 | |
|---|---|---|---|---|
| a (6 + 5) parameter model 2. | ||||
| KΔ | 7.00 × 105 M−1 | −33.36 | +3.29 | +122.9 |
| KΛ | 8.10 × 104 M−1 | −28.02 | +8.86 | +121.9 |
| yΔΔ | 1 | 0 | −6.53 | −22.9 |
| yΛΛ | 5.23 | −4.10 | −19.16 | −52.0 |
| yΔΛ | 6.17 | −4.51 | −15.37 | −36.4 |
| KΔ·yΔΔ | 7.00 × 105 M−1 | −33.36 | −3.30 | +100.8 |
| KΛ·yΛΛ | 4.82 × 105 M−1 | −32.12 | −11.28 | +69.9 |
| KΔ·yΔΔa | 9.19 × 105 M−1 | −34.04 | −1.10 | +110.5 |
| KΛ·yΛΛa | 6.84 × 105 M−1 | −33.30 | −11.28 | +73.9 |
Discussion
The general algorithm derived in this work allows quick evaluation of lattice binding models of widely varying complexity, and for the first time, mass balance equations for lattice models which, by defining multiple-ligand units, go beyond nearest-neighbor interactions, can be easily solved. As model complexity increases, however, so does the number of fitting parameters, and the physical meaningfulness of their best-fit values might rapidly deteriorate if the range of experimental data in the global fit is too narrow. As the present study is intended to show examples of general global analysis of ITC data, we have deliberately excluded titration data sets made by other experimental methods.Thus, the goal of this study is to find the binding model that gives a very good global fit to the ITC data with the smallest number of adjustable parameters. Since neither non-cooperative lattice-models (model 1–3 and 5) nor the restricted two independent site model 4 produced any reasonable global fit (see Fig. 4), we conclude that ligand–ligand interactions, whether direct or mediated by the DNA, are an absolute requirement to understand the behavior of the present system. Furthermore, since models 4 and 5, in which no neighbor interaction enthalpy is considered, require a considerably larger number of fitting parameters for acceptable fits, we conclude that for a minimal parameter model, the enthalpic contribution from ligand–ligand interactions has to be included.
Using model 1, the present dataset with extended competitive titrations gave only minor differences in intrinsic and homochiral interaction parameters compared to our earlier analysis of single titration Δ- and ΛRu-bpy ITC data.3 However, the X-ray structure evidence for the ΛRu-bpy 5′-TA-3′ selectivity suggests that the assumption in model 1 of identical intercalation pockets in poly(dAdT)2 is erroneous. Assuming that ΔRu-bpy shares the same selectivity, model 2 models poly(dAdT)2 as consisting of repeating units of 2 base pairs, to which 5′-TA-3′ selective ligands can bind with essentially no overlap, but the fit is slightly worse (nRMSD = 4.48%) than with model 1 (4.04%). It should be noted that assuming ΔRu-bpy to be homo-chiral non-cooperative (i.e. reducing the binding parameters from 7 to 6 by setting yΔΔ = 1) had a negligible influence on the fit for models 1 and 2.
Relaxing this assumption in model 3, and allowing the 5′-TA-3′ and 5′-AT-3′ intercalation sites for ΔRu-bpy to have different values for the intrinsic binding constant and homo-chiral cooperativity parameter (9 + 7 fitting parameters, nRMSD 2.45%), gave the best fit of all models tried, although at the drawback of having 2 additional binding and 2 additional enthalpy parameters. Restricting the 5′-TA-3′ and 5′-AT-3′ intercalation sites for ΔRu-bpy to have the same fitting parameter values and setting yΔΔ = 1 gave only a slightly inferior fit (6 + 5 fitting parameters, nRMSD 2.83%). The better fit of the (6 + 5) parameter model 3 compared to the (6 + 5) parameter model 2 suggests that ΔRu-bpy can intercalate 5′-AT-3′ as well as 5′-TA-3′ steps, but in view of the good overall fit of both models, conclusive evidence will require independent experimental data for the sequence preferentiality of ΔRu-bpy.
Although binding parameters variate due to the fact that the stoichiometry of binding sites is differently defined, models 1–3 show the same overall pattern: Δ itself binds non-cooperatively and has a larger (3 to 9-fold) intrinsic binding constant than Λ; the latter, on the other hand, has a stronger (3 to 6-fold) cooperative binding, both with itself and with Δ. Notably, for all models 1–3, the hetero-chiral cooperativity parameter value is close to the homo-chiral value for Λ.
Also the enthalpy parameters show a similar overall pattern for models 1–3: the intrinsic binding is endothermic (although the relative magnitude for the two enantiomers is clearly model sensitive), while the interaction enthalpies are exothermic, with ΛΛ about 2.7 and ΔΛ about 2.3 times that of ΔΔ for all three models. Comparing the enthalpy values with the associated standard free energy changes (see Table 2) clearly shows the endothermic intrinsic binding to be massively entropy driven, while the exothermic ligand–ligand interaction is nearly compensated for by a large entropy decrease.
The stronger homo-chiral cooperativity largely compensates for the smaller intrinsic binding constant for Λ, which for models 3 and 2 leads to a very similar ratio KΔyΔΔ/KΛyΛΛ = 1.4 ± 0.05. The value of the product of the intrinsic binding constant and the homo-chiral cooperativity parameter Ky is essentially the effective binding constant in the vicinity of saturation of the intercalation sites, where the curvature of the ITC curve changes rapidly. Hence, the value of Ky, and the value of the corresponding enthalpy change, can both be expected to be the best determined quantity form the fit to the data. Indeed, as seen in the last rows of Table 2, where models 2 and 3 are compared, these values show relatively small variations between the models Thus, we can draw the conclusion, independent of whether ΔRu-bpy discriminates between the two base pair steps or not, that the binding of ΔRu-bpy next to a bound ΔRu-bpy is almost entirely driven by entropy, and that the binding of ΛRu-bpy next to a bound ΛRu-bpy is to about one third driven by enthalpy.
A simple allosteric explanation of the lower intrinsic binding constant and higher cooperativity for the Λ enantiomer would be that, due to the seemingly less good steric fit compared to the Δ enantiomer,32Λ pays a free energy penalty by widening the groove upon intercalation, which pays back for the second Λ enantiomer intercalating from the already widened groove. However, this simple allosteric model does not explain the hetero-chiral cooperativity, since by hypothesis the better fitting, non-cooperative Δ enantiomer does not need to widen the groove upon intercalation. Although allosteric interactions undoubtedly play an important role, we suggest that ligand–ligand interactions also make a significant contribution. Fig. 6 shows models of the different combinations of Ru-bpy enantiomers intercalating (from the minor groove, as suggested by X-ray structures) two base pairs apart on DNA. We can distinguish three essentially different types of arrangements of the close-by bipyridine moieties: ΔΔ: face to face; ΛΛ: edge to edge; ΔΛ: face to edge. These three types of arrangements can be expected to be significantly different with regard to direct, mainly enthalpic interactions such as pi-stacking and electrostatic repulsion, but also with respect to entropy-contributing effects of water solvation and the counter-ion distribution. We believe that it presently would be premature to attempt to do a more detailed correlation between structural differences and changes in the thermodynamic quantities.
Conclusions
By developing a new simple algorithm, no longer restricted by the complexity of the binding system and general enough to be implemented to any biopolymers, we have been able to demonstrate a method that can capture the most essential effects of the nearest-neighbor interactions between ligands. This has allowed us to critically examine different binding models for the analysis of competitive calorimetric binding isotherms for the enantiomers of Ru(bpy)2dppz2+, for which we find a significant hetero-chiral binding cooperativity. It is our hope that this method will contribute in the future search for better pharmacological therapeutics and biotechnological applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge Swedish Research Council (Vetenskapsrådet) grant 2012-1661 and 2016-05421 and Chalmers Area of Advance Nano for funding, as well as COST Action CM1105 for providing a forum for stimulating discussions.Notes and references
- V. H. Le, R. Buscaglia, J. B. Chaires and E. A. Lewis, Anal. Biochem., 2013, 434, 233–241 CrossRef CAS PubMed.
- J. Andersson, L. H. Fornander, M. Abrahamsson, E. Tuite, P. Nordell and P. Lincoln, Inorg. Chem., 2013, 52, 1151–1159 CrossRef CAS PubMed.
- A. K. F. Mårtensson and P. Lincoln, Dalton Trans., 2015, 44, 3604–3613 RSC.
- P. Lincoln, Chem. Phys. Lett., 1998, 288, 647–656 CrossRef CAS.
- J. A. Hartley, K. Reszka, E. T. Zuo, W. D. Wilson, A. R. Morgan and J. W. Lown, Mol. Pharmacol., 1988, 33, 265–271 CAS.
- A. Jamalian, A. Shafiee, B. Hemmateenejad, M. Khoshneviszadeh, R. Miri, A. Madadkar-Sobhani, S. Z. Bathaie and A. A. Moosavi-Movahedi, J. Iran. Chem. Soc., 2011, 8, 1098–1112 CrossRef CAS.
- G. Marverti, M. Cusumano, A. Ligabue, M. L. Di Pietro, P. A. Vainiglia, A. Ferrari, M. Bergomi, M. S. Moruzzi and C. Frassineti, J. Inorg. Biochem., 2008, 102, 699–712 CrossRef CAS PubMed.
- T. A. K. Prescott, I. H. Sadler, R. Kiapranis and S. K. Maciver, J. Ethnopharmacol., 2007, 109, 289–294 CrossRef CAS PubMed.
- A. Banerjee, J. Singh and D. Dasgupta, J. Fluoresc., 2013, 23, 745–752 CrossRef CAS PubMed.
- S4SD – AFFINImeter 2017, accessed 20 October 2017, http://https://www.affinimeter.com/site/.
- N. J. Buurma and I. Haq, J. Mol. Biol., 2008, 381, 607–621 CrossRef CAS PubMed.
- P. Lincoln, A. Broo and B. Nordén, J. Am. Chem. Soc., 1996, 118, 2644–2653 CrossRef CAS.
- R. M. Hartshorn and J. K. Barton, J. Am. Chem. Soc., 1992, 114, 5919–5925 CrossRef CAS.
- I. Haq, P. Lincoln, D. C. Suh, B. Nordén, B. Z. Chowdhry and J. B. Chaires, J. Am. Chem. Soc., 1995, 117, 4788–4796 CrossRef CAS.
- A. E. Friedman, J. C. Chambron, J. P. Sauvage, N. J. Turro and J. K. Barton, J. Am. Chem. Soc., 1990, 112, 4960–4962 CrossRef CAS.
- H. Song, J. T. Kaiser and J. K. Barton, Nat. Chem., 2012, 4, 615–620 CrossRef CAS PubMed.
- H. Niyazi, J. P. Hall, K. O'Sullivan, G. Winter, T. Sorensen, J. M. Kelly and C. J. Cardin, Nat. Chem., 2012, 4, 621–628 CrossRef CAS PubMed.
- J. P. Hall, et al. , J. Am. Chem. Soc., 2013, 135, 12652–12659 CrossRef CAS PubMed.
- J. P. Hall, P. M. Keane, H. Beer, K. Buchner, G. Winter, T. L. Sorensen, D. J. Cardin, J. A. Brazier and C. J. Cardin, Nucleic Acids Res., 2016, 44, 9472–9482 CrossRef CAS PubMed.
- P. Lincoln and B. Nordén, J. Phys. Chem. B, 1998, 102, 9583–9594 CrossRef CAS.
- J. G. Liu, B. H. Ye, H. Li, L. N. Ji, R. H. Li and J. Y. Zhou, J. Inorg. Biochem., 1999, 73, 117–122 CrossRef CAS.
- L. Wang, J. Z. Wu, G. Yang, T. X. Zeng and L. N. Ji, Transition Met. Chem., 1996, 21, 487–490 CAS.
- J. G. Liu, Q. L. Zhang, X. F. Shi and L. N. Ji, Inorg. Chem., 2001, 40, 5045–5050 CrossRef CAS PubMed.
- B. Y. Wu, L. H. Gao, Z. M. Duan and K. Z. Wang, J. Inorg. Biochem., 2005, 99, 1685–1691 CrossRef CAS PubMed.
- D. Lawrence, V. G. Vaidyanathan and B. U. Nair, J. Inorg. Biochem., 2006, 100, 1244–1251 CrossRef CAS PubMed.
- A. W. McKinley, J. Andersson, P. Lincoln and E. M. Tuite, Chem. – Eur. J., 2012, 18, 15142–15150 CrossRef CAS PubMed.
- M. Scott Vandiver, et al. , Inorg. Chem., 2010, 49, 839–848 CrossRef CAS PubMed.
- C. G. Mikek, J. I. DuPont, V. R. Machha, J. C. White, L. R. Martin, N. Alatrash, F. M. MacDonnell and E. A. Lewis, Eur. J. Inorg. Chem., 2017, 3953–3960 CrossRef CAS.
- Y. D. Chen, Biopolymers, 1990, 30, 1113–1121 CrossRef CAS PubMed.
- J. D. McGhee and P. H. von Hippel, J. Mol. Biol., 1974, 86, 469–489 CrossRef CAS PubMed , correction J. D. McGhee and P. H. von Hippel, J. Mol. Biol., 1976, 103, 679 CrossRef.
- F. R. Gantmacher, Applications of the theory of matrices, Interscience Publishers, Inc., New York, 1959 Search PubMed.
- J. K. Barton, A. T. Danishefsky and J. M. Goldberg, J. Am. Chem. Soc., 1984, 106, 2172–2176 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp03184j |
| This journal is © the Owner Societies 2018 |