Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New insight into the effect of mass transfer on the synthesis of silver and gold nanoparticles†
Maximilian O.
Besenhard
 a,
Razwan
Baber
a,
Alec P.
LaGrow
a,
Razwan
Baber
a,
Alec P.
LaGrow
 b,
Luca
Mazzei
b,
Luca
Mazzei
 a,
Nguyen T. K.
Thanh
a,
Nguyen T. K.
Thanh
 *bc and
Asterios
Gavriilidis
*bc and
Asterios
Gavriilidis
 *a
*a
aDepartment of Chemical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK. E-mail: a.gavriilidis@ucl.ac.uk
bUCL Healthcare Biomagnetic and Nanomaterials Laboratories, 21 Albemarle Street, London W1S 4BS, UK
cBiophysics Group, Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK. E-mail: ntk.thanh@ucl.ac.uk
First published on 4th October 2018
Abstract
The fact that mass transfer affects noble metal nanoparticle (NP) syntheses is well known, not least because the scale-up of batch processes is anything but trivial. Therefore, this work studies the synthesis of silver and gold nanoparticles in batch reactors using constant reactant concentrations, but different process conditions to alter the mass transfer during the synthesis. Silver NPs were synthesized by reduction of silver nitrate via sodium borohydride in the presence of trisodium citrate. Gold NPs were synthesized using the Turkevich method, reducing tetrachloroauric acid via trisodium citrate. Four synthesis conditions for each NP system were used to investigate the mass transfer effects on the size and dispersity of the NPs. These were the i) slow or ii) fast addition of the concentrated reducing agent to the dilute precursor and the iii) slow and iv) fast addition of the concentrated precursor to dilute reducing agent solutions. Slow addition was performed by adding the reagent dropwise at a rate of 0.5 ml min−1 from a tube suspended above the stirred bulk solution, while fast addition was achieved by adding the reagent near the stir bar tip at a rate of 50 ml min−1 from a tube submerged in the stirred bulk solution. Mixing times of 209 ms for slow and 46 ms for fast reagent addition were determined using the Villermaux–Dushman protocol in combination with a mixing model. The silver NP size ranged from 6.7 to 11.5 nm for the four mixing conditions tested, with the smallest NPs being synthesized by fast addition of sodium borohydride to a silver nitrate solution. Stabilization of the initially formed particles was key to producing smaller and less polydisperse silver NPs in the case of slow reagent addition. The gold NP size ranged from 13.1 to 18.0 nm, with the smallest NPs being synthesized by fast addition of the trisodium citrate solution to the tetrachloroauric acid precursor solution. Faster reagent addition reduced polydispersity, due to a sharper separation of nucleation and growth. The results for both systems highlight the importance of mass transfer in determining the size and degree of polydispersity in batch synthesis of NPs and indicate that the effects are system-dependent.
1. Introduction
Noble metal nanoparticles (NPs) offer unique properties as compared to their bulk counterpart, offering potential for a variety of applications. Silver NPs for instance are successfully used in catalysis,1,2 surface enhanced Raman scattering,3,4 electronics,5,6 and as antimicrobial or anti-inflammatory agents7–10 and sensors.11,12 Likewise, gold NPs have been utilised for biological/biomedical,13–18 electrochemical,19,20 catalytic,21,22 and optical applications.23,24 Since the properties of NPs depend on their shape and size (and polydispersity), a well-controlled synthesis is key for satisfactory NP performance.There are many studies, mostly in batch systems, showing how precursor concentrations and different synthetic conditions (e.g., temperature, synthesis duration, sequence of reagent addition, etc.) affect the size of NPs. One factor that is rarely investigated in depth for batch synthesis is mass transfer, i.e., the transport of reagent molecules, particles, volumes of fluid, etc., from one location to another. This is associated with the rate and order of reagent addition and the mixing time. The latter can be categorised into macromixing time, relating to the timescale of bulk homogenization (order of seconds for lab-scale reactors), mesomixing time, relating to the dispersal of reagent plumes, and micromixing time, relating to the molecular diffusion or fluid engulfment on the smallest scales of motion, where flow is no longer turbulent (order of milliseconds)25,26 Which timescale affects the synthesis does depend on the reaction timescale of the synthesis.27
Micromixing times, for example, cannot be neglected for fast reactions, such as the reduction of noble metal precursors by strong reducing agents. It has been shown that with sodium borohydride as the reducing agent precursor reduction is completed within less than 200 ms during the synthesis of gold NPs28 and similarly in the case of silver NPs.29,30 The reaction timescale, therefore, is shorter than typical mixing timescale. It is thus essential to understand the effect of mixing conditions on the NP properties to develop scalable batch protocols and reproducible syntheses (not least in different laboratories with varying equipment).
Probably the most common synthesis for silver NPs is the reduction of silver nitrate via sodium borohydride and for gold NPs, the Turkevich method, i.e., the reduction of tetrachloroauric acid via trisodium citrate at elevated temperatures, which are both studied in this work. However, for both systems there are no benchmark synthesis conditions, including the sequence of reagent addition. In this work we refer to the addition of the reducing agent to a precursor solution as the “standard method”, and the addition of the precursor to a reducing agent solution as the “inverse method”. The standard method for silver NP synthesis was investigated by Ryu et al. Highly concentrated silver NP solutions (up to 40 wt%) with NPs in the range of 1–35 nm were synthesized by reducing ice cold silver nitrate by slow addition of sodium borohydride and/or hydrazine monohydrate in the presence of polyelectrolytes.31 Pinto et al. synthesized silver NPs in the size range of 3–10 nm by the addition of sodium borohydride to a mixture of silver nitrate and trisodium citrate.32 On increasing the sodium borohydride to silver nitrate molar ratio (by increasing the amount of 1 mM NaBH4 solution added to a 0.25 mM AgNO3/Na3C6H5O7 solution), the size of the nanoparticles decreased and the concentration of the nanoparticles increased based on UV-Vis spectroscopy analysis. The standard deviation of the absorbance maximum increased with increasing sodium borohydride molar amount, demonstrating lower reproducibility between experiments. Shirtcliffe et al. reduced silver nitrate using sodium borohydride and sodium hydroxide using the standard and inverse methods for the synthesis of silver NPs in the range of 15–77 nm.33 In their work, pipettes were used to mix reagents within a cuvette at 2 °C and it was shown that the method and order of mixing had a significant effect on the NP size distribution. The addition of silver nitrate to a mixture of sodium borohydride and sodium hydroxide produced the narrowest and most reproducible peaks using UV-Vis analysis (though the TEM images showed quite large and polydisperse NPs, possibly because no stabilizer was used in the system).
The inverse method was studied by Song et al.34 Silver NPs between 30 and 40 nm were synthesised by adding silver nitrate to a solution of sodium borohydride and sodium dodecyl sulfate.34 The authors observed that after exceeding a [NaBH4]/[AgNO3] ratio of 5, higher sodium borohydride concentrations resulted in well-dispersed silver NPs. It was suggested that an excess amount of NaBH4 yields a [BH4]− ion layer preventing the boron hydroxide (generated due to the hydrolysis of NaBH4), which is assumed to provoke aggregation, from adsorbing onto the surfaces of silver nanoparticles. The fact that sodium borohydride is not only a reducing agent but also a stabilizer is in agreement with the work of Polte et al.29 This detailed study of the silver nanoparticle formation mechanism during the NaBH4 reduction method describes a metastable phase, i.e., particles are stable for several minutes after initial coalescence-based particle growth in the absence of any stabilizer. A subsequent (after ∼10 min) decrease of stability, i.e., the continuation of coalescence/aggregation, was suspected to be driven by a changing ratio of [BH4]−/[B(OH)4]−, the increasing pH, or a combination of both. Thøgersen et al. synthesized silver NPs between 6–19 nm by slowly dropping an ice cold AgNO3 solution into an ice cold solution of sodium borohydride.35 They found an increase in NP size due to an increase of the molar ratio of silver nitrate to sodium borohydride. Agnihotri et al. synthesized silver NPs in the range of 5–100 nm by adding silver nitrate to a heated solution of sodium borohydride and trisodium citrate (60 °C) and further heating the solution to 90 °C.36 Monodispersed NPs could be synthesized, which was assigned to a two-step growth mechanism, where sodium borohydride produced small seeds through coalescence of small silver clusters followed by a surface reduction type growth via citrate reduction to grow the NPs into a more monodispersed product. The authors were able to synthesize NPs with a wide range of sizes by varying the concentrations of the various components used in the system. In general, altering the ratio of the reducing agent to precursor was the main method to achieve control of the size of the NPs, highlighting the importance of reagent concentration in the resultant silver NP size.
In their original work, Turkevich et al. tested a variety of different methods for the synthesis of gold NPs, but found the sodium citrate method to be the most repeatable, typically producing gold NPs in the range between 15 and 20 nm.37 A minimum size was observed at 80 °C while a lower citrate concentration resulted in an increase in NP size. The standard Turkevich method was later studied by Frens, where gold NPs were synthesised in the range of 12–150 nm by varying the amount of citrate injected into a boiling tetrachloroauric acid solution.38 The final NP size was found to be determined by the number of nuclei formed (hence, the initial nuclei size), which is why higher amounts of citrate yielded smaller gold NPs. Goodman et al. observed a similar trend when increasing citrate concentration, with the gold NP size ranging between 21 and 80 nm.39 Chow and Zukoski synthesised gold NPs with sizes between 16 and 52 nm for non-agglomerated particles (very large agglomerated NPs were seen in cases where the synthesis of gold NPs did not reach completion).40 In a recent study, Kettemann et al. synthesised gold NPs between 11 and 18 nm using the standard method. A modification in the reducing agent composition was shown to improve the reproducibility of the synthesis significantly.41
The inverse method was studied by Sivaraman et al., who synthesised gold NPs in the range of 5–10 nm by adding a small volume of highly concentrated tetrachloroauric solution to a large volume of citrate solution.42 These authors found that for citrate to gold molar ratios of <5, the mean size of the NPs was not significantly affected whereas for ratios >5, there was a significant reduction in the size of the NPs. Piella et al. synthesised monodisperse gold NPs in the range of 3–13 nm based on a modification of the inverse method involving the use of tannic acid together with sodium citrate as the reducing agent.24 Also Schulz et al. synthesized gold NPs of ∼12 nm with a low polydispersity of 5–8% using an inverse method.43
Ojea-Jiménez et al. synthesised gold NPs in the range of 9–37 nm comparing the standard method to the inverse method (swapping the reagent addition order). These authors found that NPs were smaller when tetrachloroauric acid was added to hot citrate.44 Also Wuithschick et al. studied both the standard and inverse methods. Gold NPs were synthesised in the range of 11–42 nm investigating the effect of temperature, ionic strength, pH, variation of reactant concentrations, and the order of reagent addition.45 The authors' detailed theoretical and experimental work revealed that the final particle size is governed by the size of the initially formed seeds. The seed size itself was shown to depend on the rather complex reduction chemistry and was found to be smaller for the inverse method under the synthesis conditions used. A minimum size was achieved at 60 °C and the synthesis time decreased with increasing temperature. A pH window between 2.8 and 4 was found to produce the lowest polydispersity index of around 10% with the minimum size of 10.8 nm achieved.
The large number of studies on the silver nitrate reduction synthesis by sodium borohydride and the Turkevich method provide an advanced understanding of the mechanisms of these two syntheses providing several options to control the NP size distribution. As shown in this introduction, size control was successfully achieved e.g., by changing reaction temperatures, reactant concentrations, or pH values. Nevertheless, there is a lack of studies which focus specifically on mass transfer and how it affects the resultant NP size and polydispersity. Therefore, this study investigates the two most common methods for the synthesis of silver NPs and gold NPs, with a focus on the role of mass transfer in the resultant size and polydispersity of the respective NP system. Various mixing configurations and orders of addition of the reagents are investigated to study a variety of reaction conditions.
2. Materials and methods
2.1 Chemicals
Silver nitrate (AgNO3, 0.01 M stock solution), trisodium citrate ((HOC(COONa)(CH2COONa)2·2H2O), powder form), sodium borohydride solution (NaBH4, ∼12 wt% in 14 M NaOH stock solution), gold(III) chloride hydrate (HAuCl4·xH2O, powder form), potassium iodide (KI, 99%), potassium iodate (KIO3, 98%) and boric acid (H3BO3, 99.5%) were obtained from Sigma Ltd. Sulfuric acid (H2SO4, 3 M stock solution) was obtained from Alfa Aesar Ltd. All chemicals were used without further purification and solutions were prepared with ultrapure water (resistivity 15.0 MΩ cm).2.2 Experimental setup
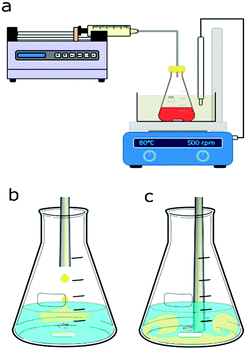
Syringe pumps (Pump 11 Elite OEM module, Harvard Apparatus) connected to a 0.5 mm internal diameter (I.D.) 316L stainless steel tube for silver NP synthesis and to a 0.5 mm I.D. PTFE tube for gold NP synthesis were used to feed one of the reagents into the batch vessel which was a 50 ml small-neck glass Erlenmeyer flask (Fisher Scientific). A digital hotplate stirrer unit with a temperature controller (Stuart, Cole-Parmer LLC) was used together with PTFE stir bars (15 mm × 1.5 mm) to heat and mix the reagents in the vessel. For the synthesis of gold NPs, a glycerine bath was used to heat the reagents to 80 °C in the batch vessel. A cap, through which the stainless steel or PTFE tube for reagent addition was inserted, covered the vessel. The height of the tube in the vessel could be adjusted to allow addition of reagents above the solution or into the solution near the tip of the magnetic stir bar. Fig. 1 shows a schematic of the experimental setups for silver and gold NP syntheses.2.3 Nanoparticle synthesis conditions
For the silver NP syntheses, 20 ml of one reagent were placed in the batch vessel and stirred at 500 rpm. To this reagent solution, 0.6 ml of the other reagent was added via the syringe pump either dropwise at 0.5 ml min−1 above the solution through a stainless-steel tube, see Fig. 1b, or at once with a feed rate of 50 ml min−1 through the tube inserted into the solution within the vessel near the stir bar tip, as shown in Fig. 1c. The reagents were a silver nitrate solution with trisodium citrate serving as a capping agent (the precursor solution) and a sodium borohydride solution (the reducing agent solution). Sodium borohydride was stored in 14 M sodium hydroxide (as received) leading to a NaOH concentration being 3.21 times higher than the sodium borohydride concentration in all silver NP syntheses. The order of reagent addition was tested by switching which reagent was initially placed in the batch vessel, either 20 ml of the precursor solution or 20 ml of the sodium borohydride solution, to which then 0.6 ml of the other reagent was fed. The concentrations of the reagent initially placed in the vessel and the fed reagent were changed based on their volumes, to have equal nominal concentrations after mixing. Details of used concentrations for the silver NP synthesis are provided in section 3.1.Similarly, for the gold NP syntheses, 20 ml of one reagent was placed in the batch vessel and 0.6 ml of the other reagent was added through PTFE tubing. Either 20 ml of tetrachloroauric acid solution (the precursor solution) or 20 ml of trisodium citrate (the reducing agent solution) were initially placed in the batch vessel. The vessel was placed in the glycerine bath which was heated to 80 °C. To test how long it takes to heat 20 ml of solution to 80 °C, the temperature was measured over time after inserting the solution at room temperature into the glycerine bath. For all cases, 7 min was sufficient to reach the steady state of 80 °C. The reagent solution in the vessel was always kept at this temperature under stirring for 15 min before the addition of 0.6 ml of the other reagent. Details of used concentrations for the gold NP synthesis are provided in section 3.2.
2.4 Characterization of nanoparticles
NPs were analysed using a UV-Vis spectrometer (USB 2000+ spectrometer and DT-Mini-2-GS light source, Ocean Optics). Silver NPs were analysed within an hour of synthesis (the signal of the samples was stable in this time window). Gold NPs were analysed over time till the signal had stabilized (usually 1–2 days). The shown UV-Vis results from gold NPs relate to stabilized samples only. NP samples were diluted with additional ultrapure water to be in the linear absorbance range. Online UV-Vis measurements using the same spectrometer during the synthesis of silver NPs were implemented by recirculating the solution from the reaction vessel via a peristaltic pump and passing it through a UV-Vis flow cell (details are shown in the ESI,† section 5). Transmission electron microscopy (TEM) images were captured using a JEOL 1200 EX microscope with an acceleration voltage of 120 kV. The samples were prepared within an hour of the synthesis completion for silver NPs and when the sample was stable for gold NPs by pipetting 5 μl of the sample onto carbon coated copper TEM grids, which were allowed to dry at room temperature. Particle size distributions (insets for each TEM image presented) have the following nomenclature: d is the average diameter, δd is the standard deviation of the NP size distribution and n is the number of particles counted to obtain the particle size distribution. Dynamic light scattering (DLS) size and zeta potential measurements were performed with a DelsaMax-Pro (Beckman Coulter) using the available flow cell system in batch mode at 22 °C. DLS measurements were performed at least five times, with a data acquisition time of 10 s.2.5 Mixing characterization
Characterization of mixing within the batch vessel was carried out using the Villermaux–Dushman reaction scheme. In this reaction system, sulfuric acid is added to a buffer solution consisting of a mixture of orthoboric acid, sodium hydroxide, potassium iodide and potassium iodate ions. The reaction scheme of the Villermaux–Dushman protocol is as follows:| H2BO3− + H+ ↔ H3BO3 | (1) |
| 5I− + IO3− + 6H+ ↔ 3I2 + 3H2O | (2) |
Reactions (1) and (2) compete for protons supplied by the sulfuric acid. The neutralization reaction of dihydrogen borate (1) is considered to be instantaneous, while reaction (2), which yields iodine, is fast but slower than reaction (1). Therefore, in the limit of instantaneous mixing, only reaction (1) occurs. Slower mixing results in local depletion of dihydrogen borate, thus allowing reaction (2) to occur. The selectivity of this reaction scheme therefore relates to the micromixing (and mesomixing) timescale. The generated iodine can then be quantified, since it reacts in an equilibrium reaction (3) with excess iodide to triiodide.
| I2 + I− ↔ I3− | (3) |
The triiodide concentration can be easily quantified due to its absorption in the UV-Vis-range, typically at a wavelength of 353 nm. Its value allows determination of the degree of mixing efficiency, which is related to the extent to which reaction (2) has occurred. Once the selectivity of the reaction scheme is known, the order of magnitude of the mixing time can be estimated using a mixing model.
The mixing model is required to relate the triiodide concentration (= model output), which depends on the initial concentrations of sulfuric acid, orthoboric acid, sodium hydroxide, potassium iodide and potassium iodate (= model inputs), to the mixing time (= model variable). In this study, the interaction by exchange with the mean (IEM) mixing model was used. For the mixing experiments, 1 ml of 0.14 N sulfuric acid was added to 20 ml of a buffer solution consisting of 181.8 mM orthoboric acid, 90.9 mM sodium hydroxide, 11.67 mM potassium iodide and 2.33 mM potassium iodate. The stirrer speed was set to 500 rpm (as used for all syntheses) and the two mixing configurations used in the NP synthesis were tested, i.e., acid was injected from the centre above the buffer solution or near the stir bar tip. Fig. 1b and c show the schematics of the two configurations. The final triiodide concentration was obtained using an extinction coefficient of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209 l mol−1 cm−1. This extinction coefficient was determined using solutions of a known iodine concentration as described in the ESI,† section 1. Experiments were repeated three times for each mixing configuration. The mixing time averaged over the three repetitions was 209 ms for the dropwise injection above the solution and 46 ms in the case of injection near the stir bar tip. Details on the mixing model used to assign the mixing time values to the measured triiodide concentrations are provided in the ESI,† section 2. The measured reduction in the mixing time when injecting near the stir bar tip was expected because of the higher shear rates near the stir bar tip and the high flow rate (50 ml min−1) used for the addition.
209 l mol−1 cm−1. This extinction coefficient was determined using solutions of a known iodine concentration as described in the ESI,† section 1. Experiments were repeated three times for each mixing configuration. The mixing time averaged over the three repetitions was 209 ms for the dropwise injection above the solution and 46 ms in the case of injection near the stir bar tip. Details on the mixing model used to assign the mixing time values to the measured triiodide concentrations are provided in the ESI,† section 2. The measured reduction in the mixing time when injecting near the stir bar tip was expected because of the higher shear rates near the stir bar tip and the high flow rate (50 ml min−1) used for the addition.
3. Results and discussion
3.1 Silver nanoparticle synthesis
Silver NPs were synthesized in the batch vessel by the reduction of silver nitrate via sodium borohydride in the presence of the stabilizer trisodium citrate. The effect of changing a) the mixing configuration and b) the order of reagent addition (swapping the reagent placed in the batch vessel) on the size and polydispersity of the NPs was investigated. As described above, for all syntheses 20 ml of one reagent was stirred in the batch vessel while feeding 0.6 ml of the second reagent into the vessel via the stainless-steel tubing. Hence, four different syntheses were performed, which we refer to as Ag-R-s, Ag-R-f, Ag-P-s, and Ag-P-f. R and P refer to the order of reagent addition: R is for adding reducing agent solution, while P is for adding precursor solution. The mixing configurations are denoted by the letters s (slow) and f (fast). Slow (i.e., slow addition) is for the reagent added dropwise at a rate of 0.5 ml min−1 from above, while fast (i.e., fast addition) is for the reagent added quickly near the stir bar tip with a feed rate of 50 ml min−1. For example, the synthesis condition Ag-R-s describes the addition of 0.6 ml of the reducing agent at a rate of 0.5 ml min−1 to 20 ml of precursor solution. Table 1 summarizes the concentrations for each mixing condition (5 to 1 molar ratio of sodium borohydride to silver nitrate was used in all cases). The precursor concentrations of the conditions Ag-P-s and Ag-P-f had to be chosen slightly lower due to the low concentration of the (as received) silver nitrate solution and the solubility of sodium citrate in aqueous solutions, limiting the maximal concentrations of the precursor solution to 9.1 mM.| Condition | Reducing agent | Volume | Conc. after mixing | Precursor/capping agent | Volume | Conc. after mixing |
|---|---|---|---|---|---|---|
| Ag-R-s | 63.3 mM | 0.6 ml | 1.84 mM | 0.38/0.38 mM | 20 ml | 0.37/0.37 mM |
| Ag-R-f | 63.3 mM | 0.6 ml | 1.84 mM | 0.38/0.38 mM | 20 ml | 0.37/0.37 mM |
| Ag-P-s | 1.36 mM | 20 ml | 1.32 mM | 9.1/9.1 mM | 0.6 ml | 0.27/0.27 mM |
| Ag-P-f | 1.36 mM | 20 ml | 1.32 mM | 9.1/9.1 mM | 0.6 ml | 0.27/0.27 mM |
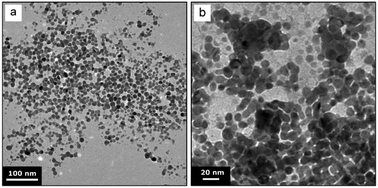
UV-Vis spectroscopy performed subsequent to the synthesis (>20 min after feeding of the precursor or reducing agent solution was completed) showed a surface plasmon absorption peak at 387.3 nm, 388.5 nm, 388.8 nm, and 388.6 nm for the conditions Ag-R-s, Ag-R-f, Ag-P-s, and Ag-P-f, respectively. The syntheses Ag-P-s and Ag-R-f exhibited a significantly higher reproducibility in terms of the surface plasmon peak position (lower standard deviation, experiments performed in triplicate) than the syntheses Ag-R-s and Ag-P-f. The details of this UV-Vis analysis, including a comparison of the absorbance values, are summarized in Fig. S4.†Fig. 2 shows the TEM images of the synthesized silver NPs exhibiting an average particle diameter of 11.1 ± 3.0 nm, 6.7 ± 1.7 nm, 9.5 ± 1.4 nm, and 11.5 ± 2.4 nm for the conditions Ag-R-s, Ag-R-f, Ag-P-s and Ag-P-f, respectively. The difference in the NP diameters obtained from the TEM studies is statistically significant comparing all four synthesis conditions (i.e., six combinations) via an unpaired t-test and Welch's unpaired t-test (assuming unequal sample variances) with a 5% significance level. Due to the large number of analysed particles, even the diameters for the conditions Ag-R-s and Ag-P-f were found to be statistically different.
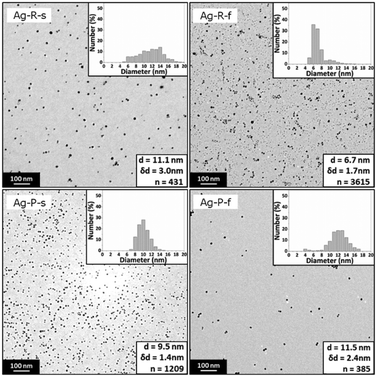 | ||
| Fig. 2 Representative TEM images and statistics of silver NPs synthesized via the four synthesis conditions Ag-R-s, Ag-R-f, Ag-P-s, and Ag-P-f. Details of these conditions are listed in Table 1. | ||
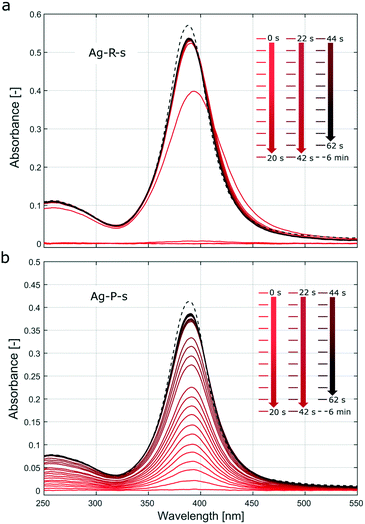
Fig. S7† showing UV-Vis spectra recorded during stepwise addition of the reducing agent, as described in section 5 of the ESI,† indicates that the particle formation was almost complete (not referring to morphological changes) after adding <20% of the final amount. In Fig. 3a, the UV-Vis spectra recorded during the first 5–10 s exhibit a shift of the surface plasmon absorption band to longer wavelengths compared to the subsequent spectra. This could be assigned to aggregated particles during the initial phase or a decrease of the electron density on the silver NP surface upon chemisorption of Ag+ as described, e.g., by Henglein et al.46 These authors reported a significant shift to larger wavelengths for Ag+ concentrations that were two orders of magnitude lower than the AgNO3 concentration used in Ag-R-s. Video analysis of the synthesis Ag-R-s showed a dark brown plume immediately on addition of the first drop of sodium borohydride solution, which then turned to a bright yellow colour (videos of all silver syntheses can be downloaded from the journal's website). This immediate reduction during Ag-R-s, as confirmed via video and online UV-Vis studies, is not surprising, as sodium borohydride is known to have the potential to reduce more than its own stoichiometric equivalent of silver ions, since it can provide multiple electrons in the reduction reaction.47–49 Hence, for Ag-R-s most of the silver precursor was reduced with the first drops of the reducing agent solution (i.e., the first ∼0.01 ml and a molar ratio of AgNO3/NaBH4 ∼12).
In contrast, Fig. 3b (and Fig. S8,† showing UV-Vis spectra during stepwise addition of the precursor solution) shows that the absorption during the synthesis Ag-P-s increased in proportion to the quantity of added precursor solution. This indicates that the particles that precipitated after the first drop of precursor solution was added had similar absorption (here not distinguished from scattering) properties to those formed after addition of the last drop. As the precursor solution was added dropwise, the synthesis Ag-P-s did not allow a large amount of AgNO3 to be reduced at the same time (and space). The UV-Vis results suggest that each drop of silver nitrate reacted to form silver NPs within seconds, which were then distributed in the sodium borohydride solution. Further drops then produce new NPs which are distributed again over the vessel before the next drop arrives. The stepwise addition of the precursor solution, as during Ag-P-s, does make seed mediated growth more likely (further precursor addition and reduction on the surface of initially formed particles) compared to Ag-R-s, where most of the precursor is reduced at once leading to burst nucleation (no further growth of initially nucleated particles due to lack of unconsumed precursor).
One of the biggest differences between these syntheses was that in the case of Ag-R-s all the precursor was reduced within seconds resulting in a temporarily high release of the silver precursor compared to Ag-P-s where the fed precursor was reduced throughout the feeding time of 72 s. The other difference was that particles synthesized via Ag-R-s were not exposed to the final sodium borohydride concentration from the first drop, as was the case for the condition Ag-P-s. Since sodium borohydride also acts as a stabilizing agent,34,50 Ag-R-s can be expected to provoke agglomeration, especially during the initial phase of the synthesis (at lower sodium borohydride concentrations). Although the precursor solution did contain the capping agent trisodium citrate, the latter might not stabilize the just formed nanoparticles sufficiently against agglomeration.
Aggregation has been identified in previous studies as the main growth mechanism in the silver NP formation process using sodium borohydride reduction29,51,52 and recent publications suggest that electrostatic repulsion forces (also referred to as the aggregation barrier53 in combination with particle size) determine up to which aggregation size of metal NPs is possible, hence the final NP size. The lower concentrations of sodium borohydride during the initial phase would explain the initially lower aggregation barrier during Ag-R-s (when most if not all of the precursor was already reduced), yielding larger particles than those in the synthesis Ag-P-s (exhibiting a high sodium borohydride concentration throughout the synthesis and gradual reduction of the precursor). This is in agreement with the larger particle diameter and higher polydispersity observed for Ag-R-s.
To obtain more information on the silver NP formation mechanism during the synthesis Ag-R-s, a TEM sample was prepared immediately (<2 min) after the addition of only 0.02 ml sodium borohydride solution via an Eppendorf pipette (=3.3% of the final reducing agent solution, i.e., a molar ratio of AgNO3/NaBH4 = 6 after mixing). The TEM images in Fig. 4 show bigger particles than those synthesized via the original condition Ag-R-s, indicating reduced stabilization due to the lower sodium borohydride concentration.
In experiment Ag-R-f, concentrated sodium borohydride solution was added quickly to a dilute precursor solution. Based on the video and UV-Vis analysis for Ag-R-s showing the immediate reduction of all the precursor with just a fraction of the reducing agent solution, this synthesis condition is expected to cause a faster reduction of the precursor resulting in higher nucleation rates. Since mixing times are fast, nucleation events are not restricted to a confined space. This limits the number of NP collisions and hence possible aggregation events during the initial particle formation phase. This also explains the large difference in the silver NP size and polydispersity between the syntheses Ag-R-s and Ag-R-f.
In experiment Ag-P-f, concentrated precursor solution was added quickly to a sodium borohydride solution. Assuming that the reaction kinetics was faster than the time needed for the addition of the precursor solution (which could be expected as discussed by Polte et al.29), the reduction and hence nucleation rates would be slower than those for Ag-R-f (where all the precursor was available for reduction at the start of the synthesis) and nucleation and growth was favoured to occur simultaneously. This agrees with the larger particles observed for Ag-P-f, compared to those for Ag-R-f. For Ag-P-f and Ag-P-s silver NP sizes were comparable.
For the Ag-P-s and Ag-P-f syntheses, the DLS studies revealed particles in solution which were distinctly larger (>100 nm) than those determined from TEM images, see Fig. S9.† However, particles >100 nm were not silver NPs, since such large silver NPs would have affected significantly the TEM data and the UV-Vis spectra, which was not the case. For example, the surface plasmon absorption band would peak at around 450 nm, even for 60 nm particles.55 Therefore, the large particles measured via DLS analysis for Ag-P-s and Ag-P-f, i.e., when feeding highly concentrated AgNO3/Na3C6H5O7, are assigned to larger aggregates (not necessarily silver NPs, probably silver citrate precipitates formed in the precursor solution) present during these syntheses. Further UV-Vis and DLS studies during the preparation of the precursor solution for Ag-P-s and Ag-P-f showed a clear increase in absorption and the occurrence of a particulate phase of unknown composition with particles >100 nm as soon as the trisodium citrate solution was added to the silver nitrate solution (data not shown). This indicates precipitation in the precursor solution at high silver nitrate and trisodium citrate concentrations.
3.2 Gold nanoparticle synthesis
The effect of changing the mixing configuration and the order of reagent addition on the size and polydispersity of the gold NPs was investigated. The same four conditions as those used for silver NP synthesis were tested and described as conditions Au-R-s, Au-R-f, Au-P-s and Au-P-f. Table 2 summarizes the concentrations and fed volumes for each mixing condition (a citrate/tetrachloroauric ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was used in all four syntheses).
1 was used in all four syntheses).
| Condition | Reducing agent/capping agent | Volume | Conc. after mixing | Precursor | Volume | Conc. after mixing |
|---|---|---|---|---|---|---|
| Au-R-s | 92.7 mM | 0.6 ml | 2.70 mM | 0.56 mM | 20 ml | 0.54 mM |
| Au-R-f | 92.7 mM | 0.6 ml | 2.70 mM | 0.56 mM | 20 ml | 0.54 mM |
| Au-P-s | 2.78 mM | 20 ml | 2.70 mM | 18.5 mM | 0.6 ml | 0.54 mM |
| Au-P-f | 2.78 mM | 20 ml | 2.70 mM | 18.5 mM | 0.6 ml | 0.54 mM |
UV-Vis spectroscopy studies showed a surface plasmon absorption peak at 523.3 nm, 521.0 nm, 522.5 nm, and 521.6 nm for the conditions Au-R-s, Au-R-f, Au-P-s, and Au-P-f. The Au-P-f synthesis exhibited the highest reproducibility, when the surface plasmon peak position and absorbance were compared. The details of this UV-Vis analysis are summarized in Fig. S5.†Fig. 6 shows the TEM images of the synthesized gold NPs with an average diameter of 18.0 ± 4.8 nm, 13.1 ± 2.2 nm, 16.3 ± 3.3 nm and 16.2 ± 2.1 nm for conditions Au-R-s, Au-R-f, Au-P-s, and Au-P-f, respectively. The difference in gold NP diameters obtained from TEM studies is statistically significant comparing all four synthesis conditions via an unpaired t-test and Welch's unpaired t-test with a 5% significance level, except for the Au-P-s and Au-P-f conditions.
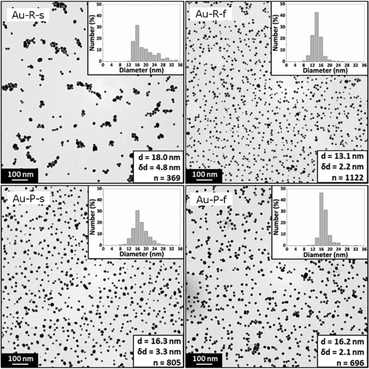 | ||
| Fig. 6 Representative TEM images and statistics of gold NPs synthesized via the four synthesis conditions Au-R-s, Au-R-f, Au-P-s, and Au-P-f. Details of these conditions are listed in Table 2. | ||
The largest and most polydisperse NPs were observed for the synthesis Au-R-s and the smallest NPs were observed via Au-R-f. Conditions Au-P-s and Au-P-f produced NPs of similar size, though Au-P-f produced more monodisperse gold NPs. Recent studies on the Turkevich synthesis method revealed its seed-mediated growth mechanism, which differs not only from the classical “nucleation–growth” mechanism, but also from the colloidal growth mechanism of the discussed silver NP syntheses using sodium borohydride as the reducing agent. The current understanding of particle formation during the Turkevich synthesis is that the initial reduction of the precursor is followed by the formation of stable seed particles of a few nm in diameter onto which remaining gold ions attach, making the nanoparticles grow.45,56 This mechanism is not intuitive since the separation of nucleation and growth, yielding the monodisperse gold NPs the Turkevich synthesis is known for, originates from the reduction of precursor reactivity just after seed formation. However, also in the case of the Turkevich synthesis, the final particle size is determined during the initial stages of the synthesis, i.e., by the size of formed seeds.
The timescale required to finish seed formation, i.e., the step determining the final NP size, was reported to be in the order of 20 s.45 Although the timescales are dependent on the precursor and citrate concentrations, temperature and pH values, it is obvious that a feeding time of 72 s (as in the case of Ag-R-s and Ag-P-s) hinders a clear separation of nucleation from growth. This is in agreement with our results showing higher polydispersity for slow mixing conditions compared to the fast mixing conditions. Other studies indicate the benefit of fast mixing during the (inverse) Turkevich synthesis for the generation of monodisperse NPs as well.43 This is consistent with the more monodisperse particles synthesized via Au-P-s.
Besides the pH, higher temperatures are known to shift the equilibrium of the gold precursor towards more hydroxylated forms as well. The effect of temperature on the citrate solution is not yet clear, but irreversible changes (based on UV-Vis spectroscopy) have been reported during heating which could be explained by the oxidation of citrate e.g., to dicarboxyacetone (DCA).45 The role of DCA is controversial in the literature. It has been postulated that the inverse method yields smaller (and more monodisperse) particles because the preheated citrate solution forms the more reactive species DCA, which therefore increases the nucleation rate.43,44 However, studies by Wuithschnick et al. performing the Turkevich synthesis adding high concentrations of DCA to the citrate solution (1 mM) prior to the synthesis showed no significant influence of DCA on the particle size. The authors attributed the smaller particles synthesized via the inverse Turkevich synthesis to different initial amounts of the reactive AuCl4− species and argued that when the inverse method was used, the precursor solution had a higher tetrachloroauric acid concentration (as was the case in this work, see Table 2) and was kept at room temperature before addition. Both would shift the AuCl4−x(OH)x− speciation equilibrium towards the most reactive AuCl4− species, i.e., the least hydroxylated form. Therefore, one can assume that for the inverse method, the nucleation rate is higher and the seed particles are smaller. However, this line of reasoning is slightly controversial, since similar argumentation would be possible discussing the higher pH of the precursor solution in the vessel (in the case of Au-R-f) in combination with the mixing kinetics.
For the condition Au-R-f, reactive species in the precursor solution in the vessel might remain sufficiently low to suppress nucleation during the initial stages of mixing with the reducing agent, i.e., mixing comes closer to completion before the onset of nucleation, which could yield higher nucleation rates later and hence smaller NPs. In comparison, nucleation is expected to occur throughout the addition of the precursor solution in the case of Au-P-f. In any case, a discussion solely based on the AuCl4− concentrations is insufficient, since the interaction between the precursor and the citrate (and all their possible complexes) needs to be taken into consideration, and both reaction temperature and precursor solution pH do not have a monotonic effect on the particle size and polydispersity.
It is very complex to identify the intermediates involved in the reduction mechanism during the very first seconds of reagent mixing. Although timescales in the range of seconds have been reported, e.g., for the equilibration of the AuCl4−x(OH)x− species, kinetic data of the reduction are scarce. Our results show that mixing times, even in the order of milliseconds, cannot be neglected for the discussion of the final NP sizes. Although for the slow mixing conditions the inverse method (Au-P-s) produced smaller particles than the direct method (Au-R-s), the trend was reversed for the fast mixing conditions. Our results do not indicate higher reduction rates, and therefore higher nucleation rates and smaller NPs, due to intermediates formed in the citrate solution formed at elevated temperatures. The reversed trend, i.e., larger particle sizes in the case of the inverse method with fast mixing, was unexpected based on previous studies. However, it is worth noting that Sivaraman et al. reported the difference in the size of NPs synthesized by the inverse and direct methods to vanish for higher tetrachloroauric acid concentrations (at concentrations higher than 0.54 mM used in this study).42
4. Summary and conclusions
Mixing times in a batch vessel were characterized using the Villermaux–Dushman reaction system for two different mixing conditions: 1) dropwise injection of the reagent above the stirred solution in the batch vessel and 2) rapid injection of the reagent near the stir bar tip. The (micro)mixing times were found to be 209 ms when reagents were injected from above and 46 ms when they were injected near the stir bar tip. Silver NPs were synthesized by reducing silver nitrate with sodium borohydride in the presence of trisodium citrate (the stabiliser) under both mixing conditions and different orders of reagent addition, i.e., four different synthesis conditions. It was found that the addition of sodium borohydride at a fast rate near the stir bar tip produced the smallest NPs (6.7 ± 1.7 nm). Slightly bigger but more monodisperse silver NPs (9.5 ± 1.4 nm) were produced by dropwise addition of the precursor solution into the reducing agent solution. Larger and more polydisperse NPs were synthesized when the mixing conditions encouraged lower sodium borohydride concentrations. Online UV-Vis studies showed that complete precursor reduction occurred within seconds, even after adding just a small fraction (<20%) of the final reducing agent solution (final NaBH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AgNO3 ratio was 5
AgNO3 ratio was 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
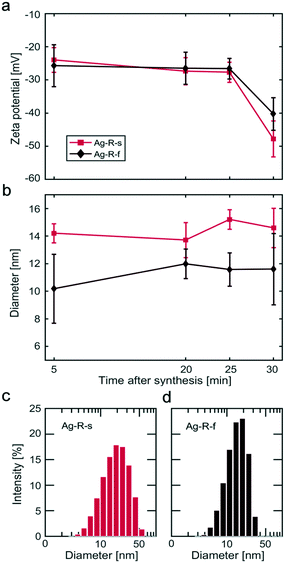
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Dynamic zeta potential studies showed a second state of stabilization, i.e., a further increase in the magnitude of the zeta potential ∼30 min after the complete addition of the second reagent. This indicates a stabilization process that is significantly slower (hours) than the formation of particles (seconds).
1). Dynamic zeta potential studies showed a second state of stabilization, i.e., a further increase in the magnitude of the zeta potential ∼30 min after the complete addition of the second reagent. This indicates a stabilization process that is significantly slower (hours) than the formation of particles (seconds).
Gold NPs were synthesized using the Turkevich method, where tetrachloroauric acid was reduced by trisodium citrate at an elevated temperature. Again, four different syntheses were tested, i.e., two mixing conditions and different orders of reagent addition. Using the same mixing configurations as those for the silver NP synthesis, the smallest NPs (13.1 ± 2.2 nm) were obtained when the reducing agent (trisodium citrate) was added to the precursor (tetrachloroauric acid) at a fast rate near the stir bar tip. These were significantly smaller than when the trisodium citrate was added at a slow rate from above the solution (18 ± 4.8 nm). For both orders of reagent addition, NP polydispersity was significantly lower for the fast mixing conditions, showing the importance of mixing for the Turkevich synthesis. For the fast addition of a concentrated precursor solution to a reservoir of preheated citric acid solution (16.2 ± 2.1 nm) a polydispersity of <8% could be achieved. Although the inverse method, i.e. adding the tetrachloroauric acid solution to the citrate solution, was reported to produce smaller and more monodisperse particles, we observed bigger particles compared to the direct synthesis in the case of fast mixing conditions (for slow mixing conditions, the results were consistent with the literature). This highlights not only the importance of mass transfer, but also the effect of preconditioning the reagents on the particle formation kinetics during the Turkevich synthesis.
In the noble metal NP syntheses investigated, different synthesis conditions yielded the most monodisperse NPs. The most monodisperse silver NPs were synthesized via the dropwise addition of a concentrated precursor solution to the reducing agent solution, whereas the most monodisperse gold NPs were synthesized via the fast addition of the concentrated precursor solution to the reducing agent solution. These syntheses showed also the highest reproducibility based on the position of the surface plasmon absorption peak, making them promising reaction conditions for further studies on the reproducible synthesis of monodisperse noble metal NPs. This study highlights the importance of mixing conditions and the order of reagent addition in determining the size and polydispersity of the synthesized NPs, even when the final nominal concentrations of the reducing agent to precursor are the same. Often, batch reactor studies state only the molar ratio of the reagents used in the syntheses, but this may be insufficient information to reproduce results, since the way reagents are mixed plays a crucial role.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank EPSRC (grant EP/M015157/1 and studentship for RB). N. T. K. Thanh thanks The Royal Society for her University Research Fellowship. Furthermore, the authors thank Dr. Joseph C. Bear (Kingston University, UK) for fruitful conversations.References
- Z.-J. Jiang, C.-Y. Liu and L.-W. Sun, J. Phys. Chem. B, 2005, 109, 1730–1735 CrossRef CAS PubMed.
- R. Mata, J. Reddy Nakkala and S. Rani Sadras, Mater. Sci. Eng., C, 2015, 51, 216–225 CrossRef CAS PubMed.
- Y. Yang, S. Matsubara, L. Xiong, T. Hayakawa and M. Nogami, J. Phys. Chem. C, 2007, 111, 9095–9104 CrossRef CAS.
- K. G. Stamplecoskie and J. C. Scaiano, J. Phys. Chem. C, 2015, 115, 1403–1409 CrossRef.
- D. Chen, X. Qiao, X. Qiu and J. Chen, J. Mater. Sci., 2009, 44, 1076–1081 CrossRef CAS.
- N. Matsuhisa, D. Inoue, P. Zalar, H. Jin, Y. Matsuba, A. Itoh, T. Yokota, D. Hashizume and T. Someya, Nat. Mater., 2017, 16, 834 CrossRef CAS PubMed.
- C. Marambio-Jones and E. M. V. Hoek, J. Nanopart. Res., 2010, 12, 1531–1551 CrossRef CAS.
- D. A. Gonzalez-Carter, B. F. Leo, P. Ruenraroengsak, S. Chen, A. E. Goode, I. G. Theodorou, K. F. Chung, R. Carzaniga, M. S. P. Shaffer, D. T. Dexter, M. P. Ryan and A. E. Porter, Sci. Rep., 2017, 7, 42871 CrossRef PubMed.
- C. Mitra, P. M. Gummadidala, K. Afshinnia, R. C. Merrifield, M. Baalousha, J. R. Lead and A. Chanda, Environ. Sci. Technol., 2017, 51, 8085–8093 CrossRef CAS PubMed.
- B. Le Ouay and F. Stellacci, Nano Today, 2015, 10, 339–354 CrossRef CAS.
- A. D. McFarland and R. P. Van Duyne, Nano Lett., 2003, 3, 1057–1062 CrossRef CAS.
- A. Contino, G. Maccarrone, M. Zimbone, R. Reitano, P. Musumeci, L. Calcagno and I. P. Oliveri, J. Colloid Interface Sci., 2016, 462, 216–222 CrossRef CAS PubMed.
- R. A. Sperling, P. Rivera Gil, F. Zhang, M. Zanella and W. J. Parak, Chem. Soc. Rev., 2008, 37, 1896–1908 RSC.
- L. Dykman and N. Khlebtsov, Chem. Soc. Rev., 2012, 41, 2256–2282 RSC.
- S. Noimark, K. Page, J. C. Bear, C. Sotelo-Vazquez, R. Quesada-Cabrera, Y. Lu, E. Allan, J. A. Darr and I. P. Parkin, Faraday Discuss., 2014, 175, 273–287 RSC.
- G. Bodelón, C. Costas, J. Pérez-Juste, I. Pastoriza-Santos and L. M. Liz-Marzán, Nano Today, 2017, 13, 40–60 CrossRef.
- T. J. Macdonald, K. Wu, S. K. Sehmi, S. Noimark, W. J. Peveler, H. du Toit, N. H. Voelcker, E. Allan, A. J. MacRobert, A. Gavriilidis and I. P. Parkin, Sci. Rep., 2016, 6, 39272 CrossRef CAS PubMed.
- X. Zhang, Cell Biochem. Biophys., 2015, 72, 771–775 CrossRef CAS PubMed.
- S. Guo and E. Wang, Anal. Chim. Acta, 2007, 598, 181–192 CrossRef CAS PubMed.
- B. Hafsi, A. Boubaker, D. Guerin, S. Lenfant, S. Desbief, F. Alibart, A. Kalboussi, D. Vuillaume and K. Lmimouni, Org. Electron., 2017, 50, 499–506 CrossRef CAS.
- M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346 CrossRef CAS PubMed.
- B. S. Takale, M. Bao and Y. Yamamoto, Org. Biomol. Chem., 2014, 12, 2005–2027 RSC.
- N. Li, P. Zhao and D. Astruc, Angew. Chem., Int. Ed., 2014, 53, 1756–1789 CrossRef CAS PubMed.
- J. Piella, N. G. Bastús and V. Puntes, Chem. Mater., 2016, 28, 1066–1075 CrossRef CAS.
- G. Caygill, M. Zanfir and A. Gavriilidis, Org. Process Res. Dev., 2006, 10, 539–552 CrossRef CAS.
- J. Bałdyga and J. R. Bourne, Turbulent Mixing and Chemical Reactions, Wiley, Chichester, 1999 Search PubMed.
- P. N. Sharratt, Handbook of Batch Process Design, Springer Science & Business Media, London, 1997 Search PubMed.
- J. Polte, R. Erler, A. F. Thünemann, S. Sokolov, T. T. Ahner, K. Rademann, F. Emmerling and R. Kraehnert, ACS Nano, 2010, 4, 1076–1082 CrossRef CAS PubMed.
- J. Polte, X. Tuaev, M. Wuithschick, A. Fischer, A. F. Thuenemann, K. Rademann, R. Kraehnert and F. Emmerling, ACS Nano, 2012, 6, 5791–5802 CrossRef CAS PubMed.
- D. L. Van Hyning, W. G. Klemperer and C. F. Zukoski, Langmuir, 2001, 17, 3128–3135 CrossRef CAS.
- B. H. Ryu, Y. Choi, H. S. Park, J. H. Byun, K. Kong, J. O. Lee and H. Chang, Colloids Surf., A, 2005, 270, 345–351 CrossRef.
- V. V. Pinto, M. J. Ferreira, R. Silva, H. A. Santos, F. Silva and C. M. Pereira, Colloids Surf., A, 2010, 364, 19–25 CrossRef CAS.
- N. Shirtcliffe, U. Nickel and S. Schneider, J. Colloid Interface Sci., 1999, 211, 122–129 CrossRef CAS PubMed.
- K. C. Song, S. M. Lee, T. S. Park and B. S. Lee, Korean J. Chem. Eng., 2009, 26, 153–155 CrossRef CAS.
- A. Thøgersen, J. Bonsak, C. H. Fosli and G. Muntingh, J. Appl. Phys., 2011, 110, 044306 CrossRef.
- S. Agnihotri, S. Mukherji and S. Mukherji, RSC Adv., 2014, 4, 3974–3983 RSC.
- J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- G. Frens, Nat. Phys. Sci., 1973, 241, 20–22 CrossRef CAS.
- S. L. Goodman, G. M. Hodges, L. K. Trejdosiewicz and D. C. Livingston, J. Microsc., 1981, 123, 201–213 CrossRef CAS PubMed.
- M. K. Chow and C. F. Zukoski, J. Colloid Interface Sci., 1994, 165, 97–109 CrossRef CAS.
- F. Kettemann, A. Birnbaum, S. Witte, M. Wuithschick, N. Pinna, R. Kraehnert, K. Rademann and J. Polte, Chem. Mater., 2016, 28, 4072–4081 CrossRef CAS.
- S. K. Sivaraman, S. Kumar and V. Santhanam, J. Colloid Interface Sci., 2011, 361, 543–547 CrossRef CAS PubMed.
- F. Schulz, T. Homolka, N. G. Bastús, V. Puntes, H. Weller and T. Vossmeyer, Langmuir, 2014, 30, 10779–10784 CrossRef CAS PubMed.
- I. Ojea-Jiménez, N. G. Bastús and V. Puntes, J. Phys. Chem. C, 2011, 115, 15752–15757 CrossRef.
- M. Wuithschick, A. Birnbaum, S. Witte, M. Sztucki, U. Vainio, N. Pinna, K. Rademann, F. Emmerling, R. Kraehnert and J. Polte, ACS Nano, 2015, 9, 7052–7071 CrossRef CAS PubMed.
- A. Henglein, Chem. Mater., 1998, 10, 444–450 CrossRef CAS.
- J. Shen, Z. Li, Q. Yan and Y. Chen, J. Phys. Chem., 1993, 97, 8504–8511 CrossRef CAS.
- J. C. Fanning, B. C. Brooks, A. B. Hoeglund, D. A. Pelletier and J. A. Wadford, Inorg. Chim. Acta, 2000, 310, 115–119 CrossRef CAS.
- R. Baber, L. Mazzei, N. T. K. Thanh and A. Gavriilidis, Nanoscale, 2017, 9, 14149–14161 RSC.
- D. L. Van Hyning, W. G. Klemperer and C. F. Zukoski, Langmuir, 2001, 17, 3120–3127 CrossRef CAS.
- M. Takesue, T. Tomura, M. Yamada, K. Hata, S. Kuwamoto and T. Yonezawa, J. Am. Chem. Soc., 2011, 133, 14164–14167 CrossRef CAS PubMed.
- D. L. Van Hyning and C. F. Zukoski, Langmuir, 1998, 14, 7034–7046 CrossRef CAS.
- M. Wuithschick, S. Witte, F. Kettemann, K. Rademann and J. Polte, Phys. Chem. Chem. Phys., 2015, 17, 19895–19900 RSC.
- A. P. LaGrow, T. M. D. Besong, N. M. AlYami, K. Katsiev, D. H. Anjum, A. Abdelkader, P. M. F. J. Costa, V. M. Burlakov, A. Goriely and O. M. Bakr, Chem. Commun., 2017, 53, 2495–2498 RSC.
- K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677 CrossRef CAS.
- J. Polte, CrystEngComm, 2015, 17, 6809–6830 RSC.
- X. Ji, X. Song, J. Li, Y. Bai, W. Yang and X. Peng, J. Am. Chem. Soc., 2007, 129, 13939–13948 CrossRef CAS PubMed.
- I. Ojea-Jiménez and J. M. Campanera, J. Phys. Chem. C, 2012, 116, 23682–23691 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ce01014e |
| This journal is © The Royal Society of Chemistry 2018 |