The thermal expansion coefficients of the alpha and beta polymorphic forms of p-aminobenzoic acid in relation to their bulk crystal chemistry

Abstract

The thermal expansion behaviour of the alpha and beta polymorphs of para-aminobenzoic acid are presented and discussed in terms of the bulk crystal chemistry and the associated strengths of the constituent intermolecular synthons for these two materials. Analysis of temperature dependant powder diffraction data over the temperature range 298.15–403.15 K facilitates calculation of the linear thermal expansion coefficients: α_a = 8.36 × 10⁻⁰⁶ K⁻¹, α_b = 94.5 × 10⁻⁰⁶ K⁻¹ and α_c = 9.91 × 10⁻⁰⁶ K⁻¹ for the alpha polymorph and α_a = 21.5 × 10⁻⁰⁶ K⁻¹, α_b = 48.5 × 10⁻⁰⁶ K⁻¹ and α_c = 2.22 × 10⁻⁰⁶ K⁻¹ for the beta polymorph. The exceptionally large increase in the thermal expansion of the b axis for the alpha form reflects the weak dispersive interactions which propagate along this axis. In contrast, the a and c axes contain relatively strong hydrogen bonds which stabilise the lattice and limit thermal expansion. The thermal expansion of the beta form reflects the more isotropic nature of the intermolecular synthons for this polymorph in comparison to the alpha form. The thermal expansion of the b axis of the beta form is larger than that of the a and c axes but to a much lesser extent than that observed for the alpha form. This is rationalised through identification of a hydrogen bonding component which contributes to the stabilisation of the b axis in comparison to the almost fully dispersive nature found in the alpha structure.

---

Introduction

The thermal expansion of solids, uniaxial and isotropic, can generally be explained through the increased vibrational motion of atoms or molecules within their periodic arrangement in a lattice structure during heating. Positive thermal expansion and negative thermal expansion¹ have been the subject of much research, particularly for metal organic frameworks,² alloys of metals, and inorganic materials.³ Materials with tuneable physical properties using external stimuli, such as temperature and pressure, are of great interest to engineering and science due to their possible application in sensor equipment, thermomechanical actuators and aerospace engineering components.⁴ Considering the advancements in understanding thermal expansion of inorganic materials, there is still much to be explored regarding organic materials⁵ and, in particular, the mechanism and quantification of thermal expansion within organic molecular crystals. The grand challenge of crystal engineering of organic materials through molecular design can only be achieved through quantification of the three dimensional intermolecular interactions which contribute to a crystalline material's lattice energy and hence its physical properties. This together with a crystallographic understanding of these vector quantities could facilitate a material by design approach, through tailoring the specific molecular functional groups to give a desired level of interaction anisotropy.⁴

This communication presents the determination of the linear thermal expansion coefficients, of the two enantiotropically⁶ related alpha and beta polymorphs of para-aminobenzoic acid (PABA), along their principle crystallographic axes. PABA, H₂NC₆H₄CO₂H, is a small organic molecule m_r = 137.14, and an attractive model system for fine chemical and pharmaceutical sector. The alpha (AMBNAC01)⁷ and beta (AMBNAC04)⁸ polymorphs both crystallise in the P2₁/n space group, where the alpha form has a bimolecular asymmetric unit resulting in a unit cell containing 8 molecules. The alpha crystal chemistry is characterised by a carboxylic acid dimer motif and head to head π–π stacking interactions of the benzene rings, shown in Fig. 1a) and b). In contrast, the beta polymorph has a unimolecular asymmetric unit in a unit cell of 4 molecules. The beta crystal chemistry is comprised of head to tail π–π stacking interactions of the benzene rings and a 4 membered ring of OH–N, NH–O hydrogen bonds shown in Fig. 1c) and d). Much research has been undertaken in recent years to determine the nucleation and growth kinetics^9–12 of the material, together with an extensive molecular modelling effort¹³ in an attempt to understand more about the nucleation and growth pathway for both polymorphs.

Fig. 1 a) Packing diagram for the alpha polymorph viewed along b axis highlighting the carboxylic acid dimers, b) the alpha polymorph viewed down the c axis to highlight the b axis π–π stacks of benzene rings, c) packing diagram for the beta polymorph viewed down the a axis showing the 4 membered hydrogen bonding ring structure, d) the beta polymorph viewed down the a axis and extended to highlight the isotropic hydrogen bonding ring structure.

Experimental

The samples of alpha PABA was used as supplied from Sigma Aldrich purity >99%. The beta sample was prepared by slurry conversion from the alpha form. A slurry of the alpha polymorph was prepared in 200 ml of deionised water to a slurry concentration of 10 wt% at 5 °C in a jacketed crystalliser under constant magnetic stirring at 200 rpm. The temperature of the slurry was controlled through a PT100 thermocouple connected to a Julabo F25 circulation bath. The interconversion was monitored offline through sampling methods with analysis of phase composition through powder X-ray diffraction.

The thermal expansion behaviour of the two PABA polymorphs was measured using a Panalytical X'pert¹⁴ powder diffractometer. Samples of the two polymorphs were first carefully ground to a powder using a mortar and pestle and mounted into a temperature controlled sample holder, which was connected to a liquid nitrogen supply to provide cooling down to −60° at 10⁻⁴ mbar. The samples were subjected to a temperature ramp at a heating rate of 10 K min⁻¹ from 298.15 K to 403.15 K for the alpha form and 298.15 K to 343.15 K for the beta form, diffraction patterns from 5–40° 2θ with a step size of 0.0334° were taken in 10 K increments for the alpha polymorph and 5° K increments for the beta polymorph. Rietveld refinement was carried out on the collected diffraction patterns using Highscore Plus,¹⁴ which involved a Marquadt least squares fit of the data and the structure was refined based on the corresponding crystallographic structures for the two polymorphs.

The thermal expansion coefficient, α, was calculated using eqn (1), where L₀ is the reference length of the specific crystallographic axis, l is the measured crystallographic axis at temperature T.

Results & discussion

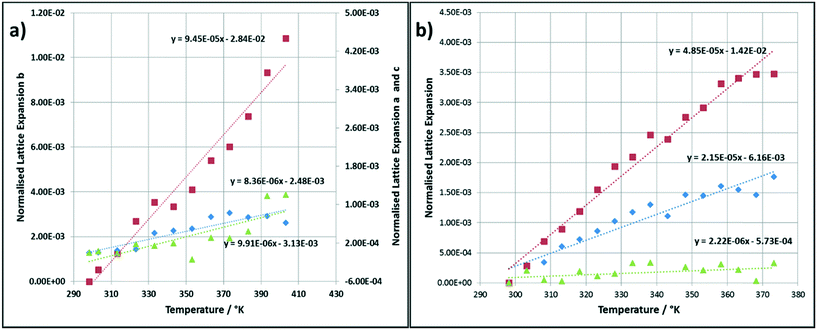
The thermal expansion of the lattice directions for the alpha and beta polymorphs of PABA as a function of temperature are presented in Fig. 2a) and b) respectively. The thermodynamically stable beta polymorph undergoes a well-studied phase transformation⁶ to the alpha form beginning at around 343.15 K. This is observable in the thermal expansion where the expansion of all axes begins to deviate from a linear function above this temperature. In this case the thermal expansion coefficients were calculated during the linear range of thermal expansion only. The data indicates that the a and c axes of the alpha polymorph expand relatively equally whereas the b axis expands much more rapidly in comparison. The linear thermal expansion of the beta crystallographic axes were found to be quite different along the three principle axes.

Fig. 2 The normalised linear thermal expansion in the various crystallographic axes as a function of temperature, a) alpha polymorph, b) beta polymorph (blue diamond's = a axis, red squares = b axis, green triangles = c axis).

The slope of the fitted linear function presented for the thermal expansion data in Fig. 1, represents the coefficients of thermal expansion in each crystallographic direction, these values are tabulated in Table 1. The average α values for both polymorphs is 6.37 × 10⁻⁰⁵ K⁻¹ which falls in a medium range for most organic materials and agrees well with α values measured for other similar compounds such as urea¹⁵ and α-chloroacetic acid.¹⁶ Interestingly the b axis of the alpha polymorph displays a much larger thermal expansion coefficient, 94.5 × 10⁻⁰⁶ K⁻¹, an order of magnitude more so than the a and c axis; 8.36 × 10⁻⁰⁶ and 9.91 × 10⁻⁰⁶ K⁻¹ in comparison. Table 1 also presents the calculated values of α for the beta polymorph crystallographic axes. The data shows that the c axes undergoes the least thermal expansion over the temperature range studied where α = 2.90 × 10⁻⁰⁶ K⁻¹, an order of magnitude lower than the b axes which has a calculated α value of 57.3 × 10⁻⁰⁶ K⁻¹.

Table 1 The calculated linear thermal expansion coefficients for the alpha and beta polymorph

Lattice axis	α/K^−1	Synthon contribution after ref. 13	Dominant interaction type
α polymorph
a	8.36 × 10^−06	Aα, Dα	H-Bond: OH–O (dimer), NH–O + dispersive
b	94.50 × 10^−06	Bα	Dispersive only
c	9.91 × 10^−06	Aα, Dα	H-Bond: OH–O (dimer), NH–O + dispersive
β polymorph
a	27.70 × 10^−06	Bβ, Cβ	H-Bond: OH–N + NH–O
b	57.30 × 10^−06	Aβ	Dispersive only
c	2.90 × 10^−06	Aβ, Bβ, Cβ	H-Bond: OH–N + NH–O + dispersive

---

To understand the measured differences in the ease of thermal expansion in the various crystallographic axes in the two polymorphs, the crystal chemistry of the two polymorphs was examined in terms of identifying the important intermolecular bonds/synthons which are involved along the principle axes of the two structures drawing down upon previous work by Rosbottom et al.¹³ using molecular and synthonic modelling tools.^17–20

The top four strongest interactions found in the two crystal structures are presented in Fig. 3, where within the alpha lattice structure the carboxylic acid hydrogen bonded dimer, Aα, was found to contribute most to the calculated lattice energy, followed by a dispersive head to head π–π stacks Bα, an NH–O short contact Cα and a NH–O hydrogen bonding interaction Dα. The synthon analysis also found that within the beta lattice structure a dispersive head to tail π–π stacking interaction, Aβ, contributed most to the lattice energy followed by Bβ an OH–N hydrogen bonding interaction then Cβ, a NH–O hydrogen bonding interaction and finally Dβ, an offset head to tail dispersive π–π stacking interaction.

Fig. 3 The top four strongest intermolecular synthons in the crystal structures of the alpha and beta polymorphs of PABA highlighting the synthon label, the type of intermolecular interaction and the calculated intermolecular interaction energy (adapted from Rosbottom et al.¹³).

This research also found that in the alpha crystal structure the a and c axis contain H-bonds in plane, where strong COOH hydrogen bonded dimer interactions and NH–OH-bonds run ∼45° to plane normal down the a and c axis, these are highlighted as interactions Aα and Dα in Fig. 3. In comparison the b axis of the alpha structure contains no H-bonds but much weaker dispersive π–π stacking interactions, interaction Bα in Fig. 3. This analysis correlates well with the increased ease of expansion in the b axis lattice direction with temperature, when compared to the a and c axis.

Returning to the crystallographic synthon analysis by Rosbottom et al.,¹³ it was found that the strongest intermolecular synthons which contribute to the lattice energy of the beta form are head to tail π–π stacks of the aromatic rings, interaction Aβ in Fig. 3, and OH–NH bonds, interaction Bβ in Fig. 3, both of which run almost in plane with the c axis. Additionally the c axis contains interaction Cβ, an NH–OH-bonding interaction, totalling three of the top four interactions in Fig. 3 and providing an explanation as to the relative observed stability of the c axis with respect to thermal expansion. In comparison, the dominant interaction in the b axis is the dispersive Aβ head to tail interaction hence the thermal expansion in this lattice direction is comparatively larger than the a or c axis. The b axis does however, have a much lower thermal expansion than the b axis of the alpha structure due to a slight contribution from highly offset OH–N and NH–O hydrogen bonds which will likely provide a small stabilisation effect in comparison to the fully dispersive component of the b axis in the alpha polymorph.

This data on the calculated synthonic interaction strength correlates well with the measured linear thermal expansion coefficients for both polymorphs of PABA, providing a molecular-based explanation for the thermal expansion properties of this organic molecular crystal. This combination of experimental work and molecular modelling also highlights a useful potential workflow component that could be used to design organic materials with specific physical properties through consideration of the detailed intermolecular structure and synthon motifs which stabilise the 3-D crystal lattice of the material.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors gratefully acknowledge the UK's Engineering and Physical Sciences Research Council for the funding of this research through a joint collaborative Critical Mass project between the Universities of Leeds and Manchester (grant references EP/IO14446/1 and EP/IO13563/1). This work was carried out during the doctoral studies of one of us (TDT).

References

1. G. D. Barrera, J. A. O. Bruno, T. H. K. Barron and N. L. J. Allan, J. Phys.: Condens. Matter, 2005, 17, R217.
2. W. Zhou, H. Wu, T. Yildirim, J. R. Simpson and A. R. H. Walker, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054114.
3. J. C. Hancock, K. W. Chapman, G. J. Halder, C. R. Morelock, B. S. Kaplan, L. C. Gallington, A. Bongiorno, C. Han, S. Zhou and A. P. Wilkinson, Chem. Mater., 2015, 27, 3912.
4. D. Das, T. Jacobs and L. J. Barbour, Nat. Mater., 2010, 9, 36.
5. K. M. Hutchins, R. H. Groeneman, E. W. Reinheimer, D. C. Swenson and L. R. MacGillivray, Chem. Sci., 2015, 6, 4717.
6. S. Gracin and A. C. Rasmuson, Cryst. Growth Des., 2004, 4(5), 1013.
7. T. F. Lai and R. E. Marsh, Acta Crystallogr., 1967, 22, 885.
8. S. Gracin and A. Fisher, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61(5), O1242.
9. R. A. Sullivan and R. J. Davey, CrystEngComm, 2015, 17, 1015.
10. D. Toroz, I. Rosbottom, T. D. Turner, D. M. C. Corzo, R. B. Hammond, X. Lai and K. J. Roberts, Faraday Discuss., 2015, 179, 79.
11. T. D. Turner, D. M. C. Corzo, D. Toroz, A. Curtis, M. M. Dos Santos, R. B. Hammond, X. Lai and K. J. Roberts, Phys. Chem. Chem. Phys., 2016, 18, 27507.
12. R. A. Sullivan, R. J. Davey, G. Sadiq, G. Dent, K. R. Back, J. H. ter Horst, D. Toroz and R. B. Hammond, Cryst. Growth Des., 2014, 14, 2689.
13. I. Rosbottom, K. J. Roberts and R. Docherty, CrystEngComm, 2015, 17, 5768.
14. http://www.panalytical.com, (accessed March 2018).
15. R. B. Hammond, K. Pencheva, K. J. Roberts, P. Mougin and D. Wilkinson, J. Appl. Crystallogr., 2005, 38, 1038.
16. R. Hoseneder and G. Hartel, Mater. Chem. Phys., 2001, 68, 278.
17. K. J. Roberts, R. B. Hammond, V. Ramachandran and R. Docherty, in Computational Approaches in Pharmaceutical Solid State Chemistry, ed. Y. Abramov, Wiley, New Jersey, USA, 2016, ch. 7, ISBN 9781118700747.
18. V. Ramachandran, D. Murnane, R. B. Hammond, J. Pickering, K. J. Roberts, M. Soufian, B. Forbes, S. Jaffari, G. P. Martin, E. Collins and K. Pencheva, Mol. Pharmaceutics, 2014, 12(1), 18.
19. J. Pickering, R. B. Hammond, V. Ramachandran, M. Soufian and K. J. Roberts, in Engineering Crystallography: From Molecule to Crystal to Functional Form, ed. K. J. Roberts, R. Docherty and R. Tamura, Springer, Netherlands, Dordrecht, 2017, ch. 11, pp. 155–176.
20. I. Rosbottom and K. J. Roberts, in Engineering Crystallography: From Molecule to Crystal to Functional Form, ed. K. J. Roberts, R. Docherty and R. Tamura, Springer, Netherlands, Dordrecht, 2017, ch. 7, pp. 109–131.

---