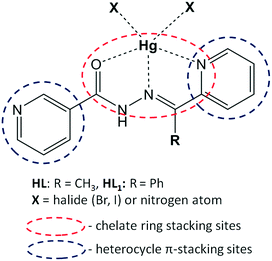
Recurrent supramolecular motifs in discrete complexes and coordination polymers based on mercury halides: prevalence of chelate ring stacking and substituent effects

Abstract

In recent years, the crystal engineering library has been enriched with a number of previously unrecognized or unnoticed intermolecular interactions, such as agostic, tetrel, chalcogen, pnicogen bonding and chelate ring stacking – collectively referred to as “unconventional interactions”. Many open questions remain unaddressed regarding their ability to form synthon interactions, specificity, and cooperativity, for example with π–π stacking interactions. In this work, we throw light on the formation of chelate ring stacking in metal–organic assemblies of nicotinohydrazide ligands (N′-(1-(2-pyridyl)ethylidene)nicotinohydrazide (HL) and N′-(phenyl(pyridin-2-yl)methylene)nicotinohydrazide (HL₁)) with mercury(II) halide (HgBr₂, HgI₂) salts. Their reaction produced five compounds, namely [Hg(μ-L)BrHgBr₂]_n (1), [Hg(μ-L₁)Br]_n (2), [Hg(L)I₂] (3), [Hg(HL₁)I₂]·(CH₃OH) (4), and [Hg(μ-L₁)I]_n (5). Crystal structure analysis reveals that chelate ring stackings are formed in four of the reported metal–organic compounds, and are common also in the literature precedents. The energies of chelate ring stackings and π–π heterocycle stackings have been computed and analyzed by means of DFT calculations, and the results were verified using Bader's theory of “atoms in molecules”. These results provide a rationale for preferential formation of both unconventional and conventional stackings and allow us to conclude that chelate ring interaction may be considered as a synthon interaction for nicotinohydrazide metal complexes. Interpretations for packing differences imposed by the substituent effect (substitution of methyl group in HL for phenyl group in HL₁) were provided based on the Hirshfeld surface analysis and 2D fingerprint plots of the crystal structures reported here.

---

Introduction

Although the strength of single π–π stacking interactions¹ (either face-to-face or edge-to-face) is low when compared to that of, for example, classical strong hydrogen bonding,² the consequences deriving from the existence of those interactions are widespread and in fact fundamental for all living organisms. Double strands of DNA are stabilized by vertical base-to-base π stacking;³ aromatic side chains of amino acids such as phenylalanine, tyrosine or histidine, which participate in the construction of proteins, are found to preferentially align their (hetero)aromatic rings in a cofacial orientation, which in turn has a profound influence on nucleic acid tertiary and quaternary structure.⁴ The therapeutic effect of some drugs⁵ and also the carcinogenic properties of fused-ring aromatic compounds such as benzopyrene and their metabolites share the same underlying intercalation mechanism, based on π–π stacking interactions.⁶ With all confidence, the immense importance of these interactions is not limited to biological systems only; indeed, the stacking of aromatic systems predetermines a wide variety of physicochemical and spectroscopic properties. To name only a few of them, stacked organic or metal–organic assemblies often reveal characteristic spectroscopic and physical phenomena, such as excimer or exciplex formation,⁷ light harvesting,⁸ and improved dynamics of electron/hole transport in organic electronics,⁹ which are all of great application importance.

In-depth understanding of π stacking-related properties mentioned above would not be possible without inputs from methods of structural and computational chemistry.¹⁰ At present, it can be stated that interactions, such as π–π stacking interactions, are very well characterized experimentally and theoretically, both in terms of structure–property relationships and from a purely structural point of view. On the other hand, in recent years, interactions referred to as “unconventional” or “nonclassical” have emerged. In these interactions, one can include agostic,¹¹ σ- or π-hole – based tetrel,¹² chalcogen,¹³ and pnicogen bondings,¹⁴ as well as – chelate ring stackings involving transition and main group metals;¹⁵ recent works suggest that these interactions cannot be perceived just as interesting crystallographic facts, but are equal or even dominating contributors to the inorganic and metal–organic crystal structure formation. Clearly, the knowledge on unconventional interactions is still in its formative years;¹⁶ thus, our efforts are focused on the detailed exploration of fundamental aspects of all of these interactions, mainly employing Schiff-base complexes with d- and p-block elements as crystalline test systems.

In this contribution, we aim to explore and explain the crucial role of chelate ring stacking in the self-assembly of five metal–organic assemblies of nicotinohydrazide ligands (N′-(1-(2-pyridyl)ethylidene)nicotinohydrazide (HL) and N′-(phenyl(pyridin-2-yl)methylene)nicotinohydrazide (HL₁) depicted in Scheme 1) with mercury(II) halide (HgBr₂, HgI₂) salts: [Hg(μ-L)BrHgBr₂]_n (1), [Hg(μ-L₁)Br]_n (2), [Hg(L)I₂] (3), [Hg(HL₁)I₂]·(CH₃OH) (4), and [Hg(μ-L₁)I]_n (5). The structural features and expected coordination behaviour of the applied ligands are summarized in Scheme 1. Indeed, the crystallographic analysis of the obtained crystal structures suggested a strong preference for the formation of unconventional chelate ring stacking, along with conventional heterocycle π–π stacking. In this manuscript, we use the term “unconventional π-stacking” for the chelate ring⋯chelate ring stacking to differentiate from the classical π–π stacking between aromatic rings. Additionally, we noted significant substituent effects (namely, the steric effect of the phenyl group of ligand HL₁) especially pronounced in 4. To gain insight into these structural features, we employed our characterization toolbox involving classical structure description, Hirshfeld surface analysis and detailed DFT calculations of interaction energies. These characterization techniques allow us to address the following points. (i) What are the energies of the noted recurrent supramolecular motifs and what is their relative participation in the stabilization of the investigated structures? (ii) What is the impact of these interactions on the final structure? (iii) Can the chelate ring stacking be considered a synthon interaction for these and similar metal-organic systems?

Scheme 1 The structures of nicotinohydrazide ligands HL and HL₁. Dashed dark blue and red ovals indicate the structural fragments responsible for heterocycle π-stacking and chelate ring stacking, respectively. Dashed lines show the coordination bonds formed upon complexation with mercury(II) halides.

The choice of nicotinohydrazides HL and HL₁ as ligands for complexes and coordination polymers needs to be explained. Firstly, the hydrazide fragment of these ligands is responsible for their chelating properties (Scheme 1);¹⁷ due to their flexibility, ligands can adopt different conformations with respect to the relative orientations of the carbonyl group.¹⁸ Assuming chelation involving oxygen atom, these ligands are predisposed to form two kinds of chelate rings: OCNN and NCCN. Secondly, from the structures of the ligands, it can be inferred that nitrogen atoms will be engaged not only to form coordination bonds but also to participate in hydrogen bonding (through a donor N–H fragment) interactions with counterions, neighboring ligand molecules and cocrystallized solvents.¹⁹ A possibility of structure expansion is provided by the nitrogen atom of the 3-pyridyl (“nicotino”) fragment, which may serve as an additional docking site to the mercury center, thereby forming a bridge and giving an access to polymeric coordination compounds.

Experimental

Materials and general methods

All the reagents other than ligands were purchased commercially and used as received without further purification. FT-IR spectra (4000–400 cm⁻¹ region) were recorded from KBr pellets with a Bruker Tensor 27 spectrometer. Microanalyses were performed using a Heraeus CHN-O-Rapid analyzer.

Synthesis of the complexes

Crystals of 1–5 were isolated by mixing the corresponding ligand with mercury(II) bromide or mercury(II) iodide, following a method exemplified for compound 1. This complex was synthesized by the reaction of organic ligand HL (0.302 g, 0.5 mmol) and HgBr₂ (0.5 mmol), both placed in the main arm of a branched tube. Methanol (15 ml) was carefully added to fill the arms. The tube was sealed and immersed in an oil bath at 60 °C, while the branched arm was kept at ambient temperature. After 5 days, crystals of 1 were formed in the cooler arm, filtered off, washed with acetone and ether, and finally dried in air.

[Hg(μ-L)BrHgBr₂]_n (1). Yield: 87%. m. p. 225 °C. Anal. calc. for C₁₃H₁₂Br₄Hg₂N₄O: C, 16.25; H, 1.26; N, 5.83%. Found: C, 16.34; H, 1.12; N, 5.65%. FTIR (cm⁻¹) selected bands: 698(s); 769(m); 1025(m); 1136(s); 1326(m); 1430(m); 1528(s); 1590(m); 1659(m); 2815(w); 2923(w); 3060(w); 3145(w).

[Hg(μ-L₁)Br]_n (2). Yield: 81%. m. p. 289 °C. Anal. calc. for C₁₈H₁₃BrHgN₄O: C, 37.16; H, 2.25; N, 9.63%. Found: C, 37.01; H, 2.31; N, 9.71%. FTIR (cm⁻¹) selected bands: 693(s); 786(m); 1027(m); 1126(s); 1333(m); 1422(m); 1471(s); 1593(m); 1641(m); 2926(w); 2925(w); 3058(w).

[Hg(L)I₂] (3). Yield: 65%. m. p. 233 °C. Anal. calc. for C₁₃H₁₂I₂HgN₄O: C, 22.48; H, 1.74; N, 8.07%. Found: C, 22.55; H, 1.81; N, 8.19%. FTIR (cm⁻¹) selected bands: 705(s); 777(m); 1011(m); 1098(s); 1326(m); 1417(m); 1589(s); 1543(m); 1620(m); 2851(w); 3032(w); 3053(w).

[Hg(HL₁)I₂]·(CH₃OH) (4). Yield: 91%. m. p. 245 °C. Anal. calc. for C₁₉H₁₈I₂HgN₄O₂: C, 28.93; H, 2.30; N, 7.10%. Found: C, 29.01; H, 2.35; N, 7.13%. FTIR (cm⁻¹) selected bands: 693(s); 784(m); 1022(m); 1153(s); 1298(m); 1428(m); 1546(s); 1581(m); 1648(m); 2854(w); 2925(w); 3055(w); 3445(w).

[Hg(μ-L₁)I]_n (5). Yield: 67%. m. p. 288 °C. Anal. calc. for C₁₈H₁₃IHgN₄O: C, 34.38; H, 2.08; N, 8.91%. Found: C, 34.21; H, 2.12; N, 9.02%. FTIR (cm⁻¹) selected bands: 697(s); 771(m); 1022(m); 1110(s); 1331(m); 1423(m); 1509(s); 1591(m); 1665(m); 2854(w); 2925(w); 3055(w).

X-ray crystallography

Diffraction data were collected at room temperature (2–4), 193(1) K (1) and 100(1) K (5) by the ω-scan technique using Bruker four-circle diffractometers (APEX-II CCD for 1, 3 and 4 and SMART1000 CCD for 2 and 5) with graphite-monochromated MoK_α radiation (λ = 0.71069 Å). The detector frames were integrated using the program SAINT,²⁰ and empirical absorption corrections were performed using the SADABS program.²¹ The structures were solved with SHELXT²² and refined with the full-matrix least-squares procedure on F² by SHELXL.²² All non-hydrogen atoms were refined anisotropically, and the positions of all hydrogen atoms were placed in idealized positions and refined as ‘riding model’ with isotropic displacement parameters set to 1.2 (1.5 for methyl groups) times U_eq of appropriate carrier atoms. The structures of 2 and 5, which are isomorphous, were both refined as twins;²² BASF factors converged at 0.13(3) for 2 and at 0.295(1) for 5. In the structure of 4, the disordered solvent, methanol molecule, has been found; site occupation factors for the alternative positions of methyl groups were fixed at 0.5. The details of crystallographic data collection and refinement parameters are given in Table 1.

Table 1 Crystal data and refinement details of 1–5

Compound	1	2	3	4	5
Formula	C13H12Br4Hg2N4O	C18H13BrHgN4O	C13H12HgI2N4O	C18H13HgI2N4O·CH3OH	C18H13HgIN4O
Formula weight	961.09	581.82	694.66	788.76	628.81
Crystal system	Monoclinic	Monoclinic	Monoclinic	Triclinic	Monoclinic
Space group	P21/n	P21/n	P21/c	P1̄	P21/n
a (Å)	8.7230(15)	10.8009(10)	9.4971(10)	9.9325(18)	10.7093(10)
b (Å)	14.244(2)	15.0130(13)	19.796(2)	10.233(2)	15.1214(14)
c (Å)	16.507(3)	11.3474(10)	9.2661(10)	12.755(3)	11.4424(11)
α (°)	90	90	90	91.65(2)	90
β (°)	100.782(3)	108.659(2)	96.913(10)	110.98(2)	110.2750(10)
γ (°)	90	90	90	106.46(2)	90
V (Å^3)	2014.8(6)	1743.3(3)	1729.4(3)	1148.5(4)	1738.2(3)
Z	4	4	4	2	4
d x (g cm^−3)	3.17	2.22	2.67	2.28	2.40
F(000)	1704	1088	1248	724	1160
μ (mm^−1)	23.16	11.13	12.47	9.41	10.65
Θ range (°)	1.90–25.10	2.27–26.00	2.06–28.00	2.10–26.25	2.25–28.31
hkl range	−10 ≤ h ≤ 10	−13 ≤ h ≤ 13	−12 ≤ h ≤ 12	−11 ≤ h ≤ 10	−14 ≤ h ≤ 13
	−16 ≤ k ≤ 16	−18 ≤ k ≤ 18	−26 ≤ k ≤ 26	−12 ≤ k ≤ 12	−20 ≤ k ≤ 20
	−19 ≤ l ≤ 19	−13 ≤ l ≤ 13	−12 ≤ l ≤ 12	−15 ≤ l ≤ 15	−15 ≤ l ≤ 15
Reflections
Collected	13 846	33 100	75 755	8336	10 487
Unique (Rint)	3496 (6.06%)	3419 (6.57%)	4179 (2.62%)	4252 (12.73%)	7894 (4.40%)
With I > 2σ(I)	2881	2709	3652	1782	6656
No. of pars.	218	227	192	253	227
R(F) [I > 2σ(I)]	0.0323	0.0758	0.0254	0.0622	0.0365
wR(F^2) [I > 2σ(I)]	0.0734	0.2154	0.0753	0.1458	0.0749
R(F) [all data]	0.0447	0.0876	0.0352	0.1182	0.0491
wR(F^2) [all data]	0.0776	0.2154	0.0779	0.1577	0.0799
Goodness of fit	1.023	1.974	1.055	0.8253	1.026
Max/min Δρ (e Å^−3)	1.10/−1.64	3.13/−3.44	1.59/−1.31	1.29/−2.25	2.35/−1.31

---

Hirshfeld surface analysis

Hirshfeld surface (HS)²³ and 2D fingerprint plot²⁴ analyses can be considered as fundamental methods for the exploration of intermolecular contacts of supramolecular²⁵ and coordination compounds.²⁶ Each point on the HS has a well-defined distance from the nearest atom inside the surface (d_i), and analogously, a distance from the nearest atom outside of the surface (d_e). Mathematical treatment of d_e and d_i values with selected functions (i.e. d_norm, shape index, and curvedness) allows particular structural information (π–π stacking, hydrogen bonding) to be highlighted using the color mapping of the HS. In the case of the d_norm function, red spots are associated with the contacts between atoms on both sides of the HS, which are shorter than the sum of van der Waals radii, and for this reason are frequently used to visualize short contacts, e.g. hydrogen bonds. Additionally, plotting the histogram of all (d_i, d_e) contacts gives two-dimensional (2D) fingerprint plot, which can be treated as a graphical ‘summary’ of the contact distances to the HS; consequently, their shapes are diagnostic for given intermolecular contacts.

The properties of Hirshfeld surfaces and 2D fingerprints (where applicable) of all compounds were explored using the Crystal Explorer package ver. 3.1.²⁷ Crystal structures were imported from CIF files. Hirshfeld surfaces were generated using high resolution and mapped with the d_norm and shape-index functions. 2D fingerprint plots were prepared using the same software.

Theoretical methods

The geometries of the complexes included in this study were computed at the M06-2X/def2-TZVP level of theory using the crystallographic coordinates within the TURBOMOLE program.²⁸ This level of theory is adequate for studying noncovalent interactions dominated by dispersion effects like π-stacking. The basis set superposition error for the calculation of interaction energies has been corrected using the counterpoise method.²⁹ “Atoms-in-molecules” (AIM)³⁰ analysis of the electron density has been performed at the same level of theory using the AIMAll program.³¹

Results and discussion

Supramolecular and coordination features of structures 1–5

The crystallographic details are summarized in Table 1, and the selected bond lengths and angles are gathered in Table S1.†

The molecular structure with an atom-labeling scheme for 1 is shown in Fig. 1a, and the 1D polymer chains are presented in Fig. 1b. The 3D packing can be simplified as parallel stacking of T-shaped prisms (see Fig. S1 in the ESI†). In complex 1, two crystallographically different Hg(II) metal centers are present. The five-coordinate Hg1 ion is surrounded by one oxygen and two nitrogen atoms of HL, one terminal (Br1) and one bridging (Br2) bromide ligands. The coordination environment of the Hg1 center is a highly distorted square pyramid, which is confirmed by the value of the τ₅ parameter (0.24).³² The Hg2 ion is coordinated by three bromide ligands and one nitrogen atom of HL. The structural index parameter τ₄ equals 0.71, which can indicate that the coordination environment around Hg2 is a very distorted tetrahedron.³³ However, the Hg2 center can be better described as a seesaw with θ₆ = 95.90°. The N1–Hg2–Br2 and Br3–Hg2–Br4 planes are almost perpendicular, with a dihedral angle of about 89.36°. The Hg1 and Hg2 metal centers are connected via the bridging μ-Br(2) ligand. However, there are no M⋯M interactions, because the Hg⋯Hg distance (4.181(1) Å) is much longer than the sum of the van der Waals radii of Hg(II) (3.41 Å).³⁴ Long distance interactions exist between the metal center and the bromide ions, Hg(1)⋯Br(3) (3.621(2) Å) and Hg(2)⋯Br(1)^1b and Hg(2)^1c⋯Br(1) (3.558(2) Å) [symmetry codes: (1b) −x, −1/2 + y, −1/2 − z; (1c) −x, 1/2 + y, −1/2 − z]. These distances are close to the sum of the van der Waals radii of Hg–Br (3.40 Å).³⁵ The structure is stabilized by weak C–H⋯Br hydrogen bonds (see Fig. 1b)³⁶ which leads to the formation of infinite chains running parallel to the [001] direction (see Table S2† for the structural features of the H-bonds in 1). The 3D packing is also stabilized by chelate ring π-stacking interactions, which are further discussed in detail in the DFT and HS study.

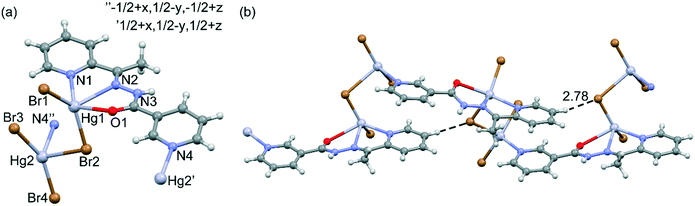Fig. 1 (a) Asymmetric unit of compound 1 and the atomic numbering scheme. (b) Projection of the polymeric 1D chain and C–H⋯Br interaction. Distance in Å.

Compounds 2 and 5 are isostructural; they both crystallize in the P2₁/n space group with very similar unit cell parameters (cf.Table 1); the geometry and packing of the molecules are almost identical. The comparisons of the molecular structure and crystal packing of both compounds are shown in Fig. 2.

Fig. 2 Comparison of molecular (left) and crystal (right) structures of 2 (red) and 5 (blue).

The coordination polymers are formed along the [101] direction (Fig. 3), and are formed from Hg ions coordinated to two different sides of the ligand molecule (N1, N8, and O10 on one side and N13 on the other side). The metal center is five-coordinated, in a distorted tetragonal-pyramid fashion. A view of the 3D crystal packing is given in Fig. S2 in the ESI.† For the details of the hydrogen bonding structural features of both complexes, see Table S2.†

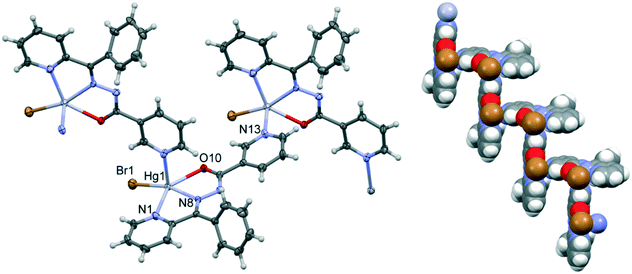Fig. 3 A fragment of the coordination polymer in 2; ellipsoids are drawn at the 50% probability level, and hydrogen atoms are shown as spheres of arbitrary radii.

Compound 3 is not polymeric, and in its structure, the Hg(II) center is coordinated via two nitrogen atoms and one oxygen atom of HL and two iodine ions (see Fig. 4). The value of index parameter (τ₅) equals 0.04, which can indicate that the coordination polyhedron has an ideal square pyramidal structure with C_4v symmetry. However, this geometry is associated with α = β = 180°, whereas for complex 3 the angles are closer to D_3h symmetry. This indicates that the coordination environment of the Hg1 center has as a highly asymmetric geometry intermediate between square pyramid and trigonal bipyramid (Fig. 4a). In 3, the N–H⋯N hydrogen bonds (see Table S2†) between the N–H groups of the hydrazone moieties and pyridine nitrogen atoms are responsible for the formation of the zigzag chain packing pattern along [001] exhibiting a C(6) graph-set motif.³⁷ In this compound, self-assembled π-stacked dimers are also formed in the solid state, exhibiting chelate ring⋯π stacking interactions, which are further discussed below. The final 3D architecture of this compound can be simplified as parallel stacking of trapezoidal prisms, see Fig. S3 in the ESI.†

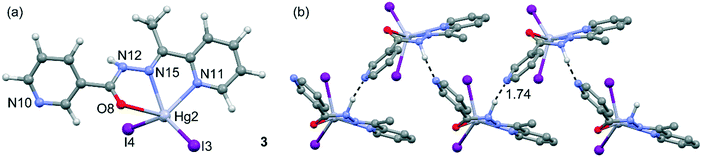Fig. 4 (a) Asymmetric unit of compound 3 and the atomic numbering scheme. (b) Detail of the polymeric 1D chain and the N–H⋯N interaction. Distance in Å.

In structure 4, the geometry of the Hg(II) center shows a five-coordinate stereochemistry, which can be described as a highly distorted trigonal bipyramidal geometry as evidenced by the value of the geometric index τ₅ (0.52). The metal ion is surrounded by two nitrogen atoms and one oxygen atom and two terminal iodine ligands (Fig. 5). Methanol molecule is linked to the [Hg(L)I₂] moiety via the intermolecular O–H⋯N hydrogen bond with a pyridine nitrogen atom as the proton acceptor. Moreover, disordered methanol molecule is engaged in the formation of dimeric units through the O–H⋯N and N–H⋯O hydrogen bonds, where it is both the donor and acceptor of proton (see Fig. 5b and Table S2†), generating cyclic hydrogen-bonded motifs with the graph-set notation R⁴₄(16).³⁷ The structure is also stabilized by weak intermolecular C–H⋯O and C–H⋯I hydrogen bonds, as well as C–H⋯π interactions. The C(19A)–H(19B)⋯Cg5 (Cg5 is the centroid of the phenyl formed from C(7)–C(12) atoms, d_C⋯Cg = 3.575(1), ∠_C–H⋯Cg = 143°) stacking interactions occur in the centrosymmetric hydrogen bond ring. The presence of weak intermolecular C–H⋯O hydrogen bonds leads to the formation of a two-dimensional network, see Fig. S4 in the ESI.†

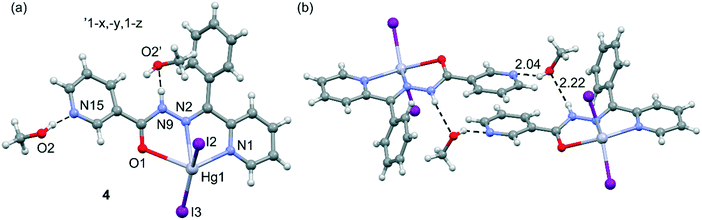Fig. 5 (a) Asymmetric unit of compound 4 and the atomic numbering scheme. (b) Dimeric units through O–H⋯N and N–H⋯O hydrogen bonds (represented by the dashed lines). Distances in Å.

Hirshfeld surface analysis

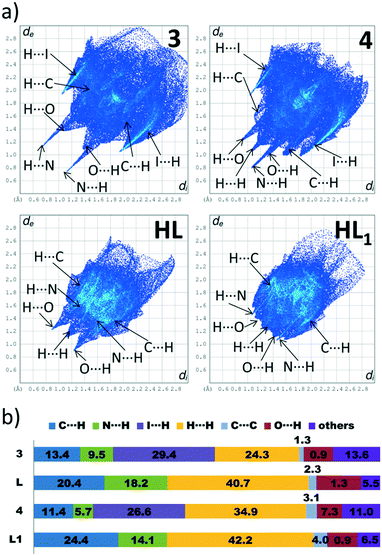
In this paper, we have divided considerations on the Hirshfeld surface (HS) properties into two parts, taking as a criterion the dimensionality of the metal–organic hybrids. As presented in the “Supramolecular and coordination features of structures 1–5” section, among compounds 1–5, the 3 and 4 are 0D complexes. The discrete nature of those compounds allows for both qualitative (that is, assignments of respective contacts to certain regions of d_norm and/or shape-index-mapped HS) and quantitative (determination of percentage contributions of contacts to the HS) analysis. On the other hand, compounds 1, 2 and 5 are 1D coordination polymers. The polymeric structure of those compounds makes the HS analysis more challenging, since it has to be conducted on the subjectively chosen fragment of the coordination chain. The choice of a fragment, in turn, has a profound influence on percentage contributions of the participating contacts. Additionally, drawing the HS on the part of coordination chain results in obtaining unusually low d_i and d_norm values since these parameters reflect not only the intermolecular interactions, but also the coordination/covalent bonds that “perforate” the drawn HS. For these reasons, the HS analysis of compounds 1, 2 and 5 has mainly qualitative characteristics.

To explore effects of the HgI₂ coordination on the landscape of the participating contacts to the HS, we have compared properties 2D fingerprint plots of complexes 3 and 4 with those of the corresponding ligands, L (CSD refcode YIRFAH)³⁸ and L1 CSD refcode HEWJUP).³⁹

A strong characteristic feature of the 2D fingerprint plots of compounds 3 and 4 is the significantly scattered d_i and d_e values, which results in larger areas occupied by histograms. As can be seen in Fig. 6, the d_e and d_i values are reaching maximal values of 2.9 and 2.85 Å in compounds 3 and 4, respectively. In contrast, the 2D fingerprints drawn for ligands occupy much smaller areas – here, the maximal d_e and d_i values are found for ligand L1 (2.7 Å). This observation can be explained on the basis of the analysis of decomposed 2D fingerprint plots. Examining the decomposed H⋯I and H⋯C fingerprint plots of 3 and 4 in Fig. S5 and S6, ESI,† shows that the H⋯I contacts form much broader “wings” than the C⋯H ones, so their overlap yields a much broader contact distribution. This can be explained on the basis of the differences between the atomic radii of iodine and carbon atoms, in which the former is much higher, so the d_i and d_e distances increased.

Fig. 6 a) 2D fingerprint plots and b) percentage contributions of contacts to the Hirshfeld surface in the structures calculated from the crystal structures of complexes 3 and 4 and ligands HL and HL₁.

A distinct difference between the 2D fingerprint plots of 3 and 4 is the lack of symmetry across the diagonal for the latter one (Fig. 6a). In our previous papers, we have noted that this behaviour is characteristic of crystal structures, which comprise more than one molecular component, e.g. in structures featured by two crystallographically independent molecules⁴⁰ or in solvates.⁴¹ Indeed, this is the case for compound 4, in which a methanol molecule is present. Its presence imparts strong accepting H⋯N contacts and donor accepting H⋯O contacts formed from the complex molecule (Fig. S6, in the ESI†). Note that in compound 3, due to lack of any solvent molecule that could form strong hydrogen bonds, the donor and accepting traces corresponding to H⋯N contacts are at the same level.

The calculation of contact contributions to the relative Hirshfeld surface areas suggests that the most prevalent interactions in 3 and 4 are the I⋯H and H⋯H ones (Fig. 6b). When I⋯H and H⋯H contacts are considered together, these two interactions made up around 60% of the entire HS; on the other hand, there are significant differences in their individual contributions. In 3, the content of I⋯H contacts is higher by 5% than of that of the H⋯H ones (I⋯H – 29.4%, H⋯H – 24.3%), while in 4 the trend is reverse (I⋯H – 26.6%, H⋯H – 34.9%). The corresponding d_norm-mapped Hirshfeld surfaces of the complexes are drawn in Fig. 7, along with the assignments of all discussed contacts.

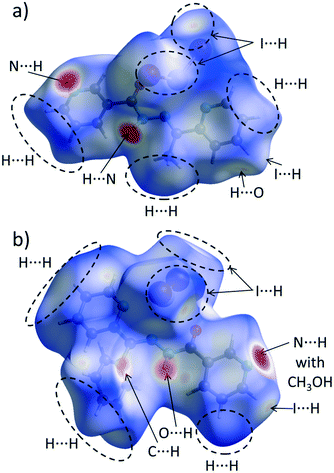Fig. 7 Hirshfeld surface of a) 3 and b) 4 mapped with the d_norm function. Regions of most important intermolecular contacts are indicated by the dashed ovals and/or arrows.

We suggest that the described above variations in the H⋯H/H⋯I contact distributions can have two different origins. Firstly, we attribute the presence of the phenyl ring in 4 instead of the methyl group (in 3) as a possible factor responsible for the increased share of the H⋯H contacts, since the phenyl ring is capable of forming dispersive contacts at a much larger area than the relatively small methyl group (Fig. 7). As an additional support for this hypothesis, we compared the contact contributions calculated from the crystal structures of ligands L and L1 (Fig. 6b). In line with the above reasoning, ligand L1 is featured by a larger amount of H⋯H and C⋯H contacts than L (42.2% vs. 40.7 and 24.4% vs. 20.4, respectively), which highlights the role of bulkiness of a phenyl ring and, in the broader context, of the substituent effect. It is worth stressing that due to the phenyl ring steric hindrance, no chelate ring stacking is present, which causes the HS of 4 to not possess flat regions (in contrast to 1–3 and 5).

Secondly, we wondered why the participation of I⋯H contacts to the HS is smaller in 4 when compared to 3. Here, as an essential contributing factor, we regard the fact that methyl hydrogen atoms of a methanol molecule (in 4) interact with iodine atoms of the HgI₂ fragment (Fig. 7b). Due to this interaction, iodine atoms are “shielded” from the other complex molecules. This causes the HS of this compound to accept mainly I⋯H contacts, consequently decreasing the overall share of the I⋯H contacts in the entire HS.

We now move to the overview of the interchain interactions within coordination polymers 1, 2 and 5. Fig. S7, ESI,† presented fragments coordination chains, on which the HSs were drawn. Those surfaces are featured by a number of C⋯H, H⋯H, Br⋯H (in 1 and 2), and I⋯H (in 5) contacts. Nevertheless, the common feature of those coordination polymers is the presence of the conventional and unconventional (chelate ring) stacking interactions, as shown in Fig. S8, ESI.† While d_norm-mapped surfaces do not provide much information on the stacking interactions, the shape-index-mapped surfaces reveal a set of four blue-colored triangles, each placed in the center of the stacked ring: either aromatic (phenyl/pyridyl) or formed via coordination. The observation of these features served as a foundation for the considerations provided in the next section.

Theoretical results

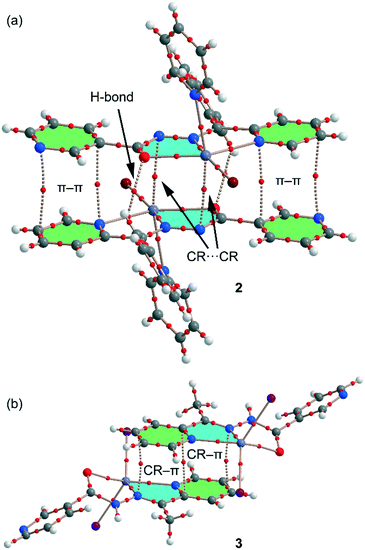
We have focused the theoretical study on the comparison of the energetic features of the different types of π-stacking interactions (chelate ring–π and π–π) observed in the crystal packing of compounds 1–3 and 5. Conventional π-stacking interactions usually involve organic aromatic molecules.⁴² However, the other planar molecular fragments can also participate in more “unpredictable” stacking interactions.⁴³ Among them, chelate rings with delocalized π-bonds establish stacking⁴³ interactions similar to those of aromatic organic molecules⁴² in transition-metal complexes. The chelate-ring–π interactions have been associated to the aromaticity of planar chelate rings with delocalized π-bonds.⁴⁴

In the crystal packing of compounds 1, 2 and 5, the 1D polymeric chains form self-assembled supramolecular entities in the solid state governed by the formation of antiparallel chelate ring⋯chelate ring (CR⋯CR) and conventional π–π interactions. These interactions are highlighted in Fig. 8, and it can be observed that the square planar pyramidal geometry of the Hg atom in compounds 2 and 5 facilitates the approximation of the chelate rings, resulting in shorter CR⋯CR interactions.

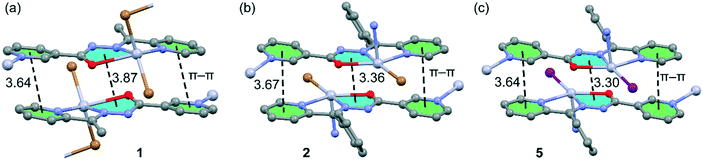Fig. 8 Conventional and unconventional π–π interactions in the self-assembled stacked 1D polymeric chains present in 1 (a), 2 (b) and 5 (c). Distances in Å. H atoms are omitted for clarity.

In this theoretical study, we have used monomeric models of the polymeric chains of compounds 1, 2 and 5 in order to estimate the interactions. In the isostructural compounds 2 and 5, we have computed the interaction energy of the self-assembled π-stacked dimers, shown in Fig. 9a, where a pyridine ring has been used as an axial Hg ligand in the monomeric model. The self-assembled dimers are stabilized by a combination of H-bonds (blue dashed lines), π–π and CR⋯CR stacking interactions. The dimerization energies in 2 and 5 (ΔE₁ = −24.6 kcal mol⁻¹ and ΔE₄ = −26.2 kcal mol⁻¹, respectively) are large due to the contribution of the three interactions. In an effort to calculate the contribution of the different forces that govern the formation of the self-assembled dimers, we have computed a theoretical model in which the uncoordinated pyridine rings have been replaced by H atoms (see the small arrows in Fig. 9b), and consequently the π–π stacking interactions between the coordinated and uncoordinated pyridine rings are not formed. As a result, the interaction energies are reduced to ΔE₂ = −14.2 kcal mol⁻¹ and ΔE₅ = −15.7 kcal mol⁻¹ for 2 and 5, respectively. Therefore, the contribution of both symmetrically equivalent π–π stacking interactions can be roughly estimated by difference (they are −10.4 and −10.5 kcal mol⁻¹ for 2 and 5, respectively). Furthermore, we have used an additional dimer, where the phenyl ring that participates in the C–H⋯O H-bonding interactions have been replaced by a hydrogen atom, and consequently, the H-bonding interactions are not formed. The resulting interaction energies are further reduced to ΔE₃ = −10.6 kcal mol⁻¹ and ΔE₆ = −11.7 kcal mol⁻¹ for 2 and 5, respectively, which corresponds to the contribution of the CR–CR π-stacking interactions. The contribution of both H-bonding interactions can be estimated by difference (they are −3.6 and −4.0 kcal mol⁻¹ for 2 and 5, respectively).

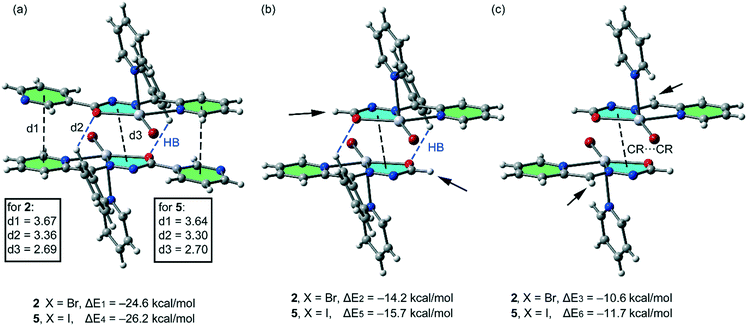Fig. 9 (a) Interaction energies of the self-assembled π-stacked dimers observed in the solid state of compounds 2 and 5. (b and c) Interaction energies in several theoretical models of 2 and 5.

For the polymeric compound 1, we have used for the calculations the monomeric unit shown in Fig. 10a. It is used to estimate the interaction energy of the self-assembled π-stacked dimer that is responsible for the inter-connection of the 1D chains in the solid state. The self-assembled dimer is stabilized by the combination of N–H⋯Br H-bonds and π-stacking interactions (π–π and CR⋯CR). The dimerization energy ΔE₇ = −36.6 kcal mol⁻¹ is larger than that found for compounds 2 and 5 likely due to the stronger ability of the N–H groups to establish H-bonding interactions. To calculate the contribution of the different forces that govern the formation of the self-assembled dimer, we have computed a theoretical model where the uncoordinated pyridine rings have been replaced by H atoms (see the small arrows in Fig. 10b), and consequently the π–π stacking interactions between the coordinated and uncoordinated pyridine rings are not formed. As a result, the interaction energy is reduced to ΔE₈ = −26.3 kcal mol⁻¹. Therefore, the contribution of both symmetrically equivalent π–π stacking interactions can be roughly estimated by difference (−10.3 kcal mol⁻¹) that is comparable to those obtained for 2 and 5. Furthermore, we have used an additional dimer, where the bromido ligands that participate in the H-bonding interactions have been replaced by hydride, and consequently, the H-bonding interactions are not formed. The resulting interaction energy is further reduced to ΔE₉ = −16.3 kcal mol⁻¹, which corresponds to the contribution of the CR⋯CR stacking interaction. The contribution of both H-bonding interactions can be estimated by difference (−10.0 kcal mol⁻¹). Therefore, the H-bonding interactions are stronger in compound 1 than in 2 or 5, which is in agreement with the stronger ability of N–H than C–H group to participate in H-bonding interactions.

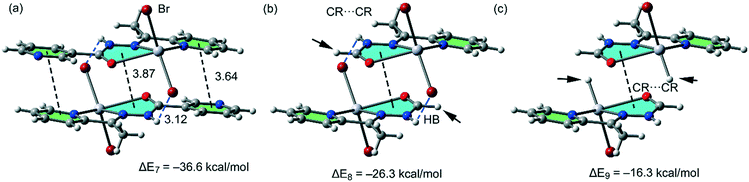Fig. 10 (a) Interaction energies of the π-stacked dimers observed in the solid state of compound 1. (b and c) Interaction energies presented in several theoretical models of 1.

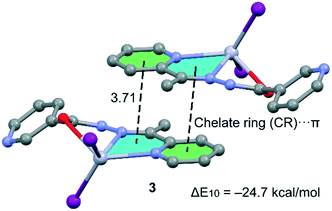
Compound 3, which is not polymeric, forms self-assembled dimers in the solid state governed by the formation of two symmetrically equivalent chelate ring (CR)⋯π interactions (see Fig. 11). The chelate ring that participates in the CR–π interaction in this compound is not the same one that participates in CR–CR interactions in compounds 1, 2 and 5, because the Hg–O–C–N–N chelate ring is not planar due to the rotation of the amido group. The interaction energy of this dimer is ΔE₈ = −18.5 kcal mol⁻¹; thus each CR–π interaction contributes −9.25 kcal mol⁻¹ similar to the CR⋯CR interactions computed for compounds 1, 2 and 5 and confirms the importance of unconventional π-stacking interactions in the crystal packing of these compounds.

Fig. 11 Self-assembled CR⋯π stacked dimer in compound 3. Distance in Å.

In order to provide additional evidence for the existence of the unconventional π–π stacking interactions between the chelate-ring interactions we have analysed the self-assembled π-stacked dimer of compounds 2 and 3 (as exemplifying models) using Bader's theory of “atoms in molecules” (AIM),⁴⁵ which provides an unambiguous definition of chemical bonding. The AIM theory has been successfully used to characterize and understand a great variety of interactions including those described herein. In Fig. 12, we show the AIM analysis of compounds 2 and 3. In 2 it can be observed that each conventional π–π interaction (pyridine rings) is characterized by the presence of two bond critical points that interconnect two atoms of the coordinated pyridine ring to two atoms of the uncoordinated ring, thus confirming the interaction. Furthermore, the distribution of critical points reveals the existence of two symmetrically related C–H⋯O H-bonding interactions. Each one is characterized by a bond critical point and a bond path connecting one H atom of the CH group with the O atom of the chelate ring. Finally, the unconventional CR⋯CR interaction is confirmed by the presence of two bond critical points interconnecting two atoms of the chelate rings. In 3, the CR–π interactions are characterized by the presence of three bond critical points and bond paths that interconnect the rings. The value of the Laplacian of the charge density at the bond critical points is positive, which is common in closed-shell interactions.

Fig. 12 AIM analysis of the self-assembled dimers retrieved from the X-ray structures of compounds 2 (a) and 3 (b). Only the bond critical points are represented by red spheres. The bond paths connecting the bond critical points are also represented by dashed lines.

Conclusions

Understanding the variances in the structural properties of systematically modified crystalline materials assists in the rational design of new materials with predictable crystal structure. For this reason, we have prepared and structurally characterized five new metal complexes of a Hg(II) metal center with two hydrazine-based ligands (HL and HL₁). Four compounds exhibit remarkable chelate ring–chelate ring and π–π heterocycle stacking interactions in the solid state. Analysis of energies associated to the interactions, including the estimation of contributions of the different forces, has been conducted using DFT calculations, and further corroborated with Bader's theory of “atoms in molecules”. The results gave ample evidence for preferential formation of both unconventional and conventional ring stackings, and allow us to conclude that chelate ring interaction may be considered as a synthon interaction for nicotinohydrazide metal complexes. The interaction energies reported herein confirm that the chelate–chelate interactions are stronger than those reported for classical π–π complexes.⁴²

Hirshfeld surface analysis and 2D fingerprint plots of the crystal structures reported here gave an insight into packing differences imposed by the substituent effect. The most significant effects result from the presence of a phenyl ring in 4 instead of a methyl group (in 3). It is attributed as an origin for the increased share of dispersive H⋯H contacts in the former compound, since the phenyl ring is capable of forming dispersive contacts at a much larger area than the much smaller methyl group. Apart from that, the phenyl substituent in 4 hampers the formation of chelate ring stacking, which is reflected in the shape and properties of the d_norm-mapped Hirshfeld surface.

The interactions studied in this work are important to understand the formation of metal–organic assemblies in the solid state. The results reported herein might be useful to understand the solid state architecture of materials that contain M(II)-chelate rings and organic aromatic molecules.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

GM is grateful to the University of Maragheh for the financial support of this research. AB and AF thank the MINECO of Spain (project CTQ2014-57393-C2-1-P and CTQ2017-85821-R, FEDER funds) for funding and the CTI (UIB) for free allocation of computer time. JKZ acknowledges financial support from the Wrocław University of Science and Technology.

References

1. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534.
2. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
3. C. F. Matta, N. Castillo and R. J. Boyd, J. Phys. Chem. B, 2006, 110, 563–578.
4. G. B. McGaughey, M. Gagné and A. K. Rappé, J. Biol. Chem., 1998, 273, 15458–15463.
5. R. Martinez and L. Chacon-Garcia, Curr. Med. Chem., 2005, 12, 127–151.
6. A. Wolfe, G. H. Shimer and T. Meehan, Biochemistry, 1987, 26, 6392–6396.
7. (a) H. Yoo, J. Yang, A. Yousef, M. R. Wasielewski and D. Kim, J. Am. Chem. Soc., 2010, 132, 3939–3944; (b) D. Ananias, A. D. G. Firmino, R. F. Mendes, F. A. A. Paz, M. Nolasco, L. D. Carlos and J. Rocha, Chem. Mater., 2017, 29, 9547–9554; (c) Z. Xu, N. J. Singh, J. Lim, J. Pan, H. N. Kim, S. Park, K. S. Kim and J. Yoon, J. Am. Chem. Soc., 2009, 131, 15528–15533.
8. E. A. Mikhalyova, A. V. Yakovenko, M. Zeller, M. A. Kiskin, Y. V. Kolomzarov, I. L. Eremenko, A. W. Addison and V. V. Pavlishchuk, Inorg. Chem., 2015, 54, 3125–3133.
9. R. Rathore, S. H. Abdelwahed and I. A. Guzei, J. Am. Chem. Soc., 2003, 125, 8712–8713.
10. M. Swart, T. van der Wijst, C. Fonseca Guerra and F. M. Bickelhaupt, J. Mol. Model., 2007, 13, 1245–1257.
11. (a) J. Saßmannshausen, Dalton Trans., 2012, 41, 1919–1923; (b) M. A. Sajjad, K. E. Christensen, N. H. Rees, P. Schwerdtfeger, J. A. Harrison and A. J. Nielson, Dalton Trans., 2017, 46, 16126–16138; (c) G. Mahmoudi, A. Bauzá and A. Frontera, Dalton Trans., 2016, 45, 4965.
12. (a) O. T. Summerscales and J. C. Gordon, RSC Adv., 2013, 3, 6682–6692; (b) G. Mahmoudi, L. Dey, H. Chowdhury, A. Bauzá, B. K. Ghosh, A. M. Kirillov, S. K. Seth, A. V. Gurbanov and A. Frontera, Inorg. Chim. Acta, 2017, 461, 192–205; (c) G. Mahmoudi, A. Bauzá, M. Amini, E. Molins, J. T. Mague and A. Frontera, Dalton Trans., 2016, 45, 10708.
13. (a) S. Scheiner, Faraday Discuss., 2017, 203, 213–226; (b) D. Franz and S. Inoue, Dalton Trans., 2016, 45, 9385–9397; (c) G. Mahmoudi, A. Castiñeiras, P. Garczarek, A. Bauzá, A. L. Rheingold, V. Kinzhybalo and A. Frontera, CrystEngComm, 2016, 18, 1009.
14. (a) A. C. Legon, Phys. Chem. Chem. Phys., 2017, 19, 14884–14896; (b) J. Fanfrlík, W. Zierkiewicz, P. Švec, Z. Růžičková, J. Řezáč, M. Michalczyk, A. Růžička, D. Michalska and P. Hobza, J. Mol. Model., 2017, 23, 328; (c) L. Brammer, Faraday Discuss., 2017, 203, 485–507; (d) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Commun., 2015, 51, 1491–1493; (e) A. Bauzá, R. Ramis and A. Frontera, J. Phys. Chem. A, 2014, 118, 2827–2834; (f) A. Bauzá, A. Frontera and T. J. Mooibroek, Nat. Commun., 2017, 8, 14522; (g) A. Báuza, A. Frontera and T. J. Mooibroek, Cryst. Growth Des., 2016, 16, 5520–5524; (h) A. Bauzá, A. V. Sharko, G. A. Senchyk, E. B. Rusanov, A. Frontera and K. V. Domasevitch, CrystEngComm, 2017, 19, 1933–1937.
15. (a) D. P. Malenov, G. V. Janjić, V. B. Medaković, M. B. Hall and S. D. Zarić, Coord. Chem. Rev., 2017, 345, 318–341; (b) R. Rakshit and C. Mukherjee, Eur. J. Inorg. Chem., 2016, 2016, 2731–2737; (c) A. P. McKay, W. K. C. Lo, D. Preston, G. I. Giles, J. D. Crowley, J. E. Barnsley, K. C. Gordon and D. A. McMorran, Inorg. Chim. Acta, 2016, 446, 41–53; (d) Y. P. Singh, R. N. Patel, Y. Singh, D. Choquesillo-Lazarte and R. J. Butcher, Dalton Trans., 2017, 46, 2803–2820; (e) H. R. Masoodi, S. Bagheri and R. Ranjbar-Karimi, Chem. Phys. Lett., 2017, 667, 327–331; (f) W. Chen, G. Li and Y. He, Phys. Chem. Chem. Phys., 2014, 16, 7907–7912.
16. E. R. T. Tiekink, Coord. Chem. Rev., 2017, 345, 209–228.
17. (a) G. Xu, B. B. Tang, L. Hao, G. L. Liu and H. Li, CrystEngComm, 2017, 19, 781–787; (b) A. Mandal, B. K. Patel, R. Shukla and D. Chopra, CrystEngComm, 2017, 19, 1607–1619; (c) B.-B. Tang, H. Ma, G.-Z. Li, Y.-B. Wang, G. Anwar, R. Shi and H. Li, CrystEngComm, 2013, 15, 8069–8073.
18. D. Hean, T. Gelbrich, U. J. Griesser, J. P. Michael and A. Lemmerer, CrystEngComm, 2015, 17, 5143–5153.
19. F. A. Afkhami, A. A. Khandar, G. Mahmoudi, W. Maniukiewicz, A. V. Gurbanov, F. I. Zubkov, O. Şahin, O. Zafer Yesilel and A. Frontera, CrystEngComm, 2017, 19, 1389–1399.
20. SAINT Plus, Data Reduction and Correction Program, v. 6.01, Bruker AXS, Madison, Wisconsin, USA, 1998.
21. SADABS v. 2.01, Bruker/Siemens Area Detector Absorption Correction Program, Bruker AXS, Madison, Wisconsin, USA, 1998.
22. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
23. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
24. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816.
25. (a) J. K. Zaręba, M. J. Białek, J. Janczak, J. Zoń and A. Dobosz, Cryst. Growth Des., 2014, 14, 6143–6153; (b) E. Önal, T. M. Okyay, G. Ekineker, Ü. İşci, V. Ahsen, S. Berber, Y. Zorlu and F. Dumoulin, J. Mol. Struct., 2018, 1155, 310–319; (c) D. Pogoda, J. Janczak and V. Videnova-Adrabinska, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 263–273; (d) A. Bulut, M. Worle, Y. Zorlu, E. Kirpi, H. Kurt, J. Zubieta, S. Grabowsky, J. Beckmann and G. Yucesan, Acta Crystallogr., Sect. B: Struct. Sci., 2017, 73, 296–303; (e) A. Pietrzak, J. Modranka, J. Wojciechowski, T. Janecki and W. M. Wolf, Cryst. Growth Des., 2018, 18, 200–209; (f) S. R. Maidur, J. R. Jahagirdar, P. S. Patil, T. S. Chia and C. K. Quah, Opt. Mater., 2018, 75, 580–594.
26. (a) B. Morzyk-Ociepa, K. Szmigiel, R. Petrus, I. Turowska-Tyrk and D. Michalska, J. Mol. Struct., 2017, 1144, 338–346; (b) P. Rogala, A. Jabłońska, K. Kazimierczuk Wawrzycka, A. Borek, A. Błażejczyk, J. Wietrzyk and B. Barszcz, J. Mol. Struct., 2016, 1126, 74–82; (c) P. M. Chhetri, X.-K. Yang and J.-D. Chen, Cryst. Growth Des., 2017, 17, 4801–4809; (d) M. Montazerozohori, A. Masoudiasl, Th. Doert and H. Seykens, RSC Adv., 2016, 6, 21396–21412; (e) M. Koc, Y. Zorlu, U. Isci, S. Berber, V. Ahsen and F. Dumoulin, CrystEngComm, 2016, 18, 1416–1426.
27. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, Crystal Explorer ver. 3.1, University of Western Australia, Perth, Australia, 2013.
28. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
29. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
30. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
31. T. A. Keith, AIMAll (Version 13.05.06), TK Gristmill Software, Overland Park KS, USA, 2013.
32. A. W. Addison, N. T. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356.
33. L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964.
34. J.-Y. Wu, H.-Y. Hsu, C.-C. Chan, Y.-S. Wen, C. Tsai and K.-L. Lu, Cryst. Growth Des., 2009, 9, 258–262.
35. S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885.
36. (a) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 49–76; (b) G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997.
37. J. Bernstein, R. E. Davis, L. Shimoni and N.-L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555–1573.
38. F. Yi-Min and T. Xi-Shi, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64, o65.
39. M. Kuriakose, M. R. P. Kurup and E. Suresh, Spectrochim. Acta, Part A, 2007, 66, 353–358.
40. G. Mahmoudi, J. K. Zaręba, A. V. Gurbanov, A. Bauzá, F. I. Zubkov, M. Kubicki, V. Stilinovic, V. Kinzhybalo and A. Frontera, Eur. J. Inorg. Chem., 2017, 2017, 4763–4772.
41. (a) G. Mahmoudi, A. A. Khandar, J. K. Zaręba, M. J. Białek, M. S. Gargari, M. Abedi, G. Barandika, D. van Derveer, J. Mague and A. Masoumi, Inorg. Chim. Acta, 2015, 429, 1–14; (b) M. Abedi, O. Z. Yeşilel, G. Mahmoudi, A. Bauzá, S. E. Lofland, Y. Yerli, W. Kaminsky, P. Garczarek, J. K. Zaręba, A. Ienco, A. Frontera and M. S. Gargari, Inorg. Chim. Acta, 2016, 443, 101–109.
42. (a) A. K. Tewari and R. Dubey, Bioorg. Med. Chem., 2008, 16, 126–143; (b) P. Mignon, S. Loverix, J. Steyaert and P. Geerlings, Nucleic Acids Res., 2005, 33, 1779–1789; (c) J. Sponer, K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2595–2610; (d) X. J. Wang, L. C. Gui, Q. L. Ni, Y. F. Liao, X. F. Jiang, L. H. Tang, L. H. Zhang and Q. Wu, CrystEngComm, 2008, 10, 1003–1010; (e) S. L. Cockroft, C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Am. Chem. Soc., 2005, 127, 8594–8595; (f) T. Sato, T. Tsuneda and K. Hirao, J. Chem. Phys., 2005, 123, 104307–104317; (g) S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434; (h) M. Rubeš, O. Bludsky' and P. Nachtigall, ChemPhysChem, 2008, 9, 1702–1708; (i) E. C. Lee, D. Kim, P. Jurecka, P. Tarakeshwar, P. Hobza and K. S. Kim, J. Phys. Chem. A, 2007, 111, 3446–3457; (j) M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 1065610668; (k) R. Podeszwa, R. Bukowski and K. Szalewicz, J. Phys. Chem. A, 2006, 110, 10345–10354; (l) M. Pitonak, P. Neogrady, J. Rezac, P. Jurecka, M. Urban and P. Hobza, J. Chem. Theory Comput., 2008, 4, 1829–1834.
43. (a) B. D. Ostojić, G. V. Janjić and S. D. Zarić, Chem. Commun., 2008, 6546–6548; (b) Z. D. Tomić, S. B. Novaković and S. D. Zarić, Eur. J. Inorg. Chem., 2004, 11, 2215–2218; (c) D. N. Sredojević, Z. D. Tomić and S. D. Zarić, Cent. Eur. J. Chem., 2007, 5, 20–31; (d) Z. D. Tomić, D. N. Sredojević and S. D. Zarić, Cryst. Growth Des., 2006, 6, 29–31; (e) D. N. Sredojević, G. A. Bogdanović, Z. D. Tomić and S. D. Zarić, CrystEngComm, 2007, 9, 793–798; (f) A. Castineiras, A. G. Sicilia-Zafra, J. M. Gonzales-Perez, D. Choquesillo-Lazarte and J. Niclos-Gutierrez, Inorg. Chem., 2002, 41, 6956–6958; (g) E. Craven, C. Zhang, C. Janiak, G. Rheinwald and H. Lang, Z. Anorg. Allg. Chem., 2003, 629, 2282–2290; (h) U. Mukhopadhyay, D. Choquesillo-Lazarte, J. Niclos-Gutierrez and I. Bernal, CrystEngComm, 2004, 6, 627–632; (i) D. Pucci, V. Albertini, R. Bloise, A. Bellusci, A. Cataldi, C. V. Catapano, M. Ghedini and A. Crispini, J. Inorg. Biochem., 2006, 100, 1575–1578; (j) S. P. Mosae, E. Suresh and P. S. Subramanian, Polyhedron, 2009, 28, 245–252; (k) X. J. Wang, H. X. Jian, Z. P. Liu, Q. L. Ni, L. C. Gui and L. H. Tang, Polyhedron, 2008, 27, 2634–2642; (l) S. Chowdhury, M. G. B. Drew and D. Datta, Inorg. Chem. Commun., 2003, 6, 1014–1016; (m) X. Wang, O. V. Sarycheva, B. D. Koivisto, A. H. McKie and F. Hof, Org. Lett., 2008, 100, 297–300.
44. (a) H. Masui, Coord. Chem. Rev., 2001, 219−221, 957–992; (b) M. K. Milčić, B. D. Ostojić and S. D. Zarić, Inorg. Chem., 2007, 46, 7109–7114.
45. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.

---

Footnote

† Electronic supplementary information (ESI) available: CCDC 1583981–1583985 contain the supplementary crystallographic data for 1–5. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ce02166f

---