Chemical micromotors self-assemble and self-propel by spontaneous symmetry breaking

Abstract

Self-propelling chemical motors have thus far required the fabrication of Janus particles with an asymmetric catalyst distribution. Here, we demonstrate that simple, isotropic colloids can spontaneously assemble to yield dimer motors that self-propel. In a mixture of isotropic titanium dioxide colloids with photo-chemical catalytic activity and passive silica colloids, light illumination causes diffusiophoretic attractions between the active and passive particles and leads to the formation of dimers. The dimers constitute a symmetry-broken motor, whose dynamics can be fully controlled by the illumination conditions. Computer simulations reproduce the dynamics of the colloids and are in good agreement with experiments. The current work presents a simple route to obtain large numbers of self-propelling chemical motors from a dispersion of spherically symmetric colloids through spontaneous symmetry breaking.

---

Artificial microswimmers show great potential to study fundamental questions in active matter and self-organization, and at the same time promise important applications as autonomous carriers or motors to localize, pick-up and deliver cargo, and as active materials.^1–11 Chemically active colloids have emerged as a model system for self-propulsion.^3,12–14 They operate by converting chemical energy into translational motion via a heterogeneous catalytic reaction that proceeds at the surface of the colloids. A requirement for propulsion is that the colloid shows an anisotropic distribution of the reacting species.^3,6 Almost all examples of self-propelled colloids are therefore Janus particles that show a different reactivity on the respective halves of the particle. In a suitable fuel the resultant asymmetric distribution of chemicals around the colloid drives flows that in turn cause the colloid to swim.^3,15,16 Symmetry breaking is a requirement for propulsion and is generally engineered into the colloids.^3,5,6,15,16 However, many Janus particles, require processing steps that involve deposition onto a substrate, which limits the number of particles that can be obtained and thus also limits the types of chemical motors that can be fabricated.^14,17 It is therefore interesting to explore whether spontaneous symmetry breaking can give rise to self-propelling chemical motors without the need for complex Janus-particle fabrication methods.^18,19

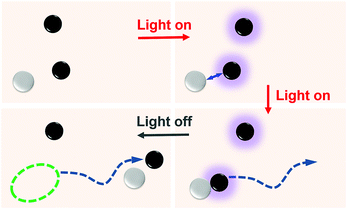
Here, we show that self-assembly can lead to the spontaneous formation of chemical motors. Two species of isotropic colloids that cannot self-propel by themselves interact to form self-assembled Janus-dimers that swim. The chemically active colloids are photocatalytic microspheres that form a uniform chemical gradient when immersed in a chemical fuel and illuminated with UV light. The gradient causes phoretic interactions with a surrounding passive colloid, which form a dimer by diffusiophoresis. The self-assembled dimers consisting of an active and a passive particle are naturally symmetry-broken polar Janus structures that start to swim. The sequence of the self-assembly process is schematically shown in Fig. 1. The propulsion of dimers is known,²⁰ however, the spontaneous formation of active dimers starting from isotropic microspheres is unique to this study. The mechanism is elucidated by particle-based mesoscale computer simulations.

Fig. 1 Schematic view for fabrication of self-propelling motors self-assembled from non-motile colloid particles by light control. The chemically active (black) and passive (white) particles are non-motile without light but they form a self-propelling dimer when the light is on.

We used commercially available isotropic photocatalytic anatase TiO₂ and (passive) SiO₂ microspheres of diameters 1.2 μm and 2 μm, respectively. Scanning electron microscope (SEM) images of the particles are provided in the ESI,† Fig. S1. Photo-active titanium dioxide and passive silica colloids were mixed in the ratio 3 : 1 and dispersed in an aqueous 2.5% hydrogen peroxide and 1 mM tetramethylammonium hydroxide (H₂O₂ and TMAH, pH ≈ 7) solution. The colloids sediment and exhibit Brownian motion near the glass surface. Further details of the experimental setup and the sample preparation protocols can be found in ref. 21. The distribution of colloids in the absence of any UV-light can be seen in Fig. 2(a). When the UV-light (365 nm, 320 mW cm⁻²) is switched on, the TiO₂ colloids become chemically active and cause the photocatalytic decomposition of H₂O₂ at the TiO₂ surface.^21–23 Nevertheless, the chemically-active colloids remain non-motile. However, proximity to a passive silica colloid gives rise to an attractive interaction between the active and the passive colloid, which subsequently join and form dimers. Fig. 2(b) shows such dimers with a pair of active–passive colloids that have formed within a few seconds after the light was turned on. Once the dimers are formed, the symmetry-broken polar particle is clearly seen to self-propel (see Fig. 2(c)). The corresponding experimental video showing the dimer formation and swimming behavior is provided in the ESI† as Movie S1. The average speed of the dimers was measured to be 2.2 μm s⁻¹, which is comparable with the speed of Janus TiO₂–SiO₂ particles.²¹ The speed of the dimers is a function of the light intensity as is seen in Fig. S2 of the ESI.† When the light is switched-off the dimer instantly breaks apart and the individual colloids revert to their Brownian state (see Fig. 2(d)).

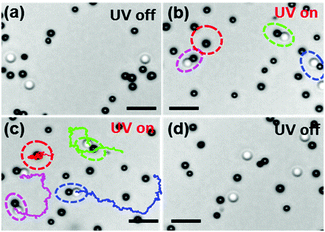Fig. 2 Snapshots from the experiment showing different states of the system when light is on and off (Movie S1, ESI†). (a) Chemically active (black) and passive (white) colloids without light illumination in the presence of fuel (H₂O₂). The particles exhibit Brownian motion. (b) When light is on, the active and passive particles self-assemble to form dimers by diffusiophoresis (highlighted with dotted circles). (c) Self-assembled dimers self-propel exhibiting directional motion (magenta, blue, green). The trajectories are taken for 28 s. For comparison, the movement of a single active colloid (encircled with red dashed lines) was also tracked. The separated active particles show Brownian motion with no propulsion. (d) When light is off, the dimers separate into the respective active and passive, which undergo Brownian motion. The scale bar corresponds to 5 μm.

The dynamics of the colloidal particles and the formation of the dimers may be explained by a diffusiophoretic mechanism.^3,15,16 Thermophoresis and optical effects are ruled out by control experiments in pure water at the same UV light intensities (see Movie S2, ESI†), and experiments with Janus TiO₂–SiO₂ colloids at high salt concentrations (Fig. S4 in ESI†) show that electrophoretic effects are not responsible for the propulsion of the dimers. Based on these observations, we perform mesoscopic simulations with diffusiophoretic mechanisms. A particle-based simulation method combining molecular dynamics (MD) for the particle motion and multiparticle collision dynamics (MPCD) for the interaction with the fluid²⁴ is adopted to describe the motion, the hydrodynamic interactions and to capture the thermal fluctuations. We consider two spheres, a catalytically active sphere (S_a, TiO₂) with a radius R_a and a non-catalytic (passive) sphere (S_p, SiO₂) with radius R_p separated by a distance L. The surrounding fluid is composed of A (e.g. H₂O₂) and B (e.g. H₂, O₂) molecules and they are involved in the reaction A + S_a → B + S_a on the catalytic sphere with an intrinsic rate constant. The system is maintained in a steady state by converting B to A far from the spheres due to the finiteness of the system.

The spheres interact with the fluid particles (chemicals A and B) in MD through repulsive Lennard-Jones (LJ) potentials, U = 4ε[(σ/r)¹² − (σ/r)⁶] + ε for r < 2^1/6σ and U = 0 otherwise. Here, ε and σ are, respectively, the parameters for the interaction energy and the distance. The size of the non-catalytic sphere is taken to be twice that of the catalytic sphere, σ_p = 2σ_a, which is expected to provide a maximum speed of the dimer motor.^20,25 We assume that the spherical colloids are a small distance σ_p away from a wall. Further, the two spherical particles have excluded volume interactions with σ_s = σ_a + σ_p. The radius of the spheres is considered to be R_i = 2^1/6σ_i (i = a, p). By assuming different interaction energies of A and B with the non-catalytic sphere S_p (ε_B < ε_A) and also different interactions with the catalytic sphere (ε^cat_B < ε^cat_A), simulations may explain experimental observations such that non-catalytic particles experience diffusiophoresis and catalytic particles repel each other. The choice of small ε_B indicates that the B chemical species plays the role of a chemoattractant, which implies that the non-catalytic sphere moves towards the catalytic sphere. Results are reported in dimensionless units and further details are given in the ESI.†

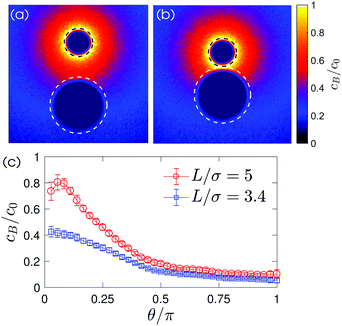
Fig. 3 presents snapshots from the simulation with and without light illumination. When the light is switched on, the catalytic sphere converts chemicals A to B, by which the concentration field is created by the catalytic particle (see Fig. 4). When the nearby non-catalytic particle feels this concentration field, it moves towards the catalytic particle by diffusiophoresis. The spherical catalytic colloid also exhibits a motion towards the non-catalytic particle (Fig. 3(a)) which is attributed to the flow drag generated by the non-catalytic particle.²⁶ The active and the passive particle approach each other and eventually form a dimer (Fig. 3(b)). The dimer is stable and shows directional motion over long times and distances (Fig. 3(c)). When the light is switched off, the concentration gradient disappears and the attractive force between the two particles ceases. The dimer then separates and the two colloids only show Brownian motion (Fig. 3(d), see also Movie S3, ESI†).

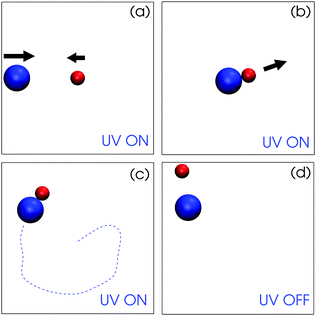Fig. 3 Simulation snapshots showing the dynamics of the spherical active (red, TiO₂) and passive particle (blue, SiO₂) when light is on and off. (a) Two spheres approach and meet by diffusiophoretic mechanisms when light is on. (b) The dimer forms. (c) The dimer self-propels stably and constantly. The dashed line indicates a schematic dimer trajectory for visualization. (d) When the light is off, the dimer is split to two separated particles being in Brownian motion (see Movie S3, ESI†).

Fig. 4 Normalized concentration field c_B/c₀ for (a) the two spheres at a separation distance L/σ = 5 and for (b) the dimer L/σ = 3.4. The black and white dashed lines indicate the radius of the catalytic and non-catalytic spheres, R_a = 2^1/6σ and R_p = 2^1/6(2σ), respectively. (c) Plots of c_B/c₀ along the polar angle θ at the surface of the non-catalytic particle. The polar angle runs from the axisymmetric axis, the line joining the center of two spheres, and the θ = 0 corresponds to the position near the catalytic sphere.

The dynamics can be understood in terms of the chemical gradient. Fig. 4(c) shows the distribution of chemical concentration around the passive particle sitting in the vicinity of the chemically-active particle. This chemical gradient induces a slip flow around the particle. Since there is no external force on the system, the particle propels in an opposite direction of the slip flow to conserve momentum. The motion of the non-catalytic particle alters the flow such that a part of this flow is directed from the catalytic to the non-catalytic particle. Hence, the catalytic particle is dragged to the non-catalytic colloid and the two particles appear to be attracted towards each other. (A more detailed explanation for the particle dynamics can be found in ref. 26.)

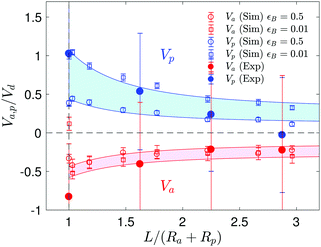
The velocity of the catalytic and the non-catalytic spheres as a function of their separation is plotted in Fig. 5. In simulations, we change the ratio of the interaction potentials of A and B with the non-catalytic sphere from 2 up to 100, i.e. ε_B = 0.01 to 0.5 while ε_A = ε^cat_A = ε^cat_B = 1, to cover a broad range of possible energy differences in experiments. Note that the change of the interaction energy on the catalytic sphere does not significantly influence the particle dynamics since the homogeneous concentration fields in the vicinity of the catalytic sphere are only disturbed when two spheres are very close (see Fig. S7 in ESI†). The experimental results show the same trend as the simulations and are captured by the L⁻² lines, which are theoretical approximations when the two spheres are far apart.²⁶ Once a dimer is formed, it propels with a constant average velocity V_d since the concentration gradients do not change during its motion.^20,25,27

Fig. 5 The velocity of catalytic V_a and non-catalytic sphere V_p as a function of separation distance L before the dimer formation. The open symbols (circles and squares) are simulations and the filled circles are experimental results. The light blue and red regions enclosed by L⁻² lines correspond to that ε_B varies from 0.01 to 0.5 when ε_A = ε^cat_A = ε^cat_B = 1. The opposite signs of the velocity indicate that the catalytic and non-catalytic particles move in an opposite direction.

The degree of dimer formation depends on the strength of the chemical gradient and the average separation of the colloids. The distance dependence of the concentration field (Fig. 4) and the resultant velocity of the particles (Fig. 5) confirm that the formation of dimers will be difficult if the particles are too far apart. The separation between the active and passive particles can be controlled by adjusting the particle density in the system. In our case a favorable particle density was found to be 2%, when dimers formed in a reasonably short time. The interaction between active and passive particles can also lead to the attachment of more than one passive particle to a single active particle, especially at higher densities. This can alter the swimming behavior, as structures other than dimers are formed. The motion can cease when too many passive particles attach to an active colloid. However, this can be avoided when there are more active than passive particles, e.g. a ratio of 3 : 1. In that case, once the dimer is formed, it will be surrounded by more active particles, which show weak repulsive interactions, and thus do not attach to the dimer (see also Movie S4, ESI†). Fig. 6 shows snapshots of a dimer approaching an active particle followed by a turn that avoids their collision. The system is therefore quite robust and we observed that more than 60% of dimers swam for more than 20 s after they formed (see ESI,† Fig. S3).

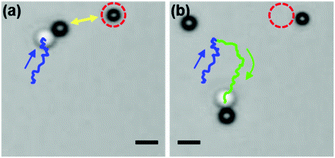Fig. 6 Dimers are repelled from active particles (Movies S4 and S5, ESI†). (a) A dimer head moves towards another active particle (encircled with red dashed lines). (b) An arrangement of two active particles causes a deflection. The trajectory of the dimer before and after interactions with active colloids is presented in blue and green, respectively. The scale bar corresponds to 2 μm.

It is considered that the deflection of the dimer and the repulsion among the catalytic spheres observed in experiments arises from the effects combined by diffusiophoresis on the catalytic spheres and chemical and hydrodynamic interactions occurring in multi-particle systems. By setting energy parameters in simulations by ε^cat_A = 1 > ε^cat_B = 0.01 and ε_A = 1 > ε_B = 0.1, we observe a similar behavior as shown in experiments (see Movie S5, ESI†). Note that for opposite values of the potential energy (ε^cat_A = 0.01 < ε^cat_B = 1), the dimer is also deflected with slightly reduced strength but not deflected by an equal value (ε^cat_A = ε^cat_B). In addition, it is notable that the self-assembling and self-propelling dynamics in a mixture of active and passive particles are not restricted to specific material composition such as SiO₂ and TiO₂ but are valid in general. For example, a mixture of polystyrene (PS) and TiO₂ particles works well with no change of other conditions (see Movie S6, ESI†).

In conclusion, we have presented a simple strategy how self-propelling chemical motors can self-assemble. Whereas up to now most self-propelling structures required the fabrication of Janus particles, which is only possible in relatively small numbers, we show that “Janus-like” dimers can self-assemble spontaneously. This is highly scalable as isotropic spherical colloids can be obtained in large quantities. The chemical field around a chemically-active symmetric colloid causes the binding of an inactive (passive) colloid by diffusiophoretic interactions to form a symmetry-broken dimer that propels. Self-propelling colloids are building blocks for active matter, and are of interest for the efficient and directed delivery of cargo. Now it is possible that such structures form by themselves. Spontaneous symmetry breaking is of fundamental interest in a number of fields as it provides a mechanism of how complexity can arise from simple building blocks. We have shown such a mechanism in active matter.§

T. Yu, D. P. Singh and P. Fischer acknowledge funding from the DFG (Projektnummer 253407113 under the SPP program 1726) and the Max Planck Society. S. Y. Reigh greatly thanks S. Dietrich and the Max-Planck-Institute for Intelligent Systems for support. S. Thakur acknowledges funding from the SERB, India. The computational work was carried out at the HPC facility in IISER Bhopal, India. The authors are grateful to R. Kapral for helpful discussions. Open Access funding provided by the Max Planck Society.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. J. Wang, Nanomachines: Fundamentals and Applications, Wiley-VCH, Weinheim, Germany, 2013.
2. W. Wang, W. Duan, S. Ahmed, T. E. Mallouk and A. Sen, Nano Today, 2013, 8, 531–554.
3. P. H. Colberg, S. Y. Reigh, B. Robertson and R. Kapral, Acc. Chem. Res., 2014, 47, 3504.
4. J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601.
5. C. Bechinger, R. D. Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006.
6. A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001.
7. D. A. Wilson, R. J. M. Nolte and J. C. M. van Hest, Nat. Chem., 2012, 4, 268.
8. S. Palagi, A. G. Mark, S. Y. Reigh, K. Melde, T. Qiu, H. Zeng, C. Parmeggiani, D. Martella, A. Sanchez-Castillo, N. Kapernaum, F. Giesselmann, D. S. Wiersma, E. Lauga and P. Fischer, Nat. Mater., 2016, 15, 647.
9. J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936.
10. D. P. Singh, W. E. Uspal, M. N. Popescu, L. G. Wilson and P. Fischer, Adv. Funct. Mater., 2018, 28, 1706660.
11. A. C. Hortelão, T. Patiño, A. Perez-Jiménez, À. Blanco and S. Sánchez, Adv. Funct. Mater., 2017, 28, 1705086.
12. W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. S. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424.
13. J. Vicario, R. Eelkema, W. R. Browne, A. Meetsma, R. M. L. Croisa and B. L. Feringa, Chem. Commun., 2005, 3936.
14. S. Sánchez, L. Soler and J. Katuri, Angew. Chem., Int. Ed., 2015, 54, 1414–1444.
15. B. V. Derjaguin and G. P. Sidorenkov, Kolloidn. Zh., 1947, 9, 335–347.
16. J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99.
17. H. Wang and M. Pumera, Chem. Rev., 2015, 115, 8704–8735.
18. B. Jurado-Sánchez, M. Pacheco, J. Rojo and A. Escarpa, Angew. Chem., Int. Ed., 2017, 56, 6957.
19. M. Pacheco, B. Jurado-Sánchez and A. Escarpa, Anal. Chem., 2018, 90, 2912.
20. L. F. Valadares, Y.-G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Small, 2010, 6, 565.
21. D. P. Singh, U. Choudhury, P. Fischer and A. G. Mark, Adv. Mater., 2017, 29, 1701328.
22. F. Mou, L. Kong, C. Chen, Z. Chen, L. Xua and J. Guan, Small, 2016, 8, 4976–4983.
23. R. Dong, Q. Zhang, W. Gao, A. Pei and B. Ren, ACS Nano, 2016, 10, 839–844.
24. A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613.
25. S. Y. Reigh and R. Kapral, Soft Matter, 2015, 11, 3149–3158.
26. S. Y. Reigh, P. Chuphal, S. Thakur and R. Kapral, Soft Matter, 2018, 14, 6043.
27. M. N. Popescu, M. Tasinkevych and S. Dietrich, Europhys. Lett., 2011, 95, 28004.
28. F. Schmidt, B. Liebchen, H. Löwen and G. Volpe, 2018, arXiv:1801.06868v1.

---

Footnotes

† Electronic supplementary information (ESI) available: Movies from experiments (Movies S1, S2, S4 and S6) and simulations (Movies S3 and S5). See DOI: 10.1039/c8cc06467a

‡ These authors contributed equally to this work.

§ The authors have recently become aware of a publication on arxiv that also discusses cluster formation, albeit in more complex and non-chemical colloidal systems.²⁸

---