Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The growth and fluorescence of phthalocyanine monolayers, thin films and multilayers on hexagonal boron nitride†
Manal
Alkhamisi
a,
Vladimir V.
Korolkov
a,
Anton S.
Nizovtsev
bc,
James
Kerfoot
a,
Takashi
Taniguchi
d,
Kenji
Watanabe
 d,
Nicholas A.
Besley
b,
Elena
Besley
d,
Nicholas A.
Besley
b,
Elena
Besley
 b and
Peter H.
Beton
b and
Peter H.
Beton
 *a
*a
aSchool of Physics & Astronomy, University of Nottingham, Nottingham NG7 2RD, UK. E-mail: peter.beton@nottingham.ac.uk
bSchool of Chemistry, University of Nottingham, Nottingham NG7 2RD, UK
cNikolaev Institute of Inorganic Chemistry, Siberian Branch of the Russian Academy of Sciences, Academician Lavrentiev Avenue 3, 630090, Novosibirsk, Russian Federation
dNational Institute for Materials Science, 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan
First published on 9th October 2018
Abstract
Free-base phthalocyanine forms distinct interfacial phases and thin films on hexagonal boron nitride including a monolayer arrangement as determined using high resolution atomic force microscopy. The phases reveal significant differences in photoluminescence with an intense peak for monolayer coverages of flat-lying molecules which is red-shifted in agreement with theoretical models.
The organisation of organic materials on a surface is important in realising their potential as electronic and optoelectronic devices, and is a major focus of supramolecular chemistry and materials science.1,2 In this study we investigate the influence of surface organisation on the fluorescence of free-base phthalocyanine (H2Pc; see inset in Fig. 1(b)). Phthalocyanines, both the free-base and metallated variants, have been widely exploited in organic electronics and gas-sensing, and also provide a prototypical example of an organic semiconductor on which many fundamental studies have been undertaken.3–12 Specifically we have investigated the adsorption of H2Pc on hexagonal boron nitride (hBN) and find that well-ordered monolayers can be formed in which the molecules lie flat with lattice vectors which are aligned with a high symmetry axis of the substrate, but additional layers grow in a three-dimensional morphology which is much less ordered. While the monolayer H2Pc gives rise to a narrow intense fluorescence peak the emission from the multilayers is much broader and significantly red-shifted.
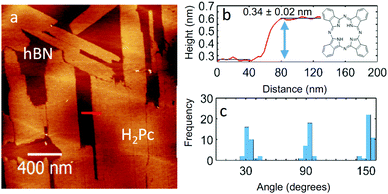 | ||
| Fig. 1 (a) AC mode AFM image of 0.7 ML of H2Pc on hBN, (b) the height profile of an island along the red line marked in panel (a). (c) Histogram of island orientations. | ||
H2Pc powder was purchased from Sigma-Aldrich and sublimed, under vacuum (base pressure ∼ 10−7 mbar), onto hBN flakes which had been exfoliated, transferred to a supporting Si/SiO2 substrate and cleaned following the procedures summarised in ESI† and our recent work.13 The deposition rate was ∼0.5 monolayers per min. hBN is chosen as a substrate since it is compatible with the formation of 2D supramolecular layers, and the acquisition of images with molecular resolution using atomic force microscopy (AFM) under ambient conditions. Since hBN is an insulator the fluorescence of the adsorbed molecular layers may also be measured, facilitating investigations of the correlation between morphology and optical properties.14,15
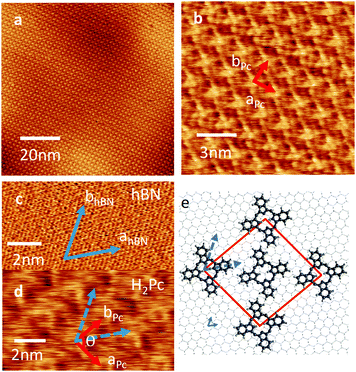
Fig. 1(a) shows the surface after 0.7 monolayer (ML) of H2Pc was deposited on hBN while the substrate was held at room temperature. Rectangular islands are observed with typical lengths ranging from 0.3 to 2 μm, and widths from 0.2 to 0.4 μm. The profile in Fig. 1(b) shows that the height of the islands is 0.34 ± 0.02 nm, consistent with the formation of a monolayer of H2Pc with the molecular plane lying parallel to the surface. The elongated island facets are oriented along specific directions – see histogram in Fig. 1(c) which has three peaks separated by 60°. This suggests that the major axes of the islands are aligned with a high symmetry axis of hBN.
If the substrate temperature is increased to 100 °C, or higher, the growth self-terminates after the formation of a monolayer. The resulting islands are large (micron scale) and it is possible to acquire images with molecular scale resolution – see Fig. 2(a, b and d). The lattice vectors are marked in Fig. 2(b); we find that aPc = bPc = 2.18 ± 0.05 nm and the angle θ = 86°. The H2Pc molecules appear as topographically bright features with a ‘cross-like’ shape similar to the molecular structure (Fig. 1(b) inset). The orientation of the lattice vectors (red arrows) of the H2Pc monolayer and the hBN (blue arrows) can be determined by comparing AFM images of the H2Pc and the hBN lattice (see Fig. 2(c and d)). The lattice vectors of hBN may be resolved in Fig. 2(c) (parallel to the blue arrows) and are overlaid on the H2Pc molecules in Fig. 2(d). From these images we determine that the lattice vector bPc is aligned at angle of 30° to both hBN lattice vectors, one of the high symmetry directions of the hBN substrate, consistent with the histogram in Fig. 1(c). The axis of the H2Pc molecules (parallel to the C–H bonds within the central ring of the macrocycle) is misaligned from the hBN lattice vector by 4 ± 2°.
A schematic of the H2Pc layer overlaid on hBN is shown Fig. 2(e). The molecules appear alternately bright (at the corners of the unit cell in Fig. 2(b and e)) and dark (at the centre of the unit cell). We suggest the reason for the differing AFM contrast of molecules is due to a variation in adsorption site; in our previous studies of molecular overlayers on hBN we have reported the appearance of moiré patterns13 in AFM images arising from a mismatch in lattice constants, and thus variations of local adsorption site. The H2Pc unit cell is similar to that previously reported on other substrates.16–19
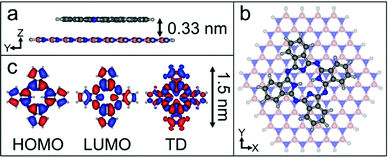
We have calculated the adsorption energy and geometry of H2Pc using density functional theory (DFT). The structure of H2Pc on hBN is optimised using the range-separated hybrid ωB97X-D functional,20 which includes an empirical dispersion correction, in combination with the correlation-consistent cc-pVDZ basis set.21 The atomic positions of a model hBN monolayer flake consisting of 65 boron atoms and 65 nitrogen atoms were initially optimized and frozen in subsequent calculations. The optimized structure for a single H2Pc molecule on hBN is shown in Fig. 3 and confirms a planar adsorption geometry with a molecule-surface separation, d = 0.33 nm and adsorption energy, EA = 3.35 eV. In common with our images the calculations show the molecular axis misaligned with the hBN lattice vector, but by a larger angle, 13°. We attribute this difference to a combination of a low barrier for rotation and the role of intermolecular interactions. Full details of the calculations, which are performed within the QCHEM package,22 are included in ESI.†
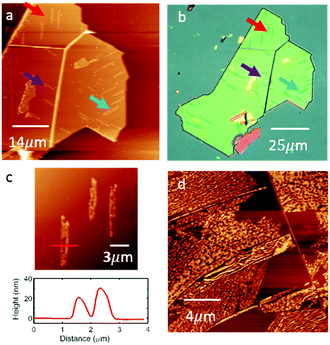
As the H2Pc coverage is increased we observe the formation of clusters of large needle-like crystallites with a rather disordered morphology. Fig. 4(a) shows a large area AFM image of an hBN flake in which several large islands (identified by arrows) are formed following the deposition of H2Pc (thickness 1 nm; 1 ML is approximately equivalent to 0.33 nm). These islands have a height of 20–30 nm (see Fig. 4(c)) and typical length of 10–20 μm, and can be resolved using optical microscopy; Fig. 4(b) shows the same hBN flake. Interestingly the islands have a direction which is locally correlated and oriented in one of three directions subtended by 60°. Following the deposition of thicker layers (Fig. 4(d)) the needle-like islands merge to cover a greater proportion of the surface, but are highly disordered. We are not able to obtain images with molecular-scale resolution in these regions. Overall our results show an abrupt transition to the growth of three-dimensional crystallites following the completion of a highly ordered monolayer. A likely explanation for this is that molecules switch from the flat-lying adsorbed state in the monolayer to a geometry in which the molecular plane is at an angle to the hBN substrate in higher layers, thus forming one-dimensional crystallites in which molecules are co-planar, maximising π–π interactions. Such a switch from a flat-lying to upright morphology has been observed previously in studies of adsorbed H2Pc.4
To measure the optical properties of a H2Pc thin film, a Horiba LabRAM system was used in conjunction with a 660 nm laser (photon energy 1.88 eV) with a spot size ∼ 1 μm2 as an excitation source (see ESI† for further details). In Fig. 5 the photoluminescence spectra of H2Pc films with varying thickness are shown. For a thickness of 0.7 ML, in which all molecules adsorb in a flat-lying configuration, we observe a narrow intense peak centred at 1.75 eV, which we attribute to the zero phonon (0–0) peak, together with broader, less intense vibronic peaks at 1.67 and 1.58 eV. These peaks are also present for a sample with H2Pc thickness of 1 nm (as in Fig. 2), but undergo a small shift; the 0–0 peak is centred on 1.76 eV. There are small differences between the spectra acquired when the laser spot is incident either on or off a multilayer H2Pc island. In particular, an additional peak centred at 1.38 eV is slightly more intense on these islands. This peak is much more intense for a thicker sample (32 nm), for which the peaks associated with the flat-lying monolayer may no longer be clearly resolved. We have also measured the spectrum of H2Pc powder on a glass slide which showed a broad peak at 1.42 eV (light blue line in Fig. 5) and we attribute the peak observed at 1.38 eV for the 32 nm thick H2Pc layer to the existence of a bulk-like H2Pc phase on the surface.
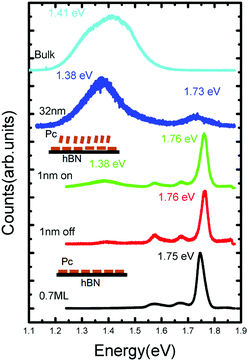 | ||
| Fig. 5 The photoluminescence spectra of free-base phthalocyanine films with different thickness on and off the islands. | ||
The 0–0 peak for H2Pc is red-shifted by ΔE = 0.13 eV as compared with a molecule in the gas phase23 (0–0 peak at 1.876 eV). As we,14,15 and others,24–26 have recently discussed this red-shift can be understood from a combination of effects arising from interactions with the substrate and with nearest neighbours. A non-resonant contribution to the shift due to the substrate can be calculated using time-dependent density functional theory (TD-DFT). The molecule is optimized in the excited (S1) state both on (adsorbed) and off (gas phase) the hBN surface and the transition to the ground state (S0) is calculated in each case (see ESI† for more details). The calculated transition energies for a molecule on the hBN surface, and in the gas phase are, respectively, 1.76 eV and 1.87 eV. These values are close to the measured peaks in fluorescence and their difference implies a non-resonant red-shift ΔEnr = 0.11 eV due to adsorption on hBN.
There are also contributions to the red-shift from resonant interactions with the substrate and neighbouring molecules. We have recently argued15 that these effects depend on the refractive index, n, of the substrate and include a ‘gas-surface’ red-shift given by ΔEsubs = f(d)(n2 − 1)μ2/4πε0(n2 + 1)d3, where μ is the transition dipole moment and d is the molecule–substrate separation, which from our DFT calculations (see ESI†) are, respectively, 8.0 Debye and 0.33 nm (for the anisotropic hBN substrate we use a geometric average15n = 1.87; the reduction factor f(d) is related to the molecular geometry as discussed below). This shift arises from a coupling of the transition dipole moment of the adsorbed molecule with the dielectric hBN substrate and may be described semi-classically as an interaction with an image dipole (see Kerfoot et al.15).
In the point dipole approximation f(d) = 1; this is satisfied if d is much greater than the molecular dimensions. However, this condition is violated for H2Pc (see dimensions in Fig. 3); instead we treat the dipole moment as arising from an oscillating charge density,27 the transition density, T(r), equal to the product of the wave functions of the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO). Previously15 we have used the extended dipole model to determine an approximate expression for f(d), however this is expected to be valid only for linear molecules. For the cross-shaped H2Pc molecule we instead calculate the reduction factor due to the interaction of the charge density described by T(r) with its image, T′(r′), given by 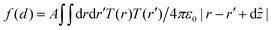 , where the constant A = μ2/4πε0d3 and T′(x′, y′, z′) = T(x′, y′, −z′). The isosurfaces of the HOMO, LUMO and the transition density are shown in Fig. 3. Evaluating numerically this double integral using the transition density calculated using DFT gives, for d = 0.33 nm, f(d) = 0.106 and ΔEsubs = 0.03 eV.
, where the constant A = μ2/4πε0d3 and T′(x′, y′, z′) = T(x′, y′, −z′). The isosurfaces of the HOMO, LUMO and the transition density are shown in Fig. 3. Evaluating numerically this double integral using the transition density calculated using DFT gives, for d = 0.33 nm, f(d) = 0.106 and ΔEsubs = 0.03 eV.
We might also expect a red-shift due to a screened resonant interaction with neigbouring molecules;24 the characteristic energy for a pairwise interaction is ΔEnn = μ2/2(n2 + 1)πε0rnn3, where rnn = 1.5 nm, the nearest neighbour separation. We find ΔEnn = 5 meV; this red-shift is expected for molecules which have aligned transition dipole moments. From our DFT calculations we find that the transition dipole moment for H2Pc is oriented close to perpendicular to the C–H bonds within the central ring of the macrocycle. From our images we are unable to determine whether the molecules are aligned (i.e. whether the C–H bonds within all molecules have a common alignment). However, the contrast of the islands, which may be resolved in optical microscopy, shows no dependence on polarisation indicating that the transition dipole moments are not ordered. Assuming a random alignment, the total red-shift due to N nearest neighbours is ∼χ2NΔEnn/2 where χ2 is the Franck Condon factor.24 Since χ2 ≤ 1 we estimate that this contribution to the gas-surface red-shift is ∼10 meV. Combining the various calculated contributions to the red-shift gives ΔEtot = ΔEnr + ΔEsubs + ΔEnn in the range 0.14–0.15 eV in excellent agreement with the experimental value, 0.13 eV.
Overall our results demonstrate that the optoelectronic properties of molecules on surfaces depends strongly on their adsorption geometry and environment as determined, with molecular resolution, using atomic force microscopy. The absorption of H2Pc in a flat lying geometry results in a narrow intense emission peak, but evolves to a broad emission feature for multilayer samples.
This work was supported by the Engineering and Physical Sciences Research Council [grant number EP/N033906/1]; the Leverhulme Trust [grant number RPG-2016-104]. Nottingham Nanoscale and Microscale Research Centre enabled access to the Horiba LABRAM instrument. K. W. and T. T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and the CREST (JPMJCR15F3), JST. EB acknowledges the financial support of an ERC Consolidator grant. The University of Nottingham and the HPC Midlands Plus Centre are gratefully acknowledged for providing computational resources.
Conflicts of interest
There are no conflicts of interest to declare.References
- D. P. Goronzy, M. Ebrahimi, F. Rosei, Arramel, Y. Fang, S. De Feyter, S. L. Tait, C. Wang, P. H. Beton, A. T. S. Wee, P. S. Weiss and D. F. Perepichka, ACS Nano, 2018 DOI:10.1021/acsnano.8b03513.
- K. S. Mali, N. Pearce, S. De Feyter and N. R. Champness, Chem. Soc. Rev., 2017, 46, 2520–2542 RSC.
- C. W. Tang, Appl. Phys. Lett., 1986, 48, 183–185 CrossRef CAS.
- Z. Bao, A. Lovinger and A. Dodabalapur, Appl. Phys. Lett., 1996, 69, 3066–3068 CrossRef CAS.
- J. Puigdollers, C. Voz, M. Fonrodona, S. Cheylan, M. Stella, J. Andreu, M. Vetter and R. Alcubilla, J. Non-Cryst. Solids, 2006, 352, 1778–1782 CrossRef CAS.
- J. Nelson, The physics of solar cells, World Scientific Publishing Co. Inc., 2003 Search PubMed.
- A. Fujii, Y. Ohmori and K. Yoshino, IEEE Trans. Electron Devices, 1997, 44, 1204–1207 CrossRef CAS.
- A. Wilson and J. D. Wright, Mol. Cryst. Liq. Cryst., 1992, 211, 321–326 CrossRef CAS.
- G. de la Torre, C. G. Claessens and T. Torres, Chem. Commun., 2007, 2000–2015 RSC.
- B. Doppagne, M. C. Chong, H. Bulou, A. Boeglin, F. Scheurer and G. Schull, Science, 2018, 361, 251–255 CrossRef CAS PubMed.
- H. Imada, K. Miwa, M. Imai-Imada, S. Kawahara, K. Kimura and Y. Kim, Nature, 2016, 538, 364–367 CrossRef CAS PubMed.
- Y. Zhang, Y. Luo, Y. Zhang, Y.-J. Yu, Y.-M. Kuang, L. Zhang, Q.-S. Meng, Y. Luo, J.-L. Yang, Z.-C. Dong and J. G. Hou, Nature, 2016, 531, 623–627 CrossRef CAS PubMed.
- V. V. Korolkov, M. Baldoni, K. Watanabe, T. Taniguchi, E. Besley and P. H. Beton, Nat. Chem., 2017, 9, 1191–1197 CrossRef CAS PubMed.
- V. V. Korolkov, S. A. Svatek, A. Summerfield, J. Kerfoot, L. Yang, T. Taniguchi, K. Watanabe, N. R. Champness, N. A. Besley and P. H. Beton, ACS Nano, 2015, 9, 10347–10355 CrossRef CAS PubMed.
- J. Kerfoot, V. V. Korolkov, A. S. Nizovtsev, R. Jones, T. Taniguchi, K. Watanabe, I. Lesanovsky, B. Olmos, N. A. Besley, E. Besley and P. H. Beton, J. Chem. Phys., 2018, 149, 054701 CrossRef PubMed.
- H. Yanagi, T. Kouzeki, M. Ashida, T. Noguchi, A. Manivannan, K. Hashimoto and A. Fujishima, J. Appl. Phys., 1992, 71, 5146–5153 CrossRef CAS.
- X. Lu, K. W. Hipps, X. D. Wang and U. Mazur, J. Am. Chem. Soc., 1996, 118, 7197–7202 CrossRef CAS.
- M. D. Upward, P. H. Beton and P. Moriarty, Surf. Sci., 1999, 441, 21–25 CrossRef CAS.
- S. K. Hämäläinen, M. Stepanova, R. Drost, P. Liljeroth, J. Lahtinen and J. Sainio, J. Phys. Chem. C, 2012, 116, 20433–20437 CrossRef.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kus, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C. M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. Distasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T. C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S. P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. Oneill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y. C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z. Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J. Da Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C. P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- C. Murray, N. Dozova, J. G. McCaffrey, N. Shafizadeh, W. Chin, M. Broquier and C. Crépin, Phys. Chem. Chem. Phys., 2011, 13, 17543 RSC.
- M. Müller, A. Paulheim, A. Eisfeld and M. Sokolowski, J. Chem. Phys., 2013, 139, 044302 CrossRef PubMed.
- A. Eisfeld, C. Marquardt, A. Paulheim and M. Sokolowski, Phys. Rev. Lett., 2017, 119, 097402 CrossRef PubMed.
- R. Forker, T. Dienel, A. Krause, M. Gruenewald, M. Meissner, T. Kirchhuebel, O. Gröning and T. Fritz, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 165426 CrossRef.
- B. P. Krueger, G. D. Scholes and G. R. Fleming, J. Phys. Chem. B, 1998, 102, 5378–5386 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of sample preparation; details of experimental techniques; details of calculations; additional images. See DOI: 10.1039/c8cc06304d |
| This journal is © The Royal Society of Chemistry 2018 |