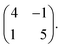Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Periodic and nonperiodic chiral self-assembled networks from 1,3,5-benzenetricarboxylic acid on Ag(111)†
Joshua
Lipton-Duffin
 *ab,
Maryam
Abyazisani
*ab,
Maryam
Abyazisani
 a and
Jennifer
MacLeod
a and
Jennifer
MacLeod
 *ab
*ab
aSchool of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology (QUT), Brisbane, 4001 QLD, Australia. E-mail: josh.liptonduffin@qut.edu.au; jennifer.macleod@qut.edu.au
bInstitute for Future Environments, Queensland University of Technology (QUT), Brisbane, 4001 QLD, Australia
First published on 25th June 2018
Abstract
Surface-catalyzed reactions provide a versatile route to synthesizing new 2D materials. Here, we show that the statistical nature of an activated reaction can lead to a diversity of intermolecular bonding motifs through partially-reacted molecules. With increasing annealing, we observe different periodic, well-defined phases of 1,3,5-benzenetricarboxylic acid on Ag(111), where the surface structure in each case is defined by the degree of deprotonation of the carboxylic groups. Over a wide range of deprotonation levels (∼50% to near 100%), we observe a granular alloy comprising two distinct phases in a continuous network. This ordered phase lacks well-defined translational symmetry, is stabilized through both intermolecular interactions and epitaxy, and demonstrates a design approach to creating non-crystalline phases by capitalizing on the chemical diversity of partially reacted molecules on a surface.
Molecular self-assembly at surfaces provides a rapid, scalable route to 2D films with tailored chemical, electronic and topological characteristics.1,2 This level of nanoscale control is a key enabling capability for next-generation applications in sensing, electronics and energy conversion and storage,3,4 and direct observation of these molecular systems through scanning tunnelling microscopy (STM) has provided a depth of fundamental understanding of the factors that drive molecular self-assembly at surfaces.5,6 A core approach to generating this understanding has been a focus on model molecular systems, such as 1,3,5-benzenetricarboxylic acid (trimesic acid, TMA). TMA is a C3-symmetric hydrogen bonding unit that tends to form strong R22(8) cyclic dimers or somewhat weaker R33(12) trimeric associations in 2D assemblies.7 On unreactive surfaces, such as graphite, graphene, or Au(111), these bonding motifs define the long-range molecular arrangements.8–12 On more reactive surfaces, such as copper, the –COOH groups can catalytically deprotonate to –COO−, creating the possibility for ionic hydrogen bonding and metal-coordinated bonding.13–17 Similarly, partial deprotonation occurs when TMA is solution-deposited onto Cu- or Ag-modified Au(111).18,19 At room temperature on Ag(111), TMA self-assembles through hydrogen bonding, and annealing to 420 K produces a partially-deprotonated TMA phase comprising dense planar dimers stabilized by ionic hydrogen bonds;20–22 a theoretical model for this system suggests that the molecules are one-third deprotonated.20
Annealing TMA/Ag(111) to higher temperatures produces a range of phases with different appearances,23 but a detailed exploration of the structure and chemistry of these phases has not yet been made. Here, we use a combination of STM and X-ray photoelectron spectroscopy (XPS) to show that annealing to temperatures between 460 K and 490 K produces a nonperiodic phase that can accommodate a range of deprotonation states of TMA. In recent years, disordered and quasicrystalline 2D self-assembled phases have gained attention, largely for their fundamental interest.24,25 In these investigations, disorder has been, e.g., structural, arising from multiple available bonding geometries26 or compositional, arising from bicomponent mixing.27 Recent work also showed that the presence of multiple vertex geometries in a metal–organic network can stabilize quasicrystallinity.28 In the present case, we find that after annealing TMA on Ag(111), a locally-crystalline phase without long-range order forms due to the range of chemical states of the TMA precursor, which is accommodated by the seamless integration of two distinct epitaxially-constrained assembly motifs. We hypothesize that the structure incorporates both metal-coordination and hydrogen bonding. This phase elucidates the potential for chemical and topological complexity in a molecular assembly formed from a single, simple precursor molecule.
All experiments were performed in an ultrahigh vacuum system (ScientaOmicron GmbH) incorporating both a twin-anode X-ray source (DAR 400) and analyser (iSphera) and a variable-temperature scanning tunnelling microscope (VT-AFM/XA). A (111)-oriented single-crystal Ag substrate (Mateck, GmbH) was cleaned with repeated Ar+ sputter/anneal cycles, and sample cleanliness was verified with XPS. TMA (Tokyo Chemical Industry) was evaporated from an organic effusion cell (MBE Components OME40) held at 425 K. Samples were annealed at the specified temperatures for five minutes. STM images were processed with the WSxM software.29
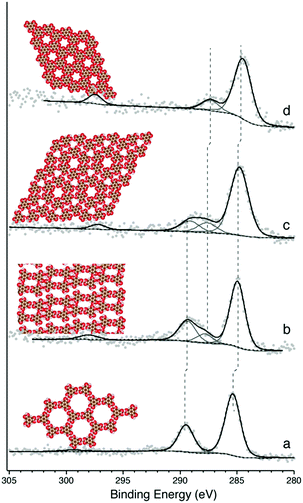
Following the deposition of ∼1 monolayer (ML) of TMA onto a room-temperature (RT) Ag(111) substrate, phases typical of hydrogen bonded self-assembly were observed (see ESI† for STM).20,21 XPS confirmed that the TMA molecule was intact (Fig. 1a). This is evident in the C1s core level, which contains a primary spectral contribution associated with the benzene ring at ∼284.8 eV, and a smaller component associated with the carboxylic groups at ∼288.9 eV, in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity ratio.20 The 4.1 eV spacing between these two peaks is expected for intact TMA,20 and is corroborated by the O1s region, which shows near-identical intensities for the –OH and
1 intensity ratio.20 The 4.1 eV spacing between these two peaks is expected for intact TMA,20 and is corroborated by the O1s region, which shows near-identical intensities for the –OH and ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O contributions (see ESI†). Annealing the sample to 430 K produced a dimer phase, similar to one identified in previous studies as an ionic hydrogen-bonded assembly (see ESI† for STM).20,21 XPS revealed that this phase corresponds to a partial deprotonation of the carboxylic acid groups, evidenced by the appearance of a spectral contribution at ∼288 eV (Fig. 1b), which is consistent with –COO−;17,20 again, this observation is corroborated by the O1s region (see ESI†). The spectral intensity observed in C1s suggests ∼25% deprotonation, which is close to the 33% deprotonation level of the proposed model for this system.20
O contributions (see ESI†). Annealing the sample to 430 K produced a dimer phase, similar to one identified in previous studies as an ionic hydrogen-bonded assembly (see ESI† for STM).20,21 XPS revealed that this phase corresponds to a partial deprotonation of the carboxylic acid groups, evidenced by the appearance of a spectral contribution at ∼288 eV (Fig. 1b), which is consistent with –COO−;17,20 again, this observation is corroborated by the O1s region (see ESI†). The spectral intensity observed in C1s suggests ∼25% deprotonation, which is close to the 33% deprotonation level of the proposed model for this system.20
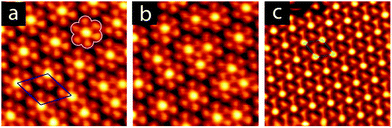
Annealing to higher temperature increases the average deprotonation of the TMA. Fig. 1c shows the C1s region after annealing to 475 K: at this point, the TMA is 50% deprotonated, and STM reveals the presence of a new phase on the surface (shown schematically in Fig. 1c, with a typical STM image in Fig. 2a). We refer to the dominant bonding motif in this phase as “discrete pinwheel”. The basic building block is a hexamer of TMA arranged around a bright central protrusion, outlined in white in Fig. 2a. The hexamer possesses an intrinsic chirality associated with a slight rotation (∼20°) of each TMA molecule with respect to the high symmetry directions of the hexagonal unit cell of the pinwheel structures. We interpret the hexamers as arising from the coordination of six –COO− groups around one or more silver adatoms, with the remaining twelve carboxylic groups around the outside of the pinwheel intact. This geometry provides a plausible hydrogen-bonding interaction between the intact –COOH groups at the perimeter of the pinwheel. Gas-phase DFT calculations at the B3LYP/6-31G(d,p) level (see ESI†) suggest that a stabilization energy of −2.2 kcal mol−1, which is substantially weaker (by a factor of 20) than per-molecule tabulated values for TMA in R22(8) dimeric associations,30 but is nevertheless bound even in the gas phase. This hydrogen bonding interaction appears to propagate chirality, resulting in enantiomerically pure domains. The metal coordination at the centre of the pore is beyond the scope of our gas-phase DFT. However, the presence of one or more adatoms is implied through the brightness of the central protrusion across all bias voltages in STM imaging, and is consistent with the behaviour of deprotonated TMA in other surface-confined systems, where the formation of metal–organic phases is frequently observed.13,14,17 Furthermore, the O1s core level energetics suggest metal coordination, which has previously been shown to modify the observed binding energy of the carboxylate component (see ESI†).31
In theory, the discrete pinwheel phase should correspond to a TMA deprotonation level of 33% (one –COO− per molecule). However, our XPS indicates a higher deprotonation level. This is consistent with the fact that, in several repeated experiments, we never observed pure-phase domains of discrete pinwheel. In all cases, the discrete pinwheel domains contained some molecules in a more advanced state of deprotonation (see below). This could be due to poor preparation parameters (consistently overshooting the desired phase), or to an intrinsic kinetic barrier to formation of the discrete pinwheel phase as a pure phase, e.g., if the nucleation of the domain requires the presence of some further-deprotonated structures.
Annealing to 495 K results in complete deprotonation of the molecule, as shown in Fig. 1d, where all spectral weight associated with –COOH has been lost, and the ratio of benzene carbon to –COO− falls slightly below 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (see ESI†). This chemical state of the molecule corresponds to a change in the observed structure, shown schematically in Fig. 1d and in the STM image in Fig. 2c. This phase is structurally similar to the discrete pinwheel phase, but comprises an increased density of bright metal-atom centres, consistent with complete deprotonation of the TMA and the replacement of all hydrogen bonds with the metal-coordination geometry at the centre of the discrete pinwheel phase. We therefore refer to this phase as “knitted pinwheel”. Like its companion phase, it possesses an intrinsic chirality related to a rotation of the individual TMA molecules with respect to the high-symmetry direction of the knitted pinwheel unit cell (shown in green in Fig. 2c. See ESI† for additional images demonstrating chirality).
1 (see ESI†). This chemical state of the molecule corresponds to a change in the observed structure, shown schematically in Fig. 1d and in the STM image in Fig. 2c. This phase is structurally similar to the discrete pinwheel phase, but comprises an increased density of bright metal-atom centres, consistent with complete deprotonation of the TMA and the replacement of all hydrogen bonds with the metal-coordination geometry at the centre of the discrete pinwheel phase. We therefore refer to this phase as “knitted pinwheel”. Like its companion phase, it possesses an intrinsic chirality related to a rotation of the individual TMA molecules with respect to the high-symmetry direction of the knitted pinwheel unit cell (shown in green in Fig. 2c. See ESI† for additional images demonstrating chirality).
Knitted pinwheels are present as a minority structure in all observed domains of the discrete pinwheel. At deprotonation levels near 50%, the discrete pinwheel structure dominates. However, at deprotonation levels increasing from 50% towards 100% we find a continuum of hybrid domain structures where the discrete pinwheel phase coexists with an increasing concentration of knitted pinwheels. A typical STM image is included as Fig. 2b. The knitted pinwheel sub-domains vary in size, and lack long-range ordering. We therefore refer to this phase as a nonperiodic granular alloy. Like both the discrete and knitted pinwheel phases, this phase is chiral.
The seamless transition from discrete to knitted pinwheels suggests that the two phases have an intrinsic commensurability. Based on STM images where we could visualize the knitted pinwheel structure and the underlying Ag(111) lattice in the same frame, we can use image autocorrelation (see ESI†) to assign the following epitaxy matrix:
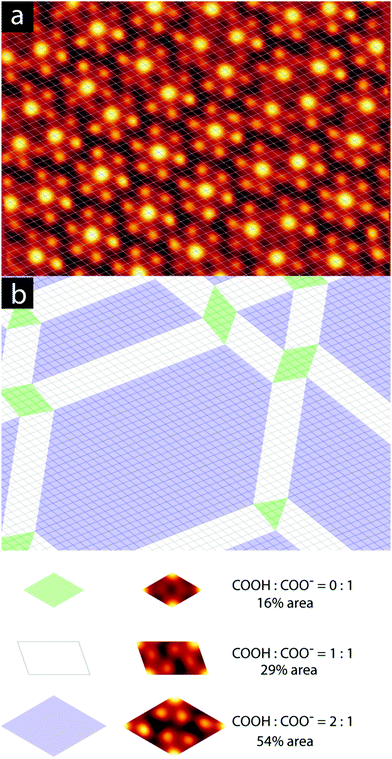
We have observed extended domains of this granular alloy phase. The image in Fig. 4 shows a 60 × 60 nm2 image that showcases the seamless integration of the two sub-phases. The assigned epitaxy matrices indicate that there is a slight rotation between the packed and knitted pinwheel phases, and this is captured in the inset 2D-FFT, which shows that the three primary periodicities, associated with the discrete and knitted pinwheels and the individual molecules, are all rotated with respect to one another. This creates a chiral signature in the FFT.
This work demonstrates that a simple molecule can form the basis for complex, multi-interaction structures in a 2D self-assembled system. The nonperiodic phase defined by partially deprotonated TMA on Ag(111) demonstrates a number of interesting characteristics, including chirality and tolerance for a continuum of chemical states. The formation of this granular alloy phase is dependent on the geometrical compatibility of the epitaxial basis for the two phases, which emphasizes the important role of the substrate in this system. In future work we hope to elucidate more details of the metal-coordinated stabilization of the pinwheel phases, and to explore whether similar phases exist on other metal substrates or with other metals acting as the coordination centre.
Some of the data reported in this paper were obtained at the Central Analytical Research Facility (CARF) operated by the IFE at QUT. Computing resources and support were made available through QUT's High Performance Computing (HPC) centre. The authors acknowledge funding from the Australian Research Council through DE170101170 (JMM) and DP160103116 (JLD).
Conflicts of interest
There are no conflicts of interest to declare.Notes and references
- K. S. Mali, N. Pearce, S. De Feyter and N. R. Champness, Chem. Soc. Rev., 2017, 46, 2520–2542 RSC.
- J. MacLeod and F. Rosei, Small, 2014, 10, 1038–1049 CrossRef PubMed.
- M. Gobbi, S. Bonacchi, J. X. Lian, Y. Liu, X.-Y. Wang, M.-A. Stoeckel, M. A. Squillaci, G. D’Avino, A. Narita and K. Müllen, Nat. Commun., 2017, 8, 14767 CrossRef PubMed.
- L. Sosa-Vargas, E. Kim and A.-J. Attias, Mater. Horiz., 2017, 4, 570–583 RSC.
- R. Gutzler, L. Cardenas and F. Rosei, Chem. Sci., 2011, 2, 2290–2300 RSC.
- K. Hipps and U. Mazur, Langmuir, 2017, 34, 3–17 CrossRef PubMed.
- O. Ivasenko and D. F. Perepichka, Chem. Soc. Rev., 2011, 40, 191–206 RSC.
- S. Griessl, M. Lackinger, M. Edelwirth, M. Hietschold and W. M. Heckl, Single Mol., 2002, 3, 25–31 CrossRef.
- J. MacLeod, J. Lipton-Duffin, D. Cui, S. De Feyter and F. Rosei, Langmuir, 2015, 31, 7016–7024 CrossRef PubMed.
- Q. Zhou, Y. Li, Q. Li, Y. Wang, Y. Yang, Y. Fang and C. Wang, Nanoscale, 2014, 6, 8387–8391 RSC.
- V. Iancu, K.-F. Braun, K. Schouteden and C. Van Haesendonck, Langmuir, 2013, 29, 11593–11599 CrossRef PubMed.
- Y. Ye, W. Sun, Y. Wang, X. Shao, X. Xu, F. Cheng, J. Li and K. Wu, J. Phys. Chem. C, 2007, 111, 10138–10141 CrossRef.
- J. Barth, J. Weckesser, N. Lin, A. Dmitriev and K. Kern, Appl. Phys. A: Mater. Sci. Process., 2003, 76, 645–652 CrossRef.
- N. Lin, A. Dmitriev, J. Weckesser, J. V. Barth and K. Kern, Angew. Chem., Int. Ed., 2002, 41, 4779–4783 CrossRef PubMed.
- A. Dmitriev, N. Lin, J. Weckesser, J. Barth and K. Kern, J. Phys. Chem. B, 2002, 106, 6907–6912 CrossRef.
- L. Kanninen, N. Jokinen, H. Ali-Löytty, P. Jussila, K. Lahtonen, M. Hirsimäki, M. Valden, M. Kuzmin, R. Pärna and E. Nommiste, Surf. Sci., 2011, 605, 1968–1978 CrossRef.
- T. Classen, M. Lingenfelder, Y. Wang, R. Chopra, C. Virojanadara, U. Starke, G. Costantini, G. Fratesi, S. Fabris and S. De Gironcoli, J. Phys. Chem. A, 2007, 111, 12589–12603 CrossRef PubMed.
- I. Cebula, H. Lu, M. Zharnikov and M. Buck, Chem. Sci., 2013, 4, 4455–4464 RSC.
- H. Aitchison, H. Lu, R. O. de la Morena, I. Cebula, M. Zharnikov and M. Buck, Phys. Chem. Chem. Phys., 2018, 20, 2731–2740 RSC.
- D. Payer, A. Comisso, A. Dmitriev, T. Strunskus, N. Lin, C. Wöll, A. DeVita, J. V. Barth and K. Kern, Chem. – Eur. J., 2007, 13, 3900–3906 CrossRef PubMed.
- M. S. Baviloliaei and L. Diekhöner, Phys. Chem. Chem. Phys., 2014, 16, 11265–11269 RSC.
- N. Lin, D. Payer, A. Dmitriev, T. Strunskus, C. Wöll, J. V. Barth and K. Kern, Angew. Chem., Int. Ed., 2005, 44, 1488–1491 CrossRef PubMed.
- M. Gastaldo and S. Kiel, MSc thesis, Aalborg University, 2013.
- Z. Zhou and K. D. Harris, ChemPhysChem, 2006, 7, 1649–1653 CrossRef PubMed.
- N. A. Wasio, R. C. Quardokus, R. P. Forrest, C. S. Lent, S. A. Corcelli, J. A. Christie, K. W. Henderson and S. A. Kandel, Nature, 2014, 507, 86 CrossRef PubMed.
- H. Zhou, H. Dang, J.-H. Yi, A. Nanci, A. Rochefort and J. D. Wuest, J. Am. Chem. Soc., 2007, 129, 13774–13775 CrossRef PubMed.
- J. M. MacLeod, J. Lipton-Duffin, C. Fu, T. Taerum, D. F. Perepichka and F. Rosei, ACS Nano, 2017, 11, 8901–8909 CrossRef PubMed.
- J. I. Urgel, D. Écija, G. Lyu, R. Zhang, C.-A. Palma, W. Auwärter, N. Lin and J. V. Barth, Nat. Chem., 2016, 8, 657 CrossRef PubMed.
- I. Horcas, R. Fernández, J. Gomez-Rodriguez, J. Colchero, J. Gómez-Herrero and A. Baro, Rev. Sci. Instrum., 2007, 78, 013705 CrossRef PubMed.
- J. M. MacLeod, O. Ivasenko, C. Fu, T. Taerum, F. Rosei and D. F. Perepichka, J. Am. Chem. Soc., 2009, 131, 16844–16850 CrossRef PubMed.
- S. L. Tait, Y. Wang, G. Costantini, N. Lin, A. Baraldi, F. Esch, L. Petaccia, S. Lizzit and K. Kern, J. Am. Chem. Soc., 2008, 130, 2108–2113 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional STM images, O1s XPS, details of DFT calculations. See DOI: 10.1039/c8cc04380a |
| This journal is © The Royal Society of Chemistry 2018 |