Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical and in silico tuning of the magnetisation reversal barrier in pentagonal bipyramidal Dy(III) single-ion magnets†
Angelos B.
Canaj
 a,
Mukesh Kumar
Singh
a,
Mukesh Kumar
Singh
 b,
Claire
Wilson
b,
Claire
Wilson
 a,
Gopalan
Rajaraman
a,
Gopalan
Rajaraman
 *b and
Mark
Murrie
*b and
Mark
Murrie
 *a
*a
aWestCHEM, School of Chemistry, University of Glasgow, University Avenue, Glasgow, G12 8QQ, UK. E-mail: mark.murrie@glasgow.ac.uk
bDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai, Maharashtra 400076, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 10th July 2018
Abstract
Two new air-stable axial Dy(III) single-ion magnets, [Dy(H2O)5(HMPA)2]Cl3·HMPA·H2O (1) and [Dy(H2O)5(HMPA)2]I3·2HMPA (2) (HMPA = hexamethylphosphoramide), exhibit magnetic hysteresis which remains open up to 9 K for 1@Y and 10 K for 2@Y, respectively. Ab initio calculations, using step-by-step elimination of fragments to generate a series of model complexes, reveal that the secondary coordination sphere plays a key role in controlling the magnetisation reversal barrier and predict that the removal of outer-sphere molecules and anions will enhance the barrier further.
Controlling the coordination environment/geometry at the level of a single metal ion is a challenging task for synthetic chemists, but of great importance for the miniaturisation of data storage.1 Single-Molecule Magnets (SMMs) are magnetically independent molecules in which the magnetic moment resists reorientation upon removal of an external magnetising field, which results in the appearance of magnetic hysteresis of molecular origin.2 These unique molecules are considered amongst the best candidates for advanced quantum-based devices (devices for data storage, quantum computing and spintronics).3 Mononuclear SMMs (usually referred to as Single-Ion Magnets (SIMs)) comprise one or more ligands binding at a single metal site to control the coordination geometry.4 The large single-ion magnetic anisotropy and unquenched orbital angular momentum of the f-elements have established them as enticing targets for the construction of SMMs/SIMs.5 It has been recently demonstrated that for lanthanide-based SMMs, the prerequisites for large energy barriers for the reorientation of magnetisation (Ueff) and magnetic hysteresis at higher temperatures are the double degeneracy of the largest mJ ground substate and a large separation from the first and higher excited states.6 According to computationally-demanding theoretical calculations (CASSCF-SO) and elegant electrostatic models, it has become clear that for improved dysprosium(III) based SMMs/SIMs, the type of coordination environment has to possess a strongly axial character.7 In this way, shortcuts through the energy barrier can be suppressed and higher energy barriers are achieved for thermal relaxation.8 Complexes with a high-order symmetry axis such as square antiprismatic (D4d),9 trigonal bipyramidal (D3h),10 sandwich type11 (with cyclooctatetraene (COT) and cyclopentadienyl (Cp) anionic ligands) and pentagonal bipyramidal (D5h),12 have been suggested as an effective way to favour slower relaxation by reducing transverse anisotropy, thus suppressing Quantum Tunnelling of the Magnetisation (QTM). Additionally higher-order symmetry also helps to align the gzz axis of the excited state co-linear to the ground state, which leads to relaxation via higher excited states and hence larger magnetisation reversal barriers.13
Recently, we reported a trigonal bipyramidal Ni(II) complex with an unprecedented axial magnetic anisotropy by using bulky axial ligands.14 Motivated by these results, we have investigated a wide range of bulky monodentate ligands to synthesise axial Dy(III) systems. Herein we report the synthesis, structure, magnetic properties and ab initio studies of [Dy(H2O)5(HMPA)2]Cl3·HMPA·H2O (1) and [Dy(H2O)5(HMPA)2]I3·2HMPA (2) {HMPA = hexamethylphosphoramide, [(CH3)2N]3PO}, which represent new examples of Dy(III) SMMs with close to ideal pentagonal bipyramidal geometry. We also report the diamagnetic yttrium analogues; [Y(H2O)5(HMPA)2]Cl3·HMPA·H2O (3) and [Y(H2O)5(HMPA)2]I3·2HMPA (4) and the Dy-doped yttrium analogues (see ESI†).15 We find that the strong axial crystal field promoted by the two axial HMPA ligands in complexes 1 and 2 leads to hysteresis loops that remain open until 9 K for the Dy-doped yttrium chloride analogue (1@Y), and 10 K for the Dy-doped yttrium iodide analogue (2@Y). In terms of a large barrier Ueff and magnetic hysteresis temperature, these complexes are amongst the best air-stable SMMs.
The synthesis of 1 and 2 was accomplished by treatment of the hexamethylphosphoramide ligand (HMPA) with DyCl3 and DyI3, respectively, in hot THF under aerobic conditions. Work-up and crystallization (see ESI†) from dichloromethane/toluene (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
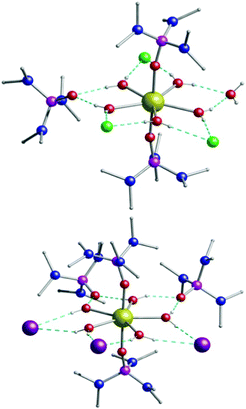
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) produces large colourless prismatic crystals of [Dy(H2O)5(HMPA)2]Cl3·HMPA·H2O (1) and [Dy(H2O)5(HMPA)2]I3·2HMPA (2) (Fig. 1). The phase purity of the bulk samples was confirmed by powder X-ray diffraction (Fig. S1–S4, ESI†).
1) produces large colourless prismatic crystals of [Dy(H2O)5(HMPA)2]Cl3·HMPA·H2O (1) and [Dy(H2O)5(HMPA)2]I3·2HMPA (2) (Fig. 1). The phase purity of the bulk samples was confirmed by powder X-ray diffraction (Fig. S1–S4, ESI†).
The chloride analogue 1 crystallises in the monoclinic space group P21/c with the asymmetric unit containing two [Dy(H2O)5(HMPA)2]Cl3·HMPA·H2O units (Table S1 and Fig. S6, S7, ESI†). The seven coordinate Dy(III) centre is in a pentagonal bipyramidal geometry (D5h symmetry) for both crystallographically independent Dy centres, as confirmed via continuous shape measures analysis,16 which provides an estimate of the distortion from the perfect polyhedron, giving a value of 0.154 for Dy1 (1a) and 0.284 for Dy2 (1b) (where 0 corresponds to the ideal structure) (Fig. S5 and Table S4, ESI†). Two HMPA ligands occupy the axial positions with five water molecules in the equatorial positions (Fig. S6, ESI†). The charge is balanced by three chloride anions in the second coordination sphere, with one HMPA and one H2O co-crystallised (Fig. S8, ESI†). The axial Dy–O distances are 2.2171(14) and 2.2211(14) for Dy1 (1a) and 2.2096(15) and 2.2282(15) Å for Dy2 (1b) while the equatorial Dy–O distances fall in the range 2.3377(16)–2.3600(16) Å for Dy1 (1a) and 2.3365(16)–2.3587(17) Å for Dy2 (1b). The axial O–Dy–O angle is almost linear (∼176°) while the equatorial O–Dy–O angles range between 71.41(6)° and 72.63(6)°, close to the ideal angle of 72° (Table S2, ESI†). Extensive intermolecular hydrogen bonding is observed in 1 connecting all the moieties in the structure (Fig. S8, ESI†). Complex [Dy(H2O)5(HMPA)2]I3·2HMPA (2) is similar to 1 but crystallises in the monoclinic Cc space group. The asymmetric unit of 2 contains one Dy(III) complex, three iodide anions and two co-crystallised HMPA ligands (Fig. S9, ESI†). We note that in complex 2, the Dy(III) pentagonal bipyramidal geometry is closer to the ideal polyhedron as confirmed via continuous shape measures analysis (0.131, Table S5, ESI†).16 The axial Dy–O distances in 2 are 2.202(4) and 2.208(4) Å, while the equatorial Dy–O distances range between 2.343(4)–2.375(4) Å. The axial O–Dy–O angle is ∼178° with the equatorial O–Dy–O angles ranging from 70.91(14)° to 73.18(14)° (Table S3, ESI†). Additionally, analysis of the crystal packing reveals that between discrete molecules the nearest Dy⋯Dy distance for 1 is 9.026 Å, while for 2 the Dy(III) centres are better isolated (11.767 Å) with only intramolecular hydrogen bonding observed (Fig. S10, ESI†).
The dc magnetic susceptibility measurements for complexes 1 and 2 are described in the ESI† (Fig. S11 and S12). The χMT profiles (i.e. the practically unchanged χMT product between 290–7 K and the sharp drop at low temperature) are similar to reported high performance Dy-SMM complexes.17 The field cooled (FC) and zero-field cooled (ZFC) magnetic susceptibility (Fig. S13 and S14, ESI†) diverge at 7 K and 8 K for 1 and 2 respectively, while the maxima are observed at ∼7 K for both complexes, indicative of the magnetic blocking temperature, TB.
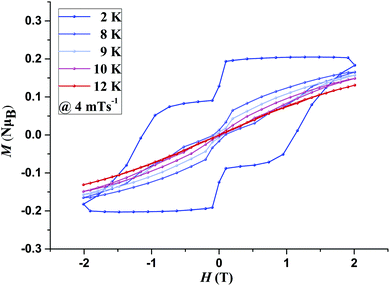
The presence of magnetic blocking was further confirmed by field dependent magnetisation measurements, M(H) loops, carried out at different temperatures, with an average sweep rate of ∼4 mT s−1 (for a full cycle). Both 1 and 2 display clear magnetic hysteresis which remains open up to 6 K (9 K for 1@Y) (Fig. S15–S17, ESI†) and 9 K (10 K for 2@Y), respectively (Fig. 2 and Fig. S18, ESI†). The shape of the M(H) loops is strongly affected by the faster relaxation around zero field arising due to unsuppressed Quantum Tunnelling of the Magnetisation. The M(H) loops display a large coercivity of 1 T for 1@Y and 1.1 T for 2@Y at 2 K.
Ac susceptibility measurements between 1–1488 Hz in zero external dc field with a small oscillating ac field of Hac = 3 Oe were performed to investigate the slow magnetic relaxation. The in phase χM′ and out of phase χM′′ magnetic susceptibility data show frequency dependent peaks with well-defined maxima at 30 K for 1 (Fig. S19 and S20, ESI†) and 38 K for 2 (Fig. S21 and S22, ESI†) for a frequency of 1488 Hz, indicating high magnetisation reversal barriers. The plot of χM′′ vs. frequency yielded temperature dependent maxima in the range of 17–30 K for 1 (Fig. S23, ESI†) and 17–37 K for 2 (Fig. S24, ESI†). The relaxation times, τ, were extracted from the fittings of the Argand plots of χM′′ vs. χM′ using the generalized Debye model.18 The α parameters found are in the range of 0.013–0.10 (17–30 K) for 1 (Fig. S25, ESI†) and 0.015–0.13 (17–37 K) for 2 (Fig. S26, ESI†), indicating a narrow distribution of relaxation times. The Arrhenius plots, constructed by using the extracted relaxation times, τ, were fitted with the Arrhenius equation 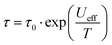 . The ln
. The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus T−1 plots were fit considering only the Orbach process, to yield an energy barrier of Ueff = 460 K, τ0 = 2 × 10−11 s for 1 (Fig. S27, top, ESI†) and Ueff = 600 K, τ0 = 1.2 × 10−11 s for 2 (Fig. S27, bottom, ESI†). In order to further understand the mechanism that governs the magnetic relaxation observed for complexes 1 and 2, we have performed ab initio calculations using the CASSCF/RASSI-SO/SINGLE_ANISO approach implemented in MOLCAS8.0 (see ESI†). This methodology has a proven track record to rationalize, and also predict at times, a reliable mechanism of magnetic relaxation.12,13,19,20 The eight Kramers Doublets (KDs), corresponding to the 6H15/2 state, span within energy ranges of 882.1 cm−1 and 919.0 cm−1, respectively for complexes 1 and 2. For both complexes, mJ = ±15/2 is the ground state with mJ = ±13/2 as the first excited state and mJ = ±1/2 as the second-excited state. It is also worth mentioning here that the second excited state for complex 1 is mixed in nature whereas for complex 2, it is pure mJ = ±1/2 (Fig. 3 and Fig. S29, ESI†). The computed ground and first-excited state magnetic anisotropy for 1 and 2 are purely Ising in nature (gzz ≈ 19.97 and 17.10 respectively, with gxx = gyy = 0, see Fig. S28 for the gzz axis of 1 and 2, ESI†) suggesting a very small operative QTM/TA-QTM within the ground and first-excited KDs (Fig. 3 and Fig. S29, Table S6, ESI†).
τ versus T−1 plots were fit considering only the Orbach process, to yield an energy barrier of Ueff = 460 K, τ0 = 2 × 10−11 s for 1 (Fig. S27, top, ESI†) and Ueff = 600 K, τ0 = 1.2 × 10−11 s for 2 (Fig. S27, bottom, ESI†). In order to further understand the mechanism that governs the magnetic relaxation observed for complexes 1 and 2, we have performed ab initio calculations using the CASSCF/RASSI-SO/SINGLE_ANISO approach implemented in MOLCAS8.0 (see ESI†). This methodology has a proven track record to rationalize, and also predict at times, a reliable mechanism of magnetic relaxation.12,13,19,20 The eight Kramers Doublets (KDs), corresponding to the 6H15/2 state, span within energy ranges of 882.1 cm−1 and 919.0 cm−1, respectively for complexes 1 and 2. For both complexes, mJ = ±15/2 is the ground state with mJ = ±13/2 as the first excited state and mJ = ±1/2 as the second-excited state. It is also worth mentioning here that the second excited state for complex 1 is mixed in nature whereas for complex 2, it is pure mJ = ±1/2 (Fig. 3 and Fig. S29, ESI†). The computed ground and first-excited state magnetic anisotropy for 1 and 2 are purely Ising in nature (gzz ≈ 19.97 and 17.10 respectively, with gxx = gyy = 0, see Fig. S28 for the gzz axis of 1 and 2, ESI†) suggesting a very small operative QTM/TA-QTM within the ground and first-excited KDs (Fig. 3 and Fig. S29, Table S6, ESI†).
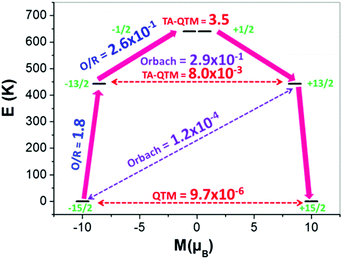 | ||
| Fig. 3 Ab initio calculated relaxation dynamics for complex 2. The arrows show the connected energy states with the number representing the matrix element of the transverse moment (see text for details). Here, QTM = quantum tunnelling of the magnetisation, TA-QTM = thermally assisted QTM, O/R = Orbach/Raman process. The numbers above each arrow represent corresponding transversal matrix elements for the transition magnetic moments as described in ref. 21 (see ESI† for further information). | ||
The Orbach process related to the ground and first excited state of opposite magnetisation is calculated to be very small (Fig. 3 and Fig. S29, ESI†). However, the second excited state for both complexes is found to have a substantial transverse magnetic component with a larger operative TA-QTM relaxation (∼0.5 and 3.5 μB for complexes 1 and 2, respectively). The computed gzz axis for both the ground and first excited states is collinear (see Fig. S28, ESI†) in complexes 1 and 2 (less than 2°). This suggests magnetic relaxation via the second excited KD (−15/2 → −13/2 → −1/2 → +1/2 → +13/2 → +15/2) with the Ucal value 584 K and 640 K for complexes 1 and 2, respectively. In complex 2, the calculated and the experimental energy barrier are in close agreement (640 K and 600 K respectively) whereas in complex 1, the agreement is not as good (584 K and 460 K, respectively). This is expected as in complex 1, the ground state QTM is larger compared to complex 2 (Fig. 3 and Fig. S29, ESI†). Furthermore, the structural parameters and LoProp22 charge analysis (see Fig. S31, ESI†) suggest a stronger axial ligand field in complex 2. Although the LoProp charges on the pentagonal plane water molecules are larger in complex 2, the even larger LoProp charges on Cl− ions found in 1, compared to I− ions in 2, result in a larger transverse ligand field in 1 (Fig. S31, ESI†). Notably, the non-axial term (Bqk, where q ≠ 0 and k = 2, 4, and 6) to the axial term (Bqk, where q = 0 and k = 2, 4, and 6) ratio is found to be smaller for complex 2 compared to 1, confirming the lower operational QTM and the larger Ucal value for 2 compared to 1 (Table S7, ESI†).20 In an attempt to evaluate how strongly the Ucal values are related to molecules/fragments in the secondary coordination sphere, we have created a number of different model systems by step-by-step elimination of each fragment to generate a series of model complexes (Fig. 4 and Fig. S32, ESI†), with the last model possessing a mono-coordinated Dy(III) with one HMPA ligand. Importantly, these models highlight that the removal of anions/molecules in the secondary coordination sphere is able to enhance the computed value of Ucal. As these outer-sphere anions/molecules are removed, this causes a lowering of the charges in the equatorial region around the Dy(III) ion and thus increases the crystal field interaction along the axial direction (Fig. S31 and Table S8, ESI†). One can in fact attain a theoretical value of ∼3100 K for a two coordinate {Dy(HMPA)2}3+ model (Fig. 4 and Fig. S32, ESI†).7 This can be attributed to the increase of the crystal field interaction along the axial direction as we move to lower-coordinate models (Fig. S34 and Table S8, ESI†). Furthermore, our calculations reveal that replacement of the halide anions, with large bulky anions, can cause a reduction in the charges in the equatorial region of the Dy(III) ion leading to larger barrier heights. Also, replacing small counter anions (X−) with large counter anions (PF6−) could potentially decrease the crowding around the Dy(III) ion by eliminating secondary coordination sphere molecules or increasing their distance from the Dy(III) ion and hence result in a lowering of the charges in the equatorial plane. Collectively both effects are expected to enhance significantly the barrier height and efforts are currently underway to achieve this in our laboratory.
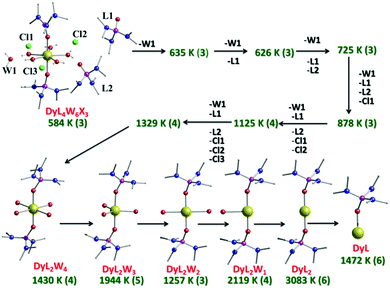 | ||
| Fig. 4 Ab initio SINGLE_ANISO computed Ucal values (in K, green text) for all the models created by stepwise removal of fragments for complex 1. The bold number in brackets for each model gives the Kramers doublet through which relaxation is expected (ground state = KD (1); first excited state = KD (2) etc.). For more information see Fig. S32 and S33 (ESI†). | ||
The UK Engineering and Physical Sciences Research Council are thanked for financial support (grant ref. EP/N01331X/1). G. R. thanks the SERB (EMR/2014/00024) and INSA for funding. MKS thanks UGC-India for a fellowship. The data which underpin this work are available at http://dx.doi.org/10.5525/gla.researchdata.625.
Conflicts of interest
There are no conflicts to declare.Notes and references
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357 CrossRef PubMed.
- J. Lu, M. Guo and J. Tang, Chem. – Asian J., 2017, 12, 2772 CrossRef PubMed; S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. S. Walsh and F. Tuna, Coord. Chem. Rev., 2017, 346, 216 CrossRef; F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150 CrossRef; S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289, 149 CrossRef; Y.-S. Meng, S.-D. Jiang, B.-W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381 CrossRef PubMed; D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef PubMed.
- G. Aromi, D. Aguila, P. Gamez, F. Luisc and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537 RSC; C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef PubMed; S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135 CrossRef PubMed; L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179 CrossRef PubMed; M. Affronte, J. Mater. Chem., 2009, 19, 1731 RSC.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcald and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010 CrossRef PubMed.
- C. Benelli and D. Gateschi, Introduction to Molecular Magnetism. From Transition Metals to Lanthanides, Wiley-VCH, Weinheim, 2015 Search PubMed; R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH, Weinheim, 2015 Search PubMed.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655 RSC; M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155 RSC.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC; L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086 RSC; S. K. Singh, T. Gupta and G. Rajaraman, Inorg. Chem., 2014, 53, 10835 CrossRef PubMed; L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043 CrossRef PubMed.
- T. Pugh, N. F. Chilton and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 11082 CrossRef PubMed; W.-B. Sun, P.-F. Yan, S.-D. Jiang, B.-W. Wang, Y.-Q. Zhang, H.-F. Li, P. Chen, Z.-M. Wang and S. Gao, Chem. Sci., 2016, 7, 684 RSC; P. Zhang, M. Perfetti, M. Kern, P. P. Hallmen, L. Ungur, S. Lenz, M. R. Ringenberg, W. Frey, H. Stoll, G. Rauhut and J. van Slageren, Chem. Sci., 2018, 9, 1221 RSC; L. Norel, L. E. Darago, B. Le Guennic, K. Chakarawet, M. I. Gonzalez, J. H. Olshansky, S. Rigaut and J. R. Long, Angew. Chem., Int. Ed., 2018, 57, 1 CrossRef PubMed; S. Demir, M. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144 CrossRef PubMed; B. S. Dolinar, D. I. Alexandropoulos, K. R. Vignesh, T. A. James and K. R. Dunbar, J. Am. Chem. Soc., 2018, 140, 908 CrossRef PubMed.
- L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092 RSC; P.-E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Chem. Commun., 2011, 47, 3751 RSC; M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874 CrossRef PubMed.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484 CrossRef PubMed; K. L. M. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, J. Am. Chem. Soc., 2017, 139, 1420 CrossRef PubMed.
- S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730 CrossRef PubMed; F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445 CrossRef PubMed; C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef PubMed.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829 CrossRef PubMed; Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071 CrossRef PubMed; J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441 CrossRef PubMed; S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191 RSC; J. L. Liu, Y. C. Chen, Y. Z. Zheng, W. Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. L. Tong, Chem. Sci., 2013, 4, 3310 RSC.
- S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Chem. Commun., 2014, 50, 15513 RSC.
- K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823 RSC.
- Z. Hou, K. Kobayashi and H. Yamazaki, Chem. Lett., 1991, 265 CrossRef; T. Imamoto, Y. Yamanoi, H. Tsuruta, K. Yamaguchi, M. Yamazaki and J. Inanaga, Chem. Lett., 1995, 949 CrossRef.
- M. Llune, D. Casanova, J. Cirera, J. Bo, P. Alemany and S. Alvarez, SHAPE (Version 2.1), Barcelona, 2013 Search PubMed.
- Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2017 DOI:10.1016/j.ccr.2017.10.030.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford Univ. Press, 2006 Search PubMed.
- M. K. Singh, N. Yadav and G. Rajaraman, Chem. Commun., 2015, 51, 17732 RSC; M. K. Singh and G. Rajaraman, Chem. Commun., 2016, 52, 14047 RSC.
- A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Coord. Chem. Rev., 2018, 367, 163 CrossRef.
- L. Ungur, M. Thewissen, J. P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328 CrossRef PubMed.
- L. Gagliardi, R. Lindh and G. Karlström, J. Chem. Phys., 2004, 121, 4494 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section, magnetic studies, crystallographic details, ab initio studies. CCDC 1835322–1835325. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8cc03929a |
| This journal is © The Royal Society of Chemistry 2018 |