Open Access Article
Open Access ArticleRole of conformational dynamics in the evolution of novel enzyme function
Miguel A.
Maria-Solano
 a,
Eila
Serrano-Hervás
a,
Eila
Serrano-Hervás
 a,
Adrian
Romero-Rivera
a,
Adrian
Romero-Rivera
 a,
Javier
Iglesias-Fernández
a,
Javier
Iglesias-Fernández
 a and
Sílvia
Osuna
a and
Sílvia
Osuna
 *ab
*ab
aCompBioLab Group, Institut de Química Computacional i Catàlisi and Departament de Química, Universitat de Girona, Carrer Maria Aurèlia Capmany, 69, 17003 Girona, Catalonia, Spain. E-mail: silvia.osuna@udg.edu
bICREA, Pg. Lluís Companys 23, 08010 Barcelona, Spain
First published on 14th May 2018
Abstract
The free energy landscape concept that describes enzymes as an ensemble of differently populated conformational sub-states in dynamic equilibrium is key for evaluating enzyme activity, enantioselectivity, and specificity. Mutations introduced in the enzyme sequence can alter the populations of the pre-existing conformational states, thus strongly modifying the enzyme ability to accommodate alternative substrates, revert its enantiopreferences, and even increase the activity for some residual promiscuous reactions. In this feature article, we present an overview of the current experimental and computational strategies to explore the conformational free energy landscape of enzymes. We provide a series of recent publications that highlight the key role of conformational dynamics for the enzyme evolution towards new functions and substrates, and provide some perspectives on how conformational dynamism should be considered in future computational enzyme design protocols.
1. Introduction
Most enzymes are accurate, specific, and highly efficient in accelerating biotransformations. Their extraordinary catalytic power arises from their precisely pre-organised active sites that properly position the catalytic residues for efficient transition state (TS) stabilisation.1 This precise positioning of the catalytic machinery2 could be related to a lack of versatility. However, enzymes present a marked adaptability as shown by their capability of catalysing additional promiscuous side-reactions,3 and in their ability to evolve and acquire novel functions. In fact, the evolvability of enzymes has been associated with their inherent dynamic nature.4 The ability of enzymes to visit different thermally accessible conformations, i.e. the enzyme conformational dynamics, plays a key role in enzyme promiscuity, regulation and inhibition, but also in essential steps in enzyme catalysis such as substrate binding and product release.5 The existence of a link between active site dynamics and catalysis of the chemical steps of the reaction has also long been debated.1a,6 This observation is, however, totally independent to the fact that enzymes adopt multiple conformations along the catalytic cycle.Conformational changes in enzymes occur in a variety of timescales.7 Bond vibration (10–100 fs) and side-chain conformational changes (ps to μs) take place on the shortest timescales, whereas loop motions often key for substrate binding and product release occur in the nanosecond up to millisecond timescales. On the longest timescales, slow domain motions and allosteric transitions can take place (μs to s).8 All these motions can precede or occur after the chemical steps, and indeed in some natural and laboratory-evolved enzymes conformational change is found to be rate-limiting.9 Many examples have been provided in the literature highlighting the importance of engineering flexible loops and domains for novel function.10 Recent studies based on the analysis of static X-ray structures along evolutionary pathways and in ancestral protein reconstruction,11 nuclear magnetic resonance (NMR) experiments,9b,12 and computational studies based on molecular dynamics (MD) simulations7c,13 have provided further support of enzymes as an ensemble of thermally accessible conformations. All these evidences emphasise the crucial role of the enzyme conformational dynamics for its function.
Initial attempts to computationally engineer enzymes towards non-natural reactions or substrates were based on protocols that (re)designed the active site of some natural scaffolds by mutating a subset of residues while maintaining most of the enzyme structure as rigid.14 Despite the initial successes, computationally designed enzymes display quite poor catalytic activities,14a and need to be further evolved by means of experimental techniques such as directed evolution (DE).15 The strategy of combining computational protocols and DE has been shown to be successful in designing enzymes for a broad scope of challenging transformations.2,16 The origin behind the poor activities of computational designs has been attributed to the imperfect realisation of the ideal arrangement of the catalytic residues for TS stabilisation,17 and the tendency to consider only the chemical steps while overlooking essential conformational changes for substrate binding and product release.5a The latter observation suggests that the consideration of conformational dynamics in enzyme design could aid greatly the field. In fact, most recent enzyme design protocols take into consideration multiple states to better represent the enzyme conformational heterogeneity.18
Advances in the available biophysical techniques and computational tools have contributed to a deeper understanding of the conformational dynamics of enzymes and their key role for activity.13a,19 In this feature article, we provide an overview of the existing techniques that can be applied for characterising the enzyme free energy landscape. We describe how by introducing mutations to the enzyme sequence the populations of the conformational states in the free energy landscape can be shifted for: enhancing a novel or promiscuous reaction, accepting alternative industrially-relevant substrates, and altering the enzyme inherent enantioselectivity. We provide some representative examples recently published in the literature, combined with some recent publications from our lab.
2. The conformational free energy landscape of proteins: theory and methodologies
The broad range of conformations that enzymes can adopt in solution can be mapped into the so-called free energy landscape (see Fig. 1A). In this free energy landscape, the different conformational states (or sub-states) in thermal equilibrium are represented as well as the barriers separating them, thus obtaining information on the thermodynamics and kinetics of the system. The conformational sub-states in the free energy landscape are populated following statistical thermodynamic distributions. The regions with high populations of specific conformers correspond to either the local or global energy minima. The height of the barriers that separate the different conformational states dictate how fast or slow a conformational transition is. Therefore, conformational states separated by small energy barriers require ps–ns timescales to exchange, whereas if connected through high energy barriers the transition becomes slower and less likely to take place. It is also worth mentioning that a particular free energy is linked to a specific protein sequence and defined values of temperature, pressure, and solvent conditions. Manipulating these parameters (e.g. single point mutation or a temperature increase) will result in dramatic changes in the relative conformational distributions or population shifts, but also in the kinetics of the conformational state interconversions.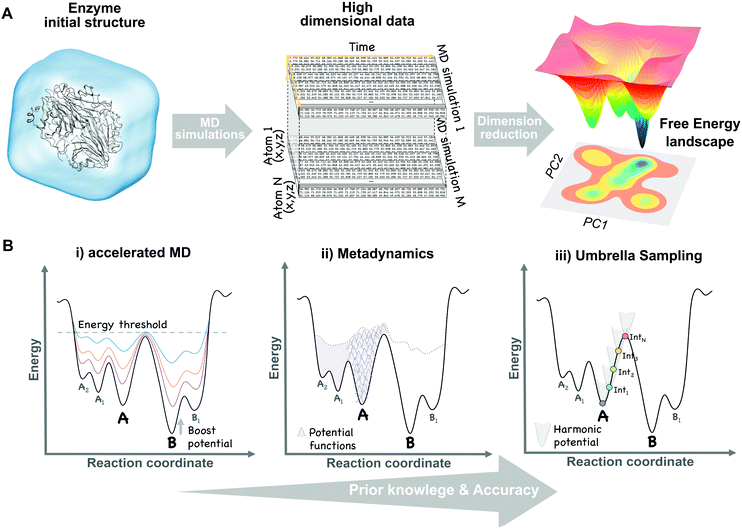 | ||
| Fig. 1 Schematic view of the dimensional reduction process of multiple unbiased MD simulation data (A) and the main biased methods (B) used to construct the conformational free energy landscape. | ||
The different conformational states that exist in the free energy landscape of enzymes and their rates of interconversion can be indirectly characterised through experimental methods. Collective or slow motions in proteins can be analysed thanks to X-ray crystallography, although there is a requirement for homogeneous crystals of individual states. Structural ensembles can be directly analysed thanks to cryo-electron microscopy, obviating the requirement for homogenous crystals, although at lower atomic resolution. This technique has been applied to determine the conformational energy landscape of yeast ribosome, together with RNA translocation as a function of time.20 NMR techniques, although also lacking the resolution of X-ray crystallography, provide structural together with kinetic data in a timescale range of picoseconds to seconds.9b,21 Finally, biophysical techniques, such as fluorescence, circular dichroism, Raman spectroscopy, among others give kinetic information complementary to other structural methods.22
Computational methods are particularly useful in reconstructing the free energy landscape of enzymes. The free energy (G) can be defined as the negative logarithm of the population distribution (P) in kBT units (e.g. kcal mol−1 K−1; see eqn (1)), therefore a maximum in the distribution corresponds to a minimum in the free energy landscape. By switching back and forth between stable states, their relative populations can be estimated.23 If the number of transitions increases, the error in the population estimation can be significantly reduced.
G ∼ −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(P) log(P) | (1) |
Molecular dynamics (MD) techniques allow to sample the population distribution of individual atoms or biomolecules by integrating Newton's laws of motion. This enables the recovery of thermodynamic properties such as the free energy. Unfortunately, as a result of the large number of atoms present in simulations (ca. 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms for a protein of regular size in an explicit solvent environment), this probability is defined in an extremely high dimensional space (see Fig. 1A). A natural solution to this limitation is to focus on a reduced set of global or collective degrees of freedom (DOFs), while less relevant atomic motions are averaged over the chosen DOFs. These DOFs can be any explicit function of the coordinates of the enzyme, relevant to the process of interest, such as distances between catalytic residues, backbone dihedral angles, or the RMSD of a loop. High dimensional data obtained from MD simulations can be projected onto these collective DOFs obtaining the probability distributions and reconstructing the associated free energy landscape (eqn (1)).
000 atoms for a protein of regular size in an explicit solvent environment), this probability is defined in an extremely high dimensional space (see Fig. 1A). A natural solution to this limitation is to focus on a reduced set of global or collective degrees of freedom (DOFs), while less relevant atomic motions are averaged over the chosen DOFs. These DOFs can be any explicit function of the coordinates of the enzyme, relevant to the process of interest, such as distances between catalytic residues, backbone dihedral angles, or the RMSD of a loop. High dimensional data obtained from MD simulations can be projected onto these collective DOFs obtaining the probability distributions and reconstructing the associated free energy landscape (eqn (1)).
Reducing the dimensionality of our data to only a few DOFs can omit essential kinetic or thermodynamic information relevant to the process under study. Besides, choosing an appropriate set of DOFs requires a detailed knowledge of our system. Approaches to automatically reduce the dimensionality of the data while preserving as much information as possible have been developed. For example, Principal Component Analysis (PCA)24 performs a dimensionality reduction accounting for as much variance in the data set as possible. In a nutshell, if we define variance as the deviation of an atom from its mean position along the MD, then each principal component will be a linear combination of strongly correlated atomic motions with large oscillations. The resulting low dimensional PCA space can be used to reconstruct the associated free energy landscape (see Fig. 1A). For example, PCA has been applied in several studies of protein folding and allostery.25 However, transitions with the highest variance do not strictly correlate with the slowest (i.e. kinetically relevant) processes. Contrary to PCA, the time-structure independent component analysis (tICA) seeks to lower the dimensionality of our data while minimising the loss of kinetic information.26 This is done by considering the time correlation of the data instead of the variance. Alternative approaches to reduce dimensionality include Diffusion Maps,27 the variational approach,28 Sketch-Map,29 among others.
The time-dependent properties gathered from MD simulations can only be connected with experimental observables if all relevant states or conformations of the system are visited (i.e. ergodic principle).23 In practical situations, this is not normally the case. To properly integrate the equations of motion, atomistic MD calculations using empirical force fields typically use time steps of the order of femtoseconds (i.e. 10−15 seconds), being able to compute few nanoseconds with a personal computer, but far from the millisecond to second timescales of domain motions and allosteric transitions occurring in some enzymes, as mentioned in the introduction.30 This timescale gap frustrates direct comparison with experimental data, encouraging for alternative approaches, which can be broadly classified in unbiased and biased methods.
a. Unbiased MD methods
After more than 40 years since the first MD simulation of a protein was performed,31 the basic MD algorithm remains unaltered. Then, the question is, how can we increase the accessible timescales to make reliable connections with experiments? Here we detail some of the most commonly used strategies:(i) CPU parallelisation leads to an enormous increase in the accessible simulation timescales. This strategy is used to simulate extremely large systems during moderately long simulation times thanks to a divide and conquer approach (i.e. the system is broken down into smaller entities, each one being computed on the different connected CPU). This approach was used in a MD simulation of a complete solvated tobacco mosaic virus capsid with up to 1 million atoms.32
(ii) The Anton supercomputer was specifically developed as a special purpose computer by D. E. Shaw and coworkers to perform single long MD simulations of biological systems. The first atomistic millisecond MD simulation of a protein (WW domain) was performed with Anton.33 This computer has also been used to study the fold of a series of small proteins,34 allosteric transitions in G-protein membrane receptors,35 ligand binding kinetics,36 among others.
(iii) GPU based clusters offer an affordable alternative to increase MD accessible timescales by running either single long and/or multiple short simulations of the same system. Some MD codes have been specifically designed to run on GPUs, such as AceMD37 and OpenMM,38 whereas others have been ported to GPUs (Amber,39 Gromacs,40 and NAMD41). The idea behind multiple MD runs is to promote infrequent transitions or rare events by running several MD simulations from different initial structures and combine them to recover the associated conformational free energy landscape (see Fig. 1A). However, dealing with the resulting flood of data, comprised of hundreds or even thousands of simulations, becomes a challenge. Markov State Models (MSMs) arise as an approach to analyse large MD data sets in an objective methodological way to recover thermodynamic and kinetic parameters between conformational states. MSMs are also based on a dimensional reduction (e.g. tICA) to recover the free energy landscape associated with slow collective DOFs and the kinetics of the process. Quantitative predictions from MSMs can be compared with available experimental data.42 In particular, this approach has recently been used to study serine protease Trypsin43 and Bruton tyrosine kinase conformational plasticity.44 Besides, MD simulations together with MSMs were also used to guide a regioselective switch in a nitrating P450 from Streptomyces scabies.45
(iv) Replica exchange or parallel tempering46 is an alternative strategy based on running several copies of the same system at different temperatures and exchanging conformations at certain time intervals. Probability distributions are only meaningful at room temperatures and can be recovered by projecting atomic coordinates onto some selected DOFs (see Fig. 1A), as explained before, whereas high temperatures facilitate barrier crossing. This approach has been widely used for protein folding,47 although the number of replicas required to ensure temperature exchanges is proportional to the number of atoms, thus making it unaffordable for large systems.
b. Biased MD methods
It is possible to increase the frequency with which barriers separating stable states are crossed by introducing external energy potentials into our MD simulations. The selection of the proper biased method can be guided by the amount of structural information that we have about our system. For instance, to study the transition of a protein domain from an open (A) to a closed (B) conformation, two main questions can be formulated: (1) do we have enough structural information of A and B to define some DOFs, (e.g. dihedral angles), describing the transition? (2) Do we have intermediate structures between the two states? Based on the answer to both questions a proper biased method can be chosen:(i) Only one conformational state is known (e.g. A) and, therefore, no clear information about the transition is available. In this situation, methods to explore biomolecular conformations without a priori structural knowledge, such as accelerated MD (aMD),48 are advantageous. In aMD, a bias potential (i.e. boost potential) is added to raise the energy minima while keeping high energy regions almost unaffected, therefore, smoothing the free energy landscape and enhancing conformational exchanges (see Fig. 1B). aMD becomes really useful when few structural information is available, although a non-trivial post-processing is needed to recover unbiased free energy values. This method has been applied to fold a set of small proteins49 and to study the conformational dynamics of biomolecules, such as the maltose binding protein.50
(ii) Both conformational states (A and B) are known, but no clear information about intermediate states is available. In this case, methods that explore all possible transitions between A and B along a set of DOFs (e.g. distance between two residues or the RMSD of a domain region) are the proper choice. Metadynamics51 is based on the addition, at a regular number of MD steps, of small repulsive potentials to a selected set of DOFs (see Fig. 1B). These potentials discourage the system from visiting prior configurations, forcing it to escape from energy minimum A to explore B through the lowest energy path. In addition to accelerate transitions between states, metadynamics allows to recover the free energy associated with the A to B transition by the sum of all the repulsive potentials added along the MD. This method usually provides higher accuracy than previous biased approaches, but can also experience convergence issues since it is not easy to decide when to stop a simulation, avoiding the addition of useless repulsive terms. It has the advantage that only a few structural information is required to set up the simulation, although choosing a proper set of DOFs can sometimes be tricky. Metadynamics has been widely used to study the conformational landscapes of proteins52 and the effect of pathogenic mutations in cancer related kinases.52,53
(iii) Both conformational states (A and B) are known together with intermediate conformations. If detailed structural knowledge is available, independent MD simulations at states A and B together with a spectrum of intermediate conformations can be performed. In umbrella sampling (US),54 for example, several MD simulations are computed with restraining bias potentials added at small increments along the reaction coordinate, forcing the system to sample all the desired conformational states, therefore cancelling the effect of energy barriers and exploring low probability regions (see Fig. 1B). Overlapping umbrella sampling simulations can be analysed together to recover probability distributions and the free energy within the A to B transition.55 This method provides good estimates of the free energy, since each point on the transition is equally sampled, but detailed structural knowledge is required to define a suitable set of starting conformations describing a continuous pathway between A and B.56
3. Effect of mutations and/or ligand binding on the free energy landscape
The free energy landscape reveals the multiple thermally accessible conformations other than the native state (i.e. the lowest energy state) that the enzyme can adopt in solution. As described in the conformational selection model,57 all these weakly populated conformations may be of importance for recognising the substrate. After inhibitor or substrate binding, a redistribution of the populations of the conformational states exists, i.e. a population shift occurs.57 Within the population shift or conformational selection concept, the binding event does not induce a conformational change, but rather a redistribution of the populations of the conformational states that already exist in the absence of ligand. This is in contrast to the 60 year old Koshland induced fit model,58 in which the binding of the substrate induces a conformational transition from the apo to the holo conformation of the enzyme. The induced fit model overlooked the fact that in solution the enzyme can pre-exist in multiple conformations in addition to the apo conformational state.59 In recent years, the population shift concept originated from the Monod–Wyman–Changeux model of allostery60 has become more popular than the induced fit model. Recently, Kovermann and coworkers provided evidence for a conformational selection pathway in the adenylate kinase (AdK) enzyme.61 As shown by X-ray crystallography, AdK adopts an open conformation in absence of ligand, whereas a catalytically competent closed conformation is required for catalysis. According to the conformational selection model, this high in energy closed conformational state should also be visited in the absence of ligand, albeit with a lower frequency. By introducing a disulfide bond, they succeeded in arresting AdK in a closed conformation in the apo state. The X-ray structure provided a definitive proof of the closed conformation of the enzyme being also sampled in the absence of any ligand, thus highlighting that higher in energy functionally relevant states are visited even in the apo state.High in energy conformational states relevant for substrate binding can also be important for conferring the enzyme the ability to accelerate additional promiscuous reactions,4 or for the enzyme evolution towards novel function.11a,13d,62 Similar to substrate binding, introduction of mutations to the enzyme sequence can induce a shift in the populations of the pre-existing conformational states (see Fig. 2). This was elegantly demonstrated with a recent example by Tokuriki and Jackson through an impressive collection of X-ray structures.11a They demonstrated that the change in function from a phosphotriesterase into an arylesterase is achieved by gradual population of pre-existing conformational states, i.e. a population shift occurs along the evolutionary pathway. Their study established that minor states that conferred the natural enzyme some arylesterase activity were gradually stabilised to become major states in the evolved arylesterases.11a A similar finding was obtained by Jackson in evaluating how ancestral binding proteins evolved into specialist binders.11b An ancestral arginine-binding protein was crystallised in complex with L-arginine and L-glutamine revealing that the promiscuous binding of L-glutamine was possible due to alternative conformational states. These alternative conformational states were further populated along evolution to produce the contemporary L-glutamine specific protein binders. Finally, some of us were able to elucidate the role of distal mutations in recapitulating the allosteric regulation exerted by an acyl-carrier protein on the acyltransferase enzyme LovD by means of MD simulations.7c,13c The analysis of the conformational dynamics of the stand-alone LovD enzyme along the evolutionary pathway indicated that the introduced mutations induced a gradual population of the catalytically active conformational states. These studies support the idea that the underlying principle that guides enzyme evolution lies in the population shift of the conformational states that pre-exist in solution.
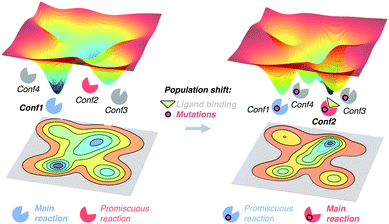 | ||
| Fig. 2 Schematic representation of the population shift induced by ligand binding and/or by the introduction of mutations in the enzyme free energy landscape. | ||
The effect of introducing mutations to the enzyme sequence for their evolution towards new functions and novel substrate scope has a high similarity to substrate binding and allosteric regulation processes.11a,62,63 In all cases, a redistribution of the populations of the conformational sub-states exists, but in the particular case of enzyme evolution this population shift should favour the catalytically competent conformational states for the new target reaction. The challenge lies in the rational prediction of mutations required to favour the desired population shift. Different computational enzyme design strategies have been developed such as the inside-out protocol with Rosetta,14a,64 multi-state design,18a CASCO (Catalytic Selectivity by Computational design),65 and discrete molecular dynamics (DMD)66 to predict active site mutations. Some recent methodologies, based on empirical valence bond (EVB), have also been proposed to mimic the experimental directed evolution.67 EVB and quantum mechanics/molecular mechanics (QM/MM) calculations can be used to elucidate the effect of active site mutations on the catalytic activity of the enzyme regarding enzyme conformational dynamics.1c,68 Additionally, the calculation of catalytically competent poses observed along MD simulations7c,13c,65 has been used to rationalise how active site and distal mutations affect the catalytic activity of enzymes (see ref. 13b for a complete description of the available computational techniques for rationalising the effect of mutations on laboratory-evolved enzymes).
Many examples have been provided in the literature demonstrating that mutations located at remote positions from the active site can have a large impact on the catalytic activity of the enzyme.13c,69 For instance, the effect of distal mutations has been nicely demonstrated experimentally and computationally in cyclophilin A.25b,70 Indeed, no correlation is found between the influence of a given mutation on the catalytic constant of the enzyme and its proximity to the active site.71 Due to the broad sequence space of enzymes, the computational prediction of distal mutations has proven to be challenging.13c,69b The key role exerted by remote mutations on the active site of the enzyme suggests that allostery (i.e. regulation of enzyme function by distal positions) might be an intrinsic characteristic of enzymes,72 which might be exploited for enzyme evolution.13d As discussed in the next section, our group has recently shown that correlation-based tools usually employed for elucidating allosteric processes can be successfully applied in the enzyme design field, identifying key distal positions that might influence the enzyme activity.13d
4. The population shift concept in enzyme evolution
Among all available computational tools,13b MD simulations have been shown to be crucial for characterising the enzyme's free energy landscape and population shifts induced by mutations. In the next sections, we provide a series of examples based on MD that emphasise the importance of the population shift concept induced by both active site and distal mutations for: evolving the enzyme towards novel or promiscuous reactions, broadening its substrate scope, and reverting its enantioselectivity.a. Towards novel enzyme function
Most of the examples provided in the previous sections are based on enzymes that present some residual (promiscuous)3 activity for the reaction under interest. For instance, the evolution of a phosphotriesterase into an arylesterase was achieved by introducing mutations via DE to further enhance the activity for the second reaction.11a As previously described, these mutations modified the free energy landscape of the phosphotriesterase enzyme and enhanced its residual arylesterase activity by populating pre-existing conformational states. However, what if the original enzyme has no residual activity for the target reaction? There are many interesting reactions that have no precedent in Nature, which makes the enzyme design task quite challenging. In this scenario, de novo computational protocols have been shown to be extremely useful for designing new enzyme variants, based on different scaffolds, achieving some initial activity for the desired reactions.13b,73One of the most representative cases of de novo computationally-designed enzymes was the creation of Kemp eliminases, which catalyse a proton abstraction from a carbon by a base. The first designs were generated using the inside-out protocol16b that combines Rosetta software74 and the theozyme concept, although other designs employing other methodologies have also been published.75 The inside-out Kemp eliminases exhibited quite low activities, due to the lack of precision to generate the perfect arrangement of the active site for catalysis.2,64 The different computational designs were further optimised through DE, making use of iterative design protocols that yielded new variants containing 10–15 mutations and exhibiting higher activities.16b,d,76 However, the most proficient Kemp eliminase reported so far was recently created by Kamerlin, Sanchez-Ruiz, and coworkers using an alternative approach. They showed that through a single hydrophobic-to-ionizable mutation an ancestral β-lactamase could be efficiently converted into a Kemp eliminase.77 It was remarkable that with 1–2 mutations this new variant was more efficient in accelerating the Kemp elimination than any of the previously designed Kemp eliminases. Of particular interest for the topic of this feature article is that such high activities were achieved mainly due to the conformational flexibility of the ancestral enzyme. This study further confirms that conformational heterogeneity should be explicitly taken into account for computationally designing novel enzyme functions.
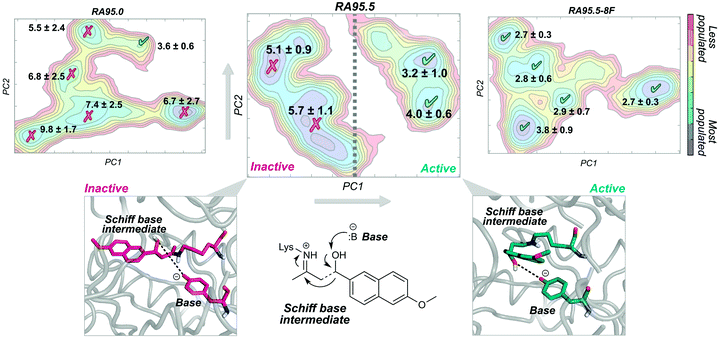
A nice example of the importance of enzyme conformational dynamics and the population shift concept for acquiring new function was reported for retro-aldolases (RA). The inside-out protocol was applied for generating these mechanistically complex RA enzymes.16e The designed RAs catalyse the cleavage of methodol substrate by a multistep reaction involving a Schiff base intermediate, between the catalytic lysine and the substrate (see Fig. 3). Hilvert and coworkers applied DE on the computationally designed RAs to enhance their modest activities towards methodol cleavage. One of the most important mutations was the introduction of a new catalytic lysine on the binding pocket in the second evolved variant (RA95.5). The introduced mutations completely remodelled the active site, allowing a better positioning of the Schiff base intermediate for catalysis. Recently, a highly active RA variant (RA95.5-8F) was generated after multiple rounds of DE, which exhibits comparable activities to those of natural class I aldolases.69a RA95.5-8F features a sophisticated catalytic tetrad responsible for the enhanced efficiency of the enzyme. These series of studies show the great power of DE in converting the original computational designs into highly proficient enzymes reaching activities similar to those of natural enzymes. It is worth mentioning that all these experiments were supported by X-ray structures.69a
The development of such a proficient RA enzyme, from the computational designs, prompted some of us to explore through microsecond timescale MD simulations the different RAs variants generated along the evolutionary pathway.13d The free energy landscape of the variants was reconstructed through the application of the PCA technique to the MD simulations (see Fig. 3). By measuring the distance between the base and the Schiff base intermediate in the different conformational states sampled along the MD simulations, we were able to distinguish catalytically inactive and active conformational states (Fig. 3). The least active variant (i.e. the computational design RA95.0) sampled only a few catalytically active conformations. The population of the catalytically active conformational states was raised along the evolutionary pathway. The most prominent shift was observed for the last evolved variant showing that all the conformations explored were catalytically competent (RA95.5-8F). The analysis of the conformational landscape of the variants highlighted that the conformational heterogeneity of the computational and less evolved variants was tuned to progressively stabilise the catalytically active conformational sub-states, which become major in the most evolved variants. Interestingly, the RA intermediate variants that exhibit a high degree of conformational flexibility were found to be highly promiscuous.16h,i
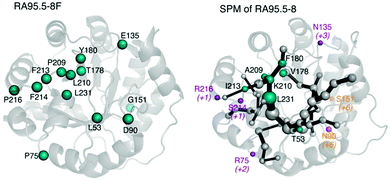
One of the biggest questions related to MD simulations is their predictive power, i.e. can we develop a MD-based tool capable of a priori identifying target residues to mutate for novel functionality? The alteration of enzyme function by introducing mutations is to some extent comparable to allosteric regulation, as mutations shift the populations of individual conformational sub-states of the enzyme. Given the high similitude of both processes we hypothesised that tools developed for studying allostery, (i.e. based on correlation measures from the MD simulations),78 could also be useful for enzyme design. Our group developed DynaComm.py python code that explores residue-by-residue correlated movements and inter-residue distances for predicting active site and distal positions that by mutation can induce a population shift.13d The output obtained is a shortest path map (SPM), which contains pairs of residues that have a higher contribution to the communication pathway. By comparing the outcome from SPM analysis with the positions mutated along the evolutionary pathway, we observed that our tool was able to predict most of the mutation points introduced in the different rounds of DE (see Fig. 4). Therefore, SPM is a very promising tool for the generation of “small but smart” libraries for the rational design of enzymes. The success of SPM in RAs may be related to the natural scaffold chosen, an indole 3-glycerol phosphate synthase, known to be an allosterically regulated enzyme. Of note is that designed RAs are (βα)8 barrel enzymes, which is a fold shared by many enzymes in the Protein Data Bank,78 suggesting that the application of our tool might be quite broad. We are now testing the possibility of applying SPM tool to engineer other allosterically-regulated enzymes.
b. Towards novel substrate scope
Substrate specificity is a crucial property of enzymes. Traditionally, the general idea that enzymes were restricted to accommodate only the ideal substrate was accepted, i.e. the famous lock and key model by Fischer.79 However, many natural enzymes are also capable of transforming a range of substrates related to its primary function, and thus present a broad substrate scope. Such enzymes are usually known as multi-specific enzymes.80In general, laboratory evolution is applied to increase the ability of enzymes to accept bulkier substrates that are usually the precursors of compounds of pharmacological interest. It has been postulated that bulky substrates have a higher dependency on the conformational dynamics of the binding site, in contrast to small substrates that are better recognised in more conformationally restricted active site cages.81 By mutation, the flexibility of the binding pocket can be modulated, (e.g. active site volume fluctuations), and conformational states more suitable for recognising and stabilizing a particular substrate can be populated. For instance, in the P450 enzyme family, CYP2A6 shows a quite narrow substrate scope, and is indeed quite rigid, whereas CYP3A4 is highly promiscuous and flexible.4 Particularly interesting is monoamine oxidase from Aspergillus niger (MAO-N) whose substrate scope was substantially enhanced by DE. The Turner lab evolved the wild-type enzyme providing a series of variants capable of accommodating a variety of small and bulky chiral amine substrates. These variants present mutations not only restricted at the hydrophobic cage of the enzyme, but also at remote positions that impact the catalytic activity of the enzyme.82
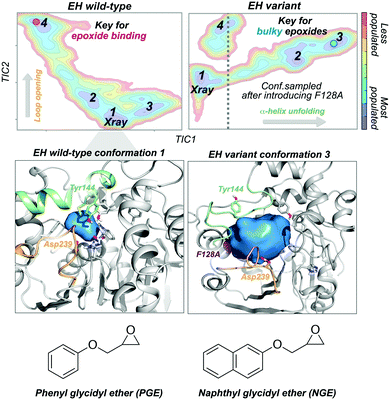
Epoxide hydrolases (EH) have been widely explored for engineering substrate selectivity. In this regard, Kong and coworkers were able to expand Bacillus megaterium EH (BmEH) substrate scope towards more sterically demanding epoxide substrates by introducing single mutations at positions located near the active site.83 EH enzymes catalyse the enantioselective hydrolysis of racemic epoxides to their corresponding vicinal diol. BmEH has attracted an increasing interest due to its (R)-selectivity towards phenyl glycidyl ether (PGE) substrates,84 but also because some of its engineered variants display promising activities towards the propranolol precursor (i.e. naphthyl glycidyl ether, NGE).83 Because of the aforementioned, some of us decided to explore the conformational heterogeneity of BmEH wild-type and two single point variants using microsecond timescale MD simulations. We have recently observed how mutations introduced in non-catalytic positions of BmEH lead to relevant conformational rearrangements that are responsible for the acceptance of pharmacologically relevant bulky substrates. Using tICA as a dimensional reduction technique, we constructed the associated free energy landscape revealing that the wild-type enzyme can display four major conformational states.85 The analysis of these conformational states in combination with active site volume calculations, provided evidence that the most populated wild-type conformations, in which the catalytic machinery is well-positioned for catalysis,86 present small active site pocket volumes (see Fig. 5). However, interesting conformational changes were observed in higher in energy conformational states. Especially important is the dynamic behaviour of a loop containing one of the catalytic Asp239 that is able to adopt an open conformation, which leads to substantially wider active site volumes. We hypothesised that this conformational state, not previously reported in the literature, plays a key role in binding the phenyl glycidyl ether (PGE) substrate. In contrast to BmEH natural enzyme, single mutations introduced in the variants induced an extra partial disorder on some of the α-helices that surround the active site pocket of the enzyme (particularly important is the α-helix that contains the catalytic Tyr144). Interestingly, this mutation-induced disorder in combination with the catalytic Asp239 loop opening seem to be key for the acceptance of bulkier epoxides (i.e. NGE) in these engineered variants (see Fig. 5).
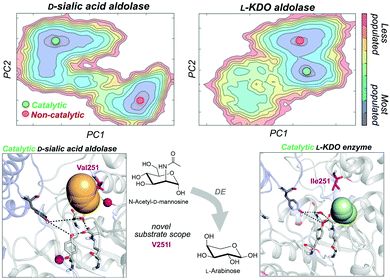
As noted in the introduction, DE experiments usually result in the insertion of multiple remote mutations from the active site.13c,69 In most cases, the direct effect of distal mutations on the catalytic properties of the enzyme is hard to rationalise. In a very recent study, some of us explored how distal mutations introduced via DE converted a D-sialic acid aldolase into an L-KDO aldolase.87D-Sialic acid aldolase is a dimeric enzyme complex that catalyses the reversible aldol reaction of N-acetyl-D-mannosamine (ManNAc) and pyruvate to produce D-sialic acid via an ordered sequential Bi-Uni kinetic mechanism. The engineered L-KDO enzyme variant accepts the smaller L-arabinose substrate to perform the reaction.
We explored the free energy landscape of both D-sialic and L-KDO aldolase and identified that distal mutations led to a population shift in the conformational states sampled.88 In both enzymes, only one of the two conformational states displayed an active site well pre-organised for catalysis (see Fig. 6). Most importantly, the analysis of substrate accessibility, active site interactions, and tunnel calculations on the conformational states sampled by the enzymes provided new insights into the change of specificity induced by mutation. Interestingly, the conformational states of L-KDO aldolase present much narrower active site and substrate access tunnels, which induce a change in the substrate scope of the enzyme. In the L-KDO aldolase, the access of the bulkier natural substrate into the enzyme active site is substantially more hindered, as shown by the computed substrate access barriers on the different conformational states. Of particular importance is the distal mutation introduced at V251 position, which is located at the bottleneck of the substrate access channel. Remarkably, among all introduced mutations in the DE experiment mutation, V251I was shown to play the most important role.89
c. Towards novel enantioselectivity
Natural enantioselective enzymes evolved to act on pro-chiral substrates for precisely yielding the optically pure enantiomer requested. Even though enzymes exist in multiple conformations, this conformational heterogeneity does not translate into a lack of enantioselectivity. In fact, the conformations explored by enzymes present stable binding pocket conformations that favour the formation of only one particular enantiomer. In this dynamic view of enzymes, reversing their enantioselectivity requires the introduction of mutations to alter the conformational energy landscape, which should preferentially favour the formation of the desired enantiomer.A powerful experimental method to enhance enantioselectivity and to expand substrate scope consists of a semi-rational DE approach applying iterative saturation mutagenesis (ISM) on a reduced set of relevant active site amino acids (CASTing).90 Second-sphere and distal mutations can also lead to a re-shaped binding pocket through allosteric effects.90c Theoretical QM/MM calculations and MD simulations are promising tools to discern the factors governing the improvement in enzyme enantioselectivity on a molecular level.13b Most of the computational evaluation studies are based on quantifying the frequency of the catalytically productive pro-(S) and pro-(R) orientations, which can be done by monitoring some selected angles and distances between the substrate and important active site residues along the MD simulations.65,91 By combining computational design with short MD simulations, Janssen and Baker successfully (re)designed the active site of an epoxide hydrolase obtaining enhanced enantioselectivities.65 Recent studies have shown that the analysis of enzyme structure flexibility (through root mean square fluctuation, RMSF) along MD simulations can be used to identify key functionality in loop regions adjacent to the binding pocket.91c,92 By modulating the conformational dynamics of these loops the reversal of enantioselectivity can be achieved.92b
One of the most explored enzymes for the reversal of enantioselectivity are alcohol dehydrogenases (ADHs). ADHs are zinc-dependent enzymes that use NAD(P)H as a cofactor, which delivers its hydride ion to the carbonyl group on the Re or Si-face of the pro-chiral ketone substrate yielding the corresponding (S) or (R)-alcohol (see Scheme 1).
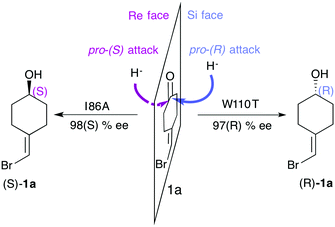 | ||
| Scheme 1 Representation of the pro-(R) and pro-(S) hydride attack for substrate 1a, together with the experimentally reported enantioselectivity of the engineered variants TbADHW110T and TbADHI86A by Reetz and coworkers.93 | ||
In an inspiring study from Lamed and coworkers, the active site shape of a thermophilic ADH enzyme from Thermoethanolicus brockii (TbSADH) was speculated. They suggested that its structure would consist of two differently-sized active site pockets, one being larger than the other to accommodate the bulkier alkyl group of the pro-chiral ketone substituent.94 Interestingly, this hypothesis was later confirmed with the resolution of the crystal structure.95 Phillips rational site-specific mutagenesis studies indeed reported that by changing the size of the active site pockets the enantioselectivity and the substrate scope of the enzyme can be modulated.96 Reetz and coworkers successfully engineered the enantioselectivity of TbSADH on a rich array of substrates by applying CASTing, guided by the available crystal structure and Phillips studies.93,97
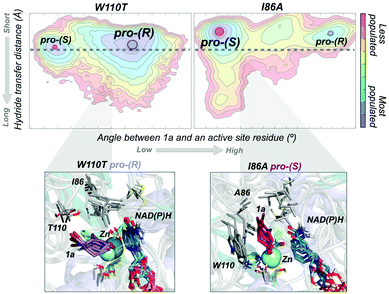
In most experimental studies published, W110 and I86 positions located at the active site have been found to be key for enhancing the activity and reversing the enantioselectivity towards diverse bulky ketones.93,96–98 We hypothesised that these single point mutations might induce a significant shift on the conformations sampled by the enzyme, which may enable the accommodation of non-natural substrates and preferentially favour the formation of one enantiomer over the other. To shed further light on the enhanced enantioselectivity contribution of these two mutations, we decided to evaluate the conformational dynamics of TbSADH wild-type, and the singly-mutated TbSADHW110T and TbSADHI86A variants in the presence of the pro-chiral ketone 4-alkediene cyclohexanone (1a, see Scheme 1) studied by Reetz and coworkers.93 Experimentally, it was found that TbSADH is able to produce the corresponding (R)-alcohol but only with modest enantioselectivity (66 (R) % ee). In contrast, TbSADHW110T exhibited (R)-enantioselectivity with 97 (R) % ee, whereas TbSADHI86A displayed reversed enantioselectivity with 98 (S) % ee.93 Our MD simulations constrained the substrate 1a bound to the Zn metal ion by imposing a force constant within the bonded model.91b,99 This approach allows us to rationalise the preferences of the accommodation of 1a in the active site along the simulation time. MD simulations coupled to active site volume calculations with POVME100 and the analysis of the most relevant non-covalent interactions with NCIplot101 permits to elucidate how favourable are the pro-(R) and pro-(S) conformations.91b
The conformational states sampled by the wild-type enzyme can position 1a in a catalytically competent orientation for both pro-(R) and pro-(S) hydride transfer, thus leading to a poor enantioselectivity. The substitution of W110 by threonine alters the large binding pocket of the conformational states sampled, becoming even wider (see Fig. 7). The extra space released after mutation stabilises those conformational states that adopt the catalytically productive pro-(R) positioning of the ketone. In contrast, the substitution of I86 by alanine enlarges the small binding pocket, thus favouring the population of those conformational states that better accommodate the pro-(S) productive orientation of 1a (see Fig. 7). The analysis of the non-covalent interactions occurring on the most populated conformational states sampled revealed how the active site pocket is remodelled to better stabilise the pro-(S) or pro-(R) orientations.91b These recent advances highlight the feasibility of MD simulations coupled with other computational tools for the engineering of natural enzyme active sites for enhanced enantioselectivity.
5. Conclusions and perspectives
As anticipated by Tokuriki and Tawfik a few years ago, conformational dynamism and evolvability are highly intertwined.4 This feature article provides multiple examples highlighting the key role played by the enzyme conformational dynamics for its function, specificity, and enantioselectivity, but also for its evolvability. Laboratory and naturally evolved enzyme variants have taught us that rarely populated, high in energy conformational states can be gradually enriched, becoming predominant in the most evolved variants. In other words, unexpected enzyme capabilities, related to hidden conformational states, can override natural enzyme functions by introducing mutations to enhance their relative populations.Recent studies on ancestral enzyme reconstruction have also provided key information on how evolution has achieved our actual enzymes.11a The large conformational heterogeneity found in ancestral enzymes and their ability to accelerate a wide range of promiscuous reactions contrasts with specialised enzymes that have low levels of promiscuity and restricted conformational dynamics.80 By taking advantage of the high level of conformational flexibility and promiscuity of ancestral enzymes, the generation of novel enzyme function can be achieved with a few mutations, as shown by Kamerlin, Sanchez-Ruiz, and coworkers with the Kemp elimination.77 We agree that the Kemp elimination is a rather simple reaction, but still the fact that the new variants based on ancestral scaffolds are more active than any of the previously evolved variants is highly appealing.
Current computational strategies are not capable of designing enzymes as active as the natural and/or laboratory-engineered variants.14a Semi-rational approaches have been shown to be more successful in this regard.2,16a In these semi-rational strategies, computational protocols are used to confer the enzyme some initial activity, which is then further enhanced by laboratory evolution. In this laboratory evolution, the catalytically competent conformational states are then gradually populated, as shown in many examples in this review. However, what if the enzyme conformational dynamics were taken more carefully into consideration in the computational protocol?
We believe that the field of computational enzyme design could benefit from the following considerations:
(i) Proper selection of the best enzyme scaffold for the target reaction. This should not be based on a static X-ray structure, but rather based on the conformational dynamics of the enzyme and how competent the different conformational states that already pre-exist in solution are for our target reaction and/or substrates. This, of course, requires a thorough analysis of the free energy landscape of many different enzymes, which has a high computational cost associated.
(ii) Mutation points should be determined for enhancing the populations of the competent conformational states and for optimising the chemical steps. Existing computational protocols can properly predict active site mutations for stabilising the transition states of the desired reactions. Improvements in the active site description of the enzyme with EVB and hybrid QM/MM approaches could bring more accurate predictions,13balbeit with a substantially higher computational cost. Directed evolution (DE) has shown that both active site and distal mutations are needed for enhanced activity. Given the vast number of possibilities that should be taken into account, distal mutations (i.e. allosteric networks) are not usually contemplated in computational enzyme design. As shown in this review, our group has developed new tools for the prediction and generation of “small but smart” libraries based on active site and distal mutations.13d
(iii) Improved enzyme ranking protocols based on machine learning algorithms. In most of current enzyme design computational protocols, there is no consensus on which are the most important computational parameters for enzymatic activity. The computational scores generated by the enzyme design software,13b together with the massive amount of data from the MD simulations of the engineered variants makes the selection of the best variants not straightforward. The application of chemoinformatic models and machine learning algorithms similarly as in the field of DE,69b could substantially improve the odds of finding the most beneficial mutations for activity.
Our hypothesis is that careful introduction of the above-mentioned considerations into available computational protocols, together with improvements in the available algorithms, methods, and hardware will bring the ‘emerging field’ of computational enzyme design one step forward.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. A. M. S. is grateful to the Spanish MINECO for a PhD fellowship (BES-2015-074964), E. S.-H. thanks the Generalitat de Catalunya for a PhD fellowship (2017-FI-B-00118), A. R. R. thanks the Generalitat de Catalunya for PhD fellowship (2015-FI-B-00165), J. I. F. is grateful to the European Community for Marie Curie fellowship (H2020-MSCA-IF-2016-753045), S. O. thanks the Spanish MINECO CTQ2014-59212-P, Ramón y Cajal contract (RYC-2014-16846), the European Community for CIG project (PCIG14-GA-2013-630978), and the funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (ERC-2015-StG-679001). We thank the Generalitat de Catalunya for the group emergent CompBioLab (2017 SGR-1707).Notes and references
- (a) S. J. Benkovic and S. Hammes-Schiffer, Science, 2003, 301, 1196–1202 CrossRef PubMed; (b) M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, Science, 2004, 303, 186–195 CrossRef PubMed; (c) S. Martí, M. Roca, J. Andrés, V. Moliner, E. Silla, I. Tuñón and J. Bertrán, Chem. Soc. Rev., 2004, 33, 98–107 RSC; (d) Z. D. Nagel and J. P. Klinman, Nat. Chem. Biol., 2009, 5, 543–550 CrossRef PubMed; (e) A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235 CrossRef PubMed.
- R. Blomberg, H. Kries, D. M. Pinkas, P. R. E. Mittl, M. G. Gruetter, H. K. Privett, S. L. Mayo and D. Hilvert, Nature, 2013, 503, 418–421 CrossRef PubMed.
- O. Khersonsky and D. S. Tawfik, Annu. Rev. Biochem., 2010, 79, 471–505 CrossRef PubMed.
- N. Tokuriki and D. S. Tawfik, Science, 2009, 324, 203–207 CrossRef PubMed.
- (a) D. D. Boehr, R. Nussinov and P. E. Wright, Nat. Chem. Biol., 2009, 5, 789–796 CrossRef PubMed; (b) G. G. Hammes, S. J. Benkovic and S. Hammes-Schiffer, Biochemistry, 2011, 50, 10422–10430 CrossRef PubMed.
- (a) G. Bhabha, J. Lee, D. C. Ekiert, J. Gam, I. A. Wilson, H. J. Dyson, S. J. Benkovic and P. E. Wright, Science, 2011, 332, 234–238 CrossRef PubMed; (b) R. G. Silva, A. S. Murkin and V. L. Schramm, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 18661–18665 CrossRef PubMed; (c) D. R. Glowacki, J. N. Harvey and A. J. Mulholland, Nat. Chem., 2012, 4, 169–176 CrossRef PubMed; (d) S. C. L. Kamerlin and A. Warshel, Proteins, 2010, 78, 1339–1375 Search PubMed.
- (a) S. Hammes-Schiffer and S. J. Benkovic, Annu. Rev. Biochem., 2006, 75, 519–541 CrossRef PubMed; (b) K. A. Henzler-Wildman, M. Lei, V. Thai, S. J. Kerns, M. Karplus and D. Kern, Nature, 2007, 450, 913–916 CrossRef PubMed; (c) S. Osuna, G. Jiménez-Osés, E. L. Noey and K. N. Houk, Acc. Chem. Res., 2015, 48, 1080–1089 CrossRef PubMed.
- (a) D. Kern and E. R. Zuiderweg, Curr. Opin. Struct. Biol., 2003, 13, 748–757 CrossRef PubMed; (b) L. D. Handley, B. Fuglestad, K. Stearns, M. Tonelli, R. B. Fenwick, P. R. Markwick and E. A. Komives, Sci. Rep., 2017, 7, 39575 CrossRef PubMed.
- (a) K. A. Henzler-Wildman, V. Thai, M. Lei, M. Ott, M. Wolf-Watz, T. Fenn, E. Pozharski, M. A. Wilson, G. A. Petsko, M. Karplus, C. G. Hübner and D. Kern, Nature, 2007, 450, 838–844 CrossRef PubMed; (b) A. Neu, U. Neu, A.-L. Fuchs, B. Schlager and R. Sprangers, Nat. Chem. Biol., 2015, 11, 697–704 CrossRef PubMed.
- B. M. Nestl and B. Hauer, ACS Catal., 2014, 4, 3201–3211 Search PubMed.
- (a) E. Campbell, M. Kaltenbach, G. J. Correy, P. D. Carr, B. T. Porebski, E. K. Livingstone, L. Afriat-Jurnou, A. M. Buckle, M. Weik, F. Hollfelder, N. Tokuriki and C. J. Jackson, Nat. Chem. Biol., 2016, 12, 944–950 CrossRef PubMed; (b) B. E. Clifton and C. J. Jackson, Cell Chem. Biol., 2016, 23, 236–245 CrossRef PubMed.
- J. M. Axe, E. M. Yezdimer, K. F. O’Rourke, N. E. Kerstetter, W. You, C.-e. A. Chang and D. D. Boehr, J. Am. Chem. Soc., 2014, 136, 6818–6821 CrossRef PubMed.
- (a) M. Orozco, Chem. Soc. Rev., 2014, 43, 5051–5066 RSC; (b) A. Romero-Rivera, M. Garcia-Borràs and S. Osuna, Chem. Commun., 2017, 53, 284–297 RSC; (c) G. Jiménez-Osés, S. Osuna, X. Gao, M. R. Sawaya, L. Gilson, S. J. Collier, G. W. Huisman, T. O. Yeates, Y. Tang and K. N. Houk, Nat. Chem. Biol., 2014, 10, 431–436 CrossRef PubMed; (d) A. Romero-Rivera, M. Garcia-Borràs and S. Osuna, ACS Catal., 2017, 7, 8524–8532 CrossRef PubMed.
- (a) G. Kiss, N. Çelebi-Ölçüm, R. Moretti, D. Baker and K. N. Houk, Angew. Chem., Int. Ed., 2013, 52, 5700–5725 CrossRef PubMed; (b) D. N. Bolon and S. L. Mayo, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14274–14279 CrossRef PubMed.
- (a) P. A. Romero and F. H. Arnold, Nat. Rev. Mol. Cell Biol., 2009, 10, 866–876 CrossRef PubMed; (b) C. Jaeckel, P. Kast and D. Hilvert, Annu. Rev. Biophys., 2008, 37, 153–173 CrossRef PubMed; (c) H. Renata, Z. J. Wang and F. H. Arnold, Angew. Chem., Int. Ed., 2015, 54, 3351–3367 CrossRef PubMed.
- (a) L. Jiang, E. A. Althoff, F. R. Clemente, L. Doyle, D. Röthlisberger, A. Zanghellini, J. L. Gallaher, J. L. Betker, F. Tanaka, C. F. Barbas, III, D. Hilvert, K. N. Houk, B. L. Stoddard and D. Baker, Science, 2008, 319, 1387–1391 CrossRef PubMed; (b) D. Röthlisberger, O. Khersonsky, A. M. Wollacott, L. Jiang, J. DeChancie, J. Betker, J. L. Gallaher, E. A. Althoff, A. Zanghellini, O. Dym, S. Albeck, K. N. Houk, D. S. Tawfik and D. Baker, Nature, 2008, 453, 190–195 CrossRef PubMed; (c) L. Giger, S. Caner, R. Obexer, P. Kast, D. Baker, N. Ban and D. Hilvert, Nat. Chem. Biol., 2013, 9, 494–498 CrossRef PubMed; (d) O. Khersonsky, G. Kiss, D. Roethlisberger, O. Dym, S. Albeck, K. N. Houk, D. Baker and D. S. Tawfik, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10358–10363 CrossRef PubMed; (e) E. A. Althoff, L. Wang, L. Jiang, L. Giger, J. K. Lassila, Z. Wang, M. Smith, S. Hari, P. Kast, D. Herschlag, D. Hilvert and D. Baker, Protein Sci., 2012, 21, 717–726 CrossRef PubMed; (f) J. K. Lassila, D. Baker and D. Herschlag, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4937–4942 CrossRef PubMed; (g) R. Obexer, S. Studer, L. Giger, D. M. Pinkas, M. G. Gruetter, D. Baker and D. Hilvert, ChemCatChem, 2014, 6, 1043–1050 CrossRef; (h) X. Garrabou, T. Beck and D. Hilvert, Angew. Chem., Int. Ed., 2015, 54, 5609–5612 CrossRef PubMed; (i) X. Garrabou, B. I. M. Wicky and D. Hilvert, J. Am. Chem. Soc., 2016, 138, 6972–6974 CrossRef PubMed.
- (a) Y. Kipnis and D. Baker, Protein Sci., 2012, 21, 1388–1395 CrossRef PubMed; (b) H. Kries, R. Blomberg and D. Hilvert, Curr. Opin. Chem. Biol., 2013, 17, 221–228 CrossRef PubMed.
- (a) J. A. Davey and R. A. Chica, Protein Sci., 2012, 21, 1241–1252 CrossRef PubMed; (b) D. J. Mandell and T. Kortemme, Curr. Opin. Biotechnol., 2009, 20, 420–428 CrossRef PubMed; (c) G. D. Friedland and T. Kortemme, Curr. Opin. Struct. Biol., 2010, 20, 377–384 CrossRef PubMed; (d) J. A. Davey, A. M. Damry, N. K. Goto and R. A. Chica, Nat. Chem. Biol., 2017, 13, 1280–1285 CrossRef PubMed; (e) R. Otten, L. Liu, L. R. Kenner, M. W. Clarkson, D. Mavor, D. S. Tawfik, D. Kern and J. S. Fraser, Nat. Commun., 2018, 9, 1314 CrossRef PubMed.
- E. C. Campbell, G. J. Correy, P. D. Mabbitt, A. M. Buckle, N. Tokuriki and C. J. Jackson, Curr. Opin. Struct. Biol., 2018, 50, 49–57 CrossRef PubMed.
- (a) A. Dashti, P. Schwander, R. Langlois, R. Fung, W. Li, A. Hosseinizadeh, H. Y. Liao, J. Pallesen, G. Sharma, V. A. Stupina, A. E. Simon, J. D. Dinman, J. Frank and A. Ourmazd, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17492–17497 CrossRef PubMed; (b) J. Frank and A. Ourmazd, Methods, 2016, 100, 61–67 CrossRef PubMed.
- A. J. Baldwin and L. E. Kay, Nat. Chem. Biol., 2009, 5, 808–814 CrossRef PubMed.
- (a) M. Diez, B. Zimmermann, M. Borsch, M. Konig, E. Schweinberger, S. Steigmiller, R. Reuter, S. Felekyan, V. Kudryavtsev, C. A. Seidel and P. Graber, Nat. Struct. Mol. Biol., 2004, 11, 135–141 CrossRef PubMed; (b) S. Myong, B. C. Stevens and T. Ha, Structure, 2006, 14, 633–643 CrossRef PubMed.
- D. M. Zuckerman, Annu. Rev. Biophys., 2011, 40, 41–62 CrossRef PubMed.
- M. Ringner, Nat. Biotechnol., 2008, 26, 303–304 CrossRef PubMed.
- (a) M. Ernst, F. Sittel and G. Stock, J. Chem. Phys., 2015, 143, 244114 CrossRef PubMed; (b) M. J. Holliday, C. Camilloni, G. S. Armstrong, M. Vendruscolo and E. Z. Eisenmesser, Structure, 2017, 25, 276–286 CrossRef PubMed.
- (a) Y. Naritomi and S. Fuchigami, J. Chem. Phys., 2013, 139, 215102 CrossRef PubMed; (b) G. Pérez-Hernández, F. Paul, T. Giorgino, G. De Fabritiis and F. Noé, J. Chem. Phys., 2013, 139, 015102 CrossRef PubMed.
- R. R. Coifman, S. Lafon, A. B. Lee, M. Maggioni, B. Nadler, F. Warner and S. W. Zucker, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7426–7431 CrossRef PubMed.
- F. Nuske, B. G. Keller, G. Pérez-Hernández, A. S. Mey and F. Noé, J. Chem. Theory Comput., 2014, 10, 1739–1752 CrossRef PubMed.
- M. Ceriotti, G. A. Tribello and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13023–13028 CrossRef PubMed.
- K. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef PubMed.
- J. A. McCammon, B. R. Gelin and M. Karplus, Nature, 1977, 267, 585–590 CrossRef PubMed.
- P. L. Freddolino, A. S. Arkhipov, S. B. Larson, A. McPherson and K. Schulten, Structure, 2006, 14, 437–449 CrossRef PubMed.
- D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. A. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Science, 2010, 330, 341–346 CrossRef PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, Science, 2011, 334, 517–520 CrossRef PubMed.
- R. O. Dror, H. F. Green, C. Valant, D. W. Borhani, J. R. Valcourt, A. C. Pan, D. H. Arlow, M. Canals, J. R. Lane, R. Rahmani, J. B. Baell, P. M. Sexton, A. Christopoulos and D. E. Shaw, Nature, 2013, 503, 295–299 CrossRef PubMed.
- A. C. Pan, D. W. Borhani, R. O. Dror and D. E. Shaw, Drug Discovery Today, 2013, 18, 667–673 CrossRef PubMed.
- M. J. Harvey, G. Giupponi and G. D. Fabritiis, J. Chem. Theory Comput., 2009, 5, 1632–1639 CrossRef PubMed.
- P. Eastman, M. S. Friedrichs, J. D. Chodera, R. J. Radmer, C. M. Bruns, J. P. Ku, K. A. Beauchamp, T. J. Lane, L. P. Wang, D. Shukla, T. Tye, M. Houston, T. Stich, C. Klein, M. R. Shirts and V. S. Pande, J. Chem. Theory Comput., 2013, 9, 461–469 CrossRef PubMed.
- R. Salomon-Ferrer, A. W. Gotz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef PubMed.
- S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef PubMed.
- (a) S. Olsson and F. Noé, J. Am. Chem. Soc., 2017, 139, 200–210 CrossRef PubMed; (b) J. H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schutte and F. Noé, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- N. Plattner and F. Noé, Nat. Commun., 2015, 6, 7653 CrossRef PubMed.
- M. M. Sultan, R. A. Denny, R. Unwalla, F. Lovering and V. S. Pande, Sci. Rep., 2017, 7, 15604 CrossRef PubMed.
- S. C. Dodani, G. Kiss, J. K. Cahn, Y. Su, V. S. Pande and F. H. Arnold, Nat. Chem., 2016, 8, 419–425 CrossRef PubMed.
- U. H. E. Hansmann, Chem. Phys. Lett., 1997, 281, 140–150 CrossRef.
- (a) P. H. Nguyen, G. Stock, E. Mittag, C. K. Hu and M. S. Li, Proteins, 2005, 61, 795–808 CrossRef PubMed; (b) J. W. Pitera and W. Swope, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7587–7592 CrossRef PubMed.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef PubMed.
- Y. Miao, F. Feixas, C. Eun and J. A. McCammon, J. Comput. Chem., 2015, 36, 1536–1549 CrossRef PubMed.
- P. R. Markwick and J. A. McCammon, Phys. Chem. Chem. Phys., 2011, 13, 20053–20065 RSC.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef PubMed.
- D. Granata, C. Camilloni, M. Vendruscolo and A. Laio, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6817–6822 CrossRef PubMed.
- G. Saladino and F. L. Gervasio, Curr. Opin. Struct. Biol., 2016, 37, 108–114 CrossRef PubMed.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef.
- N. Bansal, Z. Zheng, L. F. Song, J. Pei and K. M. Merz, Jr., J. Am. Chem. Soc., 2018, 140, 5434–5446 CrossRef PubMed.
- (a) S. Gianni, J. Dogan and P. Jemth, Biophys. Chem., 2014, 189, 33–39 CrossRef PubMed; (b) C.-J. Tsai, B. Ma and R. Nussinov, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9970–9972 CrossRef PubMed; (c) B. Ma, M. Shatsky, H. J. Wolfson and R. Nussinov, Protein Sci., 2002, 11, 184–197 CrossRef PubMed.
- D. E. Koshland, Proc. Natl. Acad. Sci. U. S. A., 1958, 44, 98–104 CrossRef.
- A. D. Vogt and E. D. Cera, Biochemistry, 2012, 51, 5894–5902 CrossRef PubMed.
- J. Monod, J. Wyman and J.-P. Changeux, J. Mol. Biol., 1965, 12, 88–118 CrossRef PubMed.
- M. Kovermann, C. Grundstrom, A. E. Sauer-Eriksson, U. H. Sauer and M. Wolf-Watz, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6298–6303 CrossRef PubMed.
- B. Ma and R. Nussinov, Nat. Chem. Biol., 2016, 12, 890–891 CrossRef PubMed.
- S. M. C. Gobeil, C. M. Clouthier, J. Park, D. Gagné, A. M. Berghuis, N. Doucet and J. N. Pelletier, Chem. Biol., 2014, 21, 1330–1340 CrossRef PubMed.
- G. Kiss, D. Röthlisberger, D. Baker and K. N. Houk, Protein Sci., 2010, 19, 1760–1773 CrossRef PubMed.
- H. J. Wijma, R. J. Floor, S. Bjelic, S. J. Marrink, D. Baker and D. B. Janssen, Angew. Chem., Int. Ed., 2015, 54, 3726–3730 CrossRef PubMed.
- F. Ding and N. V. Dokholyan, PLoS Comput. Biol., 2006, 2, 725–733 Search PubMed.
- B. A. Amrein, F. Steffen-Munsberg, I. Szeler, M. Purg, Y. Kulkarni and S. C. Kamerlin, IUCrJ, 2017, 4, 50–64 Search PubMed.
- (a) B. Karasulu and W. Thiel, ACS Catal., 2015, 5, 1227–1239 CrossRef; (b) F. Gan, R. Liu, F. Wang and P. G. Schultz, J. Am. Chem. Soc., 2018, 140, 3829–3832 CrossRef PubMed.
- (a) R. Obexer, A. Godina, X. Garrabou, P. R. E. Mittl, D. Baker, A. D. Griffiths and D. Hilvert, Nat. Chem., 2017, 9, 50–56 Search PubMed; (b) A. Currin, N. Swainston, P. J. Day and D. B. Kell, Chem. Soc. Rev., 2015, 44, 1172–1239 RSC.
- U. Doshi, M. J. Holliday, E. Z. Eisenmesser and D. Hamelberg, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4735–4740 CrossRef PubMed.
- K. L. Morley and R. J. Kazlauskas, Trends Biotechnol., 2005, 23, 231–237 CrossRef PubMed.
- K. Gunasekaran, B. Ma and R. Nussinov, Proteins, 2004, 57, 433–443 CrossRef PubMed.
- P.-S. Huang, S. E. Boyken and D. Baker, Nature, 2016, 537, 320 CrossRef PubMed.
- F. Richter, A. Leaver-Fay, S. D. Khare, S. Bjelic and D. Baker, PLoS One, 2011, 6, e19230 Search PubMed.
- (a) I. V. Korendovych, D. W. Kulp, Y. Wu, H. Cheng, H. Roder and W. F. DeGrado, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6823–6827 CrossRef PubMed; (b) M. Merski and B. K. Shoichet, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16179–16183 CrossRef PubMed.
- (a) O. Khersonsky, D. Röthlisberger, O. Dym, S. Albeck, C. J. Jackson, D. Baker and D. S. Tawfik, J. Mol. Biol., 2010, 396, 1025–1042 CrossRef PubMed; (b) O. Khersonsky, D. Röthlisberger, A. M. Wollacott, P. Murphy, O. Dym, S. Albeck, G. Kiss, K. N. Houk, D. Baker and D. S. Tawfik, J. Mol. Biol., 2011, 407, 391–412 CrossRef PubMed; (c) H. K. Privett, G. Kiss, T. M. Lee, R. Blomberg, R. A. Chica, L. M. Thomas, D. Hilvert, K. N. Houk and S. L. Mayo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 3790–3795 CrossRef PubMed; (d) R. Blomberg, H. Kries, D. M. Pinkas, P. R. Mittl, M. G. Grutter, H. K. Privett, S. L. Mayo and D. Hilvert, Nature, 2013, 503, 418–421 CrossRef PubMed.
- V. A. Risso, S. Martinez-Rodriguez, A. M. Candel, D. M. Krüger, D. Pantoja-Uceda, M. Ortega-Muñoz, F. Santoyo-Gonzalez, E. A. Gaucher, S. C. L. Kamerlin, M. Bruix, J. A. Gavira and J. M. Sanchez-Ruiz, Nat. Commun., 2017, 8, 16113 CrossRef PubMed.
- I. Rivalta, M. M. Sultan, N.-S. Lee, G. A. Manley, J. P. Loria and V. S. Batista, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1428–E1436 CrossRef PubMed.
- D. E. Koshland, Angew. Chem., Int. Ed., 1994, 33, 2375–2378 CrossRef.
- O. K. Tawfik and S. Dan, Annu. Rev. Biochem., 2010, 79, 471–505 CrossRef PubMed.
- E. M. Behiry, J. J. Ruiz-Pernia, L. Luk, I. Tuñón, V. Moliner and R. K. Allemann, Angew. Chem., Int. Ed., 2018, 57, 3128–3131 CrossRef PubMed.
- (a) S. Herter, F. Medina, S. Wagschal, C. Benhaïm, F. Leipold and N. J. Turner, Bioorg. Med. Chem., 2017, 30391–30397, DOI:10.1016/j.bmc.2017.07.023; (b) G. Li, P. Yao, R. Gong, J. Li, P. Liu, R. Lonsdale, Q. Wu, J. Lin, D. Zhu and M. T. Reetz, Chem. Sci., 2017, 8, 4093–4099 RSC; (c) D. Ghislieri, A. P. Green, M. Pontini, S. C. Willies, I. Rowles, A. Frank, G. Grogan and N. J. Turner, J. Am. Chem. Soc., 2013, 135, 10863–10869 CrossRef PubMed.
- X.-D. Kong, S. Yuan, L. Li, S. Chen, J.-H. Xu and J. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15717–15722 CrossRef PubMed.
- J. Zhao, Y. Y. Chu, A. T. Li, X. Ju, X. D. Kong, J. Pan, Y. Tang and J. H. Xu, Adv. Synth. Catal., 2011, 353, 1510–1518 CrossRef.
- E. Serrano-Hervás, G. Casadevall, M. Garcia-Borràs, F. Feixas and S. Osuna, Chem. – Eur. J., 2018 DOI:10.1002/chem.201801068.
- E. Serrano-Hervás, M. Garcia-Borràs and S. Osuna, Org. Biomol. Chem., 2017, 15, 8827–8835 Search PubMed.
- C.-C. Hsu, Z. Hong, M. Wada, D. Franke and C.-H. Wong, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9122–9126 CrossRef PubMed.
- S. Osuna, A. Romero-Rivera and J. Iglesias-Fernández, Eur. J. Org. Chem. DOI:10.1002/ejoc.201800103.
- C. Y. Chou, T. P. Ko, K. J. Wu, K. F. Huang, C. H. Lin, C. H. Wong and A. H. Wang, J. Biol. Chem., 2011, 286, 14057–14064 CrossRef PubMed.
- (a) Z. Sun, Y. Wikmark, J. E. Backvall and M. T. Reetz, Chemistry, 2016, 22, 5046–5054 CrossRef PubMed; (b) M. T. Reetz, M. Bocola, J. D. Carballeira, D. Zha and A. Vogel, Angew. Chem., Int. Ed., 2005, 44, 4192–4196 CrossRef PubMed; (c) M. T. Reetz, Angew. Chem., Int. Ed., 2011, 50, 138–174 CrossRef PubMed.
- (a) H. J. Wijma, S. J. Marrink and D. B. Janssen, J. Chem. Inf. Model., 2014, 54, 2079–2092 CrossRef PubMed; (b) M. A. Maria-Solano, A. Romero-Rivera and S. Osuna, Org. Biomol. Chem., 2017, 15, 4122–4129 RSC; (c) Z. Sun, L. Wu, M. Bocola, H. C. S. Chan, R. Lonsdale, X. D. Kong, S. Yuan, J. Zhou and M. T. Reetz, J. Am. Chem. Soc., 2018, 140, 310–318 CrossRef PubMed; (d) E. L. Noey, N. Tibrewal, G. Jiménez-Osés, S. Osuna, J. Park, C. M. Bond, D. Cascio, J. Liang, X. Zhang, G. W. Huisman, Y. Tang and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E7065–E7072 Search PubMed.
- (a) G. Li, M. A. Maria-Solano, A. Romero-Rivera, S. Osuna and M. T. Reetz, Chem. Commun., 2017, 53, 9454–9457 RSC; (b) B. Yang, H. J. Wang, W. Song, X. L. Chen, J. Liu, Q. L. Luo and L. M. Liu, ACS Catal., 2017, 7, 7593–7599 CrossRef.
- R. Agudo, G. D. Roiban and M. T. Reetz, J. Am. Chem. Soc., 2013, 135, 1665–1668 CrossRef PubMed.
- E. Keinan, E. K. Hafeli, K. K. Seth and R. Lamed, J. Am. Chem. Soc., 1986, 108, 162–169 CrossRef.
- (a) O. Kleifeld, A. Frenkel, O. Bogin, M. Eisenstein, V. Brumfeld, Y. Burstein and I. Sagi, Biochemistry, 2000, 39, 7702–7711 CrossRef PubMed; (b) C. Li, J. Heatwole, S. Soelaiman and M. Shoham, Proteins, 1999, 37, 619–627 CrossRef PubMed; (c) Y. Korkhin, A. J. Kalb, M. Peretz, O. Bogin, Y. Burstein and F. Frolow, J. Mol. Biol., 1998, 278, 967–981 CrossRef PubMed.
- (a) M. M. Musa, K. I. Ziegelmann-Fjeld, C. Vieille, J. G. Zeikus and R. S. Phillips, J. Org. Chem., 2007, 72, 30–34 CrossRef PubMed; (b) M. M. Musa, N. Lott, M. Laivenieks, L. Watanabe, C. Vieille and R. S. Phillips, ChemCatChem, 2009, 1, 89–93 CrossRef; (c) K. I. Ziegelmann-Fjeld, M. M. Musa, R. S. Phillips, J. G. Zeikus and C. Vieille, Protein Eng., Des. Sel., 2007, 20, 47–55 CrossRef PubMed; (d) M. M. Musa, J. M. Patel, C. M. Nealon, C. S. Kim, R. S. Phillips and I. Karume, J. Mol. Catal. B: Enzym., 2015, 115, 155–159 CrossRef.
- (a) Z. T. Sun, R. Lonsdale, A. Ilie, G. Y. Li, J. H. Zhou and M. T. Reetz, ACS Catal., 2016, 6, 1598–1605 CrossRef; (b) Z. T. Sun, G. Y. Li, A. Ilie and M. T. Reetz, Tetrahedron Lett., 2016, 57, 3648–3651 CrossRef.
- M. M. Musa, K. I. Ziegelmann-Fjeld, C. Vieille and R. S. Phillips, Org. Biomol. Chem., 2008, 6, 887–892 Search PubMed.
- (a) J. M. Seminario, Int. J. Quantum Chem., 1996, 60, 1271–1277 CrossRef; (b) L. Hu and U. Ryde, J. Chem. Theory Comput., 2011, 7, 2452–2463 CrossRef PubMed.
- J. D. Durrant, L. Votapka, J. Sorensen and R. E. Amaro, J. Chem. Theory Comput., 2014, 10, 5047–5056 CrossRef PubMed.
- (a) J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed; (b) E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |