Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The n → π* interaction in metal complexes†
Jorge
Echeverría

Departament de Química Inorgànica i Orgànica and Institut de Química Teòrica i Computacional IQTC-UB, Universitat de Barcelona, Martí i Franquès 1-11 08028, Barcelona, Spain. E-mail: Jorge.echeverria@qi.ub.es
First published on 2nd March 2018
Abstract
We report here, for the first time, the existence of n → π* interactions in transition metal complexes containing carbonyl ligands. This interaction has been observed to be surprisingly abundant and to stabilize precise molecular conformations that maximize the overlap between the donor and acceptor orbitals.
Noncovalent interactions are key in numerous chemical and biological processes.1–4 A particular type of weak interaction, called the n → π* interaction, has attracted much interest in recent years due to its unambiguous contribution to protein structure, but also because it dictates the conformation of a plethora of organic molecules.5,6 In a recent report, Das et al. have given further experimental evidence for an n → π* interaction in phenyl formate.7 According to the same authors, n → π* interactions can be roughly divided into two groups, n → π*Am (amide) and n → π*Ar (aromatic).6 One of the most common n → π*Am interactions is that involving two carbonyl groups with a C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance shorter than the sum of the van der Waals radii (3.27 Å).8 Such carbonyl–carbonyl interaction has the origin in the overlap of an oxygen lone pair (n) and a carbonyl empty antibonding orbital (π*) that involves some degree of electron delocalization of the first into the second.9 The energy release resulting from this orbital mixing (approximately 0.27 kcal mol−1)5 makes the interaction attractive. A great effort to unravel the nature and to understand the signatures of the n → π* interaction has been done by Raines group and others, who have extensively investigated its presence in lactones,10 collagen,11 prolines,12 aminobutyric acid,13 aspirin14 and peptoids.15
O distance shorter than the sum of the van der Waals radii (3.27 Å).8 Such carbonyl–carbonyl interaction has the origin in the overlap of an oxygen lone pair (n) and a carbonyl empty antibonding orbital (π*) that involves some degree of electron delocalization of the first into the second.9 The energy release resulting from this orbital mixing (approximately 0.27 kcal mol−1)5 makes the interaction attractive. A great effort to unravel the nature and to understand the signatures of the n → π* interaction has been done by Raines group and others, who have extensively investigated its presence in lactones,10 collagen,11 prolines,12 aminobutyric acid,13 aspirin14 and peptoids.15
However, carbonyl groups are not confined to organic compounds since they are commonly found acting as neutral ligands in transition metal complexes. A carbonyl ligand has a set of two empty π* orbitals that can, a priori, act as acceptors of electron density. In fact, carbonyl complexes have been widely used as electrophiles in catalysis.16,17 For instance, in Pd-catalyzed carbonylation reactions, a carbonyl can be attacked by an amine or alcohol to form an amide or ester group.18 Therefore, one could expect that inorganic carbonyls can participate in a n → π* interaction similarly to their organic analogues do. Here, by means of a combined structural and theoretical analysis, we show that carbonyl⋯carbonyl short contacts are in fact ubiquitous in metal complexes. Furthermore, behind such contacts there is an attractive interaction based on the electron delocalization of a lone pair of one carbonyl in the empty orbitals of the other, giving place to a n → π* interaction. These findings extend the realm of the n → π* interaction beyond the organic world and open the possibility of using it in metal complex design.
Within a metal complex, the donor group must have certain mobility to engage in the n → π* interaction, excluding thus another carbonyl ligand and pointing to candidates among more structurally complex ligands. A quick survey reveals that 3.5% of all crystal structures found in the Cambridge Structural Database (CSD)19 containing at least one metal–CO (terminal ligand) and one non-metal–CO moieties present intramolecular Metal–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(non-metal) contacts shorter than the sum of the van der Waals radii
O(non-metal) contacts shorter than the sum of the van der Waals radii 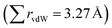 . These contacts do not show any marked directionality and only a few distances are shorter than 3 Å (see Fig. S1 in the ESI†), which is consistent with the low mobility of carbonyl ligands directly attached to the metal centre. If one looks for short non-metal–C
. These contacts do not show any marked directionality and only a few distances are shorter than 3 Å (see Fig. S1 in the ESI†), which is consistent with the low mobility of carbonyl ligands directly attached to the metal centre. If one looks for short non-metal–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O(metal) contacts, the percentage rises to 22.6%. Moreover, such contacts show a clear directionality with an O⋯C
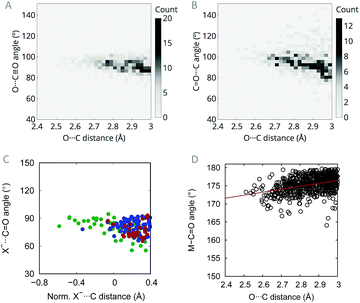
O(metal) contacts, the percentage rises to 22.6%. Moreover, such contacts show a clear directionality with an O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angle in the range 90–100° (Fig. 1A), close to the Burgi–Dunitz trajectory (O⋯C
O angle in the range 90–100° (Fig. 1A), close to the Burgi–Dunitz trajectory (O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angle = 107°), which is characteristic of the n → π* interaction.20,21 Here, the presence of the metal atom, arranged linearly with the acceptor carbonyl, involves either a ligand (e.g. in octahedral complexes) or a set of occupied orbitals (e.g. in square-planar complexes) in the region around approach angles of 107°, precluding in this way O⋯C
O angle = 107°), which is characteristic of the n → π* interaction.20,21 Here, the presence of the metal atom, arranged linearly with the acceptor carbonyl, involves either a ligand (e.g. in octahedral complexes) or a set of occupied orbitals (e.g. in square-planar complexes) in the region around approach angles of 107°, precluding in this way O⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O angles larger than 100–105°. Moreover, according to the Burgi–Dunitz trajectory, O⋯C
O angles larger than 100–105°. Moreover, according to the Burgi–Dunitz trajectory, O⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O angles around 100° should maximize the overlap between the donor lone pair and the acceptor empty π* orbitals in transition metal complexes. Previous studies of C
O angles around 100° should maximize the overlap between the donor lone pair and the acceptor empty π* orbitals in transition metal complexes. Previous studies of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O contacts in organic molecules have shown the absence of a trend in the dihedral angle between the two interacting carbonyl groups,9 a behaviour that has been reproduced here in the context of carbonyl complexes. In the present case, however, I have observed some degree of dependence between the C
O contacts in organic molecules have shown the absence of a trend in the dihedral angle between the two interacting carbonyl groups,9 a behaviour that has been reproduced here in the context of carbonyl complexes. In the present case, however, I have observed some degree of dependence between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C angle and the contact distance (Fig. 1B). However, the angle values are more variable than for the O⋯C
O⋯C angle and the contact distance (Fig. 1B). However, the angle values are more variable than for the O⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O (Fig. 1A) and, moreover, they can be imposed by the coordination geometries associated to different metal complexes.
O (Fig. 1A) and, moreover, they can be imposed by the coordination geometries associated to different metal complexes.
Previous studies have extensively investigated the nature of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O interactions demonstrating that a purely electrostatic picture cannot explain experimental and computational observations in protein residues.5 Inspired by Raines and co-workers, who analysed the origin of intimate interactions with carbonyl groups in organic compounds in terms of geometrical parameters,9 I have searched the CSD for short contacts where the donor is a halide anion (X−⋯C
O interactions demonstrating that a purely electrostatic picture cannot explain experimental and computational observations in protein residues.5 Inspired by Raines and co-workers, who analysed the origin of intimate interactions with carbonyl groups in organic compounds in terms of geometrical parameters,9 I have searched the CSD for short contacts where the donor is a halide anion (X−⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O; X = F, Cl, Br, I) to further test whether carbonyl··carbonyl interactions in transition metal complexes are of electrostatic dipolar nature. In this case, there is no dipole associated to the donor and, thus, if the interaction is dipolar one should not expect any directional short contact. Remarkably, it has been found for halides the same angular occurrence as that found when the donor is a carbonyl (Fig. 1C). This finding reinforces the orbital hypothesis since it indicates that a dipole is not needed in the nucleophile in order to establish an interaction.
O; X = F, Cl, Br, I) to further test whether carbonyl··carbonyl interactions in transition metal complexes are of electrostatic dipolar nature. In this case, there is no dipole associated to the donor and, thus, if the interaction is dipolar one should not expect any directional short contact. Remarkably, it has been found for halides the same angular occurrence as that found when the donor is a carbonyl (Fig. 1C). This finding reinforces the orbital hypothesis since it indicates that a dipole is not needed in the nucleophile in order to establish an interaction.
Another signature of the n → π* interaction is the pyramidalization of the R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety. Numerous studies have shown that short O⋯C distances along the Burgi–Dunitz trajectory involve the displacement of the electrophilic carbon out of the R2C
O moiety. Numerous studies have shown that short O⋯C distances along the Burgi–Dunitz trajectory involve the displacement of the electrophilic carbon out of the R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O plane, approaching in this way the acceptor to the donor in an incipient evolution toward an sp3 hybridization as a consequence of the orbital mixing.22 When studying terminal carbonyl ligands, one cannot analyse such pyramidalization angle, but a similar linearity loss in the M–C
O plane, approaching in this way the acceptor to the donor in an incipient evolution toward an sp3 hybridization as a consequence of the orbital mixing.22 When studying terminal carbonyl ligands, one cannot analyse such pyramidalization angle, but a similar linearity loss in the M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O framework could be expected for short O⋯C distances. Interestingly, a survey of the CSD discloses such dependence (Fig. 1D). While M–C
O framework could be expected for short O⋯C distances. Interestingly, a survey of the CSD discloses such dependence (Fig. 1D). While M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O angles are between 175 and 180° for O⋯C distances larger than 2.8 Å, for shorter distances the angles approach the 170–175° region. This change in the angle could also be due to a geometrical rearrangement to avoid repulsion between the lone pair donor orbital and the occupied π orbital of the carbonyl ligand, which also leads to a maximization of the n/π* orbital overlap.23 In any case, the observed angle variation, in one direction or the other, points toward some orbital involvement in the carbonyl⋯carbonyl short contact.
O angles are between 175 and 180° for O⋯C distances larger than 2.8 Å, for shorter distances the angles approach the 170–175° region. This change in the angle could also be due to a geometrical rearrangement to avoid repulsion between the lone pair donor orbital and the occupied π orbital of the carbonyl ligand, which also leads to a maximization of the n/π* orbital overlap.23 In any case, the observed angle variation, in one direction or the other, points toward some orbital involvement in the carbonyl⋯carbonyl short contact.
Carbonyl ligands are neutral but they also shown some degree of polarization, presenting a region of charge depletion in the carbon atom while the terminal oxygen shows a charge accumulation. Accordingly, an electrostatic contribution to the carbonyl⋯carbonyl interaction could be expected accompanying the orbital delocalization. In the case of anionic compounds, this possible O∂−⋯C∂+ interaction should be diminished, leaving the n → π* mixing as the most important stabilizing factor. Remarkably, a nice example of an intimate carbonyl interaction within an anionic complex has been found in the crystal structure of a Pt(II) square-planar complex24 (Fig. 2A). In that crystal, there is an intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O contact at 2.87 Å, considerably shorter that the sum of the vdW radii. The representation of the molecular electrostatic potential of the anionic complex shows a negative surface around the whole molecule, but it is known that the presence of countercations in the crystal structure can significantly modify the MEP picture of the anionic complex.25 Moreover, the natural charge (NPA) at the carbonyl C atom is still positive, which allows some degree of electrostatic interaction with an electron-rich donor. An NBO analysis shows a stabilizing interaction involving a lone-pair of the donor O and an empty antibonding π orbital of the acceptor carbonyl (Fig. 2B) with an associated energy of 0.58 kcal mol−1. Notably, this energy falls within the range of previous n → π* interactions found in organic compounds.5,6
O contact at 2.87 Å, considerably shorter that the sum of the vdW radii. The representation of the molecular electrostatic potential of the anionic complex shows a negative surface around the whole molecule, but it is known that the presence of countercations in the crystal structure can significantly modify the MEP picture of the anionic complex.25 Moreover, the natural charge (NPA) at the carbonyl C atom is still positive, which allows some degree of electrostatic interaction with an electron-rich donor. An NBO analysis shows a stabilizing interaction involving a lone-pair of the donor O and an empty antibonding π orbital of the acceptor carbonyl (Fig. 2B) with an associated energy of 0.58 kcal mol−1. Notably, this energy falls within the range of previous n → π* interactions found in organic compounds.5,6
 | ||
| Fig. 2 (A) Short carbonyl⋯carbonyl contact found in the crystal structure of bis(triphenylphosphine)iminium carbonyl-dichloro-(3-(methoxycarbonyl)prop-2-en-2-yl)-platinum(II)24 (CSD refcode: GEMLUF) and (B) NBO results representing the overlap between the carbonyl n and π* orbitals. | ||
Carbonyl⋯carbonyl short contacts are also found in neutral metal complexes. In Fig. 3A, we represent the short O⋯C contact (2.89 Å) between a formate and a carbonyl ligand in a Fe(II) complex.26
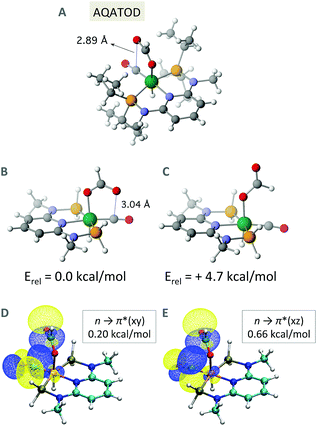 | ||
| Fig. 3 (A) Short carbonyl⋯carbonyl contact found in the crystal structure of carbonyl-(formato)-hydrido-(N,N′-(pyridine-2,6-diyl)bis(P,P-diisopropyl-N-methyl(phosphinous amide)))-iron (CSD refcode: AQATOD),26 (B and C) optimized geometries of the two isomers of the model system, and (D and E) NBO results showing the overlap between the p-type lone pair orbital of the donor carbonyl and the two π* empty orbitals of the acceptor carbonyl ligand. | ||
To further investigate intimate carbonyl interactions, a model system based on such molecule has been created. The isopropyl groups on the phosphines have been eliminated to avoid possible C–H⋯O interactions and allow free rotation of the upper formate. After full geometry optimization, the short O⋯C contact is still present at 3.04 Å (Fig. 3B). I have also built the model isomer in which there is no possibility of O⋯C contact by rotating 180° the Fe–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral (Fig. 3C). Interestingly, the zero-point corrected relative energies of the two isomers show that the interacting one is 4.7 kcal mol−1 more stable than the non-interacting one. It seems thus clear that such energy stabilization comes from the presence of the carbonyl⋯carbonyl short contact. Furthermore, its attractive nature is associated with donor–acceptor orbital interactions between lone pair and empty π* orbitals (Fig. 3D and E), i.e. a n → π* interaction. Here, conversely to what is observed in proteins and organic compounds, two perpendicular empty π* orbitals can participate as acceptors in the interaction. In fact, there are also two lone pairs involved in the interaction, one with more p and the other with more s character. The four interactions derived from the four orbitals mixing account for a total energy release of 1.08 kcal mol−1 according to the NBO analysis. From a geometrical point of view, the relative position of the two carbonyl groups (C–Fe–O–C dihedral = 40.5°) seems to maximize the overlap of the two lone pairs (s and p) with the two π* (xy and xz) orbitals. Note that in the case of a dipolar interaction such deviation of the dihedral angle from 0° should, in principle, not be observed.
O dihedral (Fig. 3C). Interestingly, the zero-point corrected relative energies of the two isomers show that the interacting one is 4.7 kcal mol−1 more stable than the non-interacting one. It seems thus clear that such energy stabilization comes from the presence of the carbonyl⋯carbonyl short contact. Furthermore, its attractive nature is associated with donor–acceptor orbital interactions between lone pair and empty π* orbitals (Fig. 3D and E), i.e. a n → π* interaction. Here, conversely to what is observed in proteins and organic compounds, two perpendicular empty π* orbitals can participate as acceptors in the interaction. In fact, there are also two lone pairs involved in the interaction, one with more p and the other with more s character. The four interactions derived from the four orbitals mixing account for a total energy release of 1.08 kcal mol−1 according to the NBO analysis. From a geometrical point of view, the relative position of the two carbonyl groups (C–Fe–O–C dihedral = 40.5°) seems to maximize the overlap of the two lone pairs (s and p) with the two π* (xy and xz) orbitals. Note that in the case of a dipolar interaction such deviation of the dihedral angle from 0° should, in principle, not be observed.
I have next analyzed substitution effects both in the interacting and the non-interacting units of the formate ligand of the model molecule. The results are shown in Table 1. The first observation is that replacing the oxygen donor with sulphur reinforces the n → π* interaction, increasing the associated energy in 0.71 kcal mol−1. The enhancing effect of including a better donor, but a poorer dipole, as S can be considered as evidence of the orbital nature of the n → π* interaction.5 The presence of S also leads to the most dramatic change in the M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O angle (171.9°), which could be due to the increased steric demand of the thiocarbonyl group. If we keep the same donor atom (O) and we modify the non-interacting unit, some changes are also observed. The presence of an electron-withdrawing group as CF3 attached to the donor carbonyl reduces its capability as a nucleophile,10 which is reflected in a decrease on the energy of the interaction (0.21 kcal mol−1 weaker). Conversely, attaching an electron-donor group as tert-butyl reinforces the n → π* interaction.
O angle (171.9°), which could be due to the increased steric demand of the thiocarbonyl group. If we keep the same donor atom (O) and we modify the non-interacting unit, some changes are also observed. The presence of an electron-withdrawing group as CF3 attached to the donor carbonyl reduces its capability as a nucleophile,10 which is reflected in a decrease on the energy of the interaction (0.21 kcal mol−1 weaker). Conversely, attaching an electron-donor group as tert-butyl reinforces the n → π* interaction.
| Int. unit | Non-int. unit | Norm. dO⋯C (Å) | O⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O angle (°) O angle (°) |
M–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O angle (°) O angle (°) |
E (2) ns → π* | E (2) np → π* |
|---|---|---|---|---|---|---|
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
–H | −0.23 | 104.8 | 175.4 | 0.22 | 0.86 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
–H | −0.12 | 101.7 | 171.9 | 0.26 | 1.53 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
–CF3 | −0.19 | 104.1 | 175.2 | 0.19 | 0.68 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
–CMe3 | −0.33 | 103.6 | 175.0 | 0.33 | 1.22 |
The geometry of the complex is also affected by the substituents at the non-interacting group. Remarkably, there is a nice linear correlation between the donor–acceptor (O⋯C) distance and the energy release due to the n → π* interaction (see Fig. S2 in the ESI†). For C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O donors, the interaction distances are between 0.19 and 0.33 Å shorter than the sum of the vdW radii. In the case of the sulphur (C
O donors, the interaction distances are between 0.19 and 0.33 Å shorter than the sum of the vdW radii. In the case of the sulphur (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S donor) the contact distance is only 0.12 Å shorter than the sum of the vdW radii, which could be attributed to the larger size of S orbitals and the consequent Pauli repulsion between the lone pair and the filled π orbital of the acceptor carbonyl.23 It is worth noting that all calculated donor⋯C
S donor) the contact distance is only 0.12 Å shorter than the sum of the vdW radii, which could be attributed to the larger size of S orbitals and the consequent Pauli repulsion between the lone pair and the filled π orbital of the acceptor carbonyl.23 It is worth noting that all calculated donor⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O angles (101–105°) are very close to the Burgi–Dunitz trajectory and in good agreement with the previous structural analysis.
O angles (101–105°) are very close to the Burgi–Dunitz trajectory and in good agreement with the previous structural analysis.
Summarizing, it has been reported here, for the first time, the existence of intramolecular n → π* interactions in transition metal complexes. These interactions are ubiquitous, stronger than similar ones in proteins and can determine the internal conformation of carbonyl complexes. It has also been shown that the interaction strength can be modulated by modification of the substituents attached to the donor carbonyl. These findings might have multiple consequences since metal complexes are important as molecular magnets, spin crossover systems or catalysts. For example, one of the Fe(II) complexes studied here (Fig. 3A), which is stabilized by a n → π* interaction, is a crucial intermediate in the catalytic hydrogenation of CO2.26 Moreover, I anticipate that n → π* interactions in metal compounds are not confined to intramolecular contacts, and intermolecular interactions might also play a role in the formation of solid-state structures. Future research could be directed to other common ligands similar to carbonyl as cyano and nitrosyl.
The author thanks the Spanish Ministerio de Economía y Competitividad (MINECO) for funding (IJC-2014-20097 and CTQ2015-64579-C3-1-P). The calculations were carried out using resources provided by the Centre de Supercomputació de Catalunya (CSUC).
Conflicts of interest
There are no conflicts to declare.Notes and references
- E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 CrossRef CAS PubMed.
- K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168 CrossRef.
- A. Bauzá, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517 CrossRef PubMed.
- Y. Zhao, Y. Cotelle, N. Sakai and S. Matile, J. Am. Chem. Soc., 2016, 138, 4270–4277 CrossRef CAS PubMed.
- R. W. Newberry and R. T. Raines, Acc. Chem. Res., 2017, 50, 1838–1846 CrossRef CAS PubMed.
- S. K. Singh and A. Das, Phys. Chem. Chem. Phys., 2015, 17, 9596–9612 RSC.
- S. K. Singh, K. K. Mishra, N. Sharma and A. Das, Angew. Chem., Int. Ed., 2016, 55, 7801–7805 CrossRef CAS PubMed.
- S. Alvarez, Dalton Trans., 2013, 42, 8617–8636 RSC.
- K. J. Kamer, A. Choudhary and R. T. Raines, J. Org. Chem., 2013, 78, 2099–2103 CrossRef PubMed.
- R. W. Newberry and R. T. Raines, ACS Chem. Biol., 2014, 9, 880–883 CrossRef CAS PubMed.
- L. E. Bretscher, C. L. Jenkins, K. M. Taylor, M. L. DeRider and R. T. Raines, J. Am. Chem. Soc., 2001, 123, 777–778 CrossRef CAS PubMed.
- R. W. Newberry, B. VanVeller, I. A. Guzei and R. T. Raines, J. Am. Chem. Soc., 2013, 135, 7843–7846 CrossRef CAS PubMed.
- S. Blanco, J. C. López, S. Mata and J. L. Alonso, Angew. Chem., Int. Ed., 2010, 49, 9187–9192 CrossRef CAS PubMed.
- C. Cabezas, J. L. Alonso, J. C. López and S. Mata, Angew. Chem., Int. Ed., 2012, 51, 1375–1378 CrossRef CAS PubMed.
- B. C. Gorske, B. L. Bastian, G. D. Geske and H. E. Blackwell, J. Am. Chem. Soc., 2007, 129, 8928–8929 CrossRef CAS PubMed.
- T. J. Mooibroek, L. Schoon, E. Bouwman and E. Drent, Chem. – Eur. J., 2011, 17, 13318–13333 CrossRef CAS PubMed.
- P. W. N. M. van Leeuwen, M. A. Zuideveld, B. H. G. Swennenhuis, Z. Freixa, P. C. J. Kamer, K. Goubitz, J. Fraanje, M. Lutz and A. L. Spek, J. Am. Chem. Soc., 2003, 125, 5523–5539 CrossRef CAS PubMed.
- X.-F. Wu, RSC Adv., 2016, 6, 83831–83837 RSC.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef PubMed.
- H. B. Burgi, J. D. Dunitz, J. M. Lehn and G. Wipff, Tetrahedron, 1974, 30, 1563–1572 CrossRef.
- H. B. Burgi, J. D. Dunitz and E. Shefter, J. Am. Chem. Soc., 1973, 95, 5065–5067 CrossRef.
- R. W. Newberry, G. J. Bartlett, B. VanVeller, D. N. Woolfson and R. T. Raines, Protein Sci., 2014, 23, 284–288 CrossRef PubMed.
- C. E. Jakobsche, A. Choudhary, S. J. Miller and R. T. Raines, J. Am. Chem. Soc., 2010, 132, 6651–6653 CrossRef PubMed.
- C. Allevi, L. Garlaschelli, M. C. Malatesta and F. Ganazzoli, J. Chem. Soc., Dalton Trans., 1988, 1949–1955 RSC.
- A. Bauzá, A. Frontera and T. J. Mooibroek, Nat. Commun., 2017, 8, 14522 CrossRef PubMed.
- F. Bertini, N. Gorgas, B. Stöger, M. Peruzzini, L. F. Veiros, K. Kirchner and L. Gonsalvi, ACS Catal., 2016, 6, 2889–2893 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details and Cartesian coordinates of all optimized structures. See DOI: 10.1039/c8cc00763b |
| This journal is © The Royal Society of Chemistry 2018 |