Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Giant exchange coupling and field-induced slow relaxation of magnetization in Gd2@C79N with a single-electron Gd–Gd bond†
G.
Velkos
 a,
D. S.
Krylov
a,
K.
Kirkpatrick
a,
D. S.
Krylov
a,
K.
Kirkpatrick
 b,
X.
Liu
b,
X.
Liu
 b,
L.
Spree
a,
A. U. B.
Wolter
a,
B.
Büchner
a,
H. C.
Dorn
b,
L.
Spree
a,
A. U. B.
Wolter
a,
B.
Büchner
a,
H. C.
Dorn
 *bc and
A. A.
Popov
*bc and
A. A.
Popov
 *a
*a
aLeibniz Institute for Solid State and Materials Research, Dresden 01069, Germany. E-mail: a.popov@ifw-dresden.de
bDepartment of Chemistry, Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24061, USA
cVirginia Tech Carilion Research Institute, Roanoke, Virginia 24016, USA. E-mail: hdorn@vt.edu
First published on 2nd March 2018
Abstract
Magnetic properties of the azafullerene Gd2@C79N are studied by SQUID magnetometry. The effective exchange coupling constant jGd,e between the Gd spins and the spin of unpaired electron residing on the single-electron Gd–Gd bond is determined to be 170 ± 10 cm−1. Low temperature AC measurements revealed field-induced millisecond-long relaxation of magnetization.
Coupling magnetic atoms into larger clusters is a viable strategy towards molecular magnets. This approach is very successful for transition metals, which can exhibit exchange interactions reaching tens or even hundreds of cm−1. In lanthanides, the 4f shells are rather compact, and the overlap of 4f-orbitals with other valence orbitals is very weak. As a result, exchange coupling constants in polynuclear lanthanide compounds rarely exceed 1 cm−1. Although even weak interactions strongly affect magnetic properties of polynuclear lanthanide molecular magnets at low temperatures, their vast majority still can be described as a combination of loosely bound spins, rather than a single giant-spin (the concept usually employed for transition metal clusters such as single molecule magnets {Mn12} or {Fe8}).1
The coupling can be enhanced by radical bridges. An exchange coupling of lanthanides with organic radicals (JLn,R) can reach several cm−1.2 The largest JGd,R values‡ were reported in Gd-nitroxide compounds (6.2 cm−1 in ref. 3a and −6.0 cm−1 in ref. 3b), and dinuclear Gd complexes with bridging radicals (−10 cm−1 for bipyrimidyl and −27 cm−1 for N23−).4 Yet, the lanthanide-radical couplings exceeding 5 cm−1 are rare and are usually considered as very strong.
Direct bonding between lanthanide atoms can potentially lead to much stronger coupling of their magnetic moments. Lanthanides are not known to form Ln–Ln bonds in molecular compounds, but carbon cages can stabilize otherwise non-existent species5 and enable formation of dimetallofullerenes (di-EMFs) with covalent Ln–Ln bonds in encapsulated metal dimers.6 A stabilization of single-electron metal–metal bonds in di-EMFs is well described for the fullerene C80-Ih. This cage usually acts as an acceptor of six electrons, which are transferred to the fullerene orbitals from metals, and forms closed-shell di-EMFs with early lanthanides. However, starting from the middle of the lanthanide row, the Ln2 dimers give only 5 electrons to C80-Ih, leaving one electron on the Ln–Ln bonding orbital.7 Such Ln2@C80 molecules are not stable because of the open-shell electronic structure of the fullerene. Their stable forms can be obtained by addition of a surplus electron,7a quenching the unpaired spin on the cage by an organic radical,6f,8 or by substitution of one carbon atom with nitrogen giving azafullerenes Ln2@C79N (Fig. 1).6a,b Once the fullerene cage is stabilized, these di-EMFs can be very stable molecules despite the presence of the single-electron metal–metal bond.
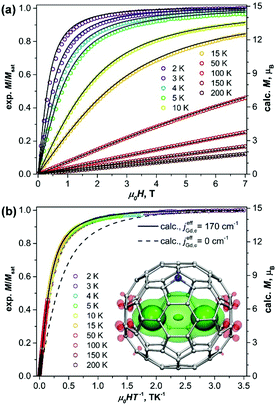 | ||
| Fig. 1 (a) Magnetization curves of Gd2@C79N measured at different temperatures. (b) Magnetization versus the quotient μ0HT−1. Dots are experimental points, solid lines are simulations using eqn (1) and the jeffGd,e value of 170 cm−1, the dash line in (b) is a simulation for the [Gd3+–e–Gd3+] system with non-interacting spins. The inset in (b) shows molecular structure and DFT-computed spin density distribution in Gd2@C79N (see footnote §) visualized with isovalues ±0.015 a.u. (solid) and ±0.0012 a.u. (semi-transparent). Three well-seen maxima of the spin density correspond to Gd atoms and unpaired electron spin (see also Fig. S3, ESI†). | ||
Magnetic interactions in di-EMFs featuring single-electron Gd–Gd bonds can be formally described by a three-center system [Gd3+–e–Gd3+] (see Fig. 1 for the spin-density distribution in Gd2@C79N [see footnote §]) with the spin Hamiltonian:
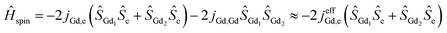 | (1) |
DFT computational studies showed giant ferromagnetic (FM) coupling between localized Gd spins and the unpaired electron spin with jGd,e values of 177 cm−1 in Gd2@C80−,9 181–184 cm−1 in Gd2@C80(CH2Ph),6f and 200 cm−1 in Gd2@C79N.10 The Gd–Gd coupling is antiferromagnetic and weak, on the order of −1 cm−1 or less, and its neglect gives the approximate form of eqn (1) with the effective coupling constant jeffGd,e. Thus, theory predicts that the lanthanide-radical coupling in di-EMFs is huge and is much larger than in any other lanthanide-radical compound studied so far. An EPR spectroscopic study of Gd2@C79N revealed the ground state with the spin S = 15/2,6a proving the FM coupling of all individual spins. The Dy-electron exchange coupling constant of jeffDy,e = 32 cm−1 was determined experimentally in Dy2@C80(CH2Ph), a single molecule magnet with a high blocking temperature of magnetization.6f Here, we report on the static and dynamic magnetic properties of Gd2@C79N (see footnote ¶) and analysis of the exchange coupling. When this manuscript was completed, Gao et al. reported the study of the quantum coherence in Gd2@C79N and determined the jGd,e value of 175 ± 10 cm−1, which is very close to the results of this work discussed below.11
Fig. 1 shows magnetization curves of Gd2@C79N measured at different temperatures. The compound exhibits typical paramagnetic behavior. The plot of the magnetization versus the quotient H/T (Fig. 1b) shows that the data measured at different temperatures overlays on a single curve, and only the lowest-temperature points deviate slightly. This proves that Gd2@C79N has very low magnetic anisotropy.
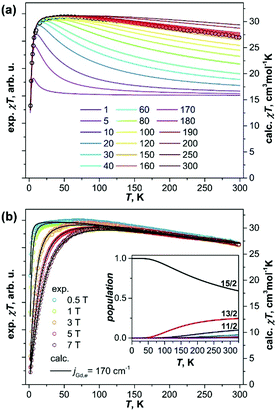
Fig. 2 plots the product χ·T measured at different temperatures in different constant fields. At low temperatures the χ·T values quickly reach the maximum (the temperature of the maximum depends on the magnetic field), then remain constant up to 50–100 K, followed by a slow almost linear decrease at higher temperatures. At 300 K, χ·T values drop to ca 90% of their 100 K counterparts (absolute values of χ·T cannot be determined precisely with the low mass of the fullerene available for the measurements). Such a temperature dependence of χ·T corresponds to the slowly decreasing magnetic moment, which is consistent with the large coupling predicted for Gd2@C79N.
To estimate the constant jeffGd,e, we simulated χ·T curves for the [Gd3+–e–Gd3+] system12 using the approximate Hamiltonian in eqn (1) with addition of Zeeman term, magnetic susceptibility was computed using exact fundamental equation for molecular magnetism. The g-factor of 1.978 and the positive sign of jeffGd,e are adopted from the EPR measurements,6a and the jeffGd,e values are varied from 1 to 300 cm−1. When jeffGd,e is small, the χ·T curves have a sharp peak at low temperature with a fast decay at higher temperature to the χ·T limit of the non-coupled system (16 cm3 mol−1 K). With the increase of jeffGd,e, the peak is growing and becomes less sharp, whereas the higher-temperature decay becomes less steep. It means, the temperature range in which the fully coupled spin system (χ·T = 31 cm3 mol−1 K) has the dominant contribution is increasing with jeffGd,e. Likewise, the decay of χ·T, caused by a thermal population of the lower-spin states, becomes more gradual because the gap between the high-spin ground state and lower-spin excited states is also increasing. The experimental χ·T curve in the field of 1 T agrees well with the curves simulated for the jeffGd,e values in the range of 160–180 cm−1 (Fig. 2a), in good agreement with DFT-predictions and recent report by Gao et al.11 More precise determination of the jeffGd,e constant is hardly possible because the variation of the computed curves within the interval is comparable to the experimental uncertainties. The constant of jeffGd,e = 170 cm−1 was then used to simulate χ·T curves measured in different fields (Fig. 2b) as well as to calculate magnetization curves. For both sets of data, very good agreement between experiment and theory is obtained (Fig. 1 and 2).
The spectrum of the approximate Hamiltonian in eqn (1) produced with the jeffGd,e constant of 170 cm−1 spans the energy range of 15jeffGd,e = 2550 cm−1. The eigenstates are grouped into 15 “giant-spin” states with S = 15/2, 13/2,…,1/2, 1/2, 3/2,…,13/2. The gaps between the states are all equal jeffGd,e except for the two S = 1/2 states with the energy gap of 2jeffGd,e. The states within each manifold are (2S + 1)-degenerate, but magnetic field lifts the degeneracy, and the 15-line EPR spectrum observed at low temperature6a corresponds to transitions within the S = 15/2 manifold with weak zero-field splitting. The inset in Fig. 2b shows temperature dependence of the spin populations. The only state to be considered below 50 K is the S = 15/2, hence the giant-spin approximation is valid at these temperatures. Magnetization curves computed using eqn (1) and for a single spin S = 15/2 show small deviations only above 100 K (Fig. S4, ESI†). The S = 13/2 manifold gains significant population above 50 K, and the S = 11/2 state should be also considered above 150 K, although the ground state is still the dominant one (>60%) up to room temperature. Thus, in the experimentally relevant temperature range, magnetic properties of Gd2@C79N are essentially determined by the S = 15/2, S = 13/2, and to a lesser extent S = 11/2 manifolds and their relative populations.
Eqn (1) does not take into account magnetic anisotropy, but the EPR measurements revealed very small ZFS parameter D of 70 mT.6a,11 Such a small value cannot be resolved in magnetization data (Fig. S5, ESI†), and thus cannot influence the jeffGd,e value. More important is the effect of the Gd–Gd coupling. The spectrum of the exact Hamiltonian in the eqn (1) computed with the constants jGd,Gd = −1 cm−1 and jGd,e = 170 cm−1 is similar to that of the approximate version with jeffGd,e = 170 cm−1, but the energy gaps between the spin states are reduced (Fig. S6, ESI†). The energies of the S = 13/2 and S = 11/2 states have become jGd,e + 14jGd,Gd and 2jGd,e + 26jGd,Gd, respectively, instead of jeffGd,e and 2jeffGd,e. Since the χ·T values are affected by the populations of only two-three lowest energy states, we conclude that the effective coupling constant estimated from the χ·T curves is related to the jGd,e value as jeffGd,e ≈ jGd,e + 14jGd,Gd. If the DFT-predicted negative sign of the jGd,Gd constant is correct, the real exchange coupling between Gd spins and the unpaired spin residing on the Gd–Gd bonding orbital is even larger than 170 cm−1. The structure of the Hamiltonian spectrum implies that when jGd,e is large, and jGd,Gd is too small to induce strong changes in the order of the energy levels as it is the case for Gd2@C79N, the fitting of jGd,e and jGd,Gd independently would be an ill-defined problem. The [Gd3+–N23−–Gd3+] complex with inner-sphere K+ ion is an example of the situation when two parameters can be determined independently.4c With the jGd,R and jGd,Gd constants of −27 and −2 cm−1, respectively, the effect of the antiferromagnetic Gd–Gd superexchange is sufficient to strongly alter the order of the spin states.
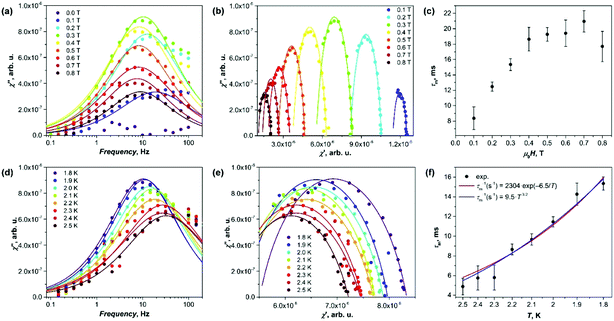
Although Gd is isotropic, millisecond-long field-induced relaxation of magnetization has been observed in some of its salt, single-chain magnets, and molecular magnets.13 Our AC susceptibility measurements showed that near 2 K and in the presence of the magnetic field, Gd2@C79N gives a signal in the out-of-phase susceptibility χ′′ (Fig. 3). Fig. 3a shows χ′′ curves obtained at 1.8 K with various DC magnetic fields between 0 and 0.8 T. Zero-field measurements did not give detectable χ′′ responses, but the peak emerged when the field of 0.1 T was applied. Its amplitude grows with the field till the maximum at 0.3 T, and then decreases again at higher fields. Fitting of the data with the generalized Debye model (Fig. 3b) gave relaxation times (τm), varying from 8 ms at 0.1 T to 18–22 ms in the field of 0.4–0.8 T (Fig. 3c).
The temperature dependence was measured in the field of 0.3 T between 1.8 and 2.5 K (Fig. 3d–f; the signal could not be measured reliably at higher temperature due to the amplifier disturbing the low-intensity signals at frequencies above 100 Hz). The relaxation times dropped from 16 ms at 1.8 K to 5 ms at 2.5 K. The temperature dependence of τm is shown in Fig. 3f with both exponential and power law fits. Both functions give a comparable agreement. The exponential dependence τm−1 = τ0−1 exp(−Ueff/T) corresponds to the Orbach relaxation mechanism with the barrier Ueff = 6.5 ± 0.5 K and τ0 = 4 ± 1 × 10−4 s. This Ueff value is larger than zero-field splitting of the S = 15/2 manifold estimated from EPR data (∼3 K), and Zeeman splitting in the field of 0.3 T (∼2.3 K).
The fit of experimental relaxation rates fitted with the power function τm−1 ∼ ATn gives the n value of 3.2 ± 0.2 (Fig. 3f). At low T, relaxation often follows the direct mechanism (τm−1 ∼ T), in which the spin flip is accompanied by the emission/absorption of the phonon with the frequency, matching the splitting of the spin levels.14 However, if the number of spins is much larger than the number of resonant phonons, the energy dissipation is hampered resulting in a phonon bottleneck,15 which elongates the relaxation with complex temperature dependence (τm−1 ∼ Tb, 1 ≤ b ≤ 4).16 Finally, the Raman mechanism with τm−1 ∼ T9 dependence for Kramers systems is plausible at higher temperatures.14 Thus, the value of n = 3.2 determined for Gd2@C79N may be an indication of the bottlenecked direct relaxation mechanism near 2 K, but in the view of significant uncertainties of the values this conclusion remains tentative. Earlier, the phonon bottleneck was often recognized as the most plausible reason for a long relaxation in several other Gd compounds.13b–f
To conclude, the giant exchange coupling between the localized 4f-spins of Gd and the spin of the unpaired electron residing on the Gd–Gd bond is found in Gd2@C79N. The exchange coupling constant jeffGd,e of 170 cm−1 is the largest constant ever observed for molecular lanthanide compounds. The inner space of the fullerene provides the perfect environment for unprecedented spin states of lanthanides.
The authors acknowledge the European Research Council under the European Union's Horizon 2020 programme (Grant No. 648295 “GraM3”) and Deutsche Forschungsgemeinschaft (grant PO 1602/4-1). K. Kirkpatrick acknowledges financial support from a Luther & Alice Hamlett Scholarship.
Conflicts of interest
There are no conflicts to declare.Notes and references
- (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS; (b) D. Gatteschi, R. Sessoli and A. Cornia, Chem. Commun., 2000, 725 RSC.
- (a) S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149 CrossRef CAS; (b) T. Gupta, T. Rajeshkumar and G. Rajaraman, Phys. Chem. Chem. Phys., 2014, 16, 14568 RSC.
- (a) T. Kanetomo, T. Yoshitake and T. Ishida, Inorg. Chem., 2016, 55, 8140 CrossRef CAS PubMed; (b) T. Kanetomo, T. Kihara, A. Miyake, A. Matsuo, M. Tokunaga, K. Kindo, H. Nojiri and T. Ishida, Inorg. Chem., 2017, 56, 3310 CrossRef CAS PubMed.
- (a) S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546 CrossRef CAS PubMed; (b) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538 CrossRef CAS PubMed; (c) K. R. Meihaus, J. F. Corbey, M. Fang, J. W. Ziller, J. R. Long and W. J. Evans, Inorg. Chem., 2014, 53, 3099 CrossRef CAS PubMed.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989 CrossRef CAS PubMed.
- (a) W. Fu, J. Zhang, T. Fuhrer, H. Champion, K. Furukawa, T. Kato, J. E. Mahaney, B. G. Burke, K. A. Williams, K. Walker, C. Dixon, J. Ge, C. Shu, K. Harich and H. C. Dorn, J. Am. Chem. Soc., 2011, 133, 9741 CrossRef CAS PubMed; (b) T. Zuo, L. Xu, C. M. Beavers, M. M. Olmstead, W. Fu, T. D. Crawford, A. L. Balch and H. C. Dorn, J. Am. Chem. Soc., 2008, 130, 12992 CrossRef CAS PubMed; (c) N. A. Samoylova, S. M. Avdoshenko, D. S. Krylov, H. R. Thompson, A. Kirkhorn, M. Rosenkranz, S. Schiemenz, F. Ziegs, A. U. B. Wolter, S. Yang, S. Stevenson and A. A. Popov, Nanoscale, 2017, 9, 7977 RSC; (d) A. A. Popov, S. M. Avdoshenko, A. M. Pendás and L. Dunsch, Chem. Commun., 2012, 48, 8031 RSC; (e) W. Shen, L. Bao, Y. Wu, C. Pan, S. Zhao, H. Fang, Y. Xie, P. Jin, P. Peng, F.-F. Li and X. Lu, J. Am. Chem. Soc., 2017, 139, 9979 CrossRef CAS PubMed; (f) F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed.
- (a) A. Velloth, Y. Imamura, T. Kodama and M. Hada, J. Phys. Chem. C, 2017, 121, 18169 CrossRef CAS; (b) Z. Wang, R. Kitaura and H. Shinohara, J. Phys. Chem. C, 2014, 118, 13953 CrossRef CAS.
- I. E. Kareev, V. P. Bubnov and E. B. Yagubskii, Russ. Chem. Bull., 2008, 57, 1486 CrossRef CAS.
- A. Mansikkamäki, A. A. Popov, Q. Deng, N. Iwahara and L. F. Chibotaru, J. Chem. Phys., 2017, 147, 124305 CrossRef PubMed.
- (a) F. Cimpoesu, B. Frecus, C. I. Oprea, H. Ramanantoanina, W. Urland and C. Daul, Mol. Phys., 2015, 113, 1712 CrossRef CAS; (b) G. Rajaraman, M. K. Singh and N. Yadav, Chem. Commun., 2015, 51, 17732 RSC.
- Z. Hu, B.-W. Dong, Z. Liu, J.-J. Liu, J. Su, C. Yu, J. Xiong, D.-E. Shi, Y. Wang, B.-W. Wang, A. Ardavan, Z. Shi, S.-D. Jiang and S. Gao, J. Am. Chem. Soc., 2018, 140, 1123 CrossRef CAS PubMed.
- PHI code: N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS PubMed.
- (a) C. F. Davis, M. W. P. Strandberg and R. L. Kyhl, Phys. Rev., 1958, 111, 1268 CrossRef CAS; (b) R. J. Holmberg, L. T. A. Ho, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, Dalton Trans., 2015, 44, 20321 RSC; (c) A. Arauzo, A. Lazarescu, S. Shova, E. Bartolome, R. Cases, J. Luzon, J. Bartolome and C. Turta, Dalton Trans., 2014, 43, 12342 RSC; (d) T. Yoshida, G. Cosquer, D. C. Izuogu, H. Ohtsu, M. Kawano, Y. Lan, W. Wernsdorfer, H. Nojiri, B. K. Breedlove and M. Yamashita, Chem. – Eur. J., 2017, 23, 4551 CrossRef CAS PubMed; (e) M. Orendáč, L. Sedláková, E. Čižmár, A. Orendáčová, A. Feher, S. A. Zvyagin, J. Wosnitza, W. H. Zhu, Z. M. Wang and S. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214410 CrossRef; (f) P. I. Girginova, L. C. J. Pereira, J. T. Coutinho, I. C. Santos and M. Almeida, Dalton Trans., 2014, 43, 1897 RSC.
- R. Orbach, Proc. R. Soc. A, 1961, 264, 458 CrossRef CAS.
- J. H. Van Vleck, Phys. Rev., 1941, 59, 724 CrossRef CAS.
- E. Bartolomé, A. Arauzo, J. Luzón, J. Bartolomé and F. Bartolomé, in Handbook of Magnetic Materials, ed. E. Brück, Elsevier, 2017, p. 1 Search PubMed.
- X. Liu, T. Zuo and H. C. Dorn, J. Phys. Chem. C, 2017, 121, 4045 CAS.
- (a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS; (b) D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5, 2229 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental details, HPLC separation, simulation. See DOI: 10.1039/c8cc00112j |
| ‡ We use −2J12S1S2 formalism to describe exchange interactions; in the −J12S1S2 formalism, which is also often used, the J12 values are twice larger. |
| § PBE0/TZ2P-DKH level, Orca code.18 |
¶ Gd2@C79N was isolated from commercial Gd3N@C80 (95% purity, Luna Innovations). The major by-product of this commercial sample is Gd2@C79N (∼3–5%). Gd2@C79N transfers only 5 electrons to the fullerene cage; whereas, Gd3N@C80 transfers 6 electrons. This provides a significant chromatographic retention difference between these two EMFs since the pentabromobenzyl (PBB) chromatographic stationary phase is sensitive to the fullerene carbon cage number and the number of electrons transferred from the internal cluster.17 With a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of toluene/ortho-dichlorobenzene as the chromatographic solvent system for the PBB chromatographic phase ∼1 mg of Gd2@C79N was purified from 100 mg of Gd3N@C80. See ESI† for further details. 1 mixture of toluene/ortho-dichlorobenzene as the chromatographic solvent system for the PBB chromatographic phase ∼1 mg of Gd2@C79N was purified from 100 mg of Gd3N@C80. See ESI† for further details. |
| This journal is © The Royal Society of Chemistry 2018 |