Exploiting coordination geometry to selectively predict the σ-donor and π-acceptor abilities of ligands: a back-and-forth journey between electronic properties and spectroscopy

Abstract

Through an analysis of eighty tetrahedral and square-planar metal carbonyls of general formula [M(CO)(L′)(L)₂] including newly synthesized chlorocarbonyl rhodium complexes with chelating atropoisomeric diphosphanes, we show how coordination geometry can switch the carbonyl stretching frequency into a selective probe of the σ-donor and π-acceptor abilities of the ligands. We thus provide a framework whereby the σ-donation and π-backdonation constituents of the Dewar–Chatt–Duncanson model can be quantitatively predicted through spectroscopic data on coordinated CO moieties and vice versa.

---

Understanding the detailed metal–ligand bonding features in coordination complexes is of fundamental importance in organometallic chemistry, especially with a view to controlling the activation of substrates and thus driving the outcome and efficiency of catalytic reactions.^1–3 Since their introduction in the early fifties, the concepts of σ-donation and π-backdonation rooted in the Dewar–Chatt–Duncanson (DCD) model of the η² coordination of ethene to a coinage-metal atom^4,5 have entered the standard tool set by which chemists analyze and rationalize the electronic properties of the ligand and metal fragments. However, also due to the difficulty in unambiguously defining σ donation and π backdonation from a quantum-mechanical point of view (see for instance ref. 6), establishing whether selected experimental observables may be used as selective probes of the metal–ligand detailed bonding features is still an open issue.^7–10 Pioneering in this respect have been Tolman's landmark works proposing the (symmetric) carbonyl stretching frequency in nickel carbonyls of formula [Ni(CO)₃(L)] as a probe of the bonding properties of L.^11,12

In terms of the DCD bond constituents, the coordination bond between carbon monoxide CO and a transition metal M involves a σ-donation charge flow from the CO lone pair on the carbon side (represented by the CO highest occupied molecular orbital, HOMO) to empty orbitals of σ symmetry available at the metal center, and a π-backdonation charge flow from the filled d orbitals of π symmetry of M to the lowest unoccupied molecular orbital (LUMO) of CO having π symmetry and antibonding character.¹³ As clearly pointed out in a recent work coauthored by one of us on a series of symmetric linearly coordinated [Au(CO)(L)]^0/+ complexes, the carbonyl stretching frequency in this class of complexes responds solely (and quantitatively) to the changes in the electron cloud of π symmetry, thus suggesting that this frequency can effectively be used to selectively probe the π-acceptor ability of L.¹⁴ Based on a combined orbital-space/real-space bond-analysis scheme¹⁵ allowing for singling out the σ-donation, Δρ_σ-don, and π-backdonation, Δρ_π-back, contributions to the overall charge rearrangement upon bond formation and quantifying them along the interaction axis z by a simple integration in space of the associated electron-density difference‡

we could recently address the more complex case of chelation bonding in [Ni(CO)₂(PP)] complexes with PP being one of the atropoisomeric chelating diphosphane ligands¹⁸ detailed in the ESI,† with a focus on the relation between the (symmetric) carbonyl stretching frequency and the detailed features of the metal–ligand coordination bond.¹⁹ For the reader's convenience and for a better understanding of the ideas contained in this communication, the results of this work are summarized in Fig. 1. After isolating the σ-donation contribution Δρ_σ-don to the overall charge rearrangement (see a volume-rendering representation in panel a) and building for each complex the related charge-displacement (CD) profile (panel b) along the z axis bisecting the angle, we found that the extent of the charge displaced upon bond formation due to σ donation was inversely proportional to the (symmetric) carbonyl stretching frequencies ν_CO(sym) in the complexes. This result is an eye-catching feature as can be seen in panel b, where the color scale used for the curves (which are positive throughout the z axis and thus depict a charge flux from right to left) reflects the order of the frequencies. On a more quantitative ground, estimates of the σ-donation charge transfers CT_σ-don, extracted from the CD profiles at z = 0.7 bohr, were found to be in tight correlation (R² = 0.988) with ν_CO(sym) (panel c) while no such relation was found for the charge transfers associated with the remaining bond components. In other words, we found that it was the σ-donation component (and not the π backdonation as mentioned above for linearly coordinated complexes) that drove the carbonyl-stretching response to the metal–ligand bond formation.

Fig. 1 (a) Charge rearrangement Δρ_σ-don (red volume: depletion, blue volume: accumulation) associated with the P → Ni σ donation in the [Ni(CO)₂(PP)] complex with PP = bifurp. (b) CD profiles of Δρ_σ-don for the considered PP along the z axis bisecting the angle. (c) Correlation between the symmetric carbonyl stretching frequencies ν_CO(sym) and the σ-donation charge transfers CT_σ-don extracted from the CD profiles at z = 0.7 bohr. Note that labels ‘bifurp1’ and ‘bifurp2’ refer to two conformers of the bifurp complex of comparable energy.

The rationale of these apparently puzzling results is that, as one can easily verify by inspecting panel a, due to the tetrahedral coordination geometry of the metal centre, it is the charge flow resulting from each P → Ni σ donation that pushes electron charge into the carbonyl LUMO of π* symmetry with respect to the C–O bond axis, thus weakening this bond and lowering the associated stretching frequency. This triggered the idea – the verification of which shall be the subject of this communication – that if one switches to a coordination geometry where the out-of-plane π-backdonation charge flow correlates with the symmetry of the carbonyl LUMO (as, for instance, in square-planar [Rh(CO)(Cl)(PP)] complexes), then the carbonyl stretching frequency should be selectively influenced by this bond component. This is concisely sketched in Scheme 1 for the general case of tetrahedral/square-planar complexes of formula [M(CO)(L′)(L)₂].

Scheme 1 Metal–ligand charge-flow component pushing (left)/drawing (right) charge into/from the carbonyl LUMO in tetrahedral/square-planar [M(CO)(L′)(L)₂] complexes.

Before synthesizing square-planar analogues of the above considered nickel complexes and verifying the hypothesis against experimental carbonyl stretching frequencies, we decided to perform an extensive theoretical analysis for the general case of ligand pairs in lieu of chelating ligands. With the aim of assessing whether and to what extent Scheme 1 is a valid model, we considered a wide and varied class of 34 ligands, resulting in a total of 68 complexes. Calculations were performed as detailed in the ESI† by means of density-functional theory where vibrational anharmonic corrections, that are mandatory to get accurate predictions, were obtained at a modest additional computational cost through a reduced-dimensionality anharmonic perturbative treatment.^20–22 The results of our analysis are concisely summarized in Fig. 2. Panels a and b display the CD profiles associated with the L → Ni σ donation in tetrahedral [Ni(CO)₂(L)₂] complexes and with the Rh → L out-of-plane π backdonation in square-planar [Rh(CO)(Cl)(L)₂] complexes, respectively, both evaluated along the z axis bisecting the angle. The complete set of ligands is listed in the key of each plot (see ESI† for an explanation of abbreviated names) in ascending order of computed ν_CO(sym) for panel a, and in descending order of computed ν_CO for panel b. A color scale reflecting this order is also used for drawing the CD profiles (note that the positive regions of the CD profile denote a positive charge flux from right to left while the negative regions of the CD profile denote a positive charge flux from left to right). As apparent from the two plots, and perfectly in line with our hypothesis, the extent of the displaced charge is in both cases proportional to the carbonyl stretching frequency (see the curves getting darker as the extent of the related charge-flow grows). More specifically, larger σ-donation profiles in tetrahedral complexes correspond to lower frequencies, while larger out-of-plane π-backdonation profiles in square-planar complexes correspond to higher frequencies. This finding is put on a more quantitative ground by extracting CT estimates from the related profiles at z = 0.7 bohr and correlating them to the related carbonyl stretching frequencies (panels c and d). Considering the great variety of the examined complexes (a range of about 300 cm⁻¹ is spanned by the calculated frequencies, for a charge-transfer range of 0.7 e), the results are rather satisfactory, with R² = 0.848 for the correlation of CT_σ-donvs. ν_CO(sym) in the tetrahedral complexes, and R² = 0.725 for the correlation of CT_π-backvs. ν_CO in the square-planar complexes. It is worth stressing here that no symmetry constraints have been used on the geometries of the examined systems. As a result, the σ and even more markedly the π character of the bond components in some of the complexes emerged less clearly (this also explains why the correlation of panel d is lower than that of panel c). Indeed, upon restricting the analysis to a narrower series of homologues such as OH⁻, F⁻, SH⁻, Br⁻, Cl⁻, and I⁻ where this issue is minimized (see filled points in panels c and d and the related best-fitting solid lines) the correlation substantially improves, yielding R² = 0.920 for data in panel c and R² = 0.983 for data in panel d. Furthermore, test calculations reported in the ESI† on analogous complexes, coordinating the same subset of ligand pairs where Ni was replaced with Pd and Rh with Co, indicate that the correlations hold reasonably well even beyond the specific case of Ni and Rh complexes considered herein.

Fig. 2 CD profiles associated with (a) the L → Ni σ donation in tetrahedral [Ni(CO)₂(L)₂] complexes and (b) the Rh → L out-of-plane π backdonation in square-planar [Rh(CO)(Cl)(L)₂] complexes, both evaluated along the z axis bisecting the angle. Correlation between the (symmetric) carbonyl stretching frequencies and (c) the σ-donation charge transfers evaluated at z = 0.7 bohr in Ni complexes; (d) the out-of-plane π-backdonation charge transfers evaluated at z = 0.7 bohr in Rh complexes.

Encouraged by these results, we synthesized and characterized square-planar complexes of formula [Rh(CO)(Cl)(PP)] with PP being each of the above considered chelating diphosphanes (these were chosen because similar complexes have already been used to characterize the electronic properties of chelating diphosphanes²³ and because they share with the [Ni(CO)₂(PP)] complexes the ease of synthesis). A summary of the experimental data as well as of some calculated properties of these complexes is given in Table 1 (a full account is provided in the ESI†) while results of the bond analysis are reported in Fig. 3. In panel a, a volume-rendering representation of the out-of-plane π-backdonation bond component is given. Panel b shows, in a color scale reflecting the order of the carbonyl stretching frequencies, the CD profile associated with this component for each of the considered complexes. Panel c provides a quantitative picture of the correlation between estimates of CT_π-back and ν_CO. As evident, the extent of the out-of-plane π-backdonation charge flow is directly proportional to the carbonyl stretching frequency and the correlation between this quantity and the extracted CT's at z = 0.7 bohr is impressive (R² = 0.974). This suggests that the values of CT_σ-don and CT_π-back in tetrahedral and square-planar complexes, respectively, can be predicted by means of simple model equations

CT_σ-don = mν^Ni_CO(sym) + q CT_π-back = nν^Rh_CO + p (2)

with parameters m, q, n and p to be determined via best fitting. Using, for example, the experimental frequencies of tetrahedral nickel complexes¹⁹ and square-planar rhodium complexes (Table 1) together with the theoretically obtained CT_σ-don and CT_π-back, best-fitting parameters m = 2.360 × 10⁻³e cm⁻¹, n = 1.553 × 10⁻³e cm⁻¹, p = 4.895 e and q = −2.967 e are obtained and, as shown in Fig. 4, these data can be used to get a clear and consistent picture of the relative σ-donor/π-acceptor ability of ligands within a given class. On the other hand, the same model eqn (2) can as well be used to get quantitative predictions of the carbonyl stretching frequencies from the computed charge-transfer values.

Table 1 Experimental and calculated properties of the Rh complexes^a

PP	ν ^expCO/cm^−1	ν ^calcCO/cm^−1	β/°	θ/°	r ^calcCO/bohr
a β, calculated bite angle. θ, calculated P–P–Cl–C dihedral angle with the first P being that on the side of C. Note that, as typical, the calculated frequencies have an average blue-shift of about 30 cm^−1 with respect to the experimental values.
bitiop	2009	2029	91.7	−22.3	2.184
binap	2012	2043	91.0	−15.7	2.181
tmbitianp	2019	2050	91.3	−11.8	2.179
bitianp	2020	2054	90.7	−8.9	2.178
bifurp	2027	2059	90.6	−3.0	2.177
bimip	2035	2065	92.9	−6.4	2.175

---

Fig. 3 (a) Charge rearrangement Δρ_π-back (red volume: depletion, blue volume: accumulation) associated with the Rh → P out-of-plane π backdonation in the [Rh(CO)(Cl)(PP)] complex with PP = bifurp. (b) CD profiles of Δρ_π-back for the considered PP along the z axis bisecting the angle. (c) Correlation between the carbonyl stretching frequencies ν_CO and the out-of-plane π-backdonation charge transfers CT_π-back extracted from the CD profiles at z = 0.7 bohr.

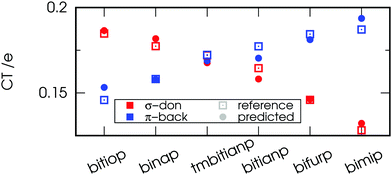Fig. 4 Reference (obtained by theoretical analysis) and predicted (via the model eqn (2) using experimental carbonyl stretching frequencies) values for the σ-donation and out-of-plane π-backdonation charge transfers in [Ni(CO)₂(PP)] and [Rh(CO)(Cl)(PP)] complexes, respectively.

The results presented in this communication demonstrate for the first time that coordination geometry can be effectively exploited to switch the carbonyl stretching frequency into a selective probe of the σ-donation and π-backdonation constituents of the DCD model in coordination complexes. Through model equations of striking simplicity, electronic properties are quantitatively related to spectroscopic data and vice versa, casting light from a novel perspective on the relation between spectroscopic observables and bonding properties, and contributing to a deeper understanding of one of the most popular models for chemical bonding.

The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement No. [320951].

Conflicts of interest

There are no conflicts to declare.

References

1. A. S. Hashmi, Angew. Chem., Int. Ed., 2010, 49, 5232–5241.
2. J. Jover and N. Fey, Chem. – Asian J., 2014, 9, 1714–1723.
3. K. Arumugam, B. Varghese, J. N. Brantley, S. S. M. Konda, V. M. Lynch and C. W. Bielawski, Eur. J. Org. Chem., 2014, 493–497.
4. M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, C71–C79.
5. J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939–2947.
6. G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717–774.
7. M. N. Golovin, M. M. Rahman, J. E. Belmonte and W. P. Giering, Organometallics, 1985, 4, 1981–1991.
8. L. Triguero, A. Föhlisch, P. Väterlein, J. Hasselström, M. Weinelt, L. G. M. Pettersson, Y. Luo, H. Ågren and A. Nilsson, J. Am. Chem. Soc., 2000, 122, 12310–12316.
9. G. Bistoni, L. Belpassi and F. Tarantelli, Angew. Chem., Int. Ed., 2013, 52, 11599–11602.
10. J. Jover and N. Fey, Dalton Trans., 2013, 42, 172–181.
11. C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2953–2956.
12. C. A. Tolman, Chem. Rev., 1977, 77, 313–348.
13. R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, John Wiley & Sons, Inc., 6th edn, 2014, pp. 98–102.
14. G. Bistoni, S. Rampino, N. Scafuri, G. Ciancaleoni, D. Zuccaccia, L. Belpassi and F. Tarantelli, Chem. Sci., 2016, 7, 1174–1184.
15. G. Bistoni, S. Rampino, F. Tarantelli and L. Belpassi, J. Chem. Phys., 2015, 142, 084112.
16. L. Belpassi, I. Infante, F. Tarantelli and L. Visscher, J. Am. Chem. Soc., 2008, 130, 1048–1060.
17. S. Rampino, L. Storchi and L. Belpassi, J. Chem. Phys., 2015, 143, 024307.
18. G. Facchetti, E. Cesarotti, M. Pellizzoni, D. Zerla and I. Rimoldi, Eur. J. Inorg. Chem., 2012, 4365–4370.
19. M. Fusè, I. Rimoldi, E. Cesarotti, S. Rampino and V. Barone, Phys. Chem. Chem. Phys., 2017, 19, 9028–9038.
20. V. Barone, J. Chem. Phys., 2005, 122, 014108.
21. V. Barone, M. Biczysko, J. Bloino, M. Borkowska-Panek, I. Carnimeo and P. Panek, Int. J. Quantum Chem., 2012, 112, 2185–2200.
22. V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759–1787.
23. S. Jeulin, S. Duprat de Paule, V. Ratovelomanana-Vidal, J.-P. Genêt, N. Champion and P. Dellis, Angew. Chem., Int. Ed., 2004, 43, 320–325.

---

Footnotes

† Electronic supplementary information (ESI) available: Methods and computational details, complete results of the NOCV/CD analysis, Experimental section, and optimized structures in XYZ format. See DOI: 10.1039/c7cc09627e

‡ The resulting function, herein referred to as charge-displacement (CD) profile, gives for each z point the exact amount of electron charge that upon bond formation has flown from right to left across a plane orthogonal to the z axis through that point.^16,17

---