Challenges and advances in the computational modeling of biological phosphate hydrolysis

Abstract

Phosphate ester hydrolysis is fundamental to many life processes, and has been the topic of substantial experimental and computational research effort. However, even the simplest of phosphate esters can be hydrolyzed through multiple possible pathways that can be difficult to distinguish between, either experimentally, or computationally. Therefore, the mechanisms of both the enzymatic and non-enzymatic reactions have been historically controversial. In the present contribution, we highlight a number of technical issues involved in reliably modeling these computationally challenging reactions, as well as proposing potential solutions. We also showcase examples of our own work in this area, discussing both the non-enzymatic reaction in aqueous solution, as well as insights obtained from the computational modeling of organophosphate hydrolysis and catalytic promiscuity amongst enzymes that catalyze phosphoryl transfer.

---

Dušan Petrović

Dušan Petrović studied Chemistry and Biochemistry at the University of Belgrade, Serbia and North Dakota State University, USA. As an Otto-Bayer and Jürgen-Manchot fellow, he performed his PhD studies in Computational Biochemistry at the Research Center Jülich and Heinrich Heine University Düsseldorf, Germany. He is currently a postdoctoral researcher in the group of Prof. Lynn Kamerlin at Uppsala University, Sweden, where he works on the structural and dynamical aspects of enzyme evolution and enzyme design.

Klaudia Szeler

Klaudia Szeler obtained her Master of Engineering in Bioinformatics at the Wroclaw University of Technology in Poland. She is currently a PhD student under the supervision of Prof. Lynn Kamerlin at Uppsala University in Sweden. Her main research goal is understanding the promiscuity and evolution of enzymes, mainly organophosphatase hydrolases.

Shina Caroline Lynn Kamerlin

Lynn Kamerlin received her Master of Natural Sciences from the University of Birmingham (UK), in 2002, where she remained to complete a PhD in Theoretical Organic Chemistry under the supervision of Dr John Wilkie (awarded 2005). Subsequently, she was a postdoctoral researcher in the labs of Stefan Boresch at the University of Vienna (2005–2007) and Arieh Warshel at the University of Southern California (2007–2010). She is currently a Professor of Structural Biology at Uppsala University, a Fellow of the Royal Society of Chemistry, a Wallenberg Academy Fellow, and the former Chair of the Young Academy of Europe.

---

1 Introduction

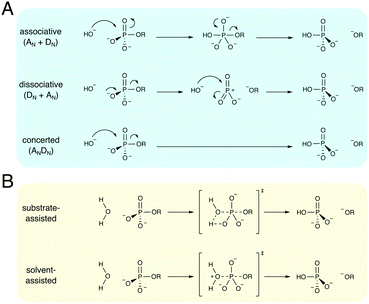
Phosphate esters are the building blocks of life, participating in a wide range of biological processes, from cellular signaling, to protein synthesis, to maintaining the integrity of genetic material, to name just a few examples.^1–3 These compounds are among the most stable on earth, and the half-lives for their hydrolyses in water can exceed millions of years,⁴ making the corresponding enzymes that catalyze these reactions among the most proficient on the planet.^4–8 Therefore, phosphatases – enzymes that hydrolyze phosphate esters – are of great interest to study from both a biochemical and a biomedical perspective, as they are either directly or indirectly the target of a substantial proportion of all drugs currently on the market.^9–11 As a result, both the non-enzymatic and enzymatic hydrolysis of phosphate esters has been the subject of substantial research effort for several decades, as reviewed in detail in, for example, ref. 1–3.

There exists a broad physical organic chemistry toolkit for the experimental elucidation of reaction mechanisms, including, for example, studying linear free energy relationships,^12,13 isotope effects,¹⁴ or entropic effects.¹² From a computational perspective, there have been substantial improvements in not just computer power but also computational algorithms for modeling (bio)chemical function and reactivity using quantum and classical mechanical approaches.^15,16 Therefore, it would be reasonable to assume that after several decades of research effort, the fundamental mechanisms for the hydrolysis of phosphate esters should be well understood. However, the fine details of phosphate ester hydrolysis remain controversial, both in terms of disagreements between experimental and computational interpretations of the same data,^2,3 and also between different computational studies that have suggested vastly different mechanisms (sometimes even for the hydrolysis of the same compound) depending on the level of theory and specific approaches used.³ The underlying causes of this controversy are manifold: (1) the low-lying d-orbitals on the phosphorus atom can potentially become involved in the chemical reaction, making phosphate esters highly versatile compounds, where even the simplest of compounds can potentially react through multiple plausible reaction mechanisms (Fig. 1), (2) because of the low-lying d-orbitals and the polarizability of the phosphorus atom, a high level of theory with a large basis set needs to be used in quantum chemical studies of phosphates, and modeling the reactivity of these compounds in a reliable way is a non-trivial problem, resulting also in severe basis set dependence of the results, (3) the high charge of these compounds means that a pure implicit solvent model (as often used in quantum chemical calculations) can be inadequate to describe the associated transition states, and either mixed implicit/explicit or fully explicit solvent models are needed,¹⁷ and, finally, (4) very few of the computational studies have directly compared all possible mechanisms at the same level of theory, which is critical when multiple potential pathways (that can be theoretically quite similar in energy^18–20) are involved.

Fig. 1 Multiple mechanisms for the hydrolysis of phosphate monoester dianions. (A) A comparison of different mechanistic pathways for hydroxide attack on a simple phosphate monoester dianion. The reaction can hypothetically proceed through either associative (A_N + D_N), dissociative (D_N + A_N), or concerted (A_ND_N) mechanisms. These pathways involve either full phosphorane (A_N + D_N) or metaphosphate (D_N + A_N) intermediates, or a single concerted transition state (A_ND_N), which can itself be either associative or dissociative in nature, depending on the degree of bond formation to the nucleophile and bond cleavage to the leaving group. (B) In the case of water-attack, the mechanistic options are further complicated because not only do all different mechanistic options highlighted in (A) also apply to this reaction, but the reaction can further be either substrate- or solvent- (general-base) assisted, as described in the main text. Finally, while all the different mechanisms shown here operate via in-line nucleophilic attack, non-inline pathways are, in principle, also feasible.

Despite this, recent years have seen substantial advances in the computational modeling of both enzymatic and non-enzymatic phosphoryl (and more recently the related sulfuryl) transfer reactions, using a range of computational approaches. In this review, we will present work, by both ourselves and others, that has advanced our understanding of both the non-enzymatic hydrolysis of a range of phosphate esters, as well as the corresponding enzyme catalyzed reactions. Our focus will be on a range of biological systems that have been of particular interest to our research group. In doing so, we will highlight not only the computational challenges that are particular to studying these compounds, but also the contributions that computation can make to further advancing our understanding of the mechanisms and catalysis of this biologically critical class of reactions.

2 Modeling non-enzymatic phosphoryl transfer

The non-enzymatic hydrolysis of phosphate esters has been the subject of substantial experimental and computational research effort,^2,3 with particular focus on the hydrolysis of phosphate mono- and diesters, as well as polyphosphates as models for biological guanosine triphosphate (GTP) and adenosine triphosphate (ATP) hydrolysis. Phosphate triesters have also been studied, albeit to a lesser extent,² in particular in the context of the degradation of organophosphate pesticides and nerve agents.²¹ As shown in Fig. 1, even the simplest of phosphate esters can be hydrolyzed through multiple different mechanisms. This includes dissociative (D_N + A_N), associative (A_N + D_N) or concerted (A_ND_N) pathways, as well as both substrate and solvent-assisted pathways. The preferred mechanism will, in turn, also depend on the esterification level of the phosphate, in addition to environmental effects such as solvent and pH,^2,3,22 further complicating attempts to obtain a clear mechanistic picture. We will focus this section primarily on the hydrolysis of phosphate monoesters and related compounds, as these have been both extensively studied experimentally,^2,3 and also have been of particular interest to us in our recent work.^{17,20,23–25}

Experimentally, the hydrolysis of phosphate monoesters is believed to proceed through loose, dissociative transition states, on the basis of the steep slope of the linear free energy relationship for the hydrolyses of these compounds (β_lg = −1.23),¹³ near-zero activation entropies,²⁶ as well as, in the case of p-nitrophenyl phosphate (pNPP) hydrolysis, kinetic isotope effects (KIE)^14,27 that show a large normal isotope effect on the bridging oxygen at the position of bond-cleavage (i.e., the oxygen in the axial position, bridging the phosphorus atom and the leaving group, O_lg, ¹⁸k_bridge = 1.0189), an inverse isotope effect (¹⁸k_nonbridge = 0.9994) on the non-bridging oxygens (i.e., the oxygen atoms in the equatorial positions, O_nb), and a ¹⁵k isotope effect that is close to the maximum value that would be expected for breaking the bond to the leaving group at the transition state (¹⁵k = 1.0028). Computational studies, however, have been less conclusive, with both associative and dissociative transition states being proposed for the hydrolysis of these compounds,^18,28–31 including an apparent leaving-group dependence for the preferred mechanism of hydrolysis.^{18,20,29–31} A second controversial issue has revolved around nucleophile activation: while one would normally assume general-base catalysis in a solvent-assisted pathway, the pK_a of the non-bridging oxygens of phosphate monoesters and triphosphates such as ATP or GTP (in the range of around 6–7³²) make a substrate-assisted pathway also plausible, as shown in Fig. 1, and whether such a pathway is in fact possible has been the subject of substantial debate in the literature.^2,31,33–36

Our starting point for exploring the competing mechanisms of phosphate ester hydrolysis has been a comparison of the non-enzymatic hydrolysis of pNPP and p-nitrophenyl sulfate (pNPS).²³ This study was motivated by a general interest in catalytic promiscuity amongst enzymes that catalyze phosphoryl and sulfuryl transfer.^37,38 Furthermore, these two experimentally well-studied compounds served as model systems for understanding these classes of reactions,^{12–14,26,27,39} at a time when minimal computational work had been performed on these reactions.^40,41

The hydrolyses of these two compounds have virtually identical reaction rates (1.6 × 10⁻⁸ s⁻¹ (ref. 12) for pNPP and 1.87 × 10⁻⁹ s⁻¹ (ref. 27) for pNPS hydrolysis, respectively), as well as very similar ¹⁸k_bridge, ¹⁸k_nonbridge, and ¹⁵k KIE (1.0189, 0.9994, and 1.0028 for pNPP, and 1.0210, 0.9951, and 1.0026 for pNPS).^14,26,27 Taking into account their similar ground state geometries, it has been argued in the literature that the two reactions proceed via identical loose transition states.^26,27 However, the activation entropies for the two reactions are very different, at +3.5 eu for the pH-independent hydrolysis of pNPP, and −18.5 eu for the pH-independent hydrolysis of pNPS,^14,26 where “eu” refers to entropy units, with 1 eu corresponding to 1 cal K⁻¹ mol⁻¹. In addition, the differences between P–O and S–O equilibrium bond lengths and the polarizability of the corresponding phosphate and sulfate anions suggest that all might not be as simple as it seems, and that there are larger differences involved between the two compounds.

In our initial work on this topic,²³ we generated 2D energy landscapes for the hydrolysis of the two compounds in implicit solvent, using density functional theory. We obtained energy landscapes indicating a loose dissociative transition state for pNPS hydrolysis, in agreement with experimental predictions.²⁷ In the case of pNPP hydrolysis, however, our energy landscapes predicted a more associative, substrate-assisted pathway, in disagreement with experiment, but in agreement with previous computational studies of related compounds.^29,42 The approximate transition state geometries, from the energy landscapes, were subjected to unconstrained geometry optimization in order to find the actual transition states. The transition states structures were then characterized by frequency calculations as well as following the intrinsic reaction coordinate (IRC)⁴³ in the reactant and product directions. The predicted activation free energies were in reasonable agreement with experiment, and additional calculations of the corresponding activation free energies in explicit solvent could reproduce the large difference between the experimental activation free energies.²³ However, while the calculations could quantitatively reproduce the experimental KIE for pNPS hydrolysis to a reasonable degree, they could not reproduce the corresponding KIE for pNPP hydrolysis. That is, in contrast to the experimental values,^14,27 the calculations predicted small normal KIE of 1.002 and 1.004 for ¹⁸k_bridge and ¹⁵k, respectively, which would indicate a transition state with very little bond breaking to the leaving group, in agreement with the calculations. In addition, as discussed in ref. 23, our energy landscapes in pure implicit solvent did not show a clear saddle point for pNPP hydrolysis. These major discrepancies suggested that our initial calculations are only telling part of the story when it comes to understanding the hydrolyses of these prototypical compounds.

To address this issue, we experimented with mixed-solvent models in subsequent work,¹⁷ by including between one and eight explicit water molecules to microsolvate the system and provide explicit hydrogen bonding interactions in addition to the implicit solvent model. Fig. 2 shows a comparison of the calculated energy landscapes for pNPP and pNPS hydrolysis in the presence of two explicit water molecules embedded into implicit solvent, as well as the associated transition states obtained from unconstrained geometry optimization. As can be seen from this figure, the energy landscapes for pNPP and pNPS hydrolysis are largely in agreement with our previous work,²³ suggesting a substrate-assisted mechanism for pNPP hydrolysis and a solvent-assisted mechanism for pNPS hydrolysis. Therefore, (1) once explicit solvent molecules are included, it is possible to see a clear saddle point on the energy landscape for pNPP hydrolysis, and (2) the energy landscape for pNPP hydrolysis does not indicate the existence of a solvent-assisted pathway. Perturbing the solvent-assisted transition state for pNPS hydrolysis by simply substituting S for P and re-optimizing this transition state, however, reveals the corresponding solvent-assisted transition state for pNPP hydrolysis. This transition state is marginally more dissociative than the transition state for the solvent monoester, but at 27.2 kcal mol⁻¹, the activation free energy for this pathway is also substantially lower than that calculated for the substrate assisted pathway (34.9 kcal mol⁻¹). In addition, unlike the substrate-assisted transition state, KIE calculations on the solvent-assisted transition state yield values that are in excellent agreement with experiment.

Fig. 2 Energy landscapes (in kcal mol⁻¹) for the hydrolyses of (A) p-nitrophenyl phosphate (pNPP) and (B) p-nitrophenyl sulfate (pNPS), calculated at the M06-2X/6-311+G**(SMD)//M06-2X/6-31+G*(SMD) level of theory. The corresponding transition states for the (C) substrate- and (D and E) solvent-assisted hydrolyses of pNPP and pNPS, highlighting the relevant bond distances to the incoming nucleophile and departing leaving group (in Å). As discussed in the main text, the solvent-assisted transition state for pNPP hydrolysis, shown in panel (B), cannot be observed on the calculated energy landscape (A), and can only be obtained by re-optimizing the transition state for the hydrolysis of the sulfate monoester, following a single-atom perturbation between the two transition states. Panels (A and B) are modified from ref. 17, copyrighted to the American Chemical Society. The coordinates for panels (C–E) come from the ESI of the same paper.

The major reason for this discrepancy, and the “missing transition state” on the energy landscape for pNPP hydrolysis, arises simply due to the problems with compressing a multidimensional surface onto two projected coordinates, including compressing the proton transfer onto a More O’Ferrall–Jencks plot^44,45 that takes into account only the P–O distances to the incoming nucleophile and departing leaving group to generate the reaction coordinate. This problem was anticipated almost four decades ago,⁴⁶ and it remains just as relevant now as it was then. Ideally, one would instead want to generate a reaction cube, which is, at present, far too computationally costly to be realistically feasible. One way to partially circumvent such problem is to examine different slices through the energy landscape rather than the full reaction cube, as has been done in elegant work by Warshel and coworkers.⁴⁷ However, this discrepancy highlights the problems with drawing mechanistic conclusions from a simple 2D projection of a complex multidimensional landscape.

In addition to examining the competition between different pathways, ref. 17 also explored the role of explicit solvent molecules in the calculations, a topic of some prior debate in the literature.^48–50 We demonstrated that, for these highly charged compounds, a pure implicit solvent model is inadequate for correctly capturing the activation free energies, and the calculated values are, unsurprisingly, highly sensitive to the inclusion of additional explicit water molecules. However, once all potential hydrogen bond donors/acceptors were saturated, the calculated activation free energies also seemed to converge, such that the inclusion of additional water molecules had less impact. The changes in energy were quite dramatic, from a difference of 9.2 kcal mol⁻¹ between the two pathways for pNPP hydrolysis in pure implicit solvent, to only 2 kcal mol⁻¹ once sufficient explicit water molecules had been added to the system. Interestingly, the calculated KIE were largely insensitive to the explicit water molecules, and were thus a much more reliable marker of mechanistic preference than the actual calculated energies.

Based on this initial work,^17,23 we have addressed a range of related problems, including the effect of leaving group variation on phosphate monoester hydrolysis,²⁰ the effect of metal ions on the hydrolysis of methyl triphosphate and acetyl phosphate,²⁵ and the reactions of substituted pyridinio-N-phosphonates with pyridine,²⁴ which eliminates the challenges involved in addressing the competition between substrate- and solvent-assisted mechanisms. In the case of phosphate monoester hydrolysis with different leaving groups, we observe a leaving-group dependent mechanistic shift,²⁰ in line with previous computational work.^18,29,31 Our calculations suggest that for most phosphate monoester dianions, a solvent-assisted pathway dominates, although a substrate-assisted pathway becomes viable only for very poor leaving groups.²⁰ This is borne out also in our study of the effect of metal ions on phosphate hydrolysis,²⁵ where the solvent-assisted pathway is consistently energetically preferred, in line with our studies of phosphate monoesters. Finally, in the case of the pyridinio-N-phosphonates,²⁴ where proton transfer is no longer an issue, we obtain loose symmetrical transition states for the reaction with pyridine, in agreement with prior experimental work.⁵¹

Merging these studies with our previous work on the alkaline hydrolysis of compounds such as phosphate diesters,⁵² fluorophosphates,⁵³ and sulfonate monoesters,⁵⁴ enabled us to construct the More O’Ferrall–Jencks diagram shown in Fig. 3. From this figure, it can be seen that all compounds of interest react through loose transition states, although there is movement of the transition state for different compounds as the leaving group stability varies. As discussed in detail in ref. 24, this does not appear to follow the predictions of a simple analysis, for example in terms of linking leaving group ability to transition state structure. However, as also noted in ref. 24, many of the compounds presented in Fig. 3 do not include an identity reaction, and involve reactions with hydroxide. This may explain why such transition states appear to have dissociative character but lie far from the diagonal of the plot, where the identity reaction would have to fall if the reaction were to pass through a single transition state during the reaction. Nevertheless, taken together, this data gives us a detailed computational overview of the reactivity of different phosphate esters (and related compounds), and provided us with a strong foundation from which to address the more complex issue of enzymatic phosphoryl transfer.

Fig. 3 More O'Ferrall–Jencks plot indicating the shifting nature of the transition states calculated for the hydrolysis reactions of five groups of compounds obtained in our previous studies. The calculated Wiberg bond indices⁶² for the P(S)-leaving group and P(S)-nucleophile bonds were used as reaction coordinates (bond breaking and bond forming, respectively). This figure is adapted from ref. 24.

3 Alkaline phosphatases and catalytic promiscuity

A key feature of many enzymes that catalyze phosphoryl transfer is that they are catalytically promiscuous, and able to catalyze the reactions of a range of chemically distinct substrates in addition to their native activities.^38,55 Already in 1976, Jensen proposed that catalytic promiscuity is important to the evolution of new enzyme functions (Fig. 4),⁵⁶ a hypothesis that has been validated by extensive later studies, including seminal work in ref. 57 and 58, amongst others. For historical reasons, the alkaline phosphatase (AP) superfamily has been a particularly important model system for understanding catalytic promiscuity and protein evolution,^{15,38,55,59,60} and therefore we will discuss both our computational work and that of others in this section.

Fig. 4 A schematic illustration of the evolutionary tree of a hypothetical primordial generalist enzyme ancestor (light green node). As the ancestral enzyme was promiscuous, the mutations it accumulated during evolution led to many modern more specialized enzymes (dark blue nodes), each carrying a specific activity, but many retaining some (or all) of their initial promiscuous activities, albeit at lower levels.

The AP superfamily is a large superfamily of enzymes that catalyze the hydrolysis of phospho- and sulfo-moieties (i.e., catalyzing the cleavage of P–O, S–O, and P–C bonds).^55,61 They achieve this using similar catalytic apparatus, involving at least one divalent metal center (typically Ca²⁺, Zn²⁺, or Mn²⁺),³⁸ as well as an alcohol or alkoxide nucleophile (e.g., the side chains of Ser, Thr, or post-translationally modified formylglycine, Fig. 5A).¹⁵ The requirement for metal ions is absolute. In addition, these enzymes are not only catalytically promiscuous, but also cross-promiscuous, such that the native reaction for one superfamily member is often a promiscuous side reaction in other superfamily members (Fig. 5B), and, in some cases, the promiscuous activities can compete with the native activity in terms of catalytic proficiency.⁵⁹ Therefore, this superfamily provides an excellent model system for mapping the evolution and emergence of new enzyme functions.

Fig. 5 (A) The active sites of E. coli alkaline phosphatase (AP, PDB ID: 1ED9), X. citri nucleotide pyrophosphatase/phosphodiesterase (NPP, PDB ID: 2GSN), R. leguminosarum phosphonate monoester hydrolase (PMH, PDB ID: 2VQR), and P. aeruginosa arylsulfatase (AS, PDB ID: 1HDH). (B) Catalytic proficiencies (log₁₀(k_cat/K_M)) for the native and cross-promiscuous activities (i.e., phosphomonoesterase, phosphodiesterase/pyrophosphatase, phosphonate monoesterase, and arylsulfatase) of the four different members of the alkaline phosphatase superfamily, shown in blue, red, green, and orange, respectively. The data was taken from Table 1 of ref. 59, see this work and references cited therein.

Challenges in modeling alkaline (and related) phosphatases

In additional to the general challenges with studying phosphoryl transfer outlined in the previous section, there are two major challenges when studying this group of enzymes computationally. The first of these is the overall size of the systems, as these enzymes can be (large) monomers, dimers or even tetramers.^38,55,63 While this issue can be addressed by performing simulations using truncated systems (either fully truncating the system in quantum chemical cluster models or by only allowing part of the system to be mobile), as has been done by both ourselves and others in previous work,^63–66 a bigger problem (from a computational perspective) is the absolute dependence of these enzymes on metal ions for their catalytic activities.³⁸ That is, while the arylsulfatase (AS) from Pseudomonas aeruginosa (PAS) is a Ca²⁺-dependent enzyme,^37,67,68 which is relatively straightforward to model computationally, the name-giving member of the superfamily, AP, is a Zn²⁺-dependent phosphomonoesterase, with an additional Mg²⁺ ion in close proximity of the active site,^69,70 that demonstrates promiscuous phosphodiesterase and, to a lesser extent, sulfatase activity.^71,72 Nucleotide pyrophosphatase/phosphodiesterase (NPP), in contrast, is a preferential phosphodiesterase, although this enzyme is also Zn²⁺-dependent.^73,74 Finally, the phosphonate monoester hydrolases (PMH) from Rhizobium leguminosarum and Burkholderia caryophilli (RlPMH and BcPMH, respectively) preferentially hydrolyze phosphonate monoesters and phosphate diesters, although they use the same post-translationally modified formylglycine residue that is common to all sulfatases.^75,76 The precise catalytic metal ion used by the latter two enzymes remains unclear, although the most likely candidate is Mn²⁺, with some degree of metal promiscuity.^75,76

Clearly, the metal ions pose challenges for both classical and quantum mechanical models, both in terms of correctly describing the structural properties of these metal ions, as well as the corresponding electrostatic properties.^77,78 An example of this, in the case of alkaline phosphatases, can be seen in the debate surrounding the relative stability of the catalytic metal ions in AP and NPP.¹⁵ We have attempted to avoid these problems in our simulations by using a multisite model, originally developed by Åqvist and Warshel to explore free-energy relationships in metalloenzymes (i.e., exploring free energies of metal substitution in Staphylococcal nuclease in particular).⁷⁹ Based on the original work by Warshel, we have developed refined multisite models for Ca²⁺, Mg²⁺, Fe²⁺, Zn²⁺, Co²⁺, Ni²⁺, and Mn²⁺,⁸⁰ followed by a multisite model for Cu²⁺ that takes into account the Jahn–Teller distortion of this metal.⁸¹ Finally, we used Merz’ 12-6-4 Lennard-Jones potential, which takes into account ion-induced dipole interactions,⁸² to develop new multisite modes for highly charged metal ions.⁸³ These models have allowed us to explore the activities and selectivities of a range of organophosphate hydrolases, including methyl parathion hydrolase (MPH),⁸⁴ and phosphonate monoester hydrolases,⁶³ as described in the following section.

Modeling the specificity and promiscuity of alkaline phosphatases using the empirical valence bond approach

Our initial interest in modeling the specificity and promiscuity of alkaline phosphatases was based on experimental work on PAS, which showed that this enzyme is not only a proficient sulfatase but also that its promiscuous phosphodiesterase activity is of a level that is comparable to the native activity.⁶⁷ In addition, experimental studies of phosphate mono- and diesters and a sulfate monoester with p-nitrophenyl leaving groups showed that PAS is a much less proficient phosphomonoesterase than a phosphodiesterase. This observation indicates that this enzyme prioritizes the charge similarity of monoanionic phosphate diester substrates to the “native” monoanionic sulfate monoester substrate, over the geometric similarity of dianionic phosphate monoester substrates to the native substrate.⁶³ Such an effect is in good agreement with previous studies that used metal fluoride transition state analogues to demonstrate that anionic charge is prioritized over geometry in enzymes catalyzing phosphoryl transfer.⁸⁵

Our methodology of choice for studying the specificity and promiscuity of this enzyme specifically, and phosphatases in general, has been the empirical valence bond (EVB) approach of Warshel and coworkers.^86,87 This approach, which is reviewed in detail in e.g., ref. 88–90, is a multiscale empirical VB/MM approach, that uses classical force fields to describe chemical reactivity within a quantum mechanical framework. EVB is, therefore, computationally very efficient, allowing for the extensive conformational sampling necessary to obtain convergent free energies. At the same time, well-parameterized force fields can carry a tremendous amount of chemical information with which to describe (bio)chemical reactivity. The postulated reaction mechanism and active site of PAS is shown in Fig. 6. Our calculations⁶³ suggested that the phosphatase activity of this enzyme proceeds through a substrate-assisted mechanism, similar to that suggested for other phosphatases^{34–36,91,92} (although this data will need revisiting in light of our more recent studies of model systems^20,25,63). In contrast, the sulfatase activity of this enzyme appears to utilize the active site histidine, H115, as a general base with which to deprotonate the active site nucleophile. In addition, significant differences were observed experimentally in the k_cat/K_M pH rate profiles of the sulfatase and phosphomonoesterase activities, which we postulated arose from differences in the protonation state of a key active site lysine, K113, upon binding mono- vs. dianionic substrates.⁹³

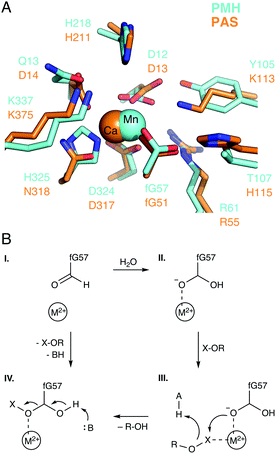Fig. 6 (A) Overlay of the active sites of the phosphonate monoester hydrolase from R. leguminosarum (RlPMH, PDB ID: 2VQR, cyan) and the arylsulfatase from P. aeruginosa (PAS, PDB ID: 1HDH, orange). (B) A generalized schematic of the corresponding reaction mechanism, where the relative active site acid and base are shown as A and B respectively. The figure is modified with permission from figures originally published in ref. 63. Copyright the American Chemical Society.

Globally, our calculations suggested that the promiscuity of this enzyme arises due to “electrostatic flexibility”,⁶³i.e., the ability of individual amino acids to take on more than one catalytic role during transition state stabilization and to compensate for each other upon binding of different substrates with different requirements for efficient catalysis. This is in agreement with experimental work on the organophosphate hydrolase serum paraoxonase 1 (PON1),^94–96 which has also pointed to catalytic versatility of individual active site residues, and is further supported by our subsequent computational work on different PMHs.⁶³ Finally, a comparison of structural and physico-chemical properties of the active sites of different alkaline phosphatases vs. the number of known activities for these enzymes shows a correlation between larger active site volume and polar solvent accessible surface area with a greater number of promiscuous activities. Overall, what our work suggests is that, in the case of the AP superfamily, as long as the number of available interactions is greater than the number of necessary interactions for efficient transition state stabilization, these enzymes are able to be catalytically promiscuous.⁶³

Due to its importance in understanding catalytic promiscuity and protein evolution, the AP superfamily has, in fact, been the subject of numerous computational studies, some highlights of which we will mention here. Cui and coworkers showed that, for APs, the substrate binds the enzyme in a conformation that partially resembles the transition state (deformed ground state),⁹⁷ and that the leaving group can be stabilized by different interactions as a consequence of the P–O_lg cleavage degree.⁹⁸ From a methodological perspective, this system has provided a valuable “stress test”, both for the treatment of transition metal ions in hybrid simulations,^99–102 as well as for the parameterization of the approximate density functional theory, DFTB3, for modeling magnesium and zinc ions in biological applications.¹⁰³ Also, we refer interested readers to ref. 99–103, which among other issues explore the effect of environment on transition state variability, both relative to the non-enzymatic reaction and across a series of compounds, using alkaline phosphatases as a model system. In addition, several important experimental studies recently focused on, e.g., the AP superfamily architecture or interdependence of the catalytic residues.^104–107

4 Modeling the evolution of organophosphate hydrolases

Organophosphate hydrolases (OPases) such as the bacterial phosphotriesterase (PTE), serum paraoxonase 1 (PON1), and methyl parathion hydrolase (MPH) (among other systems) are a class of enzymes that have evolved the capacity to hydrolyze neurotoxic organophosphate compounds.^108–112 These compounds, which inhibit the enzyme acetylcholine esterase, block key pathways in neurotransmission and are a major cause of death worldwide through accidental, malicious, or deliberate exposure.^113,114 From a biochemical perspective, these enzymes are particularly interesting as organophosphates are anthropogenic compounds that have only had widespread usage for less than a century,^115–117 and yet a variety of enzymes from different organisms and different protein folds have evolved the ability to hydrolyze these compounds with respectable catalytic proficiencies¹¹⁵ (in the case of PTE, the hydrolysis of paraoxon by this enzyme is diffusion limited¹¹⁸). Unsurprisingly, these enzymes have been the subject of significant experimental and computational work; due to the large volume of work in this area, we will not provide here all studies but rather refer the reader to reviews such as ref. 59, 119, and 120, and references cited therein for examples of key literature. Our interest in this topic, as in the case of the members of the alkaline phosphatase superfamily, has been in both mechanisms as well as in the molecular drivers for the evolution of organophosphatase activity. In this section, we will discuss some of our work in this area,^84,94,95,121 as well as the associated methodological challenges, and how were they overcome.

A key feature of OPases is their catalytic promiscuity, in that many OPases can also hydrolyze a range of cyclic and/or acyclic esters, as well as other related compounds, in addition to their native organophosphate hydrolase activity.^120,122,123 In many cases, for example, OPase activity emerged from lactonase activity, in enzymes with either deep buried active sites, or active site loops that act as lids, sequestering the active site from solvent.^95,124 In addition, in the case of the OPase methyl parathion hydrolase (MPH, Fig. 7), this enzyme is not only catalytically promiscuous, but also metal-promiscuous. Metal-ion substitutions have been demonstrated to not just lead to changes in the specificity pattern of this enzyme, but also the emergence of cryptic promiscuous actives not observed with the native metal ion.⁸⁴ From a computational perspective, this is a challenging system to study, as (1) there are not one but two metal ions in the active site (Fig. 7A), (2) these metal ions are “non-trivial” to model, including Co²⁺, Ni²⁺, and Mn²⁺, and (3) there is an additional question of what the reaction mechanism is. The main mechanistic question is whether the nucleophile is a bridging hydroxide ion between the two metal ions (as has been proposed in the related case of PTE^120,125,126 that has a quite similar active site¹²⁷), or is it a terminal hydroxide ion, which is more reasonable for MPH in terms of steric constraints in the active site, limiting viable substrate binding conformations (Fig. 7B).

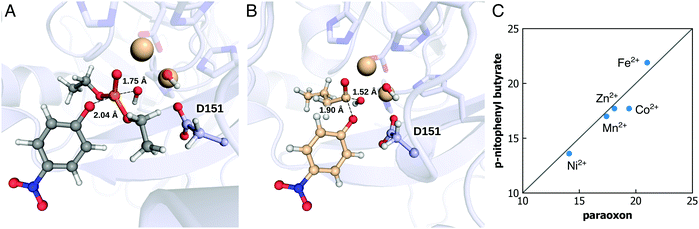Fig. 7 The transition states of methyl parathion hydrolase (MPH), with two metal ions in the active site and with (A) paraoxon or (B) p-nitrophenyl butyrate. (C) The calculated activation free energy for hydrolysis of two different substrates by MPH, in the presence of different metal ions (i.e., Ni²⁺, Mn²⁺, Zn²⁺, Co²⁺, and Fe²⁺). Panels (A) and (B) are reproduced with permission from ref. 84. Figure originally published in the Philos. Trans. R. Soc., A under a Creative Commons CC-BY license. Panel C is assembled from the data published in the same reference.

We recently performed a detailed EVB study of both the arylesterase and the organophosphatase activities of MPH in complex with five different metal ions (Zn²⁺, Fe²⁺, Co²⁺, Ni²⁺, and Mn²⁺, Fig. 7C).⁸⁴ A key difference between the two substrates is the preferred angle of attack between the oxygen atom of the incoming nucleophile, the C/P atom of the relevant substrate, and the oxygen atom of the bond being cleaved; in the case of the organophosphate substrate, this is preferentially in-line at 180°, whereas in the case of the arylester, the preferred angle of attack is a Bürgi–Dunitz angle at least of 90°.⁸⁴ As discussed in our previous work,⁸⁴ this affects the preferential substrate binding pose for efficient chemistry, and, thus, the key stabilizing interactions at the transition state. Therefore, differences in catalytic efficiency between the different substrates are to be expected. However, understanding differences in catalytic efficiency for the same substrate between the different metal ions is more challenging. Our multi-site model was able to reproduce experimental data with excellent accuracy, but both the transition states and the stabilizing interactions were extremely similar between the different metal ions (for each substrate). Despite these similarities, our calculations could reproduce the up to 4 kcal mol⁻¹ differences in activation free energy between the different metal ions.

What our model suggested was that rather than major structural differences at the transition state or changes in interactions between the transition state and the surrounding enzyme, the biggest difference between the different systems was the electrostatic properties of the metal ions themselves, which were implicitly accounted for in the parameterization of our multi-site models, and which led to different degrees of transition state stabilization, depending on which metal ion was being considered. This observation points to electrostatic flexibility. However, contrary to what we see in the case of the alkaline phosphatases,⁶³ in the case of MPH we observed a local electrostatic flexibility in terms of the properties of the metal ions, driving the evolution of new functions and emergence of cryptic promiscuous activities.⁸⁴

Other systems of interest to us have been serum paraoxonase 1 (PON1)^94,95 and diisopropyl fluorophosphatase (DFPase).¹²¹ Both enzymes are six-blade β-propellers, with the active site located in the central tunnel of the propeller (Fig. 8).^128–131 In addition, both enzymes bind two Ca²⁺ ions that are 7.4 Å apart in PON1 and 9.4 Å apart in DFPase.¹³¹ The Ca²⁺ ion buried more deeply into the central tunnel of the β-propeller plays a primarily structural role, whereas the more solvent exposed Ca²⁺ ion is catalytically important.¹³¹ In addition, PON1 (but not DFPase) associates with high density lipoprotein (HDL) in vivo, and is dependent on lipid association for its biological function, as the tertiary structure otherwise quickly and irreversibly unfolds.^132,133 Indeed, experiments with this system are typically conducted in the presence of lipid or detergent micelles,^134–136 or reconstituted HDL (rHDL).^94,133

Fig. 8 Comparison of serum paraoxonase 1 (PON1, blue) and DFPase (brown), highlighting also their respective Ca²⁺ ions and active site residues. Here, H1 and H2 denote the H1 and H2 helices, discussed in the text. On the right side, a closer view of the active site with the key catalytic residues is shown. This figure is modified with permission from ref. 121. Copyright the American Chemical Society.

There have been a number of computational studies of both PON1 and DFPase that have primarily focused on either (1) trying to elucidate the catalytic mechanism for this enzyme,^{94,95,120,128,137} or (2) to obtain insights into either membrane association^94,138 or the dynamics of a catalytically important active site loop^95,139 that is far more flexible in PON1 than in DFPase.¹⁴⁰ In our case, we have addressed a number of issues using a combination of EVB simulations and structural bioinformatics tools. As our starting point, we explored the mechanisms of both organophosphate (paraoxon) and lactone (5-thiobutyl butyrolactone, TBBL) hydrolysis by this enzyme, as a baseline to indirectly probe the effect of membrane binding on the catalytic activity. Specifically, experimental data shows that the native lactonase activity of PON1 is substantially stimulated (enhanced) when binding to rHDL compared to lipid and detergent micelles, whereas the corresponding promiscuous organophosphatase activity is barely affected.⁹⁴ We would like to point out that there is no structure of PON1, or indeed any other enzyme, in complex with HDL, which prevents building appropriate models. Therefore, we decided to examine this problem indirectly, by creating models of PON1 in which perturbed structures of the membrane-binding helices (highlighted in Fig. 8) were obtained through normal mode analysis, mimicking the structural perturbations caused by membrane binding. These perturbed conformations were then restrained in subsequent EVB simulations of the catalytic activity. Our simulations showed, in agreement with the experimental data, that these structural perturbations had a much more radical impact on the lactonase than the organophosphatase activity, and both experiment and computation pointed to the origin of this effect being the rigidification of a key catalytically important hydrogen bonding network that extends over 15 Å from the surface H2 helix (K192) of PON1, through the catalytic calcium ion (Fig. 8). It would appear that membrane association freezes out catalytically unfavourable motions along this hydrogen-bonding network, thus increasing the likelihood of PON1 being found in a catalytically competent conformation.⁹⁴

We have, in addition, performed a combined experimental and computational study of the relationships between the flexibility of the PON1 active site loop and the catalytic activity of this enzyme through mutations of a key residue, Y71, that sits at the tip of this loop and forms a hydrogen bonding interaction with D183 (Fig. 8). Residue D183 is a key participant in the hydrogen bonding network along the central tunnel of PON1, as it forms hydrogen bonding interactions with several other residues, including Y71, N168, H184, and K192. Therefore, substitutions of this residue have been experimentally shown to be drastic for the catalytic activity of this enzyme.^94,95 As would be expected, mutations of Y71 result in the loss of this hydrogen bonding interactions, and a concomitant increase in loop flexibility and solvent-accessibility of the active site (Fig. 9). These mutations result in a minimal effect on the native lactonase activity (which would be expected to be more robust), whereas they have a detrimental effect of up to 2.8 kcal mol⁻¹ increase in activation free energy (Y71G) for the promiscuous organophosphatase activity.⁹⁵ Both substrates are large, “greasy” molecules, where one would expect increased solvation of the active site to have a negative impact on the corresponding catalytic activities. However, our calculations⁹⁵ (Fig. 9) suggest that the active site of even wild-type PON1 is already far more solvated when TBBL is bound than when paraoxon is bound, and therefore the differential upon mutating Y71 is much larger for paraoxon than for TBBL, leading to the much greater loss in catalytic activity. There are several examples of lactonases that have evolved the ability to hydrolyze organophosphates,^141–145 and a comparison of different organophosphates in the literature shows a general tendency to either have deep buried active sites, or “floppy” active site loops that can sequester the active site from solvent (see discussion in ref. 59 and 95). Based on our data and other examples in the literature, we proposed that active site hydrophobicity, which is a necessary feature for the hydrolysis of hydrophobic substrates such as lactones, is a key driver in the evolution of organophosphatase activity.⁹⁴

Fig. 9 Active site of serum paraoxonase 1 (PON1) WT and Y71G mutant with paraoxon (A and B) and 5-thiobutyl butyrolactone (TBBL, panels C and D) in the transition state. Mutation to glycine shows stronger solvation of the active site. Figure is reproduced with permission from ref. 95. Copyright the American Chemical Society.

Finally, we have performed a detailed mechanistic study of the hydrolysis of DFP by DFPase, considering not just EVB simulations of the chemical step of catalysis, but also mutational, temperature, and pH effects on the calculated activation free energies.¹²¹ Having established that DFPase and PON1 hydrolyze organophosphates through identical chemical mechanisms, this raises the question of why two enzymes with the same mechanism and with very similar active sites are not cross-promiscuous? That is, while both DFPase and PON1 are efficient catalysts of the hydrolysis of DFP and paraoxon, respectively, they are poor catalysts of the hydrolysis of each other's substrates.¹²¹ We performed a detailed analysis of the (lack of) cross-promiscuity between these two systems, illustrating in particular that in addition to expected structural and dynamical differences between the two enzymes, a key functional residue in PON1, D183, discussed above, is in fact severely detrimental to the DFPase activity of this enzyme due to electrostatic repulsion between the aspartate side chain and the fluoride leaving group.¹²¹ Understanding such differences in specificity at the fine molecular detail is an important first step towards re-engineering organophosphate hydrolases that can more efficiently break down highly neurotoxic organophosphate nerve agents with challenging leaving groups such as sarin (fluoride) or VX (thiol).

5 Understanding the mechanisms of biological GTP hydrolysis

We would like to touch upon some of the associated challenges with understanding the mechanisms of biological GTP hydrolysis. GTPases are a broad superclass of biologically crucial enzymes involved in all cellular functions, from signaling to protein synthesis to programmed cell death.^22,146,147 Many GTPases have similar active sites and constellations of key catalytic residues (Fig. 10),^148–152 and yet as with DFPase and PON1, small but subtle differences can be enough to result in substantially different catalytic efficiencies, in line with the different demands of their varied biological functions. The fine details of the mechanisms of GTP hydrolysis by this enzyme have been the subject of substantial debate, focusing on not just the nature of the transition state (associative vs. dissociative),²² but also the feasibility of substrate- vs. general-base assisted catalysis,^{34–36,92,153–157} as well as the involvement of one vs. two water molecules at the transition state for GTP hydrolysis.²² The broad disagreements in the literature highlight the challenges involved in studying these compounds, and why better computational tools that can distinguish between the different mechanistic pathways in a definitive way are clearly needed. We have examined these systems to some extent, using computational Eyring plots as a powerful tool to discriminate between different mechanistic alternatives,¹⁵⁸ as associative vs. dissociative transition states give very different thermodynamic parameters, and there is excellent experimental data available on these systems.^{91,92,146–148,150–152,154,159–161} Clearly, in order to make mechanistic conclusions, it is essential to be able to reproduce a range of (and ideally all) available experimental markers, and thus understanding the mechanisms of biological GTP hydrolysis remains not just a biochemically important problem that is not yet fully resolved, but also an excellent test of the quality of computational methodologies and their ability to make meaningful chemical predictions.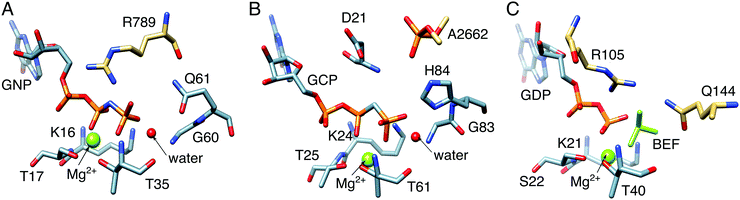

Fig. 10 Comparison between the active sites of (A) Ras GTPase activating protein (RasGAP) in complex with phosphonate guanosine diphosphate analogue (GNP, PDB IDs: 1CTQ and 1WQ1), (B) elongation factor Tu (EF-Tu) with guanosine triphosphate analogue (GCP, PDB ID: 2XQD), and (C) human Rab 1 in complex with GTPase-activating protein (GAP) and BeF₃²⁻ (PDB ID: 4HLQ). The key residues in these systems are the: (A) arginine finger, R789, (B) phosphate, A2662, from the sarcin–ricin loop (SRL) on the ribosome, and (C) arginine–glutamine finger, i.e., R105 and Q144, from the corresponding GAP.

6 Overview and conclusions

The controlled formation and cleavage of phosphate ester bonds lies at the heart of biology, and yet the mechanisms of these reactions have remained controversial and often poorly understood. The controversies are in part driven by the inherent mechanistic complexity of these reactions, and in part by the apparent contradictions between experimental and computational (and also computational vs. computational) predictions (often for the same system). Understanding the mechanisms, specificity, and evolution of biological phosphate hydrolysis has been a topic of great interest to our research team, and an area where we have invested substantial computational effort. We have discussed herein some of the major computational challenges involved in studying these mechanistic chameleons, using examples from our own work as showcase systems. We also demonstrate that advances in both computer power and new computational approaches have allowed us (and others) to address problems that would have been unthinkable just a decade ago. These advances make it possible to not only provide more rigorous models for existing open questions, such as understanding the fundamental mechanisms of phosphate transfer in key systems, but also to address increasingly challenging problems such as the fine details of molecular evolution,^60,63,121 or the operation of molecular machines.^162,163 The latter point is provided, however, that the computational approaches are sufficiently accurate in their description of structural and energetic changes in the systems of interest, in order to be able to reliably capture the subtle differences that can control the switch from one function to another. At present, even the best computational approaches do not provide accuracies of better than 1 kcal mol⁻¹, if even that, for large biomolecular systems. Therefore, although phosphate hydrolysis is by now an “old” reaction, there remain many new paths to follow, and we believe the coming years will be an exciting time for the field, both in terms of resolving existing mechanistic controversies as well as in tackling new biological problems, such as for instance designing novel phosphatases with tailored catalytic properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by a Wallenberg Academy Fellowship to SCLK from the Knut and Alice Wallenberg Foundation (KAW 2013.0124).

References

1. F. H. Westheimer, Science, 1987, 235, 1173–1178.
2. J. K. Lassila, J. G. Zalatan and D. Herschlag, Annu. Rev. Biochem., 2011, 80, 669–702.
3. S. C. Kamerlin, P. K. Sharma, R. B. Prasad and A. Warshel, Q. Rev. Biophys., 2013, 46, 1–132.
4. R. Wolfenden, Chem. Rev., 2006, 106, 3379–3396.
5. A. Radzicka and R. Wolfenden, Science, 1995, 267, 90–93.
6. R. Wolfenden, C. Ridgway and G. Young, J. Am. Chem. Soc., 1998, 120, 833–834.
7. C. Lad, N. H. Williams and R. Wolfenden, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5607–5610.
8. G. K. Schroeder, C. Lad, P. Wyman, N. H. Williams and R. Wolfenden, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 4052–4055.
9. P. Cohen, Nat. Rev. Drug Discovery, 2002, 1, 309–315.
10. S. Zhang and Z.-Y. Zhang, Drug Discovery Today, 2007, 12, 373–381.
11. A. J. Barr, Future Med. Chem., 2010, 2, 1563–1576.
12. A. J. Kirby and W. P. Jencks, J. Am. Chem. Soc., 1965, 87, 3209–3216.
13. A. J. Kirby and A. G. Varvoglis, J. Am. Chem. Soc., 1967, 89, 415–423.
14. A. C. Hengge, W. A. Edens and H. Elsing, J. Am. Chem. Soc., 1994, 116, 5045–5049.
15. F. Duarte, B. A. Amrein and S. C. Kamerlin, Phys. Chem. Chem. Phys., 2013, 15, 11160–11177.
16. M. W. van der Kamp and A. J. Mulholland, Biochemistry, 2013, 52, 2708–2728.
17. F. Duarte, J. Åqvist, N. H. Williams and S. C. Kamerlin, J. Am. Chem. Soc., 2015, 137, 1081–1093.
18. J. Florián and A. Warshel, J. Phys. Chem. B, 1998, 102, 719–734.
19. J. Åqvist, K. Kolmodin, J. Florian and A. Warshel, Chem. Biol., 1999, 6, R71–R80.
20. F. Duarte, A. Barrozo, J. Åqvist, N. H. Williams and S. C. Kamerlin, J. Am. Chem. Soc., 2016, 138, 10664–10673.
21. E. Ghanem and F. M. Raushel, Toxicol. Appl. Pharmacol., 2005, 207, 459–470.
22. A. T. P. Carvalho, K. Szeler, K. Vavitsas, J. Åqvist and S. C. L. Kamerlin, Arch. Biochem. Biophys., 2015, 582, 80–90.
23. S. C. Kamerlin, J. Org. Chem., 2011, 76, 9228–9238.
24. A. Pabis, N. H. Williams and S. C. L. Kamerlin, Org. Biomol. Chem., 2017, 15, 7308–7316.
25. A. Barrozo, D. Blaha-Nelson, N. H. Williams and S. C. L. Kamerlin, Pure Appl. Chem., 2017, 89, 715–727.
26. A. C. Hengge, Acc. Chem. Res., 2002, 35, 105–112.
27. R. H. Hoff, P. Larsen and A. C. Hengge, J. Am. Chem. Soc., 2001, 123, 9338–9344.
28. T. Yamamoto, Chem. Phys. Lett., 2010, 500, 263–266.
29. M. Klähn, E. Rosta and A. Warshel, J. Am. Chem. Soc., 2006, 128, 15310–15323.
30. S. C. Kamerlin, J. Florián and A. Warshel, ChemPhysChem, 2008, 9, 1767–1773.
31. N. Iché-Tarrat, M. Ruiz-Lopez, J.-C. Barthelat and A. Vigroux, Chem. – Eur. J., 2007, 13, 3617–3629.
32. P. Thaplyal and P. C. Bevilacqua, in Methods in Enzymology, ed. D. H. Burke-Aguero, Academic Press, 2014, vol. 549, pp. 189–219.
33. S. J. Admiraal and D. Herschlag, J. Am. Chem. Soc., 2000, 122, 2145–2148.
34. W. Dall'Acqua and P. Carter, Protein Sci., 2000, 9, 1–9.
35. S. Pasqualato and J. Cherfils, Structure, 2005, 13, 533–540.
36. T. Schweins, M. Geyer, K. Scheffzek, A. Warshel, H. R. Kalbitzer and A. Wittinghofer, Nat. Struct. Biol., 1995, 2, 36–44.
37. L. F. Olguin, S. E. Askew, A. C. O'Donoghue and F. Hollfelder, J. Am. Chem. Soc., 2008, 130, 16547–16555.
38. S. Jonas and F. Hollfelder, Pure Appl. Chem., 2009, 81, 731.
39. J. Purcell and A. C. Hengge, J. Org. Chem., 2005, 70, 8437–8442.
40. L. Zhang, D. Xie, D. Xu and H. Guo, Chem. Commun., 2007, 1638–1640.
41. D. E. C. Ferreira, B. P. D. Florentino, W. R. Rocha and F. Nome, J. Phys. Chem. B, 2009, 113, 14831–14836.
42. J. Florían and A. Warshel, J. Am. Chem. Soc., 1997, 119, 5473–5474.
43. S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Int. J. Quantum Chem., 2015, 115, 258–269.
44. W. P. Jencks, Chem. Rev., 1985, 85, 511–527.
45. R. A. M. O'Ferrall, J. Chem. Soc. B, 1970, 274–277.
46. I. H. Williams and G. M. Maggiora, THEOCHEM, 1982, 89, 365–378.
47. R. B. Prasad, N. V. Plotnikov and A. Warshel, J. Phys. Chem. B, 2013, 117, 153–163.
48. S. C. L. Kamerlin, M. Haranczyk and A. Warshel, ChemPhysChem, 2009, 10, 1125–1134.
49. E. Nikitina, V. Sulimov, F. Grigoriev, O. Kondakova and S. Luschekina, Int. J. Quantum Chem., 2006, 106, 1943–1963.
50. G. Brancato, N. Rega and V. Barone, J. Chem. Phys., 2008, 128, 144501.
51. N. Bourne and A. Williams, J. Am. Chem. Soc., 1984, 106, 7591–7596.
52. E. Rosta, S. C. L. Kamerlin and A. Warshel, Biochemistry, 2008, 47, 3725–3735.
53. A. Alkherraz, S. C. L. Kamerlin, G. Feng, Q. I. Sheikh, A. Warshel and N. H. Williams, Faraday Discuss., 2010, 145, 281–299.
54. F. Duarte, T. Geng, G. Marloie, A. O. Al Hussain, N. H. Williams and S. C. L. Kamerlin, J. Org. Chem., 2014, 79, 2816–2828.
55. M. F. Mohamed and F. Hollfelder, Biochim. Biophys. Acta, Proteins Proteomics, 2013, 1834, 417–424.
56. R. A. Jensen, Annu. Rev. Microbiol., 1976, 30, 409–425.
57. P. J. O'Brien and D. Herschlag, Chem. Biol., 1999, 6, R91–R105.
58. O. Khersonsky and D. S. Tawfik, Annu. Rev. Biochem., 2010, 79, 471–505.
59. A. Pabis, F. Duarte and S. C. L. Kamerlin, Biochemistry, 2016, 55, 3061–3081.
60. A. Pabis and S. C. Kamerlin, Curr. Opin. Struct. Biol., 2016, 37, 14–21.
61. A. Kim, M. M. Benning, S. OkLee, J. Quinn, B. M. Martin, H. M. Holden and D. Dunaway-Mariano, Biochemistry, 2011, 50, 3481–3494.
62. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
63. A. Barrozo, F. Duarte, P. Bauer, A. T. Carvalho and S. C. Kamerlin, J. Am. Chem. Soc., 2015, 137, 9061–9076.
64. J. Luo, B. van Loo and S. C. Kamerlin, FEBS Lett., 2012, 586, 1622–1630.
65. T. Mariano, N. Russo and M. Toscano, Chem. – Eur. J., 2013, 19, 2185–2192.
66. R.-Z. Liao and P. E. M. Siegbahn, Inorg. Chem., 2015, 54, 11941–11947.
67. A. C. Babtie, S. Bandyopadhyay, L. F. Olguin and F. Hollfelder, Angew. Chem., Int. Ed., 2009, 48, 3692–3694.
68. I. Boltes, H. Czapinska, A. Kahnert, R. von Bülow, T. Dierks, B. Schmidt, K. von Figura, M. A. Kertesz and I. Usón, Structure, 2001, 9, 483–491.
69. M. L. Applebury and J. E. Coleman, J. Biol. Chem., 1969, 244, 308–318.
70. J. E. Coleman, Annu. Rev. Biophys. Biomol. Struct., 1992, 21, 441–483.
71. P. J. O'Brien and D. Herschlag, J. Am. Chem. Soc., 1998, 120, 12369–12370.
72. P. J. O'Brien and D. Herschlag, Biochemistry, 2001, 40, 5691–5699.
73. R. Gijsbers, H. Ceulemans, W. Stalmans and M. Bollen, J. Biol. Chem., 2001, 276, 1361–1368.
74. J. G. Zalatan, T. D. Fenn, A. T. Brunger and D. Herschlag, Biochemistry, 2006, 45, 9788–9803.
75. S. Jonas, B. van Loo, M. Hyvönen and F. Hollfelder, J. Mol. Biol., 2008, 384, 120–136.
76. B. van Loo, S. Jonas, A. C. Babtie, A. Benjdia, O. Berteau, M. Hyvönen and F. Hollfelder, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2740–2745.
77. L. Banci, Curr. Opin. Chem. Biol., 2003, 7, 143–149.
78. P. Li and K. M. Merz, Jr., Chem. Rev., 2017, 117, 1564–1686.
79. J. Åqvist and A. Warshel, J. Am. Chem. Soc., 1990, 112, 2860–2868.
80. F. Duarte, P. Bauer, A. Barrozo, B. A. Amrein, M. Purg, J. Åqvist and S. C. L. Kamerlin, J. Phys. Chem. B, 2014, 118, 4351–4362.
81. Q. Liao, S. C. Kamerlin and B. Strodel, J. Phys. Chem. Lett., 2015, 6, 2657–2662.
82. P. Li and K. M. Merz, Jr., J. Chem. Theory Comput., 2014, 10, 289–297.
83. Q. Liao, A. Pabis, B. Strodel and S. C. L. Kamerlin, J. Phys. Chem. Lett., 2017, 8, 5408–5414.
84. M. Purg, A. Pabis, F. Baier, N. Tokuriki, C. Jackson and S. C. L. Kamerlin, Philos. Trans. R. Soc., A, 2016, 374, 20160150.
85. N. J. Baxter, G. M. Blackburn, J. P. Marston, A. M. Hounslow, M. J. Cliff, W. Bermel, N. H. Williams, F. Hollfelder, D. E. Wemmer and J. P. Waltho, J. Am. Chem. Soc., 2008, 130, 3952–3958.
86. A. Warshel and R. M. Weiss, J. Am. Chem. Soc., 1980, 102, 6218–6226.
87. A. Warshel, Computer modeling of chemical reactions in enzymes and solutions, Wiley, New York, 1991.
88. Theory and Applications of the Empirical Valence Bond Approach: From Physical Chemistry to Chemical Biology, ed. F. Duarte and S. C. L. Kamerlin, Wiley, Chichester, West Sussex, 2017.
89. S. C. L. Kamerlin and A. Warshel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 30–45.
90. A. Shurki, E. Derat, A. Barrozo and S. C. L. Kamerlin, Chem. Soc. Rev., 2015, 44, 1037–1052.
91. A. J. Scheidig, C. Burmester and R. S. Goody, Structure, 1999, 7, 1311–1324.
92. T. Zor, M. Bar-Yaacov, S. Elgavish, B. Shaanan and Z. Selinger, Eur. J. Biochem., 1997, 249, 330–336.
93. J. Luo, B. van Loo and S. C. L. Kamerlin, Proteins: Struct., Funct., Bioinf., 2012, 80, 1211–1226.
94. M. Ben-David, J. L. Sussman, C. I. Maxwell, K. Szeler, S. C. L. Kamerlin and D. S. Tawfik, J. Mol. Biol., 2015, 427, 1359–1374.
95. D. Blaha-Nelson, D. M. Krüger, K. Szeler, M. Ben-David and S. C. L. Kamerlin, J. Am. Chem. Soc., 2017, 139, 1155–1167.
96. M. Ben-David, M. Elias, J.-J. Filippi, E. Duñach, I. Silman, J. L. Sussman and D. S. Tawfik, J. Mol. Biol., 2012, 418, 181–196.
97. D. Roston and Q. Cui, J. Am. Chem. Soc., 2016, 138, 11946–11957.
98. D. Roston, D. Demapan and Q. Cui, J. Am. Chem. Soc., 2016, 138, 7386–7394.
99. V. López-Canut, M. Roca, J. Bertrán, V. Moliner and I. Tuñón, J. Am. Chem. Soc., 2010, 132, 6955–6963.
100. V. López-Canut, M. Roca, J. Bertrán, V. Moliner and I. Tuñón, J. Am. Chem. Soc., 2011, 133, 12050–12062.
101. G. Hou and Q. Cui, J. Am. Chem. Soc., 2013, 135, 10457–10469.
102. G. Hou and Q. Cui, J. Am. Chem. Soc., 2012, 134, 229–246.
103. M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948.
104. F. Sunden, A. Peck, J. Salzman, S. Ressl and D. Herschlag, eLife, 2015, 4, e06181.
105. F. Sunden, I. AlSadhan, A. Y. Lyubimov, S. Ressl, H. Wiersma-Koch, J. Borland, C. L. Brown, Jr., T. A. Johnson, Z. Singh and D. Herschlag, J. Am. Chem. Soc., 2016, 138, 14273–14287.
106. F. Sunden, I. AlSadhan, A. Lyubimov, T. Doukov, J. Swan and D. Herschlag, J. Biol. Chem., 2017, 292, 20960–20974.
107. C. D. Bayer, B. van Loo and F. Hollfelder, ChemBioChem, 2017, 18, 1001–1015.
108. Y. Ashani, N. Rothschild, Y. Segall, D. Levanon and L. Raveh, Life Sci., 1991, 49, 367–374.
109. S. B. Bird, T. D. Sutherland, C. Gresham, J. Oakeshott, C. Scott and M. Eddleston, Toxicology, 2008, 247, 88–92.
110. L. Gaidukov, D. Bar, S. Yacobson, E. Naftali, O. Kaufman, R. Tabakman, D. S. Tawfik and E. Levy-Nissenbaum, BMC Clin. Pharmacol., 2009, 9, 18.
111. L. Raveh, Y. Segall, H. Leader, N. Rothschild, D. Levanon, Y. Henis and Y. Ashani, Biochem. Pharmacol., 1992, 44, 397–400.
112. R. C. Stevens, S. M. Suzuki, T. B. Cole, S. S. Park, R. J. Richter and C. E. Furlong, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12780–12784.
113. W. N. Aldridge and E. Reiner, Enzyme inhibitors as substrates: interactions of esterases with esters of organophosphorus and carbamic acids, North-Holland, 1972.
114. T. C. Kwong, Ther. Drug Monit., 2002, 24, 144–149.
115. K. E. LeJeune, J. R. Wild and A. J. Russell, Nature, 1998, 395, 27–28.
116. D. Ecobichon, in Casarett and Doull's Toxicology: The Basic Science of Poisons, ed., C. D. Klaassen, McGraw-Hill, New York, 1996, pp. 643–689.
117. F. M. Raushel, Curr. Opin. Microbiol., 2002, 5, 288–295.
118. S.-B. Hong and F. M. Raushel, Biochemistry, 1999, 38, 1159–1165.
119. G. Schenk, I. Mateen, T.-K. Ng, M. M. Pedroso, N. Mitić, M. Jafelicci, Jr., R. F. C. Marques, L. R. Gahan and D. L. Ollis, Coord. Chem. Rev., 2016, 317, 122–131.
120. A. N. Bigley and F. M. Raushel, Biochim. Biophys. Acta, Proteins Proteomics, 2013, 1834, 443–453.
121. M. Purg, M. Elias and S. C. L. Kamerlin, J. Am. Chem. Soc., 2017, 139, 17533–17546.
122. O. Khersonsky and D. S. Tawfik, Biochemistry, 2005, 44, 6371–6382.
123. M. Elias and D. S. Tawfik, J. Biol. Chem., 2012, 287, 11–20.
124. M. Goldsmith, Y. Ashani, Y. Simo, M. Ben-David, H. Leader, I. Silman, J. L. Sussman and D. S. Tawfik, Chem. Biol., 2012, 19, 456–466.
125. S.-L. Chen, W.-H. Fang and F. Himo, J. Phys. Chem. B, 2007, 111, 1253–1255.
126. J. Kim, P.-C. Tsai, S.-L. Chen, F. Himo, S. C. Almo and F. M. Raushel, Biochemistry, 2008, 47, 9497–9504.
127. S. D. Aubert, Y. Li and F. M. Raushel, Biochemistry, 2004, 43, 5707–5715.
128. T. Wymore, M. J. Field, P. Langan, J. C. Smith and J. M. Parks, J. Phys. Chem. B, 2014, 118, 4479–4489.
129. J. C.-H. Chen, M. Mustyakimov, B. P. Schoenborn, P. Langan and M. M. Blum, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 1131–1138.
130. M.-M. Blum, M. Mustyakimov, H. Rüterjans, K. Kehe, B. P. Schoenborn, P. Langan and J. C.-H. Chen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 713–718.
131. M. Harel, A. Aharoni, L. Gaidukov, B. Brumshtein, O. Khersonsky, R. Meged, H. Dvir, R. B. Ravelli, A. McCarthy, L. Toker, I. Silman, J. L. Sussman and D. S. Tawfik, Nat. Struct. Mol. Biol., 2004, 11, 412–419.
132. C.-L. Kuo and B. N. La Du, Drug Metab. Dispos., 1998, 26, 653–660.
133. L. Gaidukov and D. S. Tawfik, Biochemistry, 2005, 44, 11843–11854.
134. R. C. Sorenson, C. L. Bisgaier, M. Aviram, C. Hsu, S. Billecke and B. N. La Du, Arterioscler., Thromb., Vasc. Biol., 1999, 19, 2214–2225.
135. S. Deakin, I. Leviev, M. Gomaraschi, L. Calabresi, G. Franceschini and R. W. James, J. Biol. Chem., 2002, 277, 4301–4308.
136. D. Josse, C. Ebel, D. Stroebel, A. Fontaine, F. Borges, A. Echalier, D. Baud, F. Renault, M. le Maire, E. Chabrières and P. Masson, J. Biol. Chem., 2002, 277, 33386–33397.
137. Q. A. T. Le, S. Kim, R. Chang and Y. H. Kim, J. Phys. Chem. B, 2015, 119, 9571–9585.
138. M. C. Patra, S. N. Rath, S. K. Pradhan, J. Maharana and S. De, Eur. Biophys. J., 2014, 43, 35–51.
139. K. Amine, L. Miri, A. Naimi, R. Saile, A. El Kharrim, A. Mikou and A. Kettani, Bioinf. Biol. Insights, 2015, 9, 129–140.
140. M.-M. Blum, F. Löhr, A. Richardt, H. Rüterjans and J. C.-H. Chen, J. Am. Chem. Soc., 2006, 128, 12750–12757.
141. M. M. Meier, C. Rajendran, C. Malisi, N. G. Fox, C. Xu, S. Schlee, D. P. Barondeau, B. Höcker, R. Sterner and F. M. Raushel, J. Am. Chem. Soc., 2013, 135, 11670–11677.
142. Y. Zhang, J. An, W. Ye, G. Yang, Z.-G. Qian, H.-F. Chen, L. Cui and Y. Feng, Appl. Environ. Microbiol., 2012, 78, 6647–6655.
143. M. Elias, J. Dupuy, L. Merone, L. Mandrich, E. Porzio, S. Moniot, D. Rochu, C. Lecomte, M. Rossi, P. Masson, G. Manco and E. Chabriere, J. Mol. Biol., 2008, 379, 1017–1028.
144. C. Roodveldt and D. S. Tawfik, Biochemistry, 2005, 44, 12728–12736.
145. O. Khersonsky and D. S. Tawfik, Biochemistry, 2005, 44, 6371–6382.
146. A. B. Jaffe and A. Hall, Annu. Rev. Cell Dev. Biol., 2005, 21, 247–269.
147. S. J. Heasman and A. J. Ridley, Nat. Rev. Mol. Cell Biol., 2008, 9, 690–701.
148. A. Seshadri, L. Samhita, R. Gaur, V. Malshetty and U. Varshney, Tuberculosis, 2009, 89, 453–464.
149. T. J. P. van Dam, F. J. T. Zwartkruis, J. L. Bos and B. Snel, J. Mol. Evol., 2011, 73, 209–220.
150. J. Colicelli, Sci. Signaling, 2004, 2004, RE13.
151. K. Wennerberg, K. L. Rossman and C. J. Der, J. Cell Sci., 2005, 118, 843–846.
152. C. Kötting and K. Gerwert, FEBS Lett., 2013, 587, 2025–2027.
153. R. Langen, T. Schweins and A. Warshel, Biochemistry, 1992, 31, 8691–8696.
154. T. Zor, R. Andorn, I. Sofer, M. Chorev and Z. Selinger, FEBS Lett., 1998, 433, 326–330.
155. M. Kosloff and Z. Selinger, Trends Biochem. Sci., 2001, 26, 161–166.
156. A. J. Adamczyk, J. Cao, S. C. Kamerlin and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 14115–14120.
157. J. Åqvist and S. C. Kamerlin, Biochemistry, 2015, 54, 546–556.
158. J. Åqvist and S. C. L. Kamerlin, Sci. Rep., 2015, 5, 15817.
159. C. Allin, M. R. Ahmadian, A. Wittinghofer and K. Gerwert, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7754–7759.
160. R. M. Voorhees, T. M. Schmeing, A. C. Kelley and V. Ramakrishnan, Science, 2010, 330, 835–838.
161. D. S. Tourigny, I. S. Fernández, A. C. Kelley and V. Ramakrishnan, Science, 2013, 340, 1235490.
162. S. Mukherjee and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14876–14881.
163. S. Mukherjee and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20550–20555.

---

Footnote

† These authors contributed equally to this work.

---