Open Access Article
Open Access ArticleEstimating and correcting interference fringes in infrared spectra in infrared hyperspectral imaging
Ghazal
Azarfar
 a,
Ebrahim
Aboualizadeh
a,
Ebrahim
Aboualizadeh
 b,
Nicholas M.
Walter
b,
Nicholas M.
Walter
 b,
Simona
Ratti
c,
Camilla
Olivieri
c,
Alessandra
Norici
c,
Michael
Nasse
d,
Achim
Kohler
e,
Mario
Giordano
b,
Simona
Ratti
c,
Camilla
Olivieri
c,
Alessandra
Norici
c,
Michael
Nasse
d,
Achim
Kohler
e,
Mario
Giordano
 c and
Carol J.
Hirschmugl
c and
Carol J.
Hirschmugl
 *ab
*ab
aDepartment of Electrical Engineering, University of Wisconsin-Milwaukee, Milwaukee, WI, USA
bDepartment of Physics, University of Wisconsin-Milwaukee, Milwaukee, WI, USA. E-mail: cjhirsch@uwm.edu; Tel: +1-414-229-5748
cDipartimento di Scienze della vita e dell’ambiente (DISVA), Università Politecnica delle Marche, Ancona, Italy
dKarlsruhe Institute of Technology, Karlsruhe, Germany
eFaculty of Science and Technology, Norwegian University of Life Sciences, Ås, Norway
First published on 3rd September 2018
Abstract
Short-term acclimation response of individual cells of Thalassiosira weissflogii was monitored by Synchrotron FTIR imaging over the span of 75 minutes. The cells, collected from batch cultures, were maintained in a constant flow of medium, at an irradiance of 120 μmol m−2 s−1 and at 20 °C. Multiple internal reflections due to the micro fluidic channel were modeled, and showed that fringes are additive sinusoids to the pure absorption of the other components of the system. Preprocessing of the hyperspectral cube (x, y, Abs(λ)) included removing spectral fringe using an EMSC approach. Principal component analysis of the time series of hyperspectral cubes showed macromolecular pool variations (carbohydrates, lipids and DNA/RNA) of less than 2% after fringe correction.
1. Introduction
Single cell chemical imaging, along with advanced methods of data evaluation and data analysis, reveals phenotypic differences in a population of diatoms.1 The ability to detect biologically important chemical bands by mid-infrared spectroscopy, such as those due to protein (Amide I and Amide II), lipids (CH2 and CH3), and carbohydrate, without labeling, makes Fourier transform infrared spectroscopy (FTIR) a desirable technique for the comprehension of compositional responses to environmental perturbation at a single cell level.2–7 By employing a high-resolution microscope equipped with a multi element infrared detector – focal plane array (FPA) – and a bright infrared source,8,9 chemical and structural variation of cells can be rapidly and reliably observed.Live cells must usually be maintained in an aqueous environment to maintain a “normal” biochemistry. However, water is highly absorbing in the mid-infrared,10,11 this constitutes a major obstacle to the utilization of FTIR spectroscopy for live cell analyses. A microfluidic channel that retains a micrometer thickness may represent a good compromise between the requirement to maintain the cells in a physiological state and the need to restrict the impact of water absorption on the biochemical signal. However prior studies12–15 revealed free flotation and mobility of the cell in this geometry, requiring rapid measurements, that reduces spectral resolution and signal to noise ratios (S/N). For example, microchannels with wedge shaped windows, that were originally designed for measuring absorbent liquids,15 have been modified to provide a controlled environment for live cell measurement in transmission mode.16,17 However, not all microscope geometries allow for such microfluidic chambers, such as high numerical aperture, small working distance objectives that require thin cross section microfluidic chambers. One such chamber consists of submicrometer thick diamond windows that are deposited on Si wafers.18 When the windows of microfluidic channel are separated by a distance close to the wavelength of probing radiation, multiple internal reflections are common, and lead to well understood spectral features (sinusoidal fringes) that hinder the analysis of the data.19 These sinusoidal spectral features are called fringes, and can impact the data analysis, when their amplitude is comparable to the desired spectral features.
There are two categories of fringe correction techniques: software based and hardware based. In hardware based techniques, the sample is rotated so that the angle of incidence is equal to the Brewster angle in order to achieve maximum transmittance.20–22 A spectrum measured by this technique is only accurate in low absorptivity regions, and this experimental geometry is not always feasible, such as with high magnification high numerical aperture objectives that require a wide range of incidence angles.
Various software-based techniques for fringe correction can be used to minimize the disturbance of biologically relevant information by spectral fringes generated by water absorption. Among these, interferogram editing, fringe fitting and subtraction from the spectrum,23–26 low frequency filtering,27,28 synthetic background generation based on the fringes in a sample interferogram,29 and digital filtering of the spectrum along with Savitzky–Golay30 algorithm. These methods, however, are limited to special cases and cannot always be applied effectively.
We propose an innovative approach to this problem which employs combination of sub-micron thick diamond windows18 and a bright synchrotron source.8,9 For live cell monitoring with high signal to noise and diffraction limited spatial resolution a Schwarzschild objective with high numerical aperture and small working distance is employed.
Single Thalassiosira weissflogii cells were monitored over the span of 2 hours to collect high quality hyperspectral cubes containing 64 × 64 × 1037 × 8 (x × y × λ × t) pieces of information covering spatial, spectral and temporal domains. Marine diatoms are responsible for up to 20% of global CO2 fixation. Their photosynthetic efficiency is enhanced by concentrating CO2 around Rubisco, diminishing photorespiration, but the mechanism is yet to be resolved.31Thalassiosira weissflogii is a species of centric diatoms, a unicellular microalgae and a congeneric of a model organism, Thalassiosira pseudonana. Thalassiosira weissflogii has an average size compare to other algal cells, and it is thin enough that infrared light can transmit through it.
Spectral and spatial fringes are observed in the raw measurements, and dominate principal components. Here, a preprocessing approach including fringe correction is proposed for live single cell synchrotron FTIR imaging, and subsequent data analysis is briefly demonstrated. The introduced fringe correction method is fast, flexible and can be adjusted with respect to the geometry of the sample.
2. Methods
2.1. Experiment
Batch cultures of the marine diatom Thalassiosira weissflogii were acclimated to ambient (390 ppm) CO2, and 30 μM NO3−, under constant irradiance of photosynthetically active radiation (PAR), at 20 °C. The algal cells were harvested by an automatic pipette and transferred to a microfluidic channel18 that supported a controlled aqueous environment with the same conditions as in the original cultures. Measurements were conducted on three independent biological replicates (i.e. three distinct cultures).A synchrotron based source (Infrared Environmental Imaging at the Synchrotron Radiation Center) coupled to a FTIR Bruker Hyperion 3000 microspectrometer with a focal plane array(FPA) detector (64 × 64 pixels)8,9 was used to collect spectrally resolved images of the algal samples. A 20× (0.6 NA) condenser objective was used to illuminate the sample, and a 74× objective (0.6 NA) was used to collect and image the transmitted radiation onto the detector, where a geometrical sample of 0.54 × 0.54 μm2 per pixel was obtained. The images were collected every 15 minutes for at least 2-hours. Individual algal cells were monitored across the spectral range of 850 cm−1 to 3850 cm−1 with a spectral resolution of 4 cm−1. However the spectra were truncated to 948 cm−1 to 2946 cm−1 due to total absorption of water. The spectra were smoothed using a Savitzky–Golay function of order 2 with 9 points.
Infrared transmission hyperspectral data cubes were obtained by collecting two sets of images, one reference or background hyperspectral data cube, and one sample data cube. Reference data cubes were taken from a location as close as possible to the algal cell being studied. The second set of data cubes (sample data cubes) were taken from a region including the algal cell. The division of a sample data cube by a reference data cube allowed to remove the background effects and resulted in a transmittance datacube. Obviously, since the reference image must be devoid of algal cells, it is not possible to select the same location for both the sample and reference. The difference between the two locations can (and typically does) lead to slightly different water thicknesses, generating spatial variations and spectral fringes with multiple frequencies.
2.2. Simulating fringes in IR transmittance spectra obtained with the micro fluidic channel
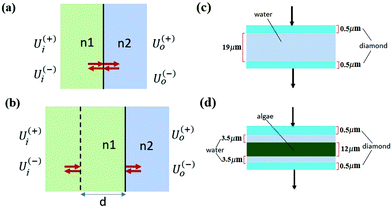
The matrix theory of optical systems32 was used to study fringe behavior in a micro fluidic channel. In this theory, the complex amplitude of the forward and backward waves through the boundaries of an optical system is calculated by use of matrix methods.33 The wave transfer matrix of a system relates the forward and backward collected waves at input and output planes of the system. The forward and backward waves collected at the input plane of the system are shown by Ui(+), and Ui(−), while Uo(+) and Uo(−) denote the forward and backward waves collected at the output plane. The wave-transfer matrix M, relates these set of forward and backward waves as follows: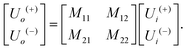 | (1) |
The wave transfer matrix of a multilayered medium, made of n layers is described by the matrix product of each single element. If the transmission matrix of each element is M1, M2, M3, … Mn, then the total transfer matrix is defined as:
| M = Mn…M2M1 | (2) |
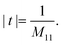 | (3) |
By solving the Maxwell's equations and applying suitable boundary conditions, the transfer matrix through a single dielectric boundary as shown in Fig. 1(a), with a refractive indexes of n1, and n2, is calculated as:33
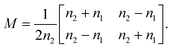 | (4) |
With the same approach, the transfer matrix through a homogeneous medium with a width of d, followed by a boundary as shown in Fig. 1(b) is described by:33
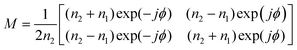 | (5) |
The water infrared spectrum was extracted from the KnowItAll spectral collection, and the algal cell standard was estimated by the method explained in the Appendix. The absorbance is defined, starting from transmittance:
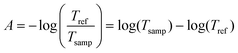 | (6) |
2.3. Fringe correction
Fringes were removed with an Extended Multiplicative Signal Correction (EMSC) method.34 EMSC is a model-based preprocessing technique that is extensively used for preprocessing of IR microspectroscopy data; it is based on Lambert–Beer law on the vibrational absorbance of materials.35 It models the absorption spectrum of a sample as the sum of its theoretical components. The EMSC model that is used to remove complex fringe patterns from spectra is the extension of the model presented by Konevskikh et al., 2015 for thin films.26 and is defined as follows: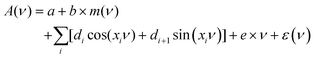 | (7) |
| A = Mscp + E | (8) |
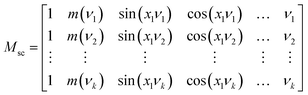 | (9) |
For the case of two parallel windows, with a distance d, a sinusoid with a constant frequency depending on the optical parameters of the assembly is added to the spectrum. Thus:
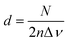 | (10) |
| ω = 4πnd | (11) |
The unit of the angular spatial frequency is rad cm, in the rest of the paper this quantity is called frequency and its unit is displayed as cm for simplicity. The corresponding angular frequency of the fringe was calculated to be 0.0327 to 0.0465 cm using eqn (11).
To determine the fringe frequencies of each measured spectrum, the Fast Fourier transform (FFT) of absorbance spectrum for the spectral region between 1766 to 2790 cm−1 was calculated. The region 1766 to 2790 cm−1 is chosen because the spectrum in this spectral range is dominated by the fringe effect and there are no absorption bands. A short spectral region in the absorbance spectrum was chosen to calculate the FFT, and then used to calculate the frequencies that expand across the entire spectral range. To accurately detect the frequency components for such a short range of information, spectra are zero padded in the wavenumber domain. FFT of a limited signal expands in Fourier domain, hence it is reasonable to select many frequencies to reconstruct the fringe and expand it across the entire spectral range. For this specific experiment the first 10 dominant frequencies larger than 0.0053 are chosen as the fringe frequencies. A low frequency band limit of 0.0053 is chosen such that the columns of matrix Msc in eqn (9) are orthogonal. Notice that for angular frequencies smaller than 0.0053, cosine columns of matrix Msc become ≈1.
In the Result and discussion section, we show that the dispersion impact was negligible in the micro channel, and the fringe pattern estimated by inserting these frequencies into eqn (7) can be extended to the other spectral regions. To remove the fringes, the approximated fringe pattern was subtracted from the raw spectrum. This procedure was repeated until no fringes were observed across the region of 1766 to 2790 cm−1.
In summary, the fringe correction algorithm is:
(a) Read the spectrum with fringes.
(b) Choose a region of spectrum where fringes are dominant, and there is no absorption band.
(c) Guess the number of dominant fringe frequencies, in the region selected in b.
(d) While there is fringe in the spectrum do:
(d.1) Calculate the FFT of the spectral region chosen in 2.
(d.2) Choose dominant fringe frequencies.
(d.3) Form matrix Msc.
(d.4) Estimate the fringe pattern across the whole spectral range by EMSC.
(d.5) Subtract the estimated fringe pattern from the spectrum.
2.4. Chemogram image
To investigate the spatial variation of the overall absorption of the sample, an integration under the spectral region (2947 cm−1–1693 cm−1 and 1585 cm−1–952 cm−1) was calculated for each pixel, excluding the water region. The resulting images, the so called chemograms, revealed the overall absorption bands and the fringes. An example is displayed in the first row of Fig. 4.2.5. Image segmentation
Fringes dominated the spectra in the regions of the image where there were no algal cells, since there are no relevant chemical absorption bands at that point in space. We used a mask to select pixels that contained algal cell absorption signatures for further chemical analysis. Our uniform approach to select the pixels within and outside the mask for each IR image is as follows: (1) generation of the image due to the Si–O peak at 1074 cm−1 (2) generation of the integrated image of silica region 1058 to 1089 cm−1 (3) addition of the two images, (4) use of Otsu's method36 to divide the pixels into two classes: class (1) cell and class (2) non-cell pixels.Otsu's method is an optimum global thresholding method based on Bayes decision rule, which maximizes between class variance of 1D array (as described below), which is a normalized histogram of an image.36 To apply Otsu's method to a given M × N image, the intensity values, I, can be grouped into L distinct levels to form a histogram, with ni the number of pixels with intensity level i. The probability of a pixel being assigned to intensity level i is then given by 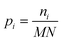 . For a given k∈[0, L], the histogram can be divided into two classes, C1, containing the pixels with intensities I∈[I0,Ik], and C2, containing the pixels with intensities I∈[Ik+1,IL−1]. The between-class variance of C1 and C2 can be maximized by finding k such that the quantity σB2 is maximized, which is defined as
. For a given k∈[0, L], the histogram can be divided into two classes, C1, containing the pixels with intensities I∈[I0,Ik], and C2, containing the pixels with intensities I∈[Ik+1,IL−1]. The between-class variance of C1 and C2 can be maximized by finding k such that the quantity σB2 is maximized, which is defined as
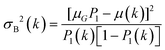 | (12) |
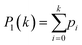 , and μ(k) is the average intensity up to level k
, and μ(k) is the average intensity up to level k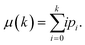 | (13) |
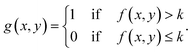 | (14) |
The threshold found by this algorithm selects 20% of the total pixels. The final mask is confirmed to be aligned with the algal cell observed in concurrently collected visible images. This approach facilitates automatic identification of all pixels within each cell at each time point.
2.6. Principal component analysis (PCA)
Principal Component Analysis (PCA) reduces the dimensionality of large data sets. When PCA is applied to spectral analysis (as a function of wavenumber) it facilitates further chemical analysis. Thus, the application of a PCA allows to decompose the spectra of the pixels selected from the masked data cubes into components. Since the spectra were not scaled, the first component is equivalent to an average spectrum of the entire data set being evaluated. The next components correspond to the variances from the average, and highlight the spectral features that are responsible for the chemical variations in the samples. The remaining components are dominated by noise. Approximately 5000 spectra were extracted from each individual algal cell (8 measurements over time span of two hours – 3 replicates) to identify the average spectrum and largest variance spatial components (PC2 and PC3). The original preprocessed spectra were fed into the MATLAB Statistics and Machine Learning Toolbox for PCA.Only wavenumber ranges of 2946 to 2489 cm−1, 2219 to 1702 cm−1, and 1581 to 950 cm−1 were considered as PCA variables to remove the impact of water and CO2 absorption bands.
3. Results and discussion
There needs to be sufficient water in the micro-fluidic chamber to maintain cells alive; too much water, however, would absorb all the incident infrared radiation across the entire bandwidth. The thin windows may bow under the pressure of the water, causing the spacing between the diamond windows to vary. This is important because amplitude and frequency of multiple internal reflection at the interface of diamond/water depends on the spacing between the diamond windows; since this spacing is not constant throughout the chamber, the extent of these reflections vary from measurement to measurement and from place to place within the assembly, and hinder the quality of chemical images.The geometry of the microfluidic channel leads to infrared images that contain both spatial variations and spectral fringes. Interpretation and statistical analysis of spectra with fringes can be misleading and even impossible. Appropriately executed fringe correction substantially improves the quality of images and spectra, and facilitates the analysis of the hyperspectral cube.
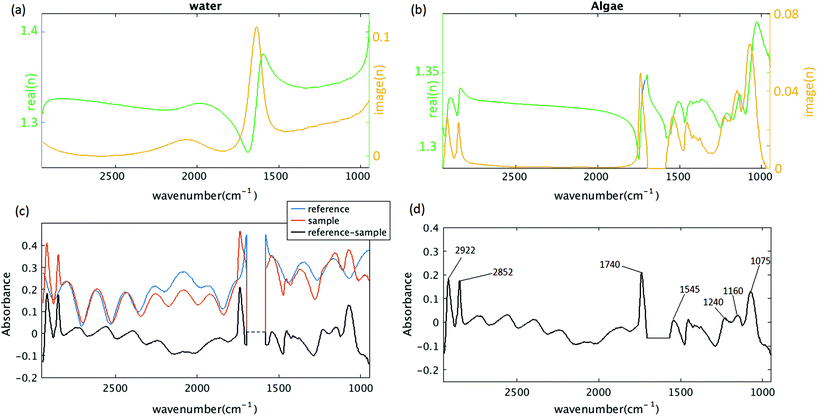
Recent work by Konevskikh et al., 201526 has demonstrated that fringes in a thin film with nominal refractive index of less than 2.4, can be determined and removed successfully from simulated data with a single frequency sinusoidal fringes impacting the spectra. Konevskikh et al.26 has shown the validity of the technique for a thin film of beef muscle tissue. Here, we have extended this work, modeling a micro fluidic channel as a seven layer assembly consisting of air, diamond window, water, algae, water, diamond window and air. The simulations show that dispersion effect are negligible in the micro fluidic channel, similar to Konevskikh et al., 201526 approach. We further extended prior work to account for multiple sinusoidal frequency components. Fig. 2(a) and (b) show the complex refractive indexes of the water, and algal cell, calculated by Kramers–Kronig. Fig. 2(c) shows simulated absorbance through the micro channel, with an algal cell (sample – red curve), compared to a region with no algal cell (reference – blue curve). The algae absorbance spectrum (black curve) is calculated by subtracting the reference from the sample spectrum using eqn (6). Fig. 2(d) shows the final simulated algal cell spectrum. In the measured data absorption is set to zero between 1580 to 1700 cm−1, since the bending vibration of the water absorption leads to a weak signal and is dominated by noise (see section B of the Appendix). The peaks at 1075 cm−1, corresponding to C–O–C/polysaccharides and Si–O of the silica shell,37 DNA–RNA at 1160 cm−1,38 P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 1240 cm−1,37 the N–H bending/Amide II for proteins at 1545 cm−1,37 C
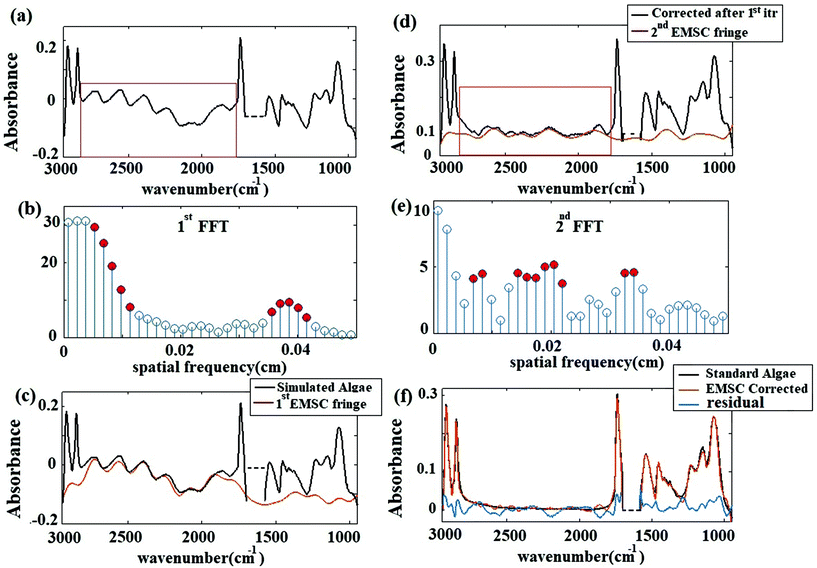
O at 1240 cm−1,37 the N–H bending/Amide II for proteins at 1545 cm−1,37 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch associated with phospholipid at 1740 cm−1(ref. 37) and CH2/lipid at 2852 cm−1 and 2922 cm−1(ref. 39) are present in the simulated data. The fringe correction algorithm applied to a simulated algal spectrum is illustrated in Fig. 3. A simulated spectrum that contains spectral fringes from multiple internal reflections is shown in Fig. 3(a). The red box shows the spectral region of 1766 to 2790 cm−1 that was dominated by fringes. The FFT of this spectral range is shown in Fig. 3(b). The first 10 dominant frequencies larger than 0.0053 were selected for fringe estimation, as discussed in section 2.3 (see section C of the Appendix). The fringe pattern shown in Fig. 3(c) was estimated by solving eqn (7). The approximated spectral fringe pattern was subtracted from the original spectrum, and is shown in Fig. 3(d). We reiterated this algorithm, until the corrected spectrum become free of fringes, between 1766 to 2790 cm−1, and the resulting spectrum did not change. In this case, the corrected spectrum was free of fringes after two repetitions of the algorithm. The FFT of the spectrum in the spectral range between 1766 and 2790 cm−1 after the first iteration of the fringe correction algorithm is shown in Fig. 3(e). To estimate fringes in the second iteration, the frequencies highlighted with red in Fig. 3(e) were selected, the first 10 dominant frequencies. The calculated EMSC fringe is shown in Fig. 3(d). The corrected spectrum was compared to the standard spectrum in Fig. 3(f), with a residual between the two spectra to highlight the differences. Fig. 3(f) shows that the corrected spectrum that is calculated by removing fringes with the EMSC approach is in a good agreement with the standard algae spectrum without fringe. It is well known that strong absorption bands (changes in indices of refraction) can induce dispersion in the spectral range.40 To determine the impact of the OH bending water absorption band on the multiple internal reflection sinusoidal fringe pattern, we inspected the residual between the corrected and standard spectra. The residual has a maximum of 15% at 1747 cm−1, and shows only noise for all frequencies. This shows dispersion is negligible. Dispersion is negligible, if the real and imaginary parts of the refractive indices of water, algae and diamond (shown in Fig. 2(a) and (b)) are less than 2.4 and 0.1, respectively. This is consistent with the simulation results published by Konveskikh et al., 2015, where there was a negligible impact on the sinusoidal fringe pattern from multiple internal reflections for real parts of indices of refraction less than 2.4. Note that the water absorption band at 1580 to 1700 cm−1 is set to zero, since it is dominated by noise in the experiment (see section B of the Appendix).
O stretch associated with phospholipid at 1740 cm−1(ref. 37) and CH2/lipid at 2852 cm−1 and 2922 cm−1(ref. 39) are present in the simulated data. The fringe correction algorithm applied to a simulated algal spectrum is illustrated in Fig. 3. A simulated spectrum that contains spectral fringes from multiple internal reflections is shown in Fig. 3(a). The red box shows the spectral region of 1766 to 2790 cm−1 that was dominated by fringes. The FFT of this spectral range is shown in Fig. 3(b). The first 10 dominant frequencies larger than 0.0053 were selected for fringe estimation, as discussed in section 2.3 (see section C of the Appendix). The fringe pattern shown in Fig. 3(c) was estimated by solving eqn (7). The approximated spectral fringe pattern was subtracted from the original spectrum, and is shown in Fig. 3(d). We reiterated this algorithm, until the corrected spectrum become free of fringes, between 1766 to 2790 cm−1, and the resulting spectrum did not change. In this case, the corrected spectrum was free of fringes after two repetitions of the algorithm. The FFT of the spectrum in the spectral range between 1766 and 2790 cm−1 after the first iteration of the fringe correction algorithm is shown in Fig. 3(e). To estimate fringes in the second iteration, the frequencies highlighted with red in Fig. 3(e) were selected, the first 10 dominant frequencies. The calculated EMSC fringe is shown in Fig. 3(d). The corrected spectrum was compared to the standard spectrum in Fig. 3(f), with a residual between the two spectra to highlight the differences. Fig. 3(f) shows that the corrected spectrum that is calculated by removing fringes with the EMSC approach is in a good agreement with the standard algae spectrum without fringe. It is well known that strong absorption bands (changes in indices of refraction) can induce dispersion in the spectral range.40 To determine the impact of the OH bending water absorption band on the multiple internal reflection sinusoidal fringe pattern, we inspected the residual between the corrected and standard spectra. The residual has a maximum of 15% at 1747 cm−1, and shows only noise for all frequencies. This shows dispersion is negligible. Dispersion is negligible, if the real and imaginary parts of the refractive indices of water, algae and diamond (shown in Fig. 2(a) and (b)) are less than 2.4 and 0.1, respectively. This is consistent with the simulation results published by Konveskikh et al., 2015, where there was a negligible impact on the sinusoidal fringe pattern from multiple internal reflections for real parts of indices of refraction less than 2.4. Note that the water absorption band at 1580 to 1700 cm−1 is set to zero, since it is dominated by noise in the experiment (see section B of the Appendix).
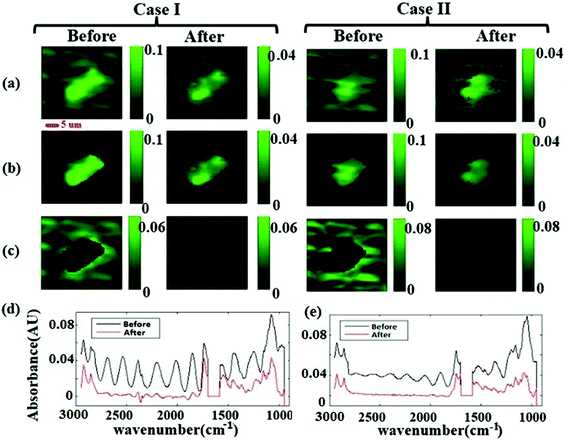
The corrected spectrum was compared to the standard spectrum in Fig. 3(f). Fig. 3(f) shows that the fringe corrected spectrum that is calculated by removing fringes with the EMSC approach is in a good agreement with the standard algae spectrum without fringe. The maximum residual of 15% was observed at 1747 cm−1. This itself is a manifestation of negligible dispersion. Small differences between the corrected and the standard algae spectrum were due to the dispersion effect33 happening at the absorption bands. A slight variation in the imaginary part of the refractive index leads to fluctuations in the real part of the refractive index, resulting in dispersion. The algal cell, water and diamond windows are sufficiently low absorbing in the spectral range 948 to 2946 cm−1, such that the dispersion due to the absorption is negligible for the scattering of infrared radiation at the micro channel. The imaginary part of the refractive indexes of water, algae and diamond (shown in Fig. 2(a) and (b)) are less than 0.1. The water absorption band at 1580 to 1700 cm−1 is blanked out, due to the limitation of the experiment (see section B of the Appendix). This simulation shows that, the absorbance spectra were sums of sinusoidal fringe contributions from multiple internal reflections and absorption bands from the imaginary part of the sample refraction index. Two different cases of fringes were observed in experimental data sets. Case I: Fringes appear with a high amplitude in the average spectrum (Fig. 4 Case I). Case II: Fringes appear with a low amplitude in the average spectrum (Fig. 4 Case II). The strength of the fringe patterns in the data appears to depend on the orientation of the diamond windows in different replicates, and will be discussed further below. To model Case I (by the method described in section 2.2) the refractive index of the diamond was set to 2.4. To model Case II, the refractive index of the diamond was set to 1.5 to model the situation in which the two diamond windows were not parallel to each other due to deformation caused by the weight of water. In the case of non-parallel diamond windows, the interference effect was smaller and resulted in fringes with smaller amplitudes. A refractive index of 1.5 for the diamond layers was used to model the situation in which the change in the refractive index of the diamond–water interface was small. This situation was assumed for the case of non-parallel windows, since in this configuration the change in the angle of incidence would give similar optical response. For such layered systems, interfaces with similar indices of refraction resulted in smaller reflections; therefore, the fringes due to multiple internal reflections have lower amplitudes. In both cases, the EMSC estimated fringe pattern, accurately modeled the fringes, which means dispersion effect is negligible in both cases. The estimated fringes in region of 1766 to 2790 cm−1 can be extended to the whole spectral region. The maximum error occurred at the water absorption peak at ∼1640 cm−1, which was excluded from PCA and further analysis of the cell.
Fig. 4(a) shows the measured chemogram images before and after fringe correction. The images were classified in “cell” and “non-cell” with Otsu's method. Fig. 4(b) and (c) shows pixels segregated within cells and background pixels. The average spectra before and after fringe correction (for the cell pixels) are plotted in Fig. 4(d). Note that there are smaller spectral variations and spatial fringes in the chemogram images and the average spectra after correction compare to the raw data. Importantly, fringe correction preserved strong absorbance features and even revealed originally known peaks (due to varying atmospheric CO2 in the optical beam path). Fig. 4(c) shows that the spatial background variation decreased after fringe correction in both cases, demonstrating that the spatial fringes were attenuated after spectral fringe correction.
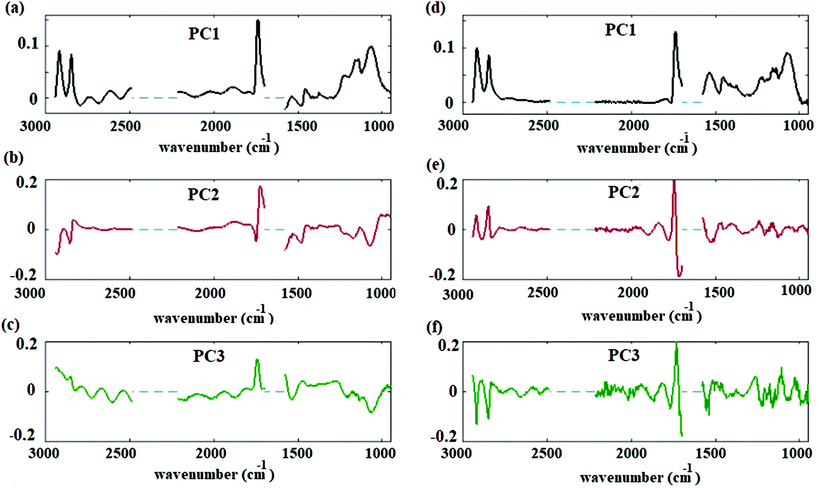
Reducing the data to principal components allows an overall assessment of data before and after correction. The spectral results of the PCA before and after fringe correction are shown in Fig. 5. Fig. 5(a), (b) and (c) show the first, second, and third principal components of the hyperspectral cube corrected by basic EMSC model,41,42 respectively; Fig. 5(d), (e) and (f) shows the first, second, and third principal components after fringe correction. Original data variances were dominated by fringes. (Similar results were obtained for PCA of spectra with significant scattering contributions. Scattering features can dominate spectral principal components before preprocessing corrections.) Once the spectral fringes were removed for each individual spectrum, spatial variations and spectral fringes were greatly reduced in the frequency dependent loadings of principal components (average, second and third principal components). After removing the fringes and applying PCA, the frequency dependent variance spectra showed signatures corresponding to lipid and carbohydrate associated bands of the spectra Fig. 5(d)–(f). The contributions of the second and third principal components to describing the overall spectra are less than 2% of the total variation. This result suggests that changes in the lipid and carbohydrate macromolecular pools are minimal, as one would expect for a cell maintained at constant, controlled conditions, and measured over a period of several hours.18 Detecting these small variations is possible only after applying data preprocessing algorithms. The results (PC loadings) of the analysis on three replicates are consistent and prove the reliability of the procedure.
4. Conclusions
A single Thalassiosira weissflogii cell mounted in a micro fluid channel was monitored by FTIR imaging, under controlled condition for 75 minutes by FTIR imaging. Fringes due to multiple internal reflections of the light in the macro channel were modeled by matrix theory of multi layer media. We showed that the dispersion effect was negligible in this geometry. Fringes behaved as additive sinusoidal in the spectral range between 950 and 2950 cm−1, and were removed from hyperspectral cube of data by extended multiplicative signal correction. Principal component analysis of ∼4000 spectra afforded significant improvement in spectral loading components after fringe correction. Our results demonstrate that lipid and carbohydrate macromolecular pools have minimal changes for the algal cell maintained at constant controlled conditions.Conflicts of interest
There are no conflicts of interest to declare.Appendix
A. Standard spectrum
To estimate a standard spectrum (denoted by m in eqn (1)) with no fringes similar to what is presented in ref. 26, the following steps are taken:(1) Water absorption regions of 2946–2489 cm−1, 2219–1702 cm−1, and 1581 to 950 cm−1 are set to zero.
(2) The average spectrum of the hyperspectral data is calculated, as the base of the standard spectrum. It is considered that there is minimum fringes present in the average spectrum.
(3) Regions of [1585, 962] and [2780, 1766] cm−1 are separately, baseline corrected.
(4) The region of 1766 to 2790 cm−1 is replaced with corresponding region of standard matrigel.
(5) The resulting spectrum is normalized at Si–O peak at 1076 cm−1.
B. Algal cell measurement
The size of the algal cell is an important factor, chosen for several reasons. The first was to match an area that could be imaged simultaneously with the infrared camera and the microscope. The second was such that the thickness of the water/media layer to maintain the viability of the cell would be thin enough to transmit infrared photons across a majority of the infrared spectral range. Since there are strong absorption bands at 1630 cm−1 and above 3000 cm−1 for water, and a thick layer of water is known to absorb strongly across the entire infrared spectral range, limiting the thickness of the water layer combined with using a bright infrared source of light is critical to being able to detect the remaining mid-infrared signatures of the algal cell while viable.Fig. 6 shows raw measured absorbance spectra from two distinct pixels, one from water region and the other from algal cell. In both cases, the signal is unreliable between spectral ranges of 3654 to 3100 cm−1, 1700 to 1580 cm−1, which correspond to the OH stretching and OH bending vibrations. Those spectral regions are neglected for further analysis and the experiment did not provide any information about the water absorption bands or the protein amide I bands that overlap this same frequency.
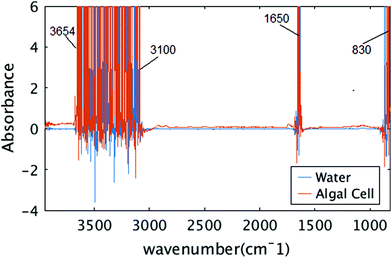 | ||
| Fig. 6 Raw measured spectra. Two raw spectra in spectral range of 850 to 3950 cm−1 are shown, one from algal cell, and one from water. | ||
C. Fringe frequencies
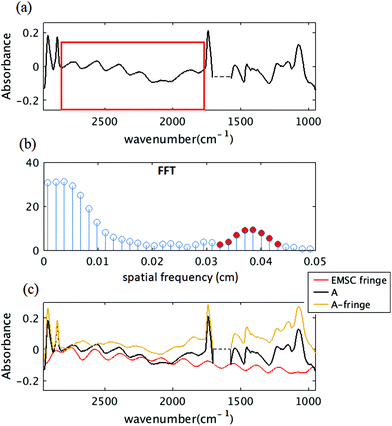
In Fig. 3(b), the first 10 dominant fringe frequencies are chosen for fringe correction. Fig. 7 shows the result of simply including the fringes that would arise from the frequencies ∼0.04 cm as it was suggested by Griffiths et al. (2007).43Fig. 7(a) shows the simulated spectrum with the method of section 2.2. and the region chosen for taking the FFT. Fig. 7(b) shows the FFT of the signal, the red circles show the frequencies that are selected for calculating the fringes. Fig. 7(c) shows the simulated spectrum (black), the estimated fringe by EMS (red) using the frequencies Fig. 7(b) and the corrected spectrum (yellow brown). Clearly, the corrected spectrum is still hindered by a fringe pattern with additional frequency components. This is reasonable, since the frequencies are calculated from a FFT of a limited spectral range, many frequency components will be needed to accurately predict the correct fringe pattern due to the uncertainty principle.Acknowledgements
The authors acknowledge UWM Physics department, NSF grants CHE-1508240 and CHE-1112433 and GAČR 16-16343S for their support.References
- H. Y. N. Holman, H. A. Bechtel, Z. Hao and M. C. Martin, Anal. Chem., 2010, 82, 8757–8765 CrossRef PubMed.
- K. Loutherback, G. Birarda, L. Chen and H.-Y. Holman, Protein Pept. Lett., 2016, 23, 273–282 CrossRef PubMed.
- L. M. Miller, Q. Wang, T. P. Telivala, R. J. Smith, A. Lanzirotti and J. Miklossy, J. Struct. Biol., 2006, 155, 30–37 CrossRef PubMed.
- A. Didonna, L. Vaccari, A. Bek and G. Legname, ACS Chem. Neurosci., 2011, 2, 160–174 CrossRef PubMed.
- G. Grenci, G. Birarda, E. Mitri, L. Businaro, S. Pacor, L. Vaccari and M. Tormen, Microelectron. Eng., 2012, 98, 698–702 CrossRef.
- E. Lipiec, G. Birarda, J. Kowalska, J. Lekki, L. Vaccari, A. Wiecheć, B. R. Wood and W. M. Kwiatek, Radiat. Phys. Chem., 2013, 93, 135–141 CrossRef.
- L. Vaccari, G. Birarda, L. Businaro, S. Pacor and G. Grenci, Anal. Chem., 2012, 84, 4768–4775 CrossRef PubMed.
- M. J. Nasse, M. J. Walsh, E. C. Mattson, R. Reininger, A. Kajdacsy-Balla, V. Macias, R. Bhargava and C. J. Hirschmugl, Nat. Methods, 2011, 8, 413–416 CrossRef PubMed.
- C. J. Hirschmugl and K. M. Gough, Appl. Spectrosc., 2012, 66, 475–491 CrossRef PubMed.
- I. Meglinski, Biophotonics for Medical Applications 2014 Search PubMed.
- K. Rahmelow and W. Hübner, Appl. Spectrosc., 1997, 51, 160–170 CrossRef.
- M. K. Kuimova, K. L. A. Chan and S. G. Kazarian, Appl. Spectrosc., 2009, 63, 164–171 CrossRef PubMed.
- K.-I. Miyamoto, P. Yamada, R.-T. Yamaguchi, T. Muto, A. Hirano, Y. Kimura, M. Niwano and H. Isoda, Cytotechnology, 2007, 55, 143–149 CrossRef PubMed.
- M. W. Peter, A. SuciaJulia and D. Vranya, Biomaterials, 1998, 19, 327–339 CrossRef.
- D. M. Wieliczka, S. Weng and M. R. Querry, Appl. Opt., 1989, 28, 1714–1719 CrossRef PubMed.
- H. Y. N. Holman, R. Miles, Z. Hao, E. Wozei, L. M. Anderson and H. Yang, Anal. Chem., 2009, 81, 8564–8570 CrossRef PubMed.
- G. Birarda, A. Ravasio, M. Suryana, S. Maniam, H.-Y. N. Holman and G. Grenci, Lab Chip, 2016, 16, 1644–1651 RSC.
- M. J. Nasse, S. Ratti, M. Giordano and C. J. Hirschmugl, Appl. Spectrosc., 2009, 63, 1181–1186 CrossRef PubMed.
- I. Amr, P.-C. Adriana and P. Chad, Can. J. Phys., 2013, 91, 910–923 CrossRef.
- P. J. Farrington, D. J. T. Hill, J. H. O'Donnell and P. J. Pomery, Appl. Spectrosc., 1990, 44, 901–903 CrossRef.
- N. J. Harrick, Appl. Spectrosc., 1977, 31, 548–549 CrossRef.
- E. Hecht, OPTICS 2002 Search PubMed.
- T. Hirschfeld and A. W. Mantz, Appl. Spectrosc., 1976, 30, 552–553 CrossRef.
- T. Hirschfeld, Appl. Opt., 1978, 17, 1400–1412 CrossRef PubMed.
- F. R. S. Clark and D. J. Moffatt, Appl. Spectrosc., 1978, 32, 547–549 CrossRef.
- T. Konevskikh, A. Ponossov, R. Blümel, R. Lukacs and A. Kohler, Analyst, 2015, 140, 3969–3980 RSC.
- A. H. Lipkus, T. J. Lenk, K. K. Chittur and R. M. Gendreau, Biopolymers, 1988, 27, 1831–1838 CrossRef PubMed.
- A. M. Pistorius and W. J. DeGrip, Vib. Spectrosc., 2004, 36, 89–95 CrossRef.
- G. C. Mellau and B. P. Winnewisser, ASP Conference Series, Grevesse, 1995, pp. 138–139.
- A. Savitzky and M. J. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef.
- K. Roberts, E. Granum, R. C. Leegood and J. A. Raven, Plant Physiol., 2007, 145, 230–235 CrossRef PubMed.
- E. Merzbacher, Quantum Mechanics, 3rd edn, 1998 Search PubMed.
- B. Saleh and M. C. Teich, Fundamentals of Photonics 2007 Search PubMed.
- H. Martens and E. Stark, J. Pharm. Biomed. Anal., 1991, 9, 625–635 CrossRef PubMed.
- N. K. Afseth and A. Kohler, Chemom. Intell. Lab. Syst., 2012, 117, 92–99 CrossRef.
- R. C. Gonzalez and R. E. Woods, Digital Image Processing Search PubMed.
- Y. Meng, C. Yao, S. Xue and H. Yang, Bioresour. Technol., 2014, 151, 347–354 CrossRef PubMed.
- T. Ramachandra and M. D. M. Madhab, in Proceedings of the 8th National Conference on Indian Energy Sector.
- D. Y. Duygu, A. U. Udoh, T. B. Ozer, A. Akbulut, I. A. Erkaya, K. Yildiz and D. Guler, Afr. J. Biotechnol., 2012, 11, 3817–3824 Search PubMed.
- P. Bassan, A. Kohler, H. Martens, J. Lee, H. J. Byrne, P. Dumas, E. Gazi, M. Brown, N. Clarke and P. Gardner, Analyst, 2010, 135, 268–277 RSC.
- H. Martens, J. P. Nielsen and S. B. Engelsen, Anal. Chem., 2003, 75, 394–404 CrossRef PubMed.
- A. Kohler, C. Kirschner, A. Oust and H. Martens, Appl. Spectrosc., 2005, 59, 707–716 CrossRef PubMed.
- P. Griffiths and J. De Haseth, Fourier Transform Infrared Spectrometry 2007 Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |