Nonadiabatic fragmentation of H2O+ and isotopomers. Wave packet propagation using ab initio wavefunctions†
Received
12th June 2018
, Accepted 16th September 2018
First published on 12th November 2018
1 Introduction
The water cation is naturally found in several environments such as the interstellar medium,1,2 and atmospheres of planets3 and comets.4,5 It can be formed in collisions of electrons, ions or photons with H2O and, given the importance of this molecule, many works have studied its ionization, and the ensuing dynamics of the remaining cation. Several experimental6–8 and theoretical9,10 works have addressed the photoionization of H2O with photon energies below 21.2 eV. At these energies, the photoelectron spectrum shows three bands that correspond to the formation of H2O+ in the electronic states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 (hereafter denoted
2B1 (hereafter denoted ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ), Ã 2A1 (Ã) and
), Ã 2A1 (Ã) and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 (
2B2 (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). These electronic states are essentially described by one-electron removal from the three outermost molecular orbitals (1b1, 3a1 and 1b2, respectively) of H2O. For photon energies higher than the dissociation threshold (18.1 eV), the vibrational levels of the
). These electronic states are essentially described by one-electron removal from the three outermost molecular orbitals (1b1, 3a1 and 1b2, respectively) of H2O. For photon energies higher than the dissociation threshold (18.1 eV), the vibrational levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state are predissociative and, accordingly, the third band of the H2O photoelectron spectrum exhibits broad peaks. The ionization of H2O above the dissociation threshold leads to the cation fragmentation into H+ + OH, H + OH+ and O+ + H + H. Following the ionization of H2O, coincidence experiments11–14 have measured the branching ratios in the formation of H+ + OH and H + OH+. Experiments of ref. 15–17 have measured the kinetic energy release distributions of the fragments formed after electron impact on water molecules, which shed light on the possible routes leading to the different fragmentation schemes.
state are predissociative and, accordingly, the third band of the H2O photoelectron spectrum exhibits broad peaks. The ionization of H2O above the dissociation threshold leads to the cation fragmentation into H+ + OH, H + OH+ and O+ + H + H. Following the ionization of H2O, coincidence experiments11–14 have measured the branching ratios in the formation of H+ + OH and H + OH+. Experiments of ref. 15–17 have measured the kinetic energy release distributions of the fragments formed after electron impact on water molecules, which shed light on the possible routes leading to the different fragmentation schemes.
Calculations on the H2O+ system include the ab initio studies18,19 of the reactions O + H2+ → OH+ + H and O + H2+ → OH + H+, and the corresponding reactions with the isotopomers D2+ and HD+. These calculations used the quasi-classical-trajectory and real-wave-packet methods, and state-of-the-art potential energy surfaces of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à electronic states. The influence of the Renner–Teller coupling on the O + H2+ proton transfer reactions was analyzed in ref. 20.
and à electronic states. The influence of the Renner–Teller coupling on the O + H2+ proton transfer reactions was analyzed in ref. 20.
In a previous paper,21 we carried out a theoretical study of the fragmentation of the water cation from the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, obtaining values for the dissociation branching ratios into OH + H+ and H + OH+ that were in excellent agreement with the experimental data of Tan et al.12 Our calculations consisted in nuclear wave-packet propagation on three electronic surfaces (
state, obtaining values for the dissociation branching ratios into OH + H+ and H + OH+ that were in excellent agreement with the experimental data of Tan et al.12 Our calculations consisted in nuclear wave-packet propagation on three electronic surfaces (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) , Ã and
, Ã and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ), using a modified version of the GridTDSE code22 to reproduce the nonadiabatic quantum nuclear dynamics. The initial condition of our dynamical calculation was the Franck–Condon (FC) wave packet, obtained by vertical ionization of the ground vibrational state of H2O. The wave-packet propagation showed that the dissociation mechanism involves nonadiabatic transitions from the state
), using a modified version of the GridTDSE code22 to reproduce the nonadiabatic quantum nuclear dynamics. The initial condition of our dynamical calculation was the Franck–Condon (FC) wave packet, obtained by vertical ionization of the ground vibrational state of H2O. The wave-packet propagation showed that the dissociation mechanism involves nonadiabatic transitions from the state ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) to à and
to à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) . The transition
. The transition ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ã takes place in a few femtoseconds in the vicinity of the conical intersection (CI) between the corresponding potential energy surfaces (PESs). The CI seam appears at angles
–à takes place in a few femtoseconds in the vicinity of the conical intersection (CI) between the corresponding potential energy surfaces (PESs). The CI seam appears at angles  in the interval 60° ≲ α ≲ 100°, while the minimum of the à PES is located at the linear geometry (α = 180°). As a consequence, the wave packet starts in
in the interval 60° ≲ α ≲ 100°, while the minimum of the à PES is located at the linear geometry (α = 180°). As a consequence, the wave packet starts in ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) , moves towards the CI and is transferred to à with an important excitation of the bending mode. At linear geometries, the states à and
, moves towards the CI and is transferred to à with an important excitation of the bending mode. At linear geometries, the states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) become the two components of the 2Πu state, and the Ö
become the two components of the 2Πu state, and the Ö![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) Renner–Teller (RT) interaction allows the population of the ground electronic state. The fragmentation can take place either by energy transfer from the bending mode into the antisymmetric stretching motion within Ã, leading to dissociation into OH + H+, or after the RT transition between à and
Renner–Teller (RT) interaction allows the population of the ground electronic state. The fragmentation can take place either by energy transfer from the bending mode into the antisymmetric stretching motion within Ã, leading to dissociation into OH + H+, or after the RT transition between à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , leading to dissociation into OH+ + H.
, leading to dissociation into OH+ + H.
Although the good agreement between our results and the experimental branching ratios indicates that the three-state (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ö
–Ö![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) mechanism explains the predissociation of the water cation, other possible nonadiabatic transitions must be ruled out. In our previous work,21 we checked that the intersystem crossing transitions from
) mechanism explains the predissociation of the water cation, other possible nonadiabatic transitions must be ruled out. In our previous work,21 we checked that the intersystem crossing transitions from ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and à to the dissociative ã 4B1 state are very slow compared to
and à to the dissociative ã 4B1 state are very slow compared to ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –à transitions. Here, we also consider the possible role of the
–Ã transitions. Here, we also consider the possible role of the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 (
2B1 (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) state in the wave packet evolution, because it exhibits a CI seam with
) state in the wave packet evolution, because it exhibits a CI seam with ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) at α = 180° and relatively large O–H distances (≈5 Bohr). Given the (large) internuclear distances at which this new CI is located, we have enlarged the grid of nuclear coordinates with respect to that of our previous calculation.
at α = 180° and relatively large O–H distances (≈5 Bohr). Given the (large) internuclear distances at which this new CI is located, we have enlarged the grid of nuclear coordinates with respect to that of our previous calculation.
Additionally, we take advantage of the PESs and nonadiabatic data obtained for H2O+ to carry out a study of isotopic effects in the fragmentation of D2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) and HDO+(
) and HDO+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). Our theoretical fragmentation branching ratios of D2O+ compare satisfactorily with the experimental results of Eland,11 and they support the small differences found between H2O+ and D2O+ species in photoelectron–photoion-coincidence experiments.13,14 With respect to HDO+, time of flight coincidence experiments23,24 in collisions of H+ and F7+ with HDO have shown a strong preference for breaking the O–H bond after both single and double ionization of the molecular species. In those experiments, it was also found that the isotopic effect is independent of the projectile, suggesting a kinematic effect at play in the post-collisional breakdown of HDO+ and HDO2+. This interpretation was only supported by wave-packet simulations for HDO2+ in a single PES,24 but one expects the fragmentation of HDO+ to be dominated by transitions between several electronic states. Here, we study the isotopic dependence in the bond cleavage preference, by carrying out 4-PESs wave packet propagation for HDO+.
). Our theoretical fragmentation branching ratios of D2O+ compare satisfactorily with the experimental results of Eland,11 and they support the small differences found between H2O+ and D2O+ species in photoelectron–photoion-coincidence experiments.13,14 With respect to HDO+, time of flight coincidence experiments23,24 in collisions of H+ and F7+ with HDO have shown a strong preference for breaking the O–H bond after both single and double ionization of the molecular species. In those experiments, it was also found that the isotopic effect is independent of the projectile, suggesting a kinematic effect at play in the post-collisional breakdown of HDO+ and HDO2+. This interpretation was only supported by wave-packet simulations for HDO2+ in a single PES,24 but one expects the fragmentation of HDO+ to be dominated by transitions between several electronic states. Here, we study the isotopic dependence in the bond cleavage preference, by carrying out 4-PESs wave packet propagation for HDO+.
In the (e–2e) + (e–e + ion) experiments of Tan et al.,12 the ionization of H2O is fast enough, compared to the characteristic rotational and vibrational periods of the molecule, that one can assume that the initial H2O+ wave packet is obtained by a FC transition from the ground state of H2O. In this work, we also address the photodissociation experiments of Harbo et al.,25 where the fragmentation starts from specific excited vibrational levels in H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). These authors carried out a crossed-beam experiment, where a H2O+ beam was crossed by a 532 nm laser. The subsequent dissociation was interpreted as due to the vibrational excitation of metastable low-lying vibrational levels of
). These authors carried out a crossed-beam experiment, where a H2O+ beam was crossed by a 532 nm laser. The subsequent dissociation was interpreted as due to the vibrational excitation of metastable low-lying vibrational levels of ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) . The experiment measured the ratio between the cross sections for production of the fragments OH + H+ and OH+ + H, obtaining a ratio value Γ:
. The experiment measured the ratio between the cross sections for production of the fragments OH + H+ and OH+ + H, obtaining a ratio value Γ:
| |  | (1) |
in contrast with the value
Γ ≈ 0.31 reported by Tan
et al.12 The calculation of
Γ with new initial conditions that simulate the experiment of Harbo
et al. is a stringent test of both the electronic structure data and the dynamical methods employed.
The paper is organized as follows. In Section 2 we summarize the method employed to calculate the PESs and the dynamical couplings. The treatment of the two conical intersections found between ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ã and
–Ã and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) PESs, which are responsible for the nonadiabatic transitions, is discussed in Section 3. In Section 4, we describe the numerical method applied to solve the time-dependent Schrödinger equation. Our main results are shown in Section 5, which includes the results of a 4-state calculation using a FC initial wave packet, the isotopic effect and the calculations with initial conditions that are excited vibrational states of the
PESs, which are responsible for the nonadiabatic transitions, is discussed in Section 3. In Section 4, we describe the numerical method applied to solve the time-dependent Schrödinger equation. Our main results are shown in Section 5, which includes the results of a 4-state calculation using a FC initial wave packet, the isotopic effect and the calculations with initial conditions that are excited vibrational states of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. A summary is presented in Section 6.
state. A summary is presented in Section 6.
2 Electronic structure calculations
We have performed ab initio calculations for the electronic states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1, Ã 2A1,
2B1, Ã 2A1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 and
2B2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 of H2O+ using the MOLPRO package.26 PESs and nonadiabatic couplings have been obtained with multireference configuration interaction calculations in the Cs symmetry point group. Configurations are generated by allocating seven valence electrons in (7a′,1a′′) molecular orbitals, previously obtained with CASSCF calculations in a space of (10a′,1a′′) orbitals. The basis set employed is aug-cc-pvqz and aug-cc-pvtz27 for oxygen and hydrogen, respectively.
2B1 of H2O+ using the MOLPRO package.26 PESs and nonadiabatic couplings have been obtained with multireference configuration interaction calculations in the Cs symmetry point group. Configurations are generated by allocating seven valence electrons in (7a′,1a′′) molecular orbitals, previously obtained with CASSCF calculations in a space of (10a′,1a′′) orbitals. The basis set employed is aug-cc-pvqz and aug-cc-pvtz27 for oxygen and hydrogen, respectively.
In this paper, we use both internal (r1,r2,α) and Jacobi (r,R,θ) coordinates to describe the molecular geometry, as depicted in Fig. 1, where r1 and r2 are the O–H distances, α is the  bond angle, R is the distance from the center of mass of the OH fragment to the remaining hydrogen, r = r1, and θ is the angle between r and R.
bond angle, R is the distance from the center of mass of the OH fragment to the remaining hydrogen, r = r1, and θ is the angle between r and R.
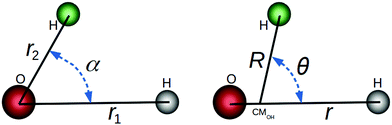 |
| | Fig. 1 Internal (left) and Jacobi (right) coordinates for the HOH nuclear framework. | |
In our calculations, the equilibrium geometry of the neutral H2O, in the ground state, is located at re = r1 = r2 = 1.79 Bohr and αe = 104.6° (θe = 107.8°). The equilibrium geometry of the ground state ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 of H2O+ is also of C2v symmetry, with no significant changes in the equilibrium coordinates (re = 1.90 Bohr and θe = 112.5°). In contrast, the equilibrium geometry of à 2A1 has D∞h symmetry (αe = 180°). The excited
2B1 of H2O+ is also of C2v symmetry, with no significant changes in the equilibrium coordinates (re = 1.90 Bohr and θe = 112.5°). In contrast, the equilibrium geometry of à 2A1 has D∞h symmetry (αe = 180°). The excited ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 state is again of C2v symmetry, but the re distance is 2.16 Bohr, larger than in the
2B2 state is again of C2v symmetry, but the re distance is 2.16 Bohr, larger than in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state, while the bond angle is θe = 80°, considerably smaller than in the
state, while the bond angle is θe = 80°, considerably smaller than in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state. These data, the energies of the corresponding potential energy minima and the dissociation energies, are given in Table 1.
state. These data, the energies of the corresponding potential energy minima and the dissociation energies, are given in Table 1.
Table 1
C
2v critical points of the first four electronic states of H2O+. The energy reference is taken as the minimum energy of the H2O+ (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1)
2B1)
| State |
r
e (Bohr) |
α
e (deg.) |
V
min (eV) |
V
∞ (eV) |
Fragments |
| gm: global minimum; lm: local minimum; sp: saddle point. |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 2B1 |
1.90 |
110.0 |
0.0gm |
5.674 |
OH+ + H |
| Ã 2A1 |
1.87 |
180.0 |
0.952gm |
6.245 |
OH + H+ |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 2B2 |
2.07 |
76.3 |
4.503gm |
7.850 |
OH+ + H |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
3.10 |
90.0 |
10.572sp |
6.245 |
OH + H+ |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
2.87 |
180.0 |
7.850sp |
|
|
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
3.42 |
30.0 |
7.388lm |
|
|
We show in Fig. 2 and 3 the contour plots of the PESs of the four adiabatic electronic states involved in the fragmentation dynamics. One can note the above-mentioned minima of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à surfaces. The changes in the slopes of the contour lines of the à and
and à surfaces. The changes in the slopes of the contour lines of the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) surfaces at α ≈ 80° are due to the CI between these surfaces. At C2v geometries, the
surfaces at α ≈ 80° are due to the CI between these surfaces. At C2v geometries, the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) surface shows two relatively shallow minima; the one at α = 180° is a saddle-point in the (r,R)-plane, as seen in the bottom-right panel of Fig. 3.
surface shows two relatively shallow minima; the one at α = 180° is a saddle-point in the (r,R)-plane, as seen in the bottom-right panel of Fig. 3.
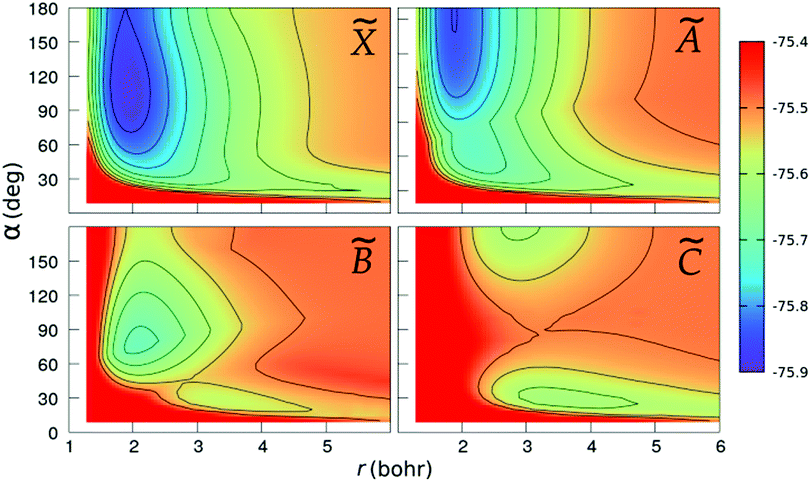 |
| | Fig. 2 Colour maps of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã, , Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) PESs of C2v geometries, as functions of the O–H distance r and the bond angle α. The numbers in the colour-box are energies in Hartree. PESs of C2v geometries, as functions of the O–H distance r and the bond angle α. The numbers in the colour-box are energies in Hartree. | |
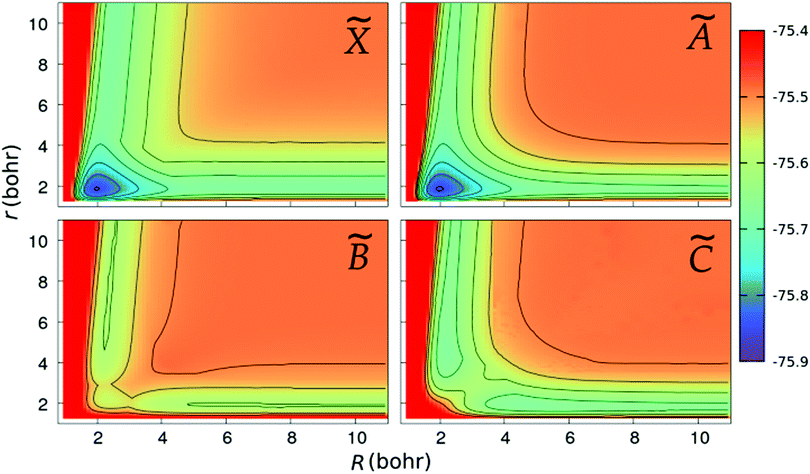 |
| | Fig. 3 Same as in Fig. 2, but for linear geometries and the PESs are plotted as functions of the Jacobi coordinates, r and R. | |
In Fig. 4 we show the electronic energies of states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) as functions of the Jacobi coordinate R, for fixed r = 1.98 Bohr, and four values of θ. In the panels corresponding to θ = 80° and θ = 100°, the energy curve of state
as functions of the Jacobi coordinate R, for fixed r = 1.98 Bohr, and four values of θ. In the panels corresponding to θ = 80° and θ = 100°, the energy curve of state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) appears above those of states
appears above those of states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and Ã, and crosses state
and Ã, and crosses state ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) at energies with small weight in the initial FC wave packet, illustrated with Gaussian shade in the second panel. At θ = 170°, the states à and
at energies with small weight in the initial FC wave packet, illustrated with Gaussian shade in the second panel. At θ = 170°, the states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) are almost degenerate up to r ≃ 5 Bohr, where the potential energy curves of states
are almost degenerate up to r ≃ 5 Bohr, where the potential energy curves of states ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) and
and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) display an avoided crossing, that turns into a CI for θ = 180°.
display an avoided crossing, that turns into a CI for θ = 180°.
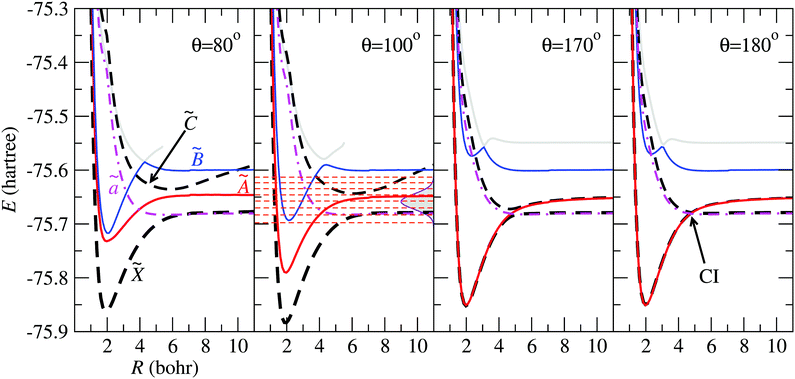 |
| | Fig. 4 Potential energy curves of the H2O+ system as functions of R for r = 1.98 Bohr and the values of θ indicated in the panels. The electronic states mentioned in the paper are labelled in the left panel, and the CI between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) is indicated for θ = 180°. In the panel for θ = 100°, the energy distribution of the Franck–Condon wave packet is depicted with a Gaussian shaded area and the horizontal dashed-lines correspond to the vibrational energies in the adiabatic is indicated for θ = 180°. In the panel for θ = 100°, the energy distribution of the Franck–Condon wave packet is depicted with a Gaussian shaded area and the horizontal dashed-lines correspond to the vibrational energies in the adiabatic ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. state. | |
3 Regularization of the conical intersections
The dynamical couplings are introduced in the numerical treatment by implementing a diabatic potential matrix in the grid representation. In fact, the nonadiabatic transitions take place in the neighbourhood of CIs, where the dynamical couplings are singular and, accordingly, a regularization procedure must be performed to remove these singularities. Given that the CIs are located in different regions of the configuration space, this regularization can be carried out for the CIs separately. The regularization procedure, already applied in our previous paper21 to treat the CI between PESs à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (henceforth referred as CI1), uses the transformation angle:
(henceforth referred as CI1), uses the transformation angle:| | 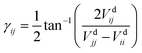 | (2) |
and the unitary transformation| | 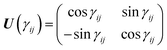 | (3) |
to build the diabatic states χd = {χdi,χdj} from the adiabatic ones χa = {χai,χaj}:The adiabatic potential energy surface matrix| | 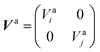 | (5) |
is transformed into the diabatic potential matrix:| | 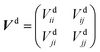 | (6) |
by
For two-centre systems the adiabatic–diabatic transformation can be carried out to completely remove the radial couplings 〈χdi|∂/∂R|χdj〉. However, for any three (or more) centre system, the diabatic states do not exist. The scope of the regularization process is to find states with small couplings near the CIs, removing the singularities. In our calculation, this is accomplished by finding a transformation angle, γij, that minimizes the nonadiabatic couplings between the diabatic states in the CI region. Explicitly, if Q is any particular nuclear coordinate, the residual coupling in the diabatic basis set is given by
| | 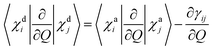 | (8) |
As seen in ref. 21, the Ö![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) CI takes place along a seam of C2v geometries, and the regularization is more easily carried out by employing the symmetry coordinates {x,y,α}
CI takes place along a seam of C2v geometries, and the regularization is more easily carried out by employing the symmetry coordinates {x,y,α}
| | 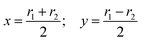 | (9) |
built from the internal coordinates
r1 and
r2 (see
Fig. 1). In these coordinates, our calculations indicate that a CI seam is located at
y = 0 for angles (in radians):
| | 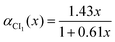 | (10) |
The transformation angle
γÃ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
is written in terms of the internal coordinates, and, similar to previous works,
28,29 the energy difference Δ
VÃ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
=
Vd![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
−
VdÃÃ is taken proportional to the distance to the CI seam in the
y = 0 plane. As
αCI1′ = d
αCI1/d
x is small in the range of
x where the interaction is sizable, the energy difference can be approximated by
| | ΔVdÃ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (x) = [α(x) − αCI1(x)]cos(αCI1′) (x) = [α(x) − αCI1(x)]cos(αCI1′) | (11) |
The interaction term is proportional to the antisymmetric coordinate
y, including a dependence on
α that gives an extra flexibility to the transformation angle to minimize the residual couplings:
| | VdÃ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (α,y) = (a0 + a1α + a2α2)y (α,y) = (a0 + a1α + a2α2)y | (12) |
where the values of the
ai parameters are given in
Table 2.
|
i
|
a
i
|
b
i
|
c
i
|
d
i
|
| 0 |
2.21 |
−0.0692 |
2.82 |
−1.57 |
| 1 |
0.94 |
1.11 |
0.367 |
−0.245 |
| 2 |
−2.88 |
2.25 |
−0.693 |
|
The second CI considered (CI2, henceforth) takes place between PESs ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) at angles α ≈ π.
at angles α ≈ π.
The symbols in Fig. 5 indicate the coordinates of the geometries with zero-energy difference between states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) . The position of the seam in the (x,y) plane is parametrized using the following expression:
. The position of the seam in the (x,y) plane is parametrized using the following expression:
| |  | (13) |
in which the values of
fi are obtained by a non-linear least-square fitting procedure of the previous equation to the points of minimum energy difference for eight values of
α. The
fi(
α) functions are fitted, independently, to the following expressions:
| | f1(α) = b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−c1(α−π)2 e−c1(α−π)2 | (15) |
| | f2(α) = b2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−c2(α−π)2 e−c2(α−π)2 | (16) |
Again,
bi and
ci parameters are obtained by a 1D-non-linear fitting procedure, and are given in
Table 2.
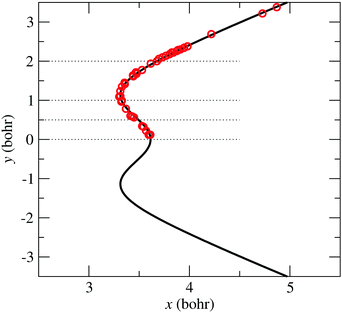 |
| | Fig. 5 Bullets: position in coordinates (x, y), eqn (9), of the zero-energy differences between states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) at α = π rad. Solid-line: CI2 seam fitted-model of eqn (13). at α = π rad. Solid-line: CI2 seam fitted-model of eqn (13). | |
The modelled diabatic potential matrix elements are finally written as
| | ΔVd![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) (α,x,y) = x − xCI2(α,y) (α,x,y) = x − xCI2(α,y) | (17) |
| | Vd![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) (α,y) = d0 (α,y) = d0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ed1y2(α − π) ed1y2(α − π) | (18) |
where
d0 and
d1 are also free parameters obtained by non-linear fitting of this model to the
ab initio couplings 〈
ψ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
|∂/∂
x|
ψ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
〉, for several values of
y, and whose values are given in
Table 2.
The ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) seam described by eqn (13) is plotted in Fig. 5, together with the position of the ab initio zero-energy difference between these states for linear geometries. Also, in Fig. 6, we compare, for α = 175°, the ab initio nonadiabatic couplings (symbols) with the values of the derivatives (solid lines) of the transformation angle γ
seam described by eqn (13) is plotted in Fig. 5, together with the position of the ab initio zero-energy difference between these states for linear geometries. Also, in Fig. 6, we compare, for α = 175°, the ab initio nonadiabatic couplings (symbols) with the values of the derivatives (solid lines) of the transformation angle γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) [see eqn (2)] obtained with the fitted model (17) and (18), for a few values of y (those corresponding to the dotted lines of Fig. 5). These figures show the satisfactory fitting of the model to the ab initio data, where the peaks of the lorentzian follow the location of the CI2 seam and their widths depend on the parameters of eqn (18). A more global view of the topology of the CI2 is shown in Fig. 7, where we plot the derivative of the transformation angle γ
[see eqn (2)] obtained with the fitted model (17) and (18), for a few values of y (those corresponding to the dotted lines of Fig. 5). These figures show the satisfactory fitting of the model to the ab initio data, where the peaks of the lorentzian follow the location of the CI2 seam and their widths depend on the parameters of eqn (18). A more global view of the topology of the CI2 is shown in Fig. 7, where we plot the derivative of the transformation angle γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) with respect to the symmetry coordinates {x,y,α}. These derivatives mimic the behaviour of the nonadiabatic couplings between the states
with respect to the symmetry coordinates {x,y,α}. These derivatives mimic the behaviour of the nonadiabatic couplings between the states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) near their CI.
near their CI.
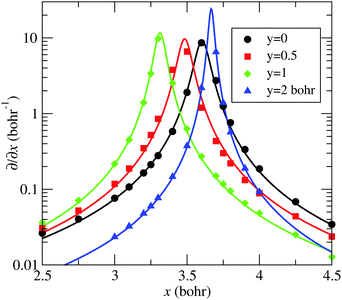 |
| | Fig. 6 Comparison between ab initio 〈Ψ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) |∂/∂x|Ψ |∂/∂x|Ψ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 〉 (symbols) and the model of eqn (13) ∂γ 〉 (symbols) and the model of eqn (13) ∂γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂x (solid-lines) as functions of x, for various values of y, labelled in the graph, and also indicated with dotted lines in Fig. 5. Modelled and ab initio data were obtained with α = 175°. /∂x (solid-lines) as functions of x, for various values of y, labelled in the graph, and also indicated with dotted lines in Fig. 5. Modelled and ab initio data were obtained with α = 175°. | |
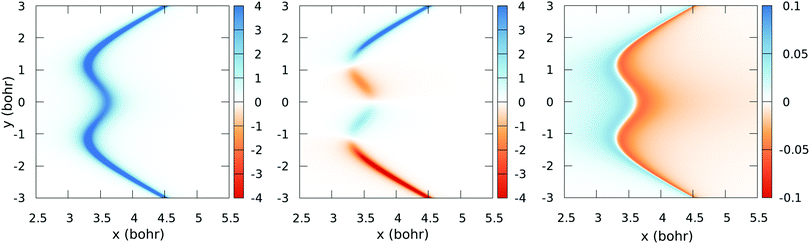 |
| | Fig. 7 Colour-map plot of ∂γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂x (left), ∂γ /∂x (left), ∂γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂y (middle) and ∂γ /∂y (middle) and ∂γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂α (right) as functions of the symmetric (x) and antisymmetric (y) coordinates for α = 175°. Colour scale values in atomic units. /∂α (right) as functions of the symmetric (x) and antisymmetric (y) coordinates for α = 175°. Colour scale values in atomic units. | |
The treatment of Ö![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) transitions, explained in our previous paper, is based on the method of Haxton et al.30,31 that yields a couple of diabatic states. Assuming a small total angular momentum, the Coriolis coupling terms are neglected and the body-fixed nuclear Hamiltonian has the form, in Jacobi coordinates:31,32
transitions, explained in our previous paper, is based on the method of Haxton et al.30,31 that yields a couple of diabatic states. Assuming a small total angular momentum, the Coriolis coupling terms are neglected and the body-fixed nuclear Hamiltonian has the form, in Jacobi coordinates:31,32
| | 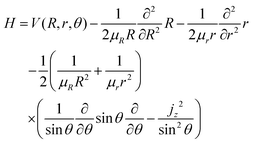 | (19) |
where
jz is the
z component of the angular momentum operator for the rotation of the diatom OH in the body-fixed frame, with
R along the
ẑ-axis. In this approximation, the nuclear wave functions are assumed to be eigenfunctions of the body-fixed operator
jz. The operator
jz2 is substituted
33 into
eqn (19) by its eigenvalue,
k2 (
k =
K −
ML), which is only defined in the
C∞v or
D∞h symmetries, where
K and
ML are the quantum numbers for the
z projections of the total and electronic angular momenta, respectively. In the present case, the electronic states Ã
2A
1 and
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2
2B
1 correlate, in the limit
θ → 180°, with the two components of the
2Π
u state, both with
Λ = |
ML| = 1. In this limit, the
χ±1 eigenfunctions of
Lz with
ML = ±1 are linear combinations of the electronic wave functions,
χà and
χ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
:
| | 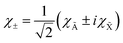 | (20) |
These two combinations are employed for all values of
θ. Considering the transformations due to the regularization of the two CIs and the transformation
(20), the unitary matrix,
U, for the transformation from the adiabatic state vector
χa = {
χa![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
,
χa![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
,
χaÃ,
χa![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
} to the diabatic one
χd = {
χd![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
,
χ+,
χ−,
χd![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
} is
| | 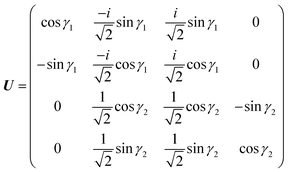 | (21) |
with
γ1 ≡
γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
and
γ2 ≡
γÃ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
.
U relates the adiabatic,
Va, and diabatic,
Vd, potentials:
4 Computational dynamics
The dynamical calculation has been carried out by means of nuclear wave packet propagation on the diabatic electronic PESs, employing a computational method (GridTDSE)22 that is adept for massive parallel calculations. This technique consists of a direct numerical collocation integration of the 3D time-dependent Schrödinger equation (TDSE):| | 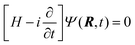 | (23) |
where H is the Hamiltonian operator of eqn (19) with the approximation of substituting jz2 by k2, as discussed in Section 3. The numerical calculation uses a lattice scheme,34 with the nuclear wave function evaluated at the points of a 3D grid. To incorporate nonadiabatic transitions, the wave function, Ψ, is written as a column vector with components {Ψi}, where i labels the (diabatic) electronic states included. The nuclear dynamics on each PES are coupled through the interaction matrix elements Hdij(R), following a procedure similar to that of Ma et al.35 This leads to the matrix equation| | HdΨ = (T + Vd)Ψ = i![[capital Psi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e13b.gif) | (24) |
where Vd stores the values of the potentials at the grid points. T, the kinetic energy operator, is a non-diagonal sparse matrix that is obtained by applying the finite differences method (see ref. 34), considering a stencil of 15 points in each dimension.
The calculations were carried out with a grid of 83 points in R ∈ [1,11] Bohr, 80 points in r ∈ [1.3,11] Bohr and 73 points in θ ∈ [ε,π–ε] rad, with ε = 2 × 10−4. In such a numerical integration scheme, the singularity at θ = 0 can be eluded by evaluating Ψ on the surroundings of the troublesome points.
The wave function vector components {Ψi}, each one referring to a different PES, were simultaneously propagated in time using a second order difference scheme (SOD), specially adapted to the present case since it conserves norm and energy, accumulating errors only in the phase.36 The errors are minimized in our calculations by setting the timestep Δt = 0.18 attosecond (7.5 × 10−3 a.u.), ensuring the stability of the norm and the correct account of the coupling terms between the evolving wave functions on each PES.
To avoid non-physical reflections of the wave function at the grid walls (Lmax = 11 Bohr), we have included a damping function37 in the propagation scheme. This function leads to a smooth decay of the wave packet for q > Lmax − δ:
| | 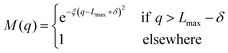 | (25) |
with
q ≡ (
R,
r),
δ = 1 Bohr and
ξ = 0.05 Bohr
−2.
Once the description of the nuclear wave packet in each electronic state is achieved, the integrated probability density 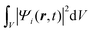 represents the time-dependent population of the electronic state i. Such populations can change either due to nonadiabatic transitions among the states included in the model, or due to the dissociating fluxes. The corresponding fragmentation probabilities ρi(t) are obtained from the continuity equation in its integral form:
represents the time-dependent population of the electronic state i. Such populations can change either due to nonadiabatic transitions among the states included in the model, or due to the dissociating fluxes. The corresponding fragmentation probabilities ρi(t) are obtained from the continuity equation in its integral form: 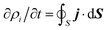 , evaluating the outgoing flux at R, r = 10.0 Bohr for the adiabatic components of the wave packet on each electronic state. Finally, the comparison with the experimental measurements is carried out at long times t > 5 ps, where the fragmentation probabilities reach asymptotic stable values.
, evaluating the outgoing flux at R, r = 10.0 Bohr for the adiabatic components of the wave packet on each electronic state. Finally, the comparison with the experimental measurements is carried out at long times t > 5 ps, where the fragmentation probabilities reach asymptotic stable values.
5 Results and discussion
5.1 Franck–Condon initial wave packet
The initial nuclear wave function is built taking the lowest vibrational eigenfunction of the electronic ground state of the water molecule. This PES was obtained with the same procedure and atomic basis set as the electronic states of H2O+ described in Section 2. In order to solve the corresponding time-independent Schrödinger equation (TISE), we employed the Lanczos scheme38 implemented in the GridTDSE code, which is based on the description of Guo et al.39 The analysis of this wave function, when projected over the eigenstates of the adiabatic ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) PES, shows that it can be described by a wave packet that spans a range of vibrational energies of about 0.1 Hartree, as shown by the vertical Gaussian curve in Fig. 4 for θ = 100°. There, the horizontal dashed-lines correspond to the vibrational energies obtained in the adiabatic
PES, shows that it can be described by a wave packet that spans a range of vibrational energies of about 0.1 Hartree, as shown by the vertical Gaussian curve in Fig. 4 for θ = 100°. There, the horizontal dashed-lines correspond to the vibrational energies obtained in the adiabatic ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) PES.
PES.
5.2 Effect of increasing the grid-size
As seen in Section 3, CI2 between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) states appears at (R,r) distances between 3 and 5 Bohr. The correct description of the nonadiabatic transitions in the vicinity of this CI requires increasing the grid size from (Rmax,rmax) ≈ 7 Bohr (GRID I21) to (Rmax,rmax) ≈ 11 Bohr (GRID II). To check the effect of size-enlargement of the grid on the time-evolution of the electronic state populations, we have reproduced our previous three-state calculation in the new grid. The comparison of the new results with those of ref. 21 are presented in Fig. 8(a). There are small differences in the probabilities between both calculations, with small changes in the probabilities, the
states appears at (R,r) distances between 3 and 5 Bohr. The correct description of the nonadiabatic transitions in the vicinity of this CI requires increasing the grid size from (Rmax,rmax) ≈ 7 Bohr (GRID I21) to (Rmax,rmax) ≈ 11 Bohr (GRID II). To check the effect of size-enlargement of the grid on the time-evolution of the electronic state populations, we have reproduced our previous three-state calculation in the new grid. The comparison of the new results with those of ref. 21 are presented in Fig. 8(a). There are small differences in the probabilities between both calculations, with small changes in the probabilities, the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state being the more affected.
state being the more affected.
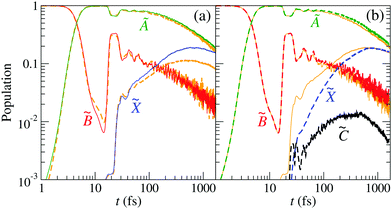 |
| | Fig. 8 Population of the electronic states of H2O+ (labelled in the panels) as a function of time. (a) The wave packet propagation includes only three electronic states. Dashed-orange lines: grid I with Lmax = 7 Bohr; solid lines: grid II with Lmax = 11 Bohr [see eqn (25)]. (b) The wave packet propagation includes four electronic states (dashed lines) in grid II with Lmax = 11 Bohr. Solid-orange lines are the solid lines of (a). | |
To study this in more detail, we show in Fig. 9 the sum of the populations of states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) for both box-sizes calculations (lines without symbols). As the size of the grid increases, there is a displacement of the population fall towards longer times, due to the damping function acting later. The inset in that figure shows the difference between both calculations, which would correspond to the wave function probability in the extra region. According to this figure, the wave packet enters this region after 50 fs, where it monotonously grows during 800 fs. After that, the amount of wave packet that leaves the extra region exceeds the amount that enters the region from shorter distances and the wave packet in the extra region fades away.
for both box-sizes calculations (lines without symbols). As the size of the grid increases, there is a displacement of the population fall towards longer times, due to the damping function acting later. The inset in that figure shows the difference between both calculations, which would correspond to the wave function probability in the extra region. According to this figure, the wave packet enters this region after 50 fs, where it monotonously grows during 800 fs. After that, the amount of wave packet that leaves the extra region exceeds the amount that enters the region from shorter distances and the wave packet in the extra region fades away.
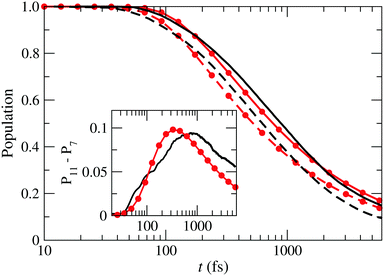 |
| | Fig. 9 Sum of the populations of the states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and , Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) as functions of time for two boxes with Lmax = 7 Bohr (– – –) and Lmax = 11 Bohr (—) compared to the probability of finding a particle described by the 1D-wave packet of eqn (26), inside a box with L = 7 Bohr (– • –) and L = 11 Bohr (—•—). Inset: Differences between the populations in the boxes with L = 11 Bohr and L = 7 Bohr for the actual calculation (—) and the 1-D model (—•—). as functions of time for two boxes with Lmax = 7 Bohr (– – –) and Lmax = 11 Bohr (—) compared to the probability of finding a particle described by the 1D-wave packet of eqn (26), inside a box with L = 7 Bohr (– • –) and L = 11 Bohr (—•—). Inset: Differences between the populations in the boxes with L = 11 Bohr and L = 7 Bohr for the actual calculation (—) and the 1-D model (—•—). | |
This behaviour can be readily modelled by the free expansion of a 1D wave packet. In this model, we consider the generic wave packet
| | | ψ(x,t) = exp[−ζ(t)(x − λ1)2]sin(λ2x) | (26) |
where the time-dependent exponential parameter
ζ(
t) is introduced to simulate the widening of the wave packet with energy above the dissociation threshold, and
With this wave packet, the probability of finding the system in the 1D box of length
L can be obtained analytically and is plotted in
Fig. 9 for the same grid size as in the three-state calculation, and with parameters (in atomic units)
λ1 = 2.5,
λ2 = 0.385,
λ3 = 0.10,
λ4 = 2.8 × 10
−3 and
λ5 = 1.2, obtained to approximately fit the time-dependent probability of the three states of H
2O
+. These results suggest that the expansion of the H
2O
+ wave packet is similar to the free wave packet expansion for the region of the space of coordinates
R,
r > 7 Bohr, as considered in our previous work.
5.3 Four-state calculation
The initial wave function shown in Section 5.1 was also propagated in the extended grid II with a Hamiltonian matrix that included four electronic states {![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ,
, ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) }. Here, the state
}. Here, the state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) is only coupled to
is only coupled to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) through nonadiabatic couplings described by the transformation angle γ
through nonadiabatic couplings described by the transformation angle γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) .
.
The time evolution of the populations of the four electronic states is displayed in Fig. 8(b), for a specific projection of the total angular momentum, K = 1. For an easy comparison, the populations obtained in the three-state calculation, in the same grid, are also included. These results show that state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) gets populated at the cost of
gets populated at the cost of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) at short times, but in the picosecond timescale, the populations of the three- and four-state calculations converge.
at short times, but in the picosecond timescale, the populations of the three- and four-state calculations converge.
As it was shown in ref. 21, the case K = 1 is a representative of the fragmentation probabilities at low temperatures. Here, the H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) main fragmentation mechanism remains the same as in the previous three-state calculation: a two-step process in which there is a fast population transfer from
) main fragmentation mechanism remains the same as in the previous three-state calculation: a two-step process in which there is a fast population transfer from ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) to à in the surroundings of CI1 and, after 30 fs, a population redistribution and decay through the following reactions:
to à in the surroundings of CI1 and, after 30 fs, a population redistribution and decay through the following reactions:
| | H2O+(Ã) ⇌ H2O+(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) k±2 ) k±2 | (29) |
while the state
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
dissociates through
| | H2O+(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) → H + OH+(3Σ−) k3 ) → H + OH+(3Σ−) k3 | (30) |
where
ki are the corresponding reaction constants. States
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
and
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
are connected by a CI, and we have
| | H2O+(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) ⇌ H2O+( ) ⇌ H2O+(![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) k±4 ) k±4 | (31) |
while
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
dissociates through
| | H2O+(![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) → H+ + OH k5 ) → H+ + OH k5 | (32) |
The direct fragmentation from
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
is
| | H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) → H + OH+(1Σ+) k6 ) → H + OH+(1Σ+) k6 | (33) |
The probability for fragmentation along each channel is shown in Fig. 10 for the wave packet propagation up to 1600 fs, and these results are used to fit a model for a first-order dissociation mechanism:
| | | pi(t) = ri(1 − e−kit) | (34) |
The parameters obtained by fitting the
ab initio data from
t = 1000 fs to
t = 1600 fs are used to draw the thin lines in
Fig. 10, and are given in
Table 3. There, the fraction of H
2O
+ that remains stable is
r0 = 1 −
r1 −
r3 −
r5 −
r6.
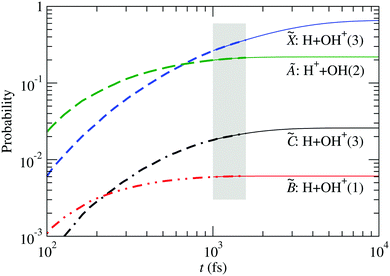 |
| | Fig. 10 Fragment probabilities as functions of time in the four-state calculation. Thick-dashed lines: result of the wave packet propagation. Thin-solid lines: fitted model [eqn (34)] using data within the shaded area. The number in brackets indicates the spin multiplicity of the diatomic species. The fitting parameters are given in Table 3. | |
Table 3 Branching ratios and rate constants for the first-order dissociation dynamics model (34) applied to reactions (28)–(33) of H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) and D2O+(
) and D2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) fragmentation
) fragmentation
|
i
|
H2O+ |
D2O+ |
|
r
i
|
k
i
(fs−1) |
r
i
|
k
i
(fs−1) |
| 0 |
0.091 |
|
0.074 |
|
| 1 |
0.219 |
2.4 × 10−3 |
0.138 |
1.3 × 10−3 |
| 3 |
0.658 |
5.1 × 10−4 |
0.786 |
6.7 × 10−4 |
| 5 |
0.026 |
1.2 × 10−3 |
— |
— |
| 6 |
0.006 |
3.7 × 10−3 |
0.002 |
1.3 × 10−3 |
In Fig. 8(b), one can note the small populations of state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) . The differences found in the populations of states à and
. The differences found in the populations of states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) by the introduction of state
by the introduction of state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) vanish as t increases, which would eventually lead to similar fragmentation branching ratios. However, one must take into account that we have extended the grid of our previous paper21 to incorporate transitions in the
vanish as t increases, which would eventually lead to similar fragmentation branching ratios. However, one must take into account that we have extended the grid of our previous paper21 to incorporate transitions in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) CI. When the grid size is increased, the system remains within the grid limits for a longer time, which, in our calculation, leads to larger populations of states à and
CI. When the grid size is increased, the system remains within the grid limits for a longer time, which, in our calculation, leads to larger populations of states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) with respect to those obtained in our previous three-state work (see Fig. 8(a)).
with respect to those obtained in our previous three-state work (see Fig. 8(a)).
Ferreira et al.16 have suggested that transitions ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) near their PESs crossing might explain their Gaussian structure around 1.8 eV in the H+ kinetic energy release distribution. However, states
near their PESs crossing might explain their Gaussian structure around 1.8 eV in the H+ kinetic energy release distribution. However, states ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) are of different symmetry (A′ and A′′, respectively) and, correspondingly, their interaction is zero in the Hamiltonian matrix. Also, we note that their leading electronic configurations are 1a212a211b23a211b21 (
are of different symmetry (A′ and A′′, respectively) and, correspondingly, their interaction is zero in the Hamiltonian matrix. Also, we note that their leading electronic configurations are 1a212a211b23a211b21 (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) and 1a212a211b223a11b14a1 (
) and 1a212a211b223a11b14a1 (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ), which are not linked by one-electron operators, and thus we expect a small
), which are not linked by one-electron operators, and thus we expect a small ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) coupling. Additionally, the fraction of the initial FC wave packet near the crossings (see Fig. 4) is very small. Therefore, we think that this mechanism is unlikely to be competitive with the formation of OH + H+via
coupling. Additionally, the fraction of the initial FC wave packet near the crossings (see Fig. 4) is very small. Therefore, we think that this mechanism is unlikely to be competitive with the formation of OH + H+via ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ã transitions.
–Ã transitions.
5.4 Isotopic effect
Having established in the previous section the small role of state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) in the fragmentation ratio, we address the calculation of the branching ratio of a FC wave packet in the
in the fragmentation ratio, we address the calculation of the branching ratio of a FC wave packet in the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state of D2O+ and HDO+ isotopomers including only three electronic states (
state of D2O+ and HDO+ isotopomers including only three electronic states (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and
, à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). For D2O+, the results are compared with those of H2O+ in Fig. 11, also including the experimental data of Eland11 for D2O+ and Tan et al.12 for H2O+, in excellent agreement with our calculation. The ratio OD+/D+ (≈5.7), larger than that of OH+/H+ (≈3.0) (see the values of r3/r1 in Table 3), can be understood in terms of kinematic effects: the D2O+ wave packet is slower and less spread than the H2O+ one, and this is particularly important in the region of linear geometries when the RT coupling transfers part of the wave packet from à to
). For D2O+, the results are compared with those of H2O+ in Fig. 11, also including the experimental data of Eland11 for D2O+ and Tan et al.12 for H2O+, in excellent agreement with our calculation. The ratio OD+/D+ (≈5.7), larger than that of OH+/H+ (≈3.0) (see the values of r3/r1 in Table 3), can be understood in terms of kinematic effects: the D2O+ wave packet is slower and less spread than the H2O+ one, and this is particularly important in the region of linear geometries when the RT coupling transfers part of the wave packet from à to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) . In D2O+, the RT coupling is less effective due to the larger reduced mass of the fragments (see eqn (19)), but the slower motion increases the interaction time, which results in a faster increase of the population of
. In D2O+, the RT coupling is less effective due to the larger reduced mass of the fragments (see eqn (19)), but the slower motion increases the interaction time, which results in a faster increase of the population of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) at the expense of Ã, and the consequent increase in the production of OD+ and decrease of that of D+.
at the expense of Ã, and the consequent increase in the production of OD+ and decrease of that of D+.
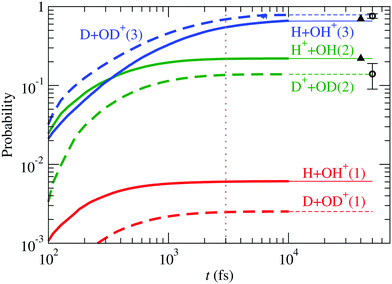 |
| | Fig. 11 Comparison between fragmentation probabilities of H2O+ and D2O+. Circles are the experimental data of Eland11 for D2O+ and triangles those of Tan et al.12 for H2O+. | |
Turning to the HDO+ system, it can fragment along four channels: OH+ + D, OD+ + H, OH + D+ and OD + H+. Here, we start with the FC wave packet as in H2O+, and follow its dynamics in the 4 PESs. The fragmentation probabilities are presented in Fig. 12, where they are compared with the coincidence-time-of-flight measurements,24 and the dynamic parameters of the first order model (34) are given in Table 4. The calculated σ(OD+)/σ(OH+) and σ(H+)/σ(D+) asymptotic ratios are 2.0 and 1.6, respectively, in excellent agreement with the experimental24 values of 2.1 ± 0.3 and 1.5 ± 0.2.
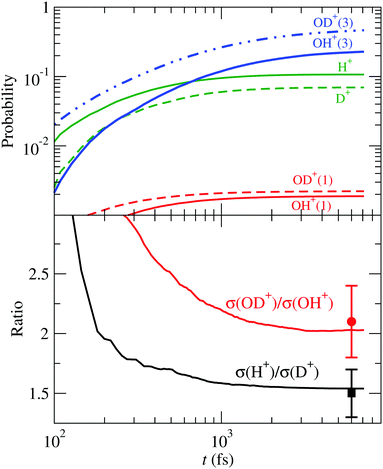 |
| | Fig. 12 Upper panel: Fragmentation probabilities of HDO+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) as functions of time. The numbers in brackets indicate the spin multiplicity of the molecular fragment species. Lower panel: Branching ratios for bond cleavage preference compared with the experimental24 ones. ) as functions of time. The numbers in brackets indicate the spin multiplicity of the molecular fragment species. Lower panel: Branching ratios for bond cleavage preference compared with the experimental24 ones. | |
Table 4 Branching ratios and rate constants for the first-order dissociation dynamics model (34) applied to the fragmentation of HDO+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) )
)
| Fragments |
r
|
k (fs−1) |
| OD+(3Σ−) + H |
0.47 |
6.1 × 10−4 |
| OH+(3Σ−) + D |
0.23 |
6.2 × 10−4 |
| OD + H+ |
0.11 |
1.4 × 10−3 |
| OH + D+ |
0.069 |
1.3 × 10−3 |
| OD+(1Σ−) + H |
0.0022 |
1.3 × 10−3 |
| OH+(1Σ−) + D |
0.0019 |
1.2 × 10−3 |
In the calculation, OH+ and OD+ are formed through the predissociation of state ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) , which is linked to the single ionization from the 1b2 molecular orbital. However, as shown by coincidence experiments,12 the dissociation into H+ + OD or D+ + OH can also take place by one-electron removal from the innermost valence orbital 2a1. In fact, the experimental branching ratios of Tan et al.12 show that the cross section for formation of protons in the photoionization of H2O is given by
, which is linked to the single ionization from the 1b2 molecular orbital. However, as shown by coincidence experiments,12 the dissociation into H+ + OD or D+ + OH can also take place by one-electron removal from the innermost valence orbital 2a1. In fact, the experimental branching ratios of Tan et al.12 show that the cross section for formation of protons in the photoionization of H2O is given by
| | | σ(H+) = 0.22σ(1b2) + 0.74σ(2a1) | (35) |
where
σ(1b
2) and
σ(2a
1) are the cross sections for ionization from the molecular orbitals 1b
2 and 2a
1, respectively. The experiments
24 were carried out at projectile energies of the order of 1 MeV u
−1, where the cross sections for ionization from both shells can be estimated by applying the Bethe–Born expression, which leads to similar contributions of the orbitals 1b
2 and 2a
1 to the formation of H
+ (see
ref. 40). Therefore, the good agreement between our calculation, which only includes the electron removal from 1b
2, and the experiment, supports the explanation that the ratio
σ(H
+)/
σ(D
+) is mainly a kinematic effect,
24 which is common to the wave packet propagation in all electronic PESs.
5.5 Time evolution of an excited vibrational state of ![[B with combining tilde]](https://www.rsc.org/images/entities/h3_char_0042_0303.gif)
In contrast with the experiment of Tan et al.,12 where the fragmentation of H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) ions is recorded just after their formation, in the experiment of Harbo et al.,25 the H2O+ ions produced by the ionization of H2O are stored for a relatively long time; most of the ions undergo fragmentation and only those with an energy below the dissociation threshold survive and are, afterwards, irradiated with a 532 nm (2.33 eV) laser, and the ensuing fragmentation branching ratios measured. The
) ions is recorded just after their formation, in the experiment of Harbo et al.,25 the H2O+ ions produced by the ionization of H2O are stored for a relatively long time; most of the ions undergo fragmentation and only those with an energy below the dissociation threshold survive and are, afterwards, irradiated with a 532 nm (2.33 eV) laser, and the ensuing fragmentation branching ratios measured. The ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state only holds two vibrational states below the lowest asymptotic energy of state
state only holds two vibrational states below the lowest asymptotic energy of state ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and the observed fragmentation was explained as due to the photodissociation of these metastable vibrational states of
and the observed fragmentation was explained as due to the photodissociation of these metastable vibrational states of ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) .
.
To simulate the experimental25 conditions, we have time-propagated an initial wave packet that corresponds to the vibrational eigenfunction whose energy lies 2.33 eV above the vibrational ground state in the adiabatic ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) surface. This vibrational state, whose probability density is shown in Fig. 14, is the seven symmetric stretch overtone. The low-lying vibrational states of the
surface. This vibrational state, whose probability density is shown in Fig. 14, is the seven symmetric stretch overtone. The low-lying vibrational states of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) electronic state have long lifetimes (≈198 μs),25 which points to ineffective nonadiabatic transitions from those states. Our simulation starts when the interaction of H2O+ ions with the laser field ends. Then, the wavefunction of the excited vibrational state has sizeable values around the Ö
electronic state have long lifetimes (≈198 μs),25 which points to ineffective nonadiabatic transitions from those states. Our simulation starts when the interaction of H2O+ ions with the laser field ends. Then, the wavefunction of the excited vibrational state has sizeable values around the Ö![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) CI and fast nonadiabatic transitions take place, leading to the ion breakdown.
CI and fast nonadiabatic transitions take place, leading to the ion breakdown.
Fig. 13 shows the evolution of this wave packet for K = 1, the quantum number for the z-component of the total angular momentum [see eqn (19)]. The comparison of the populations of Fig. 8 with those of Fig. 13(a) clearly shows similar mechanisms, but now there is a larger fragmentation into H+ + OH, which results in a faster decrease of the population of Ã. This precludes the transition to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , henceforth a smaller fragmentation into H + OH+; i.e., the initial vibrational excitation leads to a faster motion of the wave packet in the à PES and to the ensuing increase of the k1 rate constant of reaction (28).
, henceforth a smaller fragmentation into H + OH+; i.e., the initial vibrational excitation leads to a faster motion of the wave packet in the à PES and to the ensuing increase of the k1 rate constant of reaction (28).
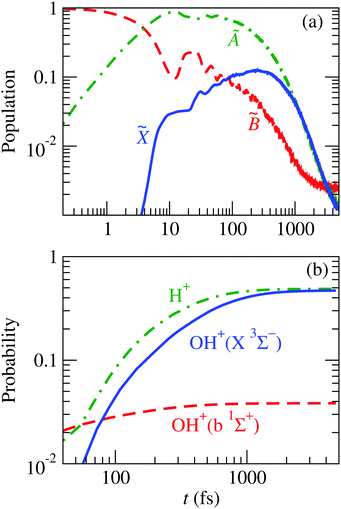 |
| | Fig. 13 Time evolution of the nuclear wave packet that is initially equal to the 8th vibrational wave function (given in Fig. 14) of the adiabatic ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. (a) Populations of the electronic states of H2O+ indicated in the figure. (b) Probabilities of the possible fragments. state. (a) Populations of the electronic states of H2O+ indicated in the figure. (b) Probabilities of the possible fragments. | |
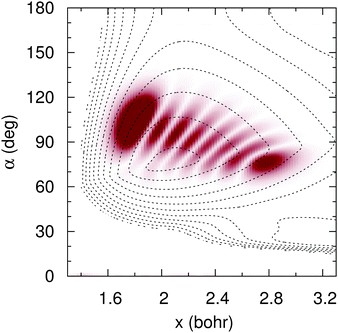 |
| | Fig. 14 Wave function probability density (shade) of the seven symmetric stretch overtone in ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) adiabatic PES (contour dotted lines), for C2v symmetries, as functions of the symmetric coordinate x = (r1 + r2)/2 and the internal angle α. adiabatic PES (contour dotted lines), for C2v symmetries, as functions of the symmetric coordinate x = (r1 + r2)/2 and the internal angle α. | |
Starting with the excited vibrational state mentioned above, our theoretical fragmentation branching ratio is Γ = σ(H+)/σ(OH+) = 0.96, in satisfactory agreement with the experimental value25 of 1.3. Furthermore, our value increases to 1.04, which falls within the ±0.3 experimental error bars, when considering only the triplet OH+ species. In both cases, these ratios are considerably larger than the 0.3 ± 0.01 value obtained in the experiments of Tan et al.12 and our theoretical21 value of 0.33 with the FC initial wave packet.
6 Conclusions
We have carried out the study of the nonadiabatic fragmentation of H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) by means of wave packet propagation in four electronic PESs (
) by means of wave packet propagation in four electronic PESs (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ), using a modified version of the GridTDSE computational code22 to simultaneously reproduce the nuclear dynamics on each surface. The values of the potential energy on each electronic state and the nonadiabatic couplings among them were calculated ab initio on exactly the same grid of points where the finite difference scheme of the GridTDSE is implemented, enhancing the accuracy of the calculations. This study extends our previous simulations21 by considering one more electronic state (
), using a modified version of the GridTDSE computational code22 to simultaneously reproduce the nuclear dynamics on each surface. The values of the potential energy on each electronic state and the nonadiabatic couplings among them were calculated ab initio on exactly the same grid of points where the finite difference scheme of the GridTDSE is implemented, enhancing the accuracy of the calculations. This study extends our previous simulations21 by considering one more electronic state (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) and a larger configuration space. Here, we have considered not only an initial FC wave packet, obtained by vertical ionization of H2O+ into the
) and a larger configuration space. Here, we have considered not only an initial FC wave packet, obtained by vertical ionization of H2O+ into the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) predissociative state of H2O+, but also vibrationally excited H2O+ ions and the fragmentation of water isotopomers.
predissociative state of H2O+, but also vibrationally excited H2O+ ions and the fragmentation of water isotopomers.
The new branching ratio for the fragmentation of H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) into OH + H+ and OH+ + H agrees with previous (
) into OH + H+ and OH+ + H agrees with previous (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) three-state calculations,21 which supports the three-state mechanism. We have also obtained an isotopic dependence of the branching ratio in agreement with the experimental11,24 data and we have discussed the unlikely role of the
) three-state calculations,21 which supports the three-state mechanism. We have also obtained an isotopic dependence of the branching ratio in agreement with the experimental11,24 data and we have discussed the unlikely role of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) transitions in the Gaussian peak of the H+ kinetic energy release measured by Ferreira et al.16
transitions in the Gaussian peak of the H+ kinetic energy release measured by Ferreira et al.16
We have carried out 4-PESs propagation of the initial FC wave packet in the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state of HDO+. The good agreement between the results of the simulation and the ion–water collision experiments24 suggests that the cleavage preference found is due to kinematic effects in the evolution of the wave packet in the surfaces that lead to dissociation (Ã and
state of HDO+. The good agreement between the results of the simulation and the ion–water collision experiments24 suggests that the cleavage preference found is due to kinematic effects in the evolution of the wave packet in the surfaces that lead to dissociation (Ã and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ). Also, we have obtained good agreement with the experiments11 in the fragmentation branching ratio of D2O+(
). Also, we have obtained good agreement with the experiments11 in the fragmentation branching ratio of D2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ), and explained the differences with respect to the fragmentation of H2O+ as due to the larger transitions between
), and explained the differences with respect to the fragmentation of H2O+ as due to the larger transitions between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à states near the linear geometry because of the slower and more compact wave packet in heavy water than in H2O.
and à states near the linear geometry because of the slower and more compact wave packet in heavy water than in H2O.
We have also considered the fragmentation of vibrationally excited H2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) ions to simulate the experimental conditions of Harbo et al.25 We have found that the initial excitation in the symmetric stretch drives the dynamics of the initial wave packet in a way that favors the dissociation from state Ã, leading to branching ratios quite different from those obtained starting with an initial FC-wave packet. In this case, our results agree with the experiments.25
) ions to simulate the experimental conditions of Harbo et al.25 We have found that the initial excitation in the symmetric stretch drives the dynamics of the initial wave packet in a way that favors the dissociation from state Ã, leading to branching ratios quite different from those obtained starting with an initial FC-wave packet. In this case, our results agree with the experiments.25
Finally, the good agreement between our calculations and the experiments paves the way for the application of this wave packet propagation technique to other three-center systems, see e.g.ref. 41.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This work has been partially supported by Ministerio de Economía and Competitividad (Spain), project ENE2014-52432-R. The Centro de Computación Científica of UAM is acknowledged for the computational hosting facilities.
References
- D. A. Neufeld, J. R. Goicoechea, P. Sonnentrucker, J. H. Black, J. Pearson, S. Yu, T. G. Phillips, D. C. Lis, M. De Luca, E. Herbst, P. Rimmer, M. Gerin, T. A. Bell, F. Boulanger, J. Cernicharo, A. Coutens, E. Dartois, M. Kazmierczak, P. Encrenaz, E. Falgarone, T. R. Geballe, T. Giesen, B. Godard, P. F. Goldsmith, C. Gry, H. Gupta, P. Hennebelle, P. Hily-Blant, C. Joblin, R. Kołos, J. Krełowski, J. Martín-Pintado, K. M. Menten, R. Monje, B. Mookerjea, M. Perault, C. Persson, R. Plume, M. Salez, S. Schlemmer, M. Schmidt, J. Stutzki, D. Teyssier, C. Vastel, A. Cros, K. Klein, A. Lorenzani, S. Philipp, L. A. Samoska, R. Shipman, A. G. G. M. Tielens, R. Szczerba and J. Zmuidzinas, Astron. Astrophys., 2010, 521, L10 CrossRef.
- E. González-Alfonso, J. Fischer, S. Bruderer, H. S. P. Müller, J. Graciá-Carpio, E. Sturm, D. Lutz, A. Poglitsch, H. Feuchtgruber, S. Veilleux, A. Contursi, A. Sternberg, S. Hailey-Dunsheath, A. Verma, N. Christopher, R. Davies, R. Genzel and L. Tacconi, Astron. Astrophys., 2013, 550, A25 CrossRef.
-
R. Wayne, Chemistry of Atmospheres: An Introduction to the Chemistry of the Atmospheres of Earth, the Planets, and Their Satellites, Oxford University Press, 2000 Search PubMed.
- M. A. Disanti, U. Fink and A. B. Schultz, Icarus, 1990, 86, 152–171 CrossRef CAS.
- S. A. Fuselier, K. Altwegg, H. Balsiger, J. J. Berthelier, A. Bieler, C. Briois, T. W. Broiles, J. L. Burch, U. Calmonte, G. Cessateur, M. Combi, J. De Keyser, B. Fiethe, M. Galand, S. Gasc, T. I. Gombosi, H. Gunell, K. C. Hansen, M. Hässig, A. Jäckel, A. Korth, L. Le Roy, U. Mall, K. E. Mandt, S. M. Petrinec, S. Raghuram, H. Rème, M. Rinaldi, M. Rubin, T. Sémon, K. J. Trattner, C.-Y. Tzou, E. Vigren, J. H. Waite and P. Wurz, Astron. Astrophys., 2015, 583, A2 CrossRef.
- C. R. Brundle and D. W. Turner, Proc. R. Soc. London, Ser. A, 1968, 307, 27–36 CrossRef CAS.
- J. E. Reutt, L. S. Wang, Y. T. Lee and D. A. Shirley, J. Chem. Phys., 1986, 85, 6928–6939 CrossRef CAS.
- S. Truong, A. Yencha, A. Juarez, S. Cavanagh, P. Bolognesi and G. King, Chem. Phys., 2009, 355, 183–193 CrossRef CAS.
- A. Lorquet and J. Lorquet, Chem. Phys., 1974, 4, 353–367 CrossRef CAS.
- M. Eroms, M. Jungen and H.-D. Meyer, J. Phys. Chem. A, 2010, 114, 9893–9901 CrossRef CAS PubMed.
- J. Eland, Chem. Phys., 1975, 11, 41–47 CrossRef CAS.
- K. Tan, C. Brion, P. V. der Leeuw and M. van der Wiel, Chem. Phys., 1978, 29, 299–309 CrossRef CAS.
- I. Powis and D. J. Reynolds, J. Chem. Soc., Faraday Trans., 1991, 87, 921–926 RSC.
- K. Norwood, A. Ali and C. Y. Ng, J. Chem. Phys., 1991, 95, 8029–8037 CrossRef CAS.
- A. L. F. de Barros, J. Lecointre, H. Luna, M. B. Shah and E. C. Montenegro, Phys. Rev. A, 2009, 80, 012716 CrossRef.
- N. Ferreira, L. Sigaud and E. C. Montenegro, Phys. Rev. A, 2017, 96, 012705 CrossRef.
- N. Ferreira, L. Sigaud and E. C. Montenegro, J. Phys. Chem. A, 2017, 121, 3234–3238 CrossRef CAS PubMed.
- M. Paniagua, R. Martínez, P. Gamallo and M. González, Phys. Chem. Chem. Phys., 2014, 16, 23594–23603 RSC.
- R. Martínez, M. Paniagua, J. Mayneris-Perxachs, P. Gamallo and M. González, Phys. Chem. Chem. Phys., 2017, 19, 3857–3868 RSC.
- P. Gamallo, P. Defazio, M. González, M. Paniagua and C. Petrongolo, Phys. Chem. Chem. Phys., 2015, 17, 23392–23402 RSC.
- J. Suárez, L. Méndez and I. Rabadán, J. Phys. Chem. Lett., 2015, 6, 72–76 CrossRef PubMed.
- J. Suarez, S. Farantos, S. Stamatiadis and L. Lathouwers, Comput. Phys. Commun., 2009, 180, 2025–2033 CrossRef CAS.
- I. Ben-Itzhak, A. M. Sayler, M. Leonard, J. Maseberg, D. Hathiramani, E. Wells, M. Smith, J. Xia, P. Wang, K. Carnes and B. Esry, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 233, 284–292 CrossRef CAS.
- A. M. Sayler, M. Leonard, K. D. Carnes, R. Cabrera-Trujillo, B. D. Esry and I. Ben-Itzhak, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 1701 CrossRef CAS.
- L. S. Harbo, S. Dziarzhytski, C. Domesle, G. Brenner, A. Wolf and H. B. Pedersen, Phys. Rev. A, 2014, 89, 052520 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. Elizaga, L. F. Errea, A. Macías, L. Méndez, A. Riera and A. Rojas, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, L697 CrossRef CAS.
- P. Barragán, L. F. Errea, A. Macías, L. Méndez, I. Rabadán, A. Riera, J. M. Lucas and A. Aguilar, J. Chem. Phys., 2004, 121, 11629–11638 CrossRef PubMed.
- D. J. Haxton, T. N. Rescigno and C. W. McCurdy, Phys. Rev. A, 2007, 75, 012711 CrossRef.
- D. J. Haxton, T. N. Rescigno and C. W. McCurdy, Phys. Rev. A, 2007, 76, 049907(E) CrossRef.
- C. Leforestier, J. Chem. Phys., 1991, 94, 6388–6397 CrossRef CAS.
- S. Carter and N. Handy, Mol. Phys., 1984, 52, 1367–1391 CrossRef CAS.
- R. Guantes and S. C. Farantos, J. Chem. Phys., 1999, 111, 10827–10835 CrossRef CAS.
- J. Ma, C. Xie, X. Zhu, D. R. Yarkony, D. Xie and H. Guo, J. Phys. Chem. A, 2014, 118, 11926–11934 CrossRef CAS PubMed.
- C. Leforestier, R. Bisseling, C. Cerjan, M. Feit, R. Friesner, A. Guldberg, A. Hammerich, G. Jolicard, W. Karrlein, H.-D. Meyer, N. Lipkin, O. Roncero and R. Kosloff, J. Comput. Phys., 1991, 94, 59–80 CrossRef.
- D. Dundas, J. F. McCann, J. S. Parker and K. T. Taylor, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 3261 CrossRef CAS.
- C. Lanczos, J. Res. Natl. Bur. Stand., Sect. B, 1950, 45, 255–282 CrossRef.
- H. Guo, R. Chen and D. Xie, J. Theor. Comput. Chem., 2002, 01, 173–185 CrossRef CAS.
- C. Illescas, L. F. Errea, L. Méndez, B. Pons, I. Rabadán and A. Riera, Phys. Rev. A, 2011, 83, 052704 CrossRef.
- A. D. Smith, E. M. Warne, D. Bellshaw, D. A. Horke, M. Tudorovskya, E. Springate, A. J. H. Jones, C. Cacho, R. T. Chapman, A. Kirrander and R. S. Minns, Phys. Rev. Lett., 2018, 120, 183003 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: A file containing the four adiabatic potential energy surfaces employed in the calculation is provided. See DOI: 10.1039/c8cp03725f |
| ‡ Present address: Dipartimento di Chimica, Università degli Studi di Milano, 20133 Milano, Italy. |
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
L.
Méndez
,
L.
Méndez
 and
I.
Rabadán
and
I.
Rabadán
 *
*
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 electronic state, allowing the participation of the
2B2 electronic state, allowing the participation of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1, Ã 2A1 and
2B1, Ã 2A1 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states in the process, is simulated using the extended capabilities of the collocation GridTDSE code to account for the nonadiabatic propagation of wave packets in several potential energy surfaces connected by nonadiabatic couplings. Molecular data are calculated ab initio. Two initial wave packets are considered to reproduce two different experiments. The isotopic effect in the fragmentation of D2O+ and HDO+ is also studied and the results show very good agreement with the experimental cleavage preference in the fragmentation of HDO+.
2B1 states in the process, is simulated using the extended capabilities of the collocation GridTDSE code to account for the nonadiabatic propagation of wave packets in several potential energy surfaces connected by nonadiabatic couplings. Molecular data are calculated ab initio. Two initial wave packets are considered to reproduce two different experiments. The isotopic effect in the fragmentation of D2O+ and HDO+ is also studied and the results show very good agreement with the experimental cleavage preference in the fragmentation of HDO+.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 (hereafter denoted
2B1 (hereafter denoted ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ), Ã 2A1 (Ã) and
), Ã 2A1 (Ã) and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 (
2B2 (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). These electronic states are essentially described by one-electron removal from the three outermost molecular orbitals (1b1, 3a1 and 1b2, respectively) of H2O. For photon energies higher than the dissociation threshold (18.1 eV), the vibrational levels of the
). These electronic states are essentially described by one-electron removal from the three outermost molecular orbitals (1b1, 3a1 and 1b2, respectively) of H2O. For photon energies higher than the dissociation threshold (18.1 eV), the vibrational levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state are predissociative and, accordingly, the third band of the H2O photoelectron spectrum exhibits broad peaks. The ionization of H2O above the dissociation threshold leads to the cation fragmentation into H+ + OH, H + OH+ and O+ + H + H. Following the ionization of H2O, coincidence experiments11–14 have measured the branching ratios in the formation of H+ + OH and H + OH+. Experiments of ref. 15–17 have measured the kinetic energy release distributions of the fragments formed after electron impact on water molecules, which shed light on the possible routes leading to the different fragmentation schemes.
state are predissociative and, accordingly, the third band of the H2O photoelectron spectrum exhibits broad peaks. The ionization of H2O above the dissociation threshold leads to the cation fragmentation into H+ + OH, H + OH+ and O+ + H + H. Following the ionization of H2O, coincidence experiments11–14 have measured the branching ratios in the formation of H+ + OH and H + OH+. Experiments of ref. 15–17 have measured the kinetic energy release distributions of the fragments formed after electron impact on water molecules, which shed light on the possible routes leading to the different fragmentation schemes.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à electronic states. The influence of the Renner–Teller coupling on the O + H2+ proton transfer reactions was analyzed in ref. 20.
and à electronic states. The influence of the Renner–Teller coupling on the O + H2+ proton transfer reactions was analyzed in ref. 20.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, obtaining values for the dissociation branching ratios into OH + H+ and H + OH+ that were in excellent agreement with the experimental data of Tan et al.12 Our calculations consisted in nuclear wave-packet propagation on three electronic surfaces (
state, obtaining values for the dissociation branching ratios into OH + H+ and H + OH+ that were in excellent agreement with the experimental data of Tan et al.12 Our calculations consisted in nuclear wave-packet propagation on three electronic surfaces (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) , Ã and
, Ã and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ), using a modified version of the GridTDSE code22 to reproduce the nonadiabatic quantum nuclear dynamics. The initial condition of our dynamical calculation was the Franck–Condon (FC) wave packet, obtained by vertical ionization of the ground vibrational state of H2O. The wave-packet propagation showed that the dissociation mechanism involves nonadiabatic transitions from the state
), using a modified version of the GridTDSE code22 to reproduce the nonadiabatic quantum nuclear dynamics. The initial condition of our dynamical calculation was the Franck–Condon (FC) wave packet, obtained by vertical ionization of the ground vibrational state of H2O. The wave-packet propagation showed that the dissociation mechanism involves nonadiabatic transitions from the state ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) to à and
to à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) . The transition
. The transition ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ã takes place in a few femtoseconds in the vicinity of the conical intersection (CI) between the corresponding potential energy surfaces (PESs). The CI seam appears at angles
–à takes place in a few femtoseconds in the vicinity of the conical intersection (CI) between the corresponding potential energy surfaces (PESs). The CI seam appears at angles 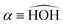 in the interval 60° ≲ α ≲ 100°, while the minimum of the à PES is located at the linear geometry (α = 180°). As a consequence, the wave packet starts in
in the interval 60° ≲ α ≲ 100°, while the minimum of the à PES is located at the linear geometry (α = 180°). As a consequence, the wave packet starts in ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) , moves towards the CI and is transferred to à with an important excitation of the bending mode. At linear geometries, the states à and
, moves towards the CI and is transferred to à with an important excitation of the bending mode. At linear geometries, the states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) become the two components of the 2Πu state, and the Ö
become the two components of the 2Πu state, and the Ö![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) Renner–Teller (RT) interaction allows the population of the ground electronic state. The fragmentation can take place either by energy transfer from the bending mode into the antisymmetric stretching motion within Ã, leading to dissociation into OH + H+, or after the RT transition between à and
Renner–Teller (RT) interaction allows the population of the ground electronic state. The fragmentation can take place either by energy transfer from the bending mode into the antisymmetric stretching motion within Ã, leading to dissociation into OH + H+, or after the RT transition between à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , leading to dissociation into OH+ + H.
, leading to dissociation into OH+ + H.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ö
–Ö![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) mechanism explains the predissociation of the water cation, other possible nonadiabatic transitions must be ruled out. In our previous work,21 we checked that the intersystem crossing transitions from
) mechanism explains the predissociation of the water cation, other possible nonadiabatic transitions must be ruled out. In our previous work,21 we checked that the intersystem crossing transitions from ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and à to the dissociative ã 4B1 state are very slow compared to
and à to the dissociative ã 4B1 state are very slow compared to ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –à transitions. Here, we also consider the possible role of the
–Ã transitions. Here, we also consider the possible role of the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 (
2B1 (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) state in the wave packet evolution, because it exhibits a CI seam with
) state in the wave packet evolution, because it exhibits a CI seam with ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) at α = 180° and relatively large O–H distances (≈5 Bohr). Given the (large) internuclear distances at which this new CI is located, we have enlarged the grid of nuclear coordinates with respect to that of our previous calculation.
at α = 180° and relatively large O–H distances (≈5 Bohr). Given the (large) internuclear distances at which this new CI is located, we have enlarged the grid of nuclear coordinates with respect to that of our previous calculation.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) and HDO+(
) and HDO+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). Our theoretical fragmentation branching ratios of D2O+ compare satisfactorily with the experimental results of Eland,11 and they support the small differences found between H2O+ and D2O+ species in photoelectron–photoion-coincidence experiments.13,14 With respect to HDO+, time of flight coincidence experiments23,24 in collisions of H+ and F7+ with HDO have shown a strong preference for breaking the O–H bond after both single and double ionization of the molecular species. In those experiments, it was also found that the isotopic effect is independent of the projectile, suggesting a kinematic effect at play in the post-collisional breakdown of HDO+ and HDO2+. This interpretation was only supported by wave-packet simulations for HDO2+ in a single PES,24 but one expects the fragmentation of HDO+ to be dominated by transitions between several electronic states. Here, we study the isotopic dependence in the bond cleavage preference, by carrying out 4-PESs wave packet propagation for HDO+.
). Our theoretical fragmentation branching ratios of D2O+ compare satisfactorily with the experimental results of Eland,11 and they support the small differences found between H2O+ and D2O+ species in photoelectron–photoion-coincidence experiments.13,14 With respect to HDO+, time of flight coincidence experiments23,24 in collisions of H+ and F7+ with HDO have shown a strong preference for breaking the O–H bond after both single and double ionization of the molecular species. In those experiments, it was also found that the isotopic effect is independent of the projectile, suggesting a kinematic effect at play in the post-collisional breakdown of HDO+ and HDO2+. This interpretation was only supported by wave-packet simulations for HDO2+ in a single PES,24 but one expects the fragmentation of HDO+ to be dominated by transitions between several electronic states. Here, we study the isotopic dependence in the bond cleavage preference, by carrying out 4-PESs wave packet propagation for HDO+.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). These authors carried out a crossed-beam experiment, where a H2O+ beam was crossed by a 532 nm laser. The subsequent dissociation was interpreted as due to the vibrational excitation of metastable low-lying vibrational levels of
). These authors carried out a crossed-beam experiment, where a H2O+ beam was crossed by a 532 nm laser. The subsequent dissociation was interpreted as due to the vibrational excitation of metastable low-lying vibrational levels of ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) . The experiment measured the ratio between the cross sections for production of the fragments OH + H+ and OH+ + H, obtaining a ratio value Γ:
. The experiment measured the ratio between the cross sections for production of the fragments OH + H+ and OH+ + H, obtaining a ratio value Γ:
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ã and
–Ã and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) PESs, which are responsible for the nonadiabatic transitions, is discussed in Section 3. In Section 4, we describe the numerical method applied to solve the time-dependent Schrödinger equation. Our main results are shown in Section 5, which includes the results of a 4-state calculation using a FC initial wave packet, the isotopic effect and the calculations with initial conditions that are excited vibrational states of the
PESs, which are responsible for the nonadiabatic transitions, is discussed in Section 3. In Section 4, we describe the numerical method applied to solve the time-dependent Schrödinger equation. Our main results are shown in Section 5, which includes the results of a 4-state calculation using a FC initial wave packet, the isotopic effect and the calculations with initial conditions that are excited vibrational states of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. A summary is presented in Section 6.
state. A summary is presented in Section 6.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1, Ã 2A1,
2B1, Ã 2A1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 and
2B2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 of H2O+ using the MOLPRO package.26 PESs and nonadiabatic couplings have been obtained with multireference configuration interaction calculations in the Cs symmetry point group. Configurations are generated by allocating seven valence electrons in (7a′,1a′′) molecular orbitals, previously obtained with CASSCF calculations in a space of (10a′,1a′′) orbitals. The basis set employed is aug-cc-pvqz and aug-cc-pvtz27 for oxygen and hydrogen, respectively.
2B1 of H2O+ using the MOLPRO package.26 PESs and nonadiabatic couplings have been obtained with multireference configuration interaction calculations in the Cs symmetry point group. Configurations are generated by allocating seven valence electrons in (7a′,1a′′) molecular orbitals, previously obtained with CASSCF calculations in a space of (10a′,1a′′) orbitals. The basis set employed is aug-cc-pvqz and aug-cc-pvtz27 for oxygen and hydrogen, respectively.
 bond angle, R is the distance from the center of mass of the OH fragment to the remaining hydrogen, r = r1, and θ is the angle between r and R.
bond angle, R is the distance from the center of mass of the OH fragment to the remaining hydrogen, r = r1, and θ is the angle between r and R.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 of H2O+ is also of C2v symmetry, with no significant changes in the equilibrium coordinates (re = 1.90 Bohr and θe = 112.5°). In contrast, the equilibrium geometry of à 2A1 has D∞h symmetry (αe = 180°). The excited
2B1 of H2O+ is also of C2v symmetry, with no significant changes in the equilibrium coordinates (re = 1.90 Bohr and θe = 112.5°). In contrast, the equilibrium geometry of à 2A1 has D∞h symmetry (αe = 180°). The excited ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 state is again of C2v symmetry, but the re distance is 2.16 Bohr, larger than in the
2B2 state is again of C2v symmetry, but the re distance is 2.16 Bohr, larger than in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state, while the bond angle is θe = 80°, considerably smaller than in the
state, while the bond angle is θe = 80°, considerably smaller than in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state. These data, the energies of the corresponding potential energy minima and the dissociation energies, are given in Table 1.
state. These data, the energies of the corresponding potential energy minima and the dissociation energies, are given in Table 1.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1)
2B1)
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1
2B1![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2
2B2![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à surfaces. The changes in the slopes of the contour lines of the à and
and à surfaces. The changes in the slopes of the contour lines of the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) surfaces at α ≈ 80° are due to the CI between these surfaces. At C2v geometries, the
surfaces at α ≈ 80° are due to the CI between these surfaces. At C2v geometries, the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) surface shows two relatively shallow minima; the one at α = 180° is a saddle-point in the (r,R)-plane, as seen in the bottom-right panel of Fig. 3.
surface shows two relatively shallow minima; the one at α = 180° is a saddle-point in the (r,R)-plane, as seen in the bottom-right panel of Fig. 3.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) PESs of C2v geometries, as functions of the O–H distance r and the bond angle α. The numbers in the colour-box are energies in Hartree.
PESs of C2v geometries, as functions of the O–H distance r and the bond angle α. The numbers in the colour-box are energies in Hartree.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) as functions of the Jacobi coordinate R, for fixed r = 1.98 Bohr, and four values of θ. In the panels corresponding to θ = 80° and θ = 100°, the energy curve of state
as functions of the Jacobi coordinate R, for fixed r = 1.98 Bohr, and four values of θ. In the panels corresponding to θ = 80° and θ = 100°, the energy curve of state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) appears above those of states
appears above those of states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and Ã, and crosses state
and Ã, and crosses state ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) at energies with small weight in the initial FC wave packet, illustrated with Gaussian shade in the second panel. At θ = 170°, the states à and
at energies with small weight in the initial FC wave packet, illustrated with Gaussian shade in the second panel. At θ = 170°, the states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) are almost degenerate up to r ≃ 5 Bohr, where the potential energy curves of states
are almost degenerate up to r ≃ 5 Bohr, where the potential energy curves of states ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) and
and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) display an avoided crossing, that turns into a CI for θ = 180°.
display an avoided crossing, that turns into a CI for θ = 180°.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (henceforth referred as CI1), uses the transformation angle:
(henceforth referred as CI1), uses the transformation angle: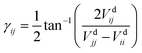
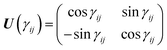
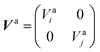
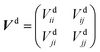
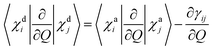
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) CI takes place along a seam of C2v geometries, and the regularization is more easily carried out by employing the symmetry coordinates {x,y,α}
CI takes place along a seam of C2v geometries, and the regularization is more easily carried out by employing the symmetry coordinates {x,y,α}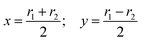
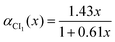
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) is written in terms of the internal coordinates, and, similar to previous works,28,29 the energy difference ΔVÃ
is written in terms of the internal coordinates, and, similar to previous works,28,29 the energy difference ΔVÃ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) = Vd
= Vd![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) − VdÃÃ is taken proportional to the distance to the CI seam in the y = 0 plane. As αCI1′ = dαCI1/dx is small in the range of x where the interaction is sizable, the energy difference can be approximated by
− VdÃÃ is taken proportional to the distance to the CI seam in the y = 0 plane. As αCI1′ = dαCI1/dx is small in the range of x where the interaction is sizable, the energy difference can be approximated by![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (x) = [α(x) − αCI1(x)]cos(αCI1′)
(x) = [α(x) − αCI1(x)]cos(αCI1′)![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (α,y) = (a0 + a1α + a2α2)y
(α,y) = (a0 + a1α + a2α2)y![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) at angles α ≈ π.
at angles α ≈ π.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) . The position of the seam in the (x,y) plane is parametrized using the following expression:
. The position of the seam in the (x,y) plane is parametrized using the following expression:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−c1(α−π)2
e−c1(α−π)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−c2(α−π)2
e−c2(α−π)2
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) at α = π rad. Solid-line: CI2 seam fitted-model of eqn (13).
at α = π rad. Solid-line: CI2 seam fitted-model of eqn (13).![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) (α,x,y) = x − xCI2(α,y)
(α,x,y) = x − xCI2(α,y)![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) (α,y) = d0
(α,y) = d0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ed1y2(α − π)
ed1y2(α − π)![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) |∂/∂x|ψ
|∂/∂x|ψ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 〉, for several values of y, and whose values are given in Table 2.
〉, for several values of y, and whose values are given in Table 2.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) seam described by eqn (13) is plotted in Fig. 5, together with the position of the ab initio zero-energy difference between these states for linear geometries. Also, in Fig. 6, we compare, for α = 175°, the ab initio nonadiabatic couplings (symbols) with the values of the derivatives (solid lines) of the transformation angle γ
seam described by eqn (13) is plotted in Fig. 5, together with the position of the ab initio zero-energy difference between these states for linear geometries. Also, in Fig. 6, we compare, for α = 175°, the ab initio nonadiabatic couplings (symbols) with the values of the derivatives (solid lines) of the transformation angle γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) [see eqn (2)] obtained with the fitted model (17) and (18), for a few values of y (those corresponding to the dotted lines of Fig. 5). These figures show the satisfactory fitting of the model to the ab initio data, where the peaks of the lorentzian follow the location of the CI2 seam and their widths depend on the parameters of eqn (18). A more global view of the topology of the CI2 is shown in Fig. 7, where we plot the derivative of the transformation angle γ
[see eqn (2)] obtained with the fitted model (17) and (18), for a few values of y (those corresponding to the dotted lines of Fig. 5). These figures show the satisfactory fitting of the model to the ab initio data, where the peaks of the lorentzian follow the location of the CI2 seam and their widths depend on the parameters of eqn (18). A more global view of the topology of the CI2 is shown in Fig. 7, where we plot the derivative of the transformation angle γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) with respect to the symmetry coordinates {x,y,α}. These derivatives mimic the behaviour of the nonadiabatic couplings between the states
with respect to the symmetry coordinates {x,y,α}. These derivatives mimic the behaviour of the nonadiabatic couplings between the states ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) near their CI.
near their CI.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) |∂/∂x|Ψ
|∂/∂x|Ψ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 〉 (symbols) and the model of eqn (13) ∂γ
〉 (symbols) and the model of eqn (13) ∂γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂x (solid-lines) as functions of x, for various values of y, labelled in the graph, and also indicated with dotted lines in Fig. 5. Modelled and ab initio data were obtained with α = 175°.
/∂x (solid-lines) as functions of x, for various values of y, labelled in the graph, and also indicated with dotted lines in Fig. 5. Modelled and ab initio data were obtained with α = 175°.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂x (left), ∂γ
/∂x (left), ∂γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂y (middle) and ∂γ
/∂y (middle) and ∂γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) /∂α (right) as functions of the symmetric (x) and antisymmetric (y) coordinates for α = 175°. Colour scale values in atomic units.
/∂α (right) as functions of the symmetric (x) and antisymmetric (y) coordinates for α = 175°. Colour scale values in atomic units.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) transitions, explained in our previous paper, is based on the method of Haxton et al.30,31 that yields a couple of diabatic states. Assuming a small total angular momentum, the Coriolis coupling terms are neglected and the body-fixed nuclear Hamiltonian has the form, in Jacobi coordinates:31,32
transitions, explained in our previous paper, is based on the method of Haxton et al.30,31 that yields a couple of diabatic states. Assuming a small total angular momentum, the Coriolis coupling terms are neglected and the body-fixed nuclear Hamiltonian has the form, in Jacobi coordinates:31,32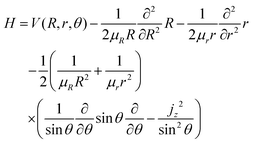
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2B1 correlate, in the limit θ → 180°, with the two components of the 2Πu state, both with Λ = |ML| = 1. In this limit, the χ±1 eigenfunctions of Lz with ML = ±1 are linear combinations of the electronic wave functions, χà and χ
2B1 correlate, in the limit θ → 180°, with the two components of the 2Πu state, both with Λ = |ML| = 1. In this limit, the χ±1 eigenfunctions of Lz with ML = ±1 are linear combinations of the electronic wave functions, χà and χ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) :
: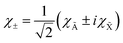
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ,χa
,χa![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ,χaÃ,χa
,χaÃ,χa![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) } to the diabatic one χd = {χd
} to the diabatic one χd = {χd![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ,χ+,χ−,χd
,χ+,χ−,χd![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) } is
} is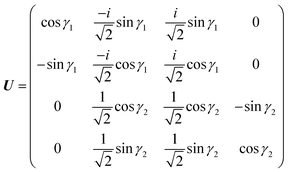
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) and γ2 ≡ γÃ
and γ2 ≡ γÃ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) . U relates the adiabatic, Va, and diabatic, Vd, potentials:
. U relates the adiabatic, Va, and diabatic, Vd, potentials: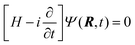
![[capital Psi, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e13b.gif)
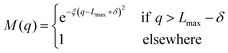
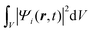 represents the time-dependent population of the electronic state i. Such populations can change either due to nonadiabatic transitions among the states included in the model, or due to the dissociating fluxes. The corresponding fragmentation probabilities ρi(t) are obtained from the continuity equation in its integral form:
represents the time-dependent population of the electronic state i. Such populations can change either due to nonadiabatic transitions among the states included in the model, or due to the dissociating fluxes. The corresponding fragmentation probabilities ρi(t) are obtained from the continuity equation in its integral form: 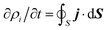 , evaluating the outgoing flux at R, r = 10.0 Bohr for the adiabatic components of the wave packet on each electronic state. Finally, the comparison with the experimental measurements is carried out at long times t > 5 ps, where the fragmentation probabilities reach asymptotic stable values.
, evaluating the outgoing flux at R, r = 10.0 Bohr for the adiabatic components of the wave packet on each electronic state. Finally, the comparison with the experimental measurements is carried out at long times t > 5 ps, where the fragmentation probabilities reach asymptotic stable values.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) PES, shows that it can be described by a wave packet that spans a range of vibrational energies of about 0.1 Hartree, as shown by the vertical Gaussian curve in Fig. 4 for θ = 100°. There, the horizontal dashed-lines correspond to the vibrational energies obtained in the adiabatic
PES, shows that it can be described by a wave packet that spans a range of vibrational energies of about 0.1 Hartree, as shown by the vertical Gaussian curve in Fig. 4 for θ = 100°. There, the horizontal dashed-lines correspond to the vibrational energies obtained in the adiabatic ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) PES.
PES.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) states appears at (R,r) distances between 3 and 5 Bohr. The correct description of the nonadiabatic transitions in the vicinity of this CI requires increasing the grid size from (Rmax,rmax) ≈ 7 Bohr (GRID I21) to (Rmax,rmax) ≈ 11 Bohr (GRID II). To check the effect of size-enlargement of the grid on the time-evolution of the electronic state populations, we have reproduced our previous three-state calculation in the new grid. The comparison of the new results with those of ref. 21 are presented in Fig. 8(a). There are small differences in the probabilities between both calculations, with small changes in the probabilities, the
states appears at (R,r) distances between 3 and 5 Bohr. The correct description of the nonadiabatic transitions in the vicinity of this CI requires increasing the grid size from (Rmax,rmax) ≈ 7 Bohr (GRID I21) to (Rmax,rmax) ≈ 11 Bohr (GRID II). To check the effect of size-enlargement of the grid on the time-evolution of the electronic state populations, we have reproduced our previous three-state calculation in the new grid. The comparison of the new results with those of ref. 21 are presented in Fig. 8(a). There are small differences in the probabilities between both calculations, with small changes in the probabilities, the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state being the more affected.
state being the more affected.

![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) for both box-sizes calculations (lines without symbols). As the size of the grid increases, there is a displacement of the population fall towards longer times, due to the damping function acting later. The inset in that figure shows the difference between both calculations, which would correspond to the wave function probability in the extra region. According to this figure, the wave packet enters this region after 50 fs, where it monotonously grows during 800 fs. After that, the amount of wave packet that leaves the extra region exceeds the amount that enters the region from shorter distances and the wave packet in the extra region fades away.
for both box-sizes calculations (lines without symbols). As the size of the grid increases, there is a displacement of the population fall towards longer times, due to the damping function acting later. The inset in that figure shows the difference between both calculations, which would correspond to the wave function probability in the extra region. According to this figure, the wave packet enters this region after 50 fs, where it monotonously grows during 800 fs. After that, the amount of wave packet that leaves the extra region exceeds the amount that enters the region from shorter distances and the wave packet in the extra region fades away.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and
, Ã and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) as functions of time for two boxes with Lmax = 7 Bohr (– – –) and Lmax = 11 Bohr (—) compared to the probability of finding a particle described by the 1D-wave packet of eqn (26), inside a box with L = 7 Bohr (– • –) and L = 11 Bohr (—•—). Inset: Differences between the populations in the boxes with L = 11 Bohr and L = 7 Bohr for the actual calculation (—) and the 1-D model (—•—).
as functions of time for two boxes with Lmax = 7 Bohr (– – –) and Lmax = 11 Bohr (—) compared to the probability of finding a particle described by the 1D-wave packet of eqn (26), inside a box with L = 7 Bohr (– • –) and L = 11 Bohr (—•—). Inset: Differences between the populations in the boxes with L = 11 Bohr and L = 7 Bohr for the actual calculation (—) and the 1-D model (—•—).![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ,
, ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) }. Here, the state
}. Here, the state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) is only coupled to
is only coupled to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) through nonadiabatic couplings described by the transformation angle γ
through nonadiabatic couplings described by the transformation angle γ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) .
.
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) gets populated at the cost of
gets populated at the cost of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) at short times, but in the picosecond timescale, the populations of the three- and four-state calculations converge.
at short times, but in the picosecond timescale, the populations of the three- and four-state calculations converge.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) main fragmentation mechanism remains the same as in the previous three-state calculation: a two-step process in which there is a fast population transfer from
) main fragmentation mechanism remains the same as in the previous three-state calculation: a two-step process in which there is a fast population transfer from ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) to à in the surroundings of CI1 and, after 30 fs, a population redistribution and decay through the following reactions:
to à in the surroundings of CI1 and, after 30 fs, a population redistribution and decay through the following reactions:![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) k±2
) k±2![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) dissociates through
dissociates through![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) → H + OH+(3Σ−) k3
) → H + OH+(3Σ−) k3![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) are connected by a CI, and we have
are connected by a CI, and we have![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) ⇌ H2O+(
) ⇌ H2O+(![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) k±4
) k±4![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) dissociates through
dissociates through![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) → H+ + OH k5
) → H+ + OH k5![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) is
is![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) → H + OH+(1Σ+) k6
) → H + OH+(1Σ+) k6
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) and D2O+(
) and D2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) fragmentation
) fragmentation
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) . The differences found in the populations of states à and
. The differences found in the populations of states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) by the introduction of state
by the introduction of state ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) vanish as t increases, which would eventually lead to similar fragmentation branching ratios. However, one must take into account that we have extended the grid of our previous paper21 to incorporate transitions in the
vanish as t increases, which would eventually lead to similar fragmentation branching ratios. However, one must take into account that we have extended the grid of our previous paper21 to incorporate transitions in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) CI. When the grid size is increased, the system remains within the grid limits for a longer time, which, in our calculation, leads to larger populations of states à and
CI. When the grid size is increased, the system remains within the grid limits for a longer time, which, in our calculation, leads to larger populations of states à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) with respect to those obtained in our previous three-state work (see Fig. 8(a)).
with respect to those obtained in our previous three-state work (see Fig. 8(a)).![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) near their PESs crossing might explain their Gaussian structure around 1.8 eV in the H+ kinetic energy release distribution. However, states
near their PESs crossing might explain their Gaussian structure around 1.8 eV in the H+ kinetic energy release distribution. However, states ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) are of different symmetry (A′ and A′′, respectively) and, correspondingly, their interaction is zero in the Hamiltonian matrix. Also, we note that their leading electronic configurations are 1a212a211b23a211b21 (
are of different symmetry (A′ and A′′, respectively) and, correspondingly, their interaction is zero in the Hamiltonian matrix. Also, we note that their leading electronic configurations are 1a212a211b23a211b21 (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) and 1a212a211b223a11b14a1 (
) and 1a212a211b223a11b14a1 (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ), which are not linked by one-electron operators, and thus we expect a small
), which are not linked by one-electron operators, and thus we expect a small ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) coupling. Additionally, the fraction of the initial FC wave packet near the crossings (see Fig. 4) is very small. Therefore, we think that this mechanism is unlikely to be competitive with the formation of OH + H+via
coupling. Additionally, the fraction of the initial FC wave packet near the crossings (see Fig. 4) is very small. Therefore, we think that this mechanism is unlikely to be competitive with the formation of OH + H+via ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –Ã transitions.
–Ã transitions.![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) in the fragmentation ratio, we address the calculation of the branching ratio of a FC wave packet in the
in the fragmentation ratio, we address the calculation of the branching ratio of a FC wave packet in the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state of D2O+ and HDO+ isotopomers including only three electronic states (
state of D2O+ and HDO+ isotopomers including only three electronic states (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã and
, à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ). For D2O+, the results are compared with those of H2O+ in Fig. 11, also including the experimental data of Eland11 for D2O+ and Tan et al.12 for H2O+, in excellent agreement with our calculation. The ratio OD+/D+ (≈5.7), larger than that of OH+/H+ (≈3.0) (see the values of r3/r1 in Table 3), can be understood in terms of kinematic effects: the D2O+ wave packet is slower and less spread than the H2O+ one, and this is particularly important in the region of linear geometries when the RT coupling transfers part of the wave packet from à to
). For D2O+, the results are compared with those of H2O+ in Fig. 11, also including the experimental data of Eland11 for D2O+ and Tan et al.12 for H2O+, in excellent agreement with our calculation. The ratio OD+/D+ (≈5.7), larger than that of OH+/H+ (≈3.0) (see the values of r3/r1 in Table 3), can be understood in terms of kinematic effects: the D2O+ wave packet is slower and less spread than the H2O+ one, and this is particularly important in the region of linear geometries when the RT coupling transfers part of the wave packet from à to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) . In D2O+, the RT coupling is less effective due to the larger reduced mass of the fragments (see eqn (19)), but the slower motion increases the interaction time, which results in a faster increase of the population of
. In D2O+, the RT coupling is less effective due to the larger reduced mass of the fragments (see eqn (19)), but the slower motion increases the interaction time, which results in a faster increase of the population of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) at the expense of Ã, and the consequent increase in the production of OD+ and decrease of that of D+.
at the expense of Ã, and the consequent increase in the production of OD+ and decrease of that of D+.


![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) as functions of time. The numbers in brackets indicate the spin multiplicity of the molecular fragment species. Lower panel: Branching ratios for bond cleavage preference compared with the experimental24 ones.
) as functions of time. The numbers in brackets indicate the spin multiplicity of the molecular fragment species. Lower panel: Branching ratios for bond cleavage preference compared with the experimental24 ones.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) )
)
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) , which is linked to the single ionization from the 1b2 molecular orbital. However, as shown by coincidence experiments,12 the dissociation into H+ + OD or D+ + OH can also take place by one-electron removal from the innermost valence orbital 2a1. In fact, the experimental branching ratios of Tan et al.12 show that the cross section for formation of protons in the photoionization of H2O is given by
, which is linked to the single ionization from the 1b2 molecular orbital. However, as shown by coincidence experiments,12 the dissociation into H+ + OD or D+ + OH can also take place by one-electron removal from the innermost valence orbital 2a1. In fact, the experimental branching ratios of Tan et al.12 show that the cross section for formation of protons in the photoionization of H2O is given by![[B with combining tilde]](https://www.rsc.org/images/entities/h3_char_0042_0303.gif)
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) ions is recorded just after their formation, in the experiment of Harbo et al.,25 the H2O+ ions produced by the ionization of H2O are stored for a relatively long time; most of the ions undergo fragmentation and only those with an energy below the dissociation threshold survive and are, afterwards, irradiated with a 532 nm (2.33 eV) laser, and the ensuing fragmentation branching ratios measured. The
) ions is recorded just after their formation, in the experiment of Harbo et al.,25 the H2O+ ions produced by the ionization of H2O are stored for a relatively long time; most of the ions undergo fragmentation and only those with an energy below the dissociation threshold survive and are, afterwards, irradiated with a 532 nm (2.33 eV) laser, and the ensuing fragmentation branching ratios measured. The ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state only holds two vibrational states below the lowest asymptotic energy of state
state only holds two vibrational states below the lowest asymptotic energy of state ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and the observed fragmentation was explained as due to the photodissociation of these metastable vibrational states of
and the observed fragmentation was explained as due to the photodissociation of these metastable vibrational states of ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) .
.
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) surface. This vibrational state, whose probability density is shown in Fig. 14, is the seven symmetric stretch overtone. The low-lying vibrational states of the
surface. This vibrational state, whose probability density is shown in Fig. 14, is the seven symmetric stretch overtone. The low-lying vibrational states of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) electronic state have long lifetimes (≈198 μs),25 which points to ineffective nonadiabatic transitions from those states. Our simulation starts when the interaction of H2O+ ions with the laser field ends. Then, the wavefunction of the excited vibrational state has sizeable values around the Ö
electronic state have long lifetimes (≈198 μs),25 which points to ineffective nonadiabatic transitions from those states. Our simulation starts when the interaction of H2O+ ions with the laser field ends. Then, the wavefunction of the excited vibrational state has sizeable values around the Ö![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) CI and fast nonadiabatic transitions take place, leading to the ion breakdown.
CI and fast nonadiabatic transitions take place, leading to the ion breakdown.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , henceforth a smaller fragmentation into H + OH+; i.e., the initial vibrational excitation leads to a faster motion of the wave packet in the à PES and to the ensuing increase of the k1 rate constant of reaction (28).
, henceforth a smaller fragmentation into H + OH+; i.e., the initial vibrational excitation leads to a faster motion of the wave packet in the à PES and to the ensuing increase of the k1 rate constant of reaction (28).
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. (a) Populations of the electronic states of H2O+ indicated in the figure. (b) Probabilities of the possible fragments.
state. (a) Populations of the electronic states of H2O+ indicated in the figure. (b) Probabilities of the possible fragments.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) by means of wave packet propagation in four electronic PESs (
) by means of wave packet propagation in four electronic PESs (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ), using a modified version of the GridTDSE computational code22 to simultaneously reproduce the nuclear dynamics on each surface. The values of the potential energy on each electronic state and the nonadiabatic couplings among them were calculated ab initio on exactly the same grid of points where the finite difference scheme of the GridTDSE is implemented, enhancing the accuracy of the calculations. This study extends our previous simulations21 by considering one more electronic state (
), using a modified version of the GridTDSE computational code22 to simultaneously reproduce the nuclear dynamics on each surface. The values of the potential energy on each electronic state and the nonadiabatic couplings among them were calculated ab initio on exactly the same grid of points where the finite difference scheme of the GridTDSE is implemented, enhancing the accuracy of the calculations. This study extends our previous simulations21 by considering one more electronic state (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) and a larger configuration space. Here, we have considered not only an initial FC wave packet, obtained by vertical ionization of H2O+ into the
) and a larger configuration space. Here, we have considered not only an initial FC wave packet, obtained by vertical ionization of H2O+ into the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) predissociative state of H2O+, but also vibrationally excited H2O+ ions and the fragmentation of water isotopomers.
predissociative state of H2O+, but also vibrationally excited H2O+ ions and the fragmentation of water isotopomers.
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) into OH + H+ and OH+ + H agrees with previous (
) into OH + H+ and OH+ + H agrees with previous (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , Ã,
, Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) three-state calculations,21 which supports the three-state mechanism. We have also obtained an isotopic dependence of the branching ratio in agreement with the experimental11,24 data and we have discussed the unlikely role of the
) three-state calculations,21 which supports the three-state mechanism. We have also obtained an isotopic dependence of the branching ratio in agreement with the experimental11,24 data and we have discussed the unlikely role of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) transitions in the Gaussian peak of the H+ kinetic energy release measured by Ferreira et al.16
transitions in the Gaussian peak of the H+ kinetic energy release measured by Ferreira et al.16![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state of HDO+. The good agreement between the results of the simulation and the ion–water collision experiments24 suggests that the cleavage preference found is due to kinematic effects in the evolution of the wave packet in the surfaces that lead to dissociation (Ã and
state of HDO+. The good agreement between the results of the simulation and the ion–water collision experiments24 suggests that the cleavage preference found is due to kinematic effects in the evolution of the wave packet in the surfaces that lead to dissociation (Ã and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ). Also, we have obtained good agreement with the experiments11 in the fragmentation branching ratio of D2O+(
). Also, we have obtained good agreement with the experiments11 in the fragmentation branching ratio of D2O+(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ), and explained the differences with respect to the fragmentation of H2O+ as due to the larger transitions between
), and explained the differences with respect to the fragmentation of H2O+ as due to the larger transitions between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à states near the linear geometry because of the slower and more compact wave packet in heavy water than in H2O.
and à states near the linear geometry because of the slower and more compact wave packet in heavy water than in H2O.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) ions to simulate the experimental conditions of Harbo et al.25 We have found that the initial excitation in the symmetric stretch drives the dynamics of the initial wave packet in a way that favors the dissociation from state Ã, leading to branching ratios quite different from those obtained starting with an initial FC-wave packet. In this case, our results agree with the experiments.25
) ions to simulate the experimental conditions of Harbo et al.25 We have found that the initial excitation in the symmetric stretch drives the dynamics of the initial wave packet in a way that favors the dissociation from state Ã, leading to branching ratios quite different from those obtained starting with an initial FC-wave packet. In this case, our results agree with the experiments.25


