Investigating the Cusp between the nano- and macro-sciences in supermolecular liquid-crystalline twist-bend nematogens

Abstract

In this article we report the first known linear liquid-crystalline hexamer and in doing so demonstrate that higher oligomers and main chain polymers, with chemical structures based upon dimers and bimesogens, can exhibit the topical twist-bend ‘nematic’ mesophase. In doing so we find that there is continuation of properties and structures across the spectrum from dimer to polymer and possibly to macroscale objects such as helical flagella. This finding highlights the cross over from nanoscience based mainly on electrostatics and other non-covalent interactions to macroscience based mainly on molecular topology, density of packing, and minimisation of the free energy.

---

Introduction

A study of the self-assembling behaviour of bimesogens possessing a bent molecular shape has been one of the most active areas of liquid crystal research in recent years.^1–24 A new enigmatic mesophase has been found in such systems, and classified as the twist-bend nematic (N_TB) phase.²⁵ The twist-bend nematic phase, theoretically predicted earlier by Dozov,²⁶ has been described as the ‘fifth nematic phase’²⁷ and as the ‘structural link’ between the uniaxial nematic mesophase (N or N_U) and the helical chiral nematic (cholesteric, N*) phase.²⁸ In the uniaxial nematic phase the molecules are, on average, oriented parallel to one another along a vector termed the director, n (Fig. 1a), whereas in the chiral nematic (N*) phase, formed via the introduction of chirality to the material, a right- or left-handed helical structure results (Fig. 1b) with a pitch of the order of hundreds of nanometers. Conversely, the twist-bend nematic phase consists of degenerate helices, with extremely short pitches of several nanometres (Fig. 1c) but formed by achiral molecules.^27–29 The spontaneous formation of helical nano-structures and the breaking of mirror symmetry pose fundamental questions that are of importance to a range of scientific disciplines such as asymmetric autocatalysis and the origin of biological homochirality.^30–34

Fig. 1 Cartoon depiction of the local structures of bimesogens in (a) an untilted uniaxial nematic phase, (b) left- and right-handed chiral nematic phase, and (c) an heliconical N_TB phase showing the local and gross structures (left- and right-hand helices are present). Images are not to scale; the pitch of (b) is typically several hundred nanometers whereas that of (c) is typically under 10 nanometers.

The discovery of a new nematic polymorph is always greeted with excitement because of the rarity of new polymorphs and the possibilities of generating new paradigms for applications, or even to replace older technologies with newer and better ones. However, in the case of the twist-bend phase the bulk properties have been found to be contrary to those of the nematic (or chiral nematic) phases exhibited by rod-like (calamitic) liquid crystals. For instance, nematic liquid crystals can be manipulated by small electric fields (<1 V μm⁻¹), whereas the N_TB phase does not exhibit any electrooptic response under these conditions. X-ray diffraction shows a lack of lamellar organisation in the N_TB phase, whereas by optical microscopy it exhibits apparent long-range order.¹⁹ The nematic phase is typically fluid, whereas the viscosity of the twist-bend nematic is significantly higher,²¹ and Brownian motion visible that is visible in the nematic phase of bimesogens is appreciably reduced upon entering the N_TB phase.^19,20 It is possible to draw freestanding films of the N_TB phase, which is something that cannot be done for calamitic nematic liquid crystals.¹⁹ Lastly, and most peculiarly, we have demonstrated that there is a linear relationship between the temperatures at which the isotropic (I) to nematic and nematic to N_TB transitions occur, irrespective of the polarity, polarisability, and lateral substitution across a range of dimeric or bimesogenic materials.³⁵ This remarkable result hints at the importance of topology and molecular shape in determining the phase structure and properties of oligomeric and supermolecular liquid crystals that exhibit N_TB phases. Differing interpretations of such experimental results have motivated several alternate descriptions of this N_TB phase.^23,36–38

To date, the N_TB phase has been exhibited mostly by liquid crystal dimers (containing two equivalent mesogenic groups) or bimesogens (containing two different mesogenic groups), where a flexible methylene spacer of odd-parity links the rigid mesogenic groups of the molecular architecture.^{20,23,39–47} Beyond simple dimers there exist examples of both covalent and non-covalent trimeric materials and one “tetrameric” material (T4₉) reported to exhibit this state of matter.^48–51 These materials are not strictly trimers or tetramers in that they are composed of identical sub units however they can be broken down into subdivisions which are broadly similar; for example the material T4₉ has four phenylbenzoate mesogenic units separated by three nonamethylene spacers and is therefore described as a tetramer.

It has been suggested that for dimers and bimesogens the propensity of a given material to exhibit the twist-bend nematic phase is highly dependent on the intermesogen angle.^17,52,53 It seems a reasonable supposition that higher oligomers of appropriate structure will exhibit the twist-bend nematic phase given its observation in three trimers and a single tetramer; but this has not yet been demonstrated experimentally. Herein we describe the synthesis of two novel oligomeric materials that exhibit the twist-bend nematic phase – a linear tetramer (O4₇) and a linear hexamer (O6₇) – and thereby demonstrate that the N_TB phase can exist across a wider range of length scales than previously reported, and that can now be extended from simple dimers to higher oligomers and, potentially, polymers. Moreover, the results reported here will enable us to further test our hypothesis that the condensed phases exhibited by supermolecular systems exhibit an increased dependence on molecular topology relative to low-molar mass materials.³⁵

Experimental

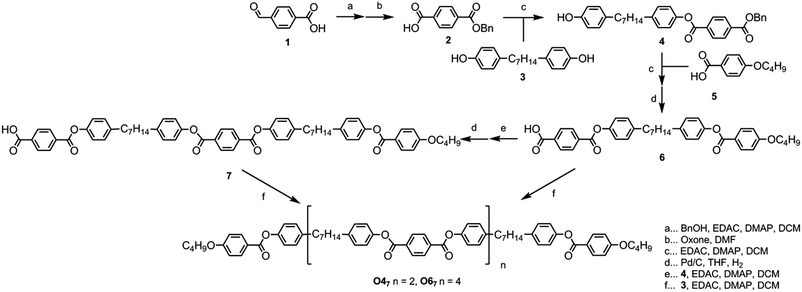
The target materials O4₇ and O6₇ shown in Fig. 2 were prepared as follows. Benzylation of 4-formylbenzoic acid followed by oxidation with oxone afforded mono-benzyl terephthalic acid in 82% yield over two steps. The esterification of 2 with 1,7-bis(4-hydroxyphenyl)heptane (compound 3, prepared in 3 steps from anisole in 63% yield as described in ref. 42) to afford the key intermediate 4 required slow addition of the EDAC–acid complex to a solution of 3 with a large excess of base to aid solubility; previously pyridine was used,⁵⁰ however, it was found that 3 equivalents of DMAP worked well, affording 4 in 66% yield. Esterification of 4 with 4-butoxybenzoic acid, followed by hydrogenolysis of the benzyl group gave the free acid (6) in a yield of 83% in 2 steps.

Fig. 2 The synthesis of O4₇ and O6₇.

Esterification of two equivalents of compound 6 with 1,7-bis(4-hydroxyphenyl)heptane (3) afforded the tetramer O4₇ in 57% yield. Esterification of 6 with 4 followed by hydrogenolysis of the benzyl protecting group afforded a ‘trimer’ system with a free benzoic acid at the terminus of one mesogenic unit (7); esterification of two equivalents 7 with 3 afforded the hexamer O6₇ in 13% yield. Although the synthesis of O6₇ was trivial, purification of the crude reaction mixture was not. For example, when attempting to purify the material by column chromatography with a gradient of either DCM/hexanes or ethyl acetate/hexanes the target compound did not elute at all, even in neat DCM (Rf_DCM ∼ 0.65). Only upon switching to neat ethyl acetate did the target material elute from the column, and then various reaction side products and impurities were also carried through. Ultimately it was found that a simple silica plug followed by preparative TLC, filtration to remove insoluble matter, and finally precipitation from THF/ethanol provided a suitable method for the purification of O6₇. This step to generate an n + 1 species, i.e. the synthesis of 7 from 6via steps e and d, may in future be used to prepare higher oligomers, however to date we have only undertaken the synthesis of O4₇ and O6₇ as a proof of concept to this approach. We note that the difficulties experienced with purification may render this method unsuitable for the preparation of higher oligomers (such as the octomer O8₇, the decamer O10₇etc.). Full experimental details, including chemical characterisation and descriptions of the instrumentation used, are available in the ESI† to this article.

Results

The liquid-crystalline behaviour of both the tetramer O4₇ and the hexamer O6₇ was studied by a combination of polarizing optical microscopy (POM), differential scanning calorimetry (DSC) and small angle X-ray scattering (SAXS). Transition temperatures, and associated enthalpies and entropies of transition were determined by DSC at a heat/cool rate of 10 °C min⁻¹. Transitional behaviour for both O4₇ and O6₇ is given in Table 1 along with that of the analogous dimer O2₇, reported by us previously,⁵⁴ with full tabulated DSC data given in the ESI† to this article.

Table 1 Transition temperatures, associated enthalpies of transition and dimensionless entropies of transition for the tetramer O4₇ and the hexamer O6₆; values are the mean of 14 cycles (6 for melting points), with standard deviations given in parenthesis. For comparative purposes the transitional behaviour of the analogous dimer (named O2₇ in this work) is shown, values were taken from ref. 54 however standard deviations were not presented

No.	n=		Cr–NTB	NTB–N	N–I
O27	0	T (°C)	87.0 (—)	79.2 (—)	85.9 (—)
		ΔH (kJ mol^−1)	36.61 (—)	1.23 (—)	0.41 (—)
		ΔS/R	12.22 (—)	0.41 (—)	0.13 (—)
O47	2	T (°C)	143.9 (0.1)	172.9 (0.24)	194.2 (0.7)
		ΔH (kJ mol^−1)	53.29 (0.49)	0.81 (0.05)	0.77 (0.03)
		ΔS/R	14.98 (0.14)	0.22 (0.01)	0.20 (0.01)
O67	4	T (°C)	174.4 (0.3)	158.9 (0.1)	188.1 (0.1)
		ΔH (kJ mol^−1)	29.76 (0.27)	0.57 (0.02)	0.35 (0.01)
		ΔS/R	7.99 (0.07)	0.16 (0.01)	0.09 (0.01)

---

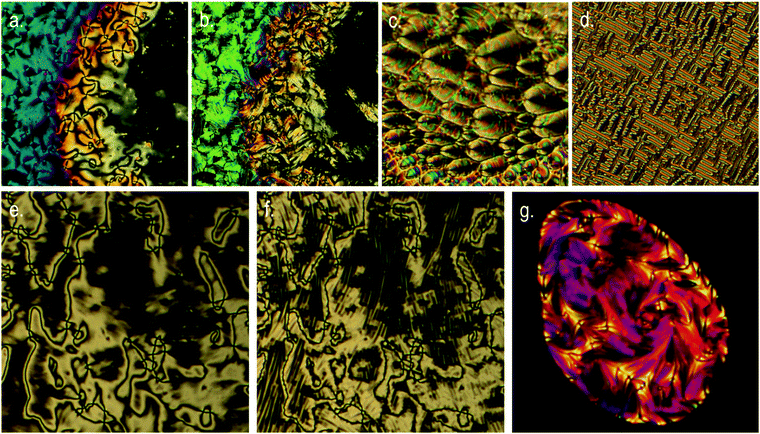
The tetramer O4₇ was found to exhibit enantiotropic nematic and twist-bend nematic phases, mirroring the mesophases exhibited by the analogous dimer O2₇. The identity of the nematic phase was based on observation of the characteristic schlieren texture (Fig. 3a). The lower temperature mesophase was identified as the twist-bend nematic by POM as follows. Upon cooling below 172.9 °C a sharp transition front was seen, yielding the ‘blocky’ texture shown in Fig. 3b. Regions that are homeotropically aligned (and thus optically extinct) in the nematic remain so in the twist bend nematic phase. In uncovered droplets the schlieren texture of the nematic phase does not yield to the ‘blocky’ texture, instead numerous parabolic defects form (Fig. 3c). When confined in a 5 μm cell with planar alignment the rope-like texture was observed (Fig. 3d). Mechanical shearing of the sample revealed it to be highly viscous in both the nematic and twist-bend phases. When studied by POM O6₇ was found to exhibit nematic and twist-bend nematic mesophases. In the analogous tetramer both mesophases are enantiotropic, but for O6₇ the twist-bend nematic phase is monotropic, being observable only by supercooling the material. The identities of both mesophases were based on the observation of a characteristic schlieren texture in the nematic phase (Fig. 3e), which subsided to the ‘blocky’ paramorphotic schlieren texture after cooling below the N_TB–N phase transition (Fig. 3f). In a different region of the slide numerous focal-conic defects could be seen embedded within the ‘blocky’ texture of the twist-bend phase. As with the tetramer (O4₇) it was observed that upon mechanical shearing the hexamer O6₇ is highly viscous, in not only the nematic and N_TB phases but also in the isotropic liquid.

Fig. 3 Photomicrographs (×100, crossed polars) of: (a) the schlieren texture and a homeotropic region of the nematic phase of O4₇ at 184 °C on an untreated glass slide; (b) the same region cooled into the N_TB phase of O4₇ at 169 °C showing the ‘blocky’ texture and a homeotropic region; (c) parabolic defects in an uncovered droplet of the N_TB phase exhibited by O4₇ at 166 °C; (d) the rope-like texture of the N_TB phase of O4₇ observed in a 5 μm cell treated for planar alignment at 128 °C; (e) the schlieren texture of the nematic phase of O6₇ at 174 °C on an untreated glass slide; (f) approximately the same region of O6₇ cooled into the N_TB phase at 156 °C showing the blocky texture; (g) a different region of the same slide showing numerous focal conic defects present alongside the blocky texture of the N_TB phase of O6₇ at 147 °C. We note that, qualitatively, these textures are almost identical with those exhibited by the dimers.

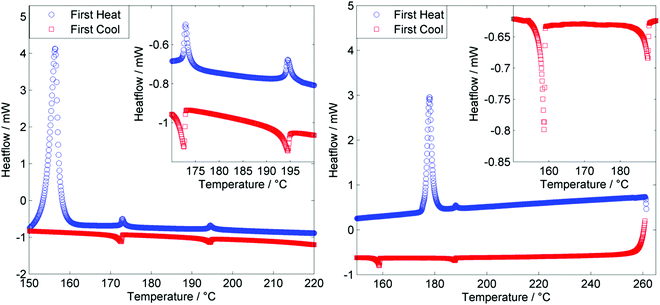
As shown in Fig. 4, for both the tetramer O4₇ and the hexamer O6₇ both the N–I and N_TB–N transitions are first order, with the enthalpy associated with the N_TB–N transition being larger than that of the N–I transition in both instances (Table 1). The enthalpy associated with the N_TB–N transition was found to be larger than that of the clearing point in the previously reported tetramer T4₉,⁵⁰ and this seems to be a universal feature of oligomeric twist-bend materials. We note that for almost all dimeric or bimesogenic materials known to exhibit nematic and twist-bend nematic mesophases the enthalpy of the former is greater than the later, the N_TB–N transition being only weakly first order. When subjected to repeated heat/cool cycles (data in ESI,† Table S1) we note that for the tetramer T_NTB–N and T_N–Iso appear to decrease marginally with successive DSC runs. This may indicate decomposition of the sample, possibly via transesterification. Conversely the hexamer does not exhibit such a strong drop in either onset temperature, possibly due to the lower T_N–I (meaning DSC cycles were run to a lower temperature of 205 °C for O6₇versus 230 °C for O4₇) of this material relative to the tetramer.

Fig. 4 DSC thermograms for O4₇ with an expansion of the region between 170–200 °C (left) and for O6₇ with an expansion of the region between 150–190 °C (right). Both thermograms were obtained using a heat/cool rate of 10 °C min⁻¹.

Both oligomeric materials, O4₇ and O6₇, were analysed by variable temperature small angle X-ray scattering (VT-SAXS, Fig. 5), with the samples filled into 0.9 mm O.D. glass capillaries and aligned in a magnetic field perpendicular to the incident X-ray beam. The wide-angle peak (small d-spacing) corresponds to the average lateral separation of molecules, whereas the small-angle scattering peak (large d-spacing) corresponds to the average end-to-end separation, but not the molecular length. For the tetramer O4₇ the contour plot of integrated SAXS intensity (Fig. 5) shows the d-spacing of the wide-angle peak decreases slightly across the entire temperature range studied, from a value of ≈0.48 nm at the N–I transition to a minimum of ≈0.43 nm at 140 °C. Conversely the d-spacing of the small angle peak of O4₇ is largely temperature independent across the entire nematic phase range with a value of 1.92 nm, but the d-spacing decreases at the N_TB–N transition, taking a temperature independent value of 1.89 nm in the N_TB phase. The hexamer O6₇ behaves analogously to the tetramer; the d-spacing of the wide-angle peak decreases in an almost linear fashion from ∼0.49 nm immediately below the N–Iso transition at 188 °C to ∼0.47 nm in the N_TB phase at 142 °C. The d-spacing of the small angle peak decreases across the nematic phase range, from 2.04 nm following the N–Iso transition to 1.99 nm immediately prior to the N_TB–N transition, before decreasing to 1.97 nm in the N_TB phase at 142 °C. It should be noted that the scattering at small- and wide-angles is diffuse for both O4₇ and O6₇, (see Fig. 5), as is typical of nematic mesophases, with the scattering at small angle being approximately 50% more intense than that at wide angles.

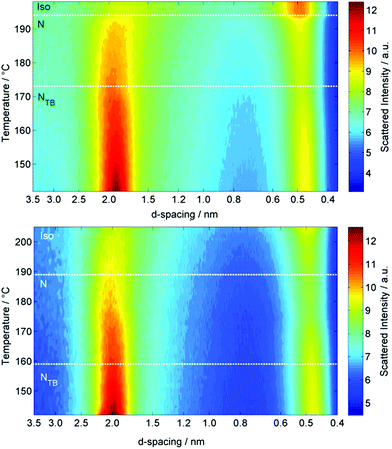Fig. 5 Contour plots of variable temperature small angle X-ray scattering (VT-SAXS) of the tetramer O4₇ (top) and the hexamer O6₇ (bottom).

The end-to-end molecular lengths of the all-trans forms of both O4₇ and O6₇ were obtained from geometries minimised at the B3LYP/6-31G(d) level of DFT, and were determined to be 8.3 nm and 12.3 nm respectively. The utility of non-resonant SAXS in studying the twist-bend phase is somewhat limited; however, what is clear from the present results is that both the nematic and N_TB phases are extensively intercalated. The d-spacing of the small angle scattering peak was essentially temperature invariant in both materials, and assuming values of 1.89 nm for the tetramer O4₇ and 1.97 nm for the hexamer O6₇, corresponding to roughly ¼ and ⅙ molecular lengths respectively. Representative two dimensional SAXS patterns for both materials are given in the ESI.†

If we compare the transition temperatures of both O4₇ and O6₇ with those of the analogous dimeric material O2₇ (heptane-1,7-diylbis(4,1-phenylene)bis(4-butoxybenzoate), shown in Table 1)⁵⁴ it can be seen that on going from a dimer to a tetramer there is a significant increase in melting point, as well as in both the N–I and N_TB–N transition temperatures. Going from the tetramer (O4₇) to the analogous hexamer (O6₇), there is a moderate increase in the melting point and a small decrease in both the clearing point and the N_TB–N transition temperatures, although the magnitudes of the changes are smaller than those going from a dimer to the tetramer. The reduced temperatures (defined here as T_NTB–N/T_N–I) are 0.98, 0.95 and 0.94 for the dimer, tetramer and hexamer systems respectively, the temperature range (and therefore the thermal stability) of the nematic phase is increasing with increasing molecular length. It has been suggested from a Landau model of the N_TB–N transition that the associated enthalpy of transition should be larger the closer the reduced temperature is to unity,⁵⁵ and this is consistent with our present results.

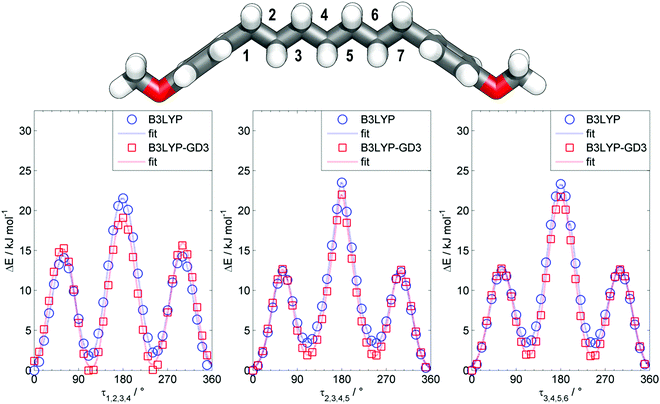
The all-trans conformer of the dimer O2₇ was calculated to have an end-to-end molecular length of 3.5 nm at the B3LYP/6-31G(d) level of DFT, which may be compared with the values of 8.3 nm and 12.3 nm obtained for the all-trans forms of O4₇ and O6₇. The previously reported N_TB tetramer (T4₉) was calculated to have something of a twisted geometry due to the non-linearity of the phenylbenzoate mesogenic units; however this is not observed for the all-trans conformers of either O4₇ or O6₇ with both compounds being linear and planar. Due to the conformational flexibility afforded to both O4₇ and O6₇ by the inclusion of multiple heptamethylene spacers there are likely to be many conformers other than the all-trans conformer that are populated, perhaps significantly at the temperatures where the liquid and liquid-crystalline phases occur. Using bis (4-methoxyphenyl)heptane as a model compound we performed relaxed scans about each of the three dihedral angles depicted in Fig. 6 using the B3LYP functional (both with and without Grimme's GD3 dispersion correction, B3LYP-GD3)⁵⁶ and the 6-31G(d) basis set, giving us some insight into the possible conformational landscape of both O4₇ and O6₇.

Fig. 6 Plots of energy (kJ mol⁻¹) vs. dihedral angle (τ_1,2,3,4, τ_2,3,4,5 and τ_3,4,5,6) obtained using the B3LYP level of DFT (blue circles) and at the B3LYP-GD3 level of DFT (red squares) with the 6-31G(d) basis set. Fits to the values are shown for guidance.

When using the B3LYP functional the all-trans conformer is the energy minimum, and assuming a simple Boltzmann distribution at 150 °C the probability of a single gauche conformer at the 1st, 2nd and 3rd torsional angles is 44%, 33% and 32%, respectively. If we include Grimme's GD3 dispersion corrections then we find that the equivalent probabilities of a single gauche conformer at these torsional angles are 71%, 45% and 41%, respectively. These results imply that the conformational landscape of oligomers such as O4₇ and O6₇ is complex, with not only the all-trans form being populated but also those with one or more gauche conformations.

Discussion

The formation of the helical structure of the N_TB phase, as with all phases of soft matter, inevitably has its origin in molecular structure. Conceptually for the twist-bend phase to be linked from the dimer through to macromolecules one would have to consider the properties of related main chain polymer equivalents. A report by Ungar et al. in 1992⁵⁷ indeed demonstrates unequivocally that nematic to nematic phase transitions occur in polymeric systems for the odd-parity (n = odd) random copolymers shown in Fig. 7. It is not clear that this lower temperature nematic phase is indeed the N_TB phase, although such an outcome has been speculated recently.²⁸ Although the aromatic units within these polymers are ethylene linked, whereas the linking groups are esters for the dimer and oligomers reported here, the overall shapes of the aromatic units in both classes can be considered to be similar.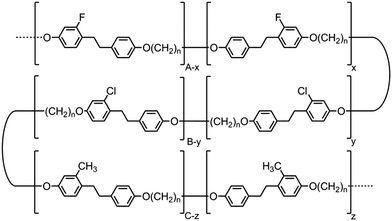

Fig. 7 Structures of copolymers reported by Ungar et al. that exhibit nematic to nematic phase transitions (denoted as N–N₂ in the text), where n is equal to 5, 7 or 9.⁵⁷

Returning to the invariant relationship between T_N–Iso and T_NTB–N that we recently reported for dimeric and bimesogenic materials,³⁵ we find that both oligomers reported here and the polymers reported by Ungar et al. follow this same relationship remarkably well despite the significant variations in chemical architectures of the materials (Fig. 8). The fitted relationships for the heptamethylene and nonamethylene systems are similar to each other although the slopes and the intercepts are different, as given by eqn (1) and (2):

T_NTB–N = 0.804T_N–I + 8.51 for heptamethylene (1)

T_NTB–N = 0.775T_N–I + 5.10 for nonamethylene (2)

If this type of relationship is taken to its logical extreme, then materials should exist where the phase sequence Iso–N_TB–N would be expected on cooling; eqn (1) and (2) suggest that such a switch would occur generally for materials with T_N–Iso values of <44 and <23 °C for heptamethylene and nonamethylene systems, respectively. The small variations of individual data points from the trends given in Fig. 8 may arise from perturbations in the molecular architectures due to differences in the aspect ratios of the dimers and bimesogens,³⁵ and the dimers as sub-units of the oligomers and polymers. Furthermore, this analysis does not take into account variations in transition temperatures that may result from either chemical purity or differences between experimental setups and procedures used to acquire the data.

Fig. 8 The general structure of ‘two-ring’ mesogenic dimers and bimesogens with various terminal groups, lateral groups and ring–ring linking groups with heptamethylene and nonamethylene spacers that provided data for plots of the T_NTB–Nversus the T_N–Iso for dimers, bimesogens and oligomers with (a) heptamethylene spacers and (b) nonamethylene spacers. Linear fits, given by eqn (1) and (2) in the text, correspond to data for pure bimesogens only (i.e. oligomers, polymers and extrapolated values were excluded from the fit, but were found to be in good agreement). In cases where differing transition temperatures were reported (CB7CB, CB9CB) we have used values from materials with the highest known chemical purity. Data was taken from ref. 23, 41, 42, 50, 51, 57, 58 and is presented in tabulated form alongside molecular structures in the ESI.†

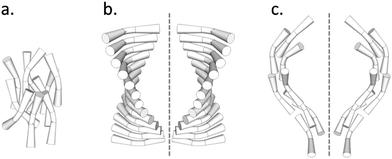
Thus the picture is complete and the twist-bend phase can be considered as a universal phenomenon that occurs over length scales from dimers through to main chain polymers, and in essence Luckhurst was correct when he stated, “Liquid Crystal dimers and trimers exhibit a range of unusual properties, which are fascinating in their own right, and which also parallel those found for semi-flexible main-chain liquid crystal polymers. This close similarity suggests that dimers and oligomers should form good model systems for their polymeric counterparts…”.⁵⁹ As the N_TB phases of dimers exhibit polymer-like properties, and helical arrangements in polymers can tend to form rope-like (fibrous) structures, it is worthwhile examining alternative structures for the twist-bend phase, given that linear oligomeric materials (which may form fibrous structures) exhibit this state of matter. For example, in a fibrous model individual helicoids of dimeric or oligomeric molecules will be twisted together as shown in the rope-like schematic structures shown in Fig. 9. In this case the resultant fibres will approximately be cylindrical with circular cross-sectional areas, and therefore will have the maximum packing together of the individual components along the fibre axes. Such packing will result in the minimisation of the free volume, and thereby the relative free energy of the system.

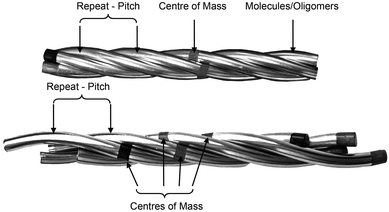Fig. 9 Schematic of the twisted fibre model of the N_TB phase, shown with commensurate (top) and incommensurate (bottom) centres of mass.

If we consider the periodic ordering revealed by the fibre model, the centres of mass of the helicoidal units can potentially be commensurate or incommensurate, as shown in Fig. 9. For commensurability there is the potential for layering resulting in long-range 1-D periodic order. Conversely for the incommensurate case, the centres of mass of each mesogenic unit are randomly organized along the fibre axis and so the periodicity of the phase arises from the pitch rather than positional ordering of the molecules. For the incommensurate model, there is an entropy gain due to the lack of positional ordering, and hence a lowering of the free energy. Thus, when the temperature is lowered and condensation of the twist-bend phase occurs, there is potential for a phase transition from an incommensurate to a commensurate N_TB phase. Furthermore, if the fibres are of similar cross-sectional area then hexagonal packing of the fibres could be likely, thereby generating a columnar nematic or N_TB phase. Experimental evidence for this phenomenon has been demonstrated for the liquid crystal phase of poly(benzyl L-glutamate) (PBLG), where X-ray data showed the formation of hexagonal ordering.^41,60 So far this type of ordering has not been observed for the twist-bend phase. The connection of the physical properties from dimer through to polymer indicates that molecular topology and minimisation of the free volume, rather than electrostatic and other non-covalent interactions, could be the dominant factors that determine the mesophase structure in condensed, self-organising phases of large molecular entities.

Conclusions

We have demonstrated two new examples of oligomeric materials exhibiting the twist-bend phase, including a tetramer and what we believe to be the first reported linear liquid-crystalline hexamer. The observation of this mesophase in these higher oligomers satisfies our earlier speculations about potential oligo-N_TB materials,⁵¹ and moreover this behaviour also appears to apply to true main chain polymers. Indeed, we speculate that one of the earliest observations of the N_TB phase, although not referred to as such at the time, was in polymers, long before its discovery in dimeric materials,⁵⁷ while the ‘conical nematic’ phase found in suspensions of helical flagella may in fact be a ‘twist-bend nematic’ mesophase.⁶¹

In addition to bridging the gap between the twist-bend phases observed separately in low-molecular weight dimers and high-molecular weight polymers, linear oligomeric materials have the potential to act as model systems for main-chain liquid-crystalline polymers. As some of the experimental results on the physical properties of the N_TB phase fit with a fibre model, we propose that this structure should be explored further, including the possible existence of commensurate and incommensurate N_TB phases. Our results indicate that the importance of electrostatics and other non-covalent interactions in dictating the structures of condensed phases of large molecular systems (e.g. dimers and above) are eclipsed by the growing importance of molecular topology. Plots of T_NTB–Nvs. T_N–Iso for dimers and bimesogens show a linear relationship for homologous series of materials, and even oligomeric materials that can be categorised within the same homologous series appear to obey the same linear relationship. Our results suggest that the cross-over from nano to macro-scale structuring and organisation is perhaps more of a continuum than a discrete step, occurring between 5 and 10 nm, and highlighting the potential for using dimers and related materials as analogues of oligomeric and polymeric systems.

Acknowledgements

RJM thanks the University of York for funding a summer research placement for FPS. The authors thank Dr Iman Khazal of the University of York for synthesising a bulk quantity of compound 3 for use in this work. The authors also thank Dr Laurence Abbott and Dr Mark Sims for discussions and insight into the packing of granular materials. Lastly we thank the Engineering and Physical Sciences Research Council (EPSRC) for support of this work via grant codes EP/K039660/1 and EP/M020584/1. Raw data pertinent to this work are available upon request from the University of York data catalogue. The authors would like to thank the referees for helpful suggestions during the peer review process.

References

1. J. W. Emsley, G. R. Luckhurst and G. N. Shilstone, Mol. Phys., 1984, 53, 1023–1028.
2. J. W. Emsley, G. R. Luckhurst, G. N. Shilstone and I. Sage, Mol. Cryst. Liq. Cryst., 1984, 102, 223–233.
3. P. J. Barnes, A. G. Douglass, S. K. Heeks and G. R. Luckhurst, Liq. Cryst., 1993, 13, 603–613.
4. M. Sepelj, A. Lesac, U. Baumeister, S. Diele, D. W. Bruce and Z. Hamersak, Chem. Mater., 2006, 18, 2050–2058.
5. M. Sepelj, A. Lesac, U. Baumeister, S. Diele, H. L. Nguyen and D. W. Bruce, J. Mater. Chem., 2007, 17, 1154–1165.
6. V. P. Panov, M. Nagaraj, J. K. Vij, Y. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Phys. Rev. Lett., 2010, 105, 167801.
7. P. A. Henderson and C. T. Imrie, Liq. Cryst., 2011, 38, 1407–1414.
8. V. P. Panov, R. Balachandran, M. Nagaraj, J. K. Vij, M. G. Tamba, A. Kohlmeier and G. H. Mehl, Appl. Phys. Lett., 2011, 99, 237804.
9. K. Adlem, M. Copic, G. R. Luckhurst, A. Mertelj, O. Parri, R. M. Richardson, B. D. Snow, B. A. Timimi, R. P. Tuffin and D. Wilkes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022503.
10. J. W. Emsley, M. Lelli, A. Lesage and G. R. Luckhurst, J. Phys. Chem. B, 2013, 117, 6547–6557.
11. J. W. Emsley, P. Lesot, G. R. Luckhurst, A. Meddour and D. Merlet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 040501.
12. C. Greco, G. R. Luckhurst and A. Ferrarini, Phys. Chem. Chem. Phys., 2013, 15, 14961–14965.
13. A. Zep, S. Aya, K. Aihara, K. Ema, D. Pociecha, K. Madrak, P. Bernatowicz, H. Takezoe and E. Gorecka, J. Mater. Chem. C, 2013, 1, 46–49.
14. P. K. Challa, V. Borshch, O. Parri, C. T. Imrie, S. N. Sprunt, J. T. Gleeson, O. D. Lavrentovich and A. Jakli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 060501.
15. D. Chen, M. Nakata, R. Shao, M. R. Tuchband, M. Shuai, U. Baumeister, W. Weissflog, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022506.
16. R. R. Ribeiro de Almeida, C. Zhang, O. Parri, S. N. Sprunt and A. Jákli, Liq. Cryst., 2014, 41, 1661–1667.
17. C. Greco, G. R. Luckhurst and A. Ferrarini, Soft Matter, 2014, 10, 9318–9323.
18. Z. B. Lu, P. A. Henderson, B. J. A. Paterson and C. T. Imrie, Liq. Cryst., 2014, 41, 471–483.
19. R. J. Mandle, E. J. Davis, C. T. Archbold, S. J. Cowling and J. W. Goodby, J. Mater. Chem. C, 2014, 2, 556–566.
20. R. J. Mandle, E. J. Davis, S. A. Lobato, C. C. Vol, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2014, 16, 6907–6915.
21. S. M. Salili, C. Kim, S. Sprunt, J. T. Gleeson, O. Parri and A. Jakli, RSC Adv., 2014, 4, 57419–57423.
22. N. Vaupotic, M. Cepic, M. A. Osipov and E. Gorecka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 030501.
23. Z. Ahmed, C. Welch and G. H. Mehl, RSC Adv., 2015, 5, 93513–93521.
24. C. T. Archbold, E. J. Davis, R. J. Mandle, S. J. Cowling and J. W. Goodby, Soft Matter, 2015, 11, 7547–7557.
25. M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. de la Fuente, D. J. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704.
26. I. Dozov, Europhys. Lett., 2001, 56, 247–253.
27. D. Chen, J. H. Porada, J. B. Hooper, A. Klittnick, Y. Shen, M. R. Tuchband, E. Korblova, D. Bedrov, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15931–15936.
28. V. Borshch, Y. K. Kim, J. Xiang, M. Gao, A. Jakli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635.
29. C. Zhu, M. R. Tuchband, A. Young, M. Shuai, A. Scarbrough, D. M. Walba, J. E. Maclennan, C. Wang, A. Hexemer and N. A. Clark, Phys. Rev. Lett., 2016, 116, 147803.
30. K. Soai, T. Shibata, H. Morioka and K. Choji, Nature, 1995, 378, 767–768.
31. J. Bailey, A. Chrysostomou, J. H. Hough, T. M. Gledhill, A. McCall, S. Clark, F. Menard and M. Tamura, Science, 1998, 281, 672–674.
32. C. Viedma, Astrobiology, 2007, 7, 312–319.
33. J. Sniechowska, P. Paluch, G. Bujacz, M. Gorecki, J. Frelek, D. T. Gryko and M. J. Potrzebowski, CrystEngComm, 2016, 18, 3561–3565.
34. C. Tschierske and G. Ungar, ChemPhysChem, 2016, 17, 9–26.
35. R. J. Mandle and J. W. Goodby, Chemistry, 2016, 22, 18456–18464.
36. E. Gorecka, M. Salamonczyk, A. Zep, D. Pociecha, C. Welch, Z. Ahmed and G. H. Mehl, Liq. Cryst., 2015, 42, 1–7.
37. A. Hoffmann, A. G. Vanakaras, A. Kohlmeier, G. H. Mehl and D. J. Photinos, Soft Matter, 2015, 11, 850–855.
38. A. G. Vanakaras and D. J. Photinos, Soft Matter, 2016, 12, 2208–2220.
39. N. Sebastian, D. O. Lopez, B. Robles-Hernandez, M. R. de la Fuente, J. Salud, M. A. Perez-Jubindo, D. A. Dunmur, G. R. Luckhurst and D. J. Jackson, Phys. Chem. Chem. Phys., 2014, 16, 21391–21406.
40. T. Ivsic, M. Vinkovic, U. Baumeister, A. Mikleusevic and A. Lesac, Soft Matter, 2015, 11, 6716.
41. R. J. Mandle, E. J. Davis, C. T. Archbold, C. C. Voll, J. L. Andrews, S. J. Cowling and J. W. Goodby, Chemistry, 2015, 21, 8158–8167.
42. R. J. Mandle, E. J. Davis, C. C. A. Voll, C. T. Archbold, J. W. Goodby and S. J. Cowling, Liq. Cryst., 2015, 42, 688–703.
43. A. A. Dawood, M. C. Grossel, G. R. Luckhurst, R. M. Richardson, B. A. Timimi, N. J. Wells and Y. Z. Yousif, Liq. Cryst., 2016, 43, 2–12.
44. T. Ivsic, M. Vinkovic, U. Baumeister, A. Mikleusevic and A. Lesac, RSC Adv., 2016, 6, 5000–5007.
45. R. J. Mandle and J. W. Goodby, Chemistry, 2016, 22, 9366–9374.
46. R. J. Mandle, C. C. A. Voll, D. J. Lewis and J. W. Goodby, Liq. Cryst., 2016, 43, 13–21.
47. R. J. Mandle and J. W. Goodby, Soft Matter, 2016, 12, 1436–1443.
48. S. M. Jansze, A. Martinez-Felipe, J. M. Storey, A. T. Marcelis and C. T. Imrie, Angew. Chem., Int. Ed. Engl., 2015, 54, 643–646.
49. Y. Wang, G. Singh, D. M. Agra-Kooijman, M. Gao, H. K. Bisoyi, C. M. Xue, M. R. Fisch, S. Kumar and Q. Li, CrystEngComm, 2015, 17, 2778–2782.
50. R. J. Mandle and J. W. Goodby, ChemPhysChem, 2016, 17, 967–970.
51. R. J. Mandle and J. W. Goodby, RSC Adv., 2016, 6, 34885–34893.
52. W. Tomczyk, G. Pajak and L. Longa, Soft Matter, 2016, 12, 7445–7452.
53. R. J. Mandle, C. T. Archbold, J. P. Sarju, J. L. Andrews and J. W. Goodby, Sci. Rep., 2016, 6, 36682.
54. C. T. Archbold, J. L. Andrews, R. J. Mandle, S. J. Cowling and J. W. Goodby, Liq. Cryst., 2017, 1, 84–92.
55. D. O. Lopez, B. Robles-Hernandez, J. Salud, M. R. de la Fuente, N. Sebastian, S. Diez-Berart, X. Jaen, D. A. Dunmur and G. R. Luckhurst, Phys. Chem. Chem. Phys., 2016, 18, 6955.
56. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
57. G. Ungar, V. Percec and M. Zuber, Macromolecules, 1992, 25, 75–80.
58. Z. P. Zhang, V. P. Panov, M. Nagaraj, R. J. Mandle, J. W. Goodby, G. R. Luckhurst, J. C. Jones and H. F. Gleeson, J. Mater. Chem. C, 2015, 3, 10007–10016.
59. G. R. Luckhurst, Macromol. Symp., 1995, 96, 1–26.
60. F. Livolant and Y. Bouligand, J. Phys., 1986, 47, 1813–1827.
61. E. Barry, Z. Hensel, Z. Dogic, M. Shribak and R. Oldenbourg, Phys. Rev. Lett., 2006, 96, 018305.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7tc00516d

---