Modulation doping of transition metal dichalcogenide/oxide heterostructures

Abstract

Control of carrier type and carrier density provides a way to tune the physical properties of two-dimensional (2D) semiconductors. Modulation doping of heterostructures can effectively inject carriers into or extract carriers from the 2D semiconductors, and eliminate the adverse effect from the ionized dopants. Here we first investigate the layer-dependent negative trion PL of 2D MoS₂, and further construct heterostructures with transition metal dichalcogenides (TMDs) and transition metal oxides (TMOs). By choosing the oxide with different charge neutrality levels (CNLs), we demonstrate effective electron injection into MoS₂ by TiO₂ doping, and electron extraction from MoS₂ by MoO₃ doping. Photoluminescence (PL) spectra and electrical characterization show that thicker MoS₂ flakes are more easily n-doped by TiO₂, while thinner MoS₂ flakes are more easily p-doped by MoO₃. Our experimental results are in good agreement with theoretical calculations. The modulation doping with TMO is compatible with conventional Si processing and highly air-stable. This method can also be extended for the controllable doping of other 2D materials.

---

Introduction

Two-dimensional (2D) layered transition metal dichalcogenides (TMDs) are of great research interest because of their unique electronic, optical and optoelectronic properties.^1–5 The modulation of carrier density in the TMDs provides a way to change their physical properties in a controllable manner. For typical TMD materials, the pristine carrier type is predominated by their intrinsic characteristics. For example, pristine MoS₂ is of the n-type while WSe₂ shows p-type or ambipolar characteristics (the carrier type of WSe₂ is dependent on its thickness).^2,6–8 Controllable injection and extraction of electrons/holes are important for effective n- and p-doping of TMDs, which are crucial for building complementary logic circuits in the future. On the other hand, the interaction between carriers and excitons enables an additional path for the PL modulation of 2D layered materials. Controlling the carrier type and density through modulation doping provides a way to switch between exciton- and trion-dominant PL and tune the PL intensity of 2D materials.⁹

Various methods have been developed to dope 2D layered TMDs,¹⁰ including substitutional doping during growth,¹¹ ion implantation,¹² plasma treating,¹³etc. Although these doping methods have been demonstrated to be effective, they inevitably result in the distortion of TMD crystal structures, introduce ionized impurity scattering canters, and degrade the charge mobility. Modulation doping has been widely used in III–V compound heterojunction superlattices to eliminate the influence of ionized impurity scattering.^14–16 In the heterojunction device, the ionized dopants and electrons are confined to two different adjacent layers. As a result, both the mobility and carrier concentration are well maintained. A variety of dopants have been studied for the surface charge transfer to TMDs, including gas molecules,¹⁷ organics,¹⁸ metal particles¹⁹ and oxides.^2,20 Among these kinds of dopants, oxide is one of the promising species due to its stability in ambience and compatibility with conventional Si processing technology.

In this work, we deposit transition metal oxide (TMO) on top of 2D MoS₂ to form a heterojunction device. We choose TiO₂ with a high charge neutrality level (CNL) and MoO₃ with a low CNL for injecting and extracting electrons, respectively. Our optical and electrical characterization, together with density functional theory (DFT) calculations, shows that TiO₂ and MoO₃ deposition gives rise to effective n-doping and p-doping, respectively. In addition, we also reveal layer-dependent negative trion photoluminescence (PL) and doping effects in 2D layered MoS₂. This approach opens up a way to control the characteristics of PL and the electrical transport of 2D layered materials.

Results and discussion

Layer-dependent negative trion PL of 2D MoS₂

Because of the extremely strong Coulomb interaction in ultrathin 2D MoS₂, optically generated excitons (i.e., electron–hole pairs) and trions (i.e., charged excitons) can exist stably at room temperature.²¹ Electrons are excited to the conducting band, leaving holes in the valence band. Electrons and holes are then bound together by Coulomb interactions to form neutrally charged excitons (electron–hole pairs). Due to the Coulomb attraction between the hole in an exciton and a third electron, the formation process of exciton to trion is energy favourable.²² Trions are formed in the presence of residual free charges. Fig. 1(a) shows the PL spectra of a 3L MoS₂ as an example. Two pronounced peaks around 1.87 eV and 2.05 eV are clearly observed, defined as the A exciton peak and the B exciton peak, respectively. As schematically depicted in the inset, the A exciton has originated from the radiative recombination of the excited electrons in the conduction band minimum (CBM) with the holes in the valence band minimum (VBM); and the B exciton has originated from the radiative recombination of the excited electrons in the CBM with the lower branch of the split VBM.²³ The A exciton of ultrathin MoS₂ can be further devolved into a neutron exciton (X) peak around 1.9 eV and a negative trion (X⁻) peak around 1.85 eV.²¹

Fig. 1 PL analysis of ultrathin MoS₂ flakes. (a) PL spectrum of 3L MoS₂. The inset shows the radiative recombination path of A and B excitons, respectively. (b) PL spectra of 1L–4L MoS₂. (c) Layer-dependent spectral weight of the X⁻ peak. (d) Layer-dependent photon energy of the X peak and the X⁻ peak in the MoS₂ samples from 1L to 5L. The inset shows the layer-dependent energy difference between the X peak and the X⁻ peak.

Fig. 1(b) shows the PL spectra of MoS₂ evolved with the layer number from 1L to 4L. The PL spectra of over 60 MoS₂ flakes were collected and are summarized in Fig. 1(c) and (d). Fig. 1(c) shows the layer-dependent spectral weight of the X⁻ peak in the whole A exciton peak, which rapidly decreases from 90% in the 1L MoS₂ to 30% in the 3L–5L MoS₂. There are two possible reasons accounting for the layer-dependent characteristic of the spectral weight of the X⁻ peak. First, electrons in MoS₂ originated from donor states introduced by surface sulfur vacancies,^24–27 which are expected to become less prominent with the increase of body thickness. Second, when the thickness of MoS₂ increases, the dielectric screening of MoS₂ increases,^28,29 which attenuates the Coulomb interaction³⁰ and reduces the binding energy of trions. With the decrease of binding energy, trion systems are less stable and can be easily decomposed into excitons. Fig. 1(d) shows the photon energy of X and X⁻ peaks as a function of MoS₂ thickness. The PL peaks exhibit a clear red-shift with an increase of MoS₂ body thickness due to the decreased bandgap. In the inset of Fig. 1(d), we present the layer-dependent energy difference (binding energy of the negative trion from the exciton) between X and X⁻ peaks. This binding energy decreases with the increase of MoS₂ thickness.

Layer-dependent n-doping of MoS₂ by TiO₂

Fig. 2 shows the PL spectra of 1L–4L MoS₂ before and after TiO₂ deposition. After 6 nm thick Atomic Layer Deposition (ALD) TiO₂ doping, we observe the characteristics of layer-dependent PL. The thicker MoS₂ sample has a smaller X⁻ spectral weight before the TiO₂ deposition, which is consistent with our previous discussions; while the X⁻ spectral weight increases more after the TiO₂ deposition. These changes in PL spectra are ascribed to the injection of electrons from TiO₂ into MoS₂, where the electron density in MoS₂ is increased by TiO₂ doping.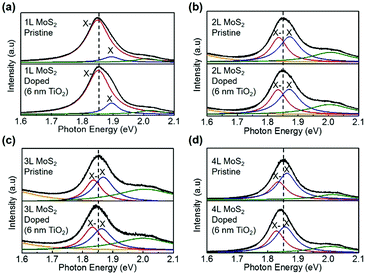

Fig. 2 PL spectra of ultrathin MoS₂ flakes before and after depositing 6 nm thick TiO₂. The thicknesses of MoS₂ samples are (a) 1L, (b) 2L, (c) 3L and (d) 4L.

To rule out the possibility that this PL change has originated from in-plain lattice strain due to oxide deposition on the surface, we also present the corresponding Raman spectra before and after doping in Fig. S1 (ESI†). As widely reported by previous research studies, the in-plane lattice strain induces the split of the E¹_2g peak and the blue-shift of both E¹_2g and A_1g peaks.³¹ However, from our Raman spectra, we observe no such Raman spectral change. Thus, it is suggested that the interlayer coupling between the TiO₂ layer and the MoS₂ surface is very weak, and this weak interaction induces negligible lattice strain to MoS₂. So the PL spectral change has not originated from the lattice strain. To confirm this speculation, we further deposited 30 nm thick TiO₂ onto 1L–3L MoS₂. The Raman and PL spectra are shown in Fig. S2 (ESI†). We still observe a more significant increase of the X⁻ spectral weight in thicker MoS₂ and a negligible shift of Raman peaks. It is noteworthy that the attenuation of Raman intensity after the doping is possibly due to the block of light of the 30 nm thick TiO₂ layer. On the other hand, the change of the dielectric environment introduced by TiO₂ deposition plays an important role in the change of the PL spectra of MoS₂. In both cases (6 nm thick and 30 nm thick TiO₂), the A exciton peak is found to be red-shifted after the TiO₂ deposition, which is more obvious in the case of 30 nm thick TiO₂ deposition. This is because the bandgap of MoS₂ is decreased in the environment with a higher dielectric constant (the dielectric constant of TiO₂ is ∼80).³⁰ Furthermore, from the point of view of enhanced dielectric screening in MoS₂ due to the deposition of the TiO₂ layer, the Coulomb interaction in MoS₂ is attenuated (similar to the effect of increasing MoS₂ body thickness). The attenuated Coulomb interaction decreases the binding energy of the negative trion, thus decreasing the stability of the trion system and the PL intensity of the X⁻ peak. However, in our experiments, the PL intensity of the X⁻ peak is obviously increased after the TiO₂ doping. Therefore, the increase of the X⁻ peak PL is due to the increase of electron density in MoS₂, which originated from the n-doping effect by TiO₂.

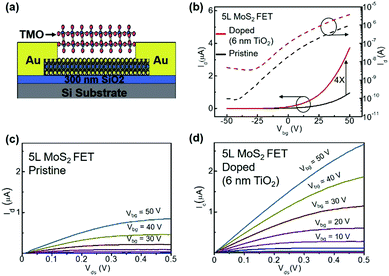
To further confirm and quantify the n-doping effect, we fabricated a back-gated MoS₂ field effect transistor (FET) and doped it with 6 nm thick ALD TiO₂. Fig. 3(a) depicts the cross-sectional schematic of a back-gated MoS₂ FET with its channel covered by TMO. Fig. 3(b) shows the transfer curve of a 5L MoS₂ FET before (black line) and after (red line) the 6 nm thick TiO₂ doping. The pristine device shows typical n-type behaviour, consistent with previous reports.^1,32 After n-doping, the ON current (I_ON) is increased by a factor of 4 at V_bg = 50 V. Fig. 3(c) and (d) show the output curves of the same device before and after doping, respectively. Again, I_ON at V_bg = 50 V is found to be amplified about 5 times. It is noteworthy that the device retains its semiconducting characteristics after the doping, indicating that the n-doping effect is non-degenerate. Furthermore, we can extract 2D sheet carrier density (n_2D) and field-effect mobility (μ_FE) according to eqn (1) and (2), where L and W are the channel length and the channel width, respectively, and C_ox is the capacitance of the gated oxide (i.e., 1.16 × 10⁻⁸ F cm⁻² for 300 nm thick SiO₂ in this study).¹ The extracted n_2D before doping is 1.17 × 10¹² cm⁻², which is consistent with previous reports,^32–35 while the extracted n_2D after the doping is 1.95 × 10¹² cm⁻². This doping level (0.78 × 10¹² cm⁻²) is comparable with other doping methods (i.e., 2 × 10¹¹ cm⁻² for OTS-doped WSe₂,³⁶ 4.6 × 10¹¹ cm⁻² for MEA-doped MoS₂,³⁷ −2 × 10¹¹ cm⁻² for FDT-doped MoS₂,³⁴ and 1 × 10¹³ cm⁻² for TiO_x-doped graphene).³⁷ The μ_FE and n_2D are extracted at V_bg = 30 V. Although the doping effect is independent of the back gate voltage, sufficient gate voltage is required to turn on the channel of the device. It is noteworthy that in these devices, the charges are free carriers without the formation of excitons or trions. Because there is no external input to excite electrons to the conduction band and the lifetimes of excitons and trions are very short, in the order of picoseconds,^38,39

Fig. 3 Electrical characterization of a MoS₂ FET for n-doping by TiO₂. (a) Cross-sectional schematic of a TMO doped MoS₂ FET. (b) Transfer curve of a 5L MoS₂ FET before (black line) and after (red line) being doped by 6 nm thick TiO₂. (c) Output curves of the FET before doping; (d) output curves of the FET after doping.

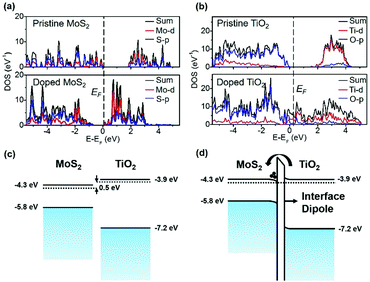
To further support our findings, DFT calculations were utilized to simulate the doping effect. The anatase phase TiO₂ structure was used in this simulation since it is a stable phase at a relatively low temperature.²⁰Fig. 4(a) and (b) show the atomic and orbital projected density of states of pristine 1H-MoS₂, 1H-MoS₂ in the TiO₂-doped MoS₂ system, anatase TiO₂, and anatase TiO₂ in the TiO₂-doped MoS₂ system. The bandgap of pristine 1H-MoS₂ is calculated to be ∼1.86 eV. And both the conduction band minimum (CBM) and the valence band maximum (VBM) of MoS₂ are populated by the 4d orbital of the Mo atom, which are highly hybridized with the 3p orbital of the S atom.²⁰ After the TiO₂ doping, the Fermi level of 1L MoS₂ is up-shifted approximately 0.76 eV towards the CBM, indicating the n-doping effect. Also, the bandgap of MoS₂ is obviously shrunken, which is due to the enhanced dielectric screening introduced by TiO₂ deposition. From Fig. 4(b), we observe a significant change in the DOS of TiO₂ after the n-doping. Compared with the pristine state, the presence of the Ti-5d level in the conduction band is dramatically decreased. This change indicates that electrons are mainly transferred from the Ti-5d level of TiO₂ to MoS₂, leaving the Ti-5d level anti-bonding. Similar findings regarding the simulation of the TiO₂ doping process can be found in the work of N. Kaushik et al.⁴⁰

Fig. 4 DFT simulation results of the n-doping process and band structures of MoS₂ and TiO₂. (a) DOS of 1L 1H-MoS₂ before (upper panel) and after doping (lower panel). (b) DOS of anatase TiO₂ before (upper panel) and after doping MoS₂ (lower panel). (c) Band alignment of 1L MoS₂ and TiO₂ before doping. (d) Band alignment of 1L MoS₂ and TiO₂ after doping. The dashed lines denote the CNL.

Fig. 4(c) shows the schematic band structures of 1L MoS₂versus anatase TiO₂. The CBM and CNL of MoS₂ are about 0.5 eV lower than those of TiO₂. Driven by this energy difference, electrons in the CB of TiO₂ flows into the CB of MoS₂, until an interface dipole pointing from MoS₂ to TiO₂ is built up (Fig. 4(d)) and then the doping process reaches its balance state. As widely acknowledged, electrons in ultrathin MoS₂ flakes have originated from surface sulfur vacancies. It is reasonable to expect that this surface effect has a smaller influence on the electronic structure of thicker MoS₂ samples. The CNL of MoS₂ thin flakes lowers when the thickness of MoS₂ increases. Considering the fact that the bandgap of MoS₂ decreases with the increase of body thickness, the CNL of thicker MoS₂ samples quickly lowers down. For thicker MoS₂ samples, the energy difference between its CNL and that of TiO₂ enlarges, thus the n-doping effect is more obvious.

Layer-dependent p-doping of MoS₂ by MoO₃

MoO₃ is one type of TMOs with a relatively low CNL. We choose it for p-doping MoS₂. Fig. 5 shows the PL spectra of 1L and 3L MoS₂ before and after 6 nm thick MoO₃ doping. In both cases, a significant decrease of the X⁻ peak spectral weight is observed. The corresponding Raman spectra of these samples are shown in Fig. S3 (ESI†). No obvious shift in the positions of Raman peaks is observed, suggesting that the interlayer coupling between the MoO₃ layer and the MoS₂ surface is also very small. Also, it is noteworthy that the dielectric constant of MoO₃ is small (∼5.5). Therefore, it has a negligible influence on the PL spectra of MoS₂.

Fig. 5 PL spectra of ultrathin MoS₂ flakes before and after being doped by 6 nm thick MoO₃. The thicknesses of MoS₂ samples are (a) 1L and (b) 3L.

Electrical characterization of MoS₂ FETs is used to further quantify the p-doping effect. Fig. 6(a) is the transfer curve of a 5L MoS₂ FET before and after p-doping. After the p-doping, the I_ON at V_bg = 50 V is decreased 5 times and the threshold voltage (V_th) is increased by ∼24 V. The extracted n_2D values are 2.3 × 10¹² cm⁻² before the doping and 1.7 × 10¹² cm⁻² after the p-doping. The electron density in MoS₂ is depleted by about 0.6 × 10¹² cm⁻², which is comparable to the doping level of 6 nm thick TiO₂ (0.78 × 10¹² cm⁻²). The corresponding output curves of the device are illustrated in Fig. 6(b) (before doping) and Fig. 6(c) (after doping). As expected, we observe a decrease of I_ON in the positive gate range (0–50 V). The gate voltage required to turn on the channel (V_ON) is clearly increased from 20 V to 30 V. The n_2D and μ_FE values of MoS₂ devices before and after the p-doping are summarized in Fig. 6(d). For thicker MoS₂ samples, the depleted electron density is smaller.

Fig. 6 Electrical characterization of a MoS₂ FET for p-doping by MoO₃. (a) Transfer curve of a 5L MoS₂ FET before (black line) and after (red line) 6 nm thick MoO₃ doping. (b) Output curves of the device before doping. (c) Output curves of the device after 6 nm thick MoO₃ doping. (d) Extracted μ_FE (left axis) and n_2D (right axis) of three MoS₂ devices before (black line) and after (red line) 6 nm thick MoO₃ doping.

This layer dependence can also be ascribed to the decrease of the CNL of MoS₂ with the increase of body thickness, as discussed in the case of n-doping by TiO₂. Due to the reduced carrier density, electrons undergo a stronger scattering effect from the interface defects, which will significantly reduce the carrier mobility.

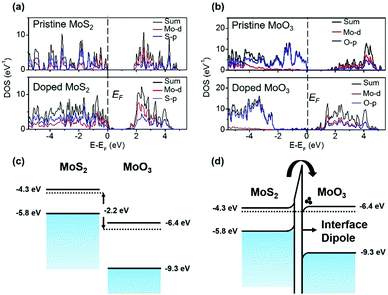
DFT calculation results of this p-doping process are shown in Fig. 7. In Fig. 7(a), the Fermi level of 1L MoS₂ is moved down towards the VB, demonstrating the p-doping effect. The DOS of MoO₃ in Fig. 7(b) shows that the population of the Mo-4d orbital is increased after the doping, indicating that electrons are transferred from the Mo-4d orbital in MoS₂ to the Mo-4d orbital in MoO₃. Fig. 7(c) illustrates the schematic band structure of 1L MoS₂versus MoO₃. The CNL of MoS₂ is 2.2 eV higher than that of MoO₃. Due to this energy difference, electrons in the CB of MoS₂ are extracted to the CB of MoO₃ until an interface dipole is built up (Fig. 7(d)). When the CNL of MoS₂ is lowered down by increasing the body thickness, the energy difference between it and the CNL of MoO₃ is decreased, thus leading to a decreased p-doping effect.

Fig. 7 DFT simulation results of the p-doping process and band structures of MoS₂ and MoO₃. (a) DOS of 1L 1H-MoS₂ before (upper panel) and after doping (lower panel). (b) DOS of pristine MoO₃ before (upper panel) and after doping MoS₂ (lower panel). (c) Band alignment of 1L MoS₂ and MoO₃ before doping. (d) Band alignment of 1L MoS₂ and MoO₃ after doping. The dashed lines denote the CNL.

Experimental

Fabrication of MoS₂ FETs

MoS₂ crystals were purchased from a commercial producer (2D semiconductors). Mechanically exfoliated MoS₂ thin flakes were used to fabricate FETs. Target substrates (300 nm thick SiO₂/Si wafer) were contacted with Scotch tape and then bathed in Acetone or Isopropyl Alcohol (IPA) at 60 °C to remove organic residues. Ultrathin flakes (<10 nm) of MoS₂ were identified using an optical microscope. The conventional photo-lithography process was performed, followed by metal deposition and lift-off processes. Metal electrodes (i.e., Ti/Au) were deposited using an electron-beam evaporator at a rate of ∼0.7 Å s⁻¹. Electrical characteristics of the FETs were measured using a Keithley 4200-SCS Semiconductor Parameter Analyser.

Deposition of TiO₂ and MoO₃ oxide layers

TiO₂ oxide layers were deposited on MoS₂ using ALD at 150 °C. The sources were tetrakis(dimethylamino)titanium (TDMAT) and H₂O. The deposition rate was ∼0.47 Å cycle⁻¹. A thermal evaporator was used to deposit MoO₃ oxide layers. The source was MoO₃ powder. The deposition rate was around 1 Å s⁻¹. The oxide layers are continuous and have small surface roughness.

DFT simulations of the doping process

DFT calculations were conducted using Quantum ESPRESSO to simulate the charge transfer process between oxide and TMDs. The ion cores were described using projector-augmented wave sets and scalar-relativistic pseudopotentials. The generalized gradient approximation Perdew–Burke–Ernzerhof (PBE) exchange–correlation was selected as the pseudopotential functional type. 2 × 1 × 1 monolayer MoO₃ was constituted on the top of 2 × 1 × 1 1H-MoS₂ along the (001) direction, and 2 × 1 × 1 TiO₂ was constituted on the 2 × 1 × 1 1H-MoS₂ along the (001) direction. Each supercell contains a 40 Å vacuum region in the z-axis to prevent the effects from the neighbouring slabs. The convergence threshold values on the total energy and force were 10⁻⁶ and 10⁻³, respectively. The kinetic energy cut-off for wave functions was 50 Ry, and the kinetic energy cut-off for charge density and potential was 200 Ry.

Conclusions

In summary, we investigate the layer dependence of n- and p-doping of MoS₂ by TMO. TiO₂ and MoO₃ are used for the n- and p-doping of MoS₂, respectively. PL and electrical characterization show that thicker MoS₂ samples are more easily n-doped by TiO₂; while thinner MoS₂ samples are more easily p-doped by MoO₃. Furthermore, the doping levels of 6 nm thick TiO₂ and MoO₃ are extracted to be 0.78 × 10¹² cm⁻² and 0.6 × 10¹² cm⁻², respectively. Our experiments characterized the doping effects and doping levels of the two mostly used oxide dopants (TiO₂ and MoO₃) and shed light on optimizing the doping strategy of TMDs by oxide layers.

Acknowledgements

This work was supported by the Research Grant Council of Hong Kong (Grant no. PolyU 152145/15E) and the Hong Kong Polytechnic University (Grant no. G-YBPS, 1-ZE25 and 1-ZVDH).

References

1. B. Radisavljevic, A. Radenovic, J. Brivio, I. V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150.
2. C. Zhou, Y. Zhao, S. Raju, Y. Wang, Z. Lin, M. Chan and Y. Chai, Adv. Funct. Mater., 2016, 26, 4223.
3. Y. Zhao, J. Qiao, P. Yu, Z. Hu, Z. Lin, S. P. Lau, Z. Liu, W. Ji and Y. Chai, Adv. Mater., 2016, 28, 2399.
4. Z. Lin, Y. Zhao, C. Zhou, R. Zhong, X. Wang, Y. H. Tsang and Y. Chai, Sci. Rep., 2015, 5, 18596.
5. C. Zhou, X. Wang, S. Raju, Z. Lin, D. Villaroman, B. Huang, H. L.-W. Chan, M. Chan and Y. Chai, Nanoscale, 2015, 7, 8695–8700.
6. W. Liu, J. Kang, D. Sarkar, Y. Khatami, D. Jena and K. Banerjee, Nano Lett., 2013, 13, 1983–1990.
7. J.-K. Huang, J. Pu, C.-L. Hsu, M.-H. Chiu, Z.-Y. Juang, Y.-H. Chang, W.-H. Chang, Y. Iwasa, T. Takenobu and L.-J. Li, ACS Nano, 2013, 8, 923–930.
8. Y. Zhang, J. Ye, Y. Matsuhashi and Y. Iwasa, Nano Lett., 2012, 12, 1136–1140.
9. S. Mouri, Y. Miyauchi and K. Matsuda, Nano Lett., 2013, 13, 5944–5948.
10. Y. Zhao, K. Xu, F. Pan, C. Zhou, F. Zhou and Y. Chai, Adv. Funct. Mater., 2016 DOI:10.1002/adfm.201603484.
11. J. Suh, T.-E. Park, D.-Y. Lin, D. Fu, J. Park, H. J. Jung, Y. Chen, C. Ko, C. Jang and Y. Sun, Nano Lett., 2014, 14, 6976–6982.
12. A. Nipane, D. Karmakar, N. Kaushik, S. Karande and S. Lodha, ACS Nano, 2016, 10, 2128–2137.
13. M. Chen, H. Nam, S. Wi, L. Ji, X. Ren, L. Bian, S. Lu and X. Liang, Appl. Phys. Lett., 2013, 103, 142110.
14. R. Dingle, H. Störmer, A. Gossard and W. Wiegmann, Appl. Phys. Lett., 1978, 33, 665–667.
15. R. People, J. Bean, D. Lang, A. Sergent, H. Störmer, K. Wecht, R. Lynch and K. Baldwin, Appl. Phys. Lett., 1984, 45, 1231–1233.
16. T. Mimura, S. Hiyamizu, T. Fujii and K. Nanbu, Jpn. J. Appl. Phys., 1980, 19, L225.
17. P. Zhao, D. Kiriya, A. Azcatl, C. Zhang, M. Tosun, Y.-S. Liu, M. Hettick, J. S. Kang, S. McDonnell, S. KC, J. Guo, K. Cho, R. M. Wallace and A. Javey, ACS Nano, 2014, 8, 10808–10814.
18. D. Kiriya, M. Tosun, P. Zhao, J. S. Kang and A. Javey, J. Am. Chem. Soc., 2014, 136, 7853–7856.
19. C.-H. Chen, C.-L. Wu, J. Pu, M.-H. Chiu, P. Kumar, T. Takenobu and L.-J. Li, 2D Mater., 2014, 1, 034001.
20. N. Kaushik, D. Karmakar, A. Nipane, S. Karande and S. Lodha, ACS Appl. Mater. Interfaces, 2015, 8, 256–263.
21. K. F. Mak, K. He, C. Lee, G. H. Lee, J. Hone, T. F. Heinz and J. Shan, Nat. Mater., 2013, 12, 207–211.
22. A. Singh, G. Moody, K. Tran, M. E. Scott, V. Overbeck and G. Berghäuser, Phys. Rev. B, 2016, 93(4), 041401.
23. G. Berghäuser and E. Malic, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 125309.
24. D. Liu, Y. Guo, L. Fang and J. Robertson, Appl. Phys. Lett., 2013, 103, 183113.
25. S. Kim, M. S. Choi, D. Qu, C. H. Ra, X. Liu, M. Kim, Y. J. Song and W. J. Yoo, 2D Mater., 2016, 3, 035002.
26. E. Rotunno, F. Fabbri, E. Cinquanta, D. Kaplan, M. Longo, L. Lazzarini, A. Molle, V. Swaminathan and G. Salviati, 2D Mater., 2016, 3, 025024.
27. A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C.-Y. Chim, G. Galli and F. Wang, Nano Lett., 2010, 10, 1271–1275.
28. X. Chen, Z. Wu, S. Xu, L. Wang, R. Huang, Y. Han, W. Ye, W. Xiong, T. Han and G. Long, 2014, arXiv:1407.5365.
29. T. Cheiwchanchamnangij and W. R. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205302.
30. Y. Lin, X. Ling, L. Yu, S. Huang, A. L. Hsu, Y.-H. Lee, J. Kong, M. S. Dresselhaus and T. S. Palacios, Nano Lett., 2014, 14, 5569–5576.
31. L. Yang, X. Cui, J. Zhang, K. Wang, M. Shen, S. Zeng, S. A. Dayeh, L. Feng and B. Xiang, Sci. Rep., 2014, 4, 5649.
32. S. Das, H.-Y. Chen, A. V. Penumatcha and J. Appenzeller, Nano Lett., 2012, 13, 100–105.
33. H.-Y. Park, M.-H. Lim, J. Jeon, G. Yoo, D.-H. Kang, S. K. Jang, M. H. Jeon, Y. Lee, J. H. Cho and G. Y. Yeom, ACS Nano, 2015, 9, 2368–2376.
34. D. M. Sim, M. Kim, S. Yim, M.-J. Choi, J. Choi, S. Yoo and Y. S. Jung, ACS Nano, 2015, 9, 12115–12123.
35. B. Radisavljevic and A. Kis, Nat. Mater., 2013, 12, 815–820.
36. D.-H. Kang, J. Shim, S. K. Jang, J. Jeon, M. H. Jeon, G. Y. Yeom, W.-S. Jung, Y. H. Jang, S. Lee and J.-H. Park, ACS Nano, 2015, 9, 1099–1107.
37. P. H. Ho, C. H. Chen, F. Y. Shih, Y. R. Chang, S. S. Li, W. H. Wang, M. C. Shih, W. T. Chen, Y. P. Chiu and M. K. Li, Adv. Mater., 2015, 27, 7809–7815.
38. Q. Wang, S. Ge, X. Li, J. Qiu, Y. Ji and J. Feng, ACS Nano, 2013, 7(12), 11087–11093.
39. D. Lagarde, L. Bouet, X. Marie, C. R. Zhu, B. L. Liu, T. Amand, P. H. Tan and B. Urbaszek, Phys. Rev. Lett., 2014, 112(4), 047401.
40. N. Kaushik, D. Karmakar, A. Nipane, S. Karande and S. Lodha, ACS Appl. Mater. Interfaces, 2015, 8(1), 256–263.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6tc04640a

---