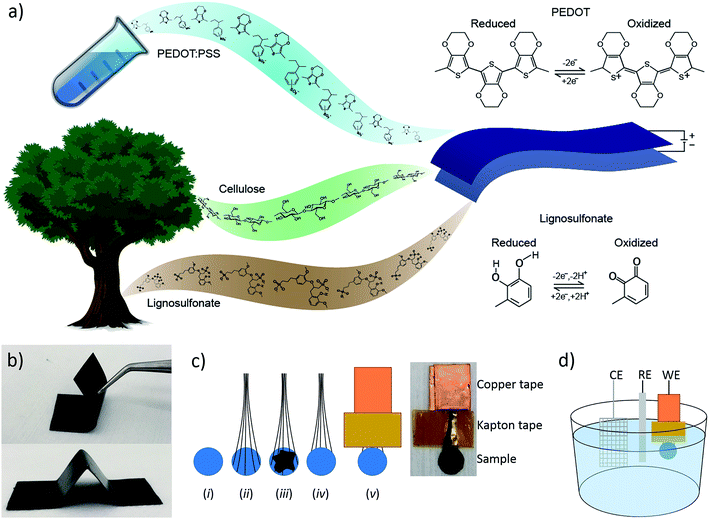
Boosting the capacity of all-organic paper supercapacitors using wood derivatives†
Jesper
Edberg
 ab,
Olle
Inganäs
c,
Isak
Engquist
ab,
Olle
Inganäs
c,
Isak
Engquist
 *a and
Magnus
Berggren
ad
*a and
Magnus
Berggren
ad
aLaboratory of Organic Electronics, ITN, Linköping University, SE-601 74 Norrköping, Sweden. E-mail: isak.engquist@liu.se
bRISE Acreo, SE-601 74 Norrköping, Sweden
cBiomolecular and Organic Electronics, IFM, Linköping University, SE-581 83 Linköping, Sweden
dStellenbosch Institute for Advanced Studies (STIAS), Wallenberg Research Center at Stellenbosch University, Stellenbosch 7600, South Africa
First published on 29th November 2017
Abstract
Printed and flexible organic electronics is a steadily expanding field of research and applications. One of the most attractive features of this technology is the possibility of large area and high throughput production to form low-cost electronics on different flexible substrates. With an increasing demand for sustainable energy production, low-cost and large volume technologies to store high-quality energy become equally important. These devices should be environmentally friendly with respect to their entire life cycle. Supercapacitors and batteries based on paper hold great promise for such applications due to the low cost and abundance of cellulose and other forest-derived components. We report a thick-film paper-supercapacitor system based on cellulose nanofibrils, the mixed ion-electron conducting polymer PEDOT:PSS and sulfonated lignin. We demonstrate that the introduction of sulfonated lignin into the cellulose-conducting polymer system increases the specific capacitance from 110 to 230 F g−1 and the areal capacitance from 160 mF cm−2 to 1 F cm−2. By introducing lignosulfonate also into the electrolyte solution, equilibrium, with respect to the concentration of the redox molecule, was established between the electrode and the electrolyte, thus allowing us to perform beyond 700 charge/discharge cycles with no observed decrease in performance.
1. Introduction
In recent years, there has been a growing interest in the development of paper-based devices for storage, generation and harvesting of energy.1,2 The motivation for using paper is its inherent mechanical strength and flexibility, porosity, large specific surface area, low cost, biocompatibility and its environmental friendliness. Some examples of devices that have been successfully integrated into paper, or that use cellulose as a binder, are supercapacitors, electrochemical batteries, lithium ion batteries, biofuel cells, thermoelectric generators, diodes, photodetectors and nanogenerators.3–8 Flexible devices have several advantages over rigid substrates in that they are less sensitive to mechanical stress, can be manufactured in high throughput roll-to-roll production and can be integrated into flexible and wearable electronic devices. The porosity of paper is advantageous in the sense that the included fibers can be coated with electronic charge transporting and redox active materials and that the space between the fibers, as well as the interior of the fibers, can provide ion transport and intercalation.9,10 These features allow us to use paper both as a separator and as the electrode material in charge storage devices.11,12 Furthermore, the large specific surface area of paper can be used to increase the number of reaction sites and therefore boost the performance of several types of devices.13 Besides economical and performance aspects, there is also an increasing demand for green and sustainable technologies, with respect to included materials, manufacturing and recycling. Cellulose is the most abundant biopolymer on earth and by using this material in electronic and electrochemical devices, one route towards environmentally friendly digital and energy technologies is constructed.14There are three reported classes of materials that have extensively been explored and also utilized as the electrodes in supercapacitors; carbon, metal oxides and conductive polymers.15–19 Carbon is the most commonly used material in commercial supercapacitors due to its abundance and low cost. Although high values of specific capacitance (>400 F g−1) has been reported for carbon nanotube materials in literature,20 commercial capacitors with activated carbons reach only 25–30 F g−1.21 The ionic conductivity of the carbon electrode is highly dependent on the porosity of the material, and can be limiting.16
Many metal oxides have been reported in literature to have very high values of specific capacitance, on the order of 1000–2000 F g−1.22 However, the best-performing metal oxides are costly and are therefore generally not used or explored in commercial applications.17 Metal oxides also suffer from poor electronic and ionic conductivity as well as short lifetime due to volumetric expansion and contraction during operation that causes cracking.19 To achieve good ion intercalation, these materials often require different types of nanostructuring, making upscaling of devices to very large volumes and dimensions difficult.
The third class of materials is the conductive polymers.23–25 The advantages of this type of material are its low resistance, mechanical flexibility and processability, which enables large area and volume fabrication at room temperature. Conducting polymers are proven easily composited with paper and provide excellent energy storage or harvesting characteristics in large-scale electrodes.14 Some conductive polymers, such as polypyrrole and polyaniline, have shown very high specific capacitance (600 (ref. 26) and 800 (ref. 27) F g−1 respectively), but are unstable and quickly degrade during electrochemical cycling due to volumetric change.16 One of the most stable conductive polymers is poly(3,4-ethylenedioxythiophene), or PEDOT. However, the theoretical specific capacitance of this polymer is only 210 F g−1 and typical reported values ranges from 80–90 F g−1.28,29
We have recently demonstrated a composite material of cellulose nanofibrils (CNF) and the conductive polymer system PEDOT:PSS (where PSS is polystyrene sulfonate) that was used to make all-organic paper-supercapacitors.30 A study of the microstructure of the material, using AFM, XPS and GIWAXS, revealed that the conductive polymer forms a cladding layer on the cellulose fibrils. We showed that this material system exhibited high electronic and ionic conductivity, good stability and that its performance as a supercapacitor scaled linearly with thickness. These characteristics enabled us to manufacture thick, flexible and self-supporting paper electrodes (Fig. 1b) to be used in supercapacitors possessing high charge storage capacity. In this report, we have introduced another redox-active organic material, lignosulfonate (LS), into this material system in order to increase the charge storage capacity of the cathode of the paper-supercapacitors. LS is a derivative of lignin, which is the second most abundant biopolymer after cellulose, and is commonly referred to as a waste product of wood pulp during paper making. This cheap and green material can store electrical energy in its phenolic groups by switching between the benzoquinone and hydroquinone states (Fig. 1a). Since LS is stable in its hydroquinone state, the molecule can be oxidized to a benzoquinone state by applying a positive potential. This means that the molecule can be used as the positive electrode in a supercapacitor/battery. However, since LS is an electronic insulator, it cannot be used by itself as the electrode material. Therefore, LS and other phenolic molecules have previously been combined with conductive polymers that enable charge transport.31–33 Ajjan et al. demonstrated a PEDOT-LS composite with excellent charge storage capacity and stability.28 However, this material system was prepared as thin films on small electrodes using chemical and electrochemical polymerization, techniques which are limited in manufacturing scalability. In this report, we investigate if LS can efficiently be integrated into a scalable and solution processable material systems, which is suitable for large-volume commercial supercapacitor systems. We also address one of the major issues with current energy storage systems based on redox-active organic compounds, namely dissolution of these molecules from the electrodes and into the electrolyte which causes the capacity to degrade over time. We demonstrate a new way of getting around this problem by incorporating the active molecules at high concentration into the electrolyte.
2. Experimental
2.1 Materials
Poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS), Clevios PH 1000, was purchased from Heraeus. Glycerol, dimethyl sulfoxide (DMSO), acetonitrile and perchloric acid (HClO4) were purchased from Sigma-Aldrich. Lignosulfonate (LC30, MW = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) was purchased from MeadWestvaco. Cellulose nanofibrills (CNF) was produced via high-pressure homogenization of cellulose dispersed in water at 1700 bar. The resulting concentration of the CNF dispersion was 0.41 wt%. The CNF dispersion was provided by RISE Bioeconomy.
400) was purchased from MeadWestvaco. Cellulose nanofibrills (CNF) was produced via high-pressure homogenization of cellulose dispersed in water at 1700 bar. The resulting concentration of the CNF dispersion was 0.41 wt%. The CNF dispersion was provided by RISE Bioeconomy.
Lignosulfonate (LS) was dissolved in 0.1 M HClO4 at a concentration of 10 mg mL−1. The solution was mixed with poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) resulting in solid content weight ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (PEDOT:PSS solution without lignosulfonate), 2
0 (PEDOT:PSS solution without lignosulfonate), 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 1
5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 of PEDOT:LS (P:L). The P:L ratios does not include the mass of PSS, and only the mass of PEDOT (PSS excluded) was taken into account for the calculation of specific capacitances.
10 of PEDOT:LS (P:L). The P:L ratios does not include the mass of PSS, and only the mass of PEDOT (PSS excluded) was taken into account for the calculation of specific capacitances.
2.2 Paper manufacturing
The conductive paper was prepared by mixing 4.7 g of PEDOT:PSS-LS mixture with 5.5 g of CNF solution, 258 mg DMSO and 36 mg glycerol. The solutions were homogenized using a T 10 basic ULTRA-TURRAX (Laboratory Mixers) after which they were degassed for 1 hour. Finally, the solutions were cast into plastic Petri dishes (5.5 cm diameter) and left to dry at 60 °C in oven. The two samples with the highest amount of lignosulfonate (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 1
5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) became very brittle and could not be lifted from the Petri dish after drying and were therefore not used in any measurements.
10) became very brittle and could not be lifted from the Petri dish after drying and were therefore not used in any measurements.
2.3 Sample preparation
The steps of the sample preparation are shown in Fig. 1c. (i) 4 mm (5 mm in the cycling experiment) diameter disks were cut out of the papers, (ii) carbon fibers were added for the electrical contacts, (iii) carbon paste was added to work as a glue between the carbon fibers and the paper, (iv) another paper disk was added on top of the carbon paste, (v) copper tape was added to the ends of the carbon fibers to ensure a good electrical contact and Kapton tape was added to prevent the electrolyte from reaching the copper. These electrodes were used as the working electrodes (WE) together with a platinum counter electrode (CE) and an Ag/AgCl reference electrode (RE) in the three-electrode electrochemical measurements (Fig. 1d). The papers were ∼50 μm thick making the final electrodes ∼100 μm thick, since two pieces were “glued” together, with an area 12.6 mm2.2.4 Measurements
The sheet resistance of the conductive paper samples was measured using a Keithley 2400 source meter in four-wire sense mode. Strips of the samples were glued on to gold electrodes using carbon paste to ensure a stable electrical contact, and the measurement apparatus was connected to the gold contacts (see Fig. SI1 in ESI†). The thickness of the samples was measured using a micrometer screw gauge and the surface roughness was characterized using a surface profilometer (see ESI†). The electronic conductivity (σ) of the samples was then calculated using eqn (1), where Rs is the sheet resistance and t is the thickness of the samples.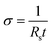 | (1) |
Electrochemical measurements were performed using a μAUTOLAB potentiostat (Metrohm) in a three-electrode setup with a [0.1 M HClO4 in water]/acetonitrile (9/1) electrolyte. The experimental setup is depicted in Fig. 1d.
3. Results & discussion
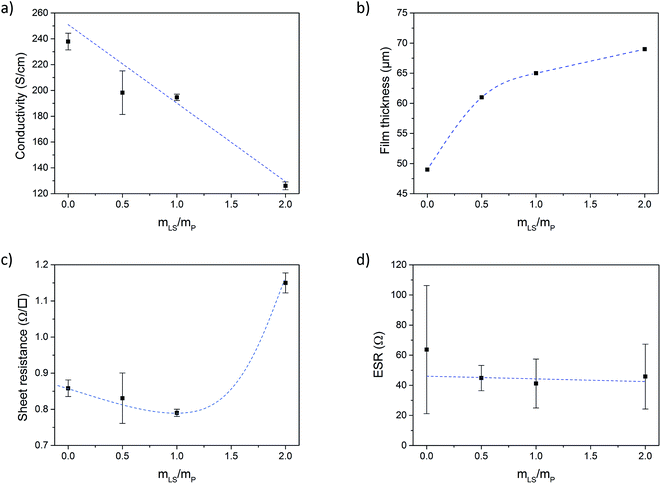
Fig. 2a shows the electronic conductivity of the conductive paper prepared with different loadings of LS. From here on, the samples will be referred to as P:L_X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y (or simply X
Y (or simply X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y in the graphs), where X is the PEDOT mass fraction (PSS excluded) and Y is the LS mass fraction. Three samples were prepared for each loading. The electronic conductivity was decreasing with increasing amount of LS, which is simply explained either by the increased thickness of the samples when adding more material and/or by that LS is forming insulating cladding phases which limits charge transport in between PEDOT domains. However, the difference in the mass (and thus thickness) of the samples cannot be explained by the addition of LS alone. During the drying process, most of the water and some of the high boiling point organic solvents (DMSO and glycerol) evaporates from the samples. By weighting the samples before and after drying, and then subtracting the mass of the solid components (PEDOT:PSS, NFC and LS), the mass of the solvents left in the samples can be estimated. Fig. SI2 in ESI† shows the weight percentage of solvents in samples with different loading of LS. The percentage of solvent increases with the amount of LS indicating that LS slows down the evaporation process or promotes binding of the solvent relatively stronger to the paper. The resulting thickness of the paper (Fig. 2b) increases as more and more LS is added and the corresponding higher amount of solvent stored in the paper explains the major part of the drop in electronic conductivity. Also, the surface roughness increased with the addition of LS, as was observed in surface profilometer measurements (see ESI†).
Y in the graphs), where X is the PEDOT mass fraction (PSS excluded) and Y is the LS mass fraction. Three samples were prepared for each loading. The electronic conductivity was decreasing with increasing amount of LS, which is simply explained either by the increased thickness of the samples when adding more material and/or by that LS is forming insulating cladding phases which limits charge transport in between PEDOT domains. However, the difference in the mass (and thus thickness) of the samples cannot be explained by the addition of LS alone. During the drying process, most of the water and some of the high boiling point organic solvents (DMSO and glycerol) evaporates from the samples. By weighting the samples before and after drying, and then subtracting the mass of the solid components (PEDOT:PSS, NFC and LS), the mass of the solvents left in the samples can be estimated. Fig. SI2 in ESI† shows the weight percentage of solvents in samples with different loading of LS. The percentage of solvent increases with the amount of LS indicating that LS slows down the evaporation process or promotes binding of the solvent relatively stronger to the paper. The resulting thickness of the paper (Fig. 2b) increases as more and more LS is added and the corresponding higher amount of solvent stored in the paper explains the major part of the drop in electronic conductivity. Also, the surface roughness increased with the addition of LS, as was observed in surface profilometer measurements (see ESI†).
In Fig. 2c the sheet resistance of the different samples is given. Since the amount of conductive material for a given area is the same for all samples (the same amount of PEDOT:PSS was added to each sample), the sheet resistance gives a measure of the total charge transport and should only increase if LS or solvents are forming insulating phases in such a way that electronic charge transport through the PEDOT phase is suppressed. The sheet resistance is more or less constant up to a mass fraction (mLS/mPEDOT) of 1, but then increases by ∼34% for a mass fraction of 2 (as compared to mass fraction 0). The results indicate that the drop in electronic conductivity, upon introducing LS, is primarily caused by an increase of the thickness of the samples, while charge transport is unaffected up to a mass fraction of 1.
The equivalent series resistance (ESR) is the total resistance of the measurement cell, including the resistance from the sample, contacts and electrolyte as well as interfacial resistances between them. One of the major advantages of supercapacitors based on conductive polymers, over inorganic materials, is their low ESR, which in turn reduces power losses thus giving a high-power density under operation.25 The ESR of our paper supercapacitors was calculated from the potential drop (U) recorded at the beginning of the galvanostatic discharge measurements using eqn (2):
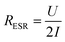 | (2) |
The constant current (I) is multiplied by a factor 2 to account for the instantaneous switch from positive to negative current during the measurement. Fig. 2d shows that the ESR of the paper supercapacitors, on average, stays relatively constant for all loadings of LS. From the measurements of sheet resistance, the resistance across a sample can be approximated as 0.4 Ω, since the samples used in the cell were twice as thick as the samples used in the resistance measurements. This mean that the ESR was two orders of magnitude higher than the resistance of the samples. Some of the resistance comes from the electrolyte between the WE and RE, however, the largest contribution to the ESR comes from the carbon fibers used to contact the samples, which had a resistance of ∼10 Ω cm−1 (for the specific wire thickness used in the experiments). Also, the carbon paste used between the fibers and the sample have a relatively high resistivity. Forming a good electrical contact which could be stable in solution for long periods of time was challenging since the samples contain a large amount of solvents. Direct contacting onto metal electrodes require the cell to be clamped, which can cause damage to the films, since they become more fragile when hydrated by the electrolyte. This method is also impractical when performing three electrode measurements. Another method was to directly contact the samples using crocodile clips. This method was also too destructive and would cause corrosion on the crocodile clip which increased the ESR over time. In future work, better contacting methods for the samples could improve the ESR.
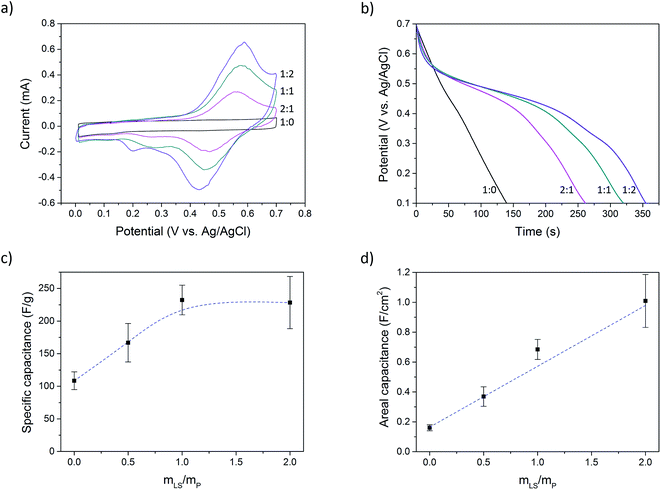
Cyclic voltammetry was performed at a scan rate of 2 mV s−1 (Fig. 3a). Electrode materials that contain lignosulfonate displays clear redox peaks, while the sample without lignosulfonate shows pure (pseudo)capacitive charging.
Using chronopotentiometry, the paper electrodes were charged up to 0.7 V at a current bias of 0.5 A g−1, calculated on the mass of PEDOT (excluding PSS) and LS, and then discharged to 0.1 V at the same rate. Fig. 3b shows the discharge curves of samples with different LS loading. The samples without LS show a linear discharge curve, indicating an ideal capacitive behavior while samples with LS show a nonlinear discharge with a voltage plateau region, indicating LS redox activity. This latter behavior is typical for a battery rather than that of a supercapacitor. However, since the voltage of this hybrid capacitor-battery still have a strong dependence on the state of charge, characterizing the material as a battery is not suitable. Instead, a capacitance is defined within a potential window which contains the electrochemical potential of LS. This method has been previously used for composites of conductive polymers and redox-active molecules.28,31–33 However, the choice of the potential window will affect the obtained capacitance, and so, to make the results comparable with previous works, the same potential window as was reported by Ajjan et al. was used in this work.28 Complete charge–discharge curves can be found in ESI (Fig. SI5†).
The capacitance (C) was calculated from the galvanostatic discharge curves using the equation C = (I × Δt)/ΔV where I is the current, Δt is the discharge time and ΔV is the change in potential. The capacitance was calculated between Vmax and 0.1 V (ΔV = Vmax − 0.1 V), where Vmax equals 0.7 V reduced by the IR-drop present at the beginning of the discharge. This IR-drop is found to be on the same level as was found and used by Ajjan et al. in their experiments.28Fig. 3c and d shows the capacitance calculated from five samples of each LS loading. Fig. 3c shows the specific capacitance, i.e. the capacitance normalized to the mass of the electroactive materials (PEDOT and LS), and Fig. 3d shows the capacitance normalized to the electrode area (areal capacitance). The specific capacitance increased from 110 F g−1 (P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) to a maximum of 230 F g−1 (P:L_1
0) to a maximum of 230 F g−1 (P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and then plateaued while the areal capacitance increased linearly from 160 mF cm−2 (P:L_1
1) and then plateaued while the areal capacitance increased linearly from 160 mF cm−2 (P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) to 1 F cm−2 (P:L_1
0) to 1 F cm−2 (P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2). The mass of PSS was not considered in the calculation of specific capacitance for two reasons: (1) PSS is a large polymer counter ion. If its mass is taken into the account, it cannot properly be compared to other PEDOT systems with small-sized and mobile counter ions, like chloride or tosylate. (2) In solution, there is an excess of PSS and one role of DMSO is to remove this excess. The amount of PSS that is ionically coupled to PEDOT is therefore much smaller than the total amount of PSS in the sample. Also, during the processing of the samples and in the electrolyte solution during measurements, PEDOT is exposed to small anions that can replace PSS as the counter ion for PEDOT, making the final amount of PSS ionically bound to PEDOT difficult to estimate. By this method of presenting the data, Fig. 3c and d give complementary information about the system; one reducing the charge storage mechanism to its most fundamental components (Fig. 3c) and the other showing the change in the total capacitance (Fig. 3d). However, to give the full picture, values of the specific capacitance calculated using different mass components can be found in Table SI1 in ESI.†
2). The mass of PSS was not considered in the calculation of specific capacitance for two reasons: (1) PSS is a large polymer counter ion. If its mass is taken into the account, it cannot properly be compared to other PEDOT systems with small-sized and mobile counter ions, like chloride or tosylate. (2) In solution, there is an excess of PSS and one role of DMSO is to remove this excess. The amount of PSS that is ionically coupled to PEDOT is therefore much smaller than the total amount of PSS in the sample. Also, during the processing of the samples and in the electrolyte solution during measurements, PEDOT is exposed to small anions that can replace PSS as the counter ion for PEDOT, making the final amount of PSS ionically bound to PEDOT difficult to estimate. By this method of presenting the data, Fig. 3c and d give complementary information about the system; one reducing the charge storage mechanism to its most fundamental components (Fig. 3c) and the other showing the change in the total capacitance (Fig. 3d). However, to give the full picture, values of the specific capacitance calculated using different mass components can be found in Table SI1 in ESI.†
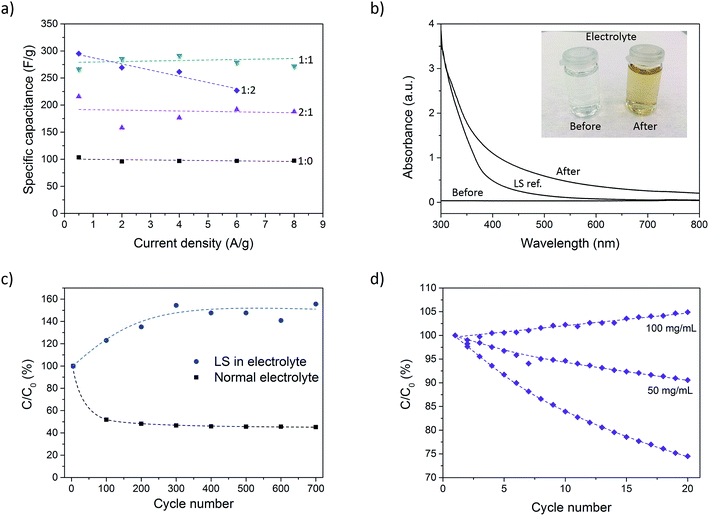
Galvanostatic discharge measurements were further performed at different current densities (0.5–8 A g−1) to investigate the rate capability of the composite. Due to the high currents in some measurements (caused by the large mass of the samples), the potential drop became significant and spanned over a large part of the total potential window. To get around this issue, the samples were charged to 0.9 V instead of 0.7 V prior to discharge. In doing so, the potential drop was confined to the potential window 0.7–0.9 V. However, for the P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 sample at 8 A g−1, the potential drop became too large even with the expanded potential window. This measurement was therefore omitted. Further increasing the potential window beyond 0.9 V was not possible since signs of overoxidation of PEDOT could be observed for such high potentials. Fig. 4a shows the specific capacitance for different current densities. The results show a constant capacitance up to 8 A g−1 for all samples except P:L_1
2 sample at 8 A g−1, the potential drop became too large even with the expanded potential window. This measurement was therefore omitted. Further increasing the potential window beyond 0.9 V was not possible since signs of overoxidation of PEDOT could be observed for such high potentials. Fig. 4a shows the specific capacitance for different current densities. The results show a constant capacitance up to 8 A g−1 for all samples except P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, indicating excellent rate capability. The highest charging rate corresponds to 7 seconds charging/discharging times for the P:L_1
2, indicating excellent rate capability. The highest charging rate corresponds to 7 seconds charging/discharging times for the P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sample and ∼15 seconds for the P:L_1
0 sample and ∼15 seconds for the P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample. The areal capacitance for different current densities can be found in ESI (Fig. SI3†).
1 sample. The areal capacitance for different current densities can be found in ESI (Fig. SI3†).
The stability of the paper composite was investigated by cycling a sample (P:L_2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 700 times at 1 A g−1 using chronopotentiometry. Fig. 4c shows C/C0 (expressed in %) where C is the capacitance of each cycle and C0 is the initial capacitance. The capacitance drops to 45% over 700 cycles, where the larger part of the drop occurs during the first 100 cycles. This level corresponds to a sample with very little or even no LS. The drop in capacitance during cycling is attributed to dissolution of LS into the electrolyte. This theory was corroborated by a discoloration of the electrolyte solution during the measurement, as can be seen in the inset of Fig. 4b. To determine if the discoloration was in fact caused by leakage of LS, we measured the UV-vis spectra of the electrolyte before and after a sample was cycled 500 times. A measurement of LS dissolved in electrolyte was also taken as a reference. From Fig. 4b it is clear that the electrolyte after cycling looks qualitatively similar to the LS reference sample. The deviation in the two spectra is believed to be caused by the conversion of phenolic hydroxyl and methoxyl groups into quinone groups during the oxidation process occurring during cycling.34 This results in a darker color compared to pristine LS, resulting in a higher absorbance.
1) 700 times at 1 A g−1 using chronopotentiometry. Fig. 4c shows C/C0 (expressed in %) where C is the capacitance of each cycle and C0 is the initial capacitance. The capacitance drops to 45% over 700 cycles, where the larger part of the drop occurs during the first 100 cycles. This level corresponds to a sample with very little or even no LS. The drop in capacitance during cycling is attributed to dissolution of LS into the electrolyte. This theory was corroborated by a discoloration of the electrolyte solution during the measurement, as can be seen in the inset of Fig. 4b. To determine if the discoloration was in fact caused by leakage of LS, we measured the UV-vis spectra of the electrolyte before and after a sample was cycled 500 times. A measurement of LS dissolved in electrolyte was also taken as a reference. From Fig. 4b it is clear that the electrolyte after cycling looks qualitatively similar to the LS reference sample. The deviation in the two spectra is believed to be caused by the conversion of phenolic hydroxyl and methoxyl groups into quinone groups during the oxidation process occurring during cycling.34 This results in a darker color compared to pristine LS, resulting in a higher absorbance.
The leakage is an effect of the high ionic conductivity of the nanopaper which is important for achieving high power density, but also easily lets ions leave the material. To stop the capacitance from degrading by LS diffusion, the initial giant gradient of LS between the sample and electrolyte must be equilibrated or, even to some extent, reversed. To this end, another sample with the same LS loading was cycled 700 times but now in an electrolyte containing 50 mg mL−1 of LS. The results are given in Fig. 4c and shows that the addition of LS to the electrolyte not only suppress the degradation completely, but in fact increases the capacitance by 50%. This is caused by the concentration of LS in the electrolyte initially being higher than inside the electrode sample, thus producing a net influx of LS into the electrodes, increasing the resulting capacitance.
The strategy of adding LS into the electrolyte was further explored for samples with an even higher LS loading (P:L_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2). Fig. 4d shows that in an electrolyte with no LS, the capacitance drops to 75% over 20 cycles. With an electrolyte including 50 mg mL−1 of LS, the capacitance still dropped, but only to 90% of the initial value. At this point, the concentration of LS in the electrolyte was still smaller (5%) as compared to the concentration within the sample electrode (∼9%). At 100 mg mL−1 (or 10%), the concentration in the electrolyte was higher than that within the sample electrode and the capacitance was found to slightly increase instead.
2). Fig. 4d shows that in an electrolyte with no LS, the capacitance drops to 75% over 20 cycles. With an electrolyte including 50 mg mL−1 of LS, the capacitance still dropped, but only to 90% of the initial value. At this point, the concentration of LS in the electrolyte was still smaller (5%) as compared to the concentration within the sample electrode (∼9%). At 100 mg mL−1 (or 10%), the concentration in the electrolyte was higher than that within the sample electrode and the capacitance was found to slightly increase instead.
4. Conclusions
The introduction of lignosulfonate (LS) into CNF-PEDOT paper supercapacitors resulted in an increase in the areal capacitance and specific capacitance on the positive electrode. The results show that LS is compatible with polymer- and paper-based supercapacitor systems possible to scale into large production and prototype volumes and therefore has the potential to be used in commercial supercapacitor applications for giant-scale electrical power applications. The charge–discharge characteristics of the electrode material start out as that of an ideal capacitor when no LS is added but becomes more and more similar to those of a battery at increasing loading of LS. The ESR of the devices was not affected by the introduction of LS and the corresponding sheet resistance measurements of the paper electrode samples indicate that LS has very little effect on the charge transport of the system. The material exhibited excellent rate performance which allowed us to charge the electrodes at high current densities of 8 A g−1 with little or no loss in capacitance. However, a loss in capacitance in the samples containing LS was seen when cycling the devices and was attributed to LS leaking out from the electrode samples into the electrolyte. This leakage was completely suppressed by adding LS also into the electrolyte solution at a concentration matching that of LS inside the electrode. This strategy solves one of the major problems with energy storage systems based on organic molecules, where dissolution of the molecules into the electrolyte limits the lifetime of the device. Other future strategies to prevent such leakage may include to crosslink LS or protecting the electrodes with membranes that are only permeable to small ions.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work was financially supported by The Knut and Alice Wallenberg foundation (Power Paper project) KAW 2011.0050, the Swedish Foundation for Strategic Research (GMT14-0058), the Önnesjö Foundation, the Swedish Energy Agency and the Advanced Functional Materials Center at Linköping University. The authors would like to acknowledge RISE Bioeconomy for their help with producing cellulose nanofibrils.References
- M. M. Pérez-Madrigal, M. G. Edo and C. Alemán, Green Chem., 2016, 18, 5930–5956 RSC
.
- Y. Z. Zhang, Y. Wang, T. Cheng, W. Y. Lai, H. Pang and W. Huang, Chem. Soc. Rev., 2015, 44, 5181–5199 RSC
.
- Y. Lin, D. Gritsenko, Q. Liu, X. Lu and J. Xu, ACS Appl. Mater. Interfaces, 2016, 8, 20501–20515 CAS
.
- T. H. Nguyen, A. Fraiwan and S. Choi, Biosens. Bioelectron., 2014, 54, 640–649 CrossRef CAS PubMed
.
- D. Sun, X. Yan, J. Lang and Q. Xue, J. Power Sources, 2013, 222, 52–58 CrossRef CAS
.
- B. Andres, S. Forsberg, A. P. Vilches, R. Zhang, H. Andersson, M. Hummelgård, J. Bäckström and H. Olin, Nord. Pulp Pap. Res. J., 2012, 27, 481–485 CAS
.
- S. Mats, T. Daniel, G. Hjalmar, S. Anurak, D. Dina, B. Magnus and P. J. Magnus, Flexible and Printed Electronics, 2016, 1, 044003 CrossRef
.
- N. Sani, X. Wang, H. Granberg, P. Andersson Ersman, X. Crispin, P. Dyreklev, I. Engquist, G. Gustafsson and M. Berggren, Sci. Rep., 2016, 6, 28921 CrossRef CAS PubMed
.
- Z. Gui, H. Zhu, E. Gillette, X. Han, G. W. Rubloff, L. Hu and S. B. Lee, ACS Nano, 2013, 7, 6037–6046 CrossRef CAS PubMed
.
- X. Chen, H. Zhu, C. Liu, Y. C. Chen, N. Weadock, G. Rubloff and L. Hu, J. Mater. Chem. A, 2013, 1, 8201–8208 CAS
.
- L. Hu and Y. Cui, Energy Environ. Sci., 2012, 5, 6423–6435 Search PubMed
.
- L. Hu, H. Wu, F. La Mantia, Y. Yang and Y. Cui, ACS Nano, 2010, 4, 5843–5848 CrossRef CAS PubMed
.
- L. Zhang, P. Zhu, F. Zhou, W. Zeng, H. Su, G. Li, J. Gao, R. Sun and C.-p. Wong, ACS Nano, 2016, 10, 1273–1282 CrossRef CAS PubMed
.
- D. Tobjörk and R. Österbacka, Adv. Mater., 2011, 23, 1935–1961 CrossRef PubMed
.
- Z. Wu, Y. Zhu and X. Ji, J. Mater. Chem. A, 2014, 2, 14759–14772 CAS
.
- G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828 RSC
.
- R. Kötz and M. Carlen, Electrochim. Acta, 2000, 45, 2483–2498 CrossRef
.
- M.-T. Lee, J.-K. Chang, Y.-T. Hsieh and W.-T. Tsai, J. Power Sources, 2008, 185, 1550–1556 CrossRef CAS
.
- J. Jiang, Y. Li, J. Liu, X. Huang, C. Yuan and X. W. Lou, Adv. Mater., 2012, 24, 5166–5180 CrossRef CAS PubMed
.
- M. Hamedi, E. Karabulut, A. Marais, A. Herland, G. Nyström and L. Wågberg, Angew. Chem., Int. Ed., 2013, 52, 12038–12042 CrossRef CAS PubMed
.
- V. V. N. Obreja, A. Dinescu and A. C. Obreja, International Review of Electrical Engineering, 2010, 5, 272–281 Search PubMed
.
- Z. Yu, L. Tetard, L. Zhai and J. Thomas, Energy Environ. Sci., 2015, 8, 702–730 CAS
.
- I. Shown, A. Ganguly, L.-C. Chen and K.-H. Chen, Energy Sci. Eng., 2015, 3, 2–26 CrossRef CAS
.
- M. Mastragostino, C. Arbizzani and F. Soavi, J. Power Sources, 2001, 97–98, 812–815 CrossRef CAS
.
- G. A. Snook, P. Kao and A. S. Best, J. Power Sources, 2011, 196, 1–12 CrossRef CAS
.
- D. P. Dubal, S. H. Lee, J. G. Kim, W. B. Kim and C. D. Lokhande, J. Mater. Chem., 2012, 22, 3044–3052 RSC
.
- T. C. Girija and M. V. Sangaranarayanan, Synth. Met., 2006, 156, 244–250 CrossRef CAS
.
- F. N. Ajjan, N. Casado, T. Rębiś, A. Elfwing, N. Solin, D. Mecerreyes and O. Inganäs, J. Mater. Chem. A, 2016, 4, 1838–1847 CAS
.
- C. Karlsson, J. Nicholas, D. Evans, M. Forsyth, M. Strømme, M. Sjödin, P. C. Howlett and C. Pozo-Gonzalo, ChemSusChem, 2016, 9, 2112–2121 CrossRef CAS PubMed
.
- A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wågberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305 CrossRef PubMed
.
- S. Admassie, F. N. Ajjan, A. Elfwing and O. Inganas, Mater. Horiz., 2016, 3, 174–185 RSC
.
- G. Milczarek and O. Inganäs, Science, 2012, 335, 1468–1471 CrossRef CAS PubMed
.
- M. Wagner, T. Rębiś and O. Inganäs, J. Power Sources, 2016, 302, 324–330 CrossRef CAS
.
- J. Wang, Y. Deng, Y. Qian, X. Qiu, Y. Ren and D. Yang, Green Chem., 2016, 18, 695–699 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta06810g |
| This journal is © The Royal Society of Chemistry 2018 |