Principles of doping ceria for the solar thermochemical redox splitting of H₂O and CO₂

Abstract

Ceria-based metal oxides are promising redox materials for solar H₂O/CO₂-splitting thermochemical cycles. Density functional theory (DFT) computations are applied to elucidate the underlying mechanism of the role of dopants in facilitating ceria based redox cycles; specifically, we explain why some dopants increase performance, while others do not. Firstly, we find that Zr and Hf dopants increase the oxygen exchange capacity of ceria because they store energy in tensilely strained Zr– or Hf–O bonds which is released upon O-vacancy formation. This finding corrects a long held assumption that Zr and Hf decrease the O-vacancy formation energy by compensating for ceria expansion upon reduction. Although the released strain energy decreases the O-vacancy formation energy, O-vacancy formation remains sufficiently endothermic to split H₂O and CO₂. Secondly, we show that two electrons must be promoted into the high energy Ce f-band during reduction if the O-vacancies are to store sufficient energy to drive the oxidative gas splitting step. This means that di- and trivalent dopants are not suitable for this process. Lastly, we show that dopants which break O bonds due to their small size or strongly covalent character, such as Ti and the pentavalent dopants, substantially decrease the O-vacancy formation energy because only three O bonds must break during reduction. These vacancies, therefore, are too low in energy to drive gas splitting. Based on these findings, we develop guidelines for new ceria doping strategies to facilitate solar thermochemical gas splitting cycles.

---

1. Introduction

The 2-step solar thermochemical redox cycle has been identified as a promising high-efficiency approach for solar fuel production.^1–4 It consists of the reduction of a metal oxide using concentrated solar process heat to liberate O₂, followed by its re-oxidation with H₂O and/or CO₂, generating H₂ and/or CO, according to:

1.1. Reduction

1.2. Oxidation

MO_x−δ + δH₂O → MO_x + δH₂ (2a)

MO_x−δ + δCO₂ → MO_x + δCO (2b)

MO_x and MO_x−δ are the oxidized and reduced forms of the metal oxide, respectively, and δ is the O nonstoichiometry, which determines the extent of product generation per cycle. For simplification, we restrict ourselves to discussing the solar thermochemical water splitting cycle (STWS, eqn (1) and (2a)); however analogous analyses are valid for the CO₂-splitting cycle (eqn (1) and (2b)). The reactions are thermodynamically favorable when their Gibbs free energy changes are negative:where the subscripts red and ox indicate the reduction and oxidation reactions, respectively, and ΔH_ws is the enthalpy of splitting water (i.e. H₂O → H₂ + 1/2 O₂). Thus, ΔH_red must be greater than 2.51 eV (242 kJ mol⁻¹) to split steam.⁵ Additionally, materials with high reduction enthalpies require high reduction temperatures and result in high H₂O conversion; conversely, materials with low reduction enthalpies reduce at lower temperatures but require a larger temperature swing between the reduction and oxidation steps or result in low H₂O conversion. Therefore, materials with intermediate reduction enthalpies, i.e. materials which balance the two reactions, are desirable. Several metal oxides have been suggested for the redox cycle, including ZnO,^6,7 mixed metal ferrites (MFe₂O₄ where M = Fe, Co, Ni, etc),^8–10 hercynite spinels (FeAl₂O₄),^5,11 perovskites (ABO₃),^12–14 and ceria (CeO₂).^15,16 Among these, ceria has become the benchmark material because of its rapid kinetics, and long term stability.^3,17,18 Some of these beneficial effects stem from the redox mechanism of ceria. For example, the release/uptake of O upon reduction/oxidation is achieved by the generation/annihilation of O-vacancies in the lattice rather than a phase change as is seen for other cycles. The lack of a phase change contributes to its stability and the presence of O-vacancies contributes to its rapid kinetics. However, ceria requires high temperatures (>1400 °C) and low oxygen partial pressures (<10⁻⁴ bar) in order to obtain a reasonable reduction extent (δ).^3,19–22 Because of this, the specific H₂ yield per unit mass of ceria is limited.

As shown in eqn (3), increasing the H₂ production capacity can be accomplished by either decreasing the reduction enthalpy or increasing the reduction entropy. Altering the reduction energy is more straight forward, and is accomplishable via doping. To this end, many researchers have attempted to dope ceria with di-, tri-, tetra- and pentavalent dopants to improve the redox performance of ceria. Di-, tri- and pentavalent dopants, including Li, Mg, Cu, Zn, Sr, Al, Sc, Cr, Mn, Fe, Co, Ni, Y, La, Pr, Sm, Gd, and Ta provide little, if any, improvement in the H₂ production capacity of ceria, although some prevent sintering and grain growth.^{16,20,23–31} Tetravalent Zr and Hf, however, have been shown to significantly improve the redox capacity of ceria.^{24,30,32–34} To date the selection of dopants for STWS is mostly based on trial and error; therefore, we attempt to bring an understanding of ceria dopants to the STWS community.

Currently, Zr and Hf dopants are thought to decrease the reduction energy of ceria, and thereby increase the reduction extent and the resulting H₂ production,^{24,30,32–34} by compensating for the expansion that ceria undergoes upon reduction.^33,35–38 The rational for this hypothesis is explained as follows. When O-vacancies form in ceria during reduction, each removed O²⁻ anion nominally releases two electrons to the ceria bulk; these electrons localize on two Ce⁴⁺ reducing them to Ce³⁺ cations, as shown in Kroger–Vink notation:

This reduction is associated with ceria expansion, which has traditionally been ascribed to the formation of Ce³⁺ cations, which are larger than Ce⁴⁺ cations.^{33,37,39–42} The presence of the smaller dopant cations, i.e. Zr and Hf, are believed to alleviate the expansive strain caused by the larger Ce³⁺ cations via the overlap of tensile and compressive strain fields; simultaneously decreasing the extent of expansion and decreasing the reduction energy.^33,35–38 This is very logical based on the cationic radius explanation for the expansion of ceria upon reduction. However, we have recently shown that the formation of Ce³⁺ cations is not responsible for ceria expansion, but rather ceria expands because of outward relaxation from the O-vacancy due to non-counterpoised forces.⁴³ This then suggests that the strain compensation theory for improved performance with Zr and Hf is incorrect. Therefore, the effects of tetravalent dopants on ceria need to be reevaluated if new and improved modifications to ceria are to be rationally designed.

In this work we develop a fundamental understanding of the role of dopants in altering the ceria O-vacancy formation energy, and therefore its redox performance for STWS, using Density Functional Theory (DFT)⁴⁴ based quantum mechanical simulations. Specifically, we investigate early transition metal di-, tri-, tetra- and pentavalent dopants, their effects on the O-vacancy formation energies in ceria and the reason for their effects. We will show that dopants alter the ceria reduction energy via three modes: (1) altering the Fermi energy of the system, and therefore the energy required to promote the electrons released upon O vacancy formation to empty bands; (2) intrinsically breaking O bonds which reduce the number of O bonds which must be severed during O-vacancy formation; and (3) storing strain energy in the dopant-O bonds which is released upon O vacancy formation. We show that only the latter mode of altering the reduction energy improves the redox performance for STWS for single element doped ceria because it suppresses the reduction energy the least and thus enables the O-vacancy to store sufficient energy to drive eqn (2a). Of all the dopants investigated, only the tetravalent Hf and Zr operate via the third mode. Lastly, we suggest guidelines for future doping strategies.

2. Computational methods

Doped ceria materials were investigated using periodic boundary condition based density functional theory quantum chemical calculations as implemented in the Quantum Espresso software package.⁴⁵ Exchange and correlation energies were calculated using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) density functional.⁴⁶ The use of ultra-soft pseudo-potentials⁴⁷ enabled us to only explicitly simulate the valance and outer core electrons while maintaining chemical accuracy. In the case of O, we only calculated the valence electrons (2s, and 2p); however, we included s and p outer core electrons for all metals and transition metals, for example the Ce 5s, and 5p electrons were calculated in addition to the valence 6s, 5d, and 4f electrons. Wave functions were based on summations of plane-waves with energies up to 530.6 eV (39 Ry) which was determined by a cut-off energy study conducted from 408.2 to 680.3 eV (30–50 Ry). The O-vacancy formation energy in CeO₂ was only 0.002 eV higher at a 530.6 eV cut-off energy as compared to the 680.3 eV cut-off energy in a 2 × 2 × 2 super cell; therefore, the less computationally demanding 530.6 eV cut-off energy was used. Due to the large super cell, and the associated extensive Brillion zone folding, all calculations were conducted at the gamma point, however, DOS and PDOS were calculated on a 2 × 2 × 2 Monkhorst–Pack k-point mesh or finer.

This investigation utilized a super cell composed of a 3 × 3 × 3 repetition of the primitive ceria fluorite cell. The 3 × 3 × 3 super cell consisted of 27 cerium and 54 oxygen ions, for a total of 81 ions. Here, super cells containing either one or two O vacancies represent 1.85% or 3.70% O-vacancy concentrations, or reduction extents of δ = 0.037 or 0.074, respectively. The replacement of one or two Ce atoms by a dopant resulted in doping concentrations of 3.7%, or 7.4%, respectively. The 3 × 3 × 3 supercell size was chosen to represent likely reduction extents, and doping concentrations, while minimizing periodic image interactions (lattice vectors of ∼11.5 Å) and computational costs. O-vacancy formation energies were calculated by:

where E_O-vac is the O-vacancy formation energy (reduction energy), E_MO2−δ is the energy of the material with an O-vacancy, E_MO2 is the energy of the fully oxidized material, and E_O2 is the energy of an O₂ molecule in vacuum. Throughout this work molecular geometry representations were generated using VESTA.⁴⁸ Bader analysis was conducted to determine the oxidation or reduction state of the ions using software written by the Henkelman group.^36,37

A Hubbard correction (DFT+U)⁴⁹ of U = 3.125 eV was imposed on the Ce f-orbitals to correct the propensity of generalized gradient approximation (GGA) based functionals, including PBE, to overly delocalize highly correlated electrons. This value was shown to be a good compromise between electronic structure accuracy and reduction energy accuracy for the Ultrasoft pseudopotential used in this work.⁴³ We additionally considered correcting the d-orbitals of the dopant elements. We determined that imposing a U correction on the dopants has almost no effect (<0.02 eV variation) on the reduction energy based on a study of the effect U_eff values ranging from 0 (no correction) to 5 eV on the d-orbitals of Nb-CeO₂, in addition to the 3.125 eV Hubbard correction on the Ce f-orbitals, as shown in (ESI) Fig. S1.† Therefore, no correction was applied to dopant ions. The nearly independent nature of the O-vacancy formation energy with respect to the correction of dopant d-states arises because the Ce f-states, rather than the dopant d-states, are largely responsible for accepting the electrons released by O-vacancy formation.

The calculations were conducted at 0 K. This assumes that the changes in energy and structure at the operational temperatures are small in comparison to the effects of doping. This is rationalized by the fact that introducing dopants into the system changes the reduction energy by up to 4 eV (see below), and it is unlikely that the formation of sub phases affects reduction energies to similar extents.

3. Results

In order to understand the effects of doping ceria on the redox cycle we first briefly discuss undoped ceria to establish a baseline for comparison. Among the dopants, we first discuss Zr and Hf tetravalent dopants which aid the redox performance,^{24,30,32–34} before discussing those dopants which do not, i.e. di-, tri-, Ti-, and pentavalent dopants,^{16,20,23–31} in that order. In each case, we investigated the elements from periodic table rows 4, 5, and 6, and detail the row 5 elements and then compare the row 4 and 6 elements to the exemplar. For each dopant, we examined an array of O-vacancy and Ce³⁺ localization configurations. All results are summarized in Table 1.

Table 1 Summary of doped ceria reduction results

		Single dopant atom (3.7%)							Two dopant atoms (7.4%)
		Ox cell length	Ox dopant–O bond length	Favorable O-vac site	E O-vac	O-vac site preference	Red cell length	Red dopant – O bond length^a	Pair preference^b	E O-vac
a Reported values do not include the distance to the O anion directly across from the vacancy, which is significantly shorter. b A positive number indicates that the paired configuration is preferred, a negative number indicates dopant repulsion. c A single number indicates that all three cell vector are the same length, a series of three shows the length of all three vectors. d Numbers separated by a slashes indicates a tetrahedral configuration, the first number is the tetrahedral bond length, the second number is the average of the remaining bond lengths. e N and F indicate a preference for the O-vacancy to neighbor the dopant or be away from the dopant, respectively. f Numbers in parenthesis correspond to the system after the formation of a second O-vacancy.
Pure	Ce	11.66	n/a	n/a	2.85	n/a	11.69^c	n/a	n/a	n/a
4+	Ti	11.64	1.92/2.67^d	N^e	1.90	0.85	11.67, 11.65, 11.67	1.93/2.50	0.73	1.49
	Zr	11.63	2.27	N	2.16	0.81	11.66	2.17/2.24	−0.01	1.52
	Hf	11.63	2.26	N	2.08	0.88	11.66	2.16/2.23	−0.03	1.33
2+^f	Ca	11.66	2.45	N	−1.20	0.35	11.67, 11.67, 11.64	2.41 (2.36)	n/a	n/a
				(N)	(2.56)	(0.08)	(11.69, 11.69, 11.72)
	Sr	11.68	2.52	N	−1.25	0.21	11.66, 11.70, 11.70	2.48 (2.49)	n/a	n/a
				(F)	(2.60)	(0.14)	(11.70, 11.74, 11.73)
	Ba	11.69	2.52	N	−0.95	0.26	11.72, 11.65, 11.72	2.54 (2.53)	n/a	n/a
				(N)	(2.47)	(0.13)	(11.72, 11.72, 11.78)
3+^f	Sc	11.63	2.31	N	0.33	0.69	11.65, 11.65, 11.64	2.26	0.44	−1.52 (2.87)
	Y	11.65	2.38	N	0.70	0.22	11.67	2.34	0.06	−1.37 (2.79)
	La	11.67	2.45	F	0.83	0.05	11.69	2.46	0.03	−1.03 (2.80)
5+	V	11.68	1.77/2.79	N	1.61	0.83	11.74, 11.64, 11.74	1.76/2.75	1.23	1.79
	Nb	11.66	1.94/2.58	N	1.84	0.90	11.69, 11.68, 11.68	1.94/2.35	0.63	1.46
	Ta	11.66	1.94/2.56	N	1.71	1.35	11.66, 11.67, 11.66	2.01/2.22	0.48	1.15

---

3.1 Reduction of undoped ceria

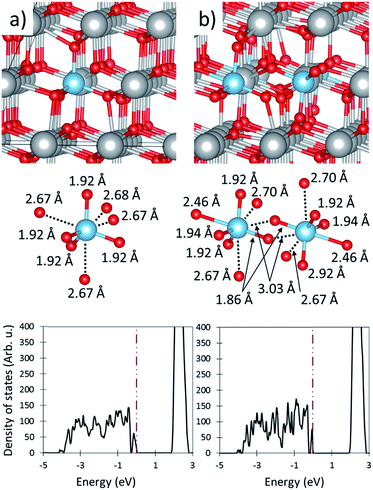
We calculate a ceria cubic lattice constant of 5.496 Å, which corresponds to lattice vectors of 11.658 Å in the 3 × 3 × 3 primitive cell based super cell used in this work and shown in Fig. 1a and tabulated in Table 1. The Ce cations are cubically (8-fold) coordinated while the O anions are tetrahedrally (4-fold) coordinated with a Ce–O bond length of 2.38 Å, and a Ce⁴⁺ to Ce⁴⁺ inter atomic distance (Ce⁴⁺–Ce⁴⁺ IAD) of 3.89 Å. The O anions are reduced while the Ce cations are oxidized, as shown by the fact that the valence band is mostly composed of O 2p states while the conduction band is composed of Ce d states, as shown in Fig. 1b, and ESI Fig. S2.† A narrow band of Ce 4f orbitals lies in the middle of the band gap. Bader change analysis confirms this, showing that O ions have charges of −1.23 while the Ce cations have charges of +2.46. The discrepancy in Bader and formal charges (−2 and +4 for O and Ce ions, respectively) arises from electron sharing in covalent bonds and the fact that charge assignment methods are imperfect.

Fig. 1 Oxidized and reduced ceria. (a) The geometric representation of the fully oxidized ceria cell, and (b) the density of states plot of the oxidized cell. (c) The geometric representation of reduced ceria, and (d) the density of states plot of the reduced cell. Large gray and small red spheres shows Ce and O ions respectively. In both (b) and (d) the insert shows the projected density of states. Projections onto the Ce orbitals is shown in ESI Fig. S2.† The purple dotted dashed line shows the Fermi level.

Ceria reduction is endothermic by 2.85 eV, however this is an underestimation of the experimentally determined values (roughly 4.5 eV at δ = 0.03)⁵⁰ due to the inclusion of the Hubbard correction. Upon reduction two electrons are promoted from the valence band to the f-band, localizing on two Ce cations that are second Ce nearest neighbors (2NN) from the O vacancy. This is confirmed by DOS analysis which shows that 74% of the two promoted electrons localized on the two 2NN Ce cations. The localization at the 2NN site is consistent with previous experimental and computational work.^43,51–54 Because the O-vacancy formation energy (i.e. reduction energy) of a metal oxide stems from both the strength of the metal–oxygen bonds and the energy required to promote the electrons donated by the removed O anion into available bonds,^55,56 it is unsurprising that ceria has a high O-vacancy formation energy owing to its relatively large band gap between the valence band and Ce f-band and strong Ce–O bonds.

The presence of an O-vacancy causes the lattice to expand to a = 11.691 Å, b = 11.688 Å, and c = 11.690 Å (a = 5.511 Å, b = 5.511 Å, and c = 5.510 Å in the cubic representation), as shown in Table 1. As detailed in our previous work,⁴³ the expansion of the O anions around the Ce³⁺ cations (O²–Ce³⁺ IAD ∼2.45 Å) is counterbalanced by a contraction of the O²–Ce⁴⁺ IAD one coordination shell away from the Ce³⁺. This results in a negligible change in the cationic lattice, as indicated by the Ce³⁺–Ce⁴⁺ IAD of 3.90 Å, which is essentially unchanged from that in oxidized ceria (Ce⁴⁺–Ce⁴⁺ IAD of 3.89 Å). Ceria expansion is caused by the outward relaxation of the vacancy neighboring Ce⁴⁺ cations (Ce_vac⁴⁺) due the non-counterpoised attraction to the O anion opposite the vacancy. This results in a Ce⁴⁺_vac–Ce⁴⁺_vac IAD of ∼4.14 Å. These results are summarized in Table 1.

We also investigated the reduction energy of ceria when only one, or zero electrons are promoted to the f-band. To do this, either one or two electrons were removed from super cells with and without an O-vacancy. When only one electron is promoted (i.e. the cell has a +1 charge) the reduction energy decreases to only 0.98 eV. The reduction energy becomes exothermic (E_O-vac = −1.09 eV) when no elections are promoted (i.e. the cell has a +2 charge). These findings demonstrate that the energy required to promote electron density into high energy f-bands is responsible for a large portion of the reduction energy of ceria. Therefore, dopants which do not require electronic promotion are expected to substantially decrease the reduction energy.

3.2 Performance improving materials: tetravalent dopants

3.2.1 Zr doped ceria. Exchanging a Ce cation in ceria for a Zr cation does not significantly alter its electronic structure because both cations are tetravalent, as shown in eqn (7); however, it does induce geometric changes to the material. As in the case of undoped ceria, the Fermi energy of the Zr doped ceria (Zr-CeO₂) lies within the band gap, as displayed in Fig. 2a, meaning that the valence O-2p states are filled while the Ce-f and the conduction bands are empty. Therefore, the reduction of Zr-CeO₂ requires the promotion of two electrons from the valence band to the Ce-f band, which is expected to be substantially uphill in energy. The presence of the Zr cation, which is smaller than Ce cations, constricts the doped material from a lattice vector of 11.66 Å in undoped ceria to 11.63 Å, as shown in Table 1. The contraction stems from the 2.27 Å Zr–O bond lengths, which is roughly 0.1 Å shorter than the Ce–O bond in both undoped ceria and Zr-CeO₂. Although Zr contracts the lattice, the Zr–O bonds are under tensile strain, as they are ∼0.07 Å longer than the 2.20 Å Zr–O bond in isostructural cubic zirconia.⁵⁷ The large amount of stress required to strain a bond by ∼3% suggests that substantial energy would be released if the bond were able to relax.

Fig. 2 Geometric and electronic characteristics of Zr-CeO₂. (a) shows the oxidized material while (b) shows the reduced materials. In both (a) and (b), the left, middle and right panels show a geometric representation of the super cell, a close up view of the Zr cation and its coordinating O anions (including Zr–O distances), and the density of states plot. The large gray, medium green, and small red spheres of the left and middle panels represent Ce, Zr, and O ions respectively. The dotted square shows the location of the O-vacancy. The vertical dotted dashed line indicates the Fermi level in the DOS plots.

The presence of the Zr cation disrupts the O anion symmetry; therefore, many unique O-vacancy sites exist. We calculated the formation energy of an O-vacancy at a site neighboring the Zr dopant (E_O-vac = 2.16 eV) and one ∼7.12 Å from the dopant (E_O-vac = 2.98 eV). In each case multiple Ce³⁺ configurations were assessed, and only the lowest energy configuration is discussed. When an O-vacancy forms in Zr-CeO₂, two electrons are promoted into the f-band regardless of the O-vacancy location, just as in the case of undoped ceria, as is shown in Fig. 2. From an electronic promotion perspective, we would expect a similar O-vacancy formation energy at either position in Zr-CeO₂ and in undoped ceria. From a bond breaking perspective we would expect that O-vacancies neighboring the Zr cation would be more unfavorable than those far from the Zr because Zr–O bonds are stronger than Ce–O bonds, based on the relative reduction energies of CeO₂ and ZrO₂.^22,58 However, neither of these predictions is correct; therefore, the difference in O-vacancy formation energies arises from geometric changes in the material, as suggested by Wang et al.⁵⁹

The formation of the O-vacancy in either position results in an expansion of the lattice from 11.63 Å to 11.66 Å. The similar expansion predicted for both O-vacancy configurations despite the large difference in reduction energy is contrary to the current explanation for the role of Zr, i.e. that the smaller Zr ionic radius compensates for Ce radius expansion and thereby lowers the reduction energy. Additionally, the Zr–Ce IAD's across the O-vacancy (4.13 Å) are larger than the Ce–Ce IAD (4.08 Å) when the O-vacancy neighbors the dopant, which is the opposite behavior than expected from the current explanation. Therefore, the current hypothesis is likely incorrect. However, other geometric changes occur when the O-vacancy neighbors the Zr cation.

The decreased O-vacancy formation energy of Zr-CeO₂ arises from the strained Zr–O bonds. When the O-vacancy forms at a site neighboring the dopant three Ce–O and one Zr–O bonds are broken. This enables significant structural relaxation of the Zr cation, and a decrease in Zr–O bond length. The O–Zr bonds of the once cubically coordinated Zr cation relax from their elongated 2.27 Å length to a coordination where four anions form a distorted tetrahedral with Zr–O bond lengths of 2.11–2.18 Å, while the remaining three anions undergo a smaller 0.02 Å contraction to roughly 2.24 Å, as shown in Fig. 2 and detailed in Table 1. The new Zr–O bond lengths are much closer to those of Zr in its monoclinic structure – which has Zr–O bond lengths of 2.06 Å (two), 2.16 Å (three), and 2.25 Å (two).⁵⁷ Consequently the Zr–O bonds in the reduced ceria are much less strained and therefore lower in energy. This released strain energy partially compensates for the energy of O-vacancy formation. When the O-vacancy is far from Zr, no Zr–O bonds are broken, and only minor relaxation of the Zr coordination occur (four O anions contract to a Zr–O IAD of 2.23 Å while four expand to a Zr–O IAD of 2.33 Å), resulting in minimal stress release, and minimal changes to the O-vacancy formation energy compared to undoped ceria.

We also investigated the behavior of Zr-CeO₂ at a higher Zr concentration (7.3%) by including a second dopant in the super cell. This enabled multiple Zr configurations, two of which we examined: (1) the Zr cations are third cationic nearest neighbors (∼6.7 Å apart) which we call the far configuration; and (2) the Zr cations are first cationic nearest neighbors (∼3.80 Å apart) which we call the near configuration. These configurations are shown in ESI Fig. 3. The far configuration does not significantly alter the reduction energetics of ceria when the O-vacancy neighbors a dopant, where both have E_O-vac = 2.16 eV, as shown in Table 1. However, the higher concentration increases the number of O anions coordinated to Zr dopants, and therefore increases the number of O-sites with a lowered reduction energy. The near configuration, where the O-vacancy neighbors both dopants, however, has a substantially decreased reduction energy (E_O-vac = 1.52 eV). The decrease arises because two Zr cations relax and thus more bond strain is released. These O-vacancies are predicted to not be redox active because their formation energy is too low to drive water splitting. Because there is almost no energy preference for one configuration or the other (the separated configuration is preferred 0.01 eV), the Zr cations are likely randomly distributed through the material, where the isolated dopant cations facilitate STWS while paired dopants do not. This explains the initial increase and subsequent decrease in STWS performance of Zr-CeO₂ with increasing Zr content.^30,50 At low concentrations there are more isolated Zr cations and therefore many O-sites capable of splitting water, but as the concentration increase the portion of O-sites neighboring two dopants also increases, and therefore the number of STWS active sites eventually decreases.

Fig. 3 The effects of Sr-CeO₂. (a) shows the geometry of Sr substituted ceria. The large gray and green, and small red spheres represent Ce, Sr, and O ions respectively. (b–d) show the DOS plots of Sr-CeO₂ under different reduction extents, where (b) is the DOS when all O sites are occupied, (c) shows the presence of one O-vacancy and (d) shows the presence of a second O-vacancy. The inset of (b) details the area near the valence band maximum. The dotted–dashed purple vertical line indicates the location of the Fermi level.

Overall, the decrease in reduction energy of Zr-CeO₂ stems from strain stored in the Zr–O bonds which is released upon O-vacancy formation, rather than size compensation between the smaller Zr⁴⁺ cations and the enlarged Ce³⁺ cations, as is often suggested.^33,35–38 This finding builds on the work of Wang et al., who suggested that structural relaxation is the driver for the decreased reduction energy,⁵⁹ by explaining that the energy released during structural relaxation stems from strain release of the Zr–O bonds. The promotion of two electrons into the Ce f-orbitals and breakage of four O-cation bonds results in an O-vacancy formation energy that is high enough to drive water splitting when the vacancy is filled. This explains the improved behavior or Zr-CeO₂ for STWS.^{24,30,32–34} Additionally, there is no attraction between Zr-dopants and therefore no driving force for the formation of O-sites with two Zr neighbors which have reduction energies too low for water splitting.

3.2.2 Hf doped ceria. Hf-CeO₂ behaves very similarly to Zr-CeO₂, which is unsurprising because of their similar size and electronic properties. Therefore, Hf is not described in detail, but the results are summarized in Table 1. The difference between the two is merely in the extent of bond strain and the resulting reduction energies where Hf–O bonds (2.26 Å) are more strained than the Zr–O bonds as compared to its native oxide (2.20 Å)⁶⁰ and therefore Hf-CeO₂ reduction (E_O-vac = 2.08 eV) is less endothermic than in Zr-CeO₂ (E_O-vac = 2.16 eV). This explains the improved reducibility of Hf-CeO₂ as compared to Zr-CeO₂, as seen experimentally and computationally.^30,36 Ti, however, behaves differently than Hf and Zr. The changes Ti induces in CeO₂ are so large that we predict that Ti doping will not increase the STWS performance of CeO₂ and it is, therefore, described in Section 3.3.5, along with the other non-STWS-improving dopants.

3.3 Non-performance improving materials

Here we discuss dopants which do not substantially increase the H₂ production capacity of ceria. First we discuss di- and trivalent dopants, as they behave similarly, before discussing Ti and pentavalent dopants as they behave similarly, although by a different mechanism than the di- and trivalent dopants. All results are summarized in Table 1 and only major differences between dopants are highlighted.

3.3.1 Divalent Sr-doped ceria. The substitution of a Sr cation onto a Ce lattice site alters ceria both electronically and geometrically, as shown in Fig. 3 and Table 1. Because Ce is tetravalent in CeO₂ the presence of divalent Sr results in the under reduction of the O anions. This is demonstrated by Kroger–Vink notation shown in eqn (8) and explicitly shown in the PDOS of Fig. 3b. As seen in the PDOS plot, the Fermi energy sits within the valence band near the valence band maximum. The unfilled valence states are mainly of O 2p character, as is expected from the fact that Sr donates a maximum of two electrons to the system rather than the four of Ce. Additionally, a Sr dopant causes the lattice to expand from 11.656 Å to 11.681 Å, because the Sr–O bonds are longer (2.52 Å) than the Ce–O bonds (2.38 Å), see Table 1, although they are shorter than the Sr–O bonds in SrO₂ (2.57 Å).⁶¹

The formation of a charge compensating O-vacancy is exothermic at sites both neighboring (E_O-vac = −1.25 eV) and away (E_O-vac = −1.04 eV) from the Sr dopant. The formation of the oxygen vacancies results in the elimination of the empty O-2p states present in the over oxidized super cell and the movement of the Fermi level into the band gap, as shown in Figures Fig. 3b and c. The formation of O vacancies is favorable as no electrons must be promoted into the high energy f-orbitals, and the remaining O anions reduce towards their preferred −2 oxidation state. The exothermic O-vacancy formation energy indicates the spontaneous formation of O-vacancies in the lattice by Sr doping. The O-vacancy preferentially neighbors Sr cations because of the relative strengths of Sr–O bonds and Ce–O bonds. The Sr–O bonds are weaker than the Ce–O bonds because of the lower ionic attraction between O²⁻ and Sr²⁺ than O²⁻ and Ce⁴⁺; therefore, when the O-vacancy localizes next to the Sr dopant, an additional more stable Ce⁴⁺–O²⁻ bond is maintained. As the formation of charge compensating O-vacancies is favorable, they cannot store energy, and therefore cannot drive water splitting.

A second O-vacancy was introduced into the lattice to investigate non-exothermic O-vacancy formation. Because of the strong site preference discussed above, an O-vacancy was maintained next to the Sr cation, while the second O-vacancy was subsequently placed on O lattice sites either near the Sr – but not directly next to the previous O-vacancy – or far from it. We calculate a reduction energy of 2.74 and 2.60 eV in the near and far configurations, respectively. The formation of the second O-vacancy formally results in the reduction of two Ce⁴⁺ cations to Ce³⁺ cations. This is shown in PDOS of Fig. 3d, where the Fermi energy has moved into the Ce f-orbital band. As in the case of pure ceria, the occupied Ce f-orbitals sit below the band of unoccupied Ce f-orbitals, indicating localized, rather than delocalized Ce³⁺ states.

The formation energy for the second, non-charge-compensating, vacancy (E_O-vac = 2.60 eV) is only slightly lower than that of the undoped ceria (E_O-vac = 2.85 eV). This is because in both cases two elections must be promoted into the high energy Ce f-states, and minimal strain energy is released (see Table 1). The charge compensating O-vacancies form spontaneously upon doping, therefore only non-charge compensating O-vacancies form at high temperatures. These vacancies have O-vacancy formation energies that are only 9% lower than in undoped ceria, which explains the similar STWS behavior of Sr-CeO₂ and undoped CeO₂,²⁴ even though Sr-CeO₂ has intrinsic vacancies.

3.3.2 Divalent Ca and Ba doped CeO₂. Doping CeO₂ with Ca or Ba results in very similar behavior to that of Sr-CeO₂, as shown in Table 1. This is unsurprising given their similar valence state. The divalent cation's O-vacancy formation energy is ordered 0 > Ba > Sr > Ca. Just as the case of Sr, the formation of a second O vacancy in Ba- and Ca-CeO₂ is endothermic (2.65 and 2.58 eV) and results in a less than a 10% decrease in the O-vacancy formation energy of undoped ceria (2.85 eV), suggesting once again that these materials will behave similarly to pure ceria in STWS. These results are consistent with previous work.⁶²

3.3.3 Trivalent Y-doped ceria. Doping ceria with trivalent Y (see Fig. 4a) also results in the under reduction of the O anions, but to a lesser degree than the divalent dopants because Y cations provide three electrons to the system rather than only two. This can be seen in the PDOS plot of Fig. 4b and written in eqn (9). The PDOS is similar to that of the divalent dopants in that the Fermi-energy lies within, but near the top of, the valence band, resulting in an unoccupied O 2p state. However, the Fermi energy lies higher in the valence band than in the divalent cases, because the Y-CeO₂ is only missing a single electron. This, as before, indicates that the O anions are not fully reduced.

Fig. 4 The effects of Y-CeO₂. (a) shows the geometry of Y substituted ceria. The large gray, medium olive green, and small red spheres represent Ce, Y, and O ions respectively (b–f) shows DOS plots of Y-CeO₂ under different doping concentrations and reduction extents, where (b) is the DOS when all O sites are occupied, (c) shows the presence of one O-vacancy, (d) shows the presence of a second dopant, (e) shows the presence of an O-vacancy in a cell with two Y cations, and (f) shows the cell with two O-vacancy and two Y dopants. The insets of (b) and (d) detail the area near the valence band maximum. The dotted–dashed purple vertical line indicates the location of the Fermi level.

Given the similar size of Y³⁺ and Ce⁴⁺, it is unsurprising that the structure undergoes little geometric change upon doping. The Y–O bonds are very slightly elongated, ∼2.384 Å, from the pure ceria Ce–O bond length of ∼2.379 Å, but they are substantially longer than the bonds in Y₂O₃ which range from 2.223 to 2.294 Å depending on the site.⁶³ This suggests that the Y–O bonds are under tensile strain. Although the Y–O bonds are slightly elongated, the lattice vectors shrink slightly from 11.658 to 11.652 Å, as shown in Table 1, which we attribute to the under reduction of the O anions and the corresponding slightly decreased ionic attraction.

O-vacancy formation in Y-CeO₂ is endothermic, and the O-vacancy preferentially occupies a site neighboring the dopant (0.74 eV), rather than far from the dopant (0.98 eV). The formation of the O vacancy next to the Y dopant allows the Y cation to move towards the remaining O-anions, decreasing the average bond length by 0.06 Å to 2.32 Å, which is closer to the Y–O bond lengths in Y₂O₃ (2.223 to 2.294 Å). We attribute the 0.24 eV site preference to the release of energy stored in the strained Y–O bond and the weaker ionic attraction of the +3 Y cation as compared to the +4 Ce cation. Upon formation of an O-vacancy, the electron density previously associated with the removed O anion redistributes through the material and only one electron is promoted to the Ce f-band, see Fig. 4c. The promotion of only one electron to the f-band, rather than two in undoped ceria, is responsible for the ∼2 eV decrease in reduction energy of Y-CeO₂. The low energy of O-vacancy formation energy suggests that these vacancies are incapable of splitting water.

The presence of a second Y dopant results in two missing electrons in the valence band when all O sites are occupied, as shown in Fig. 4d. This suggests that the material should behave similarly to divalently doped ceria. Indeed, the O-vacancy formation energy in doubled Y-CeO₂ is exothermic by −1.20 eV. Upon O-vacancy formation the Fermi energy moves back into the band gap. The formation of a second O-vacancy is endothermic by 2.79 eV which is similar (∼2% difference) to that of undoped ceria. This means that only the second O-vacancy is STWS redox active as the first is incapable of splitting water. Additionally, because the second O-vacancy has a formation energy similar to that of undoped ceria, they should have similar STWS activities, as is seen experimentally.^24,31,64

3.3.4 Trivalent Sc and La doped ceria. Because they are isovalent with Y, Sc- and La-CeO₂ behaves very similarly to Y-CeO₂, and only major differences are discussed here while calculation results are summarized in Table 1. While the O-vacancy preferentially neighbors Y and Sc, there is a slight (0.05 eV) preference for the O-vacancy not to neighbor the La dopant. The bifurcation of site preference stems from relative sizes. Sc cations, like Y cations, are smaller than the Ce⁴⁺ host cations, while La³⁺ cations are roughly of equal size to Ce³⁺ cations. The O-vacancy prefers to neighbor the Sc cation because in this configuration the Sc cation relaxes towards the remaining O anions and closer to its preferred bond length. La³⁺ behaves similarly to Ce³⁺ cations in undoped ceria, where the vacancy preferentially occupies sites away from the +3 cations,⁴³ enabling the smaller, and more positively charged Ce⁴⁺ cations neighboring the vacancy to move closer to the anionic O²⁻ rather than compressing the larger La³⁺ and Ce³⁺ ions.

When a second +3 dopant is present, the O-vacancy formation becomes exothermic for both La (−0.96 eV) and Sc (−1.52 eV) and are incapable of splitting water. Therefore, only additional, non-charge compensating O-vacancies which have similar energies to those in undoped ceria, as shown in and Table 1, are STWS active. Base on their O-vacancy formation energies, trivalent dopants are not expected to significantly improve to the STWS behavior of ceria which is seen experimentally.^24,31,64 From these results, and those of charged undoped ceria, and divalently doped ceria, we can see that the energy input associated with double electron promotion to the f-band is necessary for storing enough energy in ceria to split water.

3.3.5 Tetravalent Ti-CeO₂. The introduction of a Ti cation into CeO₂ induces large geometric changes to the system which lower the reduction energy past the point of being capable of splitting water. The significantly smaller size of Ti cations as compared to Ce cations disrupts the cubic configuration of its coordinating O anions. After restructuring, four coordinating O anions form a tetrahedral configuration around the dopant (Ti–O bond length of ∼1.92 Å which is close to the 1.95 Å in TiO₂ (ref. 65)), while the remaining four anions are substantially further from the dopant (Ti–O IAD of ∼2.67 Å), as shown in Fig. 5a and compared in Table 1. This configuration is preferred by 0.68 eV compared to the un-restructured configuration, and is in agreement with experimental studies.⁶⁶ The long distance indicates that the Ti is, at most, only weakly bound to these anions, and results in dangling O-bonds. These dangling bonds are higher in energy than the other O 2p states, as can be seen in the new states in the PDOS of Fig. 5a, which are slightly higher in energy than rest of the valence band. While the valence band of Ti-CeO₂ remains filled, the presence of the Ti cation results in the under-coordination of four O anions.

Fig. 5 The effects of Ti-CeO₂. (a) and (b) show the fully oxidized material with 3.7 and 7.4% doping concentrations respectively. In both (a) and (b), the top, middle and bottom panels show a geometric representation of the super cell, a close up view of the Ti cation and its coordinating O anions (including Ti–O distances), and the density of states plot. The large gray, medium blue and small red spheres of the top and middle panels represent Ce, Ti, and O ions respectively. The vertical dotted dashed line indicates the Fermi level in the DOS plots.

The presence of a single Ti dopant decreases the reduction energy to 1.87 eV and 2.75 eV when the dopant neighbors or is far from the cation, respectively. The decrease in O-vacancy formation energy does not arise from Ti–O bond strain release as the bond length of the tetrahedrally coordinating O anions remains essentially unchanged before (1.92 Å) and after O removal (1.91 Å), as shown in Table 1. Instead, we attribute the decreased reduction energy to the under-coordinated of O anions. This is counter to previous work which suggest that the size of Ti compensates for expansion upon reduction.³⁵ To remove an O anion, only three Ce–O bonds must break rather than four when the anions are fully coordinated. The O-vacancy formation energies of Ti-, Hf-, and Zr-CeO₂ (1.90, 2.08, and 2.16 eV respectively) would indicate that doping ceria with Ti should slightly improve the water splitting performance over Hf-, and Zr-CeO₂; however, this is not the case.

Ti cations in CeO₂ attract each other and thereby generate sites with very low O-vacancy formation energies. It is downhill in energy by 0.70 eV for two Ti cations to be cationic nearest neighbors as compared to two separated cations (i.e. one super cell with two neighboring cations and one without dopants vs. two super-cells containing one Ti cation each) as shown in Table 1. This suggests that most, if not all, Ti dopants will pair. For example, less than 1% of Ti cations are predicted to be unpaired at 1500 °C, based on a Boltzmann distribution. Therefore, the paired state must be the one considered for evaluating the doping effect of Ti on CeO₂. When the Ti cations pair, each maintains its tetrahedral coordination to four O anions, while the remaining four of the previously eight coordinating anions relax outwards. Because the Ti dopants share two coordinating O anions, the relaxation of one of the Ti away from an O anion enables the anion to relax closer to the other Ti cation, as is shown in Fig. 5b. The associated of one O anion with each Ti is responsible for the greater stabilization of paired Ti cations. This drive for pairing also explain the low solubility of Ti in CeO₂. In the paired configuration, the O-vacancy formation energy is suppressed to only 1.52 eV, or roughly half that of undoped ceria. The substantially decreased O-vacancy formation energy at sites neighboring two dopants arises because O anions at these sites are only 3-fold rather than 4-fold coordinated, and their removal enables further favorable structural relaxation. After O-vacancy formation the tetrahedral coordination remains, but the bond lengths to the remaining three O anions decrease, as shown in ESI Fig. S4.† The O-vacancy formation energy at these sites is so low that the vacancy cannot store sufficient energy to drive water splitting. Therefore, even if Ti were substantially soluble in ceria, which it is not, it would be unlikely to facilitate STWS.

3.3.6 Pentavalent Nd doped ceria. Nb-CeO₂ behaves similarly to Ti-CeO₂ despite bringing an extra electron to the system. As seen in Fig. 6a, the presence of the Nb dopant causes substantial geometric reconfiguration, resulting in a structure similar to that of Ti-CeO₂. The Nb dopant supplies five valence electrons to the host ceria lattice. Because only four electrons are necessary to fully reduce the O anions in the system the additional electron originally associated with Nb associates with a cation. As is shown in the PDOS of Fig. 6 and eqn (10), this extra electron occupies a Ce f-state. The filled f-state sits high in the valence band – f-band gap and is separated from the remainder of the f-band. Additionally, a second, but unfilled, state appears in the gap between the filled f-states and the remainder of the f-bands. Both of these states are lower in energy than the filled f-states associated with ceria reduction. The appearance of a shoulder in the valance band is once again attributed to the under coordinated O anions as described below.

Fig. 6 The effects of Nb-CeO₂. (a) and (b) show the fully oxidized material with 3.7 and 7.4% doping concentrations respectively. In both (a) and (b), the top, middle and bottom panels show a geometric representation of the super cell, a close up view of the Nb cation and its coordinating O anions (including Nb–O distances), and the density of states plot. The large gray, medium green and small red spheres of the top and middle panels represent Ce, Nb, and O ions respectively. The vertical dotted dashed line indicates the Fermi level in the DOS plots. The insets of the bottom panels shows the PDOS of the cations.

The relatively small ionic radius of Nb and the more covalent character of the Nb–O bonds result in large structural modifications of its coordinating O anions, as seen in Fig. 6. Similarly to Ti doping, the Nb cation is tetrahedrally coordinated, with Nb–O bond lengths of 1.94 Å and the remaining four O anions relaxing outward to an Nb–O IAD of ∼2.58 Å, as shown in Table 1. This suggests that there is only a bond between the Nb and the tetrahedrally positioned O anions, while the remaining O anions are under-coordinated and have dangling bonds. The high energy dangling bonds, therefore, are the cause of the valance band shoulder, and suggest that these O anions have a substantially reduced O-vacancy formation energy, as was seen in for Ti-CeO₂.

The large distortions caused by the presence of a Nb dopant drastically decreases the O-vacancy formation energy to 1.84 eV and 2.75 eV for vacancy sites neighboring and far from the dopant, respectively. As is the case for Ti-CeO₂, the under coordinated O anions in Nb-CeO₂ are more easily removed from the lattice because only three bonds must be broken (i.e. the O–Ce bonds), rather than the four in undoped ceria. The similarity in behavior of Ti and Nb with respect to bond lengths and reduction energies, suggests that the extra electron of Nb has little effect on the behavior of Nb-CeO₂, but rather that the geometric effects of the smaller Nb and Ti cations are the main cause for the modified ceria behavior.

Just as in the case of Ti, Nb cations attract each other, where Nb dopants preferentially occupy nearest cation neighbor sights by 0.63 eV compared to separated dopants. This large energy preference once again indicates that Nb dopants are likely to cluster, even at high temperatures, and that these configurations are the appropriate model for examining STWS behavior. In this configuration the O-vacancy formation energy is further decreased to 1.43 eV, similarly to Ti-CeO₂, and is incapable of driving water splitting. Therefore, only secondary O-vacancies, such as those far from Nb centers are predicted to be STWS active, and the redox behavior of Nb-CeO₂ is predicted to be similar to undoped ceria.

3.3.7 Pentavalent V and Ta doped ceria. V- and Ta-CeO₂ behave very similarly to Nb-CeO₂ as is expected given their similar sizes and electronic configurations. The calculated results are compiled in Table 1. In all cases there is massive driving force for dopant pairing, and these configurations are unlikely to be STWS active due to their very low O-vacancy formation energies. Overall, the smaller size of the pentavalent dopants results in significant restructuring of the ceria cell and the suppression of O-vacancy formation energy below that which is required for STWS. This means that the presence of pentavalent dopants is not predicted to improve the STWS performance of CeO₂. The prediction that Ta doping does not increase the performance of CeO₂ matches experimental findings.³¹

4. Discussion

Dopants alter the reduction energy of ceria, and therefore its STWS ability, through three effects: modifying the energy required to promote the electrons released by O-vacancy formation, inducing bond strain within the material, and inherently breaking O bonds. The latter two both arise from cationic size mismatch but the extent of the mismatch results in significant differences in their behaviors. The modification of promotion energy depresses the O-vacancy formation energy the most, followed by inherent bond breaking and finally O-dopant bond strain, as can be seen in Fig. 7. We will briefly comment on each of these effects and how they facilitate or hinder STWS.

Fig. 7 O-vacancy formation energy of doped ceria. The O-vacancy formation energy of undoped ceria with various charges are shown in solid black lines. Dashed lines are added to guide the eye. Solid markers show single O-vacancies, empty markers indicate two O-vacancies. Squares, diamonds, circles, and triangles mark di-, tri-, tetra- and pentavalent cations, respectively. The gray square shows two trivalent dopants with one O-vacancy.

4.1 Decreasing electron promotion energy

The energy required to promote electrons to available bands upon reduction largely determines the O-vacancy formation energy. Doping ceria with di- and trivalent cations, or removing electrons from pure ceria, results in the under-reduction of the O-anions, and the generation of empty low energy O-2p states. Therefore, when an O vacancy forms, less (or no) electron density must be promoted into high energy Ce-f states. The more electron density that has to be promoted, the higher the energy penalty is for O-vacancy formation. The trivalent dopants are excellent examples of this because the number of missing electrons is controllable via the number of dopants. When two trivalent dopants are present, and therefore no electrons must be promoted, O-vacancy formation is exothermic. Additionally, the exothermicity almost exactly matches that of the divalent dopants and is quite similar to the pure CeO₂ with two missing electrons, as shown in Fig. 7. This shows that despite slightly different ion sizes and charges the suppression of reduction energy is caused by the lack of electronic promotion. When only one trivalent dopant is present (i.e. one electron promotion to a Ce f-orbital) the reduction energy is roughly half way between the reduction of undoped ceria and ceria with two trivalent dopants. Lastly, when two O-vacancy form in divalent or doubly trivalent doped ceria, two electrons once again must be promoted to the f-band upon reduction, and the resulting O-vacancy formation energy is quite close (<10% difference) to that of undoped ceria. This shows that without the promotion of two electrons to the Ce-f band upon reduction, ceria reduction is exothermic or only slightly endothermic, in agreement with previous work,^62,67–69 and therefore does not store sufficient energy to drive water splitting. Therefore, any modifications to ceria in an attempt to increase its redox behavior should require the promotion of two electrons into Ce-f orbitals.

4.2 Breaking O bonds

The introduction of dopants with four or more valence electrons enables the full reduction of the O-anions and, therefore, ceria reduction requires the promotion of two electrons into high energy Ce-f bands. However, if the dopant cation is very small, or its O bonds have strong covalent character, it induces large structural reconfiguration and substantially weakens, if not fully brakes, O-cation bonds. This is seen in cases of Ti and the pentavalent dopants in Fig. 7. The O-vacancy formation energy at sites neighboring the dopant are significantly suppressed because an O-cation (the dopant) bond is already broken, and therefore only three O-cation (Ce) bonds must be severed to form an O-vacancy rather than four in undoped ceria. This substantially decrease the O-vacancy formation energy; as a result, these O-vacancies do not store enough energy to abstract an O atom from H₂O molecules and consequently cannot drive STWS. Additionally, these rearrangements seem to lead to dopant clustering which further suppresses the O-vacancy formation energies. As in the case of under-reduction, only secondary O-vacancies with formation energies similar to undoped ceria are expected to be capable of driving water splitting. This means that bond breaking dopants do not increase the STWS capacity of ceria, and such doping strategies should be avoided.

4.3 Straining O-bonds

Dopants which are slightly smaller than Ce⁴⁺ cations and fully reduce the O anions, such as Zr and Hf, pull their eight coordinating O anions inward without inducing changes to its coordination. If these bonds are longer than their ideal bond length because the O anions remain coordinated to three Ce cations, the bonds are strained and thus are high energy. The generation of an O-vacancy enables the dopant cations to relax towards the remaining O anions, decreasing the associated bond lengths and thus releasing the stored energy. This released energy in turn compensates for some of the energy required to break the four O-cation bonds and promote electron density into the Ce-f bands. The fact that strained bonds reduces the ceria reduction energy corrects a long held misunderstanding that they compensate for ceria expansion.^33,35–38 Additionally, this explanation provides the fundamental understanding for why the geometric relaxation of Zr-CeO₂ during reduction is associated with a decreased O-vacancy formation energy.⁵⁹ While the energy released is sizable, it does not decrease the reduction energy to the same extent as the presence of pre-broken bonds or decreased electron promotion energy. Therefore, sufficient energy is still stored in the O-vacancies to split water. New ceria doping strategies which induce bond strain or otherwise slightly weaken the cation-O bond without breaking O-bonds or decreasing the electron promotion energy should be developed to increase STWS capacity.

5. Conclusions

Using density functional theory, we investigated how doping ceria alters its ability to drive the H₂O and CO₂ splitting redox cycle. We showed that Zr and Hf dopants decrease the O-vacancy formation energy by storing energy in strained Zr–O or Hf–O bonds which is released when O-vacancies form. This corrects a long standing misunderstanding of the role of Zr and Hf dopants. We also show that dopants which result in the under-reduction of the O anions, i.e. di- and trivalent dopants, severely decrease the O-vacancy formation energy because electron density does not have to be promoted to the Ce-f orbitals upon reduction. It is the energy associated with two high energy electrons which drives water splitting. Lastly, we showed that dopants which result in under-coordinated O anions, due to their small size or highly covalent bonding character, also severely decrease the O-vacancy formation energy. To store sufficient energy for driving the redox cycle, four O-cation bonds have to be broken. From the understanding developed in this work, several guidelines for ceria modification to improve its redox performance are derived. First, the modification should result in the complete reduction of the O anions, and therefore O-vacancy formation should entail the promotion of two electrons into the f-orbitals. This then requires the dopants to be tetravalent or higher. Second, the dopants should not cause local restructuring which leaves O anions under-coordinated. Therefore, small cations with highly covalent O bonds are to be avoided. Third, dopants which decrease the strength, or increase the energy (i.e. tensile stain) of the O-dopant bond while remaining consistent with the above listed guidelines are desirable. Based on the properties of the elements, finding a single (non-Zr or -Hf) dopant that meets these criteria is unlikely. Therefore, doping strategies that modify both the behavior of ceria and the dopants themselves may meet the doping guidelines outlined above and should be sought.

Acknowledgements

We gratefully acknowledge the financial support by the European Research Council under the European Union's ERC Advanced Grant (SUNFUELS – No. 320541). The DFT calculations were performed at the High-Performance Computation cluster of ETH Zürich.

References

1. A. Steinfeld, Sol. Energy, 2005, 78, 603–615.
2. C. Perkins and A. W. Weimer, Int. J. Hydrogen Energy, 2004, 29, 1587–1599.
3. C. L. Muhich, B. D. Ehrhart, I. Al-Shankiti, B. J. Ward, C. B. Musgrave and A. W. Weimer, Wiley Interdiscip. Rev.: Energy Environ., 2016, 5, 261–287.
4. M. Romero and A. Steinfeld, Energy Environ. Sci., 2012, 5, 9234–9245.
5. C. L. Muhich, B. D. Ehrhart, V. A. Witte, S. L. Miller, E. N. Coker, C. B. Musgrave and A. W. Weimer, Energy Environ. Sci., 2015, 8, 3687–3699.
6. A. Steinfeld, Int. J. Hydrogen Energy, 2002, 27, 611–619.
7. E. Koepf, W. Villasmil and A. Meier, Appl. Energy, 2016, 165, 1004–1023.
8. T. Nakamura, Sol. Energy, 1977, 19, 467–475.
9. P. Lichty, X. Liang, C. Muhich, B. Evanko, C. Bingham and A. W. Weimer, Int. J. Hydrogen Energy, 2012, 37, 16888–16894.
10. M. D. Allendorf, R. B. Diver, N. P. Siegel and J. E. Miller, Energy Fuels, 2008, 22, 4115–4124.
11. J. R. Scheffe, J. H. Li and A. W. Weimer, Int. J. Hydrogen Energy, 2010, 35, 3333–3340.
12. A. H. McDaniel, A. Ambrosini, E. N. Coker, J. E. Miller, W. C. Chueh, R. O'Hayre and J. Tong, Energy Procedia, 2014, 49, 2009–2018.
13. M. Takacs, M. Hoes, M. Caduff, T. Cooper, J. R. Scheffe and A. Steinfeld, Acta Mater., 2016, 103, 700–710.
14. A. H. McDaniel, E. C. Miller, D. Arifin, A. Ambrosini, E. N. Coker, R. O'Hayre, W. C. Chueh and J. H. Tong, Energy Environ. Sci., 2013, 6, 2424–2428.
15. S. Abanades and G. Flamant, Sol. Energy, 2006, 80, 1611–1623.
16. W. C. Chueh and S. M. Haile, Chemsuschem, 2009, 2, 735–739.
17. W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801.
18. S. Ackermann, L. Sauvin, R. Castiglioni, J. L. M. Rupp, J. R. Scheffe and A. Steinfeld, J. Phys. Chem. C, 2015, 119, 16452–16461.
19. B. Bulfin, F. Call, M. Lange, O. Lübben, C. Sattler, R. Pitz-Paal and I. V. Shvets, Energy Fuels, 2015, 29, 1001–1009.
20. H. Kaneko, T. Miura, H. Ishihara, S. Taku, T. Yokoyama, H. Nakajima and Y. Tamaura, Energy, 2007, 32, 656–663.
21. B. D. Ehrhart, C. L. Muhich, I. Al-Shankiti and A. W. Weimer, Int. J. Hydrogen Energy, 2016, 41, 19881–19893.
22. R. J. Panlener, R. N. Blumenthal and J. E. Garnier, J. Phys. Chem. Solids, 1975, 36, 1213–1222.
23. S. Abanades, A. Legal, A. Cordier, G. Peraudeau, G. Flamant and A. Julbe, J. Mater. Sci., 2010, 45, 4163–4173.
24. Q.-L. Meng, C.-i. Lee, T. Ishihara, H. Kaneko and Y. Tamaura, Int. J. Hydrogen Energy, 2011, 36, 13435–13441.
25. Q.-L. Meng, C.-i. Lee, S. Shigeta, H. Kaneko and Y. Tamaura, J. Solid State Chem., 2012, 194, 343–351.
26. H. Kaneko, H. Ishihara, S. Taku, Y. Naganuma, N. Hasegawa and Y. Tamaura, J. Mater. Sci., 2008, 43, 3153–3161.
27. Q. Jiang, G. Zhou, Z. Jiang and C. Li, Sol. Energy, 2014, 99, 55–66.
28. E. V. Ramos-Fernandez, N. R. Shiju and G. Rothenberg, RSC Adv., 2014, 4, 16456–16463.
29. A. Le Gal, S. Abanades, N. Bion, T. Le Mercier and V. Harlé, Energy Fuels, 2013, 27, 6068–6078.
30. J. R. Scheffe, R. Jacot, G. R. Patzke and A. Steinfeld, J. Phys. Chem. C, 2013, 117, 24104–24114.
31. A. Le Gal and S. Abanades, J. Phys. Chem. C, 2012, 116, 13516–13523.
32. A. Le Gal, S. Abanades and G. Flamant, Energy Fuels, 2011, 25, 4836–4845.
33. J. Scaranto and H. Idriss, Top. Catal., 2015, 58, 143–148.
34. Y. Hao, C.-K. Yang and S. M. Haile, Chem. Mater., 2014, 26, 6073–6082.
35. D. A. Andersson, S. Simak, N. V. Skorodumova, I. Abrikosov and B. Johansson, Appl. Phys. Lett., 2007, 90, 1909.
36. D. A. Andersson, S. Simak, N. V. Skorodumova, I. Abrikosov and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 174119.
37. G. Balducci, J. Kašpar, P. Fornasiero, M. Graziani, M. S. Islam and J. D. Gale, J. Phys. Chem. B, 1997, 101, 1750–1753.
38. S. R. Bishop, D. Marrocchelli, W. Fang, K. Amezawa, K. Yashiro and G. W. Watson, Energy Environ. Sci., 2013, 6, 1142–1146.
39. I. Al-Shankiti, F. Al-Otaibi, Y. Al-Salik and H. Idriss, Top. Catal., 2013, 56, 1129–1138.
40. S. Hull, S. T. Norberg, I. Ahmed, S. G. Eriksson, D. Marrocchelli and P. A. Madden, J. Solid State Chem., 2009, 182, 2815–2821.
41. S. R. Bishop, Acta Mech. Sin., 2013, 29, 312–317.
42. E. Aneggi, M. Boaro, S. Colussi, C. de Leitenburg and A. Trovarelli, Handb. Phys. Chem. Rare Earths, 2016, 50, 209–242.
43. C. L. Muhich, J. Phys. Chem. C, 2017, 121, 8052–8059.
44. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138.
45. G. Paolo, B. Stefano, B. Nicola, C. Matteo, C. Roberto, C. Carlo, C. Davide, L. C. Guido, C. Matteo, D. Ismaila, C. Andrea Dal, G. Stefano de, F. Stefano, F. Guido, G. Ralph, G. Uwe, G. Christos, K. Anton, L. Michele, M.-S. Layla, M. Nicola, M. Francesco, M. Riccardo, P. Stefano, P. Alfredo, P. Lorenzo, S. Carlo, S. Sandro, S. Gabriele, P. S. Ari, S. Alexander, U. Paolo and M. W. Renata, J. Phys.: Condens. Matter, 2009, 21, 395502.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
47. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
48. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
49. J. Hubbard, Proc. R. Soc. London, Ser. A, 1963, 276, 238–257.
50. M. Takacs, J. R. Scheffe and A. Steinfeld, Phys. Chem. Chem. Phys., 2015, 17, 7813–7822.
51. B. Wang, X. Xi and A. N. Cormack, Chem. Mater., 2014, 26, 3687–3692.
52. G. E. Murgida, V. Ferrari, M. V. Ganduglia-Pirovano and A. M. Llois, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115120.
53. J. E. Sutton, A. Beste and S. H. Overbury, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144105.
54. J.-F. Jerratsch, X. Shao, N. Nilius, H.-J. Freund, C. Popa, M. V. Ganduglia-Pirovano, A. M. Burow and J. Sauer, Phys. Rev. Lett., 2011, 106, 246801.
55. A. M. Deml, V. Stevanovic, C. L. Muhich, C. B. Musgrave and R. O'Hayre, Energy Environ. Sci., 2014, 7, 1996–2004.
56. A. M. Deml, A. M. Holder, R. P. O'Hayre, C. B. Musgrave and V. Stevanović, J. Phys. Chem. Lett., 2015, 6, 1948–1953.
57. C. J. Howard, R. J. Hill and B. E. Reichert, Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 116–120.
58. A. S. Foster, V. B. Sulimov, F. Lopez Gejo, A. L. Shluger and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 224108.
59. H.-F. Wang, X.-Q. Gong, Y.-L. Guo, Y. Guo, G. Z. Lu and P. Hu, J. Phys. Chem. C, 2009, 113, 10229–10232.
60. G. M. Rignanese, X. Gonze, G. Jun, K. Cho and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 184301.
61. P. A. O'Day, M. Newville, P. S. Neuhoff, N. Sahai and S. A. Carroll, J. Colloid Interface Sci., 2000, 222, 184–197.
62. A. B. Kehoe, D. O. Scanlon and G. W. Watson, Chem. Mater., 2011, 23, 4464–4468.
63. J. Zhang, F. Paumier, T. Höche, F. Heyroth, F. Syrowatka, R. J. Gaboriaud and H. S. Leipner, Thin Solid Films, 2006, 496, 266–272.
64. J. R. Scheffe and A. Steinfeld, Energy Fuels, 2012, 26, 1928–1936.
65. J. Muscat, V. Swamy and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 224112.
66. G. Zhou, J. Hanson and R. J. Gorte, Appl. Catal., A, 2008, 335, 153–158.
67. D. E. P. Vanpoucke, P. Bultinck, S. Cottenier, V. Van Speybroeck and I. Van Driessche, J. Mater. Chem. A, 2014, 2, 13723–13737.
68. M. Nolan, J. Mater. Chem., 2011, 21, 9160–9168.
69. Z. Hu and H. Metiu, J. Phys. Chem. C, 2011, 115, 17898–17909.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta04000h

---