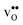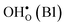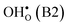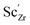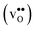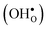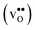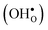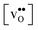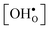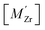Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect segregation to grain boundaries in BaZrO3 from first-principles free energy calculations
Anders
Lindman
 *a,
Tor S.
Bjørheim
*a,
Tor S.
Bjørheim
 b and
Göran
Wahnström
b and
Göran
Wahnström
 a
a
aDepartment of Physics, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden. E-mail: anders.lindman@chalmers.se
bCentre for Materials Science and Nanotechnology, Department of Chemistry, University of Oslo, FERMiO Gaustadalléen 21, 0349 Oslo, Norway
First published on 14th June 2017
Abstract
Acceptor-doped BaZrO3 is currently the most promising ceramic proton conductor for application in electrolyzers and reactor membranes. Its overall proton conductivity is, however, limited by space-charge formation due to defect segregation to grain boundaries (GBs). In this contribution, we determine the vibrational contribution to the free energy of GB formation and defect segregation in the symmetric Σ3 (112)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] tilt GB in BaZrO3 in order to elaborate on the high temperature GB defect chemistry. We consider segregation of several different defect species: oxygen vacancies
10] tilt GB in BaZrO3 in order to elaborate on the high temperature GB defect chemistry. We consider segregation of several different defect species: oxygen vacancies 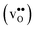 , protons
, protons 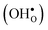 and the four trivalent acceptor dopants Sc, In, Y and Gd
and the four trivalent acceptor dopants Sc, In, Y and Gd 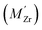 . The calculations reveal that the segregation free energy of
. The calculations reveal that the segregation free energy of 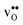 decreases with temperature while it remains fairly constant for
decreases with temperature while it remains fairly constant for 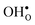 , which increase the relative stability of
, which increase the relative stability of 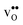 with respect to
with respect to 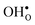 with increasing temperature. As a consequence the onset for hydration of the GB core is shifted towards lower temperatures. For the dopants we find that both the segregation energy and entropy correlate with the ionic radius, where they are positive for the smaller dopants (Sc and In) while negative for the larger (Y, Gd). In turn, this leads to similar segregation free energies for all species, which are close to zero, at high temperatures where dopants are mobile, implying that dopant segregation is almost entirely driven by segregated positively charged defects. Neglecting the phonon contribution erroneously leads to the conclusion that the thermodynamic driving force for dopant segregation increases with increasing dopant radii, and it is therefore important to consider free energies when predicting the high temperature defect chemistry of BaZrO3 GBs.
with increasing temperature. As a consequence the onset for hydration of the GB core is shifted towards lower temperatures. For the dopants we find that both the segregation energy and entropy correlate with the ionic radius, where they are positive for the smaller dopants (Sc and In) while negative for the larger (Y, Gd). In turn, this leads to similar segregation free energies for all species, which are close to zero, at high temperatures where dopants are mobile, implying that dopant segregation is almost entirely driven by segregated positively charged defects. Neglecting the phonon contribution erroneously leads to the conclusion that the thermodynamic driving force for dopant segregation increases with increasing dopant radii, and it is therefore important to consider free energies when predicting the high temperature defect chemistry of BaZrO3 GBs.
1 Introduction
Proton-conducting perovskite-structured oxides such as BaZrO3 have attracted considerable attention over the last decade due to their high partial proton conductivity, and find application as electrolytes and membranes in electrochemical applications such as solid oxide fuel cells, electrolyzers and chemical reactors.1 Acceptor-doped BaZrO3 has emerged as the most promising proton-conducting oxide at intermediate temperatures (400–700 °C) as it combines high bulk proton conductivity with chemical stability towards CO2.2–4 Several recent advances in this field are based on ceramic cells that use derivatives of BaZrO3 as the electrolyte,5–8 which emphasize the importance of this material.Polycrystalline BaZrO3, however, exhibits resistive grain boundaries (GBs), which ultimately deteriorates the overall performance of BaZrO3-based devices. This phenomenon has been investigated intensively and it is generally accepted that the high GB resistance is due to positively charged GB cores, resulting in space-charge regions surrounding the cores which are effectively depleted of protonic charge carriers.9–11 Theoretical studies of a variety of different GBs,12–20 and also a recent experiment using atom-probe tomography,21 have shown that the charged GBs stem from accumulation of both doubly charged oxygen vacancies 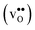 and protons
and protons 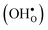 . None of these theoretical studies, however, consider free energies of defect segregation, but rather the energy at zero Kelvin thus neglecting the temperature dependence and zero-point vibrational contribution to defect segregation energies. The phonon contribution to defect formation and segregation in BaZrO3 has recently been determined for the bulk material,22–24 surfaces and thin films25,26 showing that vibrational contributions affect the relative stability of
. None of these theoretical studies, however, consider free energies of defect segregation, but rather the energy at zero Kelvin thus neglecting the temperature dependence and zero-point vibrational contribution to defect segregation energies. The phonon contribution to defect formation and segregation in BaZrO3 has recently been determined for the bulk material,22–24 surfaces and thin films25,26 showing that vibrational contributions affect the relative stability of 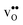 and
and 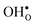 . One might therefore suspect that such contributions may be important also for prediction of GB defect chemistry, especially at the high temperatures employed for preparation of polycrystalline materials (typically above 1700 K).
. One might therefore suspect that such contributions may be important also for prediction of GB defect chemistry, especially at the high temperatures employed for preparation of polycrystalline materials (typically above 1700 K).
Segregation of acceptor dopants 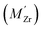 to GBs has also been observed experimentally, especially in samples prepared at high temperatures.9,10,21,27–29 This phenomenon has not yet been considered from a theoretical point of view and it is not clear whether dopant segregation is driven only by the attractive space-charge potential, or if dopants are thermodynamically stabilized at the GB core in the same way as
to GBs has also been observed experimentally, especially in samples prepared at high temperatures.9,10,21,27–29 This phenomenon has not yet been considered from a theoretical point of view and it is not clear whether dopant segregation is driven only by the attractive space-charge potential, or if dopants are thermodynamically stabilized at the GB core in the same way as 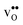 and
and 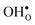 . For surfaces, yttrium dopants have been shown to favour the surface plane BaZrO3 (ref. 30–32) and one may foresee that this also is the case for GBs.
. For surfaces, yttrium dopants have been shown to favour the surface plane BaZrO3 (ref. 30–32) and one may foresee that this also is the case for GBs.
In this contribution, we assess the free energy of defect segregation to the symmetric Σ3 (112)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] tilt GB in BaZrO3 through first-principles phonon calculations. This GB displays a low formation energy and can be represented in a fairly small supercell,12,15 which makes it suitable for the present study due to the demanding nature of free energy calculations. This choice is further justified by the fact that the same GB has been observed experimentally with high-resolution transmission electron microscopy in cubic SrTiO3,33 which is structurally similar to BaZrO3. In addition to
10] tilt GB in BaZrO3 through first-principles phonon calculations. This GB displays a low formation energy and can be represented in a fairly small supercell,12,15 which makes it suitable for the present study due to the demanding nature of free energy calculations. This choice is further justified by the fact that the same GB has been observed experimentally with high-resolution transmission electron microscopy in cubic SrTiO3,33 which is structurally similar to BaZrO3. In addition to 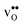 and
and 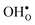 , we consider segregation of four typical trivalent acceptor dopants with different ionic radii: Sc, In, Y, and Gd. The segregation properties are evaluated in a thermodynamic space-charge model in order to obtain equilibrium defect concentrations in the GB core and the resulting potential barriers, at different temperatures.
, we consider segregation of four typical trivalent acceptor dopants with different ionic radii: Sc, In, Y, and Gd. The segregation properties are evaluated in a thermodynamic space-charge model in order to obtain equilibrium defect concentrations in the GB core and the resulting potential barriers, at different temperatures.
2 Methodology
Density functional theory (DFT) calculations have been carried out using the projector augmented wave method34,35 as implemented in VASP.36–39 The semi-local PBE40 functional was used to describe exchange and correlation and the plane wave cutoff energy was set to 500 eV. An 8 × 8 × 8 Monkhorst–Pack grid was used for k-point sampling of the BaZrO3 primitive bulk cell, which yields a lattice constant of a0 = 4.236 Å. The smallest GB supercell with sufficient GB separation, which we here on refer to as the primitive GB cell, contains 90 atoms and the unrelaxed cell dimensions are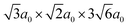 , where the principal axes are [11
, where the principal axes are [11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], [
], [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] and [112], respectively (see Fig. 1). Both this primitive cell and a 1 × 2 × 1 supercell expansion (180 atoms) were considered for calculating GB properties, while only the larger supercell was considered for the defect calculations. Initially, a 6 × 6 × 1 k-point grid was used for the primitive GB cell, in accordance with grid size used for the bulk system. Further convergence tests showed, however, that a 4 × 4 × 1 grid was sufficient and the corresponding k-point density was later used in the defect calculations. The convergence criteria for electronic relaxation was set to 10−8 eV, and both ionic and volume relaxations were performed until residual forces were below 0.4 meV Å−1.
10] and [112], respectively (see Fig. 1). Both this primitive cell and a 1 × 2 × 1 supercell expansion (180 atoms) were considered for calculating GB properties, while only the larger supercell was considered for the defect calculations. Initially, a 6 × 6 × 1 k-point grid was used for the primitive GB cell, in accordance with grid size used for the bulk system. Further convergence tests showed, however, that a 4 × 4 × 1 grid was sufficient and the corresponding k-point density was later used in the defect calculations. The convergence criteria for electronic relaxation was set to 10−8 eV, and both ionic and volume relaxations were performed until residual forces were below 0.4 meV Å−1.
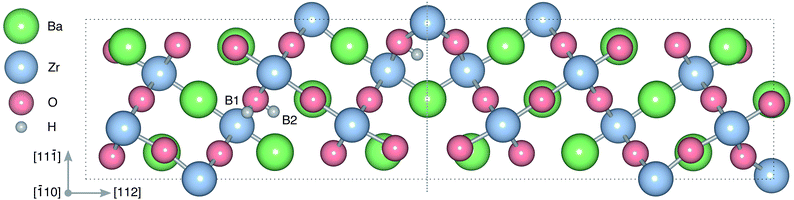 | ||
Fig. 1 Atomic structure of the Σ3 (112)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] tilt GB. The vertical gray dotted line indicates the position of the GB plane. The protons in the figure mark the unrelaxed positions of the three protonic defect sites considered here (where the two sites in the bulk region are denoted B1 and B2), and the two oxygen ions to which the protons form bonds are the sites considered for oxygen vacancy formation. The figure was produced using VESTA.41 10] tilt GB. The vertical gray dotted line indicates the position of the GB plane. The protons in the figure mark the unrelaxed positions of the three protonic defect sites considered here (where the two sites in the bulk region are denoted B1 and B2), and the two oxygen ions to which the protons form bonds are the sites considered for oxygen vacancy formation. The figure was produced using VESTA.41 | ||
Segregation free energies were evaluated according to
| ΔsegGdef(T) = ΔfGGBdef(T) − ΔfGbulkdef(T), | (1) |
| ΔsegGdef(T) = ΔsegEeldef + ΔsegFvibdef(T) | (2) |
| = ΔsegEeldef + ΔfFvib,GBdef(T) − ΔfFvib,bulkdef(T), | (3) |
| ΔsegSdef(T) = ΔfSvib,GBdef(T) − ΔfSvib,bulkdef(T). | (4) |
In the calculations all structures have been completely relaxed (i.e. ionic positions, and cell volumes and shapes), which implies that free energies are calculated at constant pressure (zero pressure) conditions.22 Phonon calculations have been performed using phonopy,42 where force constants have been determined within the harmonic approximation using finite displacements of 0.005 Å. The vibrational contribution to the free energy and entropy is given by
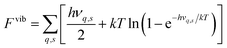 | (5) |
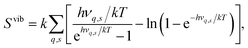 | (6) |
The segregation entropy ΔsegSdef is given by the change of the frequencies νq,s between the configuration with the defect located at the GB and in the bulk region. Differentiating the expression for the entropy with respect to the frequency νq,s yields
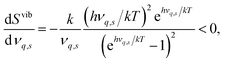 | (7) |
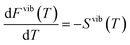 | (8) |
3 Results and discussion
3.1 Grain boundary properties
First, we consider the defect free symmetric Σ3 (112)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] GB. In contrast to previous studies12,15 of this GB, where cell relaxation only was permitted perpendicular to GB interface, here we perform a full relaxation of the cell shape and structure. We find that the GB expansion is 0.17 Å per GB, which is slightly larger than found previously,12,15 while the area of the GB is reduced by 0.2%. The GB expansion is more significant than the GB area reduction and the net effect of the GB formation is a volume expansion of 0.4% per GB in the primitive GB cell.
10] GB. In contrast to previous studies12,15 of this GB, where cell relaxation only was permitted perpendicular to GB interface, here we perform a full relaxation of the cell shape and structure. We find that the GB expansion is 0.17 Å per GB, which is slightly larger than found previously,12,15 while the area of the GB is reduced by 0.2%. The GB expansion is more significant than the GB area reduction and the net effect of the GB formation is a volume expansion of 0.4% per GB in the primitive GB cell.
The GB formation free energy is determined according to the expression γ(T) = [GGB(T) − Gbulk(T)]/2A, where GGB and Gbulk are the free energies of the GB and bulk systems, respectively, and A is the GB area of the relaxed GB structure. An equivalent expression is used for calculating the GB formation entropy (interchange G with S). For the bulk system we use a supercell with the same orientation and number of atoms as for the GB system that allows us to perform phonon calculations at the same q-points in both systems. At zero Kelvin we obtain γ(0) = 52 meV Å−2, which is slightly higher than previously reported values for this GB.12,15
The vibrational frequencies projected onto the ions in the GB plane are subject to a redshift, while the frequencies associated with the ions next to the interface are blueshifted, especially those for Ba and O. The overall effect is a blueshift and, hence, a negative entropy and the free energy increases as function of temperature (see Fig. 2).
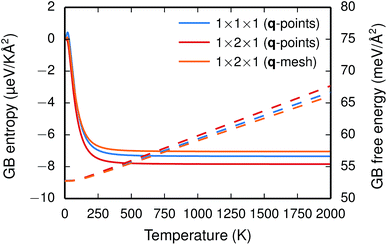 | ||
| Fig. 2 GB formation entropy (solid lines) and free energy γ(T) (dashed lines) calculated for different supercells and q-point sampling schemes. | ||
The two considered system sizes, the GB primitive cell (1 × 1 × 1) and the 1 × 2 × 1 supercell expansion, yield very similar GB formation entropies and free energies (see Fig. 2), which suggest that the results are converged. Additionally, further convergence tests were performed with the supercell in order to study the effect of the q-point sampling scheme. Two different schemes were considered: (1) using only the explicit q-points resulting from the supercell expansion (q1 = [0, 0, 0] and q2 = [0, 1/2, 0]) and (2) using a mesh of q-points along the expanded dimension with frequencies obtained through interpolation. The rather good agreement between the two (see Fig. 2) suggests that using the explicit q-points in the present case is adequate for obtaining free energies and entropies with sufficient accuracy.
3.2 Defect segregation
Next, we consider segregation of defects to the GB starting with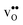 and
and 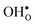 followed by the acceptor dopants Sc, In, Y and Gd. All defect calculations are performed with the 1 × 2 × 1 supercell and phonons are only evaluated at the Γ point, a choice that is justified by q-point convergence for the defect free system (see Section 3.1).
followed by the acceptor dopants Sc, In, Y and Gd. All defect calculations are performed with the 1 × 2 × 1 supercell and phonons are only evaluated at the Γ point, a choice that is justified by q-point convergence for the defect free system (see Section 3.1).
The insertion of a defect into the GB supercell causes a symmetry reduction, which gives rise to an increase in the number of displacements required to compute the vibrational frequencies for the defective system. This is most prominent for a single proton, which requires 1086 displacements, as to be compared with the 83 displacements required for the defect free GB. However, since there are two identical GBs in the supercells (due to the periodic boundary conditions), it is possible to reduce the number of displacements by inserting two defects symmetrically into the supercell and thereby preserving an amount of symmetry in the system. In the present case this operation reduced the number of displacements by a factor of two for all defects. For this approach to be feasible the two defects need to be far enough apart so that there is no interaction between them. We have considered both one and two defects for 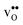 and
and 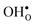 and, as will be shown in Fig. 4, this approach works remarkably well with very similar segregation entropies and free energies per defect for the supercells containing one and two defects. We therefore only performed phonon calculations with two defects in the supercell for the acceptor dopants.
and, as will be shown in Fig. 4, this approach works remarkably well with very similar segregation entropies and free energies per defect for the supercells containing one and two defects. We therefore only performed phonon calculations with two defects in the supercell for the acceptor dopants.
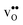 and
and 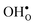 in the Σ3 (112)[
in the Σ3 (112)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] GB have been studied previously and it is well established that the most favorable site for both defects is located in the plane next to the GB plane12,15 (see Fig. 1). We therefore only consider this site here. As a representation of the defects in bulk we consider the oxygen site that is furthest away from the GB interface. There are, however, two distinct proton sites at this oxygen ion due the lower symmetry of the GB supercell and we refer to them as B1 and B2 (see Fig. 1).
10] GB have been studied previously and it is well established that the most favorable site for both defects is located in the plane next to the GB plane12,15 (see Fig. 1). We therefore only consider this site here. As a representation of the defects in bulk we consider the oxygen site that is furthest away from the GB interface. There are, however, two distinct proton sites at this oxygen ion due the lower symmetry of the GB supercell and we refer to them as B1 and B2 (see Fig. 1).
The segregation energy of 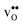 is found to be −1.53 eV, while for
is found to be −1.53 eV, while for 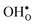 it is −0.83 eV and −0.79 eV with the B1 and B2 sites as bulk reference, respectively. A less negative segregation energy using B2 implies that this configuration is lower in energy by 0.04 eV compared to B1. These segregation energies are all slightly more negative than found previously for the same GB at constant volume.12,15 Defect formation volumes have also been determined, both in the bulk region and at the GB core. The formation volumes are given in terms of the chemical expansion coefficient, which is calculated as described in the work by Jedvik et al.43 The expansion coefficients for defects in the bulk region are in good agreement with the corresponding ones in bulk supercells22,43 (see Table 1), which further indicates that the present GB supercell size is sufficient. The expansion coefficient at the GB is similar compared to bulk for
it is −0.83 eV and −0.79 eV with the B1 and B2 sites as bulk reference, respectively. A less negative segregation energy using B2 implies that this configuration is lower in energy by 0.04 eV compared to B1. These segregation energies are all slightly more negative than found previously for the same GB at constant volume.12,15 Defect formation volumes have also been determined, both in the bulk region and at the GB core. The formation volumes are given in terms of the chemical expansion coefficient, which is calculated as described in the work by Jedvik et al.43 The expansion coefficients for defects in the bulk region are in good agreement with the corresponding ones in bulk supercells22,43 (see Table 1), which further indicates that the present GB supercell size is sufficient. The expansion coefficient at the GB is similar compared to bulk for 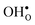 but significantly more negative for
but significantly more negative for 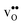 , where the latter can be explained by the removal of short O–O distances when forming the vacancy in the GB core.
, where the latter can be explained by the removal of short O–O distances when forming the vacancy in the GB core.
We now turn to the vibrational properties of the two defects. When 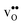 segregate to the GB core there is a redshift in the frequencies associated with Ba and O, while those for Zr are less affected. The redshift stems from that the vacancy formation relieves the system from the compressive strain that follows from the short O–O distances at the GB core. For
segregate to the GB core there is a redshift in the frequencies associated with Ba and O, while those for Zr are less affected. The redshift stems from that the vacancy formation relieves the system from the compressive strain that follows from the short O–O distances at the GB core. For 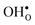 it is the high frequency OH-stretch and bend modes that are affected by the presence of the GB. The corresponding frequencies vary quite substantially at the different sites, even for B1 and B2 where the results for B1 agrees better with the corresponding frequencies in a bulk supercell22 (see Table 2). Largest differences are seen for the stretch mode and the bend mode parallel to the Zr–O–Zr axis, which are denoted ν1 and ν3 in Table 2, respectively. The frequency of the former, which is significantly reduced at the GB, correlates with the distance between the proton and the next nearest neighboring oxygen ion, where a shorter distance weakens the O–H bond and reduce the frequency. The bend mode frequency, on the other hand, is increased at GB and this is due to that the distance to the neighboring Zr ions is reduced. All modes at the three sites (B1, B2 and GB) show local vibrational motion with distinct peaks except for ν3 at B1, which interacts with the oxygen band and becomes dispersed over the frequency range 641–765 cm−1. The zero-point vibrational energies stabilize both
it is the high frequency OH-stretch and bend modes that are affected by the presence of the GB. The corresponding frequencies vary quite substantially at the different sites, even for B1 and B2 where the results for B1 agrees better with the corresponding frequencies in a bulk supercell22 (see Table 2). Largest differences are seen for the stretch mode and the bend mode parallel to the Zr–O–Zr axis, which are denoted ν1 and ν3 in Table 2, respectively. The frequency of the former, which is significantly reduced at the GB, correlates with the distance between the proton and the next nearest neighboring oxygen ion, where a shorter distance weakens the O–H bond and reduce the frequency. The bend mode frequency, on the other hand, is increased at GB and this is due to that the distance to the neighboring Zr ions is reduced. All modes at the three sites (B1, B2 and GB) show local vibrational motion with distinct peaks except for ν3 at B1, which interacts with the oxygen band and becomes dispersed over the frequency range 641–765 cm−1. The zero-point vibrational energies stabilize both 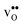 and
and 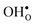 at the GB core by about 0.02 eV. They also stabilize B1 with respect to B2, however, B2 is still more favorable (see Table 2).
at the GB core by about 0.02 eV. They also stabilize B1 with respect to B2, however, B2 is still more favorable (see Table 2).
| Site | Δ seg G def(0) | O(1)–H | O(2)–H | ν 1 | ν 2 | ν 3 |
|---|---|---|---|---|---|---|
| B1 | 0.00 | 0.98 | 2.09 | 3542 | 873 | 641–765 |
| B2 | −0.02 | 0.99 | 1.85 | 3302 | 943 | 963 |
| GB | −0.85 | 1.03 | 1.49 | 2610 | 887 | 1220 |
| Bulk22 | — | 0.98 | 2.10 | 3547 | 869 | 642–759 |
With the phonon spectra, we can now consider entropies and free energies. The formation entropies of 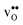 and
and 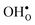 are given by a difference between two systems with different number of vibrational modes and will therefore not approach a temperature independent value at high temperatures.44,45 The formation entropy in the bulk region for
are given by a difference between two systems with different number of vibrational modes and will therefore not approach a temperature independent value at high temperatures.44,45 The formation entropy in the bulk region for 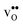 and
and 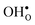 is shown in Fig. 3. For
is shown in Fig. 3. For 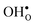 at the B1 site and for
at the B1 site and for 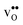 it agrees very well with the bulk supercell counterpart,22 which suggests that the supercell is sufficiently large for the purpose of studying defect segregation. The entropy at B2, on the other hand, is slightly different, which can be explained by the frequencies of the local proton vibrational modes (see Table 2). The largest contribution to the entropy is given by the lowest frequency, which is similar for B1 and the bulk supercell and correspond to the ν3 mode. For B2, however, the frequency of the same mode is increased by about 200 cm−1 and the entropy therefore decreases. The difference in entropy between B1 and B2 affects the relative stability of the two sites and above 300 K the free energy of B1 becomes lower. As all practical applications using acceptor-doped BaZrO3 operate above room temperature B1 will be considered as the bulk reference site from here on. This choice is further motivated by the fact that both the vibrational properties and the chemical expansion for B1 are in better agreement with calculations for bulk supercells (see Tables 1 and 2).
it agrees very well with the bulk supercell counterpart,22 which suggests that the supercell is sufficiently large for the purpose of studying defect segregation. The entropy at B2, on the other hand, is slightly different, which can be explained by the frequencies of the local proton vibrational modes (see Table 2). The largest contribution to the entropy is given by the lowest frequency, which is similar for B1 and the bulk supercell and correspond to the ν3 mode. For B2, however, the frequency of the same mode is increased by about 200 cm−1 and the entropy therefore decreases. The difference in entropy between B1 and B2 affects the relative stability of the two sites and above 300 K the free energy of B1 becomes lower. As all practical applications using acceptor-doped BaZrO3 operate above room temperature B1 will be considered as the bulk reference site from here on. This choice is further motivated by the fact that both the vibrational properties and the chemical expansion for B1 are in better agreement with calculations for bulk supercells (see Tables 1 and 2).
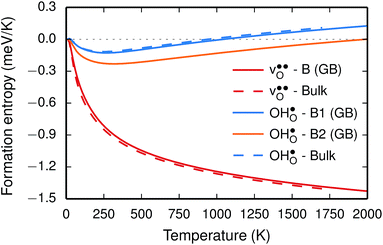 | ||
Fig. 3 Phonon contribution to the formation entropies of the oxygen vacancy 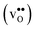 and the proton and the proton 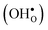 in the bulk region of the GB supercell (solid lines) as well as in a bulk supercell (dashed lines), where data for the latter is taken from ref. 22. in the bulk region of the GB supercell (solid lines) as well as in a bulk supercell (dashed lines), where data for the latter is taken from ref. 22. | ||
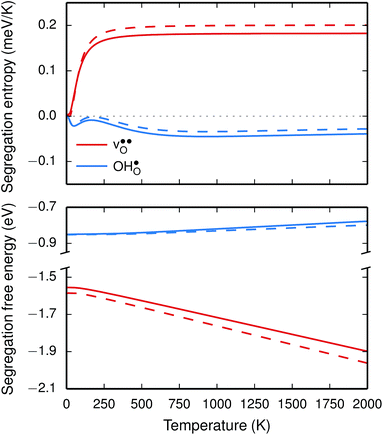
The segregation entropy for 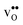 is found to be positive and converges to a value of about 0.2 meV K−1 at around 400 K (Fig. 4). As a result, the free energy decreases with increasing temperature from −1.6 eV at 0 K to about −1.9 eV at 2000 K (Fig. 4). The positive segregation entropy is a result of the aforementioned redshift, where the vibrational motion of the oxygen ions stands for the largest contribution. The proton segregation entropy is found to be negative and becomes fairly constant above 700 K, at a value of about −0.04 meV K−1. This small negative entropy leads to a segregation free energy that increases slightly with temperature and is fairly constant in the regime where protons enter the material. Similarly to the formation entropies, the negative segregation entropy is due to that ν3 is increased at the GB (see Table 2).
is found to be positive and converges to a value of about 0.2 meV K−1 at around 400 K (Fig. 4). As a result, the free energy decreases with increasing temperature from −1.6 eV at 0 K to about −1.9 eV at 2000 K (Fig. 4). The positive segregation entropy is a result of the aforementioned redshift, where the vibrational motion of the oxygen ions stands for the largest contribution. The proton segregation entropy is found to be negative and becomes fairly constant above 700 K, at a value of about −0.04 meV K−1. This small negative entropy leads to a segregation free energy that increases slightly with temperature and is fairly constant in the regime where protons enter the material. Similarly to the formation entropies, the negative segregation entropy is due to that ν3 is increased at the GB (see Table 2).
As outlined previously, the segregation entropy and free energy per defect were calculated with both one and two defects in the supercell, where the latter was considered in order to reduce the number of displacements in the phonon calculations. The difference is found to be quite small (see Fig. 4) and this justifies the choice of considering two defects in the supercell (later to be used for the acceptor dopants) and thereby decreasing the computational cost by a factor of two.
The vibrational contribution to 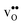 and
and 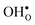 segregation has previously been calculated for the ZrO2-terminated [001] surface in BaZrO3.25 In contrast to the results we present here, the segregation entropies were found to be positive for both defects and the corresponding magnitudes were found to be larger. This surface thus behaves qualitatively different for
segregation has previously been calculated for the ZrO2-terminated [001] surface in BaZrO3.25 In contrast to the results we present here, the segregation entropies were found to be positive for both defects and the corresponding magnitudes were found to be larger. This surface thus behaves qualitatively different for  compared to the GB considered here. Both systems, however, share the property that the magnitude of segregation entropy is less pronounced for
compared to the GB considered here. Both systems, however, share the property that the magnitude of segregation entropy is less pronounced for  than
than  , which indicates that proton segregation is already quite well described at zero Kelvin.
, which indicates that proton segregation is already quite well described at zero Kelvin.
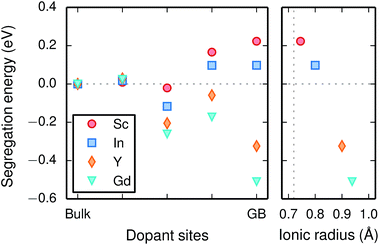
Chemical expansion coefficients have also been determined for the dopants, which are all positive and become larger with increasing ionic radius (see Table 1). The dopants that display positive segregation energies (Sc and In) have slightly larger chemical expansion coefficients in the GB plane compared to bulk while the opposite holds for Y and Gd, but the differences are quite small.
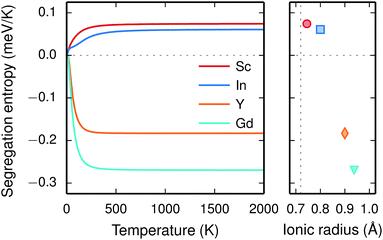
The vibrational properties are also affected by the ionic radius. The phonon contribution to the dopant formation entropies have been calculated both with the dopants situated in the bulk region and at the GB plane and all entropies are found to be positive and to attain a constant value at around room temperature (Fig. 6). For each individual site the magnitude of the entropy increases with the ionic radius and the effect is more prominent at the bulk site with entropies ranging from 0.22 meV K−1 for Sc to 0.85 meV K−1 for Gd. The corresponding interval in the GB plane is 0.30 meV K−1 to 0.60 meV K−1. The major contribution to the formation entropies stems not from the dopant itself but from the vibrational motion of O followed by that of Ba, which both experience a redshift due to the dopant induced distortion. This explains why the dopant ionic radius, which is related to the amount of strain the dopant exerts on its environment, rather than the mass of the dopant correlates with the formation entropies. Furthermore, the smaller spread in the entropies at the GB is due to that the contributions from O and Ba are more similar in this case compared with when the dopants are located in the bulk region. This indicates that the GB is less sensitive to size of the dopant and this is likely due to the GB expansion, which results in less compressive strain upon dopant formation compared with the bulk. One might suspect that the same mechanism is behind the segregation energies, i.e., that the dopant formation energies are more sensitive to the dopant species in the bulk compared to the GB region.
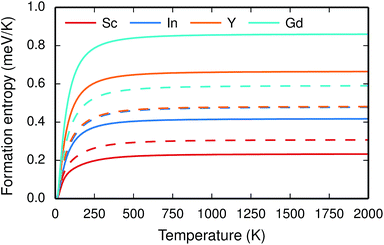 | ||
| Fig. 6 Phonon contribution to the formation entropy at constant pressure of trivalent acceptor dopant ions in the bulk (solid lines) and GB (dashed lines) regions of the GB supercell. | ||
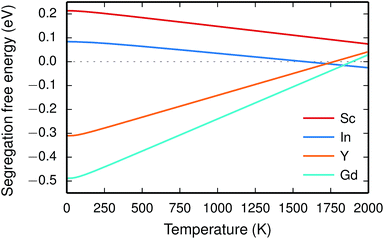
Since the range of formation entropies in the GB plane lies within the corresponding interval in bulk it follows that the formation entropy increases at the GB for Sc and In while it decreases for Y and Gd. This leads to dopant segregation entropies that become positive for Sc and In while negative for Y and Gd (Fig. 7). The segregation entropies display an almost linear correlation with the ionic radius, similar to that of the segregation energies (see Fig. 5). As a consequence of that the segregation energy and entropy depend on the ionic radius in a similar fashion, the two properties compensate each other in the free energy (see Fig. 8). This leads to segregation free energies that are almost zero for all dopants above 1700 K, which is where dopants become mobile. Noticeable dopant segregation should therefore occur only if driven by other defect species.
On a final note, the results presented here strongly suggest that the difference in dopant segregation energies and entropies for the different species is mainly a consequence of differences in the bulk phase rather than in the GB region. Hence, it is reasonable to assume that these properties are less sensitive the choice of GB and the results presented here concerning dopants may therefore transfer to other GBs in acceptor-doped BaZrO3 systems.
3.3 Space-charge modelling
Finally, we assess the defect chemistry of the Σ3 (112)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] GB from the calculated free energies of defect segregation using a space-charge model. The same GB has previously been studied using space-charge modelling in the work by Helgee et al.15 Here, however, we only consider segregation to the site with the lowest energy. Helgee et al.15 considered several sites, also those with less negative segregation energies. The present treatment will therefore reduce the number of available segregation sites.
10] GB from the calculated free energies of defect segregation using a space-charge model. The same GB has previously been studied using space-charge modelling in the work by Helgee et al.15 Here, however, we only consider segregation to the site with the lowest energy. Helgee et al.15 considered several sites, also those with less negative segregation energies. The present treatment will therefore reduce the number of available segregation sites.
For both 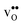 and
and 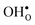 the site with the lowest energy is located in the plane next to the GB plane and there is an equivalent site on the opposite side of the GB plane (see Fig. 1). The formation of an
the site with the lowest energy is located in the plane next to the GB plane and there is an equivalent site on the opposite side of the GB plane (see Fig. 1). The formation of an 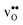 at this site leads to that the oxygen ion on the opposite side relaxes into the GB plane. It is thus very likely that segregation to the second oxygen site becomes considerably less favorable when the first site becomes occupied by a defect. Correspondingly, if an
at this site leads to that the oxygen ion on the opposite side relaxes into the GB plane. It is thus very likely that segregation to the second oxygen site becomes considerably less favorable when the first site becomes occupied by a defect. Correspondingly, if an 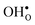 forms at the segregation site the oxygen ion on the opposite side forms an hydrogen bond with the proton and also in this case the segregation to the second site is likely to become less favorable. These two segregation sites are therefore treated as a single site in present space-charge modelling, which was not the case in the study by Helgee et al.15 This leads to a GB core site concentration of 2 per GB unit for both
forms at the segregation site the oxygen ion on the opposite side forms an hydrogen bond with the proton and also in this case the segregation to the second site is likely to become less favorable. These two segregation sites are therefore treated as a single site in present space-charge modelling, which was not the case in the study by Helgee et al.15 This leads to a GB core site concentration of 2 per GB unit for both 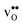 and
and 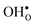 . For the acceptor dopants we only consider the Zr site in the GB plane. For Y and Gd that is the segregation site with lowest energy. Segregation of dopants were not considered by Helgee et al.15
. For the acceptor dopants we only consider the Zr site in the GB plane. For Y and Gd that is the segregation site with lowest energy. Segregation of dopants were not considered by Helgee et al.15
A description of the specific core-space-charge model used here can be found in ref. 25 and 31. The bulk hydration enthalpy and entropy were taken as −0.74 eV and −0.93 meV K−1, respectively,22 and assumed to be temperature independent. In the work of Helgee et al.15 −0.82 eV and −0.92 meV K−1 were used. The relative permittivity was taken as 75 and we considered a wet atmosphere with pH2O = 0.03 atm. The potential and concentration profiles were solved iteratively until global electroneutrality was achieved.
We first consider a fixed dopant concentration of 10 mol% at 1073 K (Fig. 9). At this temperature, the bulk oxide is mostly dehydrated such that 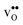 is the dominating positive defect. The GB core becomes positively charged primarily due to segregation of
is the dominating positive defect. The GB core becomes positively charged primarily due to segregation of 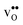 , which almost completely saturates the GB core lattice site. Accounting for the phonon contribution increases the core concentration of
, which almost completely saturates the GB core lattice site. Accounting for the phonon contribution increases the core concentration of 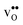 and thus the potential, leading to smaller core concentration of
and thus the potential, leading to smaller core concentration of 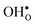 and a more pronounced depletion of
and a more pronounced depletion of 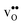 and
and 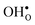 in the space-charge region.
in the space-charge region.
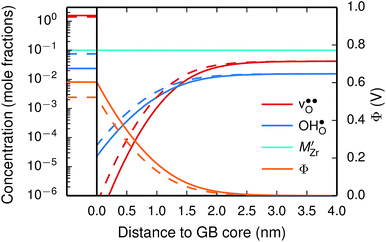 | ||
| Fig. 9 Space-charge profiles at 1073 K calculated both with (solid lines) and without (dashed lines) the vibrational free energy contribution. | ||
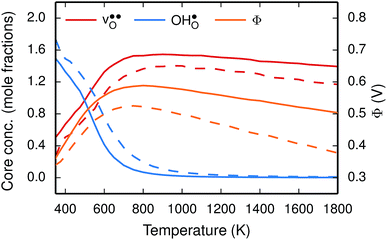
To further elaborate, the GB core concentrations and space-charge potential were calculated for the temperature interval 350–1800 K (Fig. 10). The GB core is dominated by 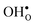 at low temperatures, while
at low temperatures, while 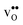 constitutes the vast majority of segregated defects at higher temperatures. Throughout the considered temperature interval, inclusion of the phonon contribution increases the core concentration of
constitutes the vast majority of segregated defects at higher temperatures. Throughout the considered temperature interval, inclusion of the phonon contribution increases the core concentration of 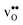 and thereby also the space-charge potential. The effect on
and thereby also the space-charge potential. The effect on 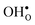 is less pronounced and the core concentration is only noticeably smaller when including phonons at the lowest temperatures within the considered range. The larger entropy of
is less pronounced and the core concentration is only noticeably smaller when including phonons at the lowest temperatures within the considered range. The larger entropy of 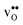 compared to
compared to 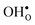 shifts the onset for when the core becomes hydrated to lower temperatures. Furthermore, the reduction in the potential at lower temperatures, which is not observed for the same GB in the work of Helgee et al.,15 is due to that the GB becomes saturated as there are fewer available segregation sites in the present model (see discussion in the beginning of this section). The segregation of
shifts the onset for when the core becomes hydrated to lower temperatures. Furthermore, the reduction in the potential at lower temperatures, which is not observed for the same GB in the work of Helgee et al.,15 is due to that the GB becomes saturated as there are fewer available segregation sites in the present model (see discussion in the beginning of this section). The segregation of 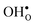 then occurs at the expense of
then occurs at the expense of  and thereby reducing the core charge and the potential. The maximum space-charge potential Φ = 0.59 V is obtained at about 800 K.
and thereby reducing the core charge and the potential. The maximum space-charge potential Φ = 0.59 V is obtained at about 800 K.
The free energy treatment becomes important when considering segregation of the dopants to the GB core, at synthesis temperatures around 1800 K (see Table 3). When excluding the phonon contribution the dopant core concentrations vary considerably (due to the different segregation energies), with Gd almost completely saturating the lattice site while the core concentration of Sc barely is enhanced compared to the bulk concentration. The space-charge potential does not display the same variation, which is due to that the dopant segregation is accompanied by additional segregation of  that compensates the negative charge of the acceptor dopants. By accounting for the phonon contribution, however, the free energies of segregation of the dopants are more similar (Fig. 8) and the dopant dependency on the defect core concentrations diminishes. The potential is slightly higher here due to that phonons stabilize
that compensates the negative charge of the acceptor dopants. By accounting for the phonon contribution, however, the free energies of segregation of the dopants are more similar (Fig. 8) and the dopant dependency on the defect core concentrations diminishes. The potential is slightly higher here due to that phonons stabilize  in the core. Furthermore, since the potential is positive there is in both cases also an accumulation of dopants in the space-charge region next to the GB core.
in the core. Furthermore, since the potential is positive there is in both cases also an accumulation of dopants in the space-charge region next to the GB core.
Due to dopant segregation the space-charge potential is reduced by 0.2 V, from 0.50 V to 0.31 V at 1800 K. This is consistent with the increase of the conductivity seen for the annealed samples in ref. 28; the activation barrier for the GB conductivity is decreased by a about 0.3 eV. Furthermore, our finding that the dopant core concentration is similar for different dopants is also in qualitative agreement with experimental results, where Y and Gd10/Sc28 were found to segregate to the GB core in similar amounts. The actual dopant concentrations obtained here are, however, higher compared to the experimental results, where the dopant concentrations were found to be between 1.2 and 2.8 times larger at the core compared to the bulk.9,10,21,27–29 Larger core concentrations (above 2 times the bulk concentration) were found in samples that were annealed for a longer time at higher temperatures,28,29 which should more closely resemble equilibrium conditions and are thus more comparable to our results.
The overestimation of core concentrations can be related to the neglect of strain interactions since the space-charge model treats defect–defect interactions in a purely electrostatic manner. This should be most prominent for  since the core concentration is almost saturated for this species (see Table 3). Including strain interactions between
since the core concentration is almost saturated for this species (see Table 3). Including strain interactions between 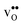 will most likely lead to less negative segregation energies at high concentrations that in turn would limit the overall accumulation of
will most likely lead to less negative segregation energies at high concentrations that in turn would limit the overall accumulation of 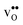 in the core. Consequently, the resulting space-charge potential will be smaller and fewer acceptor dopants will therefore segregate. The influence of vacancy–dopant interactions is probably weaker since they appear both at the GB and in bulk and the effect on the segregation energies would therefore be small. Nevertheless, our results are in general agreement with experimental studies on acceptor-doped BaZrO3, which indicate that dopants accumulate in the GB and space-charge layers.
in the core. Consequently, the resulting space-charge potential will be smaller and fewer acceptor dopants will therefore segregate. The influence of vacancy–dopant interactions is probably weaker since they appear both at the GB and in bulk and the effect on the segregation energies would therefore be small. Nevertheless, our results are in general agreement with experimental studies on acceptor-doped BaZrO3, which indicate that dopants accumulate in the GB and space-charge layers.
4 Conclusions
In this contribution we have determined the thermodynamics of the Σ3 (112)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] GB in BaZrO3 and the free energy of defect segregation to its core from first-principles calculations. The calculations reveal that the GB free energy is 52 meV Å−2 at zero Kelvin. The free energy increase with temperature due to a negative formation entropy and the GB thereby becomes less stable at high temperatures.
10] GB in BaZrO3 and the free energy of defect segregation to its core from first-principles calculations. The calculations reveal that the GB free energy is 52 meV Å−2 at zero Kelvin. The free energy increase with temperature due to a negative formation entropy and the GB thereby becomes less stable at high temperatures.
The GB exhibits 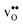 and
and 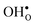 segregation energies of −1.53 and −0.83 eV, respectively, which are in line with previous theoretical studies. By including zero-point contributions both defects are slightly stabilized at the GB core with segregation enthalpies of −1.55 and −0.85 eV. The segregation free energy of
segregation energies of −1.53 and −0.83 eV, respectively, which are in line with previous theoretical studies. By including zero-point contributions both defects are slightly stabilized at the GB core with segregation enthalpies of −1.55 and −0.85 eV. The segregation free energy of 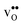 is further reduced when the temperature is increased to a value of about −1.90 eV at 2000 K, while it for
is further reduced when the temperature is increased to a value of about −1.90 eV at 2000 K, while it for 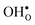 remains more or less unchanged over the same temperature interval. This can be understood from the segregation entropies, which are 0.2 and −0.04 meV K−1 in the high temperature limit for
remains more or less unchanged over the same temperature interval. This can be understood from the segregation entropies, which are 0.2 and −0.04 meV K−1 in the high temperature limit for 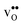 and
and 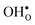 , respectively. The positive segregation entropy of
, respectively. The positive segregation entropy of 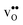 is explained by the significant lattice relaxations it induces in the GB and the following redshift of the phonon spectrum. Space-charge modelling reveals that inclusion of phonons shifts the temperature onset of hydration of the GB core to lower temperatures due to stabilization of
is explained by the significant lattice relaxations it induces in the GB and the following redshift of the phonon spectrum. Space-charge modelling reveals that inclusion of phonons shifts the temperature onset of hydration of the GB core to lower temperatures due to stabilization of 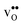 , but also affects the predicted core concentrations and the space-charge potential becomes slightly higher.
, but also affects the predicted core concentrations and the space-charge potential becomes slightly higher.
Furthermore, the considered acceptor dopants (Sc, In, Y and Gd) exhibit segregation energies to the GB plane ranging from 0.22 eV for Sc to −0.51 eV for Gd, where a larger ionic radius yields a more favorable segregation energy. The dopants also exhibit distinctly different segregation entropies, which for Gd and Y are negative while being positive for In and Sc, and these correlate with the ionic radii in the same way as the segregation energies. Hence, at temperatures above 1700 K where dopant are mobile, which correspond to synthesis conditions, their segregation free energies are nearly the same and close to zero. As a consequence, dopants only segregate due to attraction with segregated positively charged defects (in this case 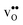 ). In the space-charge modelling this leads to very similar defect core concentrations and space-charge potentials for all dopants, as opposed to when the phonon contribution is not taken into account and the results vary considerably for the different species. The predicted dopant segregation reduces the space-charge potential with about 0.2 V, in line with experimental findings.
). In the space-charge modelling this leads to very similar defect core concentrations and space-charge potentials for all dopants, as opposed to when the phonon contribution is not taken into account and the results vary considerably for the different species. The predicted dopant segregation reduces the space-charge potential with about 0.2 V, in line with experimental findings.
To conclude, this study shows the importance of using free energies in accurate prediction of defect chemistry and space-charge formation in GBs in acceptor-doped BaZrO3. This especially concerns dopant segregation, which becomes important at the high temperatures where the material is being fabricated. The results presented here will thus be of value in the further development of BaZrO3-based materials and devices.
Acknowledgements
A. L. and G. W. acknowledge the Swedish Energy Agency (Project number: 36645-1) for financial support and the Swedish National Infrastructure for Computing (SNIC) for providing computational resources at PDC (Stockholm), C3SE (Gothenburg) and NSC (Linköping). T. S. B. acknowledges the Centre for Materials Science and Nanotechnology and Department of Chemistry, University of Oslo, for financial support, and Uninett Sigma2 for providing computational resources under the project NN4604k.References
- M. Marrony, Proton-Conducting Ceramics: From Fundamentals to Applied Research, Pan Stanford, 2015 Search PubMed.
- K. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- Y. Yamazaki, R. Hernandez-Sanchez and S. M. Haile, Chem. Mater., 2009, 21, 2755–2762 CrossRef CAS.
- E. Fabbri, L. Bi, D. Pergolesi and E. Traversa, Adv. Mater., 2012, 24, 195–208 CrossRef CAS PubMed.
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326 CrossRef CAS PubMed.
- E. Vasileiou, V. Kyriakou, I. Garagounis, A. Vourros, A. Manerbino, W. G. Coors and M. Stoukides, Top. Catal., 2015, 58, 1193–1201 CrossRef CAS.
- V. Kyriakou, I. Garagounis, A. Vourros, E. Vasileiou, A. Manerbino, W. G. Coors and M. Stoukides, Appl. Catal., B, 2016, 186, 1–9 CrossRef CAS.
- S. H. Morejudo, R. Zanón, S. Escolástico, I. Yuste-Tirados, H. Malerød-Fjeld, P. K. Vestre, W. G. Coors, A. Martínez, T. Norby, J. M. Serra and C. Kjølseth, Science, 2016, 353, 563–566 CrossRef CAS PubMed.
- C. Kjølseth, H. Fjeld, Ø. Prytz, P. I. Dahl, C. Estournès, R. Haugsrud and T. Norby, Solid State Ionics, 2010, 181, 268–275 CrossRef.
- F. Iguchi, N. Sata and H. Yugami, J. Mater. Chem., 2010, 20, 6265 RSC.
- C.-T. Chen, C. E. Danel and S. Kim, J. Mater. Chem., 2011, 21, 5435–5442 RSC.
- B. J. Nyman, E. E. Helgee and G. Wahnström, Appl. Phys. Lett., 2012, 100, 061903 CrossRef.
- J. M. Polfus, K. Toyoura, F. Oba, I. Tanaka and R. Haugsrud, Phys. Chem. Chem. Phys., 2012, 14, 12339–12346 RSC.
- A. Lindman, E. E. Helgee, B. J. Nyman and G. Wahnström, Solid State Ionics, 2013, 230, 27–31 CrossRef CAS.
- E. E. Helgee, A. Lindman and G. Wahnström, Fuel Cells, 2013, 13, 19–28 CrossRef CAS.
- A. Lindman, E. E. Helgee and G. Wahnström, Solid State Ionics, 2013, 252, 121–125 CrossRef CAS.
- J.-H. Yang, D.-H. Kim, B.-K. Kim and Y.-C. Kim, Solid State Ionics, 2013, 252, 126–131 CrossRef CAS.
- J.-S. Kim, J.-H. Yang, B.-K. Kim and Y.-C. Kim, J. Ceram. Soc. Jpn., 2015, 123, 245–249 CrossRef CAS.
- J.-H. Yang, B.-K. Kim and Y.-C. Kim, Solid State Ionics, 2015, 279, 60–65 CrossRef CAS.
- J.-S. Kim and Y.-C. Kim, J. Korean Ceram. Soc., 2016, 53, 301–305 CrossRef CAS.
- D. R. Clark, H. Zhu, D. R. Diercks, S. Ricote, R. J. Kee, A. Almansoori, B. P. Gorman and R. P. O'Hayre, Nano Lett., 2016, 16, 6924–6930 CrossRef CAS PubMed.
- T. S. Bjørheim, E. A. Kotomin and J. Maier, J. Mater. Chem. A, 2015, 3, 7639–7648 Search PubMed.
- T. S. Bjørheim, M. Arrigoni, D. Gryaznov, E. Kotomin and J. Maier, Phys. Chem. Chem. Phys., 2015, 17, 20765–20774 RSC.
- T. S. Bjørheim, A. Løken and R. Haugsrud, J. Mater. Chem. A, 2016, 4, 5917–5924 Search PubMed.
- T. S. Bjørheim, M. Arrigoni, S. W. Saeed, E. Kotomin and J. Maier, Chem. Mater., 2016, 28, 1363–1368 CrossRef.
- M. Arrigoni, T. S. Bjørheim, E. Kotomin and J. Maier, Phys. Chem. Chem. Phys., 2016, 18, 9902–9908 RSC.
- B. Groß, C. Beck, F. Meyer, T. Krajewski, R. Hempelmann and H. Altgeld, Solid State Ionics, 2001, 145, 325–331 CrossRef.
- M. Shirpour, B. Rahmati, W. Sigle, P. A. van Aken, R. Merkle and J. Maier, J. Phys. Chem. C, 2012, 116, 2453–2461 CAS.
- M. Shirpour, G. Gregori, L. Houben, R. Merkle and J. Maier, Solid State Ionics, 2014, 262, 860–864 CrossRef CAS.
- T. Tauer, R. O'Hayre and J. W. Medlin, J. Mater. Chem. A, 2013, 1, 2840–2846 CAS.
- J. M. Polfus, T. S. Bjørheim, T. Norby and R. Bredesen, J. Mater. Chem. A, 2016, 4, 7437–7444 CAS.
- J. M. Polfus, T. Norby and R. Bredesen, Solid State Ionics, 2016, 297, 77–81 CrossRef CAS.
- K. J. Dudeck, N. A. Benedek, M. W. Finnis and D. J. H. Cockayne, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 134109 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- E. Jedvik, A. Lindman, M. T. Benediktsson and G. Wahnström, Solid State Ionics, 2015, 275, 2–8 CrossRef CAS.
- P. G. Sundell, M. E. Björketun and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104112 CrossRef.
- M. E. Björketun, P. G. Sundell and G. Wahnström, Faraday Discuss., 2007, 134, 247 RSC.
| This journal is © The Royal Society of Chemistry 2017 |