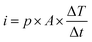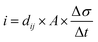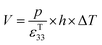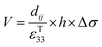Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multiscale-structuring of polyvinylidene fluoride for energy harvesting: the impact of molecular-, micro- and macro-structure
Chaoying
Wan
*a and
Christopher Rhys
Bowen
 *b
*b
aInternational Institute for Nanocomposites Manufacturing, WMG, University of Warwick, CV4 7AL, UK. E-mail: chaoying.wan@warwick.ac.uk
bMaterials and Structures Centre, Department of Mechanical Engineering, University of Bath, BA2 7AY, UK. E-mail: c.r.bowen@bath.ac.uk
First published on 6th January 2017
Abstract
Energy harvesting exploits ambient sources of energy such as mechanical loads, vibrations, human motion, waste heat, light or chemical sources and converts them into useful electrical energy. The applications for energy harvesting include low power electronics or wireless sensing at relatively lower power levels (nW to mW) with an aim to reduce a reliance on batteries or electrical power via cables and realise fully autonomous and self-powered systems. This review focuses on flexible energy harvesting system based on polyvinylidene fluoride based polymers, with an emphasis on manipulating and optimising the properties and performance of the polymeric materials and related nanocomposites through structuring the material at multiple scales. Ferroelectric properties are described and the potential of using the polarisation of the materials for vibration and thermal harvesting using piezo- and pyro-electric effects are explained. Approaches to tailor the ferroelectric, piezoelectric and pyroelectric properties of polymer materials are explored in detail; these include the influence of polymer processing conditions, heat treatment, nanoconfinement, blending, forming nanocomposites and electrospinning. Finally, examples of flexible harvesting devices that utilise the optimised ferroelectric polymer or nanocomposite systems are described and potential applications and future directions of research explored.
1. Introduction
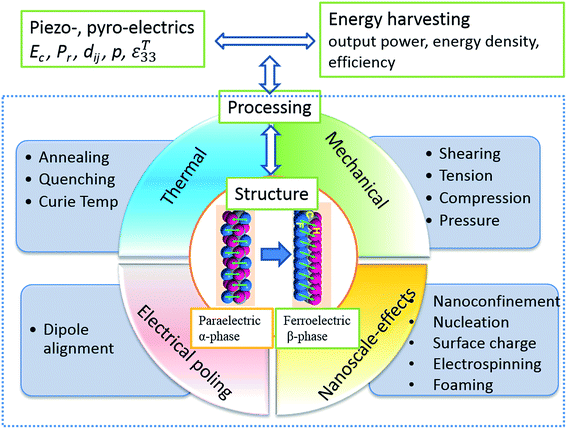
Energy harvesting is a topic of intense interest where ambient sources of energy are harvested and converted into useful electrical energy. The concept of harvesting energy covers applications that produce relatively small levels of power (nW to mW) from mechanical loads, vibrations, human motion, waste heat, light or chemical sources. The power generated by the harvesting material or device is used for applications such as low power electronics, lighting or wireless sensor systems. The ability to use energy harvesting to produce autonomous self-powered systems is of interest to reduce reliance on power cables or batteries that require regular replacement or recharging; there are also environmental benefits from reduced battery usage.Piezoelectric and pyroelectric materials are particularly attractive for a variety of energy harvesting applications. This includes the potential to convert mechanical vibrations into electrical energy via the direct piezoelectric effect and the conversion of thermal fluctuations into electrical energy via the pyroelectric effect. Since both properties are often present simultaneously, it provides a potential route to harvest energy from multiple sources so that the design of hybrid systems is possible.
A number of excellent reviews have been published in the area of piezoelectric and pyroelectric energy harvesting, which concentrate on nano-scale materials and devices, including ‘nanogenerators’,1–10 and surveys of the various potential devices.11–16 Li et al. recently presented a review on ferroelectric polymers for energy, including storage applications17 and Fan et al. reviewed flexible nanogenerators for harvesting and self-powered electronics.18 Prateek et al.19 have overviewed recent progress on ferroelectric polymer based nanocomposite for energy storage and capacitor applications. The emphasis of this review is to describe mechanically flexible systems based on polyvinylidene fluoride (PVDF) polymers for energy harvesting, with an emphasis on manipulating the properties and energy harvesting performance of ferroelectric polymers and polymer nanocomposites through structuring the materials at multiple scales. This includes effort to tailor the ferroelectric, piezoelectric and pyroelectric properties of polymer materials by manipulating the polymer processing conditions, heat treatment, nano-confinement, blending, forming nanocomposites, electrospinning and creating porous structures. PVDF is chosen in this review as it the most commonly used piezoelectric polymer due to its high piezoelectric coefficient compared with other bulk polymers. A comparison with other piezoelectric materials will be undertaken later in Table 1 and a detailed comparison of the range of piezoelectric polymers has been undertaken by Ramadan et al.20
| Polymer | Relative permittivity (εr) (frequency measurement) | d ij (pC N−1) | Electro-mechanical coupling (k33) |
|---|---|---|---|
| PVDF | 6–12 (ref. 33) | d 31 = 8–22 (ref. 31) | 0.20 (ref. 35) |
| d 33 = −24 to −34 (ref. 34) | |||
| P(VDF-co-TrFE) | 18 (ref. 36) | d 31 = 12 (ref. 32) to 25 (ref. 37) | 0.29 (ref. 35) |
| d 33 = −25 to 40 (ref. 37 and 38) | |||
| P(VDF-co-HFP) | 11 (ref. 39) | d 31 = 30 (ref. 40) | 0.36 (ref. 39) |
| d 33 = −24 (ref. 41) | |||
| P(VDF-co-CTFE) | 13 (ref. 42) | d 33 = −140 (ref. 43) | 0.36 (ref. 44) |
| P(VDF-TrFE-CFE) | 65 (ref. 45) | — | — |
| Polyurethane | 6.8 (ref. 46) | — | — |
| Polyamide 11 | 5 (ref. 47) | d 33 = 4 (ref. 47) | — |
| Polyimide | — | d 33 = 2.5–16.5 (ref. 20) | — |
| Poly-L-lactide | 3–4 (ref. 48) | d 14 = −9.82 (ref. 49) | — |
| Polyhydroxybutyrate | 2–3.5 (ref. 50) | d 33 = 1.6–2.0 (ref. 51) | — |
| Liquid crystal elastomers | — | d 33 = −70 (ref. 52) | — |
| Parylene-C | — | d 33 = 0.1–2 (ref. 20) | — |
| ZnO | — | d 33 = 12.4 (ref. 53) | 0.48 (ref. 54) |
| PZT | 500 (ref. 22) | d 33 = 225–590 (ref. 55) | 0.7 (ref. 22) |
| BaTiO3 | 1200 (ref. 22) | d 33 = 191 (ref. 56) | 0.49 (ref. 57) |
Before discussing the properties of ferroelectric PVDF-based polymers it is first of interest to introduce the mechanisms of harvesting via the piezoelectric and pyroelectric effects so that the important properties for energy harvesting can be identified.
1.1 Piezoelectric and ferroelectric materials
Piezoelectric materials undergo a change in electrical polarisation when a mechanical stress is applied and this is termed the direct piezoelectric effect. This effect can create an electrical current in an external circuit and can therefore be exploited as an electromechanical generator to harvest energy. Piezoelectric materials also undergo a mechanical strain when subjected to an electric field, this is termed the converse piezoelectric effect and is more relevant to actuator, acoustic emitter and vibration damping applications and will not discussed here.The phenomenon of piezoelectricity is best introduced by considering a crystalline solid and its distribution of ions within an individual unit cell. The most common case is when the centres of the positive and negative charges are non-centrosymmetric within the unit cell planes when no pressure is applied; this is the case in ceramics such as barium titanate (BaTiO3), lead zirconate titanate (PZT), aluminium nitride (AlN) and zinc oxide (ZnO). Of the 32 crystallographic classes that depend on the geometry and symmetry of the unit cell, 21 are non-centrosymmetric and all but one (due to other symmetry elements) exhibit piezoelectricity. It is the lack of symmetry in the distributions of ions in these crystalline materials that lead to the presence of an electrical dipole that leads to the piezoelectric response. Due to the lack of symmetry, piezoelectric materials for energy harvesting possess a well-defined polar axis and the application of stress relative to this polar axis is of importance for energy harvesting applications; the polar axis is often termed the 3-direction or z-direction.
Ferroelectrics are a subgroup of piezoelectric materials, and are characterised by a spontaneous polarisation in the unstrained state and the capability to re-orientate the polarisation direction via an applied electric field. The BaTiO3 and the PZT family of ceramic materials are commonly used ferroelectric ceramics due to their good piezoelectric properties. The subject of this review is ferroelectric polymers, such as polyvinylidene fluoride (PVDF) and its copolymers. Example copolymers include polyvinylidene-difluoride trifluoro-ethane, P(VDF-co-TrFE), and we will see later that these are crystalline polymers with aligned molecular chains where the polarity is due to the alignment of polarised covalent bonds. The temperature limits of a ferroelectric are determined by the Curie temperature (Tc) and when BaTiO3 is heated above Tc its crystal structure is cubic and since the unit cell is symmetrical there is no polarisation and the material in no longer ferroelectric. Below the Tc the unit cell is tetragonal and non-centrosymmetric, thereby leading to ferroelectric properties. A similar behaviour is observed in PVDF based materials where the ferroelectric β-phase converts to the paraelectric α-phase when the material is heated above Tc.
While a ferroelectric contains many individual unit cells with a corresponding electrical dipole, there are regions where the unit cells have equal polarisation directions, these are known as domains. When a ferroelectric is cooled below the Tc there is no net polarisation as the domains are effectively randomly distributed through the volume of the material. For the material to exhibit piezoelectricity the randomly orientated electrical dipoles are aligned in a common direction to achieve a net polarisation in a process called ‘poling’. The process of electrical alignment, or ‘poling’, is essential in converting an inactive ferroelectric polymer into a useful electromechanically active material. Poling involves the application of an electric field, often at elevated temperatures, to orientate the polar axis of the domains to those directions allowed by the crystal symmetry, which are nearest to that of the applied electric field. To further facilitate the poling process ferroelectric polymers often require mechanical stretching to enhance the alignment of the molecular chains and these factors will be discussed later in the review.
Fig. 1 shows a simple schematic of the poling process and the material initially consists of randomly orientated domains (Fig. 1a). The material is then heated to an elevated temperature below Tc, and an electric field is applied to orientate the domains (Fig. 1b). The material is then cooled to ambient temperature while the electric field remains applied. On removal of the electric field at ambient temperature, although some domains may change configuration (Fig. 1c), the material retains a net polarisation producing a poled ferroelectric with piezoelectric behaviour. Once poled, the material has a polar axis (the z- or 3-direction), which for the case in Fig. 1a–c is through the thickness of the material. The material is now piezoelectric and will exhibit the direct and converse piezoelectric effects.
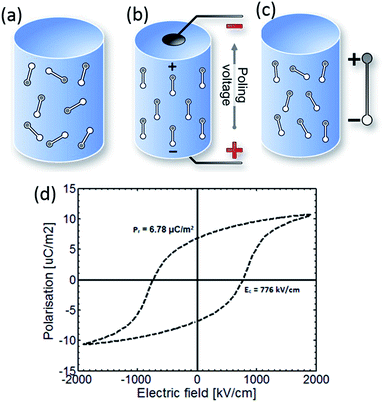 | ||
| Fig. 1 Poling of a ferroelectric. (a) The material initially has a random arrangement of domains. (b) Application of an electric field at elevated temperature aligns domains with the field. (c) Once cooled to room temperature the field is removed and a remnant polarisation and strain is observed. The poled material is piezoelectric. (d) Polarisation–electric field (P–Ef) loop of PVDF.21 | ||
A polarisation–electric field (P–Ef) loop of PVDF is shown in Fig. 1d. At point 1 the material has no net polarisation, as the dipoles are randomly orientated (as in Fig. 1a). However, as the electric field is applied the dipoles align with the applied electric field to produce a polarisation at point 2 (as in Fig. 1b). Once the electric field is removed, the PVDF has a remanent polarisation (Pr), where the material is similar to Fig. 1c and the material is piezoelectric. Clearly a high Pr is of interest to achieve a high piezoelectric activity for harvesting applications. If an electric field is applied in the opposite direction the polarisation can be returned to zero (point 4) and the polarisation direction can be reversed; which is defined as the coercive field (Ec).
1.2 Direct piezoelectric effect for energy harvesting
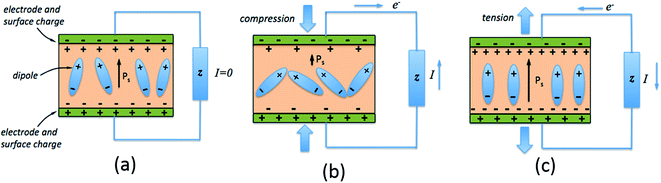
The direct piezoelectric effect, where a force leads to the production of an electrical charge, can be used for energy harvesting. The presence of a polarisation with aligned dipoles and domains leads to the presence of a charge at each surface of the material and free charges, such as ions or electrons, are attracted to the charged surfaces of the material. This is shown schematically in Fig. 2a where the polarisation of the material is observed along with its bound surface charge. No current will flow under this stress-free condition if an electrical load it connected across the surfaces. The origin of the direct piezoelectric effect stems from the behaviour of the surface charge as the material is subjected to a stress that changes the polarisation level. If the application of a compressive stress leads to a decrease in the polarisation of the material, as in Fig. 2b, the free charges at the surface generate a current across an electrical load applied to the material. In Fig. 2c the application of a tensile load in the opposite direction increases the polarisation level and current flows in the opposite direction to balance the surface charge. If an alternating stress in applied to the piezoelectric the piezoelectric will generate an AC current through the load impedance.The charge (Q) generated across the opposite faces of a piezoelectric material of area (A) when a mechanical stress (Δσ) is applied between the faces is given by eqn (1).22
| Q = d33 × A × Δσ | (1) |
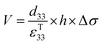 | (2) |
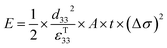 | (3) |
Therefore, for a given area and thickness the energy from an applied stress can be maximised by selecting materials with a high 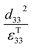 ; this is termed a harvesting figure of merit (FoM) to assess the performance of a material for vibration harvesting off-resonance. Under short circuit conditions, where the load impedance is zero, a current (I) will be generated and since
; this is termed a harvesting figure of merit (FoM) to assess the performance of a material for vibration harvesting off-resonance. Under short circuit conditions, where the load impedance is zero, a current (I) will be generated and since 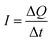 , from eqn (1) we arrive at eqn (4).
, from eqn (1) we arrive at eqn (4).
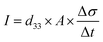 | (4) |
Measurements at both open circuit and closed circuit are commonly made in energy harvesting applications, although it should be noted at these conditions there is effectively no power since at open circuit conditions there is no current and at closed circuit conditions the potential difference is zero.
1.3 Pyroelectric effect for energy harvesting
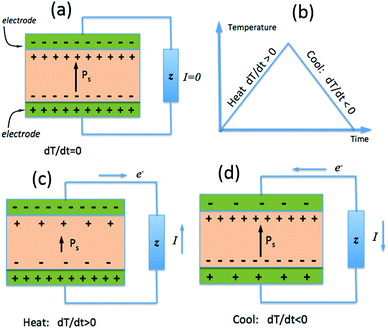
While the piezoelectric effect is the generation of charge with applied stress, the pyroelectric effect is the generation of charge with a temperature change. As with piezoelectric materials, pyroelectrics are polar materials and exhibit a spontaneous polarization in the absence of an applied electric field23 and in ferroelectric polymers the polarisation is a consequence of the alignment of polarised covalent bonds.24 As described in Section 1.2, the polarisation leads to the presence of bound charge on each surface of the material, as in Fig. 3a, and the origin of pyroelectric behaviour stems from the change in polarisation level with material temperature.23If a pyroelectric is heated (dT/dt > 0), as in Fig. 3b, there is a decrease in its polarisation as dipoles within the material lose their orientation due to thermal vibrations. This fall in the polarisation leads to a decrease in the number of free charges bound to the material surface;23 see Fig. 3c. If the material is under an open circuit condition the free charges remain at the electrode surface and an electric potential is generated across the material.25 If the material is under short circuit conditions an electric current flows between the two polar surfaces of the material. If the pyroelectric is then cooled (dT/dt < 0), as in Fig. 3b, the dipoles regain their orientation leading to an increase in the level of spontaneous polarization, thus reversing the electric current flow under short circuit conditions as free charges are now attracted to the polar surfaces; see Fig. 3d.
Eqn (5) defines the relationship between the developed pyroelectric charge (Q) due to a change in temperature (ΔT) for a material of surface area (A) with a pyroelectric coefficient (p).26
| Q = p × A × ΔT | (5) |
Since current is dQ/dt, eqn (6) provides the short circuit pyroelectric current (ip) as a function of the rate of temperature change (dT/dt)27 with electrodes orientated normal to the polar direction.
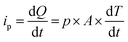 | (6) |
The pyroelectric coefficient of an unclamped material, under a constant stress and electric field, is defined by eqn (7),
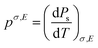 | (7) |
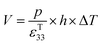 | (8) |
Under open circuit conditions the material behaves as a capacitor and the energy stored in the pyroelectric is 1/2CV2, such that the energy (E) generated from a change in temperature is given by eqn (9).
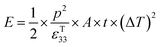 | (9) |
Therefore, for a given area and thickness the energy for a temperature change can be maximised by maximising selecting a materials with a high 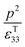 ; which is a figure of merit to asses the performance of a material for pyroelectric harvesting. This figure of merit has similarities with the vibration figure of merit
; which is a figure of merit to asses the performance of a material for pyroelectric harvesting. This figure of merit has similarities with the vibration figure of merit 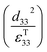 which is not surprising given the similarity in the charge generation for both mechanisms result from a change in polarisation of the material as a result of stress, dij = dPs/dσ (C N−1 or C m−2/N m−2), and temperature, p = dPs/dT (C m−2 K−1).
which is not surprising given the similarity in the charge generation for both mechanisms result from a change in polarisation of the material as a result of stress, dij = dPs/dσ (C N−1 or C m−2/N m−2), and temperature, p = dPs/dT (C m−2 K−1).
Since there is a requirement for a pyroelectric material to be polar and exhibit a level of polarisation all pyroelectric materials are piezoelectric (pyroelectrics are a sub-class of piezoelectric materials so that all pyroelectrics are also piezoelectric). In ferroelectric pyroelectric materials, such as PVDF, the orientation, and sign, of the spontaneous polarisation can be switched by reversing the direction of the applied electric field. These ferroelectrics are a sub-class of pyroelectric materials so that all ferroelectrics are both pyroelectric and piezoelectric.
Clearly for energy harvesting applications the figures of merit indicate that there is a need for high piezoelectric activity to maximise the piezoelectric coefficients (such as d33 and d31) and high pyroelectric coefficients (p); this also relates to a need for a high remnant polarisation (Pr) after the poling process. Since the origins of the piezoelectric and pyroelectric effect originate from an electrical dipole from the polymer molecule there is a need to maximise the fraction of the non-symmetrical phase of the polymer and ensure it can be easily poled. The figures or merit also indicate a low relative permittivity is beneficial for harvesting, although a large electrical dipole or ease of polarisation often leads to a high permittivity so that the optimum choice of material based on a combination of d33, d31, p and εT33 can be complex. Other factors include the Curie temperature (Tc) since it indicates the temperature at which the polymer transforms from a ferroelectric to paraelectric phase and indicates the temperature at which piezoelectric/pyroelectric properties are lost. The ferroelectric phase of polymers such as PVDF and its copolymers will now be discussed in more detail.
2. Piezo- and pyro-electric polymers
We have seen that ferroelectric and piezoelectric materials can be ceramic or polymeric. Electroactive polymers have obvious advantages over ceramics in specific applications in terms of their ease of processing at low-temperatures, low density, low stiffness, flexibility and mechanical robustness, such as toughness and high strains to failure. There are also benefits in terms of biocompatibility for implantable harvesters and sensors.30 Polymer based piezoelectrics have found diverse applications in smart and multifunctional systems which include transducers, sensors, actuators, energy harvesting and storage devices, in the form of fibres, foams, thin films, textiles and coatings. Ferroelectric polymers that contain net molecular dipole moments in their macromolecular structure are of interest for energy harvesting and storage due to their high levels of polarisation. The molecular dipoles in these materials can be spontaneously polarised and oriented by the application of an electric field, temperature variation, mechanical stretching, and via interactions with nanoparticles;31 thereby leading to piezo-and pyro-electric response of the polymers. Polarised and electroactive polymers of interest include vinylidene fluoride (VDF)-based fluoropolymers, odd-numbered nylon, poly-L-lactide, polyurethane, and liquid crystal elastomers. The electroactive performance is highly dependent on their macromolecular structure which includes aspects of their crystalline structure, chain conformation, dipole orientation in crystalline regions towards the applied poling field,31,32 processing conditions and post-treatment methods.Compared to ferroelectric ceramics, electroactive polymers tend to have a lower permittivity and lower piezoelectric coefficients. Table 1 shows typical properties of electroactive polymers along with common piezoelectric ceramics. Due to their relatively low piezoelectric activity, significant effort has been undertaken to enhance the piezoelectric coefficients of polymers and tailor the permittivity, and the approaches used to improve the electrical properties include modifying the molecular structure, forming composites, controlling processing conditions and post-treatment methods such as mechanical stretching and electrical poling. In this review we will discuss the latest research progress and strategies employed to enhance the piezo- and pyro-electric properties of electroactive polymers and composites, in particular PVDF and its copolymers due to their high piezoelectric coefficient and ease of fabrication, with a particular emphasis on energy harvesting applications.
2.1 Structure of polyvinylidene fluoride (PVDF) and polymorphs
PVDF is a thermoplastic semi-crystalline polymer and is an important ferroelectric polymer due to its unique molecular structure and variety of crystalline forms. Table 1 indicates PVDF is a polymer with high piezoelectric coefficients compared to other polymers and the origins of the negative piezoelectric coefficients of PVDF in Table 1 has recently been reported by Katsouras et al.58 The PVDF homopolymer contains 59.4 wt% fluorine and 3 wt% hydrogen.31 The presence of fluorine atoms with a large van der Waals radius (1.35 Å, versus hydrogen 1.2 Å) and electronegativity in the polymer chain [–CH2–CF2–] induces a dipole moment perpendicular to the chain in each monomer unit.32,59 PVDF has approximately 50% crystallinity, and exhibits five different polymorphs: α (phase II), β (phase I), γ (phase III), δ and ε, which are related to the molecular chain conformations. Fig. 4a shows the α, β and γ phases.42 The α-crystal phase is hexagonal, with aligned polymer chains anti-parallel to each other, in the conformation of trans–gauche–trans–gauche′ (TGTG′).42 The polar β-crystal is orthorhombic and has an all-trans planar zigzag conformation with their dipoles parallel to the b-axis, and contribute to the highest dipolar moment per unit cell (8 × 10−30 C m).60 The phase transition from the ferroelectric β-phase to the paraelectric α-phase is defined as the Curie transition, which is a process that is highly dependent on the polymer chain structure, processing condition and post-treatment. Achieving a higher β-phase fraction in PVDF leads to higher piezo-, pyro- and ferroelectric properties.31,32,34 The polar γ- and δ-phase have the conformation of TTTTGTTTG′ and TGTG′, respectively, which are also responsible for the piezo- and pyro-electric properties of PVDF, together with the β-phase.31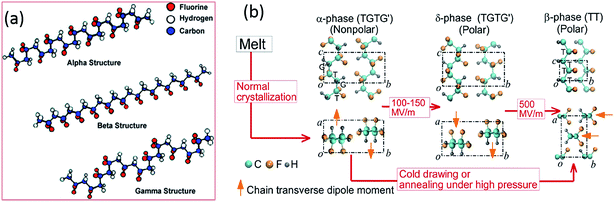 | ||
| Fig. 4 Diagrams of (a) the three α, β and γ primary polymorphic crystalline phases of PVDF. Reprinted with permission.42 Copyright 2009 American Chemical Society. (b) Electric field-induced phase transitions of PVDF. The transverse dipole moment of each polymer chain is shown using an orange arrow that points from the negatively charged fluorine atoms to the positively charged hydrogen atoms. T-trans; G-gauche.61 | ||
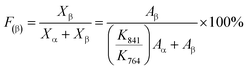 | (10) |
The polymorph can be also identified by XRD. The characteristic peaks at 2θ = 17.6°, 18.3°, 19.9°, and 26.5° correspond to the (100), (020), (110), and (021) reflections of the α-phase of PVDF. The (200) and (110) reflections of the β-phase and (021) reflection of the γ-phase overlap at 2θ = 20.4°.32,59
Differential scanning calorimetry (DSC) is often used to study the Curie transition and crystallisation behaviour of polymers during a change from the ferroelectric β-phase to the paraelectric α-phase. Measurements are generally conducted in the temperature range of 0 to 220 °C for PVDF and its copolymers, to understand the relationship of heat flow and temperature during non-isothermal and isothermal crystallisation processes. A value of 104.6 J g−1 was used as the heat of fusion of the perfect crystalline α-phase of PVDF.63 The efficiency of nucleation agents can be evaluated using eqn (11);64
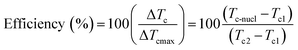 | (11) |
The melting temperature and crystalline temperature of polymers are dependent on the molecular structure, molecular weight and any annealing process. The surface morphology, chain alignment and dipole orientation, ferroelectric properties have been characterised by FTIR-grazing incident reflection absorption spectroscopy, grazing incident wide angle X-ray diffraction,65 atomic force microscopy, small-angle neutron scattering,66 dynamic contact electrostatic force microscopy, and polarization–electric field hysteresis measurements.67 Measurements of the ferroelectric and piezoelectric properties can be undertaken by polarisation–electric field measurements, piezo-response force microscopy and second harmonic generation microscopy.
The crystalline structure of PVDF has been studied during a micro-injection process and in the presence of polar additives.74 In contrast to crystallisation in the static state, the application of high stress during micro-injection promotes the formation of β-phase. The presence of polar additives also aids in the stabilization of the metastable TT conformation (as shown in Fig. 4b) via an interaction between the polar groups and the ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) CF2 groups of PVDF, which benefits the formation of β-PVDF. As a result, PVDF micro-components with rich β-phases have been injection-moulded under the combined effects of an externally applied force and polar group interaction.
CF2 groups of PVDF, which benefits the formation of β-PVDF. As a result, PVDF micro-components with rich β-phases have been injection-moulded under the combined effects of an externally applied force and polar group interaction.
The α to β transformation is highly dependent on the stretching rate and temperature. By stretching PVDF blown films biaxially or uniaxially,75 a high 86.5% content of highly oriented β-phase was achieved during drawing at 87 °C, with a drawing rate of 50 mm min−1 and a stretch ratio of 6.5. At this stretch ratio, a high d33 piezoelectric coefficient of 33 pC N−1 was obtained. Other studies have shown that the β-phase is more favourably formed in the temperature range of 70–100 °C and at a stretch ratio of 3–5.76 Higher stretching temperatures reduce the efficiency of the phase conversion to β-phase and the conversion into β-phase only takes place for stretch ratios above 5. It has also been shown that annealing of the PVDF thin films at 90 °C transforms the γ-phase to the β-phase and this is reflected in a decrease of the relative permittivity.77
Recently, nanofabrication technologies such as electrospinning, nanoimprint lithography78 and the horizontal Langmuir–Schaefer technique79 have attracted attention to produce non-volatile memory and flexible piezoelectric sensors. In particular, electrospinning can produce a high β-phase content in PVDF nanofibers via a one-step process that avoids additional processing stages such as mechanical stretching or electrical poling; this process will be described later in Section 2.2.8. In the following sections, the latest progress in understanding the effects of co-polymerisation, processing condition, post-treatment, addition of nanoparticles and electrospinning on the piezo- and pyro-electric properties of PVDF and its copolymers are discussed. Harvesting devices exploiting these optimised properties are then described.
2.2 Approaches to enhancing β-phase formation
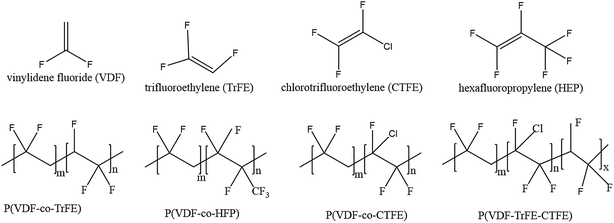 | ||
| Fig. 5 Schematic representation of the molecular structure of VDF, co-monomers and four types of copolymers. | ||
The introduction of a bulky co-monomer to PVDF chains generally facilitates the formation of ferroelectric β-phase due to a steric hindrance effect.80 For example, for P(VDF-co-TrFE) in Fig. 5a the introduction of a third fluoride atom in the TrFE [–CHF–CF2–] co-monomer unit forces the polymer chains to align in an extended planar zigzag all-trans conformation below Tc when the TrFE content is over 11 mol%.81 When the TrFE is above 20 mol%, the formation of β-phase is independent of the processing conditions and electric poling.82 For P(VDF-co-HFP), shown in Fig. 5b, the presence of bulky –CF3 groups in the PVDF chains provides more space to allow dipoles to re-orient. With a HFP content of 5 mol%, a high value of remnant polarization (Pr ∼ 80 mC m−2) was achieved for solvent cast films, resulting in a high d31 piezoelectric coefficient of 30 pC N−1.83 In the case of the P(VDF-co-CTFE) copolymer, Fig. 5c, a CTFE content lower than 16 mol% (ref. 42) led to a d33 piezoelectric coefficient as high as 140 pC N−1.43 Therefore, the advantages of PVDF copolymers over PVDF is that the β-phase is always present regardless of processing methods, which can be attributed to the steric hindrance of the co-monomer that expands the inter-chain distance and reduces the activation energy for the α to β phase transition.32,84 Additional annealing, mechanical stretching or electrical poling processes can be used to increase the degree of crystallinity and further align the CF2 dipoles, which leads to higher piezo- and pyro-electric properties than PVDF homopolymers. By introducing a chloro-containing third monomer termonomer, such as chlorotrifluoroethylene (CTFE), to P(VDF-co-TrFE) copolymers, as in Fig. 5d, some of the ferroelectric β-phase transforms to the γ-phase when the ter-monomer units reach 7 mol%.85 As a result, the Tc of the mixed ferroelectric phase polymer was reduced to almost ambient temperature and exhibits a high relative permittivity (ε′ > 70), a slim polarization hysteresis and ferroelectric relaxor behaviour.
For ter-polymers, such as poly(VDF-TrFE-TFP), the ter-monomer 3,3,3-trifluoropropene (TFP) with a bulky side group leads to –CF3 behaving as crystalline defects in the polymer chains and this results in small crystals and a small degree of crystallinity. This is reflected by a Tc that reduces from 72 °C for a conventional P(VDF-co-TrFE) copolymer to 65 °C for the terpolymer.86 The TFP is mainly an amorphous phase and the bulky –CF3 groups hinders the mobility of the chain segments, leading to an increase of the glass transition temperature (Tg) from approximately −20 °C for a standard copolymer to 0 °C for a terpolymer with 9 mol% of TFP. The effect of the ter-monomer on the polarization behaviour of copolymer thin films (20 μm) were compared for P(VDF-co-TrFE) (65/35), poly(VDF-TrFE-CTFE) (61/26/13) and poly(VDF-TrFE-TFP) (62/32/6). As shown in Fig. 6, the poly(VDF-TrFE-CTFE) exhibited a typical relaxor ferroelectric behaviour with a slim hysteresis loop and low coercive field (Ec = 13 MV m−1), remnant polarization (Pr = 10 mC m−2) and saturation polarization (Psat = 58 mC m−2). Both P(VDF-co-TrFE) and poly(VDF-TrFE-TFP) exhibited wide ferroelectric hysteresis loops with a high coercive field, Ec = 63 MV m−1, indicating that both polymers have a similar polarisation response. The poly(VDF-TrFE-TFP) has a lower Pr = 33 mC m−2 and saturation polarisation, Psat = 49 mC m−2, as compared to P(VDF-co-TrFE) copolymer, which may be due to the lower crystallinity of the terpolymer and the lower polarizability of the –CF3 group of the TFP compared to the CFE and CTFE units.86
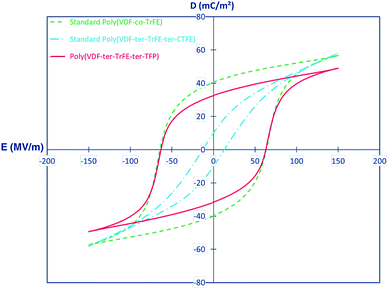 | ||
| Fig. 6 Comparison of bipolar dielectric displacement–field (D–Ef) hysteresis loops for standard annealed 65/35 poly(VDF-co-TrFE) (dotted line) and 61/26/13 poly(VDF-TrFE-CTFE) (semidotted line) with a 67/38/5 poly(VDF-TrFE-TFP) (full line). Reprinted with permission.86 Copyright 2015 American Chemical Society. | ||
A previous study89 demonstrated that Tc is 70–80 °C for a 65/35 mol% P(VDF-co-TrFE) copolymer, which was observed as a decrease in the intensity of the XRD diffraction peak at 2θ = 19.5° (β-phase), and the emergence of a second peak at 2θ = 18.2° (α-phase) as the temperature increased above 80 °C. The all-trans peak vanished at 100 °C (lower than the melting temperature, Tm ∼ 153 °C). In the temperature between Tc and Tm, the polymer chains move more freely to reorganise into higher degree of crystallinity. In comparison, a copolymer of 73/27 mol% had a Tc of 100–110 °C and the all-trans ferroelectric peak disappeared on heating to 140 °C, while Tm was 150 °C. For a 78/22 mol% copolymer, the Tc was increased further to 130–145 °C and Tm was estimated to be 149 °C.89,90 For a 81/19 mol% copolymer, the Tc was ∼120 °C, and the Tm was near 150 °C.81
During the manufacturing process, polymers suffer from tension, shearing and compression during melt-extrusion, injection moulding and compression moulding; and tension and electrical poling during the electrospinning process. In addition to mechanical stretching or electrical poling, the polar β-phase of PVDF can also be induced by application of a shearing history (shear rate, shear strain and shear temperature).91 A recent study found an increase in β-phase content from 38 to 84% for PVDF 120–150 μm thick films when sheared at 220 °C with an applied shear rate of 10 s−1 for 10 s, followed by isothermal crystallization at 155 °C. The samples sheared at a higher temperature generally had a higher nuclei density, smaller spherulites and a higher β-phase fraction, as shown in Fig. 7. A large deviation between the shearing temperature and crystallization temperature was shown to facilitate the formation of β-phase.
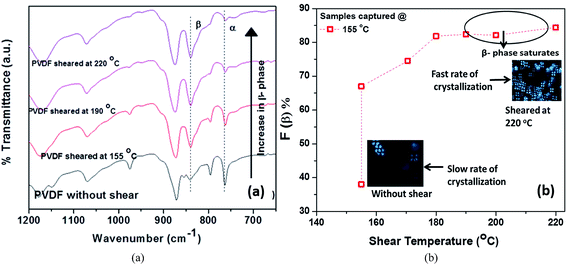 | ||
| Fig. 7 (a) FTIR spectra of pure PVDF isothermally crystallized at constant temperature of 155 °C. (b) Variation of β-phase content with shearing temperature crystallize at 155 °C with an applied shear rate of 10 s−1 for 10 s. Reprinted with permission.91 Copyright 2016 American Chemical Society. | ||
Generally, a higher annealing or crystallisation temperature and/or longer annealing time above Tc yields lamellar thickening and improved crystalline packing, lower defect density and higher crystallinity of the paraelectric α-phase. These factors result in an increase in Tm and decrease Tc.67,92 When annealing the polymer below Tc in the β-phase state, an increase of the Tc is expected.93 Solution-cast P(VDF-co-TrFE) (72/28) thin films annealed at 120 °C for 3 h (above Tc, but below Tm) had a preferential chain orientation that was aligned parallel to the substrate surface with a high degree of crystallinity, and high dipole alignment upon electrical poling. These factors lead to a large polarization in 100 nm thin films, Pr = 7.8 μC cm−2 and an Ec = 0.75 MV cm−1.67 Therefore, to achieve high piezoelectric coefficients, it is essential to control the annealing procedures through the Tc.92
As an example of the influence of such processing conditions, for a solution-cast P(VDF-co-TrFE) (81/19) copolymer that was annealed at 120 °C (close to the Tc) for 16 h the Tc increased to 128 °C but no change of Tm was observed. In contrast, the Tc increased to 125 °C and Tm increased to 151 °C after annealing at a higher temperature of 140 °C for 16 h.81 The changes of Tc were associated with changes in the Gibbs free energies in the orthorhombic β-phase and hexagonal α-phase during annealing. Annealing of the material below its Tc favors the removal of gauche defects in the ferroelectric phase which increases the degree of crystallinity and β-phase concentration. Annealing above Tc facilitates the transformation of the paraelectric α-phase into the β-phase. The β-phase concentration in the as-cast film increased from 75% to 93% after annealing at 130 °C for 2 h (Fig. 8). The increase in β-phase concentration led to higher piezoelectric activity and increased the d33 piezoelectric coefficient from an original value of 13 pC N−1 to 18 pC N−1 after 4 h of annealing with a three-fold increase in elastic modulus and 10-fold reduction of oxygen permeability.81 For energy harvesting applications high piezoelectric coefficients, such as d33, are beneficial, see eqn (2)–(4).
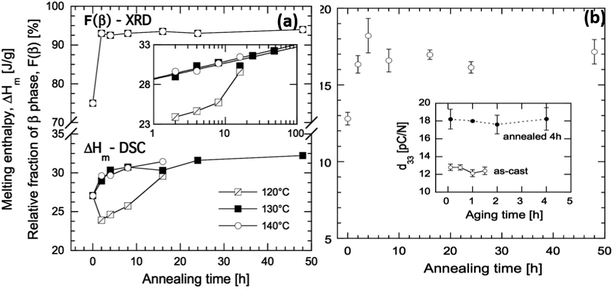 | ||
| Fig. 8 (a) Melting enthalpy of solvent cast P(VDF-co-TrFE) films as a function of annealing time at 120, 130, and 140 °C, and relative fraction of crystalline β-phase as a function of annealing time at 130 °C. The inset shows ΔHmvs. annealing time in logarithmic scale. (b) Piezoelectric d33 coefficient of solvent-cast P(VDF-co-TrFE) films as a function of annealing time at 130 °C. The inset shows the d33 coefficient of the copolymer, as-cast (open symbols) and annealed 4 h at 130 °C (black symbols), during aging at room temperature. Reprinted with permission.81 Copyright 2016 John Wiley and Sons. | ||
In the case of P(VDF-co-TrFE) copolymers with a VDF content in the range of 65–82 mol%, the Tc shows a large thermal hysteresis, it is lower during the cooling process (T↓c) compared to the heating process (T↑c). For the P(VDF-co-TrFE) 75/25 mol%, the T↓c = 57–79 °C was much lower than that of T↑c = 124 °C.35 Due to the large difference in the free energy between the hexagonal α-phase phase and orthorhombic β-phase phase at T↓c, the phase transition proceeds rapidly even when the film is cooled slowly. Therefore, TGTG′ sequences in the hexagonal α-phase phase are quenched partly in the orthogonal direction as conformational defects. When annealed above Tc, P(VDF-co-TrFE) copolymers undergo a thickening of crystallites, resulting in a strong increase in crystallinity, up to 90% or more for a VDF content in the range 70–80%.35,93,94,94–96 The Tc decreases as the TrFE content increases, and vanishes for P(VDF-TrFE) 50/50, due to cooperative movements in the ferroelectric β-phase near the transition temperature.87 A maximum β-phase fraction of 66.3% was obtained from the sequential treatment of “annealing and cooling–pressing–electrical poling” while control materials only exhibited a β-phase fraction of 45.3%.97
For a copolymer crystallising from the melt, the Tc was affected by the cooling rate, suggesting that a higher cooling rate leads to VDF-rich crystalline regions due to the TrFE units having difficulty entering into the crystal lattice. In contrast, quenching the material from the melt leads to a broader endotherm, similar to dimethylformamide (DMF) crystallized samples annealed at 120 °C.93 Melt processing, in particular extension flows, also affect the crystallization and chain orientation of polymers. For example, in P(VDF-co-TrFE) copolymers, the extensional flow at a normal stress level of 6.35 × 105 Pa produced an all-trans crystal structure in the 66/34 mol% copolymer. A 7 °C higher transition temperature and lower melting temperature was observed in the two-dimensional flow rate range of 0.002–0.03 cm2 s−1 for the 75/25 mol% copolymer.98
In both PVDF and P(VDF-co-TrFE) copolymers, the α-phase tends to form when cooling from high temperature and at high cooling rates. The presence of increasing amounts of TrFE increases the formation of β-phase. A lower fabrication temperature favours the formation of polar β- and γ-phases.99 When an as-cast P(VDF-co-TrFE) (80/20) film was heated to 200 °C for 4 h, then quenched at 100 °C, a 43% degree of crystallinity was obtained and the α-phase dominated; when quenched at −20 °C, a 56% degree of crystallinity was obtained, and almost 100% β-phase was formed. Therefore, the annealing process affects the local distribution of the TrFE comonomer units in the crystalline lattices, which is reflected by the varied Tc and crystallinity. It is largely accepted that β-phase melting occurs in the range 165–172 °C; α-phase crystals in the range 172–175 °C with the γ-phase melting between 175 and 180 °C.100
The ferroelectric behaviour of PVDF based materials have been investigated as a function of temperature and poling frequency, as shown in Fig. 9 and 10.101 For a uniaxially stretched P(VDF-co-TrFE) (50/50) film, paraelectric behavior was obtained due to the nucleation of electric field-induced ferroelectric nanodomains inside the paraelectric matrix when it was poled at a high poling frequency (1 kHz) at 100 °C and above the Tc of 64 °C. These ferroelectric nanodomains were highly reversible and could be rapidly depolarized upon removal of the poling field, as shown in Fig. 10C. At an intermediate poling frequency (10 Hz) at 100 °C, an ‘antiferroelectric-like’ behaviour was observed, which could be attributed to the competition between depolarization and polarization fields upon reversed poling, this corresponds to the behaviour in Fig. 10B. Finally, at a low poling frequency (1 Hz) at 100 °C, conventional ferroelectric behaviour with a rectangular hysteresis loop was observed since the small, reversible ferroelectric domains have sufficient time to grow into large irreversible ones. For energy harvesting applications the ability to pole the material and achieve a high remnant polarisation (Pr) which is modulated with stress or temperature is of interest for piezoelectric or pyroelectric harvesting, as in Fig. 10A. For energy storage applications, the antiferroelectric-like (Fig. 10B) or paraelectric (Fig. 10C) behaviour is more desirable due to the ability to store and recover energy, as given by the larger areas in the D–Ef loops which are indicated by the purple areas in Fig. 10.
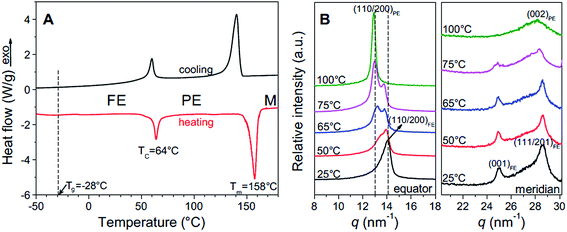 | ||
| Fig. 9 (A) First cooling and second heating DSC thermograms of P(VDF-TrFE) 50/50; (B) XRD profiles for the uniaxially stretched P(VDF-TrFE) 50/50 film at different temperatures: (left panel) along the equator and (right panel) along the meridian. Reprinted with permission.101 Copyright 2012, Elsevier. | ||
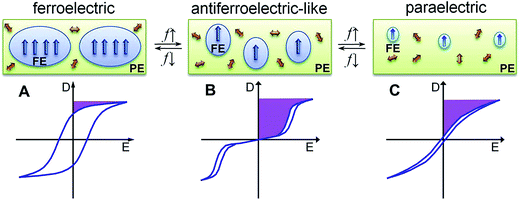 | ||
| Fig. 10 Schematic illustration of D–Ef loops and domain structure of (A) conventional ferroelectric, (B) antiferroelectric-like, and (C) paraelectric behaviour of the high temperature phase in P(VDF-co-TrFE) under different poling frequencies (f). Reprinted with permission.101 Copyright 2012, Elsevier. | ||
A β-phase content of 74% and an overall crystallinity of 42.6% was achieved for melt-quenched stretched PVDF films.102 A higher β-phase content of 82% and a d33 of 21 pC N−1 was obtained by stretching PVDF films that were solution-cast from N,N-dimethylacetamide (DMAc) solutions.103 It is reported that an overall crystallinity of 52–60% with a β-phase fraction of 53% was present in PVDF films prepared by spin coating from an acetone/DMF solution and then stretching uniaxially.104 The pyroelectricity of a ferroelectric VDF-oligomer [CF3(CH2CF2)17I]-evaporated film was investigated utilizing a low-frequency sinusoidal heat source.72 The pyroelectric coefficient (p) of the 600 nm-thick VDF oligomer film was −68 μC m−2 K−1 at 37 °C, which is larger than those reported for ferroelectric polymers. The VDF oligomer is therefore a promising material for pyroelectric thin-film infrared detectors and pyroelectric harvesting.
P(VDF-co-TrFE) (70/30) nanowires formed by templating exhibited a Pr = 7.4 μC cm−2 and Ps = 9.6 μC cm−2, that are similar to as-prepared P(VDF-co-TrFE) thin films. Maximum d33 values of −8.2 and −6.5 pm V−1 were obtained for the P(VDF-co-TrFE) and PVDF nanowires. Non-poled P(VDF-co-TrFE) thin films had a d33 of −15 pC N−1, while in comparison, poled films and bulk materials of both P(VDF-co-TrFE) and PVDF had a d33 in the range of −20 to −30 pC N−1 (or pm V−1).
A significant change in the crystallisation behaviour of P(VDF-co-TrFE) was observed when confined in a nanoporous template with pores less than 40 nm in diameter,38 as compared to the bulk material. The copolymer crystallised into an oriented ferroelectric crystal lamellae perpendicular to the pore axis. Both melting and crystallization temperatures decreased with a decrease in pore diameter, and the Tc was weakly affected. The presence of ferroelectric phase was preserved down to pore sizes as small as 15 nm. The results imply that nanoconfinement enhances the formation and orientation of the ferroelectric β-phase and can enhance ferroelectricity and piezoelectricity in nanoscale P(VDF-co-TrFE) materials.
For a P(VDF-co-TrFE) copolymer with a composition ratio of 72.2/27.8 mol%,88 the polymer chain length affects the conformations. It was found that a short polymer chain length leads to a higher crystal size and promotes a higher β-phase content; the d33 piezoelectric coefficient was enhanced by decreasing the molecular weight (Mw) of the copolymer. A maximum d33 value of −50 pC N−1 was achieved for the composition 72.2/27.8 mol% with a molecular weight of 470 kg mol−1. Interestingly, the pyroelectric properties were enhanced for the lowest polymer crystalline grain size studied. A pyroelectric coefficient of 37.8 μC m−2 K−1 was obtained with the composition 71/29 mol% with a molecular weight of 505 kg mol−1. These differences may be related to how the polarisation changes with either stress (thereby influencing the piezoelectric coefficient) or temperature (thereby influencing the pyroelectric coefficient).
When a PVDF based material is crystallised and confined in two-dimensional (2D) cylindrical anodic aluminium oxide (AAO), the crystal c-axis becomes perpendicular to the porous cylinder axes, which favours dipole switching. The polarity of the nanopore surface and the surface hydroxyl groups on the template nanopores promote the formation of the polar phase, with a β-phase content of 40.5%. As shown in Fig. 11a, the use of an oxygen plasma treatment increases the number of negatively charged OH− and O2− groups on the surface of the Al2O3 nanopore template, thereby increasing its hydrophilicity compared to the pristine template; see Fig. 11a and b. Therefore, the presence of highly polar surface increases the template interaction with the PVDF dipoles, and forces the polymer chains to arrange in a TT confirmation, leading to a polar β-phase fraction of 40.2%. The use of a 3-aminopropyltrimethoxysilane (APMS) treatment increased the hydrophobicity of the nanopore surface, and enhanced the interfacial interactions with the polymer chains, and enhanced the polar phase formation to 71%, as shown in Fig. 11c.106 However, no polar phases have been obtained from 2D confinement down to 35 nm pores after melt recrystallization.
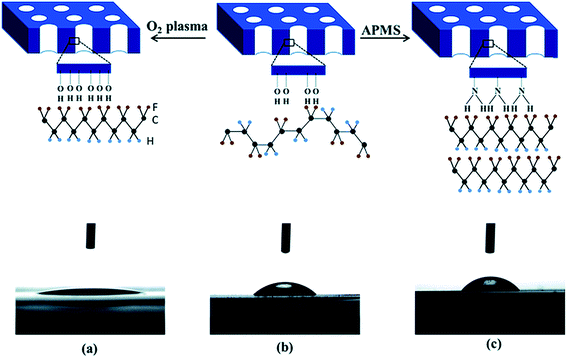 | ||
| Fig. 11 Contact angle measurements of a water droplet deposited on the surface of oxygen plasma treated (a), pristine (b) and APMS modified (c) AAO templates and corresponding schematic diagram of the polar phase formation (hydrogen, fluorine and carbon atoms are represented by blue, yellow and black spheres). Reproduced from ref. 106. Copyright 2015 Royal Society of Chemistry. | ||
When recrystallized from the melt in confined 3D polystyrene nanospheres 180 nm in diameter, PVDF exhibited both polar β- and γ-phases, rather than the kinetically favoured α-phase,107 see Fig. 12. These results indicate that PVDF can nucleate homogeneously at a high crystallization rate in the 3D nanoconfined space, which does not rely on the polarity of the substrate. The use of 3D nanoconfinement is thought to be more effective than 2D nanoconfinement in producing polar crystalline phases in PVDF.
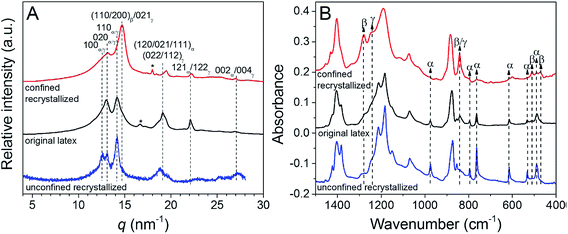 | ||
| Fig. 12 (A) WAXD profiles and (B) FTIR spectra for original latex, unconfined recrystallized (using original latex directly), and confined recrystallized (using PVDF@PS core–shell particles polymerized at 65 °C for 10.5 h) PVDF samples. Reduced with permission.107 Copyright 2014 American Chemical Society. | ||
By varying the quenching temperature, the crystal structure and properties of PVDF can be tailored for different applications, as shown in Fig. 13.108 For solution-cast films, when quenched below 0 °C, more β-phase was formed which was aligned to create a self-polarised material with a high d33 of ∼49.6 pm V−1 (see Fig. 13c). This is much higher than typical values of −20 to −35 pm V−1 produced by mechanical stretching and poling. These values are comparable to PVDF nanofibres which show a d33 coefficient of −54 pm V−1, which originates from the high γ-phase content with ∼75% crystallinity.109 The high d33 of the film was attributed to the high (∼100%) β-phase content and high crystallinity of 56%, as shown in Fig. 13a and b. Fast quenching at a low temperature induced a strong thermal field gradient, which can cause crystals to align along the thermal field direction. The interaction with polar water can also be a possible reason for the alignment of the β-crystals.109,110 The self-polarised β-phase and high piezoelectric coefficient of the PVDF films make them suitable for energy harvesting applications, such a vibration harvesting (Fig. 13d) and examples of devices are described at the end of the review (Section 3). Further details of ferroelectric polymer nanostructures under confinement has been described111 and recently nanostructured arrays of PVDF based polymers have been formed by nanoimprint lithography.112
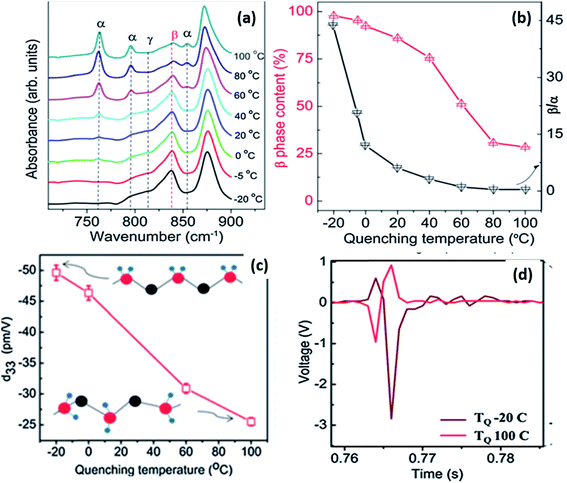 | ||
| Fig. 13 (a) FTIR spectra showing various crystalline phases; (b) β-phase content, the β/α ratio as a function of quenching temperature; (c) variation of d33 as a function of quenching temperature; (d) voltage output observed from microgenerators prepared using PVDF films quenched at −20 and 100 °C. Adapted with permission from ref. 108, Copyright 2015 Royal Society of Chemistry. | ||
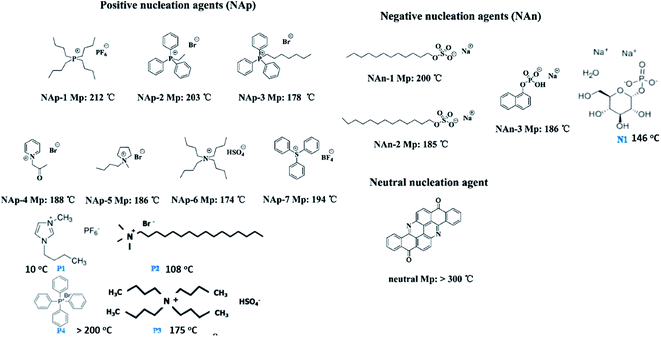 | ||
| Fig. 14 Chemical structures of organic nucleating agents with different surface charges. Adapted with permission.113 Copyright 2014 American Chemical Society. Reprinted with permission.64 Copyright 2012 American Chemical Society. | ||
Nanoparticles can also act as nucleating agent for polymers by increasing the crystallisation kinetics and degree of crystallinity. For PVDF composites filled with Na(M)Y zeolites, the negatively charged zeolite framework induces the formation of the polar γ-phase in PVDF when prepared by solution-cast and melt compression.114 The use of Na(Y) in the composite induced 100% of γ-phase in PVDF due to the negatively charged ion–dipole interactions between the zeolite framework and the PVDF. The exchangeable (M) ion size in the zeolite also affects the PVDF phase structure. The presence of small sized lithium (Li) ions increased the crystallisation of polar phases, as compared to Na(Y), while the presence of potassium (K) and cesium (Cs) has the opposite effect. This behaviour depends on the interaction competition between the alkali ion–zeolite structure and alkali ion-molecular dipoles. Using larger sized ions and stronger interactions with zeolite structures reduced the interactions with polar polymer chains, leading to a lower fraction of polar phase. The relative permittivity ranged from 47 to 3 for PVDF/Na(Li)Y and PVDF/Na(Cs)Y, respectively, while the electrical conductivity of PVDF/Na(Li)Y was three orders of magnitude higher than that of PVDF/Na(Cs)Y. An increased relative permittivity can often be related to increased conductivity in the material.
With the addition of graphene oxide (GO) nanoplatelets to PVDF,115 only the γ-phase was induced to form in PVDF when crystallized from the solution, and only α-phase forms from melt crystallization. When GO was combined with a positively charged surfactant (cetyltrimethylammonium bromide, CTAB), more γ-phase crystals were formed in PVDF during isothermal melt crystallization at 160 °C for 80 min. It is suggested that there are two distinct stages during the melt crystallization of PVDF/GO composites in the presence of CTAB, i.e., a simultaneous growth of γ- and α-phases, which is followed by an α- to γ-phase transition. The Tm was increased by 10 °C for the γ-phase PVDF/GO composites. The addition of CTAB was thought to strengthen the ion–dipole interactions between the GO and PVDF, as compared to weak π-dipole interaction between GO and PVDF.
Similarly, the effects of the surface charge on the crystal structure of PVDF were studied using nanoparticles of CoFe2O4 whose surface was treated with three types of surfactants, i.e., anionic (SDS), nonanionic (Triton X-100), and cationic (CTAB).116 A higher fraction of polar β-phase was obtained when CoFe2O4 nanoparticles with a negative electrostatic charge were added. The β-phase content reached 30% and 90% for CoFe2O4/PVDF and CoFe2O4–SDS/PVDF, respectively, with a resultant d33 of 23 and 33 pC N−1 respectively. This behavior was attributed to the interaction between the negatively charged magnetic CoFe2O4 particles and the positive polymer CH2 groups.
The ion–dipole interactions are described as (i) negatively charged surfaces with the CH2 dipoles in PVDF, or (ii) the positively charged surfaces with the CF2 dipoles in PVDF. By comparing the effects of positively- and negatively-charged organic nucleation agents,113 as in Fig. 15, the positively charged nucleation agents interact more strongly with the partially negative CF2 dipoles of PVDF, resulting in a lower nucleating energy barrier and increased crystallization kinetics and crystallization temperature for PVDF; this induces the formation of polar (β, γ) phase formation. The addition of positively charged organic molecules in solid PVDF induced a 100% of γ-phase formation, while the β-phase PVDF becomes dominant when in the molten state. Almost 100% of polar phases were formed by the addition of 3 wt% of positively charged small molecules (1-butyl-3-methylimidazolium hexafluorophosphate). The β- and γ-phases can give rise to ferro-, pyro-, and piezoelectricity for harvesting, and the γ-phase can lead to increased transparency117 and flexibility113 of PVDF.
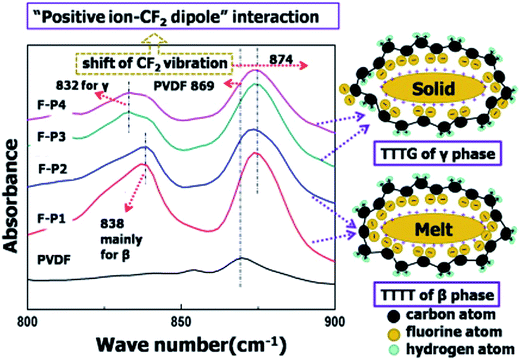 | ||
| Fig. 15 FTIR results and scheme for ion–dipole interaction between positively charged molecules and PVDF. Reprinted with permission from ref. 113. Copyright 2014 American Chemical Society. | ||
In addition to tailoring the processing conditions and heat-treatment conditions, recent approaches to tailoring the piezo- and pyro-electric properties are to use polymer blending and form nanocomposites, which will be now discussed.
For example, the miscibility of PVDF with amorphous PMMA is driven by hydrogen bonding between the carbonyl group of PMMA and CH2 of PVDF and dipole–dipole interactions between CH2 of PMMA and CF2 of PVDF.119 The blending of amorphous PMMA with PVDF decreased the crystallinity and crystal size of PVDF which were mostly in the polar β-phase when the PMMA content was above 25 wt%.118 With the assistance of rigid PMMA segments, the β-phase was easier to pole and was reversible with electric field changes. A higher PMMA content (≥40 wt%) and quenching process favoured the α- to β-phase transition. Therefore, PVDF/PMMA blends with a high β-phase content exhibited a high relative permittivity, and a low dielectric and energy loss due to the presence of PMMA.118
Semicrystalline PBS is miscible with PVDF, and can promote the formation of β-phase in PVDF, depending on the PBS content and quenching temperature.120 The β-phase fraction increased with increasing PBS content, up to 50 wt%, while the addition of greater amounts of PBS can restrict the nucleation and growth of the β-phase, thus resulting in more α-phase. Lowering the quenching temperature benefits the formation of β-phase in PVDF.
Semicrystalline PA11 has comparable coercive fields and remnant polarization with PVDF, but a low piezoelectric response (<4 pC N−1, see Table 1) at room temperature because of its higher glass transition temperature (ca. 50 °C) compared to PVDF (∼−30 °C).123,124 When blending ferroelectric PA11 and PVDF, the glass transition temperature and melting point of PA11 decreases with increasing PVDF concentration, due to the dipolar intermolecular interactions between the polar amide groups (–NH–CO–) in PA11 and the polar –CF2 groups in PVDF.121,125 It has also been found that the hydrogen-bonded structure of PA11 becomes more disordered as the PVDF concentration is increased. The PVDF developed a larger proportion of polar β- and γ-phase in blends with a high PA11 concentration compared to pure PVDF under similar melt quench conditions.121 During the uniaxial drawing process, the phase transformation of PVDF from the nonpolar α-phase to the polar β-phase is more complete, with more ordered β-crystals than in pure PVDF. These structural changes and the dipolar interactions between PA11 and PVDF lead to a 30% increase in piezoelectric properties and improved high-temperature stability of the blends at temperatures up to 160 °C.121 These properties enables this new polymeric blend material to be used in electroactive applications, such as sensing and harvesting in more hostile environments.
The formation of unique orientation textures due to confined crystal growth of PVDF in PVDF/PA6 blends of drawn films have been reported.122 Uniaxial-drawn PVDF/PA6 blends were heat-treated at 180 °C for 3 minutes to melt the PVDF component, followed by non-isothermal crystallization of PVDF at a cooling rate of 0.5 °C min−1. For PVDF/PA6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) as a 50/50 blend, stretched domains of PVDF with a diameter of 0.2–0.5 μm were dispersed in a PA6 phase. Spatial confinement of the crystal growth resulted in the alignment of the crystal b-axis along the long axis of the domains, since the PVDF crystallized as thin cylindrical domains. The orientation behaviour is different from the oriented crystallization of PVDF/PA11125 in which trans-crystallization from the interface causes an a-axis orientation in the drawing direction. It is thought that the domain size influenced the mechanism of oriented crystallization.
as a 50/50 blend, stretched domains of PVDF with a diameter of 0.2–0.5 μm were dispersed in a PA6 phase. Spatial confinement of the crystal growth resulted in the alignment of the crystal b-axis along the long axis of the domains, since the PVDF crystallized as thin cylindrical domains. The orientation behaviour is different from the oriented crystallization of PVDF/PA11125 in which trans-crystallization from the interface causes an a-axis orientation in the drawing direction. It is thought that the domain size influenced the mechanism of oriented crystallization.
A recent study showed that a P(VDF-co-HFP)/poly(ether imide) blend with a poly(ether imide) content larger than 80% created more free volume in the polymer matrix, thereby providing more space for dipole orientation polarization and providing an enhancement of the relative permittivity of the polymer blends.126
As discussed, PVDF and its copolymers contain mainly of α-phase (∼40%)127 or a trace amount of β-phase when cooled from the melt; Fig. 4. A significant body of research has demonstrated that nanoparticles with a negatively charged surface can interact with the positively charged –CH2 groups, and induce the formation of the polar β-phase, with fractions up to 100%,64,99,128 and provide high d33 piezoelectric coefficient of ∼33 pC N−1.116 Dipole-surface charge interactions have been found in various PVDF based composites systems. Examples of dielectric and conductive additives include clay, BaTiO3,129 lead zirconium titanate (Pb(Zr, Ti)O3, PZT),130 SiO2,131 ionic liquids, carbon materials (carbon nanotube, graphene, carbon fibers), metal nanoparticles (nanoparticles of Pd,132 Ag,133 Pt134), metal salts (CuO,135 ZrO2,136 TiO2, Fe3O4,137,138 BaFe12O19,139 cerium(III)-N,N-dimethylformamide-bisulfate [Ce(DMF)(HSO4)3] complex140), and conducting polymers. The effect of nanoparticle additions on the structure and piezoelectric properties of PVDF polymers generally depend on their nucleation efficiency, supercooling effect and interfacial interactions. The nucleation effect of the nanoparticle additions strongly depends on the particle size,129,135 shape,141 surface chemistry,135 concentration,130 dispersion, interfacial interaction and processing conditions.
2.2.7.1 Ceramic particles in nanocomposites. As described in Section 1, the generation of a piezoelectric potential under strain is due to the displacement of the positive and negative charges in the β-phase of PVDF. With the incorporation of ferroelectric inorganic particles, such as BaTiO3, the piezoelectric potential can be further enhanced.129 BaTiO3 hollow nanospheres141 with particle sizes of ≈20 nm and surface area of 297 m2 g−1 were surface-treated to enhance their compatibility with PVDF. Both the large specific surface area and increased surface functionality of the hollow spheres increased the β-phase content and degree of crystallinity at 16 wt% of filler. The changes in crystallinity led to a high relative permittivity of 109 and high energy density (Ue ≈ 21.7 J cm−3) with a high retained breakdown strength (Eb = 3.81 × 103 kV cm−1) compared to pristine PVDF (ε′ ≈ 11.6 and Ue ≈ 2.16 J cm−3 at 3.98 × 103 kV cm−1). Surface functionalised Ba0.6Sr0.4TiO3 nanofibers142 showed good dispersion and strong interfacial adhesion with PVDF matrix, which resulted in high relative permittivity (ε′ ∼ 12) and high breakdown strength (3900 kV cm−1) for the composite containing 2.5 vol% of nanofibers. The maximum energy storage density reached 7.5 J cm−3 for a PVDF nanocomposite under the electric field of 3900 kV cm−1, which is three times that of pure PVDF (2.8 J cm−3 at 4000 kV cm−1). A recent study on BaTi(1−x)ZrxO3 (BTZO) nanocube filled PVDF composites for harvesting reported that143 the flexible PVDF/BTZO composite films exhibit a high electrical output up to ∼11.9 V and ∼1.35 μA compared to PVDF/BaTiO3 films which had an output of 7.99 V and 1.01 μA when subjected to a cyclic stress at 21 Hz with a constant load (11 N). The doping of various amount of Zr4+ (x = 0, 0.05, 0.1, 0.15, and 0.2) into the Ti4+ site of BaTiO3 can further enhance the piezoelectric performance of the particles. The piezoelectric potential of the PVDF/BTZO composites was adjusted by varying the composition ratio of BTZO and PVDF, electrical poling and mechanical loading. The composite generators were used to measure different water velocities at an outlet pipe and the peak power of the piezoelectric nanogenerator varied from 0.2 to 15.8 nW for water velocities ranging from 31.43 to 125.7 m s−1.
2.2.7.2 Metal and metal salts in nanocomposites. For metal and metal salt filled PVDF composites, it was shown that 5 wt% of copper induced the formation of up to 90% of β-phase due to the high interfacial area between the well-dispersed nanoparticle surface and the polymer.135 Superior ferro- and piezo-electret properties in a self-poled, porous hybrid ferroelectretic polymer nanocomposite film was achieved by in situ generation of platinum nanoparticles embedded in a P(VDF-co-HFP) matrix.134 The cooperative functionality between the self-polarized β-phase and the micropores as charge trapping sites was achieved by using a simple solvent evaporation method. The resulting porous hybrid film exhibited a square-shaped hysteresis loop with large remnant polarization (Pr ≈ 61.7 μC cm−2), high piezoelectric charge coefficient (d33 ∼ −686 pC N−1), and high dielectric properties (relative permittivity ε′ = 2678 and tan
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 0.79 at 1 kHz); this high permittivity may be associated with the high loss (tan
δ = 0.79 at 1 kHz); this high permittivity may be associated with the high loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ). An open-circuit output voltage of 18 V with a 17.7 μA short-circuit current were generated under a 4 MPa stress. The high piezoelectric energy conversion efficiency (ηpiezo ≈ 0.2%) of the nanogenerator demonstrated its potential for piezoelectric-based energy harvesters.
δ). An open-circuit output voltage of 18 V with a 17.7 μA short-circuit current were generated under a 4 MPa stress. The high piezoelectric energy conversion efficiency (ηpiezo ≈ 0.2%) of the nanogenerator demonstrated its potential for piezoelectric-based energy harvesters.
The addition of metal salts, such as cerium(III)/yttrium(III) nitrate hexahydrate (1–30 wt%),144 or Fe2O3–Co3O4 nanoparticles138 to PVDF induced the formation of β-phase due to a strong ion–dipole interaction through the formation of hydrogen bonds between the water molecules of the salts and the –CF2 dipoles of the polymer chains; this led to a large permittivity. A 15 wt% SiO2-loaded PVDF film exhibited a high permittivity, due to the homogeneous dispersion and interfacial interaction of SiO2 nanoparticles in the PVDF matrix.131 For a P(VDF-co-HFP) matrix filled with mesoporous SiO2 nanorods, the anisotropic shape of the SiO2 nanorods and ordered mesopores doubled the amount of the –OH groups present. This increased the intermolecular interactions and enhanced the β-phase content and ferroelectric properties of P(VDF-co-HFP).145 Using this approach, the nucleation of the ferroelectric β-phase in PVDF can be influenced by the geometry of the fillers through the interface interactions between the local electric field of the filler and PVDF dipoles, such as ion–dipole and dipole–dipole interactions.
Ferroelectric P(VDF-co-CTFE) terminated with phosphonic acid groups were synthesised and subsequently coupled with ZrO2 fillers.136 The functional chain end-groups can form covalent coupling with the ZrO2 surface, thereby providing the nanocomposites with stability and a uniform filler dispersion. The presence of 9.1 wt% ZrO2 increased the crystallization temperature of the copolymer from 82 to 91 °C, and increased the crystallinity from 18.3 to 22.8%. As a result of the intimate coupling between the filler and matrix, the interfacial interaction regions between the polymer and ZrO2 increased the energy density at high electric fields. The energy density reached a maximum of 11.2 J cm−3 at 270 MV m−1 with 9.1 wt% of ZrO2, this was a 60% increase in comparison to the copolymer matrix. The improvement in the energy storage capability of the nanocomposite was ascribed to changes in polymer microstructure and an increase in crystallinity, the interfacial region and the rise of the electric displacement induced by the incorporation of the nanofillers.
The incorporation of a cerium(III)-N,N-dimethylformamide-bisulfate [Ce(DMF)(HSO4)3] complex140 into PVDF provided a higher yield (99%) of the polar β- and γ-phases. An enhancement of the output voltage (∼32 V) of a nanogenerator based on a non-electrically poled cerium(III) complex containing PVDF composite film was achieved by repeated human mechanical loading, whereas pure PVDF did not show any response. This high electrical output was due to the electrostatic interactions between the fluoride of PVDF and the positive charge cloud of the cerium complex via H-bonding and/or a bipolar interaction between the opposite poles of the cerium complex and PVDF, as shown in Fig. 16a–c. The capability of the composite film to charge a capacitor shows its capability as a piezoelectric-based energy harvester. The cerium(III) complex doped PVDF composite film exhibited an intense photoluminescence in the UV region, which may be due to participation of an electron cloud from the negative pole of the bipolarized PVDF. This fact may also be of interest for the development of flexible solid-state UV light emitters, as shown in Fig. 16d.
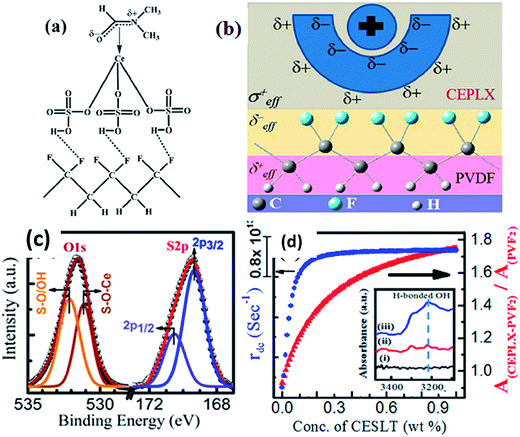 | ||
| Fig. 16 Schematic representation of (a) the formation of H-bonding with –HSO4 and CF2 dipoles; (b) the electrostatic interaction between the surface charge of the particles and the CF2 dipoles; (c) XPS of O1s and S2p core levels of cerium(III) complex and PVDF; (d) damping coefficient and the absorbance intensity ratio of the composites. Reprinted with permission from ref. 140. Copyright 2015 American Chemical Society. | ||
2.2.7.3 Nanoclay additions. Nanoclay, in particular, layered montmorillonite has been shown to provide excellent reinforcement and barrier functions to polymers. A variety of organoclays modified with cationic surfactants have been investigated for modifying PVDF-based polymers. Commercial organoclays, such as Cloisite®Na, Cloisite®6A, Cloisite®15A, Cloisite®20A, Cloisite®25A, Cloisite®30B, Lucentite STN, Nanocor Inc I.34TCN have been studied. The main difference between the organoclays above are the different surface treatment and polarity. It was found that the organoclay promotes the formation of β-phase of PVDF, while unmodified clay shows little or no influence. Solution-casting146 has been shown to facilitate dispersion and strengthening of the interaction between the organoclay and PVDF, as compared to melt-processing.
The effects of nanoclay inclusions on the crystallisation behaviour of PVDF depend on the dispersion, exfoliation and interfacial interactions of nanoclay in the PVDF matrix. Three types of organoclay modified by different surfactants were studied: ammonium (C18), pyridinium, and phosphonium. It was found that the three types of organoclay could be readily dispersed in PVDF melts. The ammonium–clay showed the best dispersion and phosphonium clay was more efficient in forming the polar β-phase.127 High β-phase fractions of ∼99% were obtained at 5 wt% of octadecyltriphenylphosphonium bromide modified clay with a 28.2 wt% organic content. In comparison, the addition of 5 wt% of unmodified clay leads to only 23% of β-phase in the composites. The presence of nanoclay also acted as a nucleating agent and enhanced the melting and crystallization temperature of PVDF by 10 and 13 °C, respectively. For the composite containing 3 wt% of nanoclay, the relative permittivity at 1 kHz was approximately 9.6 with a dielectric loss less than 0.05, the Pr was 6.3 μC cm−2, as compared to 5.0 μC cm−2 for pristine PVDF. A higher loading of nanoclay, over 5 wt%, led to a higher dielectric loss, increased leakage current and early breakdown due to the aggregation of the clay in the PVDF matrix. By tuning the surface charge and dispersion of the nanoclay in PVDF, the energy density of the PVDF/nanoclay composites was increased from 5.34 to 5.91 J cm−3 at 1 wt% clay content and the highest energy density could reach 10.2 J cm−3.147
In addition to promoting β-phase formation, organoclay platelets can also stabilize the β-phase from depolarisation.148–150 The organoclay may play three roles in influencing the crystal structure and properties of PVDF:68,149 (i) a super-cooling effect, (ii) a heterogeneous nucleating effect and (iii) intermolecular interactions between the polymer chains and silicate sheets. To investigate the role of organoclay, solution-cast PVDF/organoclay (Lucentite STN) composite films with different thermal treatments were studied. This included annealing at 160 °C/24 h, melt-quenching followed by annealing treatment 160 °C/5 h and melt-slow cooling (10 °C min−1). The as-cast samples exhibited nearly pure γ-phase irrespective of the organoclay content, the melt-slow cooled samples showed α-phase at lower clay concentration, and a mixture of α- and γ-phases at a higher clay content. The samples prepared by melt-quenching followed by annealing had a mixture of α-, β- and γ-phases across a range of clay contents. Upon heating, the β-phase initially transformed to the thermodynamically stable γ-phase before melting. The increased melt-crystallization temperature of PVDF with the addition of organoclay indicated that the clay did not show any super-cooling effect. Ultra-thin films of PVDF/organoclay (Lucentite STN) nanocomposites have been prepared by heat-controlled spin coating.71 The Lucentite STN favours the formation of β-phase and orientation in nanoscale thin films, irrespective of preparation temperature, which leads to a high remanent polarization. In comparison, thick PVDF/organoclay nanocomposites films only contained α-phase after quenching and slow-cooling from the melt, while the nanoscale thin nanocomposite films showed a mixture of β- and γ-crystalline phases without any α-crystalline phase. Therefore, the sample thickness also affects the crystal structures of the PVDF composites.
Organoclay platelets can retard the relaxation of the PVDF chains and stabilize conformation due to the presence of ion–dipole interaction between the exfoliated nanoclay layers and the PVDF. An increase of organoclay concentration should therefore increase the level of interaction. For organically modified montmorillonite (OMMT) modified PVDF, the α-phase dominates when the OMMT concentration is below 0.025 wt%, while the β-phase fraction exceeds the α-phase fraction when the OMMT concentration is between 0.025 and 0.5 wt%.151 It is found that an increase of organoclay above 0.5 wt% introduces gauche defects in the all-trans conformation and results in a mixture of β- and γ-crystals in the polymer.151 In this case, the interactions between the clay and PVDF is responsible for crystal modification rather than the heterogeneous nucleating actions and super-cooling effect.63,148,152
The presence of a second polymer which is compatible with PVDF can also benefit the formation of the polar ferroelectric phase.153 In addition to the well-studied PVDF/PMMA blends, as described in Section 2.2.6, the addition of a polymeric compatibilizer such as acrylic rubber (ACM) can facilitate the intercalation and dispersion of nanoclay in the PVDF matrix, and promote polar β- and γ-phase formation.153 A relative permittivity of 16 (at 10 Hz) was obtained for PVDF/ACM/clay (90/10/5 wt%), which was 40% higher than that of a PVDF/clay (100/5 wt%) nanocomposite without ACM.
Therefore, organically modified clays generally have good dispersion and strong interfacial interaction with PVDF. Exfoliated organoclay nanosheets promote and stabilise the epitaxial growth of the β-phase PVDF149,154 mainly by the stronger interfacial interactions rather than heterogeneous nucleating effects or super-cooling effect.149 The PVDF/clay nanocomposites have mainly β-phase, and also have γ-phases coexisting at low crystalline temperature (Tc < 155 °C), the coexistence of γ- and β-phases was found at a high crystalline temperature range (Tc > 155 °C). The β-PVDF nucleation is influenced by the geometrical factors, interactions at the interface between the nanoparticles and the PVDF dipoles and particle concentration.31,32,34
2.2.7.4 Carbon nanotubes additions. Single-walled (SWCNT) and multiwalled carbon nanotubes (MWCNT) have been used to modify PVDF and its copolymers. Utilizing a solution-mixing method using dimethylacetamide (DMAc) as the solvent,155 pristine MWCNT (diameter 10–50 nm, length 4–10 μm) induced the formation of both α- and β-phases in PVDF under sonication, while no β-phase was formed in mechanically mixed mixtures. According to density functional theory, more energy is required to form the TT β-phase, and more TGTG′ α-phase can transform to the TT conformation under sonication, and the TT molecular chains can bind the CNT surface more tightly than the TGTG′ polymer chains.
For SWCNT filled P(VDF-co-TrFE) composites prepared by solution-casting followed by annealing at 70 °C for 38 h,156 the pyroelectric coefficients of the composites were higher than that of pure P(VDF-co-TrFE) copolymer. The increase in the pyroelectric coefficients of the composites as a function of temperature is more gradual compared the copolymer, as shown in Fig. 17a. This may be due to the interfacial interactions between the SWCNTs and the polymer chains which hinder the mobility of the dipoles at higher temperatures, thereby limiting the overall contribution to pyroelectricity. The measured d31 coefficient was 25 pC N−1, which is higher than the 20 pC N−1 for the pure PVDF–TrFE film with no additions, see Fig. 17b.
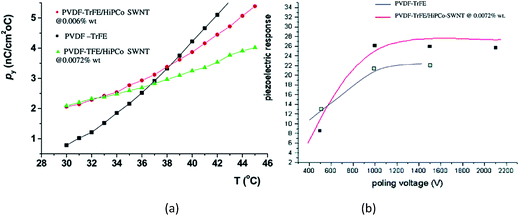 | ||
| Fig. 17 (a) Pyroelectric coefficient for P(VDF-co-TrFE) and it composites containing SWCNTs of approximately 0.01 wt%; (b) piezoelectric response (pC N−1) of composites at 0.0072 wt% as compared to the pure copolymer. Reprinted with permission from ref. 156. Copyright 2004 American Chemical Society. | ||
By directly melt-compounding PVDF with pristine MWCNTs of diameter of 20–40 nm and length 5–15 μm through a twin-screw extruder, Yuan et al.157 reported the relative permittivity of PVDF/MWCNTs composites to be as high as 3800, which is three orders of magnitude higher than pristine PVDF, while maintaining a low conductivity level at 10−5 S m−1. The enhancement was explained by a reinforced Maxwell–Wagner–Sillars effect due to the wrapping of PVDF chains on the MWCNTs surface and increased interfacial interactions, but the effect of the pristine MWCNTs on the piezoelectric active phase of PVDF was not reported and is of interest for further study.
Without additional post-treatment, only a trace amount of β-phase PVDF could be formed in PVDF/CNT nanocomposites when processed by melt-cooling158,159 and melt-spinning.160 One of the benefits of the inclusion of nanoparticles in PVDF is that the crystalline structures of PVDF can be tuned using surface modified particles, without additional annealing or electrical poling treatment. The nucleating efficiency of three types of surface functionalised MWCNTs in β-phase PVDF were compared.159 The contents of the functional groups on the MWCNTs surface were carboxyl (–COOH ∼ 3 at%), amino (–NH2 ∼ 0.5 at%) and hydroxyl (–OH ∼ 1.2 at%), respectively. It was demonstrated that the NH2–MWCNTs induced the highest percentage of β-phase (17.4%) in PVDF,159 followed by OH–MWCNT (11.6%) and unmodified MWCNTs (9.4%). The nanocomposites containing COOH–MWCNTs had the lowest amount of β-phase (4.7%). It is believed that the combined effects of the dispersion of MWCNTs and the interfacial interactions account for the formation of β-phase in PVDF, as shown in Fig. 18. The NH2–MWCNTs and COOH–MWCNTs were melt-blended with PVDF/PMMA blends,161 and only the NH2–MWCNTs favoured the formation of β-phase, where both the pure blends and COOH–MWCNTs filled composites exhibited only β-phase after melt-mixing. This was ascribed to the preferable location of the NH2–MWNTs in the amorphous phases of PVDF and in the interlamellar regions of PVDF/PMMA (70/30).
 | ||
| Fig. 18 Schematic of the role of CNTs on the formation of the β-phase in PVDF: (a) the chemical bonding between functionalized CNTs and PVDF chains; (b) the adsorbed chains of PVDF on the surface of CNTs influenced by the dispersion of CNTs. Reproduced with permission from ref. 159. Copyright 2014 Elsevier. | ||
Ionic liquids are a good dispersant for CNTs. It was found that the addition of 2 wt% of pristine MWCNTs only induced 6.1% β-phase in PVDF162 after cooling from the melt. However, when the MWCNTs were modified with an ionic liquid (1-butyl-3-methylimidazolium hexafluorophosphate [BMIM]+[PF6]−), almost 100% β-phase was achieved in PVDF. This was thought to be due to the interactions between the planar imidazolium cations of the ionic liquid that were wrapped on the MWCNTs surface with the –CF2 bonds of the PVDF, thereby improving the dispersion of MWCNTs in the PVDF melt. In comparison, the incorporation of only a ionic liquid depressed the PVDF melt crystallization due to the miscibility of ionic liquid with PVDF and led to a higher content of polar β- and γ-phase compared to using pristine MWCNTs. This indicates the synergetic effects of MWCNTs and ionic liquids on the β-phase formation in PVDF during melt cooling. MWCNT covalently modified with 3-aminoethyl imidazolium bromide162 led to the formation of 100% β-phase in PVDF at only 1 wt% concentration by both solvent-casting and melt-blending processes.163 It was concluded that covalently linked ionic liquids with MWNTs is an efficient method to induce polar phase formation in PVDF compared to physically modified ionic liquids and MWNTs.
In addition to ionic liquids, MWCNTs modified by ester groups (e.g. –COOC2H5)164 and PMMA165 have been used to fabricate PVDF/CNT nanocomposites through solution-mixing, in which the fraction of β-phase was highly dependent on the modification of MWCNTs and their dispersion in the matrix. The ester (–COOC2H5)-functionalized MWCNTs (FMWCNTs)164 were well-dispersed in the PVDF matrix and the FMWCNTs facilitated the transformation of α- to the β-phase by the interaction of the ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group in the FMWCNTs and the
O group in the FMWCNTs and the ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) CF2 group of PVDF. However, only a maximum of 50% β-polymorph PVDF was achieved, even at a high loading of the FMWCNT in the melt-cooled samples. PMMA-grafted MWNTs via nitrene chemistry could induce the formation of an almost fully β-phase PVDF at a 5 wt% loading165 from solution-cast PVDF nanocomposites.
CF2 group of PVDF. However, only a maximum of 50% β-polymorph PVDF was achieved, even at a high loading of the FMWCNT in the melt-cooled samples. PMMA-grafted MWNTs via nitrene chemistry could induce the formation of an almost fully β-phase PVDF at a 5 wt% loading165 from solution-cast PVDF nanocomposites.
For a PVDF/PMMA (50/50) blend, the introduction of a small amount of acidized CNTs (0.2 and 0.5 wt%) accelerated PVDF crystallisation, and two types of spherulites were observed in the PVDF/PMMA blends, namely ring-banded spherulites and compact spherulites. The acceleration of the crystallization of the PVDF phase was attributed to the joint effects of CNT nucleation and inducing phase fluctuation between PVDF and PMMA during the crystallization process.166 As mentioned in Section 2.2.6, the fraction of PMMA in the blends governs the origin of polymorphism in the PVDF,118 while the effect of steady shear was found more pronounced in the blends rich in α-phase crystals.167
Composites based on PVDF filled with NH2–MWNTs showed two distinct structural relaxations in dielectric loss owing to mobility confinement of PVDF chains and smaller cooperative lengths. The aspect ratio of CNTs also affect the nature of the dispersion, nucleation and reinforcement of polymers. Two MWNTs with a similar diameter of 10–20 nm, and different lengths 5–15 μm (L-MWNT) and 1–2 μm (S-MWNT) were mixed with PVDF in DMF solutions. It was found that β-phase structures were formed for L-MWNT at 2 wt%, and a mixture of α- and β-phases were detected at below 2 wt% of L-MWNT. For the short S-WMNT, a mixture of α- and β-phases coexisted at a concentration at or below 2 wt%, which is believed to be due to the high-aspect-ratio CNT surface having more zigzag carbon atoms, which match with the all-trans conformation of the β-phase.168 Post-treatment can also induce a greater α- to β-phase transition and dipole orientation in PVDF nanocomposites. By mechanical stretching,169 a high phase transformation from α- to β-phase (≥96%) was achieved for nanocomposites with greater than 1.0 wt% carbon nanofibers (CNF). The AC conductivity of CNF/PVDF composites decreased significantly when the percolation threshold was raised from 1.0 to 4.2 wt% CNFs after stretching. This was attributed to the reduced crystallinity induced by the phase transformation from α- to β-phase as well as the CNF re-orientation.
The thermal conductivity of PVDF is approximately 0.22 W mK−1, and was increased to 0.47 W mK−1 after mixing the polymer with 10 wt% of CNT. With the addition of only 1 wt% GO, the thermal conductivity of PVDF/CNT/GO nanocomposites reached 0.95 W mK−1. In comparison, the thermal conductivity of PVDF/GO with 1 wt% of GO was only ∼0.27 W mK−1. Therefore, the presence of low intrinsic thermal conductive GO (0.14–2.87 W mK−1 (ref. 170)) may be of benefit for high heat transfer rates in pyroelectric applications; for example eqn (6) indicates a high rate of temperature change are needed to produce high pyroelectric currents. Although the crystallinity of the matrix in the PVDF/CNT/GO composites is decreased in comparison with PVDF/CNT composites, a large number of polar γ-phase crystallites were induced. The presence of GO facilitated the dispersion of CNTs and the formation of a denser CNT/GO network structure in the PVDF matrix is thought to be the reason for the enhanced thermal conductivity.171
PVDF composites containing TiO2 coated MWCNTs nanoparticles have been prepared through a solution-cast method,172 followed with mechanical rolling. A highly oriented structure with both PVDF lamella and TiO2–MWCNT core–shell structures (TiO2@MWCNTs) were formed, and such an aligned structure led to enhanced breakdown strength and a piezoelectric coefficient d33 of ∼41 pC N−1 when the particle loading was at 0.3 wt%; this is almost double that of the pure PVDF (see Table 1). MWCNTs were coated with a continuous layer of TiO2 nanoparticles (TiO2@MWCNTs) by a simple hydrothermal process and TiO2@MWCNTs/PVDF composites were prepared by solution casting. Compared to the pristine MWCNTs/PVDF composites, the TiO2@MWCNTs/PVDF composites had enhanced permittivity and lower dielectric loss. In addition, the breakdown strength of the TiO2@MWCNTs/PVDF composites was also improved, which is favourable for enhanced ferroelectric properties and storage.173
Therefore, the effects of CNT on the nucleation of β-phase of PVDF is mainly dependent on the surface charge–dipole interactions (surface chemistry), the particle size and concentration, as well as processing conditions (solvent, temperature, annealing, shearing, post-treatment).
2.2.7.5 Graphene additions. Graphene and its derivatives are effective nanoparticles for the modification of PVDF and its copolymers. The oxygen functional groups on the surface of GO or reduced graphene oxide (RGO) can interact with the –CF2 in PVDF via electrostatic interaction and/or hydrogen bonding, thereby benefiting the nucleation of ferroelectric γ- or β-phase.174,175
With a solvent casting route, approximately 100% of the polar ferroelectric β-phase was formed in PVDF/GO films with a 0.1 wt% GO content,175 and 80% of β-phase formed in PVDF/RGO films,176 which led to enhanced mechanical properties, relative permittivity and electric polarization. However, PVDF/graphene nanocomposites often suffer from higher dielectric loss and lower breakdown strength compared to composites employing insulating piezoelectric ceramics, this is due to the presence of high electric fields in the composite due the presence of electrically conductive filler.177 The volume fraction of the fillers should therefore be as low as possible in order to maintain high breakdown strength and energy density.
Surface modification of graphene or GO provides a route for enhancing the dispersion and interfacial interactions with polymers, thereby leading to higher composite performance at lower filler loadings. To evaluate the effects of surface functionalisation of graphene on the formation of β-phase in PVDF,178 a thermally-reduced exfoliated graphene (EG) with various oxygen-containing functional groups including fluorination-EG, ozone-EG, and PMMA-g-EG were added to PVDF through a solution-mixing method with a 0.5 wt% filler content. The β-phase fraction of PVDF for the variety of systems was PMMA-g-EG > ozone-EG > fluorination-EG > EG and was related to its specific interaction between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group of PMMA and the CF2 group of PVDF. In the frequency range of 102 to 107 Hz, the relative permittivity of the composites showed a linear relationship with the content of the carbonyl groups of the fillers, in the order of PMMA-g-EG > ozone-EG > fluorination-EG > EG. Among all the composites studied, the PVDF/PMMA-g-EG composite had the highest relative permittivity (ε′ = 18) at 100 Hz.
O group of PMMA and the CF2 group of PVDF. In the frequency range of 102 to 107 Hz, the relative permittivity of the composites showed a linear relationship with the content of the carbonyl groups of the fillers, in the order of PMMA-g-EG > ozone-EG > fluorination-EG > EG. Among all the composites studied, the PVDF/PMMA-g-EG composite had the highest relative permittivity (ε′ = 18) at 100 Hz.
When using an ionic liquid (IL) to modify graphene, for example, 1-hexadecyl-3-methylimidazolium bromide,179 both graphene and the IL play a positive role in the crystallisation of the β-phase in PVDF. This was ascribed to the existence of graphene–cation interaction between the imidazolium cation and the aromatic carbon ring structure, and the electrostatic interaction between the –CF2 group of the polymer backbone and imidazolium cation. The addition of 3 wt% of IL functionalized GO to PVDF promoted the formation of β-phase, and increased the melting temperature and glass transition temperature.180 The maximum increase in the storage modulus (73%), Young's modulus (333%) and tensile strength (628%) was at 3% filler concentration. A sharp increase of DC-conductivity of the composite to ∼10−2 S cm−1 occurred at the percolation threshold of 0.1 wt%. The relative permittivity increased from ε′ ∼ 7.5 for pure PVDF to ε′ ∼ 13.5 for 3% filler with a percolation threshold at 0.1 wt%.
PVDF/NH2-treated graphene nanodots (GNDs)/RGO nanocomposites were developed to utilise the synergetic effects of the RGO sheets and NH2-treated GNDs.181 The RGO sheets promoted the formation of β-phase by disrupting the nucleation of α-phase in the PVDF. The –NH2 groups attached on the surfaces of GNDs to effectively interact with the PVDF, thereby stabilising the polar β- or γ-phases. The resulting PVDF/NH2-treated GND/RGO nanocomposites exhibited a higher relative permittivity (ε′ ≈ 61) and larger energy density (Ue ≈ 14.1 J cm−3) compared to pristine PVDF (ε′ ≈ 11.6 and Ue ≈ 1.8 J cm−3).
The addition of GO, magnetic iron oxide (Fe3O4) nanoparticles of size 10–12 nm, or the combination of both GO and Fe3O4 led to the transformation of PVDF from the α-phase to the β-phase, which may be due to the heterogeneous nucleating effects of the nanoparticles and interfacial interactions.182 With the addition of 5 wt% GO and 5 wt% Fe3O4, the maximum saturation polarisation was 0.065 μC cm−2, this is higher than PVDF (mainly α-phase, 0.038 μC cm−2) and PVDF/Fe3O4 (0.058 μC cm−2), but lower than that of PVDF/GO (0.1 μC cm−2), which may be due to the conducting nature of Fe3O4. A higher permittivity was observed for the composite films (ε′ = 12–19) than the pure PVDF film (ε′ ∼ 6), with a dielectric loss of approximately 0.6. The enhanced magnetic, ferroelectric, dielectric, magneto-dielectric coupling and structural properties of the PVDF/Fe3O4–GO nanocomposite films were attributed to the homogeneous dispersion and good alignment of Fe3O4 nanoparticles and GO in the PVDF matrix, along with a conversion of nonpolar α-phase PVDF to the polar β-phase.
For RGO–ZnO filled PVDF films,183 a α- to β-phase transformation was observed and a maximum content of 83% of β-phase was determined by FTIR. A decrease in the size of the spherulitic crystal structure of PVDF/RGO–ZnO nanocomposites was observed and a combination of RGO, ZnO and Fe3O4 led to approximately a 50% decrease of β-phase content in the PVDF films.176
However, with a Fe-doped RGO, a 99% of polar γ-phase was formed in PVDF when the Fe–RGO content was 2 wt%,184 which was thought to be due to electrostatic interactions among the –CH2 and –CF2 dipoles of PVDF and the delocalized π-electrons and oxygen functionalities of Fe–RGO via ion–dipole and/or hydrogen bonding interactions, as shown in Fig. 19a and b. The nanocomposite films generated an open circuit output voltage and short circuit current up to 5.1 V and 0.254 μA respectively on loading with a human finger as a piezoelectric energy harvester. In addition, the nanocomposite showed a higher electrical energy density of ≈0.85 J cm−3 at an electric field of 537 kV cm−1, higher than that of pristine PVDF of 0.27 J cm−3, as shown in Fig. 19c and d. This is of interest for combined harvesting and storage systems.
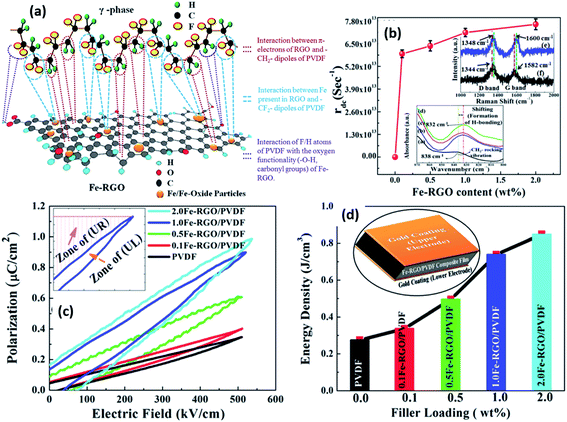 | ||
| Fig. 19 (a) Proposed interaction between the γ-phase of PVDF and an Fe–RGO nanosheet in the nanocomposites; (b) function of damping co-efficient with the filler concentration; (c) P–E loops of Fe–RGO/PVDF nanocomposites at different Fe–RGO concentrations (the inset shows the zone of released energy density (UR) and loss energy density (UL)); (d) variation in the released energy density at various filler concentrations. Adapted with permission from ref. 184. Copyright 2015 Royal Society Chemistry. | ||
A typical electrospinning apparatus consists of a syringe with a metal needle connected to a high voltage dc power supply. When the polymer solution is ejected through the metal tip at high voltage (7–30 kV), the pendant droplet at the syringe tip becomes electrified, and is distorted into a conical shape, known as the ‘Taylor cone’. This distortion is caused by the electrostatic repulsion between the surface charges and the coulombic force exerted by the external electric field.187 When the electrostatic repulsion between surface charges overcomes the surface tension of the solution, an electrified jet of polymer solution is ejected from the syringe tip and deposits onto a grounded collector, while mechanical stretching and electrical poling occur simultaneously during the fibre solidification process. Therefore, electrospinning can be a single process to induce preferential orientation and formation of ferroelectric dipoles in PVDF and its copolymers.188,189 The electrospinning parameters, such as applied voltage and electrode-to-collector distance (from less than 1 cm, up to 20 cm), solvent polarity, polymer molecular weight and concentration, and additives (BaTiO3,190 CNTs,191,192 Ag–CNT,188 clay,193 graphene, SiO2, and ionic liquid194) have considerable effects on the fibre morphology and properties. Subsequent treatments such as annealing and cooling, electrical poling, and compression can be applied to further enhance the crystallinity of the β-phase of the PVDF and its copolymers.97,191–193,195
2.2.8.1 β-phase content during electrospinning. Electrospinning favours the formation of β-phase formation or induces an α- to β-phase transformation due to its unique in situ electrical poling and mechanical stretching effects. The β-phase content in polymeric fibres is dependent on the solvent type, additives and electrospinning parameters. For example, when electrospinning PVDF from DMF solution, a β-phase fraction of 75% and a crystallinity in the range of 49–58% can be produced. It is evident that solvents with a higher dipole moment produce PVDF films with γ-phase crystallinity, while solvents with lower dipole moment result in the nonpolar α-phase. The formation of the ferroelectric β-phase can be controlled by the composition of the solvent, notably the water content.196 Using a hydrated salt in the casting solvent formed films with a high β-phase content. Table 2 summarises some typical results for effects of electrospinning parameters on the formation of the polar β-phase.
| Materials | Solvent | Mean field strength (kV cm−1) | Diameter of fibre (nm) | Comments |
|---|---|---|---|---|
PVDF (Mw = 687![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)197 000)197 |
DMF (10 wt%) | 7/15 | 200 | β-Phase content, F(β), of 75% |
PVDF (Mw = 534![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)215 000)215 |
DMSO/acetone (1/1) (18 wt%) | 14 kV rotating at 1900 rpm | 1600 | Under a tensile strain at 0.05% with a short period of 25 ms and frequency of 5 Hz, peak voltage is ∼−25 mV, peak current is ∼−7.9 nA |
| PVDF (Solef1010) | DMAA (25 wt%) | 10/15 | 400–500 | Conductivity of 1.6–2.0 × 10−3 S cm−1 |
PVDF (Mw = 275![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)216 000)216 |
DMF/acetone (4/6) (20–26 wt%) | 15/15 | 284–810 | F (β) = 85.9–82.5%. Fiber mat thickness 70 μm, output maximum of 2.2 V and 2.3 μA |
PVDF (Mw = 534![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)217 000)217 |
DMF/acetone (4/6) 16, 80, 4 wt% | 15/15 | 85 | F (β) = 85.2% rotating 800 rpm at different substrates: slide glasses, PET, PEN film and papers |
Solef 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 008, Mw = 115 008, Mw = 115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (ref. 192) 000 (ref. 192) |
DMF/acetone (6/4) (20 wt%)–CNT 0.01–0.1 wt% | 15 kV | 100 | Rotating disk collector (1500 rpm) induced highly orientated β-phase at very low SWCNT concentration as comparison to MWCNTs |
PVDF (Mw = 534![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)198,218 000)198,218 |
NMP/acetone (5/5) (16 wt%) | 7.5/10 | 100–200 | F (β) = 99% (rotating speed 800 rpm) FFES |
| P(VDF-TrFE) (65/35)219 | Methyl ethyl ketone (15 wt%) | 10/10 | 340 | Nanogenerator capable of producing an average of −0.4 to 0.4 V when deformed by 8 mN of cantilever pressure at 2 Hz and 3 Hz |
PVDF (Mw = 209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)206 000)206 |
DMF/acetone (6/4) 20 wt% [BMIM][PF6] 0–40 wt% | 20/15 | 200–400 | F (β) = 100% |
PVDF (Mw = 275![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)220 000)220 |
DMF/acetone (6/4) with Ce3+ complex/graphene | 12/10 | 80–85 | F (β) = 46%. A voltage of 11 V and 6.8 μW of maximum power have been achieved by the application of a 6.6 kPa of pressure amplitude to the ANG. For sound-driven generation, with an intensity of ∼88 dB was applied to the ANG, an AC output voltage of ∼3 V is obtained |
| P(VDF-TrFE)/PVDF (70/30)221 | DMF/acetone (6/4), 20 wt% | 12/20, and 200 rpm 1–4 inch electrode gap | — | 100% β-phase formed, and voltage outputs was enhanced by 27 fold as compared to stationary aligned fibers |
PVDF (Mn = 710![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)205 000)205 |
DMAc/THF (8/2), 29, 32, and 35 wt%, PVDF/PSF (30/70), PVDF/PAN (20/80) | 12/12 | 200 nm to 1 μm | For nonpolar PSN blend, mechanical stretching during electrospinning is more effective in inducing more ferroelectric phase; for polar PAN blend, strong intermolecular interactions plays a key role in forming β-phase |
By adjusting the electrospinning conditions to narrow the fibre diameter or increasing the electrospinning voltage, more β-phase was obtained, which is ascribed to the increased elongation and a larger electric field that acts as an increased poling field on the polymer jet.197 When electrospinning PVDF from a N-methyl-2-pyrrolidinone/acetone (5/5 v/v) mixed solution at 16 wt% concentration, PVDF nanofibers with 95% of β-phase were collected from a rotating drum at 800 rpm.198 When electrospinning 20 wt% PVDF from DMF/acetone (6/4 v/v) solution199 in the presence of 3 wt% of tetrabutylammonium chloride (TBAC), almost pure β-phase fibres were produced. The TBAC salt is believed to facilitate the degree of hydrogen bonding between water molecules and the fluorine atoms of the PVDF and hence induce more trans-conformation. In contrast, only the α- and γ-phase was detected in the spin-coated samples from the same solutions. It is believed that the TBAC additive induced local conformational changes and electrospinning promotes inter-chain interactions.
A higher fraction of polar β-phase can generally lead to higher d33 piezoelectric coefficients,34 and therefore a higher voltage output in energy harvesting applications, however the piezoelectric performance of PVDF fibers is also affected by the total dipole moment, i.e., the orientation of dipoles that is closely related to the poling effect.
2.2.8.2 Orientation of molecular dipoles during electrospinning. Given the high applied electrostatic fields and polymer jet characteristics of the electrospinning process, it is believed that electrospinning can not only facilitate more ferroelectric phase formation, but also induce dipole orientation in the polymer fibres. A number of studies have reported flexible, high-output piezoelectric nanogenerators based on PVDF fibers using near-field electrospinning (NFES) or conventional far-field electrospinning (FFES) processes.200,201,201–203 However, the effects of the electrospinning process on the dipolar orientation of the polymer fibres are still not fully understood and conflicting results have been reported.202,203
During electrospinning, a polymer solution experiences a number of forces. The first is a shear force when it flows through a capillary needle at a high rate. The second is a coulombic force when the jet is elongated and accelerated by the applied electric field. When a rotation disk collector is used to collect the fibers, a mechanical force may also be applied. These three forces can cause polymer chains to be aligned and/or stretched in the spinning direction. Using a rotating drum or disk as a fibre collector can exert an additional mechanical stretching, and promotes the formation and alignment of the c-axis of the β-phase crystallites along the fiber axis.199 One study204 reported that rotation of the collecting drum has a pivotal role in the enhancement of β-phase formation and degree of the orientation of the fibers in the electrospun mats. However, another study found that the degree of orientation and the polymorphism behaviour of the fibres did not vary significantly with either the rotating disk speed or the size of the spinneret used.199 This implies that the formation of the β-phase is likely to be caused by the coulombic force imposed by the electric field rather than the mechanical and shear force exerted by the rotation disk collector and spinnerets.
The coulombic force may cause conformational changes to the straighter TT conformation, and hence promote the formation of β-phase. To seek evidence of dipole orientation during the electrospinning process, Sun et al.198 compared electrospun PVDF nanofibers with fibres made by a force-spinning process (mechanical stretching without electrostatic force), in which the nanofibers were produced by an electrostatic force and a centrifugal force. It was found that both fibrous mats formed showed aligned PVDF fibres with a high β-phase content of 95%. However, the force-spun PVDF fibers did not show piezoelectricity, although it had a high β-phase content, since the mechanical force may only induce a phase transformation, but fails to align the ferroelectric dipoles. In comparison, the FFES process can lead to an electric poling field (∼1 kV cm−1) on the polymer jet, thus inducing polarization of the crystallites with a preferential orientation along the fibres; see Fig. 20.
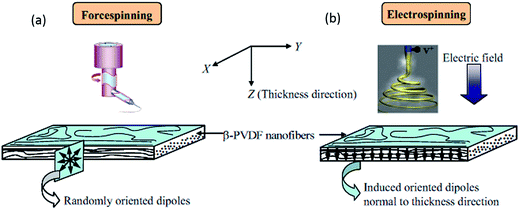 | ||
| Fig. 20 Representation of the dipole arrangement in the fibre mats produced by force-spinning (a) and electrospinning (b) reproduced with permission from ref. 198. Copyright 2015 Springer. | ||
A study on PVDF/polar polyacrylonitrile and PVDF/nonpolar polysulfone nanofibers205 concluded that mechanical stretching is more effective than electric poling to induce the formation of ferroelectric phases. The β-phase was more stable in the polar polyacrylonitrile blends than in the nonpolar polysulfone/PVDF blends, which indicates that apart from the mechanical stretching, the local electric field–dipole interactions determine the nucleation and growth of polar PVDF phases. This reflects that electrical poling is more effective than mechanical stretching in enhancing the piezoelectric properties of PVDF nanofibers.205
2.2.8.3 Synergistic effects of nanoparticles and electrospinning. While the benefits of nanocomposites have been discussed, the addition of nanoparticles has also been used in the electrospinning process. The possible mechanism of the formation of β-phase PVDF with the aid of templates with a large surface area is proposed in Fig. 21.
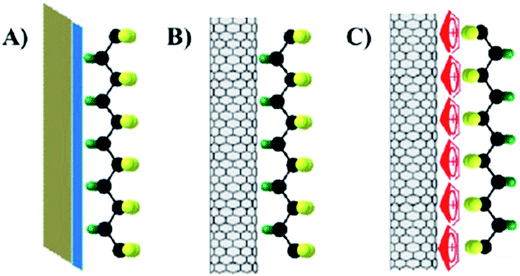 | ||
| Fig. 21 Schematic representation of formation for polar β-PVDF with the aid of the tangible templates of (A) OMMT,149 (B) pristine CNTs,155 and (C) ionic liquid modified CNTs. Reproduced with permission from ref. 206. Copyright 2014 American Chemical Society. | ||
Both OMMT149 or modified CNTs,162,206 with their intrinsically large aspect ratio, are capable of interacting with the positive charged –CH2 or negative –CF2 groups of PVDF, resulting in the large scale conformation of polar phases, in particular the β-phase. Clay can increase and stabilise the polar phase in PVDF fibres,207 and act as a processing agent to facilitate electrospinning.208 Particles with a smaller aspect ratio, such as Ag, metal salts or ionic liquid, also induce the formation of polar β-phases, but are not as effective as the particles with a high aspect ratio. Electrospun PVDF/room-temperature ionic liquid (RTIL) composite nanofibers206 based on 1-butyl-3-methylimidazolium hexafluorophosphate [BMIM][PF6], exhibited almost 100% of β-phase, which differs from the dominant γ-phases observed for melt-blended PVDF/RTIL blends.209
Two different nanoscale particles: carboxyl–MWCNTs and Ag-doped MWCNTs were used to modify the piezoelectric coefficient of PVDF electrospun fibers.188 The high voltage electrostatic field generated extensional forces on the polymer chains that aligns dipoles. The Ag–CNTs filled PVDF electrospun fibers exhibited the highest piezoelectric coefficient (d33 = 54 pm V−1) in contrast to PVDF/CNT fibers (35 pm V−1) and pure PVDF (30 pm V−1). In another study, silver nanowires (AgNWs) doped PVDF fibers were electrospun in a mixed DMF/acetone solution.210 The β-phase content in the PVDF was increased by the presence of AgNWs, and the piezoelectric coefficient d33 was 29.8 pC N−1 for the nanofibers webs containing 1.5 wt% AgNWs, which is close to that of P(VDF-co-TrFE) (77/23).
Additives can aid the electrospinning process, and also improve the piezoelectric performance of the composites fibers. The presence of inorganic salt LiCl of 0.00133 wt% in PVDF DMF/acetone (4/6) solution in 16 wt% concentration,211 decreased the fiber diameter from 340 nm to 65 nm due to the increased charge carried by the jet, and increased the β-phase formation to 93.6%. The voltage response of PVDF was increased from 1.89 V to 8 V for composite fibers with 0.00133 wt% of LiCl, which is of interest for harvesting. Alternatively, increasing the collector drum speed up to 8.4 ms−1 lead to the alignment of β-crystallites along the fiber axis without a significant effect on the formation of β-phase and output voltage. The addition of acetic acid significantly reduced the density and size of the beads, while the addition of TBAC effectively removed all traces of beads from the electrospun fibers. The β-phase enhancement induced by TBAC is likely to be caused by the hygroscopic nature of the salt, which retains water in the fibers and leads to hydrogen bonding between the water molecules and the fluorine atoms of PVDF.196
Non-woven fiber mats of PVDF/BaTiO3 nanocomposites212 with randomly oriented fiber diameters ranging between 200 nm and 400 nm have been fabricated. The PVDF electrospun mats exhibited a mixed crystalline phase consisting of both α- and β-phases. However, the addition of BaTiO3 was found to result in an increase in the β-phase content in electrospun PVDF/BaTiO3 mats. By increasing the fibre alignment in the PVDF fibrous membranes, the piezoelectric response was enhanced.213 For randomly orientated membranes with a BaTiO3 concentration of 20 wt%, the output voltage was 0.1 V and corresponded to a 7 mm displacement at 1 Hz.185 By uniaxial-alignment of the composite fibres, the piezoelectric output voltage was increased with increasing BaTiO3 concentration, and reached 0.48 V at 6 mm deflection, which is 1.7 times higher than PVDF fibers of 0.27 V when subjected to the same deformation, see Fig. 22.214 The increased piezoelectric response of uniaxial-aligned BaTiO3–PVDF nanofibers in comparison with randomly oriented PVDF fibers and thin films suggests their possible uses in energy harvesting and as power sources in miniaturized electronic devices such as wearable smart textiles and implantable biosensors.
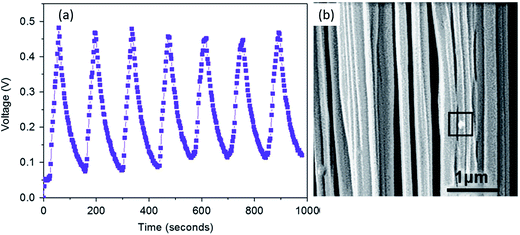 | ||
| Fig. 22 (a) Voltage generation as a function of time during cyclical fiber deflections of 6 mm using a PVDF nanofibrous bundle with 16 wt% BaTiO3; (b) SEM image of aligned PVDF/BaTiO3 fibres with 16 wt% BaTiO3. Adapted with permission from ref. 214. Copyright 2016 Elsevier. | ||
2.2.8.4 Electrospinning technology. A variety of electrospinning methods have been developed in order to produce aligned or doped nanofibers for energy applications. For example, PVDF nanofibers were produced by a bubble electrospinning technique, where the production rate of the obtained PVDF nanofibers was higher (13.93 mL h−1) than that of the reported traditional electrospinning (1–5 mL h−1).222 The crystallinity of the PVDF nanofibers was higher than in traditionally synthesized PVDF powders. PVDF fibers were also investigated via non-uniform field electrospinning where the air pressure and PET substrate thickness were varied to align the PVDF fibers, and increase the level of piezoelectricity.223 PVDF/Fe3O4 nanocomposite fibers were prepared under magnetic field assisted electrospinning.224 Two Helmholtz coils were mounted on the electrospinning apparatus to create a uniform magnetic field. The PVDF in DMF/acetone (3/1) solution with a concentration of 18 wt% were mixed with Fe3O4 nanoparticles in the size of 20–30 nm at PVDF ratios of 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 1
5, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and 1
10 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15. The application of an electromagnetic field during fiber deposition resulted in improved orientation of the polymer flow towards the grounded electrode and led to smoother fibers with diameters in the range of hundreds of nanometers. A magnetic field response of the nanofibers with higher magnetic fields was observed.
15. The application of an electromagnetic field during fiber deposition resulted in improved orientation of the polymer flow towards the grounded electrode and led to smoother fibers with diameters in the range of hundreds of nanometers. A magnetic field response of the nanofibers with higher magnetic fields was observed.
During the conventional electrospinning process, the fast evaporation of the solvent and the Coulomb forces generated among the induced charges inside the electrified jet causes the polymer jet to follow a curved shape.225 These cause the electrified jets to spin in a looping path towards the collector, and thus the bending instability results in randomly oriented nanofibers.226 Well-aligned nanofibers are often required for energy, sensor and biomedical applications,221,227 but their production by electrospinning remains technically challenging. Different techniques have been developed to produce unidirectional aligned fibers, such as modification of electrostatic field,228–230 mechanically wiring, and using a specially designed collector, including a fast rotating mandrel collector221,231 or a parallel-electrode collector.232
Centrifugal electrospinning221 applies a centrifugal force and disperses a PVDF solution through a capillary, which causes elongation and thinning of the solution jet, and the fiber is produced with no applied voltage. In a recent study, a hybrid centrifugal electrospinning process has been developed by integration of the concepts of the parallel-electrode electrospinning with centrifugal dispersion, that can produce highly aligned fibers at a large scale,221 see Fig. 23. Aligned PVDF fibers were prepared across three-inch electrode gaps at an applied voltage of 15 kV and a spinneret rotation speed of 200 rpm from a 20 wt% PVDF solution with 3 wt% TBAC. Randomly oriented fibers as well as aligned fibers produced by the parallel electrodes were also prepared. All fiber samples were 25 mm long with a cross-sectional area of 0.76 mm2. The samples were embedded in PDMS, connected via electrodes to a voltage-output analyzer and clamped onto a nanomechanical tester to produce controlled strain rates, as shown in Fig. 23a. The aligned fibers shown in Fig. 23b produced an output voltage of ∼3.04 mV at a strain of 0.10 compared to the only 0.059 mV for the randomly oriented fibers. Although the individual PVDF fibers in the randomly oriented specimen were likely to be poled, the randomly oriented poling directions in the membrane's bulk macrostructure resulted in a negligible response. A schematic of the centrifugal system is shown in Fig. 23f.
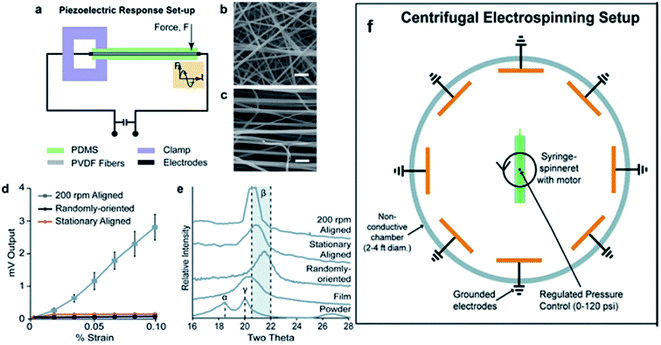 | ||
| Fig. 23 Centrifugal electrospinning for aligned PVDF nanofibers. (a) Schematic of the system employed to test the piezoelectric effect of PVDF nanofibers. Aligned nanofibers electrospun at 200 rpm, (b) randomly oriented fibers and (c) stationary spinneret-spun (parallel-electrode) fibers, all 25 mm in length were cast in PDMS, connected to electrodes, fixed via a clamp at one end and deflected at the opposite cantilever end. (d) Measured piezoelectric voltage output of fibers produced by the various fibrous systems. (e) XRD analysis of the PVDF with designated α-, β-, and γ-phases peak locations. (f) Schematic of the system configuration. Adapted with permission from ref. 221. Copyright 2012 Royal Society of Chemistry. | ||
In a rotating collector configuration, the polymer fibers are deposited and wrapped around a rotating mandrel. The degree of fiber alignment mainly depends on the mandrel rotational speed. By simply mounting two polyimide films onto a rotating cylindrical collector with a 1 mm gap from the collector surface, the air flow generated by the rotation of the collector can be redirected, and the electric field at the gap between the films can be altered; this is termed the ‘end-point’ control assembly method,233 as shown in Fig. 24. The deposition of nanofibers can therefore be controlled by the relative position of the gap and the collector. With this manufacturing setup, PVDF fiber bundles were electrospun when operated at the tip-to-collector distance of 6 cm, external applied voltage of 8 kV, and the two polyimide films separated by a distance of 5 mm. It was found that both the alignment and positioning controllability of the electrospun PVDF fibers were improved as compared with conventional electrospinning with a rotating cylindrical collector.
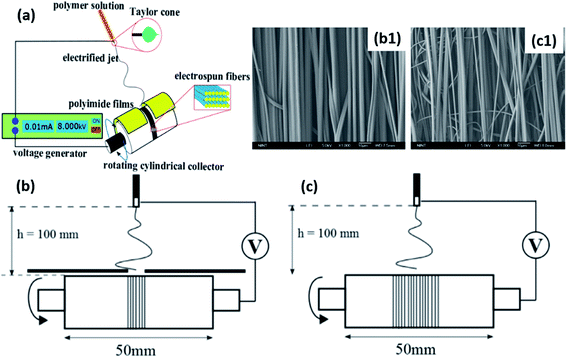 | ||
| Fig. 24 Images of (a) end-point control assembly (EpCA) electrospinning setup, where the rotating cylindrical collector was covered with two dielectric polyimide films; (b) schematics of end-point control assembly method, (c) conventional rotating collector with the width of 50 mm; SEM micrographs of PVDF fibers fabricated by (b1) the EpCA method when the gap d = 5 mm and the rotation speed was set at 3500 rpm, and (c1) the fibers fabricated by conventional electrospinning method at rotation speed 3500 rpm. Reprinted with permission from ref. 233. Copyright 2016 Elsevier. | ||
The electrospinning process can be classified according to the spinning distance, for example, near-field electrospinning (NFES, spinning distance < 1 cm), ‘short-distance’ electrospinning (spinning distance of 1–8 cm)195,234–239 and conventional electrospinning (spinning distance > 8 cm). The main characteristic of NFES is that the jet does not have a ‘whipping’ movement within the short spinning distance, and the macromolecular chains can align along the fiber length. In the conventional electrospinning process, the polymer jet undergoes whipping and solidification before it deposits on the substrate. The electrospinning of PVDF at a short spinning distance range (1–8 cm) can form highly interconnected fibers throughout the web. The mechanical properties are higher than fibers made by conventional electrospinning due to the interfiber connections stabilizing the fibrous structure.195 Both NFES and short-distance electrospun PVDF nanofibers could be more suitable for the development of robust energy harvesters.
In order to grow β-phase extended-chain crystallites in PVDF fibers, a high electric field (1.6 × 107 V m−1) elongates the polymer jet and a strong extensional force is applied when the glass tube collector rotated at 700–2100 rpm. A further introduction of CNTs enhances the β-phase formation, and the benefits of CNT additions have been discussed in Section 2.2.7.4. The PVDF fibers exhibited a large deflection under high electric field. Bending resulted in a mechanical strain (0.05–0.1%) that was distributed along the PVDF fibers, and the maximum voltage and current output of the piezoelectric energy harvesters were 43.6 mVpp and 240 nIpp at a 15 Hz impact frequency, respectively. A flexible energy harvester was made by patterning of ordered PVDF/poly(γ-methyl L-glutamate) (PMLG) composite fibers produced by NFES onto a PET film. The NFES process improved the piezoelectric properties of the PMLG/PVDF composites, resulting in better orientation of their dipoles, a high ultimate stress (27.5 MPa), and a high Young's modulus (2.77 GPa). The energy harvester could capture ambient energy with a maximum peak voltage of 0.08 V, a power of 637 pW, and the energy conversion efficiency is 3.3%. The electro-mechanical energy conversion efficiency of this PVDF/PMLG energy harvester was up to three times higher than those of pure PVDF and PMLG based energy harvesters.237 The NFES and hollow cylindrical near-field electrospinning (HCNFES) process was used to fabricate piezoelectric PVDF/MWCNT nanofibers.240 When comparing NFES and HCNFES, the HCNFES process applies a high electric field with an in situ mechanical stretching for alignment of dipoles along the longitudinal direction of PVDF nanofiber. Therefore, the PVDF nanofibers fabricated using HCNFES can be of smaller diameter and higher β-phase content with higher piezoelectric activity for harvesting.
3. Examples of structuring ferroelectric polymers in devices
This section describes some of the potential harvesting devices that exploit the properties of ferroelectric properties that have been optimised using the methods described above. The emphasis of this section is not on the design of the devices but to provide examples on how the optimisation of the ferroelectric properties of the polymers using the processes described in this review can lead to improved performance. Exploitation of the ferroelectric materials will be achieved by a combination of both harvester device design and optimisation of the structure of the piezoelectric material at a range of scales (molecular-, micro- and macro-structure). Since all pyroelectrics are piezoelectric, researchers have attempted to combine both pyroelectric and piezoelectric harvesting approaches. Table 3 compares the relevant equations for a pyroelectric subjected to a temperature change (ΔT) and piezoelectric subjected to a stress (Δσ) with similarities in the relationships between current, voltage and stored energy. Due to their similarities there is interest in hybrid piezoelectric–pyroelectric harvesting systems241–244 whereby a combination of temperature change and stress is applied. In such systems care must be taken to ensure the changes in polarisation are constructive and enhance the power generation of the harvesting device.241 As discussed by Sebald et al., the frequencies of temperature and vibration can be different and there is a need to optimise the electronics for such a hybrid system.245Flexible and stretchable piezo- and pyro-electric generators have attracted considerable attention in energy harvesting systems, especially in wearable and portable electronics, electronic skins, touch screens and electronic textiles. The challenges of flexible and stretchable nanogenerators include the limited output power generation, low efficiency at low frequency, mechanical weakness, low stability and durability. The flexibility and stretchability of the devices rely on the intrinsic mechanical properties of polymers and elastomers, or they can be realised by intelligent design of the device structures.246 For instance, through the fabrication of foam-like structures, micro-patterning,243 arch-shape assembly, electrospun membranes and textiles. The use of structuring technologies expands the range of potential materials from elastomer to semi-crystalline polymers, and hybrid nanocomposites. Nanostructuring can also enhance output power density by integration of piezo- and pyro-electric generators with other harvesting mechanisms, such as the triboelectric effect, and energy storage devices.
3.1 Curved and multi-layered structured devices
A stretchable hybrid piezo- and pyro-electric energy harvester was fabricated by using micro-patterned PDMS/CNTs composite as an electrode, which also makes the nanogenerator stretchable and flexible. Graphene was used as a top electrode for improved heat transfer, and a P(VDF-co-TrFE) copolymer layer provided piezo- and pyro-electric performance, as described in Section 2.2.1. Under the effects of a thermal gradient and mechanical strain from 0 to 30%, the pyroelectric output voltage was stable at 0.4 V.243 The potential of the material to harvest both mechanical loads (σ) and temperature changes (ΔT) was examined. The total change in polarisation is expressed as:| ΔP = (d × σ) + (p × ΔT) | (12) |
A multilayered flexible PVDF curved generator was studied by investigating the effects of using a curved structure and tailoring the substrate material.246 By stretching the device to a 1 cm displacement in the x-direction, the PVDF film, without a polyimide substrate, generated a low output voltage of only 0.1 V, while with a substrate it generated over 100 V. In addition, PVDF with a curved structure generated 86 V, in comparison to a flat PVDF film that only produced 15.7 V. As a result, the attachment to a substrate to a curved structure allowed the PVDF to be subjected to a higher external force, and induces a higher stress and produces a higher output power. The multi-layered curved nanogenerator produced a peak output voltage of ∼200 V and a peak output current of ∼2.7 mA. The output power density of the generator reached ∼17 mW cm−2, which could illuminate over 950 LED bulbs. This concept was reported to provide the groundwork to enhancing the output power of conventional piezoelectric generators, thereby enabling novel approaches to realizing self-powered systems.
A hybrid piezoelectric/triboelectric generator247 was fabricated by vertically-stacking two functional layers, as shown in Fig. 25. An arch-shaped piezoelectric generator with a Au/PVDF/Au structure on the top, and a touch-and-release type triboelectric generator with a PTFE/Al structure on the bottom. In the triboelectric generator, electrical charges are generated due to the charge transfer between two thin organic/inorganic films that exhibit a different surface electron affinity. The arch-shaped piezoelectric generator produced electricity by the d31 mode. The device had a common shared electrode as a bottom electrode of the piezoelectric generator and as a driving electrode of the triboelectric generator. With two full-wave bridge diodes connected to the hybrid generator, the piezoelectric and triboelectric outputs were effectively combined. The hybrid open-circuit output voltage and current density were approximately 370 V and 12 mA cm−2, respectively, and the output power density was ∼4.44 mW cm−2. The hybrid nanogenerator produced a high output power even at a mechanical force of as small as 0.2 N, enough to light 600 LEDs.
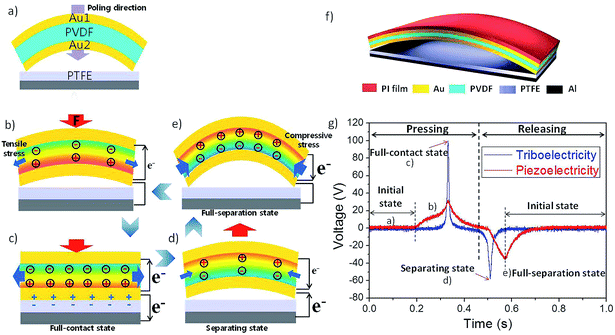 | ||
| Fig. 25 Working mechanism of the hybrid generator in a press-and-release cycle. (a) Initial state without a mechanical force. (b) Piezoelectric potential when the external force starts to be applied. (c) Piezoelectric and triboelectric charge distribution at full-contact state. (d) Negative piezoelectric and triboelectric generation at separating state. (e) Maximized negative piezoelectric potential at full-separation state. (f) Schematic view of the arch-shaped piezo/triboelectric hybrid generator. (g) A graph of the piezo/triboelectric output voltages of the hybrid generator that are simultaneously measured in a single press-and-release cycle.247 Licensed under a Creative Commons Attribution 4.0 International License. | ||
3.2 Nanoconfinement based devices
P(VDF-co-TrFE) nanowires with a diameter of approximately 196 nm were prepared by using an AAO template-wetting method,248 with the nanoconfinement promoting high crystallinity and preferential molecular dipole orientation in the polymer nanowires; as discussed in Section 2.2.4. The as-prepared self-poled polymer nanowire exhibited a peak electrical output voltage of 3 V and peak output current of 5.5 nA when subjected to a strain rate of 0.1% s−1, which is comparable to those reported highest efficiency values estimated from electrospun nanowire generators.234 The energy conversion efficiency was approximately 11%.3.3 Foam-like structured devices
Meso- and micro-porous structures are important for tailoring the mechanical energy harvesting performance of polymer films.249 Porous PVDF nanogenerators have been fabricated by templating or electrospinning methods (Section 4) to further enhance the piezoelectric properties while providing the materials with stretchability and flexibility. In addition to tailoring the crystalline structures of PVDF-based materials, the pore size and porosity of the materials can also affect the properties. By using a templating method, mesoporous PVDF thin films were prepared by casting PVDF/ZnO nanoparticles solutions, following by etching of the ZnO nanoparticles, as shown in Fig. 26A. The benefits of nanocomposites and electrospinning nanocomposites have been discussed in Section 2.2.7 and 2.2.8, respectively. The pore size and porosity of the films were controlled by the size and volume fraction of the ZnO particles.249 With a ZnO particle size of 35–45 nm, the output voltage increased from 3.5 to 11 V as the porosity increased from 6.5 to 32.6% when the ZnO mass fraction increased from 10 to 50%, but the voltage decreased to 8.3 V as the porosity further increased to 45.5% at a ZnO mass fraction of 70 wt%. The mixing of ZnO with PVDF helped to from a higher fraction of β-phase in the PVDF, and reached a maximum fraction of β-phase at a ZnO content of 50 wt%, where the output voltage and current of the porous PVDF film nanogenerator 28 μm thick was 11 V and 9.8 μA at a frequency of 40 Hz, respectively.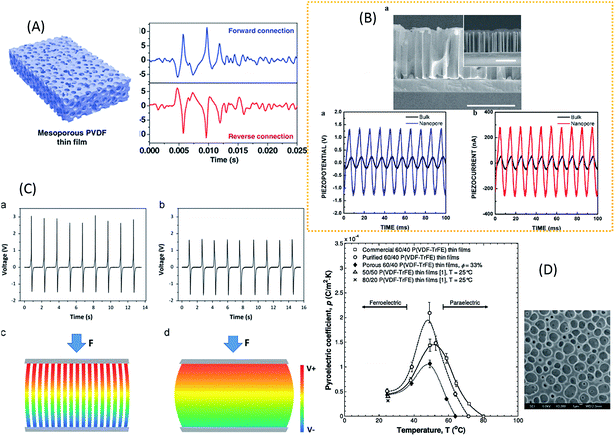 | ||
| Fig. 26 Images of (A) mesoporous PVDF thin film templated with ZnO nanoparticles, and the voltage output of a PVDF thin film NG (fabricated from a 50% ZnO mass fraction mixture) generated during one cycle of surface oscillation. The blue and red curves were collected under forward and reverse connections, respectively;249 (B) cross section SEM images. Scale bars are 5 μm. A porous PVDF nanostructure using a ZnO nanowire template, and the piezoelectric potential (blue) and piezoelectric currents (red) from the porous PVDF and bulk structure under the same force; adapted with permission from ref. 250. Copyright 2011 American Chemical Society. (C) Comparison of piezoelectric output of PVDF mesoporous film (left) and quasi-bulk film (right) after polarization under a 34 N compressive stress. Reproduced with permission from ref. 251. Copyright 2014 Elsevier. (D) Pyroelectric coefficient versus temperature for P(VDF-co-TrFE) (60/40) copolymer films, and SEM image of the film with porosity of 33%.253 | ||
Porous PVDF films were fabricated with a ZnO nanowire array template-assisted preparation method, as shown in Fig. 26B.250 With a sonic power of 100 dB at 100 Hz, the porous PVDF with a pore size of 2 μm showed an enhancement in the peak-to-peak piezoelectric potential (open circuit voltage)/piezoelectric current (short circuit current) with an output of 2.6 V/0.6 μA, which is over 5.2 times (piezoelectric potential) and six times (piezoelectric current) higher compared to that of the bulk film (0.5 V/0.1 μA). The device could produce a rectified power density of 0.17 mW cm−3. For the porous PVDF films with pores of 700–900 nm and 2.7 μm in thickness, an output voltage of 2.84 V and an electric field of 1.05 × 106 V m−1 were measured, which is ascribed to the geometrical strain confinement effect, as shown in Fig. 26C.251 The pore structure can reduce the strain on the orthogonal direction, to allow the development of strain that is confined to the axial direction. The porous structured nanogenerators showed a higher performance compared to fiber-like generators, such as a single PVDF nanofiber (30 mV/3 nA, 6.5 μm diameter/600 μm length),234 PVDF nanofibers (20 mV/0.3 nA, sample thickness and area were not indicated),202 PVDF mats (≈1 V, 100 μm thickness/1 cm2 area, output current not indicated),252 and PVDF nanofiber membranes (≈2.2 V/≈4.5 μA, 140 μm thickness/2 cm2 area).203
Porous P(VDF-co-TrFE) copolymer films have also been prepared via an immersion precipitation and phase inversion method,253 where the porosity can be varied by changing the type of solvent and nonsolvent. By using 15 wt% of P(VDF-co-TrFE) (60/40) copolymer in MEK with ethanol as a nonsolvent, a porous film with an average pore size of 2.2 μm and 33% porosity was produced. As shown in Fig. 26D, the porous film had a coercive field, Ec of 30.5 MV m−1, similar to those of commercial copolymer thin film, but the relative permittivity ε′ was 39.9 which is higher than commercially available thin film material (ε′ ∼ 28.8). The pyroelectric coefficient of commercial thin film and porous films were 4.5 × 10−5 and 4.3 × 10−5 C m−2 K−1 at room temperature, respectively, and both exhibited peak values of 1.4 × 10−4 and 1.2 × 10−4 C m−2 K−1 at 50 °C, respectively, which is the transition temperature from the ferroelectric β-phase to the paraelectric α-phase phase. In this case, the porous structure improved the thermal response of the films, but reduced the pyroelectric coefficient. Therefore, porous structure and porosity are a key features to tune the properties of the materials for harvesting applications.
3.4 Fibrous structured devices
As mentioned for electrospinning (Section 2.2.8), the NFES technique can produce in situ poled and well-aligned nanofibers in a continuous manner due to the strong electric fields (>107 V m−1)254 and stretching forces during the electrospinning process. It can realize direct-write and integrated PVDF nanogenerators with high energy conversion efficiency.234,255 The piezoelectric coefficient d33 is −63.25 pm V−1 for a single NFES fibre,238 or −57.6 pm V−1 for PVDF fibrous mats,256 which is twice as large than that reported for PVDF thin-films (about −15 pm V−1). The typical electrical outputs of the direct-write PVDF nanogenerators are 5–30 mV and 0.5–3 nA.215 In comparision, randomly distributed PVDF nanofibers prepared by conventional electrospinning process did not show a measurable electrical output. A number of serially integrated layers of the fabricated nanofiber were encapsulated in a device consisting of a PDMS polymer on a PVC substrate, and an increase of output voltage was obtained due to the increasing number of layers via a summing up the external piezoelectric potential. A nanogenerator that comprised 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rows of well-aligned PVDF NFs was able to create a peak output voltage of ∼4 V and a current of 75 nA. A three-layer integrated nanogenerator could reach a maximum output voltage and current up to 20 V and 390 nA, respectively. By attaching the nanofiber-based device on the human finger under a folding–releasing cycle at ∼45°, the output voltage and current could reach 0.8 V and 30 nA, respectively, making the nanofiber based devices promising for flexible and wearable electronics.238
000 rows of well-aligned PVDF NFs was able to create a peak output voltage of ∼4 V and a current of 75 nA. A three-layer integrated nanogenerator could reach a maximum output voltage and current up to 20 V and 390 nA, respectively. By attaching the nanofiber-based device on the human finger under a folding–releasing cycle at ∼45°, the output voltage and current could reach 0.8 V and 30 nA, respectively, making the nanofiber based devices promising for flexible and wearable electronics.238
Fig. 27a shows a hollow cylindrical near-field electrospinning setup.215 Large arrays of PVDF fibers were produced with a high concentration of β-phase. The fibers were deposited on a PET substrate and fixed with copper foil electrodes at both ends to form a flexible PVDF energy harvester, as shown in Fig. 27b. At a strain of 0.05%, a maximum peak voltage and current was measured to be 76 mV and 39 μA, respectively, as shown in Fig. 27c.215
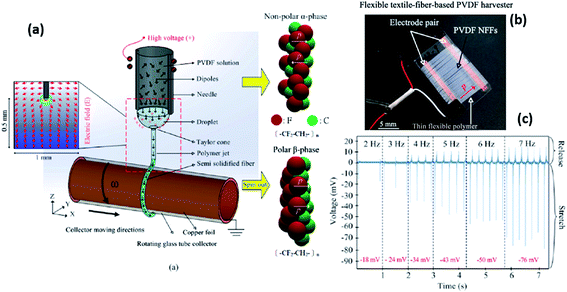 | ||
| Fig. 27 (a) Schematic of hollow cylindrical near-field electrospinning process showing possible directions of dipoles and the applied electric field; (b) design of a flexible textile-fiber-based PVDF harvester; (c) output voltage of flexible PVDF fiber-based harvester under different stretch and release cycling frequencies of 2–7 Hz with 0.05% strain.215 | ||
The co-doping of Ce3+ and graphene to PVDF electrospun nanofibers helped to align and achieve in situ poling of the polar ferroelectric crystal phases.220 The sensitivity and energy harvesting performance of the composite fibres were tested for different applications. As an ultrasensitive pressure sensor, it could detect a pressure as low as 2 Pa. As an acoustic nanogenerator, it generated an output voltage of 11 V and 6.8 μW of maximum power by the application of a 6.6 kPa of pressure amplitude, which could light up 10 blue light emitting diodes (LEDs). For sound-driven power generation, when a sound intensity of ∼88 dB was applied to the nanogenerator, an AC output voltage of approximately 3 V was obtained but no current was reported; however the device could power three blue LEDs. These properties are ascribed to the synergistic effects of graphene, Ce3+ doping and electrospinning. The electrospun nanogenerator was reported to be promising for application as a pressure sensor, mechanical energy harvester, and effective power source for portable electronic and wearable devices.
Single PVDF nanofiber prepared by NFES only show an electrical output in tens of millivolts under bending.234 With a metallic coaxial needle injector, hollow PVDF fiber tubes were produced by NFES. Near-field electrospinning was shown to enhance the energy harvesting performance of hollow PVDF piezoelectric fibers.235 The elongation of the fibre tubes was greater than that of solid PVDF fibers, with a tensile strength of 32.5 MPa. The output voltage of the fiber tubes was 71.7 mV with an external load resistance of 6 MΩ; the output power was also significantly greater (856 pW) than the solid PVDF fiber which has output voltage of 45.7 mV and the maximum output power of 347 pW. As a result, the power generation of the PVDF fiber tubes, while small in magnitude, was 2.46 times higher than that of the solid fibers. With a rotating glass tube collector, highly aligned PVDF nanofibers were produced by the NFES process.236
All-fibre piezoelectric fabrics nanogenerators257 were fabricated by assembly of knitted high β-phase (∼80%) piezoelectric PVDF monofilaments as the spacer yarn interconnected between silver coated polyamide multifilament yarn layers acting as the top and bottom electrodes. With an effective area of 15 cm × 5.3 cm, the 3D spacer piezoelectric fabrics exhibited an output power density in the range of 1.10–5.10 μW cm−2 at applied impact pressures of 0.02–0.10 MPa. This was reported to be higher than 2D woven and nonwoven piezoelectric structures. The piezoelectric fabrics can also be coupled with the knitted and screen printed supercapacitors for textile based energy harvesting storage in wearable electronics.258 Clearly, these harvesting devices demonstrate that the optimisation of PVDF at multiple scales can improve the performance of energy harvesting systems.
3.5 Copolymer and nanocomposite based devices
Copolymers and nanocomposite materials have been used to create energy harvesting devices. Bhavanasi et al. reported enhanced piezoelectric energy harvesting performance in bilayer films of poled PVDF–TrFE and graphene oxide (GO). Bilayer films of poled P(VDF-co-TrFE) and GO259 exhibited a voltage output of 4 V and power output of 4.41 μW cm−2 for energy harvesting as compared to poled P(VDF-co-TrFE) films alone that had a voltage output of 1.9 V and power output of 1.77 μW cm−2. The enhanced voltage and power output in the presence of the GO film was thought to be due to the combined effect of electrostatic contribution from the GO, residual tensile stress, enhanced Young's modulus of the bilayer films, and the presence of space charge at the interface of the P(VDF-co-TrFE) and GO films. The higher Young's modulus and relative permittivity of GO was thought to facilitate efficient transfer of mechanical and electrical energy. Zhao et al.260 produced piezoelectric nanocomposites composed of barium titanate nanoparticles with a PVDF matrix. By a simple and solvent evaporation process, the BaTiO3 nanoparticles and PVDF composites where formed with an oriented structure and the highest open-circuit voltage reached 150 V. Siddiqui et al.261 produced lead free and flexible piezoelectric nanogenerators based on a piezoelectric nanocomposite thin film of barium titanate nanoparticles embedded in a highly crystalline polyvinylidene P(VDF-TrFE) polymer for charge storage, Fig. 28. The nanocomposite with up to 40 wt% of BaTiO3 in the nanocomposite produced an output voltage of 9.8 V and output power density of 13.5 mW cm−2 under cyclic bending, comparable to the output of conventional inorganic polycrystalline lead zirconate titanate devices. The high performance of nanocomposite system was thought to be attributed to the high effective piezoelectricity of the crystalline P(VDF-TrFE) and BaTiO3.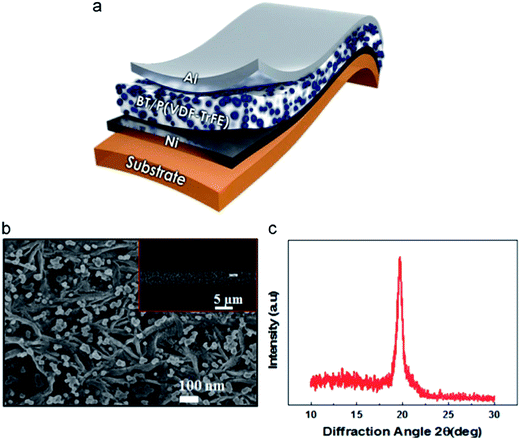 | ||
| Fig. 28 (a) Schematic nanocomposite device. (b) Top-view FE-SEM image of BaTiO3 (40 wt%)–P(VDF-TrFE) nanocomposite; (b, inset) cross-sectional FE-SEM image of the 6 mm-thick nanocomposite layer. (c) XRD spectrum of the highly crystalline P(VDF-TrFE) in the nanocomposite.261 Copyright 2015 Elsevier. | ||
4. Summary and perspective
This review has provided a detailed examination of the use of flexible PVDF based ferroelectrics for energy harvesting applications. The potential mechanisms by which a ferroelectric can harvest vibrations or thermal fluctuations has been explored. In terms of improving the ferroelectric properties for harvesting applications, a wide variety of properties of interest can be tailored. This can include the piezoelectric coefficients (such as d33 and d31), relative permittivity, pyroelectric coefficient, Curie temperature (Tc), the electric field required to activate and align dipoles in ferroelectric domains (coercive field, Ec) and the remnant polarization (Pr) which is related to the number of dipoles “locked” in after the poling process. The main ferroelectric phase of PVDF is the β-phase and approaches to maximise the fraction of the ferroelectric phase to optimise the ferroelectric, piezoelectric and pyroelectric properties of polymer materials are described in detail; these include the influence of polymer processing conditions, co-polymerisation, heat treatment, nanoconfinement, blending, porosity, ionic liquids, forming nanocomposites that contain dielectric or conductive fillers and electrospinning. A wide variety of processing conditions and methods are available to optimise the properties above for the desired application; a combination of these methods can also be exploited. While a number of these approaches have been used to design and tailor flexible material for harvesting applications, such as forming nanocomposites and electrospinning, some areas have yet to be explored, such as the use of nanoclays and ionic liquids. The majority of work concentrates on processing and experimental characterisation and opportunities exist for modelling these complex materials are a range of scales to inform the experimental efforts. The range of interactions and potential benefits are highlighted in Fig. 29. We have seen that concept of harvesting typically covers systems at relatively lower power levels (nW to mW) for applications such as low power electronics or for wireless sensors and reduce reliance on batteries, electric cables and provide autonomous sensors or devices. Less effort has considered the use of Olsen types cycle for higher power/larger thermal harvesting applications and are worthy of investigation.Applications include flexible and stretchable piezo- and pyroelectric generators have attracted considerable attention in energy harvesting systems, especially in wearable and portable electronics, electronic skin, medical devices touch screen and electronic textile with stretchable properties. Since ferroelectric polymers are both piezoelectric and pyroelectric properties, there is the prospect to harvest energy from multiple sources including vibration and thermal fluctuations so that the design of hybrid systems is possible. This can also be combined with additional ‘non-ferroelectric’ based harvesting mechanisms in polymers, such as tribo-electric effects. Ferroelectric polymers, such as PVDF and its copolymers can also be used as energy storage materials due to their high dielectric strength, permittivity and relaxor properties; therefore there is also scope for combining harvesting and storage applications, such as multi-layer structures and devices. While ceramic based materials with high Curie temperature and high ferroelectric activity are available the ability of polymers to be processed at low-temperatures, their low density, bio-compatibility, low stiffness, flexibility and mechanical robustness, such as toughness and high strains to failure will ensure there remains a number of applications where these materials are of continued interest for harvesting applications.
Acknowledgements
C. R. Bowen would like to acknowledge funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement no. 320963 on Novel Energy Materials, Engineering Science and Integrated Systems (NEMESIS).References
- Z. L. Wang and W. Wu, Angew. Chem., Int. Ed., 2012, 51, 11700–11721 CrossRef CAS PubMed.
- Z. L. Wang and W. Wu, Angew. Chem., 2012, 51, 2–24 CrossRef.
- Z. L. Wang, MRS Bull., 2012, 37, 814–827 CrossRef CAS.
- Z. L. Wang, Adv. Mater., 2012, 24, 4632–4646 CrossRef CAS PubMed.
- Z. L. Wang, R. Yang, J. Zhou, Y. Qin, C. Xu, Y. Hu and S. Xu, Mater. Sci. Eng., R, 2010, 70, 320–329 CrossRef.
- Z. L. Wang, G. Zhu, Y. Yang, S. Wang and C. Pan, Mater. Today, 2012, 15, 532–543 CrossRef CAS.
- X. Wang, Nano Energy, 2012, 1, 13–24 CrossRef CAS.
- Y. Qia and M. C. McAlpine, Energy Environ. Sci., 2010, 3, 1275–1285 Search PubMed.
- Z. L. Wang, Mater. Sci. Eng., R, 2009, 64, 33–71 CrossRef.
- P. Hiralal, H. Unalan and G. A. J. Amaratunga, Nanotechnology, 2012, 23, 194002 CrossRef PubMed.
- H. B. Radousky and H. Liang, Nanotechnology, 2012, 23, 502001 CrossRef CAS PubMed.
- K. A. Cook-Chennault, N. Thambi and A. M. Sastry, Smart Mater. Struct., 2008, 17, 043001 CrossRef.
- H. S. Kim, J. H. Kim and J. Kim, Int. J. Precis. Eng. Manuf., 2011, 12, 1129–1141 CrossRef.
- H. A. Sodano, D. J. Inman and G. Park, Shock Vib. Digest, 2004, 36, 197–205 CrossRef.
- A. Nechibvute, A. Chawanda and P. Luhanga, Smart Mater. Res., 2012, 2012, 853481 Search PubMed.
- P. D. Mitcheson, E. M. Yeatman, G. K. Rao, A. S. Holmes and T. C. Green, Proc. IEEE, 2008, 96, 1457–1486 CrossRef.
- Q. Li and Q. Wang, Macromol. Chem. Phys., 2016, 217, 1228–1244 CrossRef CAS.
- R. F. Fan, W. Tang and Z. L. Wang, Adv. Mater., 2016, 28, 4283–4305 CrossRef PubMed.
- Prateek, V. K. Thakur and R. K. Gupta, Chem. Rev., 2016, 116, 4260–4317 CrossRef CAS PubMed.
- K. S. Ramadan, D. Sameoto and S. Evoy, Smart Mater. Struct., 2014, 23, 033001 CrossRef.
- D. Zabek, J. Taylor, E. LeBoulbar, C. Bowen and R. Vaish, Adv. Energy Mater., 2015, 5, 1401891 CrossRef.
- C. R. Bowen, H. A. Kim, P. M. Weaver and S. Dunn, Energy Environ. Sci., 2014, 7, 25–44 CAS.
- S. B. Lang, Phys. Today, 2005, 58, 31–36 CrossRef CAS.
- R. W. Whatmore, Rep. Prog. Phys., 1986, 49, 1335–1386 CrossRef CAS.
- D. Lingam, A. R. Parikh, J. Huang, A. Jain and M. Minary-Jolandan, Int. J. Smart Nano Mater., 2013, 4, 229–245 CrossRef.
- C. R. Bowen, J. Taylor, E. LeBoulbar, D. Zabek, A. Chauhan and R. Vaish, Energy Environ. Sci., 2014, 7, 3836–3856 Search PubMed.
- P. Mane, J. Xie, K. K. Leang and K. Mossi, IEEE Trans. Sonics Ultrason., 2011, 58, 10–17 CrossRef PubMed.
- A. Cuadras, M. Gasulla and V. Ferrari, Sens. Actuators, A, 2010, 158, 132–139 CrossRef CAS.
- S. B. Lang and D. K. Das-Gupta, in Handbook of Advanced Electronic and Photonic Materials and Devices, ed. H. S. Nalwa, Academic Press, 2001, vol. 4, pp. 1–54 Search PubMed.
- Y. Yu, H. Sun, H. Orbay, F. Chen, C. G. England, W. Cai and X. Wang, Nano Energy, 2016, 27, 275–281 CrossRef CAS.
- H. S. Nalwa, Ferroelectric Polymers: Chemistry: Physics, and Applications, CRC Press, 1995 Search PubMed.
- P. Martins, A. C. Lopes and S. Lanceros-Mendez, Prog. Polym. Sci., 2014, 39, 683–706 CrossRef CAS.
- P. Martins, J. S. Nunes, G. Hungerford, D. Miranda, A. Ferreira, V. Sencadas and S. Lanceros-Méndez, Phys. Lett. A, 2009, 373, 177–180 CrossRef CAS.
- J. Gomes, J. S. Nunes, V. Sencadas and S. Lanceros-Mendez, Smart Mater. Struct., 2010, 19, 065010 CrossRef.
- K. Koga and H. Ohigashi, J. Appl. Phys., 1986, 59, 2142–2150 CrossRef CAS.
- H. Xu, J. Appl. Polym. Sci., 2001, 80, 2259–2266 CrossRef CAS.
- A. J. Lovinger, Science, 1983, 220, 1115–1121 CAS.
- J. L. Lutkenhaus, K. McEnnis, A. Serghei and T. P. Russell, Macromolecules, 2010, 43, 3844–3850 CrossRef CAS.
- M. Aldas, G. Boiteux, G. Seytre and Z. Ghallabi, 10th IEEE International Conference on Solid Dielectrics, 2010, DOI:10.1109/ICSD.2010.5568042.
- W. Künstler, M. Wegener, M. Seiß and R. Gerhard-Multhaupt, Appl. Phys. A: Mater. Sci. Process., 2002, 73, 641–645 Search PubMed.
- Y. Huan, Y. Liu and Y. Yang, Polym. Eng. Sci., 2007, 47, 1630–1633 CAS.
- B. Ameduri, Chem. Rev., 2009, 109, 6632–6686 CrossRef CAS PubMed.
- Z. Li, Y. Wang and Z.-Y. Cheng, Appl. Phys. Lett., 2006, 88, 062904 CrossRef.
- Z. Cheng, Q. Zhang, J. Su and M. E. Tahchi, in Piezoelectric and Acoustic Materials for Transducer Applications, ed. A. Safari and E. K. Akdoğan, Springer, US, Boston, MA, 2008, pp. 131–159, DOI:10.1007/978-0-387-76540-2_7.
- M. Lallart, P.-J. Cottinet, L. Lebrun, B. Guiffard and D. Guyomar, J. Appl. Phys., 2010, 108, 034901 CrossRef.
- K. Wongtimnoi, B. Guiffard, A. Bogner-Van de Moortèle, L. Seveyrat, C. Gauthier and J. Y. Cavaillé, Compos. Sci. Technol., 2011, 71, 885–892 CrossRef CAS.
- P. Frübing, A. Kremmer, R. Gerhard-Multhaupt, A. Spanoudaki and P. Pissis, J. Chem. Phys., 2006, 125, 214701 CrossRef PubMed.
- S. Hikosaka, H. Ishikawa and Y. Ohki, Electronics and Communications in Japan, 2011, 94, 1–8 CrossRef.
- O. Tsutomu and F. Eiichi, Jpn. J. Appl. Phys., 1998, 37, 3374 CrossRef.
- J. A. Malmonge, L. F. Malmonge, G. C. Fuzari, S. M. Malmonge and W. K. Sakamoto, Polym. Compos., 2009, 30, 1333–1337 CrossRef CAS.
- E. Fukada and Y. Ando, Int. J. Biol. Macromol., 1986, 8, 361–366 CrossRef CAS.
- W. Lehmann, N. Leister, L. Hartmann, D. Geschke, F. Kremer, P. Stein and H. Finkelmann, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 328, 437–445 CrossRef CAS.
- J. A. Christman, R. R. Woolcott, A. I. Kingon and R. J. Nemanich, Appl. Phys. Lett., 1998, 73, 3851–3853 CrossRef CAS.
- D. F. Crisler, J. J. Cupal and A. R. Moore, Proc. IEEE, 1968, 56, 225–226 CrossRef CAS.
- T. R. Shrout and S. J. Zhang, J. Electroceram., 2007, 19, 113–126 CrossRef.
- D. Berlincourt and H. Jaffe, Phys. Rev., 1958, 111, 143–148 CrossRef CAS.
- J. Zhang, Z. Wu, Y. Jia, J. Kan and G. Cheng, Sensors, 2012, 13, 367–374 CrossRef PubMed.
- I. Katsouras, K. Asadi, M. Li, T. B. van Driel, K. S. Kjaer, D. Zhao, T. Lenz, Y. Gu, P. W. M. Blom, D. Damjanovic, M. M. Nielsen and D. M. de Leeuw, Nat. Mater., 2016, 15, 78–84 CrossRef CAS PubMed.
- Z. Cui, N. T. Hassankiadeh, Y. Zhuang, E. Drioli and Y. M. Lee, Prog. Polym. Sci., 2015, 51, 94–126 CrossRef CAS.
- A. J. Lovinger, J. Appl. Phys., 1981, 52, 5934–5938 CrossRef CAS.
- Y.-J. Yu and A. J. H. McGaughey, J. Chem. Phys., 2016, 144, 014901 CrossRef PubMed.
- J. R. Gregorio and M. Cestari, J. Polym. Sci., Part B: Polym. Phys., 1994, 32, 859–870 CrossRef.
- A. Garton and M. H. George, J. Polym. Sci., Polym. Chem. Ed., 1973, 11, 2153–2167 CrossRef CAS.
- Y. Wu, S. L. Hsu, C. Honeker, D. J. Bravet and D. S. Williams, J. Phys. Chem. B, 2012, 116, 7379–7388 CrossRef CAS PubMed.
- Y. Li, S. Tang, M.-W. Pan, L. Zhu, G.-J. Zhong and Z.-M. Li, Macromolecules, 2015, 48, 8565–8573 CrossRef CAS.
- J. Yang, S. Pruvost, S. Livi and J. Duchet-Rumeau, Macromolecules, 2015, 48, 4581–4590 CrossRef CAS.
- J. S. Lee, A. A. Prabu and K. J. Kim, Polymer, 2010, 51, 6319–6333 CrossRef CAS.
- E. Yamada, A. Nishioka, H. Suzuki, G. Murasawa, K. Miyata, T. Koda and S. Ikeda, Polym. J., 2009, 41, 383–388 CrossRef CAS.
- D. Song, D. Yang and Z. Feng, J. Mater. Sci., 1990, 25, 57–64 CrossRef CAS.
- M.-M. Tao, F. Liu, B.-R. Ma and L.-X. Xue, Desalination, 2013, 316, 137–145 CrossRef CAS.
- S. Ramasundaram, S. Yoon, K. J. Kim, J. S. Lee and C. Park, Macromol. Chem. Phys., 2009, 210, 951–960 CrossRef CAS.
- N. Kei, I. Kenji, H. Toshihisa, Y. Hirofumi and M. Kazumi, Jpn. J. Appl. Phys., 2003, 42, L1334 CrossRef.
- W. J. Kim, M. H. Han, Y.-H. Shin, H. Kim and E. K. Lee, J. Phys. Chem. B, 2016, 120, 3240–3249 CrossRef CAS PubMed.
- G. Chen, M. Nie and Q. Wang, J. Vinyl Addit. Technol., 2016 DOI:10.1002/vnl.21532.
- B. Mohammadi, A. A. Yousefi and S. M. Bellah, Polym. Test., 2007, 26, 42–50 CrossRef CAS.
- T.-C. Hsu and P. H. Geil, J. Mater. Sci., 1989, 24, 1219–1232 CrossRef CAS.
- C. M. Hess, A. R. Rudolph and P. J. Reid, J. Phys. Chem. B, 2015, 119, 4127–4132 CrossRef CAS PubMed.
- J. Shklovsky, L. Engel, Y. Sverdlov, Y. Shacham-Diamand and S. Krylov, Microelectron. Eng., 2012, 100, 41–46 CrossRef CAS.
- S. Maji, P. K. Sarkar, L. Aggarwal, S. K. Ghosh, D. Mandal, G. Sheet and S. Acharya, Phys. Chem. Chem. Phys., 2015, 17, 8159–8165 RSC.
- Y. Chen, X. Chen, D. Zhou, Q.-D. Shen and W. Hu, Polymer, 2016, 84, 319–327 CrossRef CAS.
- F. Oliveira, Y. Leterrier, J.-A. Månson, O. Sereda, A. Neels, A. Dommann and D. Damjanovic, J. Polym. Sci., Part B: Polym. Phys., 2014, 52, 496–506 CrossRef CAS.
- Z. Hu, M. Tian, B. Nysten and A. M. Jonas, Nat. Mater., 2009, 8, 62–67 CrossRef CAS PubMed.
- J.-H. Cao, B.-K. Zhu, G.-L. Ji and Y.-Y. Xu, J. Membr. Sci., 2005, 266, 102–109 CrossRef CAS.
- T. Furukawa, Phase Transitions, 1989, 18, 143–211 CrossRef CAS.
- T. C. Chung and A. Petchsuk, Macromolecules, 2002, 35, 7678–7684 CrossRef CAS.
- T. Soulestin, V. Ladmiral, T. Lannuzel, F. Domingues Dos Santos and B. Ameduri, Macromolecules, 2015, 48, 7861–7871 CrossRef CAS.
- G. Teyssedre, A. Bernes and C. Lacabanne, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 879–890 CrossRef CAS.
- A. Aliane, M. Benwadih, B. Bouthinon, R. Coppard, F. Domingues-Dos Santos and A. Daami, Org. Electron., 2015, 25, 92–98 CrossRef CAS.
- A. J. Lovinger, T. Furukawa, G. T. Davis and M. G. Broadhurst, Polymer, 1983, 24, 1225–1232 CrossRef CAS.
- T. Yamada and T. Kitayama, J. Appl. Phys., 1981, 52, 6859–6863 CrossRef CAS.
- A. Gebrekrstos, M. Sharma, G. Madras and S. Bose, Cryst. Growth Des., 2016, 16, 2937–2944 CAS.
- C. Bourgaux-Leonard, J. F. Legrand, A. Renault and P. Delzenne, Polymer, 1991, 32, 597–604 CrossRef CAS.
- J. S. Green, B. L. Farmer and J. F. Rabolt, J. Appl. Phys., 1986, 60, 2690–2693 CrossRef CAS.
- T. Furukawa, J. X. Wen, K. Suzuki, Y. Takashina and M. Date, J. Appl. Phys., 1984, 56, 829–834 CrossRef CAS.
- J. F. Legrand, P. J. Schuele, V. H. Schmidt and M. Minier, Polymer, 1985, 26, 1683–1688 CrossRef CAS.
- K. Matsushige, K. Nagata, S. Imada and T. Takemura, Polymer, 1980, 21, 1391–1397 CrossRef CAS.
- J.-H. Bae and S.-H. Chang, Compo. Struct., 2015, 131, 1090–1098 CrossRef.
- B. Khomami and C. A. Langton, Polym. Eng. Sci., 1991, 31, 803–811 CAS.
- Q. Zhang, W. Xia, Z. Zhu and Z. Zhang, J. Appl. Polym. Sci., 2013, 127, 3002–3008 CrossRef CAS.
- S. Lanceros-Méndez, J. F. Mano, A. M. Costa and V. H. Schmidt, J. Macromol. Sci., Part B: Phys., 2001, 40, 517–527 CrossRef.
- R. Su, J.-K. Tseng, M.-S. Lu, M. Lin, Q. Fu and L. Zhu, Polymer, 2012, 53, 728–739 CrossRef CAS.
- A. Salimi and A. A. Yousefi, Polym. Test., 2003, 22, 699–704 CrossRef CAS.
- A. Salimi and A. A. Yousefi, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 3487–3495 CrossRef CAS.
- M. Benz and W. B. Euler, J. Appl. Polym. Sci., 2003, 89, 1093–1100 CrossRef CAS.
- V. Cauda, S. Stassi, K. Bejtka and G. Canavese, ACS Appl. Mater. Interfaces, 2013, 5, 6430–6437 CAS.
- C. Fu, X. Wang, X. Shi and X. Ran, RSC Adv., 2015, 5, 87429–87436 RSC.
- M. Pan, L. Yang, J. Wang, S. Tang, G. Zhong, R. Su, M. K. Sen, M. K. Endoh, T. Koga and L. Zhu, Macromolecules, 2014, 47, 2632–2644 CrossRef CAS.
- N. Soin, D. Boyer, K. Prashanthi, S. Sharma, A. A. Narasimulu, J. Luo, T. H. Shah, E. Siores and T. Thundat, Chem. Commun., 2015, 51, 8257–8260 RSC.
- M. Kanik, O. Aktas, H. S. Sen, E. Durgun and M. Bayindir, ACS Nano, 2014, 8, 9311–9323 CrossRef CAS PubMed.
- S. Chen, X. Li, K. Yao, F. E. H. Tay, A. Kumar and K. Zeng, Polymer, 2012, 53, 1404–1408 CrossRef CAS.
- D. Guo, F. Zeng and B. Dkhil, J. Nanosci. Nanotechnol., 2014, 14, 2086–2100 CrossRef CAS PubMed.
- J. Song, H. Lu, K. Foreman, S. Li, L. Tan, S. Adenwalla, A. Gruverman and S. Ducharme, J. Mater. Chem. C, 2016, 4, 5914–5921 RSC.
- C.-L. Liang, Z.-H. Mai, Q. Xie, R.-Y. Bao, W. Yang, B.-H. Xie and M.-B. Yang, J. Phys. Chem. B, 2014, 118, 9104–9111 CrossRef CAS PubMed.
- A. C. Lopes, I. C. Neves and S. Lanceros Mendez, J. Phys. Chem. C, 2015, 119, 5211–5217 CAS.
- Y. Li, J.-Z. Xu, L. Zhu, G.-J. Zhong and Z.-M. Li, J. Phys. Chem. B, 2012, 116, 14951–14960 CrossRef CAS PubMed.
- P. Martins, C. Caparros, R. Gonçalves, P. M. Martins, M. Benelmekki, G. Botelho and S. Lanceros-Mendez, J. Phys. Chem. C, 2012, 116, 15790–15794 CAS.
- A. C. Lopes, C. M. Costa, C. J. Tavares, I. C. Neves and S. Lanceros-Mendez, J. Phys. Chem. C, 2011, 115, 18076–18082 CAS.
- Q. Meng, W. Li, Y. Zheng and Z. Zhang, J. Appl. Polym. Sci., 2010, 116, 2674–2684 CAS.
- G. Ico, A. Showalter, W. Bosze, S. C. Gott, B. S. Kim, M. P. Rao, N. V. Myung and J. Nam, J. Mater. Chem. A, 2016, 4, 2293–2304 CAS.
- B. Wang, M. Yin, R. Lv, B. Na, Y. Zhu and H. Liu, J. Phys. Chem. B, 2015, 119, 14303–14308 CrossRef CAS PubMed.
- Q. Gao and J. I. Scheinbeim, Macromolecules, 2000, 33, 7564–7572 CrossRef CAS.
- A. Kaito, Y. Iwakura, Y. Li, K. Nakayama and H. Shimizu, Macromol. Chem. Phys., 2007, 208, 504–513 CrossRef CAS.
- R. G. Kepler and R. A. Anderson, Adv. Phys., 1992, 41, 1–57 CrossRef CAS.
- Y. Takase, J. W. Lee, J. I. Scheinbeim and B. A. Newman, Macromolecules, 1991, 24, 6644–6652 CrossRef CAS.
- Y. Li and A. Kaito, Macromol. Rapid Commun., 2003, 24, 603–608 CrossRef CAS.
- R. Ramani, V. Das, A. Singh, R. Ramachandran, G. Amarendra and S. Alam, J. Phys. Chem. B, 2014, 118, 12282–12296 CrossRef CAS PubMed.
- T. U. Patro, M. V. Mhalgi, D. V. Khakhar and A. Misra, Polymer, 2008, 49, 3486–3499 CrossRef CAS.
- P. Martins, C. M. Costa, J. C. C. Ferreira and S. Lanceros-Mendez, J. Phys. Chem. B, 2012, 116, 794–801 CrossRef CAS PubMed.
- T. G. Mofokeng, A. S. Luyt, V. P. Pavlović, V. B. Pavlović, D. Dudić, B. Vlahović and V. Djoković, J. Appl. Phys., 2014, 115, 084109 CrossRef.
- V. Tiwari and G. Srivastava, Ceram. Int., 2015, 41, 8008–8013 CrossRef CAS.
- E. Kar, N. Bose, S. Das, N. Mukherjee and S. Mukherjee, Phys. Chem. Chem. Phys., 2015, 17, 22784–22798 RSC.
- D. Mandal, K. J. Kim and J. S. Lee, Langmuir, 2012, 28, 10310–10317 CrossRef CAS PubMed.
- A. C. Lopes, S. A. C. Carabineiro, M. F. R. Pereira, G. Botelho and S. Lanceros-Mendez, ChemPhysChem, 2013, 14, 1926–1933 CrossRef CAS PubMed.
- S. K. Ghosh, T. K. Sinha, B. Mahanty and D. Mandal, Energy Technol., 2015, 3, 1190–1197 CrossRef.
- B. Dutta, E. Kar, N. Bose and S. Mukherjee, RSC Adv., 2015, 5, 105422–105434 RSC.
- J. Li, P. Khanchaitit, K. Han and Q. Wang, Chem. Mater., 2010, 22, 5350–5357 CrossRef CAS.
- O. D. Jayakumar, B. P. Mandal, J. Majeed, G. Lawes, R. Naik and A. K. Tyagi, J. Mater. Chem. C, 2013, 1, 3710–3715 RSC.
- P. Thakur, A. Kool, B. Bagchi, S. Das and P. Nandy, Phys. Chem. Chem. Phys., 2015, 17, 1368–1378 RSC.
- P. Anithakumari, B. P. Mandal, E. Abdelhamid, R. Naik and A. K. Tyagi, RSC Adv., 2016, 6, 16073–16080 RSC.
- S. Garain, T. K. Sinha, P. Adhikary, K. Henkel, S. Sen, S. Ram, C. Sinha, D. Schmeißer and D. Mandal, ACS Appl. Mater. Interfaces, 2015, 7, 1298–1307 CAS.
- S. Cho, J. S. Lee and J. Jang, Adv. Mater. Interfaces, 2015, 2, 1500098 CrossRef.
- S. Liu, S. Xiao, S. Xiu, B. Shen, J. Zhai and Z. An, RSC Adv., 2015, 5, 40692–40699 RSC.
- N. R. Alluri, B. Saravanakumar and S.-J. Kim, ACS Appl. Mater. Interfaces, 2015, 7, 9831–9840 CAS.
- P. Thakur, A. Kool, B. Bagchi, N. A. Hoque, S. Das and P. Nandy, RSC Adv., 2015, 5, 28487–28496 RSC.
- D. Yuan, Z. Li, W. Thitsartarn, X. Fan, J. Sun, H. Li and C. He, J. Mater. Chem. C, 2015, 3, 3708–3713 RSC.
- D. R. Dillon, K. K. Tenneti, C. Y. Li, F. K. Ko, I. Sics and B. S. Hsiao, Polymer, 2006, 47, 1678–1688 CrossRef CAS.
- Y. Wang, J. Li and Y. Deng, RSC Adv., 2015, 5, 85884–85888 RSC.
- D. Shah, P. Maiti, E. Gunn, D. F. Schmidt, D. D. Jiang, C. A. Batt and E. P. Giannelis, Adv. Mater., 2004, 16, 1173–1177 CrossRef CAS.
- S. Ramasundaram, S. Yoon, K. J. Kim and C. Park, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 2173–2187 CrossRef CAS.
- P. Cebe and J. Runt, Polymer, 2004, 45, 1923–1932 CrossRef CAS.
- J. Buckley, P. Cebe, D. Cherdack, J. Crawford, B. S. Ince, M. Jenkins, J. Pan, M. Reveley, N. Washington and N. Wolchover, Polymer, 2006, 47, 2411–2422 CrossRef CAS.
- M. M. Abolhasani, M. Naebe and Q. Guo, Phys. Chem. Chem. Phys., 2014, 16, 10679–10687 RSC.
- M. M. Abolhasani, F. Zarejousheghani, Z. Cheng and M. Naebe, RSC Adv., 2015, 5, 22471–22479 RSC.
- V. K. Tiwari, P. K. Kulriya, D. K. Avasthi and P. Maiti, ACS Appl. Mater. Interfaces, 2009, 1, 311–318 CAS.
- S. Yu, W. Zheng, W. Yu, Y. Zhang, Q. Jiang and Z. Zhao, Macromolecules, 2009, 42, 8870–8874 CrossRef CAS.
- N. Levi, R. Czerw, S. Xing, P. Iyer and D. L. Carroll, Nano Lett., 2004, 4, 1267–1271 CrossRef CAS.
- J.-K. Yuan, S.-H. Yao, Z.-M. Dang, A. Sylvestre, M. Genestoux and J. Bai, J. Phys. Chem. C, 2011, 115, 5515–5521 CAS.
- W. Mian, S. Jia-Hua, K. P. Pramoda and G. Suat Hong, Nanotechnology, 2007, 18, 235701 CrossRef.
- K. Ke, P. Pötschke, D. Jehnichen, D. Fischer and B. Voit, Polymer, 2014, 55, 611–619 CrossRef CAS.
- A. Lund, C. Gustafsson, H. Bertilsson and R. W. Rychwalski, Compos. Sci. Technol., 2011, 71, 222–229 CrossRef CAS.
- M. Sharma, K. Sharma and S. Bose, J. Phys. Chem. B, 2013, 117, 8589–8602 CrossRef CAS PubMed.
- C. Xing, L. Zhao, J. You, W. Dong, X. Cao and Y. Li, J. Phys. Chem. B, 2012, 116, 8312–8320 CrossRef CAS PubMed.
- A. Mandal and A. K. Nandi, ACS Appl. Mater. Interfaces, 2013, 5, 747–760 CAS.
- S. Manna and A. K. Nandi, J. Phys. Chem. C, 2007, 111, 14670–14680 CAS.
- A. Mandal and A. K. Nandi, J. Mater. Chem., 2011, 21, 15752–15763 RSC.
- C.-X. Feng, J. Duan, J.-H. Yang, T. Huang, N. Zhang, Y. Wang, X.-T. Zheng and Z.-W. Zhou, Eur. Polym. J., 2015, 68, 175–189 CrossRef CAS.
- M. Sharma, G. Madras and S. Bose, Phys. Chem. Chem. Phys., 2014, 16, 16492–16501 RSC.
- X. Huang, P. Jiang, C. Kim, F. Liu and Y. Yin, Eur. Polym. J., 2009, 45, 377–386 CrossRef CAS.
- L. L. Sun, B. Li, Z. G. Zhang and W. H. Zhong, Eur. Polym. J., 2010, 46, 2112–2119 CrossRef CAS.
- S. Timo, R. B. Brian, C. S. Niklas and P. Dimos, Nanotechnology, 2009, 20, 405704 CrossRef PubMed.
- W.-B. Zhang, Z.-X. Zhang, J.-H. Yang, T. Huang, N. Zhang, X.-T. Zheng, Y. Wang and Z.-W. Zhou, Carbon, 2015, 90, 242–254 CrossRef CAS.
- L. Yang, H. Ji, K. Zhu, J. Wang and J. Qiu, Compos. Sci. Technol., 2016, 123, 259–267 CrossRef CAS.
- L. Yang, J. Qiu, H. Ji, K. Zhu and J. Wang, Composites, Part A, 2014, 65, 125–134 CrossRef CAS.
- K. K. Sadasivuni, A. Kafy, L. Zhai, H. U. Ko, S. C. Mun and J. Kim, in Graphene-Based Polymer Nanocomposites in Electronics, 2015, pp. 67–90, DOI:10.1007/978-3-319-13875-6_4.
- M. El Achaby, F. Z. Arrakhiz, S. Vaudreuil, E. M. Essassi and A. Qaiss, Appl. Surf. Sci., 2012, 258, 7668–7677 CrossRef CAS.
- E. Abdelhamid, O. D. Jayakumar, V. Katari, B. P. Mandal, R. Rao, V. M. Naik, R. Naik and A. K. Tyagi, RSC Adv., 2016, 6, 20089–20094 RSC.
- Y. Li, X. Huang, Z. Hu, P. Jiang, S. Li and T. Tanaka, ACS Appl. Mater. Interfaces, 2011, 3, 4396–4403 CAS.
- S. Wang, L. Liu, Y. Zeng, B. Zhou, K. Teng, M. Ma, L. Chen and Z. Xu, J. Adhes. Sci. Technol., 2015, 29, 678–690 CrossRef CAS.
- Y. Hu, P. Xu, H. Gui, S. Yang and Y. Ding, RSC Adv., 2015, 5, 92418–92427 RSC.
- N. Maity, A. Mandal and A. K. Nandi, Polymer, 2015, 65, 154–167 CrossRef CAS.
- S. Cho, J. S. Lee and J. Jang, ACS Appl. Mater. Interfaces, 2015, 7, 9668–9681 CAS.
- O. D. Jayakumar, E. H. Abdelhamid, V. Kotari, B. P. Mandal, R. Rao Jagannath, V. M. Naik, R. Naik and A. K. Tyagi, Dalton Trans., 2015, 44, 15872–15881 RSC.
- B. Jaleh and A. Jabbari, Appl. Surf. Sci., 2014, 320, 339–347 CrossRef CAS.
- S. K. Karan, D. Mandal and B. B. Khatua, Nanoscale, 2015, 7, 10655–10666 RSC.
- J. Nunes-Pereira, V. Sencadas, V. Correia, J. G. Rocha and S. Lanceros-Méndez, Sens. Actuators, A, 2013, 196, 55–62 CrossRef CAS.
- S. Sharma, Adv. Mater. Lett., 2013, 4, 522–533 CrossRef.
- M. Zaccaria, D. Fabiani, A. Zucchelli and J. Belcari, 2015 IEEE Electrical Insulation Conference (EIC), 2015, 197–200 Search PubMed.
- M. Sharma, V. Srinivas, G. Madras and S. Bose, RSC Adv., 2016, 6, 6251–6258 RSC.
- D. Mandal, S. Yoon and K. J. Kim, Macromol. Rapid Commun., 2011, 32, 831–837 CrossRef CAS PubMed.
- C. Lee, D. Wood, D. Edmondson, D. Yao, A. E. Erickson, C. T. Tsao, R. A. Revia, H. Kim and M. Zhang, Ceram. Int., 2016, 42, 2734–2740 CrossRef CAS.
- H. Shao, J. Fang, H. Wang, C. Lang and T. Lin, ACS Appl. Mater. Interfaces, 2015, 7, 22551–22557 CAS.
- S. Huang, W. A. Yee, W. C. Tjiu, Y. Liu, M. Kotaki, Y. C. F. Boey, J. Ma, T. Liu and X. Lu, Langmuir, 2008, 24, 13621–13626 CrossRef CAS PubMed.
- Y.-L. Liu, Y. Li, J.-T. Xu and Z.-Q. Fan, ACS Appl. Mater. Interfaces, 2010, 2, 1759–1768 CAS.
- R. Mejri, J. C. Dias, A. C. Lopes, S. Bebes Hentati, M. M. Silva, G. Botelho, A. Mão de Ferro, J. M. S. S. Esperança, A. Maceiras, J. M. Laza, J. L. Vilas, L. M. León and S. Lanceros-Mendez, Eur. Polym. J., 2015, 71, 304–313 CrossRef CAS.
- Y. Ahn, J. Y. Lim, S. M. Hong, J. Lee, J. Ha, H. J. Choi and Y. Seo, J. Phys. Chem. C, 2013, 117, 11791–11799 CAS.
- M. Benz, W. B. Euler and O. J. Gregory, Macromolecules, 2002, 35, 2682–2688 CrossRef CAS.
- J. S. Andrew and D. R. Clarke, Langmuir, 2008, 24, 670–672 CrossRef CAS PubMed.
- T. Lei, L. Yu, G. Zheng, L. Wang, D. Wu and D. Sun, J. Mater. Sci., 2015, 50, 4342–4347 CrossRef CAS.
- W. A. Yee, M. Kotaki, Y. Liu and X. Lu, Polymer, 2007, 48, 512–521 CrossRef CAS.
- C. Chang, V. H. Tran, J. Wang, Y. K. Fuh and L. Lin, Nano Lett., 2010, 10, 726–731 CrossRef CAS PubMed.
- Z. H. Liu, C. T. Pan, L. W. Lin, J. C. Huang and Z. Y. Ou, Smart Mater. Struct., 2014, 23, 025003 CrossRef.
- B. J. Hansen, Y. Liu, R. Yang and Z. L. Wang, ACS Nano, 2010, 4, 3647–3652 CrossRef CAS PubMed.
- J. Fang, X. Wang and T. Lin, J. Mater. Chem., 2011, 21, 11088–11091 RSC.
- M. M. Abolhasani, S. Azimi and H. Fashandi, RSC Adv., 2015, 5, 61277–61283 RSC.
- G. Zhong, L. Zhang, R. Su, K. Wang, H. Fong and L. Zhu, Polymer, 2011, 52, 2228–2237 CrossRef CAS.
- C. Xing, J. Guan, Y. Li and J. Li, ACS Appl. Mater. Interfaces, 2014, 6, 4447–4457 CAS.
- R. Neppalli, S. Wanjale, M. Birajdar and V. Causin, Eur. Polym. J., 2013, 49, 90–99 CrossRef CAS.
- K. Yoon and A. Kelarakis, J. Nanomater., 2014, 367671 Search PubMed.
- C. Xing, M. Zhao, L. Zhao, J. You, X. Cao and Y. Li, Polym. Chem., 2013, 4, 5726–5734 RSC.
- B. Li, J. Zheng and C. Xu, Proc. SPIE 8793, Fourth International Conference on Smart Materials and Nanotechnology in Engineering, 2013, 879314, DOI:10.1117/12.2026758.
- F. Mokhtari, M. Shamshirsaz and M. Latifi, Polym. Eng. Sci., 2016, 56, 61–70 CAS.
- C. V. Chanmal and J. P. Jog, Int. J. Plast. Technol., 2011, 15, 1–9 CrossRef CAS.
- D. Edmondson, N. Bhattarai, S. Jana, A. Kim and M. Zhang, Appl. Phys. Lett., 2009, 94, 103101 CrossRef.
- C. Lee, D. Wood, D. Edmondson, D. Yao, A. E. Erickson, C. T. Tsao, R. A. Revia, H. Kim and M. Zhang, Ceram. Int., 2016, 42, 2734–2740 CrossRef CAS.
- Z. H. Liu, C. T. Pan, L. W. Lin, J. C. Huang and Z. Y. Ou, Smart Mater. Struct., 2014, 23, 025003 CrossRef.
- H. Shao, J. Fang, H. Wang and T. Lin, RSC Adv., 2015, 5, 14345–14350 RSC.
- B.-S. Lee, B. Park, H.-S. Yang, J. W. Han, C. Choong, J. Bae, K. Lee, W.-R. Yu, U. Jeong, U. I. Chung, J.-J. Park and O. Kim, ACS Appl. Mater. Interfaces, 2014, 6, 3520–3527 CAS.
- T. Lei, P. Zhu, X. Cai, L. Yang and F. Yang, Appl. Phys. A: Mater. Sci. Process., 2015, 120, 5–10 CrossRef CAS.
- L. T. Beringer, X. Xu, W. Shih, W.-H. Shih, R. Habas and C. L. Schauer, Sens. Actuators, A, 2015, 222, 293–300 CrossRef CAS.
- S. Garain, S. Jana, T. K. Sinha and D. Mandal, ACS Appl. Mater. Interfaces, 2016, 8, 4532–4540 CAS.
- D. Edmondson, A. Cooper, S. Jana, D. Wood and M. Zhang, J. Mater. Chem., 2012, 22, 18646–18652 RSC.
- N. Hernández-Navarro, V. González-González, I. E. Moreno-Cortez and M. A. Garza-Navarro, Mater. Lett., 2016, 167, 34–37 CrossRef.
- D. Wu, S. Huang, Z. Xiao, L. Yu, L. Wang, D. Sun and L. Lin, Smart Mater. Struct., 2014, 23, 025003 CrossRef.
- J. A. Gonzalez, R. Furlan, R. Lopez, L. M. Martinez and E. Fachini, MRS Online Proceeding Library Archive, 2014, 1659(2) Search PubMed.
- D. H. Reneker, A. L. Yarin, H. Fong and S. Koombhongse, J. Appl. Phys., 2000, 87, 4531–4547 CrossRef CAS.
- D. H. Reneker and A. L. Yarin, Polymer, 2008, 49, 2387–2425 CrossRef CAS.
- S. Agarwal, A. Greiner and J. H. Wendorff, Prog. Polym. Sci., 2013, 38, 963–991 CrossRef CAS.
- C. Hellmann, J. Belardi, R. Dersch, A. Greiner, J. H. Wendorff and S. Bahnmueller, Polymer, 2009, 50, 1197–1205 CrossRef CAS.
- D. Li, Y. Wang and Y. Xia, Nano Lett., 2003, 3, 1167–1171 CrossRef CAS.
- G. Viswanadam and G. G. Chase, Polymer, 2013, 54, 1397–1404 CrossRef CAS.
- A. Theron, E. Zussman and A. L. Yarin, Nanotechnology, 2001, 12, 384 CrossRef.
- A. Baji, Y.-W. Mai, S.-C. Wong, M. Abtahi and P. Chen, Compos. Sci. Technol., 2010, 70, 703–718 CrossRef CAS.
- D. N. Nguyen, Y. Hwang and W. Moon, Eur. Polym. J., 2016, 77, 54–64 CrossRef CAS.
- C. Chang, V. H. Tran, J. Wang, Y.-K. Fuh and L. Lin, Nano Lett., 2010, 10, 726–731 CrossRef CAS PubMed.
- C. T. Pan, C. K. Yen, S. Y. Wang, Y. C. Lai, L. Lin, J. C. Huang and S. W. Kuo, RSC Adv., 2015, 5, 85073–85081 RSC.
- Z. H. Liu, C. T. Pan, Z. Y. Ou and W. C. Wang, IEEE Sens. J., 2013, 13, 4098–4103 CrossRef CAS.
- C. T. Pan, C. K. Yen, H. C. Wu, L. Lin, Y. S. Lu, J. C. C. Huang and S. W. Kuo, J. Mater. Chem. A, 2015, 3, 6835–6843 CAS.
- Y. Xin, X. Qi, H. Tian, C. Guo, X. Li, J. Lin and C. Wang, Mater. Lett., 2016, 164, 136–139 CrossRef CAS.
- Z. H. Liu, C. T. Pan, L. W. Lin and H. W. Lai, Sens. Actuators, A, 2013, 193, 13–24 CrossRef CAS.
- Z. H. Liu, C. T. Pan, L. W. Lin, H. W. Li, C. A. Ke, J. C. Huang and P. S. Wang, The 8th Annual IEEE International Conference on Nano/Micro Engineered and Molecular Systems, 2013, 707–710 Search PubMed.
- K. Mossi, C. Green, Z. Ounaies and E. Hughes, J. Intell. Mater. Syst. Struct., 2005, 16, 249–261 CrossRef.
- Y. Yang, H. Zhang, G. Zhu, S. Lee, Z.-H. Lin and Z. L. Wang, ACS Nano, 2013, 7, 785–790 CrossRef CAS PubMed.
- J.-H. Lee, K. Y. Lee, M. K. Gupta, T. Y. Kim, D.-Y. Lee, J. Oh, C. Ryu, W. J. Yoo, C.-Y. Kang, S.-J. Yoon, J.-B. Yoo and S.-W. Kim, Adv. Mater., 2014, 26, 765–769 CrossRef CAS PubMed.
- M. Goudarzi, K. Niazi and M. K. Besharati, Mater. Phys. Mech., 2013, 16, 55–65 CAS.
- G. Sebald, E. Lefeuvre and D. Guyomar, IEEE Trans. Sonics Ultrason., 2008, 55, 538–551 CrossRef PubMed.
- W.-S. Jung, M. Lee, S.-H. Baek, I. K. Jung, S.-J. Yoon and C.-Y. Kang, Nano Energy, 2016, 22, 514–523 CrossRef CAS.
- W.-S. Jung, M.-G. Kang, H. G. Moon, S.-H. Baek, S.-J. Yoon, Z.-L. Wang, S.-W. Kim and C.-Y. Kang, Sci. Rep., 2015, 5, 9309 CrossRef CAS PubMed.
- R. A. Whiter, V. Narayan and S. Kar-Narayan, Adv. Energy Mater., 2014, 4, 1400519 CrossRef.
- Y. Mao, P. Zhao, G. McConohy, H. Yang, Y. Tong and X. Wang, Adv. Energy Mater., 2014, 4, 1301624 CrossRef.
- S. Cha, S. M. Kim, H. Kim, J. Ku, J. I. Sohn, Y. J. Park, B. G. Song, M. H. Jung, E. K. Lee, B. L. Choi, J. J. Park, Z. L. Wang, J. M. Kim and K. Kim, Nano Lett., 2011, 11, 5142–5147 CrossRef CAS PubMed.
- L. Xing, Y. Nie, X. Xue and Y. Zhang, Nano Energy, 2014, 10, 44–52 CrossRef CAS.
- D. Dhakras, V. Borkar, S. Ogale and J. Jog, Nanoscale, 2012, 4, 752–756 RSC.
- A. Navid, C. S. Lynch and L. Pilon, Smart Mater. Struct., 2010, 19, 055006 CrossRef.
- J. Chang, M. Dommer, C. Chang and L. Lin, Nano Energy, 2012, 1, 356–371 CrossRef CAS.
- Y.-K. Fuh, J.-C. Ye, P.-C. Chen, H.-C. Ho and Z.-M. Huang, ACS Appl. Mater. Interfaces, 2015, 7, 16923–16931 CAS.
- J. Pu, X. Yan, Y. Jiang, C. Chang and L. Lin, Sens. Actuators, A, 2010, 164, 131–136 CrossRef CAS.
- N. Soin, T. H. Shah, S. C. Anand, J. Geng, W. Pornwannachai, P. Mandal, D. Reid, S. Sharma, R. L. Hadimani, D. V. Bayramol and E. Siores, Energy Environ. Sci., 2014, 7, 1670–1679 CAS.
- K. Jost, D. Stenger, C. R. Perez, J. K. McDonough, K. Lian, Y. Gogotsi and G. Dion, Energy Environ. Sci., 2013, 6, 2698–2705 CAS.
- V. Bhavanasi, V. Kumar, K. Parida, J. Wang and P. S. Lee, ACS Appl. Mater. Interfaces, 2016, 8, 521–529 CAS.
- Y. Zhao, Q. Liao, G. Zhang, Z. Zhang, Q. Liang, X. Liao and Y. Zhang, Nano Energy, 2015, 11, 719–727 CrossRef CAS.
- S. Siddiqui, D.-I. Kim, L. T. Duy, M. T. Nguyen, S. Muhammad, W.-S. Yoon and N.-E. Lee, Nano Energy, 2015, 15, 177–185 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |