Open Access Article
Open Access ArticleMetal-functionalized covalent organic frameworks as precursors of supercapacitive porous N-doped graphene†
Jorge
Romero‡
a,
David
Rodriguez-San-Miguel‡
bc,
Antonio
Ribera
a,
Rubén
Mas-Ballesté
b,
Toribio F.
Otero
d,
Ilse
Manet
e,
Fabiola
Licio
f,
Gonzalo
Abellán
*ag,
Felix
Zamora
*bc and
Eugenio
Coronado
*a
aInstituto de Ciencia Molecular (ICMol), Universidad de Valencia, 46980 Paterna, Spain. E-mail: eugenio.coronado@uv.es
bDepartamento de Química Inorgánica y Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, Madrid, Spain. E-mail: felix.zamora@uam.es
cInstituto Madrileño de Estudios Avanzados en Nanociencia (IMDEA Nanociencia), 28049 Madrid, Spain
dCenter for Electrochemistry and Intelligent Materials (CEMI), Universidad Politécnica de Cartagena, Cartagena, Spain
eConsiglio Nazionale delle Ricerche – Istituto per la Sintesi Organica e la Fotoreattività (CNR-ISOF), Via Gobetti 101, 40129 Bologna, Italy
fCNR-IMM, Istituto per la Microelettronica e Microsistemi, via P. Gobetti 101, 40129 Bologna, Italy
gDepartment of Chemistry and Pharmacy, Joint Institute of Advanced Materials and Processes (ZMP), University Erlangen-Nürnberg, Henkestr. 42, 91054 Erlangen and Dr.-Mack Str. 81, 90762 Fürth, Germany. E-mail: gonzalo.abellan@fau.de
First published on 17th November 2016
Abstract
Covalent Organic Frameworks (COFs) based on polyimine with several metal ions (FeIII, CoII and NiII) adsorbed into their cavities have shown the ability to generate N-doped porous graphene from their pyrolysis under controlled conditions. These highly corrugated and porous graphene sheets exhibit high values of specific capacitance, which make them useful as electrode materials for supercapacitors.
Introduction
Supercapacitors (SCs) have attracted increased attention as energy storage devices in the scientific community because of their high reversibility, quick charge/discharge rates and excellent energy and power densities.1 The suitable selection of the electrodes is crucial in this sort of devices, as the selected material must have high specific surface area, accurate pore size distributions, good thermal stability and stable electrochemical behaviour.2 In this sense, carbonaceous materials such as activated carbon, mesoporous carbons or nanotubes occupy a privileged position.3 Traditionally, activated carbons have been used as materials for commercial SC electrodes due to their moderate cost and high capacity, but their performance is dramatically reduced with charge/discharge cycling, which is crucial to meet the current demands (electric vehicles, elevators, etc.). This reduction in performance is generally related to limitations in the transport of ions through the pores, provoking insufficient electrochemical accessibility.Nowadays, intense research effort is focused on synthesizing carbon nanomaterials with suitable pore size distributions and high values of specific surface area.3 In this context, graphene seems to be an outstanding candidate because of its unique properties, such as high surface area, excellent electrical and thermal conductivity and mechanical strength.4 Graphene has been synthesized traditionally by mechanical exfoliation of graphite, liquid-phase exfoliation, epitaxial growth on substrates, and chemical vapour deposition using catalytic surfaces. However, the non-porous graphene obtained by these routes does not exceed 200 F g−1 at 1 A g−1 when used as an electrode material in SCs. In order to synthesize highly corrugated graphene with improved porosity several synthesis routes have been developed, for example by employing a MgO template procedure using methane in a tube furnace under an argon flow.5–7 This porous graphene exhibits high specific capacity (ca. 245 F g−1 at 1 A g−1) and better performance compared to the chemically reduced graphene due to its narrow distribution of mesopores and open structure with large surface area. Additionally, highly corrugated graphene sheets have been obtained upon cooling graphene oxide in liquid nitrogen (ca. 349 F g−1 at 2 mV s−1).8 More recently, porous graphene with 3D structures has been prepared by a combined method of ion exchange and activation with NaOH using as the carbon precursor an acrylic resin ion exchanged with a metal (ca. 305 F g−1 at 0.5 A g−1).9 However, the development of scalable and cost-effective synthesis methods of porous graphene still remains a challenge. In this regard, any advance in synthesis would have a major impact in the field of energy storage and conversion and particularly in SCs.4
Recently, some of us reported the use of hybrid organic–inorganic layered double hydroxides (LDHs) as catalytic precursors of a graphitized porous carbon material exhibiting high values of specific capacitance even at high current densities (607 F g−1 at 10 A g−1).10–12 The success of this approach relies on the atomic in-plane distribution of the catalytic ions in the LDH layers, favouring the graphitisation process and subsequent formation of carbon nanoforms.13,14
Along this front, we tried to extend this concept to a different scenario in which the catalytic ions are incorporated into a laminar carbonaceous precursor instead of forming a laminar catalytic structure like in the LDH case. To this end, a suitable selection of the precursor material with an appropriate structure is required, as the overall performance in this type of calcination processes is limited by the formation of partially amorphous carbon instead of graphene.15,16 Layered covalent organic frameworks (COFs) consist of ordered structures with high carbon content, and the presence of cavities with electron donor nitrogen atoms.17 From the electrochemical point of view, the unique ability of COFs to offer uniform nanopores (and predictive design criteria to organize functional building blocks) has been also used to prepare electrodes for energy-based devices including electrochemical capacitors.18,19 Moreover, COFs could be an ideal graphene precursor, as they exhibit a laminar porous morphology and the ability to coordinate metallic ions through their imine receptors (Fig. 1).20,21 Even more appealing is the possibility to incorporate at the same time nitrogen as a dopant in the final graphene, in light of the last reports regarding the improved performance of N-doped graphene in SCs.22–25 Moreover, in contrast to conventional physico-chemical N-doping techniques (e.g. CVD and arch discharge), the use of COFs could help to incorporate N heteroatoms in a single step reaction leading to N-doped porous graphene.26,27
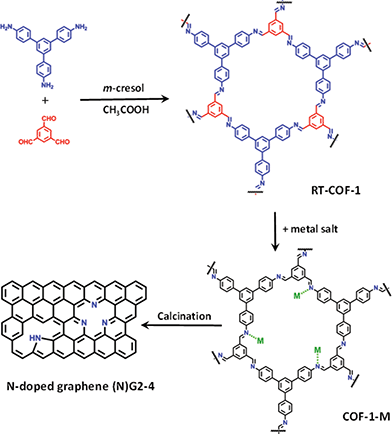 | ||
| Fig. 1 General scheme of the work showing the RT-COF-a andCOF-1-M structures, as well as the calcination process to produce N-doped graphenes. | ||
Herein, we report a method consisting of calcination at moderate temperatures (below 1000 °C) of a COF based on polyimine (Schiff base), which shows the ability to adsorb catalytic metal ions (FeIII, CoII and NiII) into its cavities. The resulting corrugated and porous N-doped graphene exhibits excellent behaviour as an electrode material for SCs under basic pH.
Results and discussion
The direct reaction between 1,3,5-tris(4-aminophenyl)benzene and 1,3,5-benzenetricarbaldehyde, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, in m-cresol at room temperature leads to a characteristic yellow gel of COF-1 (see the ESI and SI 1†).21 The material was vigorously stirred in a methanol solution of M(acac)n (M = FeIII, CoII, NiII; acac = acetylacetonate) for 24 h at 25 °C. Spectroscopic analysis of COF-1-M by FT-IR (SI 2†), as well as elemental analysis and TXRF confirm the incorporation of the metal ions into the RT-COF-1 structure. The FT-IR spectra of COF-1-M clearly show the presence of both imine C
1 molar ratio, in m-cresol at room temperature leads to a characteristic yellow gel of COF-1 (see the ESI and SI 1†).21 The material was vigorously stirred in a methanol solution of M(acac)n (M = FeIII, CoII, NiII; acac = acetylacetonate) for 24 h at 25 °C. Spectroscopic analysis of COF-1-M by FT-IR (SI 2†), as well as elemental analysis and TXRF confirm the incorporation of the metal ions into the RT-COF-1 structure. The FT-IR spectra of COF-1-M clearly show the presence of both imine C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C–C
N and C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C stretching bands at 1617 cm−1 and 1280 cm−1, respectively (SI 2†). The metal ion content was evaluated by TXRF showing that Fe(III) is incorporated in a 1
N–C stretching bands at 1617 cm−1 and 1280 cm−1, respectively (SI 2†). The metal ion content was evaluated by TXRF showing that Fe(III) is incorporated in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 Fe
280 Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N atomic ratio. For Co(II) the atomic ratio is similar (1
N atomic ratio. For Co(II) the atomic ratio is similar (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 Co
190 Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N), while Ni(II) is incorporated in a smaller ratio (1
N), while Ni(II) is incorporated in a smaller ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 Ni
760 Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
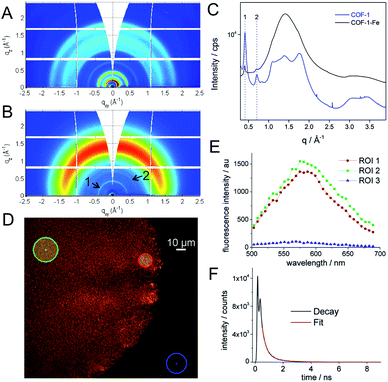
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N). These values represent 0.19–0.05% of the starting material added to the reaction. Synchrotron radiation grazing incidence X-ray diffraction (GIXRD) data of COF-1-Fe confirm the presence of the two most characteristic diffraction peaks of RT-COF-1 (named as 1 and 2 in Fig. 2B and C) with a general broadening of the peaks indicating a partial amorphization of the initial structure (SI 3†). This change is associated with the decrease of the intensity of the Bragg rings and the appearance of an amorphous halo in Fig. 2B, which could be related to a layer-to-layer separation.28 Similar observations have been reported for Pd(II) incorporation in a closely related COF.29 The incorporation of Co(II) and Ni(II) causes a more pronounced effect with a complete loss of structural order. This is probably a consequence of the high structural distortion caused by the metal ion incorporation between the RT-COF-1 layers. Furthermore, the influence of metal-functionalization was followed by confocal fluorescence imaging measurements on SiO2 substrates. After exciting RT-COF-1 at 488 nm, a green fluorescence signal peak at ca. 580 nm was observed. We also obtained a fluorescence lifetime image for excitation at 405 nm. A tail-fit of the fluorescence decay yielded two lifetimes of 0.3 and 1.1 ns with similar weight. While the observation of a short lifetime – close to the resolution limit – may be due to scattering, the second lifetime is likely due to the species giving the fluorescence spectrum peak at 580 nm (Fig. 2D–F). In turn, dramatic quenching of the fluorescence was observed after metal incorporation, probably due to the Fe(III) heavy-metal effect or metal-to-ligand charge transfer (MLCT), as previously observed for other Fe3+–imine systems (SI 4†).30–33
N). These values represent 0.19–0.05% of the starting material added to the reaction. Synchrotron radiation grazing incidence X-ray diffraction (GIXRD) data of COF-1-Fe confirm the presence of the two most characteristic diffraction peaks of RT-COF-1 (named as 1 and 2 in Fig. 2B and C) with a general broadening of the peaks indicating a partial amorphization of the initial structure (SI 3†). This change is associated with the decrease of the intensity of the Bragg rings and the appearance of an amorphous halo in Fig. 2B, which could be related to a layer-to-layer separation.28 Similar observations have been reported for Pd(II) incorporation in a closely related COF.29 The incorporation of Co(II) and Ni(II) causes a more pronounced effect with a complete loss of structural order. This is probably a consequence of the high structural distortion caused by the metal ion incorporation between the RT-COF-1 layers. Furthermore, the influence of metal-functionalization was followed by confocal fluorescence imaging measurements on SiO2 substrates. After exciting RT-COF-1 at 488 nm, a green fluorescence signal peak at ca. 580 nm was observed. We also obtained a fluorescence lifetime image for excitation at 405 nm. A tail-fit of the fluorescence decay yielded two lifetimes of 0.3 and 1.1 ns with similar weight. While the observation of a short lifetime – close to the resolution limit – may be due to scattering, the second lifetime is likely due to the species giving the fluorescence spectrum peak at 580 nm (Fig. 2D–F). In turn, dramatic quenching of the fluorescence was observed after metal incorporation, probably due to the Fe(III) heavy-metal effect or metal-to-ligand charge transfer (MLCT), as previously observed for other Fe3+–imine systems (SI 4†).30–33
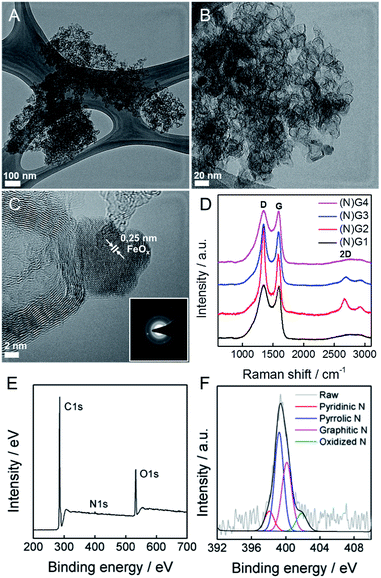
This physical change strongly suggests Fe(III) incorporation into the RT-COF-1 structure rather than physisorption. The controlled thermal treatment of the COF-1-M carried out in a tubular oven at 900 °C under a nitrogen atmosphere produces a black residue for all materials, named as (N)G1 from RT-COF-1 and (N)G2, (N)G3 and (N)G4 from COF-1-M (M = Fe (2), Co (3), Ni (4)). The pyrolysis procedure results in carbon yields in the range of 55–67% as obtained by thermogravimetric analysis (see SI 5†). The TEM analysis of (N)G1 clearly shows the formation of a partially amorphous structure. In contrast, in the other (N)G-M samples, TEM and EDAX analyses clearly show the formation of corrugated graphitic forms. The morphology of (N)G2 consists of a well-defined hierarchical structure, rather similar to that previously named as graphene nanocages (Fig. 3A–C).7 It consists of a lamellar porous material based on cages of 3–7 graphene layers exhibiting a very open structure. The iron compound is a well-known and efficient catalyst for graphitization of organic aerogels or mesoporous carbons, favouring the graphitization process.34,35 In addition, the pyrolysis and gasification processes that occur during the heat treatment of the different compounds could also play an important role in the final morphology of the materials, as gases like CO or CO2 formed during the heat-treatment could act as very efficient porogens.9,36 On the other hand, (N)G3 revealed the presence of several cage-like graphitic carbon nanoforms consisting of 5–15 layers of graphene, whereas (N)G4 exhibited less defined morphology, with a strongly disordered graphitic structure (SI 6†). The observed poorest morphologies could be related to the complete loss of the structural order exhibited by the COF-1-Co and COF-1-Ni precursors after metal functionalization, in comparison to that of COF-1-Fe. These results suggest a critical influence of the employed metal salts in the catalytic process, despite the small metal incorporation.9 In fact, a control experiment using metal sulfates instead of acetylacetonates shows a rather different behaviour with poor graphitization and the formation of micrometric metal particles after the calcination process. In any case, further studies are required to deeply understand the metal functionalization of COFs and their effect on the catalytic graphitization.
To evaluate the presence of metal residues in the final (N)G-M samples, we have performed inductively coupled plasma-optical emission spectroscopy (ICP-OES) analysis, showing that the metal content is below 0.1% for all the samples (see SI 7†). This point was also corroborated by TG analysis in air, showing the absence of any residue after calcination at 1000 °C (SI 8†). As a matter of fact, after a careful inspection of (N)G2, it was possible to find some residual metal nanoparticles, as depicted in Fig. 3C. Based on the general lattice spacing between two adjacent planes observed in the HRTEM images, the small nanoparticle seems to correspond to crystalline FeOx (Fig. 3C).14 Indeed, electron diffraction confirms the presence of the characteristic FeOx patterns.
Surface analysis by XPS confirmed the predominant sp2 character of all the graphitic samples (N)G2 being the sample with the highest C–C sp2 proportion in agreement with XRD and Raman spectroscopy, vide infra), with binding energies of 284.6 ± 0.1 eV. Moreover, no metal signal was detected in any sample, in excellent accordance with the ICP-OES, EDX and TG experiments, highlighting that the presence of the catalytic metals is residual (see SI 9†). Nitrogen could be incorporated as “lattice N” within the carbon network or “chemical N” in the form of functional groups at the periphery of the graphene plane. The high-resolution N1s spectra peaking at ca. 400 eV shows the presence of nitrogen as a dopant in all the samples, with values in the 0.8–1.9% range, similar to other recently reported N-doped graphene or microporous carbon nanosheets (Fig. 3E and SI 9†).22,37 The deconvoluted peak reveals four different N types, i.e. pyridinic-N, pyrrolic-N, graphitic-N and pyridine-N-oxide groups, the pyridinic- and graphitic-type nitrogen being predominant for all the samples (Fig. 3F). Interestingly, (N)G2 exhibited the highest amount of pyridinic-N and pyrrolic-N compared to the rest of the samples, usually related to an increase in the capacitive contribution.38 Moreover, FESEM-EDAX mappings were measured to further confirm the homogeneous distribution of nitrogen (SI 10†).
Raman spectroscopy was also used to evaluate the graphitic character of the samples. Characteristic G and D bands were observed at around 1585 and 1348 cm−1, respectively, in good accordance with that expected for N-doped graphene. The ID/IG ratios exhibited similar values (1.0–1.3) for all the samples. Moreover, there is a splitting in the G band at ca. 1613 cm−1 (D′ band) in the spectrum of (N)G2 related to the increased disorder in the sp2 content. Interestingly, the 2D band at ca. 2669 cm−1 was only present in the (N)G2 and (N)G3 samples suggesting higher crystallinity, in excellent agreement with XPS measurements (Fig. 3D).22,25 This point was further confirmed by X-ray powder diffraction (SI 11†).
Textural characterization of the samples was performed using N2 and CO2 adsorption–desorption isotherms at 77 K and 273 K, respectively (see Fig. 4, Table 1 and SI 12–13† for complete porosity metrics).
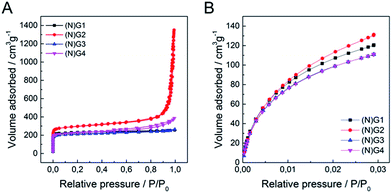 | ||
| Fig. 4 (A) N2 adsorption/desorption isotherms at 77 K of (N)G1–(N)G4, (B) CO2 adsorption/desorption isotherms at 273 K of (N)G1–(N)G4. | ||
| Sample | S BET (m2 g−1) | V t (cm3 g−1) | V μ(<0.7 nm) (cm3 g−1) | V μDR (cm3 g−1) | V meso (cm3 g−1) |
|---|---|---|---|---|---|
| a Data obtained from N2-adsorption. Specific surface area calculated by the BET method. b Total pore volume at P/P0 = 0.96. c Data obtained from CO2-adsorption. Volume of narrow micropores (<0.7 nm) calculated according to the DR method. d Micropore volume calculated from N2-adsorption using the DR method. e Mesopore volume was calculated as the difference of total (Vt) at P/P0 = 0.96 and N2 micropore volume (VμDR). | |||||
| (N)G1 | 927 | 0.959 | 0.413 | 0.354 | 0.605 |
| (N)G2 | 1147 | 0.961 | 0.471 | 0.446 | 0.515 |
| (N)G3 | 844 | 0.960 | 0.399 | 0.325 | 0.635 |
| (N)G4 | 893 | 0.959 | 0.383 | 0.343 | 0.616 |
The N2 isotherms of (N)G1–(N)G4 exhibit combined characteristics of type II and type IV isotherms. The specific surface area was measured by the Brunauer–Emmett–Teller (BET) method showing values between ca. 844 and 1147 m2 g−1, remarkably higher than those of the pristine RT-COF-1 (329 m2 g−1) and the COF-1-M (620 m2 g−1).21 Interestingly, the sample N(G)2 exhibited the highest surface area (1147 m2 g−1) and pore volume (0.961 cm3 g−1) in the series. The pore size distribution (PSD) was analysed by quenched solid density functional theory (QSDFT; SI 13†), showing a narrow distribution of micropores of ca. 1 nm, as well as mesopores in the 4–30 nm range, probably related to the nanocavities originated by the corrugation of graphene, in agreement with the HRTEM observations. We also measured CO2 adsorption at 273 K in order to evaluate the presence of narrow micropores (<0.7 nm). Also in this case (N)G2 exhibited the highest value (0.471 cm3 g−1), with a narrow micropore contribution of ca. 50% of the total pore volume of the material. Interestingly, all the samples exhibited a larger micropore volume (Vμ(<0.7 nm)), obtained from the CO2 adsorption data, than the total micropore volume (VμDR) deduced from the N2 isotherm. This phenomenon is typical of carbon molecular sieves, and clearly indicates the presence of narrow constrictions (pore opening below 0.4 nm), these kinetic restrictions being more detrimental for N2 adsorption (77 K) compared to CO2 (273 K).39,40 This hierarchical porosity can play a relevant role in the supercapacitive behaviour (vide infra).41
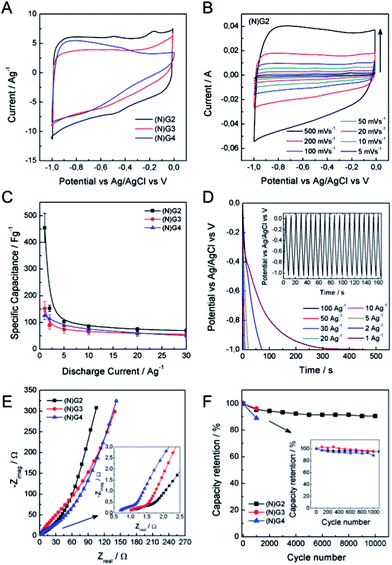
To illustrate the application of these materials in the field of supercapacitors, their electrochemical properties were evaluated in 6 M aqueous KOH using a three-electrode system. Fig. 5 shows typical cyclic voltammetry (CV) curves for the four graphitic materials from −1 to 0 V vs. Ag/AgCl at a scan rate of 50 mV s−1. The CVs of the metal-functionalized samples ((N)G2–4) exhibit a rectangular-shape, even at 500 mV s−1, indicative of a remarkable rate capability. This is more pronounced for the sample (N)G2, exhibiting the highest CV area. In turn, (N)G1 shows a triangular-like morphology indicative of a less-effective ion diffusion and the poorest conductivity (see SI 14†). According to Pumera and co-workers, the residual metal centers could play an important role, indeed the presence of transition metal traces on graphene could dramatically affect its electrochemical behavior.42,43 Along this front, we have also tested the samples under positive potential windows in order to determine whether the presence of metal residues (always below 0.1% as demonstrated by ICP-OES) has an influence or not (see SI 15†). Indeed, it is possible to observe the redox peaks arising from the cobalt and nickel traces, superimposed on that of the Ni-foam collector. This indicates that the presence of metal residues could contribute to the pseudocapacitance of the materials, despite the predominant character of the electrical double layer capacitance (EDLC) from the N-doped carbon matrix. The specific capacitance of the samples was analysed by means of galvanostatic charge/discharge measurements using several electrodes prepared from different batches in order to test the reliability of this synthesis route. From these experiments it is clear that the best performance was achieved for the (N)G2 sample under negative potentials, with an overall maximum specific capacitance of ca. 460 F g−1 at 1 A g−1, a value among the highest compared with those recently reported for related nitrogen-doped graphene-like materials or highly corrugated graphene flakes (Fig. 5C and D, SI 14†).8,25,44,45 It is worth to remark here the long tail exhibited at low discharge currents by (N)G2 and (N)G3, probably related to a pseudocapacitive effect as previously described for other N-doped carbons.46 In any case, slight carbon degradation cannot be completely excluded. The (N)G3 and (N)G4 samples showed 160 and 125 F g−1 at 1 A g−1, respectively (Fig. 5C). For positive potential windows we observed a maximum value of ca. 121 and 218 F g−1 for (N)G3 and (N)G4, respectively (SI 15.7†). Interestingly, (N)G4 exhibited ca. 200 F g−1 even at 30 A g−1, highlighting the versatility of this route to create highly active materials.
In order to shed light on the excellent electrochemical behavior of these materials we have performed blank experiments showing the negligible contribution by the Ni-foam collector to the pseudocapacitance (see SI 16†). Moreover, we have studied the sample N(G)2 using a carbon felt collector showing a similar behavior, and exhibiting a maximum capacity of ca. 545 F g−1 (see SI 17† for additional experimental information).
To further gain insights into the kinetic behavior of the different samples, we carried out electrochemical impedance spectroscopic (EIS) measurements (Fig. 5E). From the analysis of the Nyquist plots, (N)G2 displays a near vertical line compared to the other samples within the low-frequency region, indicative of a better capacitive behavior (vertical line for an ideal capacitor). The small semicircular shapes in the EIS plots in the high frequency region are related to the charge transfer resistance at the electrode/electrolyte interface (inset in Fig. 5E). All the samples exhibited similar small diameters suggesting low charge-transfer resistances, mainly attributed to the N-doping. Moreover, we have also evaluated the capacity retention of (N)G2 after 10,000 charge/discharge cycles, observing capacity retention values higher than 90%, indicative of good stability. Similar capacity retention values were observed for (N)G3–4 (Fig. 5F). It is worth noting that large measuring periods lead to partial loss of the active material from the Ni-foam.47
The excellent properties of the (N)G2 material are attributed, on the one hand, to the presence of nitrogen atoms, which enhances the surface wettability by electrolytes and also improves the charge transfer of the electrode materials.16,48 On the other hand, the laminar hierarchical porous structure allows easy electrolyte penetration, efficiently exposing the active surface of graphene to the electrolyte.9,24 In fact, (N)G2 exhibited the highest specific surface area, micro- and mesopore volumes. It is worth mentioning that the contribution of pores smaller than the size of solvated electrolyte ions (narrow micropores) could play an important role favouring the increase of double-layer capacitance in carbons.41 Overall, all the studied techniques are in good agreement pointing towards (N)G2 as the best candidate of this family of materials for the development of supercapacitors.
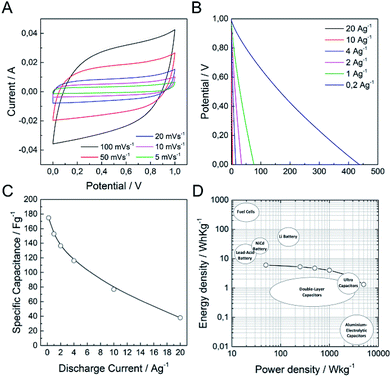
It is well-known that a test fixture configuration, like a two-electrode cell, is more closely related to the performance of commercially available packaged cells.1,49 In this sense, we have developed a preliminary test of (N)G2 in symmetric two-electrode supercapacitors. We used directly assembled electrodes, KOH 6 M as the aqueous electrolyte, and ca. 10 mg of active material in order to obtain reliable measurements.49,50Fig. 6a shows the typical rectangular-shaped cyclic voltammograms at different scan rates ranging from 5 to 100 mV s−1, and the corresponding galvanostatic discharge curves, showing an appropriate supercapacitive behavior. The maximum specific capacitance was 175 F g−1 at a current density of 0.2 A g−1, ca. 38% of that obtained in the three-electrode cell configuration (Fig. 6c). Fig. 6d shows the Ragone plot of the (N)G2//(N)G2 symmetric supercapacitors in the potential range of 0–1 V. The supercapacitive device could deliver a maximum energy density of 6.1 W h kg−1, with a corresponding power density of 50 W kg−1. In addition, when the current density increases to 20 A g−1, the maximum power density is 5000 W kg−1. These values compare favorably with other recently reported carbon-based symmetric supercapacitors working in alkaline solutions using the same electrochemical window.50–54 It is worth to remark here that additional device optimization efforts to extract the full potential of these materials are currently on going in our labs. This includes: different cell configurations, the use of other electrolytes to improve the cell voltage, or modification of the electrode contact, mass and thickness. Finally, to illustrate the performance of our system, we used two (N)G2//(N)G2 devices connected in series as the power supply for a commercial green light-emitting diode (see SI 18†).
Conclusions
The fact that the COF-1-M materials incorporate metal ions (FeIII, CoII and NiII) into the cavities of their laminar structures favours corrugated graphene formation upon controlled thermal treatment. In this sense, the structure, morphology and disposition of the COF precursor lead to the formation of a hierarchical N-doped porous structure. This strategy avoids the need for the use of any additional template, allowing the formation of corrugated graphene in a one-pot reaction from the COF-1-M precursors. These materials exhibited a promising behaviour as electrode materials in supercapacitors. Concretely, the Fe derivative ((N)G2) shows an overall specific capacity of ca. 460 F g−1 at a current density of 1 A g−1. This work paves the way for the development of highly corrugated N-doped porous graphene of great interest not only in supercapacitors, but also as Oxygen Reduction Reaction (ORR) electrocatalysts or in Li-ion batteries.Experimental information
Materials
1,3,5-Benzenetricarboxaldehyde was obtained from Manchester Organics. 1,3,5-Tris-(4′-aminophenyl)benzene was prepared according to literature procedures.21 Other chemicals and solvents were obtained from Aldrich Chemical Co. and used without further purification unless specified.Synthesis
Physical characterization
Carbon, nitrogen and hydrogen contents were determined by microanalytical procedures by using a LECO CHNS-932.The atomic composition of bulk samples was determined by means of electron probe microanalysis performed in a Philips SEM-XL30 equipped with an EDAX microprobe.
HRTEM studies of the hybrid material were carried out on a JEM-2010 microscope (JEOL, Japan) operating at 200 kV. Samples were prepared by dropping a sonicated suspension of the material in ethanol on a carbon-coated copper grid. The digital analysis of the HRTEM images was done using a Digital Micrograph 1.80.70 for GMS 1.8.0 by Gatan.
FESEM studies were performed on a Hitachi S-4800 microscope operating at an accelerating voltage of 20 kV and without metallization of the samples.
ATR-FT-IR spectra were recorded on a Perkin Elmer Spectrum 100 with a universal ATR accessory with a spectral range of 4000–650 cm−1.
Total reflection X-ray fluorescence was performed on a Bruker TXRF S2 PICOFOX spectrometer at 50 kV and 600 mA, with an acquisition time of 500 s and 10 ppm of vanadium as the internal standard.
High resolution solid-state nuclear magnetic resonance (NMR) spectra were recorded at ambient pressure on a Bruker AV 400 WB spectrometer using a triple channel (BL4 X/Y/1H) and Bruker magic angle-spinning (MAS) probe with 4 mm (outside diameter) zirconia rotors. The magic angle was adjusted by maximizing the number and amplitudes of the signals of the rotational echoes observed in the 79Br MAS FID signal from KBr. Cross-polarization with MAS (CP-MAS) was used to acquire 13C data at 100.61 MHz. The 1H ninety degree pulse widths were both 3.1 μs. The CP contact time varied from 3.5 ms. High power two-pulse phase modulation (TPPM) 1H decoupling was applied during data acquisition. The decoupling frequency corresponded to 80 kHz. The MAS sample spinning rate was 10 kHz. Recycle delays between scans were 4 s, depending upon the compound as determined by observing no apparent loss in the 13C signal from one scan to the next. The 13C chemical shifts are given relative to tetramethylsilane as zero ppm, calibrated using the methylene carbon signal of adamantane assigned to 29.5 ppm as the secondary reference.
Grazing incidence X-ray diffraction (GIXRD) measurements were carried out using COF-1 and COF-1-Fe deposited on SiO2/Si wafer at an XRD1-ELETTRA beamline at Trieste's synchrotron facility (Italy) using a monochromatic beam with a wavelength of 1 Å and size of HxV = (200 × 200) μm2. 2D-GIXRD images were collected using a 2D camera (Pilatus detector) placed normal to the incident beam at a distance of 200 mm. Several images were collected by translating the sample 0.5 mm in a direction perpendicular to the beam to probe the sample homogeneity.
Thermogravimetric analysis (TGA) of the composite was carried out with a Mettler Toledo TGA/SDTA 851 apparatus in the 25–900 °C temperature range at a 2 °C min−1 scan rate and under a nitrogen flow of 100 mL min−1.
XRPD patterns of COF-1-Co and COF-1-Ni were collected with a Bruker D8 Advance X-ray diffractometer (Cu-Kα radiation; λ = 1.5418 Å) equipped with a Lynxeye detector. Samples were mounted on a flat sample plate. Patterns were collected in the 3.5° < 2θ < 35° range with a step size of 0.016° and exposure time of 0.8 s per step.
XRPD patterns of (N)G1–4 were collected with a Siemens d-500 X-ray diffractometer (Cu-Kα radiation; λ = 1.5418 Å) equipped with a rotating anode D-max Rigaku operating at 80 mA and 45 kV. Samples were mounted on a flat sample plate. Profiles were collected in the 2.5° < 2θ < 70° range with a step size of 0.05°.
Confocal fluorescence imaging was performed on an inverted Nikon A1 laser scanning confocal microscope equipped with a CW argon ion laser for excitation at 457, 488 and 514 nm (Melles Griot, 40 mW), and a diode laser for excitation at 405 nm (LDH-D-C-405 of Picoquant GmbH Berlin, Germany) operating both in continuous mode (50 mW) and pulsed at 40 MHz (1.0 mW average power for pulse FWHM of 70 ps). Confocal fluorescence imaging was carried out on the samples at room temperature. The images were collected using a Nikon PLAN APO VC 20× NA 0.75 objective or a Nikon PLAN APO VC 60× NA 1.40 oil immersion objective. Images of 512 × 512 have been acquired applying a scan speed of 1 frame in 1–4 s and the pixel dimension of the xy plane falls in the range 0.21–0.4 μm. Hexagonal pinhole dimension was set to 1.0 au corresponding to 38 μm and optical thickness of 440 nm. A dichroic mirror reflecting 405, 488, 541 and 640 nm was used. Bandpass filters in front of the PMT selected fluorescence in the ranges of 500–550 and 560–615 nm. Spectral imaging was done with a Nikon 32-PMT array detector with resolution varying from 6 to 10 nm per channel. For fluorescence lifetime imaging a time-correlated single photon counting (TCSPC) system of Picoquant GmbH Berlin was used exciting at 405 nm. Photons were detected in TTTR mode with two Single Photon Avalanche Diodes manufactured by Micro Photon Devices (MPD), Bolzano, Italy. Fluorescence was filtered with the opportune fluorescence SEMROCK bandpass filter 520/40 nm. A PicoHarp 300 photon processor completes the TCSPC system. SymPhoTime v. 5.1 analysis software was used for image processing and lifetime fitting. A tail fit with multi-exponential functions was performed to analyze fluorescence decays of selected ROI. The system allowed measurement of fluorescence lifetimes from 300 ps up to several nanoseconds. Elemental analysis was performed in the Universidad Complutense de Madrid (CAI de Tećnicas Geoloǵicas) by inductively coupled-plasma optical emission spectroscopy (ICP-OES) on solutions prepared by treating the samples in a nitric acid/hydrochloric acid mixture in a Teflon reactor.
The Raman measurements (Jobin-Yvon LabRam HR 800 Raman Microscope) were carried out at room temperature with the 532 nm line of an Ar ion laser as an excitation source.
The porous texture of all the materials prepared was characterized by N2 adsorption at 77 K and CO2 at 273 K using an AUTOSORB-6 apparatus. Samples were degassed for 8 hours at 523 K and 5 × 10−5 bar prior to analysis. Surface areas were estimated according to the BET model, and pore size dimensions were calculated by the solid density functional theory (QSDFT) for the adsorption branch assuming a cylindrical pore model. The micropore volumes were determined by applying t-plot and DR methods to the N2 and CO2 adsorption data.
Electrochemical characterization
For the electrochemical measurements a mixture of acetylene black and PVDF in ethanol in a mass ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 was prepared and deposited on a nickel foam electrode. The as-prepared nickel foam electrodes were dried overnight at 80 °C and pressed. Each working electrode contained about 1 mg of electroactive material and had a geometric surface area of about 1 cm2. A typical three-electrode experimental cell equipped with a steel sheet as the counter electrode and a Metrohm Ag/AgCl (3 M KCl) as the reference electrode was used for the electrochemical characterization of the nanocomposite materials trapped by the working electrodes. All the electrochemical measurements were carried out in 6 M KOH (99.99%) aqueous solutions as the electrolyte. Ultrapure water was obtained from Milli-Q equipment. All the electrochemical experiments were performed at room temperature using an AUTOLAB PGSTAT 128N potentiostat–galvanostat controlled by Nova 2.0 electrochemical. The specific capacitance (C) was calculated from the cyclic chronopotentiometric curves according to eqn (1):
10 was prepared and deposited on a nickel foam electrode. The as-prepared nickel foam electrodes were dried overnight at 80 °C and pressed. Each working electrode contained about 1 mg of electroactive material and had a geometric surface area of about 1 cm2. A typical three-electrode experimental cell equipped with a steel sheet as the counter electrode and a Metrohm Ag/AgCl (3 M KCl) as the reference electrode was used for the electrochemical characterization of the nanocomposite materials trapped by the working electrodes. All the electrochemical measurements were carried out in 6 M KOH (99.99%) aqueous solutions as the electrolyte. Ultrapure water was obtained from Milli-Q equipment. All the electrochemical experiments were performed at room temperature using an AUTOLAB PGSTAT 128N potentiostat–galvanostat controlled by Nova 2.0 electrochemical. The specific capacitance (C) was calculated from the cyclic chronopotentiometric curves according to eqn (1):| C = IΔt/mΔV | (1) |
A two-electrode symmetric supercapacitor was assembled using a Swagelok cell, with a pellet consisting of a mixture of (N)G2 and Teflon (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 proportion) as positive and negative electrodes. The average mass of each electrode was about 5 mg of active material. The employed electrolyte was aqueous 6 M KOH, and a cellulose membrane was used for separating the electrodes. The test voltage range was optimized to 0–1 V. All the electrochemical tests were carried out at room temperature using a GAMRY 5000E potentiostat–galvanostat controlled by Gamry Software. The specific capacitance was calculated according to the following equation:
1 proportion) as positive and negative electrodes. The average mass of each electrode was about 5 mg of active material. The employed electrolyte was aqueous 6 M KOH, and a cellulose membrane was used for separating the electrodes. The test voltage range was optimized to 0–1 V. All the electrochemical tests were carried out at room temperature using a GAMRY 5000E potentiostat–galvanostat controlled by Gamry Software. The specific capacitance was calculated according to the following equation:
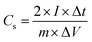 | (2) |
where Cs (F g−1) is the specific capacitance, I (A) the discharge current, Δt (s) the discharge time, and ΔV (V) the voltage window. The energy density, E (W h kg−1), and the power density, P (W kg−1), were estimated by using the following expressions, normalizing to the mass of two carbon electrodes:
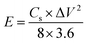 | (3) |
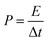 | (4) |
Acknowledgements
We are grateful to the EU (FET-OPEN 2D-INK, grant agreement 648786), the Spanish MINECO (Projects MAT2016-77608-C3-1-P, MAT-2014-56143-R, CTQ-2014-59209-P, FEDER-MAT2012-38318-C03 and Excellence Unit Maria de Maeztu, MDM-2015-0538), and the Generalitat Valenciana (Prometeo Program and ISIC-Nano). Support from the INNCIDE program through Vicerectorat d'lnvestigació i Política Científica of the University of Valencia is also acknowledged. J. R. and D. R. thank the Spanish MECD for FPI and FPU grants, respectively. G. A. thanks the EU for a Marie Curie Fellowship (FP7/2013-IEF-627386). Dedicated to Prof. Nazario Martín on the occasion of his 60th birthday.Notes and references
-
F. Beguin and E. Frackowiak, Supercapacitors: Materials, Systems and Applications, John Wiley & Sons, 2013 Search PubMed
.
- G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828 RSC
.
- X. Li and B. Wei, Nano Energy, 2013, 2, 159–173 CrossRef CAS
.
- A. C. Ferrari, F. Bonaccorso, V. Fal'ko, K. S. Novoselov, S. Roche, P. Bøggild, S. Borini, F. H. L. Koppens, V. Palermo, N. Pugno, J. A. Garrido, R. Sordan, A. Bianco, L. Ballerini, M. Prato, E. Lidorikis, J. Kivioja, C. Marinelli, T. Ryhänen, A. Morpurgo, J. N. Coleman, V. Nicolosi, L. Colombo, A. Fert, M. Garcia-Hernandez, A. Bachtold, G. F. Schneider, F. Guinea, C. Dekker, M. Barbone, Z. Sun, C. Galiotis, A. N. Grigorenko, G. Konstantatos, A. Kis, M. Katsnelson, L. Vandersypen, A. Loiseau, V. Morandi, D. Neumaier, E. Treossi, V. Pellegrini, M. Polini, A. Tredicucci, G. M. Williams, B. H. Hong, J.-H. Ahn, J. M. Kim, H. Zirath, B. J. van Wees, H. van der Zant, L. Occhipinti, A. D. Matteo, I. A. Kinloch, T. Seyller, E. Quesnel, X. Feng, K. Teo, N. Rupesinghe, P. Hakonen, S. R. T. Neil, Q. Tannock, T. Löfwander and J. Kinaret, Nanoscale, 2015, 7, 4598–4810 RSC
.
- J. Yan, Z. Fan, W. Sun, G. Ning, T. Wei, Q. Zhang, R. Zhang, L. Zhi and F. Wei, Adv. Funct. Mater., 2012, 22, 2632–2641 CrossRef CAS
.
- G. Ning, Z. Fan, G. Wang, J. Gao, W. Qian and F. Wei, Chem. Commun., 2011, 47, 5976–5978 RSC
.
- K. Xie, X. Qin, X. Wang, Y. Wang, H. Tao, Q. Wu, L. Yang and Z. Hu, Adv. Mater., 2012, 24, 347–352 CrossRef CAS PubMed
.
- J. Yan, J. Liu, Z. Fan, T. Wei and L. Zhang, Carbon, 2012, 50, 2179–2188 CrossRef CAS
.
- Y. Li, Z. Li and P. K. Shen, Adv. Mater., 2013, 25, 2474–2480 CrossRef CAS PubMed
.
- G. Abellán, E. Coronado, C. Martí-Gastaldo, A. Ribera and T. F. Otero, Part. Part. Syst. Charact., 2013, 30, 853–863 Search PubMed
.
- G. Abellán, J. G. Martínez, T. F. Otero, A. Ribera and E. Coronado, Electrochem. Commun., 2014, 39, 15–18 CrossRef
.
- G. Abellán, C. Martí-Gastaldo, A. Ribera and E. Coronado, Acc. Chem. Res., 2015, 48, 1601–1611 CrossRef PubMed
.
- G. Abellán, E. Coronado, C. Martí-Gastaldo, A. Ribera and J. F. Sánchez-Royo, Chem. Sci., 2012, 3, 1481–1485 RSC
.
- G. Abellan, J. A. Carrasco, E. Coronado, J. P. Prieto-Ruiz and H. Prima-García, Adv. Mater. Interfaces, 2014, 1, 1400184 CrossRef
.
- R. Liu, D. Wu, X. Feng and K. Müllen, Angew. Chem., Int. Ed., 2010, 49, 2565–2569 CrossRef CAS PubMed
.
- L. Zhang, Z. Su, F. Jiang, L. Yang, J. Qian, Y. Zhou, W. Li and M. Hong, Nanoscale, 2014, 6, 6590–6602 RSC
.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef PubMed
.
- C. R. DeBlase, K. E. Silberstein, T.-T. Truong, H. D. Abruña and W. R. Dichtel, J. Am. Chem. Soc., 2013, 135, 16821–16824 CrossRef CAS PubMed
.
- C. R. DeBlase, K. Hernández-Burgos, K. E. Silberstein, G. G. Rodríguez-Calero, R. P. Bisbey, H. D. Abruña and W. R. Dichtel, ACS Nano, 2015, 9, 3178–3183 CrossRef CAS PubMed
.
- S.-Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548–568 RSC
.
- A. de la Peña Ruigómez, D. Rodríguez-San-Miguel, K. C. Stylianou, M. Cavallini, D. Gentili, F. Liscio, S. Milita, O. M. Roscioni, M. L. Ruiz-González, C. Carbonell, D. Maspoch, R. Mas-Ballesté, J. L. Segura and F. Zamora, Chem.–Eur. J., 2015, 21, 10666–10670 CrossRef PubMed
.
- H. Wang, T. Maiyalagan and X. Wang, ACS Catal., 2012, 2, 781–794 CrossRef CAS
.
- Z. Wen, X. Wang, S. Mao, Z. Bo, H. Kim, S. Cui, G. Lu, X. Feng and J. Chen, Adv. Mater., 2012, 24, 5610–5616 CrossRef CAS PubMed
.
- X. Zhuang, F. Zhang, D. Wu and X. Feng, Adv. Mater., 2014, 26, 3081–3086 CrossRef CAS PubMed
.
- H. Peng, G. Ma, K. Sun, Z. Zhang, Q. Yang, F. Ran and Z. Lei, J. Mater. Chem. A, 2015, 3, 13210–13214 CAS
.
- Z. Xiang, D. Cao, L. Huang, J. Shui, M. Wang and L. Dai, Adv. Mater., 2014, 26, 3315–3320 CrossRef CAS PubMed
.
- M. Barrejón, A. Primo, M. J. Gómez-Escalonilla, J. L. G. Fierro, H. García and F. Langa, Chem. Commun., 2015, 51, 16916–16919 RSC
.
- S.-Y. Ding, J. Gao, Q. Wang, Y. Zhang, W.-G. Song, C.-Y. Su and W. Wang, J. Am. Chem. Soc., 2011, 133, 19816–19822 CrossRef CAS PubMed
.
- S. B. Kalidindi, H. Oh, M. Hirscher, D. Esken, C. Wiktor, S. Turner, G. Van Tendeloo and R. A. Fischer, Chem.–Eur. J., 2012, 18, 10848–10856 CrossRef CAS PubMed
.
- J.-Q. Wang, L. Huang, M. Xue, Y. Wang, L. Gao, J. H. Zhu and Z. Zou, J. Phys. Chem. C, 2008, 112, 5014–5022 CAS
.
- E. Hao, T. Meng, M. Zhang, W. Pang, Y. Zhou and L. Jiao, J. Phys. Chem. A, 2011, 115, 8234–8241 CrossRef CAS PubMed
.
- S. Shobana, P. Subramaniam, L. Mitu, J. Dharmaraja and S. Arvind Narayan, Spectrochim. Acta, Part A, 2015, 134, 333–344 CrossRef CAS PubMed
.
- J. Nandre, S. Patil, P. Patil, S. Sahoo, C. Redshaw, P. Mahulikar and U. Patil, J. Fluoresc., 2014, 24, 1563–1570 CrossRef CAS PubMed
.
- F. J. Maldonado-Hódar, C. Moreno-Castilla, J. Rivera-Utrilla, Y. Hanzawa and Y. Yamada, Langmuir, 2000, 16, 4367–4373 CrossRef
.
- W. Gao, Y. Wan, Y. Dou and D. Zhao, Adv. Energy Mater., 2011, 1, 115–123 CrossRef CAS
.
- M. Sevilla and A. B. Fuertes, ACS Nano, 2014, 8, 5069–5078 CrossRef CAS PubMed
.
- Z.-Y. Jin, A.-H. Lu, Y.-Y. Xu, J.-T. Zhang and W.-C. Li, Adv. Mater., 2014, 26, 3700–3705 CrossRef CAS PubMed
.
- F. M. Hassan, V. Chabot, J. Li, B. K. Kim, L. Ricardez-Sandoval and A. Yu, J. Mater. Chem. A, 2013, 1, 2904–2912 CAS
.
- R. V. R. A. Rios, J. Silvestre-Albero, A. Sepúlveda-Escribano, M. Molina-Sabio and F. Rodríguez-Reinoso, J. Phys. Chem. C, 2007, 111, 3803–3805 CAS
.
- A. Wahby, J. M. Ramos-Fernández, M. Martínez-Escandell, A. Sepúlveda-Escribano, J. Silvestre-Albero and F. Rodríguez-Reinoso, ChemSusChem, 2010, 3, 974–981 CrossRef CAS PubMed
.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed
.
- A. Ambrosi, C. K. Chua, B. Khezri, Z. Sofer, R. D. Webster and M. Pumera, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12899–12904 CrossRef CAS PubMed
.
- L. Wang, A. Ambrosi and M. Pumera, Angew. Chem., Int. Ed., 2013, 52, 13818–13821 CrossRef CAS PubMed
.
- H. M. Jeong, J. W. Lee, W. H. Shin, Y. J. Choi, H. J. Shin, J. K. Kang and J. W. Choi, Nano Lett., 2011, 11, 2472–2477 CrossRef CAS PubMed
.
- T. Lin, I.-W. Chen, F. Liu, C. Yang, H. Bi, F. Xu and F. Huang, Science, 2015, 350, 1508–1513 CrossRef CAS PubMed
.
- T. Akhter, M. M. Islam, S. N. Faisal, E. Haque, A. I. Minett, H. K. Liu, K. Konstantinov and S. X. Dou, ACS Appl. Mater. Interfaces, 2016, 8, 2078–2087 CAS
.
- G. Abellán, J. A. Carrasco, E. Coronado, J. Romero and M. Varela, J. Mater. Chem. C, 2014, 2, 3723–3731 RSC
.
- L. Sun, L. Wang, C. Tian, T. Tan, Y. Xie, K. Shi, M. Li and H. Fu, RSC Adv., 2012, 2, 4498 RSC
.
- M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294 CAS
.
- J. Patiño, N. López-Salas, M. C. Gutiérrez, D. Carriazo, M. L. Ferrer and F. del Monte, J.
Mater. Chem. A, 2016, 4, 1251–1263 Search PubMed
.
- D.-W. Wang, F. Li, M. Liu, G. Q. Lu and H.-M. Cheng, Angew. Chem. Int. Ed., 2008, 120, 379–382 CrossRef
.
- Z. Lei, Z. Liu, H. Wang, X. Sun, L. Lu and X. S. Zhao, J. Mater. Chem. A, 2013, 1, 2313–2321 CAS
.
- X. Huang, Q. Wang, X. Y. Chen and Z. J. Zhang, J. Electroanal. Chem., 2015, 748, 23–33 CrossRef CAS
.
- Y. Li and D. Zhao, Chem. Commun., 2015, 51, 5598–5601 RSC
.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details and further characterization including confocal fluorescence, FT-IR, solid-state 13C-NMR, XRD, GIXRD, TG/DTA, FESEM, EDAX, XPS, porosity metrics, and additional electrochemical experiments. See DOI: 10.1039/c6ta09296a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |