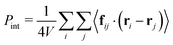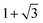Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Active Brownian equation of state: metastability and phase coexistence†
Demian
Levis
 *ab,
Joan
Codina
ab and
Ignacio
Pagonabarraga
abc
*ab,
Joan
Codina
ab and
Ignacio
Pagonabarraga
abc
aDepartament de Física de la Matèria Condensada, Universitat de Barcelona, Martí i Franquès 1, E08028 Barcelona, Spain. E-mail: demianparatodos@gmail.com
bUniversity of Barcelona Institute of Complex Systems (UBICS), Universitat de Barcelona, Barcelona, Spain
cCECAM Centre Européen de Calcul Atomique et Moléculaire, École Polytechnique Fédérale de Lausanne, Batochimie, Avenue Forel 2, 1015 Lausanne, Switzerland
First published on 31st October 2017
Abstract
As a result of the competition between self-propulsion and excluded volume interactions, purely repulsive self-propelled spherical particles undergo a motility-induced phase separation (MIPS). We carry out a systematic computational study, considering several interaction potentials, systems confined by hard walls or with periodic boundary conditions, and different initial conditions. This approach allows us to identify that, despite its non-equilibrium nature, the equations of state of Active Brownian Particles (ABP) across MIPS verify the characteristic properties of first-order liquid–gas phase transitions, meaning, equality of pressure of the coexisting phases once a nucleation barrier has been overcome and, in the opposite case, hysteresis around the transition as long as the system remains in the metastable region. Our results show that the equations of state of ABPs account for their phase behaviour, providing a firm basis to describe MIPS as an equilibrium-like phase transition.
1 Introduction
Active matter made of self-propelled particles can be found in a wide variety of contexts, both in living and synthetic systems, like bacteria or colloidal artificial swimmers.1 The fundamental difference between active and ‘passive’ matter made of thermally agitated constituents, is that the microscopic dissipative dynamics of the former breaks detailed balance and, as such, evolves far-from-equilibrium. The intrinsic out-of-equilibrium nature of active matter manifests strikingly in the presence of interactions. Self-propelled particles accumulate in regions of space where their velocity decreases as a consequence of collisions (between particles or with external obstacles). Simple models that capture in a minimal way the competition between self-propulsion and steric effects, like the so-called Active Brownian Particles (ABP) model, have provided much insight into the generic behavior of such systems. For instance, at high enough densities and activities, a purely Motility-Induced Phase Separation (MIPS) generically takes place, leading to the coexistence of an active low density gas with a high density drop in the absence of attractive forces.2–7 This out-of-equilibrium transition is reminiscent of equilibrium liquid-gas de-mixing. It is thus tempting to extend the thermodynamic description of first order phase transitions in terms of, for instance, equations of state, to ABP. However, this poses several fundamental difficulties since no thermodynamic variable is, in principle, well defined in this context. Much effort has been recently devoted to this question: the notions of effective temperature8–12 and chemical potential13 have been introduced, and special attention has been paid to the notion of pressure.14–21In spite of the above-mentioned efforts, the equality of pressure at coexistence imposed by the very existence of an equation of state (EoS) for spherical ABP,17 has not been properly confirmed neither by experiments nor simulations.15,17–20 Several numerical studies have measured the pressure in ABP, but its interpretation has raised several conceptual problems. For instance, an abrupt pressure drop at the vicinity of MIPS has been reported and it has been argued that it constitutes a distinctive feature of this transition, hindering the analogy with equilibrium phase separation.19,20 A pressure loop generically appears in phase separating finite systems in equilibrium, an effect that can be redressed by the Maxwell construction. However, this construction is violated for ABP,17,22 so there is no direct way to understand the phase behaviour of the system from the simulated EoS. The phase diagram of ABP has been discussed in terms of binodal and spinodal-like curves.5,23 While the phase separation kinetics show the hallmarks of nucleation and spinodal decomposition,5,6,24,25 the connection with (static) quantities like the EoS remains unclear. Thus, the possibility to construct from the EoS a thermodynamic description of MIPS, bridging the gap between the phase diagram, the relaxation dynamics and the pressure, is still a matter of debate.
In this work we clarify these issues, providing a full characterization of the phase behavior of spherical ABPs in terms of its EoS and show that MIPS is fully consistent with the first-order phase transition scenario. We bring out the existence of a metastability region: an hysteresis around the coexistence pressure is found as the system is quenched to the coexistence region from ‘below’ or ‘above’ MIPS. As we show, the pressure drop near MIPS disappears as the system is quenched from ‘above’, and we recover instead a flatter EoS between the binodals, showing the equality of pressure at coexistence and thus allowing to estimate the location of the low-density binodal from the extrapolation of the pressure measurements above the spinodal. We analyze both open and confined systems in order to establish the role played by the presence of a nucleation barrier in the pressure anomalies reported in previous numerical works, and the inherent difficulty of sampling the thermodynamic behaviour of the EoS of ABPs at coexistence. We find that the EoS of an open system quenched from ‘above’ approaches the behaviour of the system under confinement, showing that the difficulties in interpreting the pressure data are due to the presence of a large nucleation barrier that can be easily bypassed by including a nucleation core (a wall). Consistently, as we show, MIPS can be stabilized at much lower densities (between the binodal and spinodal line) than those reported to date, and the phase diagram can be understood from the EoS despite the absence of a Maxwell construction.
In order to show the generality of our results, we perform NVT simulations of spherical ABPs using different repulsive potentials. As we show, the location and depth of the pressure drop found for different potentials can be rationalized borrowing ideas from classical nucleation theory. Thus, we connect the structure of the dense phase and its phase separation kinetics: stiffer potentials promote the emergence of crystalline ordering accompanied by a large surface tension, explaining the presence of a large nucleation barrier and, therefore, the difficulties that have hindered the interpretation of the EoS of ABPs.
2 Model
To be specific, we consider N self-propelled particles in a 2d volume V = Lx × Ly. The model is defined by the following equations of motion for each particle at position ri = (xi,yi) and with orientation ni(t) = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi, sin
θi, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi):
θi):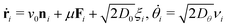 | (1) |
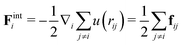 and external potentials, Fexti = −∇iw(ri). Here we compare Active Brownian (infinitely) Hard Disks (AB-HD)
and external potentials, Fexti = −∇iw(ri). Here we compare Active Brownian (infinitely) Hard Disks (AB-HD)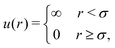 | (2) |
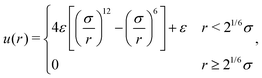 | (3) |
| w(x) = [x−12 + (Lx − x)−12]. | (4) |
The units of length and time are given by σ and Dθ−1, respectively, and fix Dθ = 3D0/σ2. The phase behavior of the model (for both AB-HD and AB-WCAD) is controlled by the following non-dimensional parameters: the packing fraction ϕ = πσ2N/(4V), which quantifies crowding effects, the Péclet number, Pe = v0/(σDθ), which quantifies the strength of self-propulsion, and the effective particle stiffness Γ = εμ/(σv0), which naturally arises from the inter-particle energy scale ε. This parameter, which quantifies to what extent particles become effectively softer as their activity increases, is irrelevant in the limit of infinitely hard-disks.
We carry out Brownian Dynamics (BD) simulations to study the evolution of the system in the absence of any external forcing. Since it is not straightforward to deal with the singular nature of hard core interactions in BD simulations, we use a variant of Event-Driven Brownian Dynamics (ED-BD) for hard spheres26 that accounts for self-propulsion.‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 We simulated systems of N = 2000,…, 8000 AB-HD using a Brownian time step τB = 0.01 which fixes D0 = τB/2 = 0.005 and thus Dθ = 0.015. Self-propulsion in the ED-BD scheme is introduced in such a way that the collisions are elastic and do not modify the orientation ni of the particles. We vary the Peclet number Pe by varying v0, from v0 = 0 (Pe = 0) to v0 = 1.5 (Pe = 100). For AB-WCAD, we use a second order stochastic Runge–Kutta algorithm as described in ref. 28 with a time step Δt = 10−5, 5 × 10−5 (used to simulate systems with the highest and the lowest Pe numbers explored, respectively). To analyze the impact of the stiffness of the potential, we simulated systems with ε = 0.4 up to ε = 250.
27 We simulated systems of N = 2000,…, 8000 AB-HD using a Brownian time step τB = 0.01 which fixes D0 = τB/2 = 0.005 and thus Dθ = 0.015. Self-propulsion in the ED-BD scheme is introduced in such a way that the collisions are elastic and do not modify the orientation ni of the particles. We vary the Peclet number Pe by varying v0, from v0 = 0 (Pe = 0) to v0 = 1.5 (Pe = 100). For AB-WCAD, we use a second order stochastic Runge–Kutta algorithm as described in ref. 28 with a time step Δt = 10−5, 5 × 10−5 (used to simulate systems with the highest and the lowest Pe numbers explored, respectively). To analyze the impact of the stiffness of the potential, we simulated systems with ε = 0.4 up to ε = 250.
3 Phase diagram
The binodal-like curves (ϕlow,ϕhigh) shown in Fig. 1 can be readily constructed from the coexisting densities. ABP with different stiffness exhibit the same qualitative phase behavior: above a critical Pe they undergo MIPS if its average density is large enough.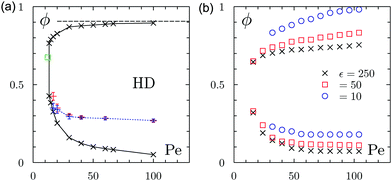 | ||
Fig. 1 Pe − ϕ phase diagram of ABP using PBC. Left: AB-HD. Black symbols show the coexisting densities ϕlow and ϕhigh defining the binodals. Red points with errorbars indicate the onset of MIPS (see Fig. 2 for details). Blue points correspond to the location of the pressure drop. We identify a critical point at Pec ≈ 12 and ϕc ≈ 0.674 (in green). The horizontal dotted line indicates the closest packing of hard disks 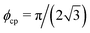 . Right: AB-WCAD for different stiffness. The symbols show the two binodals ϕlow and ϕhigh. . Right: AB-WCAD for different stiffness. The symbols show the two binodals ϕlow and ϕhigh. | ||
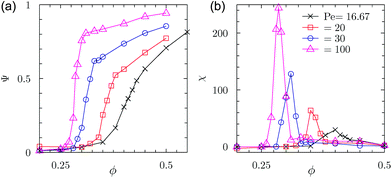
To identify MIPS for AB-HD with PBC we let the system evolve from an homogeneous initial condition and then, once the system has reached its steady-state, we measure the fraction of particles in the dense phase Ψ. We compute Ψ as the probability that a given particle belongs to the largest cluster in the system, where a cluster is defined as a connected set of neighboring particles (defined by a distance 1.05σ). In order to locate more precisely the appearance of MIPS we also compute its associated second moment
| χ = N(〈Ψ2〉 − 〈Ψ〉2). | (5) |
As shown in Fig. 2(a) this quantity grows from Ψ ≈ 0 to 0 < Ψ ≲ 1 as we increase the packing fraction at fixed Pe. The corresponding susceptibility χ shows a peak at the onset of MIPS (Fig. 2(b)), thus providing a criterion to locate it in the Pe − ϕ phase diagram. The transition points ϕn obtained using this prescription are shown by red symbols in the phase diagram Fig. 1(a). As it is clear from the figure, these transition points remain rather close to the location of the pressure discontinuity (see Section 4), shown by blue symbols. As discussed below, the location of the pressure discontinuity results in a spinodal-like curve, as shown in Fig. 1(a) by a blue dotted line, and as shown by our cluster analysis, it is accompanied by the emergence of a macroscopic cluster.
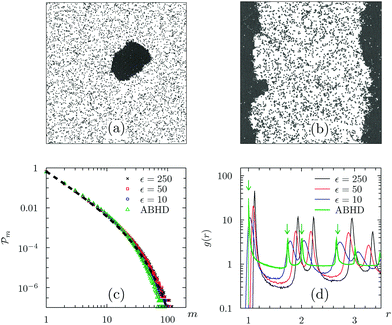
To understand the role of particle stiffness, we construct the binodals for AB-WCAD (see Fig. 1(b)). Increasing ε one observes both a decrease of ϕlow and an increase in the structure, as depicted in Fig. 5(d). This feature implies that the high-density phase has a higher degree of order for stiffer potentials. In the limit of hard disks, the high-density branch of the binodal, ϕhigh, quickly saturates at close packing, indicating that the competition between self-propulsion and excluded volume generates a nearly perfect hexagonal crystal at high activities, as shown in Fig. 5 (e.g. for Pe = 60, a dense region at ϕhigh = 0.98ϕcp coexists with a gas at ϕlow = 0.089, 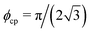 is the closest packing of disks).
is the closest packing of disks).
4 Equation of state
We identify the pressure, P, by an extension of the virial theorem that accounts for active forces:19,29| P = ρkBT + Pint + Pa |
is the standard virial expression of the collisional pressure, and
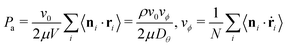 | (6) |
Following usual practice, we study the phase behavior of ABP by letting the system evolve from a homogenous initial state at some density ϕ towards its stationary state corresponding to a given value of Pe. This procedure corresponds to a quench from Pe = 0 to Pe > 0. In order to gain insight into the nature of the pressure, we compare the values obtained for a periodic system and one confined in the x-direction by two walls at x = 0 and x = Lx, and periodic boundary conditions (PBC) in the y-direction.
The P(ϕ;Pe) equations of state (normalized by the ideal gas pressure P0 and multiplied by ϕ) found in confined and open geometries are shown in Fig. 3. If the system does not phase separate, for Pe < Pec, the total pressure of AB-HD with PBC coincides with the pressure computed in confined conditions (see Fig. 3(a)). At higher activities, for PBC the pressure drops abruptly in the vicinity of MIPS,19,20 while in the confined system it displays a monotonic increase with density and remains roughly constant in the coexistence region. As shown in Fig. 3(a and b), the pressure jump becomes more pronounced as the activity and the stiffness of the particles increases (note the similarity between AB-HD with Pe = 30 and AB-WCAD with ε = 250 and Pe = 100). The formation of a macroscopic cluster, due to MIPS, coincides with the location of the pressure drop, ϕn (as discussed above). Particles are dramatically slowed down as they aggregate, making vϕ, and therefore the active pressure, to drop (see eqn (6)). The low-density branch of the binodal, ϕlow, is well below the density ϕn at which the dense phase appears.
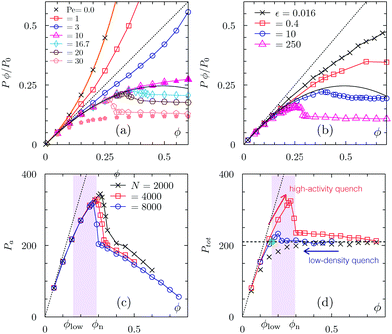 | ||
| Fig. 3 (a) Total pressure times ϕ normalized by the ideal gas pressure P0 of AB-HDs for Pe = 0,…, 30 in systems with PBC (line-open symbols) and for Pe = 10 and 30 in systems with confining walls (in filled triangular and pentagonal symbols, respectively). The continuous (orange) line corresponds to the analytical equation of state for hard disks;31 the dotted one is the ideal gas limit. The black curve shows P/P0 = 1 − ϕ. (b) Total pressure of AB-WCADs using PBC and different stiffness at fixed Pe = 100. The continuous and dotted lines are the same as in (a). (c) Active pressure for systems of AB-HDs with PBC (line-points) and confining walls (symbols) of different size for Pe = 30. (d) Hysteresis in the EoS of AB-HDs for Pe = 30: the red points are obtained by quenching the system with PBC from an homogenous state; the blue points were obtained by quenching the system with PBC from a phase separated state (at ϕ = 0.50, Pe = 30). Black points show the equation of state in the confined system. The coexistence pressure P* is represented by a flat broken-line and its intersection with the low density branch of the equation of state of the open system (blue dots) is shown by a green symbol. The light colored band in panels (c and d) shows the metastable region between the binodal ϕlow and the onset of MIPS ϕn. | ||
Above Pec, but for densities below the onset of MIPS, the equations of state collapse into a single curve which can be fitted by a first order virial expansion, P = P0(1 + b1ϕ), where P0 is the pressure in the ideal gas limit.19 The equations of state (or compressibility factor) of AB-HD in confined conditions are shown in Fig. 4. Together with the data points, we also show the Carnahan–Starling equation of state for passive Hard-Disks31 and the best fits of the simulation data at Pe > 0 by a second order virial expansion
| P/P0 = 1 + b1ϕ + b2ϕ2. | (7) |
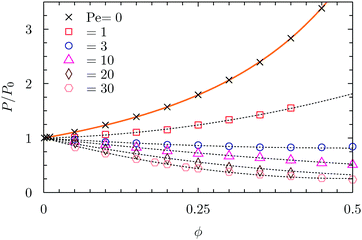 | ||
| Fig. 4 Equations of state of AB-HD confined along one direction between two hard walls for several Pe numbers. Dotted lines denote fits by a second order virial expansion. The continuous line is the Carnahan–Starling equation of state for Hard-Disks.31 | ||
Interestingly, the equations of state in confined and PBC geometries converge at large densities to a value close to the expected coexistence pressure. In equilibrium, finite-size systems display a pressure loop due to the formation of an interface between the two phases,32,33 while the loop arising in van der Waals (mean-field) theory is (thermodynamically) unstable. Accordingly, P(ϕ) shows a peak when the dense phase develops, an effect that should disappear in the thermodynamic limit. In simulations, this behavior is typically smoothed out by interface fluctuations. The sharp decrease in P for ABPs implies that interfacial fluctuations are considerably suppressed, suggesting a large interface tension (indeed AB-HD generate an interface between a dilute gas and a closed packed crystal). Hence, we can interpret the pressure drop for PBC systems as a finite size effect. For finite systems the EoS is affected both because of the interfacial contribution and a shift in the location of nucleation.§ These two effects are consistent with the data shown in Fig. 3(c). The active pressure in systems of N ≳ 4000 converges above ϕn, meaning that there is no interfacial contribution to the pressure after phase separation. It is less clear though whether the pressure jump is reduced when increasing N.20 We push thermodynamic ideas even further, and claim that the system sizes used so far are not large enough to observe how the onset of MIPS approaches the binodal. The idea behind this claim is that MIPS involves a large critical nucleus: our systems turn out to be too small to phase separate close to the binodal and thus remain metastable in a sub-region of the coexistence region.¶ The convergence of ϕn towards the binodal as the system is made larger is due to the fact that the probability to spontaneously form a cluster of size m > mc, (where mc is the critical nucleus size) increases with system size. The system sizes used need to be much larger than mc, otherwise, nucleation cannot take place and the approach of P(ϕ) to its infinite-size behavior cannot be observed. In the following we show this important claim.
5 Metastability
In order to probe metastability, we initialize the open system deeply in the coexistence region. As we expand the system, nucleation is avoided since an interface between a dense and low density phase is already present. We perform such a low-ϕ quench at fixed Pe by letting AB-HDs evolve from a steady-state at ϕ = 0.50, Pe = 30 to lower packing fractions. The equation of state we obtain is depicted in blue in Fig. 3(d). We find that: (i) the system remains phase separated at much lower densities than the ones previously reported (see Fig. 5(a) and movie in ref. 37); (ii) the pressure remains roughly constant down to ϕ ≈ ϕlow. We thus found hysteresis around MIPS, a typical signature of first-order phase transitions.Accordingly to classical nucleation theory (CNT), in the absence of a preferential site (homogeneous nucleation), phase separation can only be triggered by a rare event: the spontaneous formation of a critical nucleus of size larger than mc ∝ γ/ΔGhomo (where γ is the interface tension and ΔGhomo the free energy difference). Since our system is out-of-equilibrium, CNT cannot be directly applied. However, borrowing ideas from equilibrium systems, Redner et al. have developed an analogous theory to describe the kinetics of phase separation in ABP,24 providing a theoretical description of simulation results.25 Within this framework, 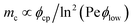 . To make a comparison with simulations, an expression ϕ(A,ϕhigh,ϕlow) for the average packing fraction in terms of the theoretical predictions is established, where A is completely determined by the cluster size distribution
. To make a comparison with simulations, an expression ϕ(A,ϕhigh,ϕlow) for the average packing fraction in terms of the theoretical predictions is established, where A is completely determined by the cluster size distribution ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) m (see eqn (11) in ref. 24). The nucleation barrier is thus controlled by two main ingredients: the location of the binodals and the structure of the clusters. We computed
m (see eqn (11) in ref. 24). The nucleation barrier is thus controlled by two main ingredients: the location of the binodals and the structure of the clusters. We computed ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) m for AB-HD and AB-WCAD with different ε and found a roughly identical distribution (see Fig. 5(c)). For stiffer potentials the structural difference between the coexisting phases is more severe. In the hard-disk limit the binodals are pushed to their limit values ϕlow → 0 and ϕhigh → ϕcp as the activity increases. Therefore, mc is expected to be very large at high Pe. As shown in Fig. 5(d), softening the particles suppresses the order of the dense phase. In turn, ϕlow is larger for softer potentials (thus mc is smaller), qualitatively explaining the reduction of the pressure drop for softer disks in Fig. 3(b).|| We did not intend to make a direct quantitative comparison between theory and simulations, but, at this level, we are able to insure that for hard ABPs, MIPS features a large nucleation barrier that discourages attempts to observe how the system escapes from metastability with BD simulations. To give further support to this idea we turn now our attention into the system in presence of hard walls.
m for AB-HD and AB-WCAD with different ε and found a roughly identical distribution (see Fig. 5(c)). For stiffer potentials the structural difference between the coexisting phases is more severe. In the hard-disk limit the binodals are pushed to their limit values ϕlow → 0 and ϕhigh → ϕcp as the activity increases. Therefore, mc is expected to be very large at high Pe. As shown in Fig. 5(d), softening the particles suppresses the order of the dense phase. In turn, ϕlow is larger for softer potentials (thus mc is smaller), qualitatively explaining the reduction of the pressure drop for softer disks in Fig. 3(b).|| We did not intend to make a direct quantitative comparison between theory and simulations, but, at this level, we are able to insure that for hard ABPs, MIPS features a large nucleation barrier that discourages attempts to observe how the system escapes from metastability with BD simulations. To give further support to this idea we turn now our attention into the system in presence of hard walls.
Confinement facilitates nucleation because of wetting. As shown in Fig. 5(b), and discuss previously in the literature, ABP accumulate at walls which thus act as natural nucleation seeds.12,21,23 The free energy associated with (heterogeneous) nucleation in a confined system is
| ΔGhet = F(α)ΔGhomo |
F(α) = (2 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)(1 − cos α)(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)2/4 α)2/4 |
Consistently, the value of the pressure obtained in the open system with PBC (using both a low-ϕ or high-ϕ quench), and in confinement, converges to the same constant value far away from the spinodal, thus defining the coexistence pressure P*. As shown by the discontinuous flat line in Fig. 3(d), the extrapolation of P* across the metastability region provides an independent numerical estimation of the location of the binodal, ϕlow* (shown by a green symbol), defined as the packing fraction at which the low density branch of the EoS (ϕ < ϕn) intersects P*. This ‘data-based’ construction provides the (approximate) location of the binodal from the pressure measurements, in agreement with the density distribution; thus connecting the EoS obtained from simulations and the coexistence phase diagram.
6 Conclusion
We have carefully examined the pressure of ABPs using different potentials, topologies and initial conditions in order to show that the EoS are fully consistent with the classical (equilibrium) first-order phase transition scenario. The equations of state of ABP do not exhibit any fundamental difference to an equilibrium system showing phase coexistence, besides: (i) the absence of a Maxwell construction on P; (ii) the extreme structural difference between the two coexisting phases, giving rise to a large nucleation barrier. Overall, our work results in a systematic way to interpret the equations of state of ABP using equilibrium-like concepts. We shed light into the first-order nature of MIPS, clarifying the analogies with liquid–gas phase separation and providing a consistent framework that brings together the phase separation kinetics, the coexistence density curves and the equations of state of spherical ABP.We have focussed on the case of isotropic Active Brownian Particles (disks), for which an equation of state exists. The existence of a metastability region with a large nucleation barrier and the equality of pressure at coexistence has been brought out by the direct comparison between the pressure in a confined and periodic system. Of course, such an approach is meaningful as long as the pressure is a state function. However, this crucial property is quite fragile in active systems and it generically fails as soon as anisotropic interactions are involved.38,39 Shape anisotropy (active particles like bacteria are often elongated) might in turn affect the MIPS scenario, since orientational ordering has to be taken into account in these systems.40,41 Therefore, the characterization of the phase behavior of anisotropic self-propelled particles using thermodynamic-like ideas, as the ones we put forward here, presents a fundamental difficulty. The nature of phase transitions in this kind of systems is still unclear, thus calling for further developments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
DL warmly thanks R. Ni, G. Redner, A. Solon, T. Speck, C. Wagner and T. Voigtmann for useful exchanges, and in particular J. Tailleur for his suggestions. DL acknowledges funding from a Marie Sklodowska-Curie Individual Fellowship (G.A. no. 657517). JC is supported by Spanish MECD fellowship FPU13/01911. IP acknowledges MINECO and DURSI for financial support under projects FIS2015-67837- P and 2014SGR-922, respectively.References
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219 CrossRef CAS.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489 RSC.
- D. Levis and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062301 CrossRef PubMed.
- D. Loi, S. Mossa and L. F. Cugliandolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051111 CrossRef PubMed.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304 CrossRef PubMed.
- G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012111 CrossRef PubMed.
- D. Levis and L. Berthier, Europhys. Lett., 2015, 111, 60006 CrossRef.
- U. M. B. Marconi and C. Maggi, Soft Matter, 2015, 11, 8768 RSC.
- M. Dijkstra, S. Paliwal, J. Rodenburg and R. van Roij, arXiv preprint arXiv:1609.02773, 2016.
- S. A. Mallory, A. Šarić, C. Valeriani and A. Cacciuto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 052303 CrossRef CAS PubMed.
- S. C. Takatori, W. Yan and J. F. Brady, Phys. Rev. Lett., 2014, 113, 028103 CrossRef CAS PubMed.
- X. Yang, M. L. Manning and M. C. Marchetti, Soft Matter, 2014, 10, 6477 RSC.
- A. P. Solon, J. Stenhammar, R. Wittkowski, M. Kardar, Y. Kafri, M. E. Cates and J. Tailleur, Phys. Rev. Lett., 2015, 114, 198301 CrossRef PubMed.
- F. Ginot, I. Theurkauff, D. Levis, C. Ybert, L. Bocquet, L. Berthier and C. Cottin-Bizonne, Phys. Rev. X, 2015, 5, 011004 Search PubMed.
- R. G. Winkler, A. Wysocki and G. Gompper, Soft Matter, 2015, 11, 6680 RSC.
- A. Patch, D. Yllanes and M. C. Marchetti, Phys. Rev. E, 2017, 95, 012601 CrossRef PubMed.
- T. Speck and R. L. Jack, Phys. Rev. E, 2016, 93, 062605 CrossRef PubMed.
- A. P. Solon, J. Stenhammar, M. E. Cates, Y. Kafri and J. Tailleur, arXiv preprint arXiv:1609.03483, 2016.
- Y. Fily, A. Baskaran and M. F. Hagan, Soft Matter, 2014, 10, 5609 RSC.
- G. S. Redner, C. G. Wagner, A. Baskaran and M. F. Hagan, Phys. Rev. Lett., 2016, 117, 148002 CrossRef PubMed.
- D. Richard, H. Löwen and T. Speck, Soft Matter, 2016, 12, 5257 RSC.
- A. Scala, T. Voigtmann and C. De Michele, J. Chem. Phys., 2007, 126, 134109 CrossRef CAS PubMed.
- R. Ni, M. A. C. Stuart and M. Dijkstra, Nat. Commun., 2013, 4, 2704 Search PubMed.
- A. C. Branka and D. M. Heyes, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 2381 CrossRef CAS.
- G. Falasco, F. Baldovin, K. Kroy and M. Baiesi, New J. Phys., 2016, 18, 093043 CrossRef.
- S. C. Takatori and J. F. Brady, Soft Matter, 2015, 11, 7920 RSC.
- D. Henderson, Mol. Phys., 1975, 30, 971 CrossRef CAS.
- J. E. Mayer and W. W. Wood, J. Chem. Phys., 1965, 42, 4268 CrossRef CAS.
- M. Schrader, P. Virnau and K. Binder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 061104 CrossRef PubMed.
- D. J. McGinty, J. Chem. Phys., 1973, 58, 4733 CrossRef CAS.
- J. K. Lee, J. A. Barker and F. F. Abraham, J. Chem. Phys., 1973, 58, 3166 CrossRef CAS.
- D. Reguera, R. K. Bowles, Y. Djikaev and H. Reiss, J. Chem. Phys., 2003, 118, 340 CrossRef CAS.
- See ESI†.
- A. P. Solon, Y. Fily, A. Baskaran, M. E. Cates, Y. Kafri, M. Kardar and J. Tailleur, Nat. Phys., 2015, 11, 673–678 CrossRef CAS.
- M. Joyeux and E. Bertin, Phys. Rev. E, 2016, 93, 032605 CrossRef PubMed.
- A. Suma, G. Gonnella, D. Marenduzzo and E. Orlandini, Europhys. Lett., 2014, 108, 56004 CrossRef.
- S. Weitz, A. Deutsch and F. Peruani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012322 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm01504f |
| ‡ The constraint that two particles cannot overlap can also be implemented by a Monte Carlo (MC) procedure.7 The MC dynamics gives rise to clusters with self-limiting size,7 while ED-BD produces clusters that coarsen by MIPS. |
§ For a first-order phase transition in equilibrium, the interface free energy density vanishes as 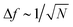 and the nucleation point is shifted by ϕn ∼ N−1/3.32 and the nucleation point is shifted by ϕn ∼ N−1/3.32 |
| ¶ Small systems should rather be thought in terms of clusters as discussed in ref. 34–36. |
| || Redner et al. predict mc ≈ 5000 at Pe = 30 and ϕ = 0.30 for AB-WCAD with ε = 1 in our units (see ref. 24). This value lies quite close to the binodal in their case while for AB-HD it falls deep into the coexistence region. |
| This journal is © The Royal Society of Chemistry 2017 |